Abstract
The planning of on-demand services requires the formation of vehicle schedules consisting of service trips and empty trips. This paper presents an algorithm for building vehicle schedules that uses time-dependent demand matrices (= service trips) as input and determines time-dependent empty trip matrices and the number of required vehicles as a result. The presented approach is intended for long-term, strategic transport planning. For this purpose, it provides planners with an estimate of vehicle fleet size and distance travelled by on-demand services. The algorithm can be applied to integer and non-integer demand matrices and is therefore particularly suitable for macroscopic travel demand models. Two case studies illustrate potential applications of the algorithm and feature that on-demand services can be considered in macroscopic travel demand models.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
In densely populated areas public transport is more efficient than private means of transport for two reasons. First, it pools the trips of several people. This leads to a high occupancy rate and thus reduces the total vehicle distance traveled. Second, service trips are concatenated to vehicle schedules. This reduces the number of required vehicles.
In contrast to traditional public transport, on-demand services in the form of carsharing or ridesplitting [definitions from Feigon and Murphy (2016)] have neither a fixed route nor a predetermined timetable. The actual vehicle schedules are only known at the end of an operating day. For the planning of on-demand services, travel demand models are used to either determine the number of served passengers for a given fleet size or to determine the required fleet size for a given demand situation.
So far, primarily microscopic travel demand models are used for modeling on-demand services (see literature review in Sect. “State of the art and related work”). Microscopic models simulate the demand of individuals and the operational processes at the level of individual vehicles using agent-based approaches. Typical input values are trip requests coming from a demand model, fleet size, vehicle capacity, and service parameters, e.g. maximum detour factor for passengers. Using some type of vehicle scheduling process, the models deliver as results indicators describing the service quality from the perspective of passengers (e.g. waiting time, in-vehicle-time, detour factor, number of passengers not served) and operators (e.g. empty and loaded vehicle kilometers, occupancy rates, revenues).
This paper presents an algorithm for the vehicle scheduling process of on-demand services, which can be embedded in macroscopic travel demand models. The presented approach is intended for long-term, strategic transport planning. For this purpose, it provides planners with an estimate of vehicle fleet size and distance travelled by on-demand services. Using a macroscopic travel demand model has advantages and disadvantages compared to a microscopic approach. Important advantages include the following:
-
Many cities, regions, and states use macroscopic travel demand models to quantify the impacts of supply changes on travel demand. Moeckel et al. (2019) report that most states in the U.S. operate macroscopic travel demand models. A survey by Rieser et al. (2018) finds that most travel demand models operated on regional and state level in German speaking countries are macroscopic models.
-
A macroscopic travel demand model replicates the demand of an average day in one model run. It works with probabilities so that every model run produces the same solution. A microscopic model simulates a certain day and requires multiple simulations to obtain results for an average day.
-
Macroscopic model implementations are usually faster.
The main disadvantage of macroscopic models is probably that they can reproduce the traffic-related decision processes of activity choice, destination choice, mode choice, departure time choice, and route choice only in a simplified way. Microscopic models can capture a more complex decision process considering household constraints, vehicle ownership, and temporal constraints coming from an activity schedule. In case average results are obtained with multiple simulations, microscopic models also give information about the variability of the results.
Looking at the pooling and vehicle scheduling processes in connection with on-demand services, macroscopic travel demand models bring a further challenge: demand is not represented as discrete trips of individuals but as a probability. This leads to a non-integer demand that is stored in demand matrices. For modelling fluctuations in travel demand over the course of a day, demand is divided into time intervals, e.g. 96 intervals of 15 min. This rather abstract representation of travel demand requires specific methods for integrating on-demand services into a macroscopic travel demand model. Friedrich et al. (2018) describe an algorithm to pool macroscopic travel demand to demanded vehicle trips (= service trips).
In this paper, we present an algorithm for the vehicle scheduling problem that uses these time-dependent vehicle trips as input. As a result, the algorithm determines the number of required vehicles and empty trips for vehicle relocation per time interval. The efficient algorithm design makes it suitable for solving large instances in short computation time, which is crucial for the use in travel demand models. Furthermore, it can be applied for both integer and non-integer demand matrices, which also allows an application to microscopic models with integer demand. A python implementation can be found in Hartleb et al. (2020).
The contribution of this paper is twofold: First, we develop a vehicle scheduling algorithm to estimate the vehicle fleet size of on-demand services efficiently. Second, we show in two case studies that the algorithm is suitable for the vehicle scheduling problem as it arises in macroscopic travel demand models.
The remainder of this paper is structured in the following way: In Sect. “State of the art and related work”, the presented approach is compared to existing research on on-demand services in travel demand models and on vehicle scheduling approaches. Section “Problem definition” defines the vehicle scheduling problem in a formalized way, followed by a description of the basic algorithm in Sect. “Algorithm”. In Sect. “Extensions”, extensions of the basic algorithm are discussed. Section “Applications” illustrates the applicability of the algorithm in two case studies. A conclusion and outlook complete the paper.
State of the art and related work
In Sect. “On-demand services in travel demand models”, we relate our work to existing research on on-demand services in travel demand models. The differences of macroscopic and microscopic travel demand models, i.e., agent-based models, are highlighted. In Sect. “Vehicle scheduling”, we report on related vehicle scheduling approaches and their solution techniques.
On-demand services in travel demand models
Travel demand models replicate the decision-making process of travelers, which is triggered by the need of people to participate in activities. According to Friedrich et al. (2016) “these decisions range from long-term to short-term decisions. Long-term decisions cover decisions concerning the place of residence and the workplace. These decisions influence subsequent medium-term decisions regarding the purchase of a car or a season ticket for public transport, which then affect later decisions on the activity locations and the transport modes. Short-term decisions on departure time, a certain route or a certain lane are taken within a short time horizon.” Most transport models cover only some of these decisions or replicate some decisions in a simplified way. Many macroscopic travel demand models capture the decisions associated with the pursuit of activities within the framework of the four-step algorithm. This framework distinguishes the steps trip generation, destination choice, mode choice and route choice (Ortúzar and Willumsen 2011; McNally 2010). To consider temporal travel patterns, macroscopic models are supplemented by a step for departure time choice. This step requires a model implementation, which distinguishes trip matrices not only by trip purpose but rather by activity pairs (e.g. Home-Work, Home-Education, Home-Shopping, Work-Shopping). For each activity pair observed temporal distributions are used to compute time-dependent trip tables. Figure 1a provides a schematic flow chart of a standard travel demand model.
While there are many approaches to model pooling and scheduling of on-demand services in general, only a limited number of modelling approaches replicate the impacts of on-demand services on travel demand, especially on destination and mode choice. Almost all of these are microscopic approaches. In their overview of demand models including one-way carsharing services, Vosooghi et al. (2017) come to the same conclusion.
Examples of microscopic approaches including on-demand services in existing travel demand models are presented by Azevedo et al. (2016) for SimMobility, Maciejewski (2016), Hörl (2017) for MATSim, Heilig et al. (2018), Wilkes et al. (2019) for mobiTopp and Martínez et al. (2017) for an agent-based model for Lisbon. A macroscopic approach is described by Richter et al. (2019).
All approaches need to deal with the challenge that the transport supply provided by on-demand services depends on the demand and is not given as a model input. Although traditional models capture the impact of demand on the supply in form of volume-delay functions, the spatial and temporal structure of the supply remains fixed. For on-demand services, however, the spatial and temporal supply structure must be adapted to the demand.
Therefore, to include on-demand services in the four-step algorithm, the travel demand model needs to be extended by an additional set of steps determining the on-demand supply. These steps replicate short-term decisions of operators which schedule the on-demand supply. Hence, the structure and availability of the on-demand supply is established in response to the trip requests of travelers. Figure 1b extends the algorithm of Fig. 1a to include the additional steps. The short-term decisions of operators can be categorized into two parts: First, pooling of passenger trip requests into vehicle trips and, second, scheduling of vehicles to serve the vehicle trips.
The pooling step converts person trip requests into vehicle trip requests, i.e., trips of vehicles carrying passengers. This step is only required for on-demand services which aim at pooling several independent travelers into one vehicle, i.e., for ridesplitting services. On-demand carsharing does not require a pooling step as users directly request a vehicle trip. Microscopic approaches to pooling algorithms can be found in Zhang et al. (2015), Bischoff et al. (2017) or Engelhardt et al. (2020), for example. A macroscopic approach is proposed by Friedrich et al. (2018).
The focus of this paper is on the vehicle scheduling step, where vehicle trip requests identified in the previous pooling step are assigned to specific vehicles. This step either determines the number of vehicles needed for serving a given demand or it defines the demand which can be served by a given vehicle fleet. The scheduling step also identifies empty vehicle trips which are required for vehicle relocation. Approaches to replicate this step differ for microscopic and macroscopic travel demand models as discussed in the following.
Microscopic or agent-based travel demand models simulate discrete choices of persons using probability distributions. Each model run replicates the demand situation of a specific day. This modelling approach is described for example by Ortúzar and Willumsen (2011) or Horni et al. (2016). Commonly, persons are assigned daily plans which are processed chronologically. In this chronological processing, the problem of vehicle scheduling can be defined as a dynamic vehicle routing problem (Maciejewski et al. 2017). At the start of the analyzed time period, not all trip requests are known. Instead, requests come in over time.
Macroscopic models, in contrast, aim to replicate an average day. This is achieved by using average trip rates for trip production and by assigning probabilities to each choice of a choice set. The results are non-integer values that represent the demand situation of a recurrent average day. As on-demand systems are designed to adapt to a specific demand situation varying from day to day, it is not helpful for planning purposes to replicate the trip requests of one specific day. Instead, an average demand situation should be used for the system design. Furthermore, it seems reasonable to assume that information on all trip requests is available at the beginning of the vehicle scheduling step. This makes the problem more similar to traditional vehicle scheduling in timetable-based public transport.
Due to their respective ways of calculating travel demand, microscopic and macroscopic approaches tend to answer different research questions: Microscopic approaches rather answer the question of how well a certain vehicle fleet can satisfy a given demand [e.g. Marczuk et al. (2015), Maciejewski et al. (2017), PTV Group (2020)]. Macroscopic approaches rather take the reverse approach and determine the required fleet size to fully satisfy a given demand.
Nevertheless, it is important to note that although the model types are prone to the uses shown, it is also possible to use them in the opposite way. Boesch et al. (2016), Wang et al. (2018) or Fagnant and Kockelman (2018), for example, confirm this by using microscopic approaches to calculate the number of vehicles needed.
Vehicle scheduling
The literature on vehicle scheduling provides many approaches to find schedules with a minimal number of vehicles. Standard models and solution approaches for vehicle scheduling in public transport are summarized in Bunte and Kliewer (2009). Recent vehicle scheduling approaches usually incorporate problem specific aspects such as variable timetables (Desfontaines and Desaulniers 2018; Lan et al. 2019) or limited range of electric vehicles and recharging strategies (Wen et al. 2016; Rogge et al. 2018). To be able to find good schedules for realistic instances, elaborate solution methods are proposed. For example, Desfontaines and Desaulniers (2018) rely on column generation, and Lan et al. (2019) combine Benders decomposition with a branch-and-price approach. With these methods, instances with up to 2100 vehicle trips could be solved within less than 1 h to optimality or close to optimality. The considered instances in Wen et al. (2016) contain up to 500 vehicle trips and are solved with an adaptive large neighborhood search within 20 min. Rogge et al. (2018) develop a genetic algorithm and provide results for instances with up to 200 vehicle trips.
Lam et al. (2016) formulate a vehicle scheduling problem specifically for a ridesharing setting with automated vehicles. Their model includes admission control and pooling of passengers, as well as a maximum route length due to a restrictive battery capacity. They use different instances constructed from taxi data from Boston with 100 trips and propose a genetic algorithm to find vehicle schedules. Lin et al. (2012) use a simulated annealing approach to find vehicle movements that are both cost-efficient and convenient for passengers in a ridesharing setting for taxis. They find that both the mileage as well as the number of vehicles can be reduced significantly by ridesharing, however, only results of a single and relatively small instance with 29 trips was discussed.
Most vehicle scheduling contributions consider an operational setting and aim at providing an optimal solution for a certain demand situation. In contrast to these approaches, our algorithm is designed for usage in an extended four-step algorithm as depicted in Fig. 1b. We intend to provide good estimates for the required fleet size and the impact on the traffic volume within short computation times. This is suitable for long-term strategic transport planning. Furthermore, most solution methods exploit that each planned trip has to be covered exactly once. Since this does not necessarily hold for macroscopic demand models, a generalized approach is required. Similar to early approaches as presented in Bodin (1983), we model the vehicle scheduling problem as a flow problem. This design choice is motivated by the huge demand data of realistic instances considered in this paper that include up to 100 million vehicle trips.
We formulate the problem as minimum-cost circulation with lower bounds. Schrijver (2003) describes a polynomial solution algorithm based on a gradual convergence by iteratively finding better routes for vehicles: First, an initial circulation is found that is not necessarily optimal. Then, the solution is iteratively improved by identifying a directed circuit with negative cost in the residual graph. The circulation is adjusted correspondingly along this circuit. To identify a directed circuit, a flow problem has to be solved. This yields a time complexity of \({\mathcal {O}}(|Z |^8 |T |^5 \log (|Z ||T |))\) for this approach, where \(Z\) and \(T\) correspond to a discretization of space and time, respectively.
In a project many vehicle schedules have to be computed since often many scenarios are considered and a feedback loop between demand estimation and supply design is common. Hence, we propose a simple heuristic approach for macroscopic on-demand problems to realize short solution times for huge instances. Our approach presented in Sect. “Algorithm” has a time complexity of \({\mathcal {O}}(|Z |^2|T |^2)\) and meets the requirements of an application in travel demand models.
Problem definition
In this section, the problem of finding a vehicle scheduling with minimal fleet size is formalized. To this end, the required input is described and the underlying network for the presented solution algorithm is introduced.
Input and notation
Passenger demand is given as demanded vehicle trips, aggregated in time and space. For ridesharing applications, passenger trips are pooled to vehicle trips in a preceding step.
The analysis period is split into time intervals of equal length. Time intervals are indexed with \(t\) and the set of time intervals is denoted by \(T = \{1,2,\dots ,|T |\}\). The examination area is divided into traffic zones, the set of traffic zones is \(Z\). A traffic zone is denoted by \(z\), or, when considering a traffic zone as origin or destination zone, by \(p\) and \(q\), respectively.
The number of demanded vehicle trips from an origin zone \(p\) to a destination zone \(q\) starting in time interval \(t\) is denoted by \(d _{p q t}\). In this setting, these requested vehicle trips are composed of pooled trips of passengers and called service trips. Further, distances \(\delta _{p q}\) between traffic zones are given as multiples of time intervals. They result from the travel time \(j\) between traffic zones and the duration of a time interval \(l\), \(\delta _{p q} = {\lceil \frac{j _{p q}}{l} \rceil }.\) For the presentation of the algorithm in this paper, two assumptions are made. First, the travel time between zones is independent of the time of day. To consider the asymmetric nature of congestion, the distance matrix can be extended by a third dimension representing the departure time interval. Second, all trips within one zone require a travel time of at most one time interval, that is \(\delta _{z z} = 1\ \forall z \in Z.\) If this assumption does not apply, the model can be extended to distinguish between waiting and traveling within a zone.
The input of an instance \({\mathcal {I}}= (\delta ,d)\) consists of a distance matrix \(\delta\) and a demand situation \(d\). By concatenating the demanded vehicle trips to vehicle schedules, the presented algorithm determines the number of required vehicles as well as empty trips for vehicle relocation per time interval as a result. The aim is to serve the entire demand with as few vehicles as possible.
Underlying network
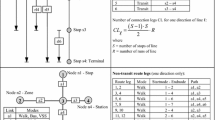
For a simpler representation of the algorithm, a time-space network \(G = (V, E)\) is introduced. Nodes can be interpreted as traffic zones at the beginning of time intervals and arcs as potential time-bound vehicle trips between zones. In the network, we depict traffic zones on the vertical and time intervals on the horizontal axis. An example network with three traffic zones and four time intervals is shown in Fig. 2a.
Formally, we introduce the set of nodes \(V = V _Z \cup V _{Z,{\overline{T}}}\) with
where \({\overline{T}} = T \cup \{ |T | + 1, \dots , |T | + \max _{p,q \in Z} \delta _{p q} \}\) is an extended set of time intervals. For each traffic zone \(z \in Z\) there is a node \(v _{z 0}\) in the network G at the beginning of the analysis period. Moreover, there is a node \(v _{z t}\) representing each traffic zone \(z \in Z\) at the beginning of each time interval \(t \in {\overline{T}}\). The nodes in \(V\) are connected by directed edges in \(E = E _Z \cup E _{Z,T}\), where
From each node \(v _{z 0}\) there is a directed edge to the node \(v _{z 1}\), which represents the traffic zone \(z\) at the beginning of the first time interval. There are also \(|T |\) edges that connect each pair of origin zone \(p\) and destination zone \(q\). These edges start in the time intervals \(t \in T\) and end in \(t + \delta _{p q} \in {\overline{T}}\), corresponding to the distance between the traffic zones.
The demand \(d _{p q t}\) can be interpreted as a lower bound on the edges \(e \in E _{Z,T}\), defining a minimum flow on these edges. The distances \(\delta _{p q}\) between the traffic zones \(p\) and \(q\) are modeled by the horizontal length of the edges. A trip from the first to the second traffic zone in the example of Fig. 2a can be covered in one time interval, the return trip needs two time intervals. Asymmetries can be caused by one-way streets or differing traffic volumes in the network. The presented vehicle scheduling algorithm is designed to find a feasible vehicle flow in this network with as few vehicles as possible, so that demand is met on all edges.
Vehicle scheduling
The flow variables \(f _{p q t} \in {\mathbb {R}}_+\) are introduced to represent a vehicle flow on the edges \({e \in E _{Z,T}}\). The value \(f _{p q t}\) can be interpreted as the number of vehicles driving from traffic zone \(p\) to \(q\), starting in time interval \(t\). To ensure that the total demand is served, the flow on each edge must be at least as large as the demand,
For the flow to be feasible, it must also be ensured that the total number of arriving and departing vehicles in each node \(v _{z t}\) is equal,
This ensures that the flow is preserved in every node and that at no time \(t\) vehicles “appear” or “disappear” in traffic zone \(z\). A feasible flow \(f\) in the network G is called a vehicle schedule. Next, the variables \(x _z \in {\mathbb {R}}_+\) are introduced to model the vehicle flow on the edges \(E _{Z}\). These correspond to the total number of vehicles leaving the traffic zone \(z \in Z\) in the first time interval, defined as
\(x _z\) as determined in Eq. (3) can be interpreted as the number of vehicles that must be available in the traffic zone \(z\) at the beginning of the analysis period. The aim is to serve the demand with as few vehicles as possible, that corresponds to minimizing the sum of vehicles leaving traffic zones in the first time interval \(\sum _{z \in Z} x _z\). Equations (1) and (2) ensure that any demand is met and the vehicle schedule is feasible.
Algorithm
Description
The basic structure of the algorithm is simple: the nodes \(v _{z t}\) in the network are processed chronologically and the vehicle flow is expanded step by step on the outgoing edges. Figure 2b–e illustrate the construction of a vehicle schedule in the example network in Fig. 2a. In each step it is ensured that the demand is met and that the vehicle flow is feasible at all processed nodes. Thus, the design of the algorithm ensures that Eqs. (1) and (2) are fulfilled step by step. While the algorithm constructs the vehicle flow chronologically, that is, from left to right in the network in Fig. 2, the flow in the previous time intervals can be amended. To perform this amendment efficiently, we maintain node labels \(a\) storing the current number of vehicles at each node during flow construction.
For a simpler representation of the vehicle scheduling algorithm, we split it into three nested parts. The basic structure is given in Algorithm 1. This part specifies that the nodes in the network are considered in a chronological order, and that at each considered node all demand on outgoing edges is met and the flow conservation holds. The flow conservation, which ensures that there is the same number of incoming and outgoing vehicles at each node, is specified in Algorithm 2. There, three cases are considered. First, the number of incoming vehicles is sufficient for the number of demanded vehicles on outgoing edges. Second, vehicles in other zones are available and can be relocated to the current traffic zone. Third, additional vehicles need to be added to the vehicle flow under construction. While the first and third case are easy to handle, the relocation of vehicles in the second case requires an amendment of the flow in previous time intervals. This amendment is described in Algorithm 3.
The nested structure means that Algorithm 1 calls Algorithm 2 to ensure the flow conservation, which in turn calls Algorithm 3 for vehicle relocation, if necessary. In the following, the pseudocode of the three algorithms is described and exemplified with the flow construction in Fig. 2.
Algorithm 1
In Algorithm 1 the basic structure of the vehicle scheduling algorithm is given as pseudocode. The loops in lines 4 and 5 scroll through the nodes \(v _{z t}\) in chronological order. Starting from the considered node, the demand is served on each outgoing edge, see line 6. This step ensures that there is sufficient vehicle flow on the demanded edges in the network, see for example Fig. 2b where a flow of 1.0 and 1.1 vehicles is set between nodes \(v _{11}\) and \(v _{12}\), and between nodes \(v _{21}\) and \(v _{32}\), respectively, to meet the demand. Then, in line 7, labels are updated at the nodes indicating how many vehicles are available in the traffic zones at the beginning of the time intervals. After the first time interval is processed in Fig. 2b, there are 1.0 and 1.1 vehicles available at nodes \(v _{12}\) and \(v _{32}\), respectively. Finally, calling the function FlowConservation() in line 8 ensures that the number of arriving and departing vehicles at the considered node \(v _{z t}\) are equal and, thus, that the vehicle flow is feasible.

Algorithm 2
Algorithm 2 is called at every node \(v _{z t}\) to ensure flow conservation. This is necessary since in Algorithm 1 only the vehicle flow on outgoing edges was set in order to meet demand. In Algorithm 2, sufficient incoming flow is ensured to match the outgoing flow, or the outgoing flow is increased if the incoming flow is predominant. To match the number of incoming and outgoing vehicles in that node, vehicles from three different sources are considered in the following priority.
-
1.
The first step is to try to satisfy as much demand as possible with vehicles available at the current node \(v _{z t}\). Vehicles are considered available at a node \(v _{z t}\) if they are idle in the traffic zone \(z\) at the beginning of the time interval \(t\). In the algorithm, the number of available vehicles at each node is stored in the label \(a _{z t}\). If more vehicles are available than needed, they wait in the traffic zone and the labels at the nodes are adjusted, see lines 3, 5, and 6 in Algorithm 2. Both usage of available vehicles and waiting in the traffic zone can be observed at the node \(v _{34}\) in Fig. 2e, for example. There, 0.1 vehicles are sent to node \(v _{25}\) to meet demand, and the remaining 1.0 available vehicles wait in the third traffic zone.

-
2.
If there are not enough vehicles available, the algorithm tries to relocate vehicles from other traffic zones \(p\) to traffic zone \(z\). For a permissible relocation, the vehicles must be available already \(\delta _{p z}\) time intervals before the considered time interval \(t\). Only in that case they can be relocated in time to meet demand at the beginning of time interval \(t\) in traffic zone \(z\). The relocation is designed in such way that demand will continue to be met on all previously considered edges and that flow will continue to be preserved in all previously considered nodes.
By relocation, it is possible to find good vehicle schedules requiring few vehicles only at the expense of empty vehicle kilometers. In the Sect. “Applications” the number of required vehicles and the length of empty trips is compared in scenarios with and without vehicle relocation. The exact procedure of vehicle relocation is described in Algorithm 3, which is called in line 10 of Algorithm 2 if there are not enough vehicles available.
-
3.
If after the relocation of vehicles from other traffic zones the total demand on outgoing edges of the considered node \(v _{z t}\) is not met, further vehicles are necessary for a feasible vehicle flow. These vehicles are inserted in the traffic zone \(z\) by increasing the variable \(x _z\) and are idle until time interval \(t\), see lines 12 and 13 in Algorithm 2. In the example network, this happens at the beginning of the analysis period, see Fig. 2b, and when processing the last time interval, see Fig. 2e. In the former, 1.0 and 1.1 vehicles are inserted in the first and the second traffic zone, respectively. In the latter, another 1.0 vehicles are inserted in the first traffic zone. There, it is possible to see how all flow variables within this zone are increased, indicating that the vehicles are idle until demanded in the fourth time interval.
Algorithm 3
Algorithm 3 describes how the relocation of vehicles is performed and the flow in previous time intervals is amended. First, it is calculated how many vehicles can be relocated, see lines 5 to 7. Then, the previously set vehicle flow is undone and the corresponding labels are updated, see lines 8 to 12. Finally, the empty vehicle trip for relocation is added to the vehicle flow, see line 13. Figure 2c, d show the relocation of vehicles from the first to the second traffic zone. Initially, 1.0 vehicles wait in the first traffic zone during the second time interval. When processing the third time interval, this flow is undone and the vehicles are relocated from the first to the second traffic zone during the second time interval to meet demand. While the basic structure in Algorithm 1 works chronologically, the relocation of vehicles in Algorithm 3 can be seen as a backward correction.

Summary
The presented vehicle scheduling algorithm is designed such that the vehicle flow is feasible at each node and the demand is served on each edge. The relocation of vehicles preserves these properties at nodes and edges that have already been processed. Therefore, the solution of the algorithm is a feasible vehicle flow \(f\), which requires as few vehicles \(x\) as possible. An implementation of the presented algorithm is available in Hartleb et al. (2020).
Solution quality
The algorithm is deterministic and provides the same solution in every call. However, it is a heuristic procedure that does not necessarily find an optimal solution. This can be seen in the example in Fig. 2. At node \(v _{23}\) not enough vehicles are available to serve the outgoing demand. Therefore, attempts are made to relocate vehicles from other traffic zones, see Fig. 2d. In this case, there are enough vehicles available in the first traffic zone, that are relocated within the second time interval. As a result of this relocation, no vehicles are available at node \(v _{14}\) in the fourth time interval. Additional vehicles must be inserted, increasing the total number of required vehicles, see Fig. 2e.
In the solution of the algorithm a total of 3.1 vehicles is required to meet the entire demand. In an optimal solution, however, only 2.1 vehicles are needed, for example, by relocating vehicles from the third instead of the first traffic zone to node \(v _{23}\). This shows that the solution quality depends, among other things, on the order of traffic zones from which vehicles are relocated. In the example described, the algorithm finds a solution that is almost 50% worse than an optimal one. However, preliminary tests have shown that the solution quality on both randomly generated and real networks is significantly higher than in this contrived example. In most practical applications the deviation from the optimal number of required vehicles was smaller than the deviation due to other modeling errors.
Complexity
In a case study many vehicle schedules need to be computed because usually several scenarios are examined and a feedback loop between demand and supply is applied within each scenario. Therefore, a heuristic approach with short running times is most practical. The vehicle scheduling algorithm presented in this paper performs \(|Z ||T |(|Z | + |Z | + |Z | + |Z | + |Z | + |Z |({\overline{\delta }} + {\overline{\delta }} + {\overline{\delta }}) + |T |)\) operations, where \({\overline{\delta }} {:}=\max _{p, q \in Z} \delta _{p q}\) is the maximum distance between two time intervals. Hence, the time complexity is in \({\mathcal {O}}(|Z |^2|T |{\overline{\delta }} + |Z ||T |^2)\). Since \({\overline{\delta }}\) is bounded by the number of time intervals \(|T |\), the presented algorithm is strongly polynomial with complexity \({\mathcal {O}}(|Z |^2|T |^2)\). This low complexity is achieved by locally improving the solution during its construction. The network has to be traversed only once.
Existing exact approaches are based on an iterative improvement of an initial circulation by identifying a directed circuit with negative cost in the residual graph. The circulation is adjusted correspondingly along this circuit. In these approaches, the graph has to be traversed multiple times, yielding a time complexity of \({\mathcal {O}}(|Z |^8 |T |^5 \log (|Z ||T |))\) (Schrijver 2003).
Extensions
In this section multiple extensions are discussed that enhance the basic algorithm. They aim at improving the solution quality or the running time of the algorithm. All extensions are implemented and each of them states how they are used in the experiments.
Consideration of the neighborhood of traffic zones The relocation of vehicles from other traffic zones results in empty trips, which should be kept as short as possible for cost reasons. This can be taken into account by adjusting the order of the neighboring traffic zones in row 3 in Algorithm 3. For all experiments, the set of traffic zones \(Z\) is replaced by a sorted neighborhood \(N (z)\) of the considered traffic zone \(z\). This means that vehicles are first requested from the traffic zones that are closest. This favours short empty vehicle trips and implicitly takes operating costs into account. The total number of vehicles required can be influenced positively or negatively.
Limitation of the relocation distance Further, it is possible to not only sort the set of all neighboring traffic zones, but also to limit it. This can, for example, prevent particularly long empty vehicle trips. This restriction can result in more vehicles being needed to meet the overall demand. In return, the length of empty trips will decrease. The trade-off between number of vehicles and empty trips is discussed in Sect. “Applications”.
Scanning of future time intervals Vehicles can be relocated if they have been available in another traffic zone for a sufficient number of time intervals. Still, it may be better to not relocate the vehicles, for example, if they are needed shortly thereafter in their current traffic zone. With scanning of future time intervals, it is possible to prevent such unnecessary vehicle relocations. However, both future incoming and outgoing edges at the nodes should be taken into account. Since this entails a high calculation effort for each additional time interval, in the current implementation only one future time interval is scanned. The total number of required vehicles can either increase or decrease, but operating costs are reduced.
Termination criterion In the current implementation, the vehicle relocation in Algorithm 3 is terminated as soon as enough vehicles have been found. This significantly reduces the runtime of the algorithm.
Applications
The applicability of the algorithm is illustrated in two case studies. Both case studies show that it is possible to consider on-demand services in macroscopic demand models by the use of the vehicle scheduling algorithm. In the first case study, the number of vehicles required for a regional carsharing system in a region in southern Germany is determined. It is assumed that carsharing is used for all private car journeys. This is not a realistic assumption, but it demonstrates the capability of the algorithm in large networks with a very large number of demanded vehicle trips. In the second case study, the required fleet size of an electric scooter rental system for operation on a university campus is computed. This case study emphasizes the importance of appropriate time interval durations for models with small spatial dimensions as well as the influence of demand symmetry on the number of vehicles needed.
Regional carsharing
The Stuttgart Region covers an area of \(80 \times 80\) kilometers with 2.7 million inhabitants living in urban and rural surroundings. The regional travel demand model is used to determine the fleet size of a regional carsharing system. The model is a macroscopic travel demand model covering the four model steps of trip generation, destination choice, mode choice and route choice in person transport. It calculates the demand on workdays for the modes car driver, car passenger, public transport, bicycle and walking with a tour-based model. The model includes \(|Z | = {1013}\) traffic zones in the examination area of the Stuttgart region. The baseline scenario assumes a situation without carsharing, which describes more or less the current state, where sharing is a rare event.
From this baseline scenario three scenarios are derived for comparison, all assume that private car journeys will be carried out with carsharing vehicles. The scenarios S02 and S03 require automated vehicles allowing driverless relocation of the vehicles. The following scenarios are distinguished:
- S00:
-
Baseline scenario without carsharing, private cars only.
- S01:
-
Carsharing rides replace car rides, Carsharing without relocation.
- S02:
-
Carsharing rides replace car rides, Carsharing with relocation aiming at a minimum number of vehicles, Duration of empty trips is not limited.
- S03:
-
Carsharing rides replace car rides, Carsharing with relocation aiming at a minimum number of vehicles, Duration of empty trips must not exceed 15 min.
The same demand situation is assumed throughout all scenarios. It considers 3.6 million private car trips that have their origin and destination in the region. Two input variables are passed to the scheduling algorithm:
-
1.
Day-time dependent demand \(d\) By using trip-purpose specific temporal distributions, the demand for car trips is divided into 96 time intervals of 15 min. This demand defines the service trips in the network.
-
2.
Distance matrix \(\delta\) This matrix describes the travel time between the traffic zones as multiples of time intervals. The values of the matrix are based on the car travel times in the congested road network. For service trips and empty trips the same travel times are assumed.
The algorithm calculates a vehicle schedule and outputs the number of vehicles required. The vehicle schedule contains all necessary information about empty trips which are needed for relocating vehicles. An assignment of the service trips and empty trips to the road network provides the vehicle kilometres traveled.
From the results of the German national travel survey 2017 (infas et al. 2017) it can be deduced that only about two thirds of all private cars in Germany are moved on an average working day. On average, these moving vehicles perform 3.2 trips per working day. This leads to about 1.1 million vehicles (without not moving vehicles) in the baseline scenario S00.
This number of vehicles is normalized in Fig. 3a to the value 100 and serves as reference for the calculated fleet sizes of scenarios S01 to S03. While demand remains constant, the number of vehicles in scenario S01 can be reduced to less than one third of the private cars required in the baseline scenario although no vehicle relocation is allowed. When including vehicle relocation in scenarios S02 and S03, the number of vehicles drops to about one eighth of the vehicles required in the baseline scenario. The limitation of the empty trip duration to 15 min in S03 implies a comparatively small increase in the number of required vehicles.
In the scenarios S00 and S01 the vehicle kilometers traveled are identical, since there are no empty trips. In the scenarios S02 and S03, however, the vehicle kilometers traveled increase due to empty vehicle trips by 9.2 and 7.7%, respectively (see Fig. 3b). In scenario S02 an average carsharing vehicle travels about 230 km per day. By limiting the empty trip duration to 15 min in S03, this daily distance goes down to 215 km. This corresponds to an average reduction of the total vehicle kilometers traveled by about 55 km per additional vehicle.
Figure 4 shows the time series of the moving vehicles in relation to the total number of required vehicles per scenario. Carsharing increases the occupancy rate of the vehicle fleet considerably, especially during peak hours. In both scenarios S02 and S03, the maximum share of empty vehicle trips per time interval is 20%. Similar to the service trips, the empty trips take place mainly during peak hours.
Sharing of electric scooters on a university campus
The University of Stuttgart plans to introduce a campus-wide shared scooter service with autonomous electric scooters. Autonomous electric scooters still require a human driver, but they are able to perform driverless empty trips to relocate or to drive to a charging station (Wenzelburger and Allgöwer 2020). To estimate the required size of such an electric scooter fleet, the demand for pedestrian traffic between bus stops, parking lots and buildings is determined for the campus of the University of Stuttgart. The basis for this estimation is a travel survey recording the choices of students and employees regarding their mode of transport (car, public transport), the exit stop or the destination car park and the time of day for their trips to and from the campus. In a baseline scenario C00, all movements between car parks or stops and university buildings are walking trips. In scenarios C01 and C02 it is assumed that walking trips longer than 400 m are no longer covered by foot, but with electric scooters. Since the demand at a university shows considerable peaks at the beginning and end of lectures, many scooters are required in the respective load direction. An automated relocation of autonomous scooters could reduce the number of scooters. This results in the following three scenarios:
- C00:
-
Baseline scenario without scooter, only walking.
- C01:
-
Scooter rides replace walking for trip lengths from 400 m,
Scooters are not relocated.
- C02:
-
Scooter rides replace walking for trip lengths from 400 m,
Scooters are relocated aiming at a minimum number of vehicles,
Duration of empty trips is not limited.
For walking trips, a speed of 4 \(\hbox {km h}^{-1}\), and for scooter rides, a speed of 10 \(\hbox {km h}^{-1}\) is assumed. With this speed, a distance matrix is created for the 150 locations on campus. Since the average time of one scooter trip on campus is only 4 min, trip times would be greatly overestimated when using time intervals of 15 min. Therefore, the demand is divided into 288 time intervals of 5 min each. Using these input variables, the algorithm can be applied as in the carsharing scenarios to find scooter schedules for the three campus scenarios.
Figure 5 shows the number of person and vehicle trips made as well as the total time spent in each of the three scenarios. On an average workday, there are almost 40000 walking trips to and from the buildings. In scenario C00, the trips are completely covered by foot. In the scenarios C01 and C02 about a third of the trips are performed with scooters. This reduces the total time spent traveling by approximately 40%. However, in scenario C01 without relocation nearly 6500 scooters are required. In scenario C02 the number of scooters can be reduced to about 500 scooters by relocation. The vehicle numbers correspond to roughly 2.2 vehicle trips per scooter and day in C01, whereas in scenario C02 a scooter is used for about 51.0 vehicle trips, of which 23.0 are empty trips.
A test shows the importance of the selected time interval length: If the demand and the distance matrix are divided into 15 min time intervals instead of 5 min time intervals, the vehicle scheduling algorithm only finds a solution with 1400 scooters for scenario C02 instead of 500 scooters due to the overestimated travel times.
Figures 5 and 6, which distinguishes the number of scooters in scenario C02 by activity (service trip, empty trip and idle) per time interval, show that the share of empty scooter trips on campus is considerably higher compared to the regional carsharing scenarios discussed in Sect. “Regional carsharing”. This can be explained by the demand structure on a university campus with strongly pronounced load directions. The more asymmetrical the demand, the more vehicles or empty trips are required to serve the same number of trip requests.
Conclusion and outlook
In this paper, we present an efficient heuristic for the vehicle scheduling problem [available at Hartleb et al. (2020)]. The aim is to find a vehicle schedule serving a given demand with as few vehicles as possible.
In contrast to most existing vehicle scheduling approaches, the presented algorithm is suitable for integration into existing macroscopic travel demand models to estimate the required vehicle fleet size and the corresponding traffic volumes of on-demand services. The presented algorithm provides two advantages compared to standard applications of vehicle scheduling.
The first difference is the problem size. Due to the simple procedure of the presented algorithm, vehicle schedules for large instance sizes can be found in short running times. This allows the analysis of large scale on-demand systems with a high number of trip requests. The second difference is the usability for integer as well as non-integer demand values. Macroscopic models deal with non-integer demand structures, which can be handled by the presented algorithm. With a high temporal resolution, it can also be used in microscopic travel demand models.
Two case studies illustrate the applicability of the algorithm in a macroscopic travel demand model with on-demand services. In the first case study, the algorithm is used to determine the number of required vehicles and the vehicle distance traveled including empty trips for a regional car sharing system. The results show that the number of required vehicles can be reduced drastically by using carsharing as a substitute for private cars. The second case study quantifies the impacts of autonomous scooters on the number of required scooters necessary for a shared scooter service. The results indicate a considerable potential for reducing the required fleet size by relocating the scooters.
One limitation of the algorithm is that travel costs can be considered only to a limited extent. We discuss extensions to the algorithm to implicitly account for these costs and illustrate the trade-off between number of vehicles and empty trips. In further extensions of the algorithm time-of-day dependent travel times and different speeds for service trips and empty trips could be considered. Both extensions allow a more detailed modeling but potentially have a negative effect on the runtime.
References
Azevedo, C.L., Marczuk, K., Raveau, S., Soh, H., Adnan, M., Basak, K., Loganathan, H., Deshmunkh, N., Lee, D.H., Frazzoli, E., Ben-Akiva, M.: Microsimulation of demand and supply of autonomous mobility on-demand. Transp. Res. Record J. Transp. Res. Board 2564(1), 21–30 (2016). https://doi.org/10.3141/2564-03
Bischoff, J., Maciejewski, M., Nagel, K.: City-wide shared taxis: a simulation study in Berlin. In: 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), IEEE, pp. 275–280 (2017)
Bodin, L.: Routing and scheduling of vehicles and crews, the state of the art. Comput. Oper. Res. 10(2), 63–211 (1983)
Boesch, P.M., Ciari, F., Axhausen, K.W.: Autonomous vehicle fleet sizes required to serve different levels of demand. Transp. Res. Rec. 2542(1), 111–119 (2016). https://doi.org/10.3141/2542-13
Bunte, S., Kliewer, N.: An overview on vehicle scheduling models. Public Transp. 1(4), 299–317 (2009)
Desfontaines, L., Desaulniers, G.: Multiple depot vehicle scheduling with controlled trip shifting. Transp. Res. Part B Methodol. 113, 34–53 (2018)
DFG–Forschergruppe 2083: Integrierte Planung im öffentlichen Verkehr (Integrated planning in public transport). https://for2083.mathematik.uni-kl.de/. Accessed 21 Oct (2020)
Engelhardt, R., Dandl, F., Bogenberger, K.: Speed-up heuristic for an on-demand ride-pooling algorithm. Presented at Informs Annual Meeting 2019 (2020) https://arxiv.org/pdf/2007.14877
Fagnant, D.J., Kockelman, K.M.: Dynamic ride-sharing and fleet sizing for a system of shared autonomous vehicles in Austin. Texas. Transp. 45(1), 143–158 (2018). https://doi.org/10.1007/s11116-016-9729-z
Feigon, S., Murphy, C.: Shared mobility and the transformation of public transit. In: TCRP Research Report 188, The National Academies Press, Washington, DC (2016). https://doi.org/10.17226/23578
Friedrich, M., Leurent, F., Jackiva, I., Fini, V., Raveau, S.: From Transit Systems to Models: Purpose of Modelling, pp. 131–234. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-25082-3_4
Friedrich, M., Hartl, M., Magg, C.: A modeling approach for matching ridesharing trips within macroscopic travel demand models. Transportation 45(6), 1639–1653 (2018). https://doi.org/10.1007/s11116-018-9957-5
Hartleb, J., Friedrich, M., Richter, E., Canales Martinez, C.R.: Vehicle Scheduling for On-demand Vehicle Fleets (2020). https://doi.org/10.5281/zenodo.4142325, https://github.com/jhartleb/VehicleScheduling/tree/v1.0.0
Heilig, M., Mallig, N., Schröder, O., Kagerbauer, M., Vortisch, P.: Implementation of free-floating and station-based carsharing in an agent-based travel demand model. Travel Behav. Soc. 12, 151–158 (2018). https://doi.org/10.1016/j.tbs.2017.02.002
Hörl, S.: Agent-based simulation of autonomous taxi services with dynamic demand responses. Procedia Comput. Sci. 109, 899–904 (2017). https://doi.org/10.1016/j.procs.2017.05.418
Horni, A., Nagel, K., Axhausen, K.W. (eds.): The Multi-agent Transport Simulation MATSim. Ubiquity Press, London (2016). https://doi.org/10.5334/baw
infas, DLR, IVT, infas 360 (2017) Mobilität in Deutschland—MiD 2017 (im Auftrag des BMVI). http://www.mobilitaet-in-deutschland.de/MiT2017.html. Accessed 5 July (2019)
Lam, A.Y., Leung, Y.W., Chu, X.: Autonomous-vehicle public transportation system: scheduling and admission control. IEEE Trans. Intell. Transp. Syst. 17(5), 1210–1226 (2016)
Lan, Z., He, S., Song, R., Hao, S.: Optimizing vehicle scheduling based on variable timetable by benders-and-price approach. J. Adv. Transp. 2, 1–13 (2019)
Lin, Y., Li, W., Qiu, F., Xu, H.: Research on optimization of vehicle routing problem for ride-sharing taxi. Procedia-Social Behav. Sci. 43, 494–502 (2012)
Maciejewski, M.: Dynamic transport services. In: The Multi-agent Transport Simulation MATSim, pp. 145–152. Ubiquity Press, London (2016). https://doi.org/10.5334/baw.23
Maciejewski, M., Bischoff, J., Hörl, S., Nagel, K.: Towards a testbed for dynamic vehicle routing algorithms. In: Proceedings of the Highlights of Practical Applications of Cyber-Physical Multi-agent Systems: International Workshops of PAAMS 2017, vol 722, Springer, Cham and s.l., pp. 69–79 (2017) https://doi.org/10.1007/978-3-319-60285-1_6
Marczuk, K.A., Hong, H.S.S., Azevedo, C.M.L., Adnan, M., Pendleton, S.D., Frazzoli, E., Lee, D.H.: Autonomous mobility on demand in simmobility: case study of the central business district in Singapore. In: 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS 2015) and IEEE Conference on Robotics, Automation and Mechatronics (RAM 2015), IEEE, Piscataway, NJ, pp. 167–172 (2015) https://doi.org/10.1109/ICCIS.2015.7274567
Martínez, L.M., Correia, GHd.A., Moura, F., Mendes Lopes, M.: Insights into carsharing demand dynamics: outputs of an agent-based model application to Lisbon, Portugal. Int. J. Sustain. Transp. 11(2), 148–159 (2017). https://doi.org/10.1080/15568318.2016.1226997
McNally, M.G.: The four-step model. In: Hensher, D.A. (ed.) Handbook of Transport Modelling, Handbooks in Transport, vol. 1, pp. 35–53. Elsevier, Amsterdam (2010). https://doi.org/10.1108/9780857245670-003
Moeckel, R., Donnelly, R., Ji, J.: Statewide transportation models in the U.S.: a review of the state of practice. In: Transportation Research Board 98th Annual Meeting (2019)
Ortúzar, J.D.D., Willumsen, L.G.: Modelling Transport, 4th edn. Wiley, Hoboken (2011)
PTV Group: PTV Visum 2020 Online Help (2020) https://cgi.ptvgroup.com/vision-help/VISUM_2020_ENG/, see demand responsive transport. Accessed 24 Nov 2020
Richter, E., Friedrich, M., Migl, A., Hartleb, J.: Integrating ridesharing services with automated vehicles into macroscopic travel demand models. In: MT-ITS 2019, IEEE, Piscataway, New Jersey (2019) https://doi.org/10.1109/MTITS.2019.8883315
Rieser, N., Tasnády, B., Friedrich, M., Pestel, E., Vries, N., Rothenfluh, M., Fischer, R.: Quality assurance for transport models and their applications (2018). https://www.mobilityplatform.ch/fileadmin/mobilityplatform/normenpool/21728_1645_Inhalt.pdf. Accessed 9 Apr 2021
Rogge, M., van der Hurk, E., Larsen, A., Sauer, D.U.: Electric bus fleet size and mix problem with optimization of charging infrastructure. Appl. Energy 211, 282–295 (2018)
Schrijver, A.: Combinatorial Optimization: Polyhedra and Efficiency, vol. 24. Springer, Berlin (2003)
Vosooghi, R., Puchinger, J., Jankovic, M., Sirin, G.: A critical analysis of travel demand estimation for new one-way carsharing systems. In: IEEE ITSC 2017, IEEE, Piscataway, NJ, pp. 199–205 (2017) https://doi.org/10.1109/ITSC.2017.8317917
Wang, B., Ordonez Medina, S.A., Fourie, P.: Simulation of autonomous transit on demand for fleet size and deployment strategy optimization. Procedia Comput. Sci. 130, 797–802 (2018). https://doi.org/10.1016/j.procs.2018.04.138
Wen, M., Linde, E., Ropke, S., Mirchandani, P., Larsen, A.: An adaptive large neighborhood search heuristic for the electric vehicle scheduling problem. Comput. Oper. Res. 76, 73–83 (2016)
Wenzelburger, P., Allgöwer, F.: A first step towards an autonomously driving e-scooter. Presented at 21. IFAC World Congress. https://www.ist.uni-stuttgart.de/institute/team/pdf/PW/IFAC20_E-Scooter.pdf. Accessed 24 Nov (2020)
Wilkes, G., Briem, L., Heilig, M., Hilgert, T., Kagerbauer, M., Vortisch, P.: Identifying service provider and transport system related effects of different ridesourcing service schemes through simulation within the travel demand model mobiTopp. In: International Conference on Mobility as a Service (iCoMaaS) (2019)
Zhang, W., Guhathakurta, S., Fang, J., Zhang, G.: The performance and benefits of a shared autonomous vehicles based dynamic ridesharing system: an agent-based simulation approach. In: Transportation Research Board 94th Annual Meeting (2015)
Acknowledgements
This research was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) as part of the research group for integrated planning in public transport (DFG 2020).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
The authors confirm contribution to the paper as follows: J. Hartleb: algorithm development and implementation, manuscript preparation; M. Friedrich: study conception and design, manuscript preparation; E. Richter: integration into demand calculation and analysis of results, manuscript preparation; All authors reviewed the results and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hartleb, J., Friedrich, M. & Richter, E. Vehicle scheduling for on-demand vehicle fleets in macroscopic travel demand models. Transportation 49, 1133–1155 (2022). https://doi.org/10.1007/s11116-021-10205-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-021-10205-4