The Gini index of demand imbalances in public transport

Abstract

The paper studies a general bidirectional public transport line along which demand varies by line section. The length of line sections also varies, and therefore their contribution to aggregate (line-level) user and operational costs might be different, even if demand levels were uniform. The paper proposes the Gini index as a measure of demand imbalances in public transport. We run a series of numerical simulations with randomised demand patterns, and derive the socially optimal fare, frequency and vehicle size variables in each case. We show that the Gini coefficient is a surprisingly good predictor of all three attributes of optimal supply. These results remain robust with inelastic as well as elastic demand, at various levels of aggregate demand intensity. In addition, we find that lines facing severe demand imbalances generate higher operational cost and require more public subsidies under socially optimal supply, controlling for the scale of operations. The results shed light on the bias introduced by the assumption of homogeneous demand in several existing public transport models.

Introduction

Short-run supply optimisation has a long-standing history at the boundary between transport planning and economics. The elementary principles of microeconomic theory suggest that, no matter which mode we consider, capacity variables¹ such as road width or service frequency should be increased up until the point where the marginal operational cost of further expansion equals the marginal benefit delivered to users. The outcome of this capacity rule in combination with usage fees capturing the marginal social cost of travelling ensure that supply maximises the economic efficiency of service provision (Small and Verhoef 2007).

In public transport, multiple variables can be considered as a representation of capacity, and the evolution of the underlying literature follows the discovery of the links between new capacity variables and the corresponding user costs. First, the tension between the cost of service frequency and average waiting time is investigated by Mohring (1972, (1976). In the second phase the literature recognises that not only waiting time, but also the in-vehicle travel time may depend on service frequency through the time required to board and alight at intermediate stops (Jansson 1980; Jara-Díaz and Gschwender 2003; Basso and Jara-Díaz 2012; Jara-Díaz and Tirachini 2013). Third, vehicle size is considered as another supply variable which determines a theoretical upper bound of vehicle loads (Jansson 1980; Basso and Silva 2014) as well as the magnitude of inconvenience of crowding (Jara-Díaz and Gschwender 2003; Tirachini et al. 2014). Further capacity variables may include the spatial density of lines (Kocur and Hendrickson 1982; Chang and Schonfeld 1991; Small 2004) and stops (Mohring 1972; Basso et al. 2011; Tirachini 2014), both affecting the time users require to access a boarding location or reach the trip destination after alighting.

The majority of the literature cited above concentrates on the derivation of optimal supply as a function of aggregate demand conditions. The representative origin-destination pair is the most usual spatial setup of the models. Exceptions include Rietveld and van Woudenberg (2007) and Pels and Verhoef (2007), for example, who do allow for fluctuations in demand along a public transport line, but these variations are exogenously fixed throughout their investigation. In terms of temporal demand patterns, some authors, including Newell (1971), Oldfield and Bly (1988), Chang and Schonfeld (1991), Rietveld et al. (2002), Jara-Díaz et al. (2017), consider daily demand variations with a fixed fleet composition. The lesson that off-peak fleet underutilisation is inevitable will be important in this paper. Several network optimisation models are also relevant to this paper. They study demand patterns on a larger spatial scale, i.e. on the level of a simple network with one transfer hub (Gschwender et al. 2016), an urban grid (Daganzo 2010), a radial network (Badia et al. 2014), or a parametric city (Fielbaum et al. 2016), and derive the optimal operational response in terms of network configuration. However, demand imbalances within individual lines are suppressed in their models, and they rather focus on the tension between transfer costs and scale economies.

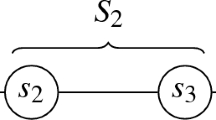
This paper can be considered as a generalisation of spatial and temporal demand imbalances. Our model recognises that operators serve multiple spatio-temporally differentiated markets along a public transport line, with the same second-best capacity generating joint costs. We analyse whether the magnitude of imbalance in demand has a predictable impact on the optimal supply strategy. Hörcher and Graham (2018) show in the simplest back-haul setting² that the asymmetry in demand between jointly served markets may have crucial impact on (1) the optimal capacity, (2) the equilibrium occupancy rate of vehicles and thus the crowding experience of passengers, (3) optimal pricing decisions, and (4) the financial and economic performance of public transport provision. In this follow-up paper we expand the spatial scope of analysis from the back-haul problem to entire public transport lines.

In this research the authors extend the analysis of the back-haul problem to a more realistic urban public transport setting: a transit line along which capacity is still indivisible due to operational constraints, but more than two origin-destination pairs have to be served. We investigate what may be a suitable measure of demand imbalances in this setting that could replace the share of main haul demand in total ridership in the back-haul problem (Hörcher and Graham 2018). We show that what matters in a network is not only the spread of demand between line sections, but also the spread of costs between them. For example, the cost of excess demand is higher on long line sections for the customers, as crowding inconvenience increases with the time spent inside the vehicle. Similarly, variable operational costs such as asset maintenance and driver costs are higher on long line sections. To characterise the joint distribution of demand and social costs, we propose the Gini coefficient of demand imbalances, a statistical index frequently used in macroeconomics as a measure of income inequality (Handcock and Morris 2006).

Delivering the core contribution of the paper, in a series of randomised numerical simulations we show that the Gini index can be identified as an important predictor of the socially optimal service frequency and vehicle size. The results are partly driven by the fact that if demand concentrates in certain sections of the line, forming a bottleneck, then crowding costs become very important relative to other user costs, and welfare maximisation requires that the operator reacts with the assignment of larger vehicles to the entire line.³ This finding remains robust in three simulation scenarios with inelastic as well as elastic demand systems. Beside their impact on optimal supply-side decision variables, demand imbalances imply that the average operational cost of transporting a passenger as well as the optimal flat (or distance-dependent) fare increase, and the operator requires more compensation from the public budget in the form of direct subsidies.

The rest of the paper is structured as follows. Section 2 sets the field with a descriptive analysis a demand patterns along real urban public transport lines. Section 3 explains the methodology of the analysis, including a detailed description of the three scenarios we investigate and the process of generating synthetic demand patterns in Sect. 3.3. Subsequently, Sect. 4 delivers the main results of the quantitative work, the three scenarios being split into separate subsections. Finally, Sect. 5 discusses our conclusions.

Descriptive insights

In order to get an empirical insight into what demand patterns transport operators face in reality, let us look at data gathered in a large Asian metro network,⁴ for illustrative purposes. The source of the illustration presented in this section is raw smart card and vehicle location data. The datasets cover one randomly selected workday when abnormal events such as major service disruptions, extreme weather phenomena or mass social events were not reported in the online media. Smart card is the only payment method in the network, and therefore our demand dataset is assumed to be comprehensive. Passenger trips are assigned to lines and then to trains using the assignment method of Hörcher et al. (2017). Finally, the throughput we derive on the train level is aggregated to 15-min intervals to even out the impact of headway deviations.

We focus on separate metro lines and time periods when capacity (i.e. the length and frequency of trains) is kept constant. In the metro network under investigation this is the case between 7.30 and 10.30, later on referred to as morning peak, and between 11.00 and 16.00 in the off-peak. Figure 1 plots the spatial and temporal distribution of demand along one particular line. The peaks in demand are clearly visible in both spatial and temporal terms. Then, Fig. 2 shows the frequency distribution of ridership in the 15-min blocks of Fig. 1, and repeats the calculation for four distinct lines differentiating the peak and off-peak operational regimes. The figures are produced with the general-purpose histogram feature of R, with manual control of the bin width.

Fig. 1

The spatial and temporal distribution of demand along a metro line. Each tile represents demand in one inter-station section over 15-min time periods

Fig. 2

Peak and off-peak demand patterns of four urban metro lines. Each observation corresponds to the passenger throughput of an interstation section in 15-min intervals

First of all, note that the histograms are surprisingly diverse; none of the standard probability distribution functions can be identified as the universal distribution of metro demand patterns. Morning peak distributions show some similarity in case of Lines 1, 3 and 4. These may be associated with a gamma or log-normal distribution, as there is a decreasing pattern towards high demand levels. Line 2 is an outlier not only in terms of the shape of the histogram, but also in the sense that mean ridership ($\mu$) is higher and the standardised measure of spread (coefficient of variation, CV) is lower than for the three other lines. The distribution of off-peak demand shows even more randomness. Lines 1 and 4 have a disproportionately high number of line sections where demand is under 1000 passengers per 15 min, Line 3 has almost a homogeneous distribution, while in case of Line 2 the demand pattern is heavily skewed towards higher ridership levels.

The lack of uniformity in demand distributions suggests that the standard measures of spread may not be appropriate for characterising demand imbalances. Also, travel times on line sections range between less than 2 min to more than 5 min, which implies that the share of inter-station markets in operational and user costs might not be uniform either. For this reason, a more compact measure of the joint distribution of demand levels and social costs will be required to study the impact of line-level demand fluctuations.

Methodology

As disaggregate demand and operational data on a large number of independent public transport lines is not available for the purpose of this research, we propose a randomised numerical approach to study regularities in the impact of line-level demand imbalances. We consider a standard bidirectional public transport line along which demand varies, both spatially and directionally. Capacity is fixed along the line, and therefore it is inevitable that supply is sub-optimal on the level of individual line sections in the sense that the first-best capacity rules do not hold in equilibrium. Section 3.1 defines the Gini index as a metric that characterises the degree of demand fluctuations. Then, Sect. 3.2 describes the second-best welfare maximising supply rule for a given demand pattern along the line. As Sect. 3.3 explains in more depth, multiple scenarios can be distinguished based on (i) whether we allow for the aggregate (line level) scale of ridership to vary, and (ii) whether demand is assumed to be responsive to the quality and price of the service. In case of the elastic demand scenario, we consider two pricing regimes (flat fares and distance based fares) as well.

Eventually, the goal of this quantitative analysis is to generate a large number of comparable, synthetic demand patterns in which the impact of demand imbalances, measured by the Gini index, on the optimal supply and the efficiency of service provision can be identified with regression techniques.

Gini index in the travel demand context

The Gini coefficient measures statistical dispersion within two frequency distributions. In the public transport context, we intend to measure the dispersion of demand along a sequence of jointly served line sections, taking into account that longer sections have a higher share in both operational and user costs. We adopt the concept of the Gini coefficient as a demand inequality measure by plotting the cumulative share of section-level demand in increasing order against the cumulative length of the sections. The resulting function is called the Lorenz curve. A stylised example is plotted in Fig. 3.

Fig. 3

Definition of the Gini coefficient in the transport demand context

The Lorenz curve is the diagonal of the graph in case of perfect equality, i.e. when both ridership and all costs are evenly distributed along the line. At the other extreme, if all demand is concentrated on a negligibly short line section, then the Lorenz curve remains flat on its initial part, and then it increases very rapidly when we finally consider the only busy section of the line. Thus, the curve moves along the two sides of the graph, representing perfect inequality. The Gini index is the fraction of the area between the actual Lorenz curve and the one belonging to perfect equality (see the shaded area A  in Fig. 3), and the area between the two extrema (that is, $A+B$). Mathematically, the Gini index is $G = A/(A+B)=2A$, where the second equality comes from the fact that $A+B=0.5$, as both variables in the graph are shares ranging between zero and unity.⁵ The resulting Gini index is 0 under perfect equality and 1 in case of perfect inequality.

The key mechanism in the supply optimisation problem is the tension between demand and social costs. Accommodating excess demand is more challenging on a line section where capacity provision is more expensive for society. The variable on the horizontal axis should therefore capture the distribution of operational and user costs among line sections The choice of this variable on the horizontal axis is not a trivial one, however, as multiple infrastructure characteristics may proxy for social costs. In this research we assume that travel time is proportional to distance in all line sections, in other words we neglect certain peculiarities of vehicle dynamics and assume that the average speed is constant. With this assumption, we define an operational cost function which depends on vehicle service hours, and therefore line length, riding time, or the share in operational costs all lead to the same Lorenz curve and Gini index, no matter what random demand pattern we consider. However, if a real service provider’s operational cost function has vehicle mileage as well as vehicle hour related components, and average speed varies along the line, then multiple unequal Gini indices can be defined depending on which variable we select on the horizontal axis. This dilemma remains open for future research, but the authors conjecture that the qualitative findings of the present research would not be affected by the choice of second variable.

Among the metro demand patterns depicted in Fig. 2, the Gini coefficient ranges between 0.18 and 0.41, hinting that their demand and line length distributions are far from perfect equality. The coefficient of variation (CV) of section-level demand and the Gini ratio do show some correlation in this sample of demand patterns, but we can also find pairs of distributions where the two metrics move in the opposite direction. For example, Line 3 in the morning peak has higher Gini index than Line 4 (0.387 and 0.378, respectively), suggesting a more unequal demand distribution, while the coefficient of variation is greater for Line 4 (0.70 and 0.71, as provided in Fig. 2). The purely demand-based CV metric contradicts the proposed alternative in which segment length is also taken into account. This implies that these lines do not have the same pattern of line lengths, and therefore it does matter whether we consider this second variable when we characterise the spread of demand.

It would be an attractive path for quantitative research to extend the sample of metro lines depicted above with additional disaggregate data from other public transport systems. Beside the administrative challenges of acquiring such a unique dataset, we see another disadvantage of working with real data. In most urban public transport systems, supply on distinct lines is not independent from each other. For example, if a metro operator intends to maintain a fleet of trains of unique size (length), then the vehicle size variable cannot be adjusted on a line level to its optimal level. Controlling for such technological constraints is challenging in the empirical analysis. By contrast, working with synthetic data enables greater transparency both in terms of the operator’s economic objective and the flexibility of decision variables, and the scale of operations can also be controlled by the researcher. In this sense what we model is the impact of demand imbalances on socially optimal supply, that is how demand fluctuations should affect supply, instead of existing operators’ decisions.

Modelling public transport operations

We generate random demand patterns for the simple service layout depicted in Fig. 4. The line has five stops (stations) and two times four inter-station sections considering both directions. Sections are indexed by subscript j, and the line serves 20 origin-destination pairs i that we define as markets with independent demand. The cycle time is $t_c = \sum _j t_j$, noting that line sections are directionally differentiated. For the sake of simplicity, dwell times are assumed to be exogenous and therefore normalised to zero.⁶ Capacity is represented by two decision variables of the model: frequency (f) and vehicle size (s). The operational cost function is defined as

$$\begin{aligned} C_{o} = t_c \, f \cdot (a + b \, s^\varepsilon ), \end{aligned}$$

(1)

where a is the coefficient of the fixed cost of vehicle service hours, while parameters b and $\varepsilon$ control the degree to which costs increase with vehicle size (i.e. train length). In particular, $\varepsilon$ is the elasticity of operational costs with respect to vehicle size. With a reference to our earlier discussion, please note that we express all operational costs in function of movement times, while in reality some expenses may depend on the distance traveled, and this matters if the average speed of vehicles differs between line sections, so there is no direct association between travel time and distance.

Fig. 4

Uniform network layout of the simulation experiment

Let us now turn to the demand side of the model. In the simulation scenarios of Sect. 4 we consider two types of demand systems. The first one is inelastic demand, in which case ridership on origin-destination pair i is denoted by $q_i$. With inelastic demand, the objective of supply optimisation is to minimise the sum of operational and user costs, in other words

$$\begin{aligned} \min _{f,s} TC = C_{o} + C_{{ user}}, \end{aligned}$$

(2)

where the aggregate user cost function has the following specification:

$$\begin{aligned} C_{{ user}} = \sum _i q_i \cdot c_i(Q,f,s) = \sum _i q_i \cdot \left[ \alpha _w \, 0.5 f^{-1} + \sum _j \delta _{ij} t_j \, \alpha _v \left( 1 + \varphi \, q_j(f s)^{-1}\right) \right] . \end{aligned}$$

(3)

Explanation: $Q= \{ q_i \}$ denotes the vector of OD demand levels, and $q_j$ is the aggregate ridership on link j, such that $q_j = \sum _i \delta _{ij} q_i$, where $\delta _{ij}=1$ if section j is part of the route taken by passengers of origin-destination pair i, and $\delta _{ij} = 0$ otherwise. Naturally, passengers take the shortest path and we neglect in this simple setup the possibility that passengers may travel backwards to secure a seat on crowded services. In the aggregate user cost function (3), $c_i(Q,f,s)$ is the individual user cost, with two components. The first one, $\alpha _w 0.5f^{-1}$, is the user cost of waiting, assuming random passenger arrivals and $\alpha _w$ denoting the monetary value of wait time. The second additive term is the total cost of travel time in monetary terms. This part of the formula adds up the in-vehicle time on all sections j that the passenger of market i travels through; $\alpha _v$ is the value of in-vehicle time. Travel time is then multiplied by a crowding dependent factor. The multiplier increases linearly in occupancy rate $q_j(fs)^{-1}$, with slope $\varphi$. This specification resembles Hörcher and Graham (2018) and earlier modelling practices in the literature.

The second demand system we consider in subsequent simulation scenarios features elastic demand. Again, we take the simplest approach by defining a linear inverse demand function $d_i (q_i)$ for each market, and declaring that in equilibrium, ridership must satisfy the following condition: $d_i (q_i) = p_i + c_i(Q,f,s)$. Thus, the vector of fares, $P = \{ p_i \}$, enters the supply optimisation problem as an additional set of decision variables affecting equilibrium demand. The social welfare oriented objective function thus modifies to

$$\begin{aligned} \begin{aligned}&\max _{f,s,P} W = B - C_{o} - C_{{ user}} = \sum _i \left[ \int _{0}^{q_i} d_{i'}(q_i') \, dq_i' \right] - C_{o} - C_{{ user}} ,\\&\text {s.t.} \quad d_i (q_i) = p_i + c_i(Q,f,s) \quad \forall i. \end{aligned} \end{aligned}$$

(4)

In the welfare function B denotes aggregate consumer benefit on all markets served. The final result of service provision is quantified by profit function

$$\begin{aligned} \pi = \sum _i p_i q_i - C_{o}. \end{aligned}$$

(5)

Simulation scenarios and their statistical evaluation

With the modelling framework introduced above, multiple simulation scenarios can be tested numerically. We propose three scenarios ranging from very simple (thus unrealistic) but transparent ones towards more complex setups in which the isolated impact of unbalanced demand can be inferred by statistical methods only. We differentiate the scenarios based on whether aggregate demand is kept constant or not, and whether OD demand levels are inelastic or elastic with respect to supply. The three scenarios are as follows.

• (a) Fixed aggregate ridership, inelastic demand

• (b) Variable aggregate ridership, inelastic demand

• (c) Elastic demand (with flat or distance dependent fares)

A key challenge of the paper’s analysis is to disentangle the impact of scale effects, aggregate scale economies from the consequences of the unbalancedness of demand along the line. Moreover, it is not trivial either what we mean by scale. The total number of passengers, passenger miles, vehicle miles as well as capacity miles may all be considered as a measure of scale. Focusing on both final output related metrics, in scenario (a) we generate synthetic demand patterns keeping the total number of passengers at $\sum _i q_i=4000$, and the total passenger mileage at $\sum _i q_i ( \sum _j \delta _{ij} t_j) = 2500$ passenger hours. With this approach we completely neutralise the impact of the scale of ridership, but of course the comparisons we thus make are quite unrealistic in the sense that we rarely find two public transport lines operating at exactly the same scale. The randomly generated demand patterns are then numerically optimised with respect to frequency (f) and vehicle size (s), according to a social cost minimising objective of (2). Without scale effects, the functional relationship between the Gini index and supply variables will be very clear, and therefore no further statistical analysis is needed.

In scenario (b) we relax the constraint of fixed aggregate demand, both in terms of total passenger volumes and the mileage travelled. In order to disentangle the impacts of the scale and the distribution of demand on supply variables, we deploy regression methods instead of simple visual observation. This turns out the be an effective strategy.

However, scenario (b) is still somewhat unrealistic in the sense that demand on various OD pairs is inelastic. The literature suggests that demand elasticities have a substantial impact on optimal supply. Thus, in scenario (c) we relax the assumption of inelastic demand as well, moving on the demand system introduced in the previous section and replacing cost minimisation with the welfare oriented objective of Eq. (4). In the random generation of demand patterns we draw the two intercepts of the linear inverse demand curves from uniform distributions. Maximum willingness to pay varies between zero and $\$20$, while maximum market size may run up to 1000 passengers an hour. The second aspect to consider is that pricing might play an important role in the system’s behaviour when demand is elastic. Thus, pricing is added to the model’s decision variables in scenario (c). We consider two pricing regimes: flat fares and distance based fares. In the former case each $p_i$ in all markets is constrained to the same uniform level, while in the second one we allow the fare to increase proportionately with travel time (distance). In this scenario we expand the range of explanatory variables with aggregate demand elasticities with respect to frequency, vehicle size and the fare level, to resemble the data that might be available in real transport networks.

In all three scenarios, the simulation algorithm runs through the following steps:

• 1. We generate 300 synthetic demand patterns,⁷ with either elastic or inelastic demand, depending on the scenario.

• 2. For each demand pattern, we define the length of each line section randomly,⁸ normalising the total length of the line to 1 h.⁹

• 3. For each demand pattern, we compute its scale (aggregate demand) measures, demand elasticities (when applicable), and the Gini index.

• 4. For each demand pattern, we derive the optimal frequency, vehicle size as well as pricing variables (when applicable) using the box constrained BFGS quasi-Newton method in the general-purpose optimisation package of R.

• 5. After steps 1–4 are performed for each synthetic demand pattern, in the resulting dataset we regress the optimal supply variables against the scale measures (when applicable), the demand elasticities (when applicable), and the Gini index.

The remaining model parameters are calibrated according to Table 1. These values are borrowed from earlier capacity optimisation studies, i.e. Rietveld et al. (2002), Jara-Díaz and Gschwender (2003) and Rietveld and van Woudenberg (2007), and $\varphi = 0.15$ is an approximation of the crowding multiplier estimated by Hörcher et al. (2017). These values are considered consensual in the literature, and are not related to specific measurements in the metro network of the illustrative example of Sect. 2.

Table 1 Notation and calibrated values of simulation parameters

Our goal in the evaluation of the randomised experiments is first of all to investigate the relevance of the Gini index as an explanatory variable of optimal supply and the efficiency of service provision. Second, we are interested in the sign of the impact that the Gini ratio has on decision variables and performance metrics, i.e. whether they increase or decrease with the magnitude of demand imbalances. The actual magnitude of the coefficients is indeed dependent on input parameters, and therefore we do not attach much importance to them.

Quantitative results

Fixed scale, inelastic demand

In the first scenario we keep aggregate demand constant, both in terms of passenger volumes and passenger miles, but the distribution of ridership is randomised, together with the length of line sections. In the sample of synthetic demand patterns, the Gini index of demand imbalances varies between 0.15 and 0.45 in the randomly generated sample, which is almost the same range as what we found for real metro lines in Fig. 2; first and third quantiles are at 0.25 and 0.33, respectively.

The four panels of Fig. 5 depict the social cost minimising frequencies and vehicle sizes, and the resulting operational cost and social cost levels, in function of the Gini index. The graphs include the best fitting nonlinear curves with local polynomial regression fitting. The main outcome of this preliminary analysis is that, fixing the scale of operations, the Gini coefficient is a surprisingly good predictor of the optimal capacity (frequency as well as vehicle size). This is confirmed quantitatively by the low RMSE values relative to the magnitude of the dependent variables. Although we do observe some noise around the best fitting nonlinear curves, suggesting that there is no deterministic link between G and the optimal supply, this noise is almost negligible. The shape of the relationships is very similar to what the authors found in the back-haul problem with only two markets served by joint capacity (Hörcher and Graham 2018).

Fig. 5

Simulation results—Optimal capacity and the resulting operational costs and social welfare

Qualitatively, as the concentration of demand increases, frequency is gradually replaced with higher vehicle size, because the disutility of crowding becomes more important than the harm caused by waiting time costs. The reduction in frequency is milder, and therefore total capacity (the product of frequency and vehicle size) is an increasing function of the Gini index. We have performed additional sensitivity analyses with respect to the crowding multiplier parameter, $\varphi$. The outcomes are in line with intuition: the optimal frequency slightly decreases while the optimal vehicle size substantially increases with travellers’ sensitivity to crowding.¹⁰ Despite the presence of scale economies in vehicle size, the optimal cost of operations also increases with the magnitude of demand imbalances, just like the aggregate cost for society. The finding that operational costs increase by almost 20% simply due the more unbalanced pattern of demand, keeping aggregate ridership constant, highlights the increased policy relevance of how demand is spreading over the public transport network.

Crowding plays an important role in the model, as the cost of crowding for users is what induces higher vehicle size when demand concentrates in specific line sections. Therefore more insights can be gained by plotting crowding related simulation variables against the Gini index. Figure 6 shows that this new measure of line-level demand imbalances explains very well the increase in crowding disutility experienced by the average passenger (weighted by the duration of their trips). As intuition suggests, the greater the asymmetry in demand between markets served by the same capacity, the higher the average crowding disutility, even at constant passenger mile performance.

Fig. 6

Simulation results—average and maximum crowding density under optimal capacity provision, in function of the Gini index

Maximum crowding density values, however, have a much wider spread around the best fitting nonlinear curve, using the Gini index as predictor variable. The ‘maximum crowding density’ curve flattens as G increases, which implies that the possibility of extreme crowding conditions becomes more unpredictable when the degree of demand imbalance is relatively high.

Varying scale, inelastic demand

In the second scenario we relax the assumption that total ridership and passenger miles must add up to the same level in the randomly generated demand patterns. We draw $q_i$ values for each origin-destination pair from normal distributions, retaining non-negative draws only. To introduce some directional imbalance along the line, demand for OD pairs in the direction $A\rightarrow E$ (see Fig. 4) are drawn from ${\mathcal {N}}(600,400)$, while demand in the opposite calm direction is ${\mathcal {N}}(300,200)$ distributed. This way we reproduce a very similar distribution of the Gini index among the randomised demand patterns. Total ridership varies between 6 and 12,000 passengers, while users spend a total of 2000–7000 h on the vehicles. Correlation between these two measures of scale and demand imbalances remains small: it is 0.08 and 0.02, respectively, meaning that greater output does not imply systematically higher inequality in demand.

Preliminary visual insights suggest that G is no longer a reliable predictor of optimal frequency and vehicle size when one does not control for the scale of operations. In other words, the plots equivalent to Fig. 5 lead to a random cloud of simulation outcomes in function of the Gin index in this case, and the best fitting nonparametric curve does not tell much about how optimal supply reacts to the distribution of demand. (For this reason, the figure is not repeated here.) This hints that the confounding effect of scale might be among the reasons why the impact of unbalanced demand is not obvious as one compares public transport services in real life, and the literature of public transport supply had assigned limited attention to the phenomenon.

To disentangle the effects of scale and the magnitude of demand imbalances, we estimate a series of regression models based on the synthetic datasets generated. We explain frequency, vehicle size, the operational cost of the average trip as well as the average social cost per trip with (i) total ridership, (ii) the average trip length, capturing the effect total passenger miles which otherwise highly correlates with total demand, and (iii) the Gini index we computed for each demand pattern. The results are plotted in Tables 2 and 3. Model I is estimated without the Gini index, in Model II it enters as a linear additive component, thus leading to a simple OLS regression, while in Model III, G is allowed to have a nonparametric specification to achieve the best possible fit. Model III is a generalised additive model (GAM) in which the degree of smoothness of model terms is estimated as part of fitting. The GAM models are estimated with the default settings of the ‘mgcv’ package of R. The values in parentheses are standard errors; all estimates are significant at the 99.9% confidence level.

Table 2 Modelling optimal supply with the Gini coefficient

Table 3 Modelling social costs with the Gini coefficient

Note that the linear models fit the data pretty well based on the $\hbox {R}^2$ values, even without adding the Gini index as an explanatory variable. Demand imbalances play a more important role in the prediction of the optimal vehicle size and operational cost, as in these models the Gini index raises the $\hbox {R}^2$ by around 10%. The signs of the coefficients are in line with expectation: optimal capacity increases with the number of users, while the negative signs of ridership in the cost models imply the presence of density economies. The average trip length has a negative effect on the optimal service frequency and a positive one on vehicle size, which is also due to the fact that the importance of crowding avoidance increases relative to the waiting time as the average passenger spends more time inside the vehicle. This raises the average operational and social cost of carrying passengers, indeed. In model specification II in which the Gini index is a linear covariate, we observe that it increases the optimal vehicle size to the expense of frequency, in line with Scenario 1 in the previous section.

Figure 7 visualises the nonparametric splines of Model III together with the predicted values of the dependent variables for each observation in the underlying dataset. It is immediately apparent that the predictive power of the Gini index improves significantly when the scale of ridership and the length of the average journey is controlled for. The predictions are scattered around the nonparametric curves more closely, especially in the range of $G \in (0.2,0.3)$. The shape of these relationships resemble the ones we got with uniform aggregate demand: the optimal frequency is a downward sloping concave, while the welfare maximising vehicle size as well as the average operator and social costs per trip are upward sloping convex functions of the Gini index.

Fig. 7

Non-parametric splines of the Gini coefficient in optimal supply and cost models

As one of the referees has pointed out, the present simulation framework also enables us to quantify the bias introduced when researchers assume a homogeneous distribution of demand along the public transport line (see e.g. Jansson et al. 2015). Let us take the aggregate demand level and average trip length of each demand pattern in our synthetic dataset, and derive the optimal frequency and vehicle size assuming that demand is homogeneously distributed over the public transport line. That is, we optimise

$$\begin{aligned} \min _{f,s} { TC} = C_{o} + C_{{ user}} = t_c \, f \cdot (a + b \, s^\varepsilon ) + \hat{Q} \cdot \left[ \alpha _w \, 0.5 f^{-1} + \bar{t} \, \alpha _v \left( 1 + \varphi \, \frac{\hat{Q}}{t_c f s} \right) \right] \end{aligned}$$

(6)

instead of (2), where $\hat{Q}$ is aggregate demand and $\bar{t}$ is the average trip length. Note that $\hat{Q}/t_c$ is the average number of passengers on board assuming a homogeneous demand distribution. The difference between the resulting biased capacity variables and the original ones derived for the unbalanced demand patterns is plotted in Fig. 8.

Fig. 8

The difference in optimal supply variables and crowding assuming a homogeneous distribution of demand, compared to the actual fluctuating demand patterns of the simulation

This figure clearly illustrates that the optimal frequency is somewhat overestimated and the vehicle size is substantially underestimated when a homogeneous demand distribution is assumed. The magnitude of this bias increases with the Gini index. In the final plot of Fig. 8 we compare the average crowding experience of passengers as predicted by the two modelling approaches. With the assumption of homogeneous demand, the predicted crowding level is lower than what passengers actually experience, which is indeed the main reason why the optimised supply variables get misled.

Elastic demand

In the third exercise of the paper we relax another constraint of the model: inelastic demand levels are now replaced with a demand function defined separately for the 20 origin-destination pairs of the network. Details of the random generation of elastic demand patterns are provided in Sect. 3.3. Let us now focus on the descriptive characteristics of the resulting dataset. We provide the distribution of the Gini coefficients and demand elasticities among the random demand patterns in Fig. 9. Indeed, it is possible to derive demand elasticities for all OD markets separately, but it would be difficult to compare that with existing empirical evidence, as normally only aggregate demand elasticities are published for public transport systems as a whole. Typically, elasticities with respect to fares range around $-0.2$ and $-0.3$, while frequency elasticities are positive and somewhat greater in magnitude (Paulley et al. 2006; Wardman 2014).

Fig. 9

Distributions of demand characteristics in the synthetic sample of network demand patterns

In this scenario we do not introduce directional demand imbalances on purpose, as the spread of the Gini index is already in the desired interval: the majority of synthetic observations vary between 0.1 and 0.5, as in the previous scenarios. The price, frequency and vehicle size elasticities of demand are calculated after the welfare maximising supply variables, including the flat fare, are found. The optimal decision variables are then marginally increased one by one, and then the elasticities are derived based on the demand levels in the new equilibria. With this numerical approximation of the elasticities, we can validate whether the synthetic demand patterns resemble reality. Price elasticities range up to $-0.7$ with a mean around $-0.2$. Frequency elasticities are mainly between 0.1 and 0.4. The vehicle size elasticity is somewhat milder, and this demand attribute is more difficult to compare with the literature, given that it is highly context specific. With these summary statistics, we are convinced that the randomised experiment can be used to draw conclusions about the properties of a representative public transport line.

With an elastic demand system pricing itself can affect the distribution of demand along the line we investigate. The first-best welfare maximising set of tariffs would require price differentiation between all markets served by the line. Hörcher and Graham (2018) derive in a very similar generalised model framework that the first-best fare in each market i would be equal to the marginal external crowding cost imposed on fellow users, a value which is proportional to the occupancy rate experienced by passengers. That is, long trips in crowded conditions should cost more for the user as well. The authors are not aware of any major public transport systems adopting differentiated first-pricing, though. Therefore in this simulation scenario we implement two of the more commonly known pricing policies: flat fares and distance-based fares. Both options imply only one decision variable in supply optimisation. We set this to its welfare maximising level after numerical optimisation.

Tables 4 and 5 present regression models of the optimal fare, frequency and vehicle size, as well as the resulting operational cost and financial profit normalised by the number of users carried. This scenario confirms again that the Gini index is a statistically significant predictor of optimal supply variables and the financial performance of service provision. The magnitude of its impact depends on the pricing regime, but the signs remain consistent in the two models. Both the optimal flat fare and the capacity variables are increasing functions of the degree of demand imbalances. It is the optimal frequency where we observe a difference relative to previous scenarios where G had a weak negative impact on f. In the present case the effect is still weak but positive, suggesting that the operator reacts to demand imbalances with both higher frequencies and vehicle capacities. One potential explanation is that in the presence of pricing incentives, substituting service frequency with even higher vehicle size is no longer required. The appearance of this new finding highlights the importance of elastic demand in public transport studies.

Table 4 Explaining optimal system characteristics with the Gini coefficient—flat fare regime

Table 5 Explaining optimal system characteristics with the Gini coefficient—distance-based pricing regime

The overall increase in capacity implies that the total operational cost of service provision is also positively impacted by the spread of demand. In terms of magnitudes, we see higher operational costs with with flat fares. The financial outcome of welfare oriented service provision is negatively impacted by demand imbalances. This applies for both pricing regimes, but the related coefficient is higher in magnitude with distance-based fares. Note that total profits are in the negative region in 89.5% of the synthetic demand patterns in our flat fare dataset, and in 97.5% of the one with distance-based fares. In other words, as theory suggests, welfare maximisation is likely to lead to financial losses, and the average traveller should receive higher subsidies if demand along the public transport line is heavily unbalanced. This result is driven by operational costs, as the fare that passengers pay actually increases with G.

It is attractive to derive qualitative conclusions about the relationship between the Gini index and the economic efficiency of service provision. A regression model explaining W predicts no significant changes in function of the Gini coefficient, unfortunately. In addition, it is difficult to control for the scale of operation in this case with elastic demand. Naturally, total ridership and social welfare are strongly correlated with each other, but it has to be noted that demand in this case is already the outcome of an equilibrium mechanism and therefore the full economic potential captured by the system of market-level demand functions might be more representative of the scale of operation. Hörcher and Graham (2018) perform a simulation in the back-haul setup in which total willingness to pay, i.e. the sum of the areas under individual inverse demand curves is kept constant. Their general finding is that social welfare in equilibrium decreases with the imbalance in maximum willingness to pay between markets, but the shape of the underlying demand functions is also an important determinant. In the present network layout with much more individual markets we cannot find a transparent method to derive more relevant results.

Conclusions

This study investigates the impact of line-level demand imbalances on the socially optimal public transport supply, including service frequency and vehicle size, and the economic and financial performance of service provision. The paper’s contributions can be summarised in three points.

• (a) We identify that the existing literature neglects the impact of network-level demand imbalances in supply optimisation. We hypothesise that this is a shortcoming of the existing literature.

• (b) We propose one potential metric to quantify network-level demand imbalances, acknowledging that many other inequality measures could be used, e.g. the ones in Handcock and Morris (2006).

• (c) In a series of numerical simulations we show that the inequality measure we selected in point (b) is a good predictor of the optimal service frequency and vehicle size. This confirms our hypothesis in point (a).

To support our conclusions, the paper documents a randomised numerical experiment with the following steps. For a predetermined network layout, first we generate a random demand pattern, i.e. demand levels for each origin-destination pair in scenarios of inelastic demand, or the parameters of the inverse demand curves from which equilibrium demand can be derived, depending on supply variables. Second, we search for the social welfare maximising fares and capacities of each of the randomly generated demand patterns. Third, we conduct a statistical analysis to identify the relationship between optimal supply and the proposed measure of demand imbalances, the Gini index. These steps are repeated in three scenarios with (i) fixed, inelastic aggregate demand, (ii) inelastic demand, but varying aggregate scale, and (iii) elastic demand functions defined for all origin-destination pairs.

The quantitative analysis confirms that the Gini index is a statistically significant and quantitatively important determinant of the socially optimal supply variables. This implies that if demand imbalances are neglected in a public transport model based on a representative OD pair, then the optimal capacity, especially vehicle size, is easily underestimated. The research shows that unbalanced demand, measured by the Gini index, does affect financial characteristics as well. More specifically, the optimal fare, operational costs, as well as the average subsidy per passenger all increase with the Gini index.

Why is the analysis of demand imbalances relevant for research and policy? Transport services make connections between geographically separated areas of a heterogeneous urban space, and are therefore affected by the spatial and temporal concentration of economic activity. Said differently, travel patterns are strongly linked to city structure, which is nearly exogenous for public transport operators in the short run.¹¹ Therefore studying demand asymmetries is essentially about how urban spatial structure affects the key operational and economic features of public transport provision. Policies that affect the spatial and temporal pattern of activities in the urban economy will influence the effectiveness of public transport provision as well, and therefore optimal public transport interventions should reflect the spatial environment of operations.

Do the results imply that operators should prefer serving lines with more homogenous demand patterns over the ones facing demand imbalances? No, the unbalanced structure of demand does not guarantee that service provision is inefficient. We suggest that investment or operational priorities should always depend on the precise account of the underlying social costs and benefits. However, the results do hint that the properties of the demand pattern should be taken into account when one benchmarks public transport services. Demand imbalances may explain differences in operational characteristics and the financial performance of services that are otherwise similar in terms of the aggregate ridership they carry.

The present analysis reveals some of the fundamental mechanisms that demand imbalances might generate. Indeed, our simple model is not suitable to replace the entire supply optimisation process of public transport operators. As one of the referees has pointed out, there are numerous additional factors that could significantly affect supply and demand. This includes the difference in global demand due to urban structure or population size, supply restrictions in the number of carriages and crew, diversity in public transport networks, track sharing by different railway companies, and various fare systems.

The analysis introduced in the paper can be extended in several ways. Let us conclude the paper with a non-exhaustive list of potential subjects for future research:

• 1. Despite the challenges enumerated in Sect. 3.1, it is an attractive path for future research to perform empirical analysis with real-world demand patterns, e.g. using smart card data.

• 2. Although our preliminary experiments suggest that the Gini coefficient is a suitable measure of demand imbalances, future research may consider more advanced inequality measures to be adopted for travel demand applications (Atkinson 1983; Handcock and Morris 2006).

• 3. The present paper as well the back-haul analysis of Hörcher and Graham (2018) consider public transport in isolation, without competing modes. If, for example, the road running in parallel with a crowded section of the rail network is heavily congested and underpriced, optimal supply should serve two goals simultaneously: one objective is to reduce crowding externalities on rail, but modal shift from the congested road is also a (conflicting) secondary goal of welfare maximisation. To the best of our knowledge, demand imbalances have not be analysed in a multimodal setup.

• 4. The ‘crowding multiplier’ approach is not the exclusive way of representing capacity shortages in a public transport model. An alternative approach often adopted in the literature is the introduction of an explicit capacity constraint. Then, demand in the critical section of the line (that is, the one with the highest demand) is expected to have a more decisive role in frequency and vehicle size setting. As a consequence, we also expect that with an explicit capacity constraint, the ratio of demand in the critical section relative to the average demand in the rest of the line might be sufficient to predict the impact of demand imbalances on optimal supply. These speculative thoughts might be justified in a dedicated model adaptation.

• 5. The present analysis has been designed to replicate the main characteristics of urban rail lines. Bus operators enjoy somewhat more flexibility in terms capacity adjustment to tackle demand imbalances, by applying short-turnings, deadheading or express lines (see Ibarra-Rojas et al. 2015), even though these techniques do not provide a general remedy against demand imbalances along bus lines. Future research might explore whether these possibilities can alter the economic consequence of unbalanced demand in bus operations.

• 6. Finally, the present paper focuses on single lines without transfers or branches. The Gini coefficient or other inequality metrics of demand patterns may be relevant on a network level as well. It is an open question whether the paper’s qualitative results remain applicable on the scale of a public transport network as well.