Abstract
Traditional approaches to travel behaviour modelling primarily rely on household travel survey data, which is expensive to collect, resulting in small sample sizes and infrequent updates. Furthermore, such data is prone to reporting errors which can lead to biased parameter estimates and subsequently incorrect predictions. On the other hand, mobile phone call detail records (CDRs), which report the timestamped locations of mobile communication events, have been successfully used in the context of generating travel patterns. However, due to their anonymous nature, such records have not been widely used in developing mathematical models establishing the relationship between the observed travel behaviour and influencing factors such as the attributes of the alternatives and the decision makers. In this paper, we propose a joint modelling framework that utilises the advantages offered by both travel survey data and low-cost CDR data to optimise the prediction capacity of traditional trip generation models. In this regard, we develop a model that jointly explains the reported trips for each individual in the household survey data and ensures that the aggregated zonal trip productions are close to those derived from CDR data. This framework is tested using data from Dhaka. Bangladesh consisting of household survey data (65,419 persons in 16,750 households), mobile phone CDR data (over 600 million records generated by 6.9 million users), and aggregate census data. The model results show that the proposed framework improves the spatial and temporal transferability of the joint models over the base model which relies on household travel survey data alone. This serves as a proof-of-concept that augmenting travel survey data with mobile phone data holds significant promise for the travel behaviour modelling community, not only by saving the cost of data collection, but also improving the prediction capability of the models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Traditional approaches to developing travel behaviour models rely on household travel surveys to establish the mathematical relationship between the choices made by the travellers, the attributes of the network and socio-demographic characteristics of the travellers. However, household surveys are often affected by low response rates and reporting errors (e.g. Rolstad et al. 2011; Groves 2006). Further, the surveys are expensive to conduct which leads to small sample sizes and lower update frequencies. Consequently, transport models designed to fit household travel survey data alone can result in biased parameters capturing the noise in the data rather than the actual relationships in the population.
On the other hand, there has been growing interest in the use of mobile phone data for mobility modelling over the last few decades. Among the various transport-related applications, such data has been widely used to estimate origin–destination matrices (e.g. Çolak et al. 2015; Iqbal et al. 2014; Pan et al. 2006; White and Wells 2002) and trip generation (e.g. Çolak et al. 2015). Since mobile phone data generally covers significant proportions of the population (GSM Association 2017), the data is able to reliably capture the aggregate travel patterns. However, due to its anonymous nature, mobile phone data is not traditionally used in developing mathematical models of travel behaviour that establish the relationship between observed travel behaviour and causal factors such as the attributes of the alternatives and the decision makers. The existing mobility models based on mobile phone data alone cannot be used to reliably test alternative or future travel demand scenarios, and yet this is one of the core roles of transport models.
We are thus in a situation where traditional survey data is small in size, potentially unrepresentative and inaccurate, but contains information on key causal variables. On the other hand, mobile phone data is larger in size, more representative and accurate but missing information on key causal variables. This situation motivates the present research where we propose a framework that brings in a third type of data, namely census information, which is representative and contains detailed socio-demographic variables but does not have travel behaviour information. We thus combine household travel survey data, aggregate census data, and mobile phone data using a combination of population synthesis techniques (to generate realistic disaggregate artificial populations to assist with forecasting) and mathematical modelling to jointly optimise the aggregate and the disaggregate fit of travel behaviour models. In terms of the aggregate fit, we seek to minimise the error between the modelled and the zonal trip productions derived from call detail record (CDR) data, while in terms of the disaggregate fit, we seek to ensure that the model parameters represent the genuine sensitivities of individuals in the population. The framework is calibrated and tested in the context of trip generation models.
In the context of trip generation, the traditional models based on household survey data establish the mathematical relationship between the number of trips made by an individual or household with the socio-demographics (see Bwambale et al. 2015 and the cited references). But the household survey data is prone to under-reporting of the number of trips (e.g. Zhao et al. 2015; Stopher et al. 2007; Itsubo and Hato 2006). Aggregating models based only on household survey data for estimating the zonal travel patterns can lead to errors, with serious consequences for the different steps of the four-stage model. This prompts us to investigate various ways of adjusting the parameter scales of the traditional trip generation model by using a joint optimisation process to combine it with the trip patterns derived from the mobile phone data. We adopt a joint optimisation approach because CDR data too is inherently noisy, and thus not error-free. Given the lack of knowledge about which datasource really represents the ground truth, it would also be unrealistic to benchmark one dataset over the other.
In the proposed joint modelling framework, the base trip generation model is first estimated using household travel survey data alone to obtain the parameter priors (i.e. the sensitivities). The parameter scales are then adjusted in three different approached (without changing the prior parameter signs). The joint models hence explain the reported trips for each individual in the household survey data and ensure that the aggregated zonal trip productions are close to those derived from CDR data. This ensures that the joint models do not lose the travel behaviour sensitivities reflected in the household survey data and is computationally tractable.
The rest of the paper is organised as follows, “Literature review” section presents a brief review of the literature, “Data” section presents the data used in this study, “Modelling framework” section presents the modelling framework, “Modelling results” section presents the model results, and “Summary and conclusions” section presents the summary and conclusions of the study.
Literature review
This section presents a brief review of the literature on related work in applying mobile phone data to trip generation and other mobility studies, as well as an overview of different population synthesis techniques.
Previous applications of mobile phone data to trip generation
The estimation of trip generation from CDR data remains a challenging area of research, with only one study so far covering this subject to the best of our knowledge (Çolak et al. 2015). This is mainly due to the spatio-temporal discontinuities in the data as it only reports mobile phone positions associated with calls (voice, message, data), thereby making it difficult to capture movements when the phone is not in use. Çolak et al. (2015) attempt to address the issue of missed movements to and from the home location by introducing a home-based trip where the first or the last reported position of the day in the CDR data is at a non-home location. Although this partly addresses the problem, the challenge still remains as several other home-based trips made during the day can be missed if the mobile phone is not in use. Nonetheless, it is important to note that CDR data is likely to become more reliable in the near future with the increasing use of apps by means of mobile internet data services (Gerpott and Thomas 2014), which will increase the frequency of recorded mobile phone positions, thereby reducing the spatio-temporal discontinuities in the data. Besides CDR data, trip generation has also been previously estimated from GSM data, which is more continuous compared to CDR data (e.g. Bwambale et al. 2019). However, GSM data remains rare as it is typically not stored by mobile network operators due to storage space constraints.
Related studies on mobile phone data and population synthesis
The availability of large-scale mobile phone data over the last few decades has motivated a lot of research in quantifying human mobility and activity patterns using synthetic data generation methods (e.g. Chen et al. 2014).
From an epidemiology perspective, Vogel et al. (2015) combined CDR data with synthetic populations to model the spread of Ebola in West African countries and obtained promising results with respect to the Ebola predictions of the Centre for Disease Control and Prevention (CDC). Still in West Africa, Cárcamo et al. (2017) developed an intelligent epidemiology simulation software based on synthetic populations made up of agents with realistic travel behaviour derived from CDR data. In France, Panigutti et al. (2017) compared the spread of a simulated epidemic using CDR and census survey travel patterns, finding greater similarity in areas with high population and connectivity, potentially due to the higher calling rates.
In the field of transport, Zilske and Nagel (2014) generated artificial CDR data from synthetic passengers in a simulated traffic scenario and re-used the data to approximate the amount of missed traffic at different calling rates to quantify the error introduced by CDR location discontinuities. The study found that the errors were inversely proportional to the calling rates and proposed scaling procedures based on observed data such as traffic counts. This led to a subsequent study where simulated CDR data and a synthetic population were combined with link traffic counts to generate all-day trip chains (Zilske and Nagel 2015). This study found that even highly biased CDR data could reasonably reproduce the traffic state across different time periods. This approach of using observed traffic counts to scale CDR data has also been tested in Dhaka in the context of transient origin–destination (OD) matrix estimation (Iqbal et al. 2014).
Calabrese et al. (2011) developed a methodology to determine the origin–destination flows utilising 829 million mobile phone locations data for 1 million devices. Those mobile phone locations data were generated using the cell tower triangulation algorithm and have a lower resolution and higher uncertainty compared to GPS data. Data of this type was the primary source of location data for Location Based Services (LBS) before smartphones began to acquire a significant share of the mobile phone market. In the case of a smartphone, location data can also be collected through different smartphone applications that use the phone’s GPS technology, WAP data, and user-provided information (Rao and Minakakis 2003; Huang et al. 2018). Therefore, smartphone LBS data provide more details (with higher resolution, and higher frequency) footprints of the user’s activities. However, the penetration rate of such application data is very low compared to CDR data. Several studies have used LBS data from different sources to implement it in transportation engineering applications. Some of the applications include travel data collection (Greaves et al. 2015; Safi et al. 2015, 2016; Patterson and Fitzsimmons 2016; Xiao et al. 2016), activity analysis (Xiao et al. 2012; Zhou et al. 2016), travel behaviour analysis (Vlassenroot et al. 2015; Ferrer López and Ruiz Sánchez 2014; Deutsch et al. 2012), and travel mode detection (Zhou et al. 2016; Wu et al. 2016; Shin et al. 2015).
Still in the field of transport, population synthesis has been applied on real-world mobile phone datasets. Ros and Albertos (2016) updated MATSim (an agent-based multi-simulation software) by fusing census and CDR data from Spain to generate synthetic populations with mobility patterns observed in the CDR data. It may be noted that in this particular case, the mobile operator also provided the age and the gender of the users, which ensured a reliable dependence structure between the travel patterns and socio-demographics in the final synthetic population. However, mobile phone data is usually anonymous, which makes direct socio-demographic linkage impossible. In our earlier work (Bwambale et al. 2019), we developed a demographic group prediction model based on mobile phone usage behaviour extracted from CDR data (as part of a latent class model for trip generation), and can potentially be used for generating synthetic populations, however, this also requires a sub-sample of CDR data with known demographics, which is rarely available.
Kressner (2017) combined consumer and anonymous mobile phone data (wireless signalling and GPS data) from the United States to generate synthetic individual-level trip diaries. The socio-demographics in the disaggregate consumer data were benchmarked against the marginal census totals, while the synthetic travel was benchmarked against the mobility patterns extracted from the aggregate mobile phone data of several operators. Although this approach performed quite well in terms of aggregate-level validation, the disaggregate dependency structure between the individual’s socio-demographics and trips could be seen as arbitrary. Zhang (2018) proposed an integrated model using Exponential Random Graph and Bayesian approaches to combine HHS and CDR data to generate a synthetic ‘connected’ population. The proposed model aims to reproduce the marginal and joint distributions of individuals and household level socio-economic characteristics, a geographical pattern of the observed community structure, and the statistics of the observed social network.
To maintain the underlying dependence structure between the individual’s socio-demographics and trips, Janzen et al. (2017) combined household travel survey data, register data (national statistics) and CDR data from France to correct the under-reporting of long-distance trips in travel surveys using population synthesis techniques. The socio-demographics in the travel survey data were matched against those in the register data, while the reported long-distance trips in the travel survey data were matched against those derived from the CDR data. However, a potential issue with this approach is that it assumes uniform under-reporting for all the respondents in the travel survey data, and yet this might vary, at least across different demographic groups, with some cases of over-reporting. Furthermore, the assumed higher reliability of CDR data versus travel survey data is contentious and needs to be approached impartially. This is why we propose an optimisation approach between the two datasets.
Existing methods of population synthesis
Population synthesis is widely applied in activity-based models, and various techniques have been proposed to do this. This section presents a brief review of these methods.
The most widely applied technique is iterative proportional fitting (IPF), which works by fitting a contingency table based on disaggregate survey data to the marginal totals in aggregate census data, constrained by a set of control variables (Beckman et al. 1996). Since its development, various improvements based on the original concept have been proposed to enhance its applicability to new challenges. These improvements have mainly focussed on addressing the zero-cell problem (Guo and Bhat 2007), simultaneous control of household and individual-level attribute distributions (Casati et al. 2015; Zhu and Ferreira Jr 2014; Ye et al. 2009; Guo and Bhat 2007), improving the computational speeds (Pritchard and Miller 2012), and non-integer conversion to integers (Choupani and Mamdoohi 2015) etc.
Another popular technique is combinatorial optimisation, which focusses on selecting a subset of households in the disaggregate sample data that closely fit the marginal distributions in the census data for the same area (Voas and Williamson 2000). This is done by randomly selecting an initial subset of households from the sample data, and iteratively replacing these with those remaining in the sample data, if and only when this leads to improvements in the fit of the subset. Although this approach has been reported to be superior (Ryan et al. 2009), the IPF method remains the most popular due to its low data requirements, reliability, and faster optimisation (Choupani and Mamdoohi 2015; Sun and Erath 2015).
Besides the two methods above, other techniques have been proposed including, the sample-free method (Barthelemy and Toint 2013), Markov chain Monte Carlo simulation (Farooq et al. 2013), and the Bayesian network framework (Sun and Erath 2015), among others.
Data
This section describes the study area, the data used, and the data processing conducted prior to model estimation. The study combines different data types (i.e. household travel survey data, census data, and CDR data) collected at different times between 2009 and 2012. Despite this limitation, these periods are considered close enough to facilitate cross-comparison.
Data description
Study area
The study location is Dhaka Metropolitan Area (DMA) in Bangladesh. The area covers approximately 303 square kilometres and is one of the world’s most crowded places with a population density of 30,551 persons per square kilometre (BBS 2013). Due to the high population density, the cell tower density is also very high. The area is served by 1361 towers, with most these located in the central business district. The average tower-to-tower distance is approximately 1 kilometre (Iqbal et al. 2014). The total daily trip production from DMA residents was approximately 20.8 million in 2010, with 85.46% of these being home-based (JICA 2010).
CDR data
The CDR data used in this study was provided by Grameenphone Ltd and covers the working days (i.e. Mondays to Thursdays) between 24 June 2012 and 07 July 2012 (2 weeks). The dataset contains information from 6.9 million anonymous users representing about 57% of the population (BBS 2012), who together generated over 600 million records during this period An excerpt of the randomised CDR data is presented in Table 1, where the location information refers to tower positions as opposed to triangulated positions.
Household travel survey data
The household travel survey data used was collected between March 2009 and March 2010 as part of the Dhaka Urban Transport Network Development Study (JICA 2010). The sampling of households in each zone was based on the population shares at a rate of approximately 1%. The total sample covers 67,461 individuals and 17,270 households, representing an average household size of approximately four persons. The collected information includes each individual’s socio-demographic details (e.g. gender, age, working status, income, household size and housing type) and a single day trip diary. Table 2 presents the summary statistics of the data.
Census data
The 2011 Bangladesh Population and Housing Census data was used (BBS 2012). The Census was conducted from 15 to 19 March 2011. The available data reports the aggregate totals of the selected person and household level attributes at different geographical scales [e.g. village, ward, and zone (Thana)].
Since we could not access the detailed census data due to privacy reasons, we used population synthesis techniques (Ye et al. 2009) to generate realistic artificial populations for the different study area zones by combining the aggregate census data with the household survey data as explained later in “Population synthesis” section.
It may be noted that the fusion of household survey data and census data could only be done at the zone (Thana) level due to differences in the study area delimitations at smaller geographical scales. The variables available in both datasets are summarised in Table 3.
Data processing and combination
General concept
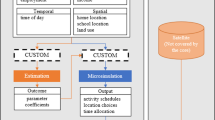
Figure 1 presents a summary of the data processing framework. The subsequent sections discuss the key aspects of this framework.
The overarching idea is to minimise the difference between the zonal trip productions derived from CDR data and those obtained by aggregating the disaggregate trip generation model, without compromising the behavioural sensitivities reflected in the household survey data. Model aggregation is based on a synthetic population generated using the Iterative Proportional Updating technique (Ye et al. 2009).
Population synthesis
Among the various software applications for population synthesis, we used PopGen (Ye et al. 2009), which is capable of conducting Iterative Proportional Updating (IPU). This algorithm simultaneously controls for both the person and the household-level attribute distributions during the fitting procedure, and has been proven to perform better than the simpler synthesis methods.
As seen in Fig. 1 (top left), the algorithm relies on two raw datasets, the household survey data and the zone level aggregate census data to generate the zone-specific synthetic populations by means of IPU. The household and individual level control variables used in the IPU process are presented in Tables 4 and 5 respectively. It may be noted that we did not use the individual’s occupation as there are differences in the definitions of the categories used in the household survey and the census data.
Figure 2 presents the distribution of the Average Absolute Relative Differences (AARD)Footnote 1 across the zones. This metric gives the mean deviation of the person weighted sums with respect to the household and person aggregate census totals (the constraints). As observed, the AARD values for most zones are concentrated in the lower ranges of the axis, an indication that the population synthesis was successful.
Furthermore, comparisons of the synthetic versus the actual estimates for each attribute at the person and the household levels are presented in Figs. 3 and 4 respectively, where the distributions are observed to have a close match.
Extraction of unscaled zonal trip productions from CDR data
The CDR data for the entire observation period was first analysed to identify each user’s home location, which was defined as the most frequently observed cell tower at night (i.e. between 8 pm and 6 am). The labelled cell towers (i.e. home/others) for each user were then arranged according to the date and observation timestamp.
Home-based trips were extracted by considering any two consecutive CDR events from different cell towers, with one of those being the home cell tower. From the CDR data, we can note the distance between adjacent towers varies between 0.02 and 7.00 kilometres. Most areas of Dhaka are densely populated and about 75% of the towers have an adjacent distance of less than 0.5 kilometres (90% have an adjacent distance of less than 1 kilometre). Furthermore, a previous study in Dhaka found that the mean walking trip distance is about 0.45 km (JICA 2010). Therefore, a lower distance threshold of 0.5 km between subsequent towers was considered as the optimum for minimising the number of very short trips within the neighbourhood and false trips due to tower jumps.Footnote 2
An upper threshold of 24 h or midnight (whichever came first) was specified based on the assumption that a user typically travels from and back to home within the same effective day. Consequently, if the first and the last CDR events for the day were not at the home cell tower, corresponding raw trips were added (Çolak et al. 2015). This led to the unscaled zonal trip productions shown in Fig. 1.
Scaling the CDR trip productions
The home cell towers derived from the CDR data were mapped to the zones with the aid of a GIS software (QGIS Development Team 2018). The total trips for each zone were then scaled using the ratio of the zonal population (from the census) to the number of users classified as residents of the zone from the CDR data (see Çolak et al. 2015 for details). We however acknowledge that this straight scaling procedure may bias the results if the CDR data sample is biased, for example in terms of the socio-economic status of the mobile phone owners.
Modelling framework
We propose an approach that combines two modelling strategies, that is, discrete choice modelling at the individual level and ordinary least squares at the aggregate level (shown in patterned text boxes in Fig. 1).
Disaggregate trip generation model (base model)
Trip generation has been found to be affected by household characteristics (e.g. household size, income, car-ownership, etc.) and composition (e.g. numbers of children, employed people, etc.) (see Bwambale et al. 2015, 2019 for details). Discrete choice models have been the most preferred approach for modelling trip generation over the last few decades (e.g. Bwambale et al. 2015; Pettersson and Schmöcker 2010; Agyemang-Duah and Hall 1997). Although the ordered response choice mechanism has been the most preferred approach for modelling trip generation, the method was intractable in this particular study where model performance is being optimised at both the aggregate and disaggregate levels through scaling as discussed later in this paper. While less appealing from a theoretical point of view, the unordered response choice mechanism was found to be a more feasible approach and was adopted. It is important to note that the unordered response choice mechanism has been found to give intuitive results even in contexts with ordered choices such as car ownership (Bhat and Pulugurta 1998).
To implement the unordered response choice mechanism, we rely on the random utility theory (Marschak 1960). Let \(U_{nt}\) be the utility of individual \(n\) making \(t\) trips. This can be expressed as;
where \(X_{n}\) is a vector of the socio-demographic attributes of individual \(n\), \(\beta_{t}\) is a vector of the model parameters to be estimated, and \(\varepsilon_{nt}\) is the random component of utility. Since the individual socio-demographics are constant across the alternatives, we specify a different set of parameters for each trip generation level to reflect the fact that each attribute has a differential impact on the utility for each trip generation level.
Under the assumption that the error terms \(\left( {\varepsilon_{nt} } \right)\) are distributed independently and identically across alternatives and individuals using a type I extreme value distribution, the trip generation choice probabilities can be calculated using the multinomial logit (MNL) model (McFadden 1974) as expressed below;
where \(P_{nt}\) is the probability of individual \(n\) making \(t\) trips.
Despite the requirements of the MNL model, it may be noted that the error terms are not likely to be independent in the real world.
If we were to rely on the household travel survey data alone, the model parameters would be estimated by maximising the log-likelihood function below.
where the dummy variable \(K_{nt} = 1\) if and only if individual \(n\) makes \(t\) trips, otherwise \(K_{nt} = 0\).
However as mentioned earlier, fitting the model to match the trips reported in the household travel survey data alone can lead to biased parameter estimates due to reporting errors, thereby resulting in misrepresentation of the aggregate travel demand as reflected in Fig. 5, where the predicted aggregate zonal trips from the base model are different from those derived from the CDR data, especially towards the right hand side of the figure.
The relative absolute errors derived from Fig. 5 were plotted on a map to check whether there is a spatial correlation to the errors as shown in Fig. 6.
From Fig. 6, it is observed that there is no obvious spatial correlation to the errors. The magnitude of the error is largest in a single central zone. But apart from that, larger magnitudes are observed both in the centre of the metropolitan area, as well as, in some outskirt areas. For the centre, the errors are most likely caused by the relatively high number of either false trips in the CDR data (due to the high tower density) or unreported short walking trips in the household survey data, while for the outskirts, the errors are most likely caused by the missed short trips that could not be captured by the CDR data due to the low tower density in those areas.
Joint trip generation model
The priors of the parameter signs and relative magnitudes are obtained from the pre-estimated base model. The parameter scales are then adjusted (without changing the prior parameter signs). The joint model thus simultaneously optimises performance at both the aggregate and disaggregate levels with respect to the CDR and the household travel survey data, respectively.
As mentioned earlier, this combined approach ensures that the resulting model does not lose the travel behaviour sensitivities reflected in the household travel survey data, by maintaining the sensitivities from the base model. Adjusting the parameter scales has an impact on the choice probabilities for each trip generation outcome, which influences the expected trip rates of the individuals. The framework of the joint trip generation model is described below. Let \(\hat{U}_{nt}\) be the updated utility of individual \(n\) making \(t\) trips. This can be expressed as;
where \(\alpha\) is a vector of the scaling factors to be estimated. The \(\beta\) parameters are priors derived from the base model, and are not re-estimated in the joint framework. The specification of the scaling factors is discussed later on.
The updated trip generation choice probability can be expressed as follows;
where \(\hat{P}_{nt }\) is the updated probability of making \(t\) trips by individual \(n\).
However, to estimate the scaling factors, we need to fulfil two objectives. The first objective is to explain the reported trips for each individual in the household survey data. The second objective is to ensure that the aggregated zonal trip productions are close to those derived from CDR data. Both outcomes have a probability attached to them and the simultaneous estimation maximises the joint probability of the two outcomes.
To estimate the aggregate zonal trip productions, we rely on the synthetic population generated in “Population synthesis” section. As mentioned earlier, the synthetic population was designed to match both the person and the household-level attribute distributions during the fitting procedure, thus making it more reliable. We have a synthetic population of \(M\) simulated individuals identified as \(m\) with \(m = 1, \ldots , M\), and a study area made up of \(Z\) zones identified as \(z\) with \(z = 1, \ldots , Z\). Let \(\hat{P}_{mt}\) denote the updated probability of making \(t\) trips by simulated individual \(m\). It may be noted that \(\hat{P}_{mt}\) is equivalent to \(\hat{P}_{nt}\) if both the simulated individual and the actual respondent in the household survey data have the same demographics (i.e. the values of \(\hat{P}_{mt}\) depend on the calculations of \(\hat{P}_{nt}\)). Now, let \(\hat{T}_{z}\) denote the aggregate zonal trip production for zone \(z\). This can be calculated by taking the weighted average trips for each simulated individual, in which the updated MNL probabilities are the weights, and summing across the zonal synthetic population as follows;
where the dummy variable \(Y_{mz} = 1\) if and only if simulated individual \(m\) belongs to zone \(z\), otherwise, \(Y_{mz} = 0\). The objective is to ensure that \(\hat{T}_{z}\) is as close as possible to the corrected CDR trip productions for zone \(z\). If \(\varphi_{z}\) denotes the corrected CDR trip productions for zone \(z\), the relationship between \(\varphi_{z}\) and \(\hat{T}_{z}\) can be expressed as follows;
where \(\omega_{z}\) is an error term which we assume follows a normal distribution with a mean of zero, \(\omega_{z} \sim N\left( {0,\sigma^{2} } \right)\). \(P(\varphi_{z} )\) is then the likelihood of observing the CDR trip productions for zone \(z\), and, from Eq. 7, this can be expressed as follows;
\(P(\varphi_{z} )\) clearly depends on \(\hat{P}_{nt}\) given that \(\hat{T}_{z}\) is a function of \(\hat{P}_{mt}\), which depends on the calculations of \(\hat{P}_{nt}\) as explained earlier. For each survey respondent in zone \(z\), we need to maximise the probability of the chosen alternative and ensure that the probabilities of all the alternatives maximise \(P(\varphi_{z} )\). Let \(t_{n}^{o}\) denote the number of trips observed for individual \(n\) in the household survey data, such that \(\hat{P}_{{nt^{o} }}\) gives the logit probability of the observed choice for individual \(n\). The overall joint likelihood \(\left( L \right)\) of the observed choices and the aggregate CDR trip productions across individuals is calculated as follows;
where the dummy variable \(H_{nz} = 1\) if and only if survey respondent \(n\) belongs to zone \(z\).
This is based on the assumption that \(\hat{P}_{nt}\) and \(P(\varphi_{z} )\) are independent. This is not unreasonable given the sources of potential errors are very different (reporting errors in case of the HHS and coarse resolution in case of the CDR) and there is no obvious source of correlation among the two probabilities. Since products are difficult to differentiate, we obtain the log-likelihood \(\left( {LL} \right)\) by applying logarithms to Eq. 9 resulting in Eq. 10.
Three parameter scaling scenarios are tested, and these are;
Model 1 | This specification applies the same \(\alpha\) scaling factor to the utility models of the different trip generation levels (see Eq. 4), i.e. \(\alpha_{t} = \alpha , \forall t\). The updated utility models have the same relative variable sensitivities as in the base model, albeit with different parameter scales |
Model 2 | This specification applies a different \(\alpha_{t}\) scaling factor to the utility model of each trip generation level. The updated utility models maintain the base model relative variable sensitivities for each particular trip generation level, however, the variable sensitivities across the different trip generation levels are adjusted with different parameter scales, and hence the relative values across levels change from the base model |
Model 3 | This specification applies a different \(\alpha_{x}\) scaling factor to each explanatory variable \(X\) (e.g. gender, age-group, and working status), however, \(\alpha_{x}\) does not change across the different trip generation levels. The updated utility models maintain the base model attribute-level relative sensitivities for a particular variable across the different trip generation levels, however, the inter-variable relative sensitivities are adjusted with different parameter scales |
Model evaluation framework
The performance of the joint models is evaluated in terms of both the temporal and the spatial transferability as presented in Figs. 6 and 7, respectively.
In terms of temporal transferability, the joint models associated with each parameter scaling scenario are estimated using the zonal aggregate CDR trip productions for week 1. The prediction capacities of the estimated joint models, as well as the base model are then compared in terms of the root mean square errors with respect to the zonal aggregate CDR trip productions for week 2 (see Fig. 7).
In terms of spatial transferability, the study area zones are randomly divided into two groups. The base and the joint models are then estimated using the data for one group of zones and applied to the other group of zones (not used for estimation). The prediction capacities of the models are then compared in terms of the predictive joint log-likelihoods, and the root mean square errors with respect to the aggregate CDR trip productions of the application zones (see Fig. 8).
Modelling results
This section presents the final model specification, as well as the model estimation and validation results.
Variable specification
The dependent variable is the number of individual home-based trips (irrespective of the trip purpose). This is because we could not reliably infer the purposes of the CDR trips. Based on distributions in the data, the trip generation levels were grouped into 0, 1–2, 3–4, and 5 + trips per day. The explanatory variables considered for possible inclusion in the model are those that were used for population synthesis. The household-level variables (i.e. household size and type) were however not included in the final model as they led to unreasonable parameter signs, potentially due to their weak influence on individual trip-making decisions.Footnote 3 The final model specification thus contains the gender, the age-group, and the working status of the individuals, coded as dummy variables.
For model identification purposes, the parameters associated with the zero trip generation level were treated as the base (for all explanatory variables). Furthermore, male non-workers in the 30–49 age-group were treated as the base demographic group, and their preferences are entirely explained by the alternative specific constants. Thus, the model parameter estimates represent the differential impact on utility with respect to the zero trip generation level and the base demographic group.
Estimation results
Base model
We first estimated the base model to assess whether the parameter estimates are in line with the expected travel behaviour. The model results are presented in Table 6.
The alternative specific constants capture the underlying differential impact on utility with respect to the zero trip generation level. All the estimates are negative, and their magnitude increases with respect to the trip generation level. Keeping all other factors constant, this reflects a general tendency to make fewer trips, especially by the base category (i.e. male, non-workers, aged 30–49 years).
The parameter estimates for females represent the differential impact on utility with respect to males. For 1-2 trips, we obtain a positive parameter estimate, while for the higher trip generation levels, we obtain negative parameter estimates. The proportion of women working in the garments industry, one of the leading sectors in Dhaka, is 64–90% (ADB and ILO 2016). This probably explains the positive parameter sign for 1–2 trips. Otherwise, males are more likely to make a higher number of trips compared to females, probably due to the average higher income levels of the former (BBS 2012) and socio-cultural factors.
The parameter estimates for the working status variables (i.e. workers and students) represent the differential impact on utility with respect to non-workers. As observed, the parameters for workers are positive, and their magnitudes increase with respect to the trip generation level, an indication that workers generally make more trips compared to non-workers. On the other hand, the parameter estimates for students are positive for 1–2 and 3–4 trips, and negative for 5 + trips. This shows that students make more trips compared to non-workers only up to a reasonable level expected for school going individuals.
Similarly, the parameter estimates for the age-group variables represent the differential impact on utility with respect to the 30–49 years age-group. As observed, the parameter estimates for all the other age-groups are negative, an indication that they generally make fewer trips compared to the base age-group (30–49 years). The active working age of white-collar workers in Bangladesh typically ranges between 29 and 60 years (i.e. the latest age for completing tertiary education and the retirement age respectively (BBS 2012)). It is therefore reasonable that persons in the 30–49 years age-group are more active travellers due to their economic vibrancy.
Finally, it is observed that the overall model (in terms of the likelihood ratio), as well as all the parameter estimates (in terms of the t-statistics) are statistically significant at the 99% level of confidence (see Ben-Akiva and Lerman 1985 for details).
Joint models
As earlier mentioned, the parameters of the base model were fixed in the joint modelling framework, and only the scaling factors were estimated. Table 7 presents the estimated scaling factors and the measures of fit for all the three models for comparison purposes. Positive scaling factors were obtained for all the three models, an indication that the resultant coefficients in the scaled joint models have the same signs as those in the base model.
A comparison of the joint convergence log-likelihoods shows that Model 3 gives the best performance, followed by Model 2, and then Model 1. This is attributed to the flexibility of the parameter scaling framework. An important point to note is that all the three joint models perform better than the base model in terms of the joint log-likelihood.
As earlier mentioned, during model optimisation, we are basically dealing with a trade-off between disaggregate and aggregate model performance. Thus, the disaggregate log-likelihood of the joint models is a little worse than that of the base model. However, if the base model parameters are directly used to estimate the joint log-likelihood, it is observed that the model yields the worst performance.
The p-values of the likelihood ratios of the joint models with respect to the base model are all less than 0.01, an indication that the improvements in performance are statistically significant at the 99% confidence level beyond the advantages offered by the additional parameters (see Ben-Akiva and Lerman 1985 for details).
Model evaluation in terms of transferability
The models based on the full sample have been presented in the previous section. To evaluate the stability and the predictive performance of the joint models as well as the base model, we compared their temporal and spatial transferability following the evaluation framework described in “Model evaluation framework” section. Tables 8 and 9 present the measures of fit in terms of the temporal and the spatial transferability, respectively.
From Table 8, it is observed that the temporal transferability of the joint models is generally higher than that of the base model in terms of the joint log-likelihoods and the root mean square errors (RMSE) with respect to the zonal CDR trips. Among the three joint models, Model 3 offers the best transferability, however, Model 2 gives the best prediction at the disaggregate level in both the estimation and the application contexts.
For spatial transferability, we tested both directions of model transfer. It may be noted that the general interpretation of the base model parameters for each group of zones did not change. From Table 9, it is again observed that the joint models are generally more transferrable compared to the base model in terms of the joint log-likelihoods and the root mean square errors for both directions.
In this particular case, it is observed that Model 2 gave the best disaggregate prediction for the zone group 1–2 transfer direction, while Model 1 gave the best disaggregate prediction for the reverse transfer direction.
An important point worth mentioning is that the superior performance of the base model at the disaggregate level is expected as it was designed to fit the travel survey data alone, but as mentioned earlier, this could be prone to reporting errors and hence less dependable.
From the results, it is clear that Model 3 gives the best overall spatial and temporal transferability, however, the disaggregate performance of Models 1 and 2 as highlighted above shows that these parameter scaling approaches offer some benefits as well. These results present initial efforts to exploit the benefits of both household travel survey and mobile phone data to optimise the performance of travel behaviour models, and there is a need for further research using data from different contexts to investigate the different parameter scaling approaches in further detail.
Model comparison in forecasting
To test the sensitivity of the models to forecasting, the base model and the different joint models have been applied to the 2019 household survey data and the predictive measures of fit for the different models have been compared. The following three performance indicators have been used in this regard:
-
Root Mean Square Error (RMSE), which has been obtained by comparing the modelled and the actual total trip productions associated with the 2019 sample data for each TAZ using the base and joint model parameters (pre-estimated using the 2010 data).
-
Average probability of correct prediction, which has been obtained by computing the mean probability of success for the 2019 sample data using the pre-estimated base and joint model parameters (pre-estimated using the 2010 data).
-
The predictive adjusted-rho square, which has been obtained using the adjusted rho-square equation below for the pre-estimated base and the joint models;
where \(k\) is the number of model parameters, \(LL\left( F \right)\) and \(LL\left( 0 \right)\) are the values of the log-likelihood function at convergence and at zero respectively.
Table 10 summarises the calculated predictive measures of fit on the 2019 forecasting sample for the base model and the different joint models.
From Table 10, it is observed that overall the joint models generally perform better than the base model in forecasting at both the aggregate and disaggregate levels. Among the three joint models, it is observed that Model 3 gives the best performance in terms of both the Root Mean Square Error and the average probability of correct prediction, while giving the least performance in terms of the predictive adjusted rho-square. However, from a forecasting point of view, aggregate performance is more critical, and Model 3 would offer more benefits.
Summary and conclusions
This paper started by highlighting the reporting errors and sampling bias associated with household travel survey data, and how these could lead to biased model parameters (e.g. Rolstad et al. 2011; Groves 2006). The paper outlines the possible consequences of such issues in the context of trip generation, where the estimated models would misrepresent the distribution of the aggregate travel demand across zones.
Although traditional travel surveys are increasingly being replaced by smartphone based surveys, which alleviate the issue of misreporting of trips, issues with sample representativeness and size remain, as well as the issue of encouraging respondents to provide a sufficiently long stream of data. On the other hand, while mobile phone call detail record (CDR) data is widely available, large in size and more representative, it is lacking information on core causal variables.
The paper demonstrates the feasibility of a joint modelling framework to find the best fit at the joint level (i.e. between the aggregate and disaggregate levels) by combining household travel survey, census, and CDR data. The census data is crucial in creating a bridge between the two other data sources. The joint modelling framework operates by adjusting the parameter scale(s) of a pre-estimated base model to jointly optimise the prediction accuracy with respect to the reported trips in travel survey data and the zonal aggregate trip productions derived from CDR data. Three different approaches of parameter scaling were investigated (i.e. uniform, alternative specific, and variable specific scaling corresponding to joint models 1, 2, and 3 respectively). All the three joint models were found to have higher temporal and spatial transferability, as well as better forecasting performance compared to the base model which relies on household travel survey data alone, thus making them more reliable. Although variable specific scaling (Model 3) produced the best overall results, there is a need for further research using data from different contexts to investigate if this finding is universally applicable. In particular, in this case, we did not have any independent measure to confirm that either of the data represented the ground truth which prompted us to give equal weight to the two types of data. This may not be the case in all contexts. More work is also needed on how to specify the joint likelihood combining the information from the two types of data and investigating the impact of the distribution of the error term, potential spatial correlation, etc.
Although the proposed framework has been tested in the context of trip generation, it has potential benefits in improving the modelling of the other transport choices (such as mode choice, route choice, departure time choice etc.). We conclude that the results of this study serve as a proof-of-concept that mobile phone data can be fused with traditional data sources to improve the temporal and spatial transferability of models. This approach is particularly important in the context of developing countries where reliable traditional data sources are scarce, and models making use of low-cost passive data to enhance their temporal and spatial transferability are invaluable.
Notes
\(AARD = \frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \frac{{\left| {w_{i} - c_{i} } \right|}}{{c_{i} }}\)
where \(c_{i}\) is the \(i{\text{th}}\) household or person-level constraint obtained from the census data (e.g. the number of men, women, and households by household size etc.), \(w_{i}\) is the weighted frequency of persons with the \(i{\text{th}}\) attribute in the generated synthetic population, and \(N\) is the total number of constraints.
A false trip occurs when the user is not making a trip but there is a change in the tower as the operator reassigns the call to a different tower (due to load management purposes).
The larger household sizes in Dhaka can often be attributed to the number of support staff members (e.g. cooks, cleaners, gardeners, housekeepers etc.) who stay and work full-time in the household. This is a potential contributing factor to the weak correlation between the numbers of people in a household and trip generation, which we appreciate is different in a more European/North American context.
References
ADB & ILO: Bangladesh: looking beyond garments: Employment diagnostic study. Asian Development Bank and International Labour Organization, Manila (2016)
Agyemang-Duah, K., Hall, F.L.: Spatial transferability of an ordered response model of trip generation. Transp. Res. Part A Policy Pract. 31, 389–402 (1997)
Barthelemy, J., Toint, P.L.: Synthetic population generation without a sample. Transp. Sci. 47, 266–279 (2013)
BBS: Community Report: Dhaka Zila: June 2012. Population and Housing Census 2011. Bangladesh Bureau of Statistics (BBS), Dhaka (2012)
BBS: District Statistics 2011 Dhaka. Bangladesh Bureau of Statistics, Dhaka (2013)
Beckman, R.J., Baggerly, K.A., Mckay, M.D.: Creating synthetic baseline populations. Transp. Res. Part A Policy Pract. 30, 415–429 (1996)
Ben-Akiva, M.E., Lerman, S.R.: Discrete Choice Analysis: Theory and Application to Travel Demand. MIT Press, Cambridge (1985)
Bhat, C.R., Pulugurta, V.: A comparison of two alternative behavioral choice mechanisms for household auto ownership decisions. Transp. Res. Part B Methodol. 32, 61–75 (1998)
Bwambale, A., Choudhury, C.F., Sanko, N.: Modelling car trip generation in the developing world: the tale of two cities. In: Transportation Research Board 94th Annual Meeting (2015)
Bwambale, A., Choudhury, C.F., Hess, S.: Modelling trip generation using mobile phone data: a latent demographics approach. J. Transp. Geogr. 76, 276–286 (2019)
Calabrese, F., Di Lorenzo, G., Liu, L., Ratti, C.: Estimating origin-destination flows using mobile phone location data. IEEE Pervasive Comput. 4, 36–44 (2011)
Cárcamo, J.G., Vogel, R.G., Terwilliger, A.M., Leidig, J.P., Wolffe, G.: Generative models for synthetic populations. In: Proceedings of the Summer Simulation Multi-Conference, 2017. Society for Computer Simulation International, 7 (2017)
Casati, D., Müller, K., Fourie, P.J., Erath, A., Axhausen, K.W.: Synthetic population generation by combining a hierarchical, simulation-based approach with reweighting by generalized raking. Transp. Res. Rec. 2493(1), 107–116 (2015)
Chen, C., Bian, L., Ma, J.: From traces to trajectories: how well can we guess activity locations from mobile phone traces? Transp. Res. Part C Emerg. Technol. 46, 326–337 (2014)
Choupani, A.A., Mamdoohi, A.R.: Population synthesis in activity-based models: tabular rounding in iterative proportional fitting. Transp. Res. Rec. 2493(1), 1–10 (2015)
Çolak, S., Alexander, L.P., Alvim, B.G., Mehndiretta, S.R., González, M.C.: Analyzing cell phone location data for urban travel: current methods, limitations and opportunities. In: Transportation Research Board 94th Annual Meeting (2015)
Deutsch, K., McKenzie, G., Janowicz, K., Li, W., Hu, Y., Goulias, K.: Examining the use of smartphones for travel behavior data collection. In: The 13th International Conference on Travel Behavior Research Toronto, Toronto (2012)
Farooq, B., Bierlaire, M., Hurtubia, R., Flötteröd, G.: Simulation based population synthesis. Transp. Res. Part B Methodol. 58, 243–263 (2013)
Ferrer López, S., Ruiz Sánchez, T.: Travel behavior characterization using raw accelerometer data collected from smartphones. Procedia Soc. Behav. Sci. 160, 140–149 (2014)
Gerpott, T.J., Thomas, S.: Empirical research on mobile internet usage: a meta-analysis of the literature. Telecommun. Policy 38, 291–310 (2014)
Greaves, S., Ellison, A., Ellison, R., Rance, D., Standen, C., Rissel, C., Crane, M.: A web-based diary and companion smartphone app for travel/activity surveys. Transp. Res. Procedia 11, 297–310 (2015)
Groves, R.M.: Nonresponse rates and nonresponse bias in household surveys. Public Opin. Q. 70(5), 646–675 (2006)
GSM Association: The mobile economy 2017 [Online]. https://www.gsmaintelligence.com/research/?file=9e927fd6896724e7b26f33f61db5b9d5&download (2017). Accessed 04 Nov 2017
Guo, J.Y., Bhat, C.R.: Population synthesis for microsimulating travel behavior. Transp. Res. Rec. 2014(1), 92–101 (2007)
Huang, H., Gartner, G., Krisp, J.M., Raubal, M., Van de Weghe, N.: Location based services: ongoing evolution and research agenda. J. Locat. Based Serv. 12(2), 63–93 (2018)
Iqbal, M.S., Choudhury, C.F., Wang, P., González, M.C.: Development of origin–destination matrices using mobile phone call data. Transp. Res. Part C Emerg. Technol. 40, 63–74 (2014)
Itsubo, S., Hato, E.: Effectiveness of household travel survey using GPS-equipped cell phones and Web diary: comparative study with paper-based travel survey (No. 06-0701) (2006)
Janzen, M., Müller, K., Axhausen, K.W.: Population synthesis for long-distance travel demand simulations using mobile phone data. In: 6th Symposium of the European Association for Research in Transportation (hEART 2017) (2017)
JICA: Dhaka Urban Transport Network Development Study (DHUTS) in Bangladesh, Final Report. Dhaka: Japan International Cooperation Agency (2010)
Kressner, J.D.: Synthetic household travel data using consumer and mobile phone Data. Final Report for NCHRP IDEA Project 184. Transportation Research Board (2017)
Marschak, J.: Binary choice constraints on random utility indications. In: Arrow, K. (ed.) Stanford Symposium on Mathematical Methods in the Social Science. Stanford University Press, Stanford (1960)
McFadden, D.: Conditional logit analysis of qualitative choice behavior. In: Zarembka, P. (ed.) Frontiers in Econometrics, pp. 105–142. Academic Press, New York and London (1974)
Pan, C., Lu, J., Di, S., Ran, B.: Cellular-based data-extracting method for trip distribution. Transp. Res. Rec. 1945(1), 33–39 (2006)
Panigutti, C., Tizzoni, M., Bajardi, P., Smoreda, Z., Colizza, V.: Assessing the use of mobile phone data to describe recurrent mobility patterns in spatial epidemic models. R. Soc. Open Sci. 4, 160950 (2017)
Patterson, Z., Fitzsimmons, K.: Datamobile: smartphone travel survey experiment. Transp. Res. Rec. 2594(1), 35–43 (2016)
Pettersson, P., Schmöcker, J.-D.: Active ageing in developing countries?–trip generation and tour complexity of older people in Metro Manila. J. Transp. Geogr. 18, 613–623 (2010)
Pritchard, D.R., Miller, E.J.: Advances in population synthesis: fitting many attributes per agent and fitting to household and person margins simultaneously. Transportation 39, 685–704 (2012)
QGIS Development Team: QGIS geographic information system [Online]. https://qgis.org/en/site/ (2018). Accessed 14 Aug 2018
Rao, B., Minakakis, L.: Evolution of mobile location-based services. Commun. ACM 46(12), 61–65 (2003)
Rolstad, S., Adler, J., Rydén, A.: Response burden and questionnaire length: is shorter better? A review and meta-analysis. Value Health 14, 1101–1108 (2011)
Ros, O.G.C., Albertos, P.G.: D5.4 enhanced version of MATSim: synthetic population module. In: Innovative Policy Modelling and Governance Tools for Sustainable Post-Crisis Urban Development (INSIGHT). Madrid, Spain: INSIGHT Consortium (2016)
Ryan, J., Maoh, H., Kanaroglou, P.: Population synthesis: comparing the major techniques using a small, complete population of firms. Geogr. Anal. 41, 181–203 (2009)
Safi, H., Assemi, B., Mesbah, M., Ferreira, L., Hickman, M.: Design and implementation of a smartphone-based travel survey. Transp. Res. Rec. 2526(1), 99–107 (2015)
Safi, H., Assemi, B., Mesbah, M., Ferreira, L.: Trip detection with smartphone-assisted collection of travel data. Transp. Res. Rec. 2594(1), 18–26 (2016)
Shin, D., Aliaga, D., Tunçer, B., Arisona, S.M., Kim, S., Zünd, D., Schmitt, G.: Urban sensing: using smartphones for transportation mode classification. Comput. Environ. Urban Syst. 53, 76–86 (2015)
Stopher, P., FitzGerald, C., Xu, M.: Assessing the accuracy of the Sydney household travel survey with GPS. Transportation 34(6), 723–741 (2007)
Sun, L., Erath, A.: A Bayesian network approach for population synthesis. Transp. Res. Part C Emerg. Technol. 61, 49–62 (2015)
Vlassenroot, S., Gillis, D., Bellens, R., Gautama, S.: The use of smartphone applications in the collection of travel behaviour data. Int. J. Intell. Transp. Syst. Res. 13(1), 17–27 (2015)
Voas, D., Williamson, P.: An evaluation of the combinatorial optimisation approach to the creation of synthetic microdata. Int. J. Popul. Geogr. 6, 349–366 (2000)
Vogel, N., Theisen, C., Leidig, J.P., Scripps, J., Graham, D.H., Wolffe, G.: Mining mobile datasets to enable the fine-grained stochastic simulation of ebola diffusion. Procedia Comput. Sci. 51, 765–774 (2015)
White, J., Wells, I.: Extracting origin destination information from mobile phone data. In: Eleventh International Conference on Road Transport Information and Control (Conf. Publ. No. 486), March 2002, pp. 30–34. IET, London (2002)
Wu, L., Yang, B., Jing, P.: Travel mode detection based on GPS raw data collected by smartphones: a systematic review of the existing methodologies. Information 7(4), 67 (2016)
Xiao, Y., Low, D., Bandara, T., Pathak, P., Lim, H.B., Goyal, D., Ben-Akiva, M.: Transportation activity analysis using smartphones. In: 2012 IEEE Consumer Communications and Networking Conference (CCNC), pp. 60–61. IEEE (2012)
Xiao, G., Juan, Z., Zhang, C.: Detecting trip purposes from smartphone-based travel surveys with artificial neural networks and particle swarm optimization. Transp. Res. Part C Emerg. Technol. 71, 447–463 (2016)
Ye, X., Konduri, K., Pendyala, R. M., Sana, B., Waddell, P.: A methodology to match distributions of both household and person attributes in the generation of synthetic populations. In: 88th Annual Meeting of the Transportation Research Board, Washington, DC (2009)
Zhang, D.: Social-enabled urban data analytics. Doctoral Dissertation, University of California Berkeley. https://digitalassets.lib.berkeley.edu/etd/ucb/text/Zhang_berkeley_0028E_17723.pdf (2018). Accessed 14 May 2020
Zhao, F., Pereira, F.C., Ball, R., Kim, Y., Han, Y., Zegras, C., Ben-Akiva, M.: Exploratory analysis of a smartphone-based travel survey in Singapore. Transp. Res. Rec. J. Transp. Res. Board 2(2494), 45–56 (2015)
Zhou, X., Yu, W., Sullivan, W.C.: Making pervasive sensing possible: effective travel mode sensing based on smartphones. Comput. Environ. Urban Syst. 58, 52–59 (2016)
Zhu, Y., Ferreira Jr., J.: Synthetic population generation at disaggregated spatial scales for land use and transportation microsimulation. Transp. Res. Rec. 2429, 168–177 (2014)
Zilske, M., Nagel, K.: Studying the accuracy of demand generation from mobile phone trajectories with synthetic data. Procedia Comput. Sci. 32, 802–807 (2014)
Zilske, M., Nagel, K.: A simulation-based approach for constructing all-day travel chains from mobile phone data. Procedia Comput. Sci. 52, 468–475 (2015)
Acknowledgements
The research in this paper used mobile phone data made available by Grameenphone Ltd, Bangladesh, household travel survey data provided by the Japan International Cooperation Agency (JICA), and aggregate census data obtained from the Bangladesh Bureau of Statistics (BBS). We would like to thank the Economic and Social Research Council (ESRC) of the UK, the Institute for Transport Studies, University of Leeds and FP7 Marie Curie Career Integration Grant of the European Union (PCIG14-GA-2013-631782) for funding this research. Stephane Hess was supported by the European Research Council through the consolidator Grant 615596-DECISIONS.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bwambale, A., Choudhury, C.F., Hess, S. et al. Getting the best of both worlds: a framework for combining disaggregate travel survey data and aggregate mobile phone data for trip generation modelling. Transportation 48, 2287–2314 (2021). https://doi.org/10.1007/s11116-020-10129-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-020-10129-5