Abstract
The benefits of cycling have been well established for several decades. It can improve public health and make cities more active and environmentally friendly. Due to the significant net benefits, many local governments in Scotland have promoted cycling. Glasgow City Council constructed four significant pieces of cycling infrastructure between 2013 and 2015, partly in preparation for the 2014 Commonwealth Games and partly to encourage cycling more generally. This required substantial capital investment. However, the effectiveness of these big new infrastructure investments has not been well examined, mostly due to data limitations. In this study, we utilised data from the activity tracking app Strava for the years 2013–2016 and fixed effects panel data regression models to examine whether the new cycling infrastructure has increased cycling volumes on these routes. Our results show that three of the infrastructure projects have a positive effect on the monthly total volume of cycling trips made by users of the app, with flows up by around 12% to 18%. Although this result is promising, it needs to be interpreted with care due to the characteristics of the data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The benefits of cycling have been well documented in several studies (Woodcock et al. 2009; Oja et al. 2011; Cavill et al. 2008). Among other things, it can improve public health and make cities more active and environmentally friendly. Even though cyclists are vulnerable to emissions and traffic accidents, several studies have found significant net health benefits of cycling and physical activities (Mueller et al. 2015; De Hartog et al. 2010; Celis-Morales et al. 2017). In many European cities, local governments have promoted cycling to make their cities more active and sustainable. For example, the cycling action plan for Scotland developed several strategies (e.g., leadership and partnership, infrastructure, integration and road safety, etc.) to achieve a vision of having 10% of everyday journeys made by bicycle by 2020, with cities being a key driver for achieving this (Transport Scotland 2017).
Glasgow City Council has also committed to cycling by increasing funding and building new infrastructure (Glasgow City Council 2015). Specifically, the strategic plan for cycling 2010–2020 included diverse action plans to prepare for the Glasgow 2014 Commonwealth Games (Glasgow City Council 2010), a major sporting event held in the city. The city council wanted to use the games as a catalyst to increase cycling and therefore also planned to install infrastructure after the games were over. As part of these efforts, several cycling infrastructure projects were undertaken between 2012 and 2015 to facilitate easier movement around the city (e.g., by providing easy and flexible access to many destinations for cyclists) and to encourage people to cycle more. This required substantial capital investment. However, the effectiveness of these big new infrastructure investments has not been well examined, partly due to data limitations. A lack of proper data also influences the quality of analysis. For example, most previous studies used a simple analytical model, focusing on specific routes. Some studies only compared two to three points in time rather than examining the effects using continuous data. This is especially important when strong seasonality effects are present, as with cycling. Therefore, the analysis should consider overall time trends and compare areas with new infrastructure and those without to evaluate the effects of new infrastructure investments properly.
Strava, a mobile phone activity tracking app with a focus on cycling, has provided new opportunities for researchers and planners to analyse cycling patterns. The app allows users to log their cycling trips and track them using GPS. Strava Metro, a division of the company behind the app, processes the raw GPS data collected from users’ devices and aggregates it into a number of products, which it then provides to researchers and planners. One of these datasets is an origin and destination (O–D) matrix of the cycling trips with added information about the routes taken by different cyclists.
Some people may argue that Strava users could be different from the general cycling population. However, several empirical studies have shown the potential value of Strava data to examine spatial variation in cycling volumes as shown in the “Literature review” section. In this paper, we utilised Strava data from 2013 to 2016 to examine whether the major, new cycling infrastructure installed around the time of the Glasgow 2014 Commonwealth Games has increased the number of cycling trips made by Strava cyclists. The significant contributions of this paper are to utilise 48 months’ worth of crowdsourced cycling data which provides information on cycling at fine temporal and spatial scales, and to employ a conservative analytical method to evaluate new cycling infrastructure investments rigorously. The methodology developed can be applied in any city. Restricting ourselves to only Strava users results in measuring only the impact of the infrastructure on a subset of cyclists. However, we present evidence suggesting that the effects measured for Strava cyclists may be generalisable to the entire population of cyclists in Glasgow.
Literature review
In this section, we review previous studies that examine the relationship between cycling infrastructure and cycling behaviour and that evaluate the effects of cycling infrastructure investments. In addition, we compare different cycling data collection efforts to discuss the strengths and weaknesses of these methods, and show how our approach could overcome some weaknesses.
Several previous studies investigated the relationship between cycling infrastructure and cycling behaviour (Hull and O’Holleran 2014; Stewart et al. 2015). For example, Lee et al. (2015) showed that the proximity to cycling lanes increases the chance of using a public bicycle for commuting in Changwon, South Korea. AMR Interactive (2009) conducted 10 focus groups and 8 in-depth telephone interviews to identify the potential barriers to cycling. They found that providing safe cycling lanes (e.g., segregated lanes, connected paths, etc.) is important in encouraging people to cycle more. Based on over 140 interviews, Christensen et al. (2012) found that new cycling infrastructure had a positive influence on cycling. Interestingly, their analysis also showed that interviewees did not often mention the lack of on-road cycle lanes as a barrier although stated that the availability of on-road cycle lanes improved their perception of safety, resulting in positive impacts on cycling.
There are several empirical studies evaluating cycling infrastructure (Pazin et al. 2016; Song et al. 2017; Jones 2012; Buehler and Pucher 2012). Most of them utilised conventional travel surveys (e.g., intercept or household surveys) or census data. Collecting such data can be costly, making it difficult to collect longitudinal data with a high spatial and temporal coverage. For example, Krizek et al. (2009) used U.S. Census data (the Census Transportation Planning Package) to examine the effects of new cycling facilities on cycling commuting behaviour between 1990 and 2000 in the Minneapolis-St. Paul area. They found positive effects of newly built cycling facilities on bicycle mode share. Goodman et al. (2014) conducted surveys before and after the construction of new cycling infrastructure [2010 (baseline), 2011 (1-year follow up) and 2012 (2-year follow-up)]. They also found an increased level of cycling activity after 2 years for those living close to the new infrastructure. In addition, the positive impacts became larger for those without cars. Thakuriah et al. (2012) conducted an intercept survey with a “time-based” user sampling approach and evaluated eight suburban bicycle and pedestrian facilities in the Chicago metropolitan area. Their result showed that these new facilities encourage people to switch to cycling from single occupant vehicle use. Goodman et al. (2013) examined the effects of town level cycling initiatives that include both capital (e.g., infrastructure) and revenue (e.g., training) investments. Their study utilised census data and a natural experimental study approach by selecting multiple comparison groups. They found a significant increase in cycling volumes but substantial differences between towns.
Some studies used data collected by other means such as automatic counters or video cameras at specific locations. For example, Skov-Petersen et al. (2017) utilised multi-year data from automatic counting stations as well as repeated surveys to examine the effects of cycling infrastructure improvements on total cycle volumes as well as cyclists’ behaviour and experience. They found significant increases on two specific routes after the improvements although there were only a small number of induced cycling trips. They argued that using a long period of count data is useful for investigating the effectiveness of cycling interventions. Deenihan et al. (2013) also utilised automatic bicycle counter data to investigate the benefits of new cycling infrastructure in a rural area in Ireland. Their results implied that this new investment is worthwhile. Although not about cycling infrastructure investments, Zangenehpour et al. (2016) collected cycling and car activity data at 23 intersections using video cameras, and examined if the intersections with cycle lanes are safer compared to those without cycle lanes. The most important benefit of the above data collection efforts is the accuracy. However, it is obvious that empirical analyses are limited because their data are limited in a spatial context. Specifically, most analyses only focus on the affected areas (e.g., specific routes or areas) rather than comparing them with large number of other unaffected areas, potentially resulting in erroneous conclusions.
Recently, new forms of data have allowed researchers to conduct detailed spatial and temporal analyses of cycling behaviour. For example, Strava Metro provides cycling activity data in one-minute intervals for all roads. In addition, a cycling O–D matrix as well as individual route information aggregated at the area level are available for researchers and transport planners (Strava Metro 2017).
Jestico et al. (2016) examined whether new types of data (i.e., crowdsourced data from fitness apps) could be utilised to investigate the spatial and temporal variations in cycling. They compared Strava count data with manual cycle counts in Victoria, British Columbia and employed statistical models to predict actual cycling counts based on Strava counts and other relevant factors (e.g., slope, street parking, etc.). They concluded that even though the sample is a small proportion of all cyclists, crowdsourced data has potential for predicting the volume of cycling trips and mapping spatial variations, especially in urban areas. Sun et al. (2017) examined the effects of diverse built environment factors on cycling behaviour with 2015 Strava data for the Glasgow Clyde Valley planning area. To validate the usefulness of Strava data for the analysis, they compared annual average daily flow data (e.g., number of cyclists) provided by the UK Department of Transport and Strava cycling counts. Their analysis showed a very high correlation between these two data sources (r = 0.83), implying that Strava data could be utilised for the spatial analysis of cyclists in general.
In sum, results from recent empirical studies imply that Strava data can be a good proxy for estimating actual cycling counts and can be used to evaluate newly created cycling infrastructures although they did not explicitly analyse if Strava users are similar to the general population. We found one recent study that utilised both intercept surveys and Strava count data to evaluate a new cycling infrastructure built near the Brisbane city centre (Heesch et al. 2016). However, they only utilised Strava count data for specific sites rather than including all other areas.
As mentioned, Glasgow held a large sporting event in 2014 and built several new cycling facilities. This provides a unique opportunity for researchers to evaluate large cycling infrastructure investments with new types of data and advanced analytical methods. In this paper, we first compared manual counts of cyclists to Strava counts to show the usefulness of Strava data for examining cycling patterns. Then, we employed 4 years’ worth of Strava data for the Glasgow area to evaluate four main new cycling facilities built between 2013 and 2015 with a fixed effects panel data regression model.
Data and method
Data
Three data sources were utilised for this study: manual counts of cyclists from a cordon count carried out in Glasgow in 2014, Glasgow cycling infrastructure data, and cycle counts from Strava for the years 2013–2016. Glasgow City Council has conducted annual surveys to monitor active travel patterns (i.e., walking and cycling) around the city centre area. They counted all cyclists and pedestrians who pass the 35 locations shown in Fig. 1 for 2 days in September, 2014. We compared data from this cordon count to counts derived from Strava for the corresponding times and places. This is to investigate whether Strava data give a sufficiently good approximation for the analysis of spatial variations in overall cycling activities, even though Strava users are a subset of cyclists.
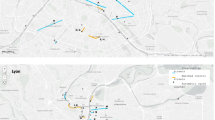
Glasgow City Council provided cycling infrastructure data with diverse information such as location, type of infrastructure (e.g., segregated, shared, etc.) and names of the infrastructure. For this study, we identified four main cycling routes opened before, during and after the Glasgow 2014 Commonwealth Games as well as their completion dates based on the inputs from Glasgow City Council. An infrastructure variable (Infra) was created based on the completion date (i.e., coded 1 after the completion date (month); 0 if not completed or if no new cycling infrastructure was introduced). Table 1 and Fig. 2 show the details of four new cycling routes.
Finally, we used the 2013–2016 Strava data to evaluate newly created cycling infrastructure. Strava Metro provides anonymized information about total cycling activities for each road segment for each minute of the day. The link counts are derived by map matching the raw GPS data onto a representation of the transport network. In this case, the GPS data were matched onto OpenStreetMap road data. Information on the origins and destinations of the cyclists is given by output area (the smallest census geography in the UK, with average populations of 150 people). The origin–destination data also includes all output areas that a cyclist traversed during a trip. That is, it includes origin output area, destination output area and all intersected output areas for a trip in our study area. Both the OpenStreetMap road data and the output areas are provided as shapefiles. A rich spatial and temporal coverage of Strava data allows us to compare it with data from the 2014 cordon count and utilise a fixed effects panel data regression model for the in-depth analysis. We obtained the above datasets from the Urban Big Data Centre (UBDC) at the University of Glasgow (http://ubdc.ac.uk/). The same data are available to other researchers upon application.
Figure 2 shows the four main infrastructure projects built between 2013 and 2015. For this study, we utilised the origin–destination data of each cycle trip to count the total volume of cycling activities at the output area level. Based on information about the timing and route of trips, we calculated monthly total cycling volumes for each output area in each month. This is to consider some potential effects of switching cycling routes due to new cycling facilities. For example, if new cycling routes are introduced close to the one that cyclists previously used, they may change their travel routes, resulting in a similar total number of cycling activities at the output area level but increased/decreased activities for other routes at the link level.
If new cycling infrastructure encourages people to cycle more, we expect that the total cycling activities made by Strava users at the output area level will increase. Our main variable of interest (New infra) was created based on the infra variable and output areas. Any output area that includes new cycling infrastructure (Infra = 1) was coded as 1 after new cycling facilities were introduced. It is worth noting that we used predefined administrative areas, therefore the modifiable areal unit problem could exist. Our final dataset includes 300,144 observations (6253 output areas * 48 months) and the average monthly total cycling volume (of Strava users) at the output area level is around 135.
Analytical model
For this study, we used a fixed effects Poisson panel regression model with cluster-robust standard errors to evaluate the effects of new cycling infrastructure on cycling activities. Negative binomial regression models have been widely used for count data. However, a fixed effects Negative binomial regression model cannot fully control for the unobserved heterogeneity of output areas in the same way that the fixed effects linear regression or fixed effects Poisson model can (Allison and Waterman 2002). In addition, we tried a fixed-effects linear regression model but several assumptions (e.g., homoscedasticity) are violated. It is worth noting that both models produced consistent results. We therefore choose to proceed with a Poisson model which accounts for the count nature of the data. We measured monthly total cycling activities for each output area over 48 months with Strava data. This results in a panel data structure. The conditional mean of our fixed effects Poisson model is given by:
where \(\lambda_{it}\) represents the number of Strava cycling trips in area i in month t, \(x_{{\text{new infra}}\_{it}}\) is a dummy variable which takes the value of 1 if new infrastructure is present and 0 otherwise, \(\mu_{i}\) is an output-area-specific effect capturing time-invariant unobserved heterogeneity (e.g., built environment, quality of roads, etc.), \(\tau_{t}\) are a series of month fixed effects (to control for factors such as seasonality and the potential changes in the number of Strava users over time). \(\beta_{\text{new infra}}\) captures the effect of the new infrastructure on monthly Strava cycling volumes in each output area.
We also examine the separate effect of each infrastructure and the fixed effects Piosson model can be written as follows:
where \(x_{{\text{new infra1}}\_{it}} ,x_{{\text{new infra2}}\_{it}} ,x_{{\text{new infra3}}\_{it}} \;{\text{and}}\;x_{{\text{new infra4}}\_{it}}\) represent the presence of Routes to Cathkin 1, Routes to Cathkin 2, South West City Way and West City Way/Connect 2 lanes, respectively.
Results
Before deploying the regression model, we conducted a correlation analysis with the cordon count data from 2014 and the corresponding Strava data. This is to evaluate the usefulness of Strava data for the spatial analysis of cycling patterns in our spatial and temporal context. We found very high correlations between the two datasets, implying that the Strava data can be a good proxy to predict actual cycling counts, even if Strava users are a biased sample of cyclists. Specifically, we calculated hourly manual counts of cyclists and Strava counts, and found a correlation of 0.816. The correlation becomes larger when data are aggregated at the daily level (r = 0.908). Figure 3 shows the relationships between cordon counts and Strava counts depending on different levels of aggregations. We can see a strong linear relationship between them, and it becomes stronger when the level of aggregation increases. When comparing the total number of cycling trips from cordon counts and that of Strava trips in 2014, our data shows that 1 Strava trip represents around 25 actual cycling trips on average. We also conducted a simple linear regression model to confirm their linear relationships. R-squared value increases from 0.67 to 0.82 when the level of aggregation increases from hourly to daily.Footnote 1 Since we employed monthly Strava counts for our analyses, we believe the relationship becomes much stronger. This also implies that the results from our analyses may be generalisable to the entire population of cyclists in our study area. In addition, our approach is to compare the volume of Strava cycling after the infrastructure is put in place with the volume of Strava cyclists before it is put in place. We are therefore comparing like with like in our models. We believe this justifies the use of monthly Strava count data for our regression analyses. It is worth noting that our model also considers output areas without new infrastructure which act as controls for our treatment group.
In Fig. 4, we consider how cycle flows have changed over time in the areas where new cycling infrastructure has been implemented. To do this, we classified output areas according to which of the four infrastructure projects passes through them (j = 1, 2, 3, 4), and one additional group for all other output areas (j = 0). In order to illustrate the changes in the monthly total cycling volume before and after the infrastructure is implemented while controlling for the overall time trend, we transformed the data in the following way:
The vertical lines represent the completion dates of new cycling infrastructure.
A number of interesting features are apparent from Fig. 4. For Routes to Cathkin 1, there appears to be a negative trend which shows that cycle volumes have grown less quickly in these output areas than in Glasgow generally. Cycling volumes in output areas associated with the other three projects tend to have grown faster than Glasgow generally. For Routes to Cathkin 2 and West City Way, there is no step-change associated with the opening of the infrastructure. There seems to be a gradual increase over the period. South West City Way shows a more marked increase after the new infrastructure opens. Interestingly, despite the fact that the overall seasonal trend has been removed from the data, a seasonal pattern is still visible in the case of Routes to Cathkin 2. This suggests that seasonal effects are stronger in these areas than in Glasgow generally.
We estimated fixed effects Poisson regression models with cluster-robust standard errors to examine both overall and separate effects of new infrastructure investments. The results are presented in Table 2. All coefficients of month dummy variables are positive and statistically significant at the 0.05 level. We expect strong seasonality effects in the model and this is evident in the estimated coefficients (e.g., larger magnitude of coefficients during the summer than the winter). That is, there are more cyclists around in the summer than in the winter. This seems reasonable when we consider the differences between the two seasons. For example, there are around 10 more hours of daylight on the longest day compared to the shortest day in Glasgow. There is also substantially more rain in the winter months.
Our main variable of interest (New Infra) in Table 2 shows a positive but statistically insignificant overall effect. The New infra coefficient is not at all significant at the 0.05 level. This means the overall effect of four new infrastructure investments is not as large as we expected.
For further analysis, we examined the separate effect of each cycling infrastructure project. Month dummy variables are consistent and show almost the same effects as before. Since time effects are dominant in our analysis, they should be consistent. Three new cycling routes (i.e., Routes to Cathkin2, South West City Way, and West City Way/Connect 2) have positive and significant influences on monthly total Strava cycling trip volume. Specifically, the result shows a 12% [exp(0.1163)] to 18% [exp(0.1656)] increase in monthly total Strava cycling activities after the new cycling infrastructure is opened. These three cycling routes are located near the city centre and include segregated cycling lanes. This result is consistent with the findings from McArthur and Hong (2019).
Routes to Cathkin 1 is the longest new cycling route and has a negative effect on monthly total cycling trips made by Strava users. This route includes several less developed areas and few people cycle from these less developed and less densely populated areas. In addition, there are no segregated lanes and most lanes are shared with other transport modes. Overall, it is reasonable to see that these areas could have a slower increase in the total number of Strava cycling trips than average. This result is also visible in Fig. 4.
Conclusion
Policy makers have used infrastructure investments as a way of increasing active travel and improving public health. Glasgow is one such city which has invested significant sums of money in installing new infrastructure across the city. A catalyst for this investment was the city’s hosting of the 2014 Commonwealth Games. The significant investments made in the run up to this event make Glasgow an interesting case study. Future investments are planned as the city tries to reach its ambitious vision for the share of journeys to be made by bicycle.
Appraisal and evaluation of such interventions can be difficult due to a lack of suitable data and analytical methods. In this paper, we investigate the use of crowdsourced cycling data from the Strava app. We began by confirming the validity of the data by comparing it to manual count data, and found high correlations and strong positive linear relationships. This implies that Strava data can be used to analyse spatial and temporal variations in cycle volumes even though Strava users are a subset of total cyclists.
Our analytical models suggested that estimating a single coefficient for all infrastructure projects (i.e., overall effect) could result in incorrect conclusions. It could be the case that while some projects have been successful in increasing the volume of cycling, other have not been. If these effects are averaged out across all four projects, it may make it more difficult to measure a statistically significant effect. Our analytical models show that three among four new projects are successful, and all of them are located close to the city centre, mostly consisting of segregated cycling lanes. This implies that in the short term, developing new cycling infrastructure inside the city area will be more effective than introducing new cycling facilities outside the developed areas. In addition, providing segregated cycling lanes should be a target of such investments. However, we should be careful. The benefits of new infrastructure in outer areas could pay-off in the future when the network becomes more extensive and people realise its existence as well as its usefulness as their normal travel option.
There are limitations to our work. Firstly, as indicated earlier, we employed predefined administrative areas as an analytical unit. The modifiable areal unit problem therefore may affect our results. Future work may consider this. Secondly, this study investigates the short/mid-term effects of new cycling facilities. It may take longer before certain types of effects are observed. For instance, once people get accustomed to the presence of cycling infrastructure they may choose to begin cycling regularly. Lastly, we should be careful when interpreting the magnitude of our results. Since Strava users are a subset of total cyclists, we need more in-depth analyses to examine how to predict actual cycling counts as precisely as possible with Strava data.
Notes
More detailed results about the validation of Strava data for cycling studies can be found in Hong et al. (2018).
References
Allison, P.D., Waterman, R.P.: Fixed-effects negative binomial regression models. Sociol. Methodol. 32, 247–265 (2002)
AMR Interactive: Research Into Barriers to Cycling in NSW. AMR Interactive Group, Sydney (2009)
Buehler, R., Pucher, J.: Cycling to work in 90 large American cities: new evidence on the role of bike paths and lanes. Transportation 39, 409–432 (2012)
Cavill, N., Kahlmeier, S., Rutter, H., Racioppi, F., Oja, P.: Economic analyses of transport infrastructure and policies including health effects related to cycling and walking: a systematic review. Transp. Policy 15, 291–304 (2008)
Celis-Morales, C.A., Lyall, D.M., Welsh, P., Anderson, J., Steell, L., Guo, Y., Maldonado, R., Mackay, D.F., Pell, J.P., Sattar, N., Gill, J.M.R.: Association between active commuting and incident cardiovascular disease, cancer, and mortality: prospective cohort study. BMJ 357, j1456 (2017)
Christensen, J., Chatterjee, K., Marsh, S., Sherwin, H., Jain, J.: Evaluation of the Cycling City and Towns Programme: Qualitative Research with Residents. AECOM, Centre for Transport & Society and the Tavistock Institute, London (2012)
De Hartog, J.J., Boogaard, H., Nijland, H., Hoek, G.: Do the health benefits of cycling outweigh the risks? Environ. Health Perspect. 118, 1109–1116 (2010)
Deenihan, G., Caulfield, B., O’Dwyer, D.: Measuring the success of the Great Western Greenway in Ireland. Tour. Manag. Perspect. 7, 73–82 (2013)
Glasgow City Council: Glasgow’s Strategic Plan for Cycling. Glasgow City Council, Glasgow (2010)
Glasgow City Council: Glasgow’s Strategic Plan for Cycling 2016–2025. Glasgow City Council, Glasgow (2015)
Goodman, A., Panter, J., Sharp, S.J., Ogilvie, D.: Effectiveness and equity impacts of town-wide cycling initiatives in England: a longitudinal, controlled natural experimental study. Soc. Sci. Med. 97, 228–237 (2013)
Goodman, A., Sahlqvist, S., Ogilvie, D., On Behalf of the iConnect Consortium: New walking and cycling routes and increased physical activity: 1- and 2-year findings from the UK iConnect study. Am. J. Public Health 104, 38–46 (2014)
Heesch, K.C., James, B., Washington, T.L., Zuniga, K., Burke, M.: Evaluation of the Veloway 1: a natural experiment of new bicycle infrastructure in Brisbane, Australia. J. Transp. Health 3, 366–376 (2016)
Hong, J., McArthur, D., Livingston, M.: The Use of Crowd-Sourced Cycling Data for Cycling Analyses (Strava). University of Glasgow, Glasgow (2018)
Hull, A., O’Holleran, C.: Bicycle infrastructure: can good design encourage cycling? Urban Plan. Transp. Res. 2, 369–406 (2014)
Jestico, B., Nelson, T., Winters, M.: Mapping ridership using crowdsourced cycling data. J. Transp. Geogr. 52, 90–97 (2016)
Jones, T.: Getting the British back on bicycles—the effects of urban traffic-free paths on everyday cycling. Transp. Policy 20, 138–149 (2012)
Krizek, K.J., Barnes, G., Thompson, K.: Analyzing the effect of bicycle facilities on commute mode share over time. J. Urban Plan. Dev. 135, 66–73 (2009)
Lee, K.H., Won, D.H., Ko, E.J.: The multiple impacts of the neighbourhood environment on the use of public bicycles by residents: an empirical study of Changwon in Korea. Int. J. Urban Sci. 19, 224–237 (2015)
McArthur, D.P., Hong, J.: Visualising where commuting cyclists travel using crowdsourced data. J. Transp. Geogr. 74, 233–241 (2019)
Mueller, N., Rojas-Rueda, D., Cole-Hunter, T., De Nazelle, A., Dons, E., Gerike, R., Götschi, T., Int Panis, L., Kahlmeier, S., Nieuwenhuijsen, M.: Health impact assessment of active transportation: a systematic review. Prev. Med. 76, 103–114 (2015)
Oja, P., Titze, S., Bauman, A., De Geus, B., Krenn, P., Reger-Nash, B., Kohlberger, T.: Health benefits of cycling: a systematic review. Scand. J. Med. Sci. Sports 21, 496–509 (2011)
Pazin, J., Garcia, L.M.T., Florindo, A.A., Peres, M.A., Guimarães, A.C.D.A., Borgatto, A.F., Duarte, M.D.F.D.S.: Effects of a new walking and cycling route on leisure-time physical activity of Brazilian adults: a longitudinal quasi-experiment. Health Place 39, 18–25 (2016)
Skov-Petersen, H., Jacobsen, J.B., Vedel, S.E., Thomas Alexander, S.N., Rask, S.: Effects of upgrading to cycle highways—an analysis of demand induction, use patterns and satisfaction before and after. J. Transp. Geogr. 64, 203–210 (2017)
Song, Y., Preston, J., Ogilvie, D.: New walking and cycling infrastructure and modal shift in the UK: a quasi-experimental panel study. Transp. Res. Part A Policy Pract. 95, 320–333 (2017)
Stewart, G., Anokye, N.K., Pokhrel, S.: What interventions increase commuter cycling? A systematic review. BMJ Open 5, e007945 (2015)
Strava Metro: Comprehensive user guide (2017). http://metro.strava.com/wp-content/uploads/2017/04/StravaMetro_5.01_User_Guide.pdf
Sun, Y., Du, Y., Wang, Y., Zhuang, L.: Examining associations of environmental characteristics with recreational cycling behaviour by street-level Strava data. Int. J. Environ. Res. Public Health 14, 644–655 (2017)
Thakuriah, V., Metaxatos, P., Lin, J., Jensen, E.: An examination of factors affecting propensities to use bicycle and pedestrian facilities in suburban locations. Transp. Res. Part D 17, 341–348 (2012)
Transport Scotland (ed.): Cycling Action Plan for Scotland 2017–2020. Edinburgh (2017). https://www.transport.gov.scot/media/10311/transport-scotland-policy-cycling-action-plan-for-scotland-january-2017.pdf
Woodcock, J., Edwards, P., Tonne, C., Armstrong, B.G., Ashiru, O., Banister, D., Beevers, S., Chalabi, Z., Chowdhury, Z., Cohen, A., Franco, O.H., Haines, A., Hickman, R., Lindsay, G., Mittal, I., Mohan, D., Tiwari, G., Woodward, A., Roberts, I.: Public health benefits of strategies to reduce greenhouse-gas emissions: urban land transport. Lancet 374, 1930–1943 (2009)
Zangenehpour, S., Strauss, J., Miranda-Moreno, L.F., Saunier, N.: Are signalized intersections with cycle tracks safer? A case–control study based on automated surrogate safety analysis using video data. Accid. Anal. Prev. 86, 161–172 (2016)
Acknowledgements
The authors would like to acknowledge support from the Economic and Social Research Council-funded Urban Big Data Centre at the University of Glasgow (Grant ES/L011921/1, ES/S007105/1).
Author information
Authors and Affiliations
Contributions
JH: research idea, data acquisition and processing, literature search and review, manuscript writing. DPM: data processing and analysis, manuscript writing and editing. ML: data acquisition, manuscript writing and editing.
Corresponding author
Ethics declarations
Conflict of interest
We confirm that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hong, J., McArthur, D.P. & Livingston, M. The evaluation of large cycling infrastructure investments in Glasgow using crowdsourced cycle data. Transportation 47, 2859–2872 (2020). https://doi.org/10.1007/s11116-019-09988-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-019-09988-4