The influence of passenger load, driving cycle, fuel price and different types of buses on the cost of transport service in the BRT system in Curitiba, Brazil

Abstract

This study analyses the influence of passenger load, driving cycle, fuel price and four different types of buses on the cost of transport service for one bus rapid transit (BRT) route in Curitiba, Brazil. First, the energy use is estimated for different passenger loads and driving cycles for a conventional bi-articulated bus (ConvBi), a hybrid-electric two-axle bus (HybTw), a hybrid-electric articulated bus (HybAr) and a plug-in hybrid-electric two-axle bus (PlugTw). Then, the fuel cost and uncertainty are estimated considering the fuel price trends in the past. Based on this and additional cost data, replacement scenarios for the currently operated ConvBi fleet are determined using a techno-economic optimisation model. The lowest fuel cost ranges for the passenger load are estimated for PlugTw amounting to (0.198–0.289) USD/km, followed by (0.255–0.315) USD/km for HybTw, (0.298–0.375) USD/km for HybAr and (0.552–0.809) USD/km for ConvBi. In contrast, the coefficient of variation ($C_{v}$) of the combined standard uncertainty is the highest for PlugTw ($C_{v}$: 15–17%) due to stronger sensitivity to varying bus driver behaviour, whereas it is the least for ConvBi ($C_{v}$: 8%). The scenario analysis shows that a complete replacement of the ConvBi fleet leads to considerable higher cost of transport service on the BRT route, amounting to an increase by 64% to 139%, depending on the bus fleet composition. Meanwhile, the service quality is improved resulting in 42% up to 64% less waiting time for passengers at a bus stop.

Introduction

Emerging automotive technologies such as hybrid-electric and plug-in hybrid-electric powertrains have gained in importance in line with efforts to mitigate anthropogenic emissions. These types of powertrains are technologically situated in-between conventional and battery-electric vehicles and offer one intermediate solution for the transition towards full-electrified transportation. While range anxiety is a considerable drawback of battery-electric vehicles, plug-in hybrid-electric vehicles prevent a potential gridlock by utilising an internal combustion engine as range extender. The use of both an energy-efficient electric motor and regenerative braking to recover excess energy during deceleration increases the vehicle’s overall energy efficiency and consequently, saves fuel compared to a conventional vehicle, e.g. up to 35% in the case of buses (Hellgren 2007). This large energy saving potential of hybrid-electric vehicles in the operation phase becomes particularly relevant when considering that between 50% (Ribau et al. 2014) and 80% (Onat et al. 2015) of a vehicle’s life-cycle energy is consumed here.

The city of Curitiba in the South Region of Brazil has a long history in innovative sustainable urban planning, particularly due to the introduction of the world-famous bus rapid transit (BRT) concept. By joining the C40 Cities Climate Leadership Group (C40) and signing the ‘C40 Cities Clean Bus Declaration of Intent’ (C40 2015), Curitiba has committed to introduce low or ultimately zero emission buses in its bus fleet. However, only 30 two-axle buses out of 1226 buses in the operating bus fleet use a hybrid-electric powertrain at present, whereas the remaining buses are of the conventional type (URBS 2018a). During 2016, two new types of buses, namely a hybrid-electric articulated bus and a plug-in hybrid-electric two-axle bus, were tested on regular bus routes (i.e. not BRT) for a test phase of six months in Curitiba (Volvo Bus Corporation 2016a, b; URBS 2017a). In addition to these physical tests on regular bus routes, first simulation tests also indicate considerable reduction potentials for energy use and greenhouse gas emissions when replacing conventional bi-articulated buses in the city’s BRT system (Dreier et al. 2018).

Meanwhile, the cost of transport service is a crucial aspect to consider as it eventually gives the fare to the paying passengers. And the fare can again influence the actual use of the BRT system as found by (Hensher and Li 2012a, b). Considering that fuel cost represent 17% of the cost of transport service for the conventional bi-articulated buses in Curitiba (URBS 2017b)—only the salaries for the personnel to operate and administrate the system are higher—there is an interest to operate as few buses as possible to meet the transport demand. In contrast, research by (dell’Olio et al. 2012) has shown that the satisfaction of passengers is increased when more buses are operated and consequently, the headway is reduced, i.e. shorter waiting time for passenger until the next bus leaves a bus stop. Furthermore, this becomes particularly relevant as more satisfaction can potentially attract more paying passengers to use the transport system. However, more passengers implies more passenger load in the buses and a consequent increase of fuel consumption (Saxe et al. 2008; Ribau et al. 2015; Yu et al. 2016). In addition to passenger load, the bus driver plays an important part, since he/she reacts upon the traffic situations. The bus driver behaviour is represented in a so-called driving cycle, which influences energy use in a bus and ultimately, the fuel cost. Moreover, the fuel price can considerably fluctuate over time (ANEEL 2018; ANP 2018) and this increases uncertainty about the fuel cost and cost of transport service of a bus, too.

Therefore, the influence of passenger load, driving cycle and fuel price are important parameters to take into account by bus operators before new buses are acquired and old buses are replaced. In regards to the C40 commitment, new buses shall be introduced that could also replace the currently operated conventional bi-articulated buses in Curitiba. Meanwhile, the selection can be made from a variety of different types of buses that potentially employ different powertrain technologies and/or possess different passenger carrying capacities. From this situation, the following two research questions arise that shall support the decision.

• i) How do passenger load, driving cycle and fuel price influence the fuel cost and cost of transport service of different types of buses?

• ii) How do replacements of the currently operated conventional bi-articulated buses by other types of buses influence the cost of transport service and service quality for the operation of a BRT route?

Thus, the first research question analyses different parameters concerning their influence on fuel cost and cost of transport service, while the second research question highlights the implications of the analysis results concerning a replacement of the current bus fleet. In this study, different types of city buses are analysed as potential alternatives to the currently operated conventional bi-articulated bus (ConvBi) in Curitiba’s BRT system, namely a hybrid-electric two-axle bus (HybTw), a hybrid-electric articulated bus (HybAr) and a plug-in hybrid-electric two-axle bus (HybTw). The study fills a gap in the existing literature by presenting the first analysis with this grade of detail for estimating energy use and fuel cost for the four different buses in comparison to each other. Moreover, uncertainties of varying parameters such as driving cycle and fuel price are quantified to enhance the understanding of their influence on fuel cost and cost of transport service. Based on the estimations, various replacement scenarios are evaluated concerning cost of transport service and service quality for the cases that the conventional bi-articulated bus fleet is partly or completely replaced by the other types of buses.

The results of this study can be of particular interest for bus operators and municipalities, e.g. C40 cities, as they consider a renewal of their bus fleets to meet the climate target. Furthermore, the estimations can provide a reference for comparison to cities in developing countries that consider the introduction of new types of buses. In fact, both the BRT concept and conventional bi-articulated buses are frequently used in developing countries (Global BRT Data 2017) due to the much lower capital costs compared to light rail transit or metro systems (Zhang 2009).

Following this introductory section, the next section presents a literature review and elaborates further on the study’s contribution to the scientific literature. Then, an overview of the methodology and input data for the analysis is provided. After this, the results are presented and discussed followed by conclusions including some indications for future work. The appendix contains a glossary for technical terms, overview of abbreviations, symbols and units as well as electronic supplementary material (in the online version).

Literature review

Extensive research has focused on the analysis and comparison of energy use and fuel cost for conventional and hybrid-electric two-axle buses (chassis length: ca. 12 m; passenger carrying capacity: ca. 80–100 passengers). For instance, (Hellgren 2007) showed a 35% fuel consumption reduction for hybrid-electric buses due to the use of regenerative braking in the case of Gothenburg in Sweden compared to conventional diesel buses. In line with this finding, but estimating a smaller difference, (Hallmark and Sperry 2012) found a fuel consumption and cost reduction of 13–21% for hybrid-electric buses compared to conventional buses in the case of the US state of Iowa. Obviously, the fuel consumption and cost advantages depend on the operation-specific driving cycle. This was also confirmed by (Lajunen 2014a), who stated that cost-efficiency depends strongly on the driving cycle.

In addition to the driving cycle, passenger load is another influential parameter as shown by (McKenzie and Durango-Cohen 2012), who found a clear advantage of using one conventional bus with a larger passenger carrying capacity instead of using two hybrid-electric buses to provide sufficient transport service to the ridership. It is therefore necessary to consider both powertrain technology and passenger carrying capacity of buses. In respect of the latter, both articulated buses (chassis length: ca. 18 m; passenger carrying capacity: ca. 150 passengers) and bi-articulated buses (chassis length: ca. 25 m; passenger carrying capacity: ca. 250 passengers) offer the possibility to transport considerably more passengers than two-axle buses and both are indeed very commonly used in various cities globally (Global BRT Data 2018a, b). However, only a few studies have been carried out to analyse energy use or fuel cost of articulated and bi-articulated buses so far. For instance, the study by (Chandler and Walkowicz 2006) compared conventional and hybrid-electric articulated buses in the case of Seattle, USA. Similarly as in the case of two-axle buses, also a hybrid-electric articulated bus can save a considerable amount of fuel due to an improved fuel economy by 21–26% compared to the conventional counterpart. While the previous studies compared similarly sized buses with different powertrain technologies, the study by (Bai et al. 2016) is one of the few studies that compared two-axle and articulated buses to each other. However, their focus was on analysing the effect of blending ratios between petroleum diesel and biodiesel on the conventional powertrain technology and not on comparing conventional and hybrid-electric powertrains.

As shown, the existing literature has been quite limited for the analysis of articulated and bi-articulated buses concerning energy use and fuel cost. However, this knowledge gap ought to be filled, especially when considering the findings of studies by (Saxe et al. 2008; Ribau et al. 2015; Yu et al. 2016), who identified the passenger load as a very influential parameter on the fuel consumption for two-axle buses. Hence, this parameter becomes presumably even more important for the cases of articulated and bi-articulated buses due to potential larger weight variations during operation as a result of their larger passenger carrying capacities. Moreover, the effect of passenger load is pronounced at slow speeds (Yu et al. 2016), which is usually the case for urban bus transport systems. And, the speed is again determined by the traffic flow and the manner a bus driver reacts on it. In this respect, changing the bus driver behaviour through eco-driving training can achieve significant amounts of fuel savings for buses amounting to 5–7% in Atlanta, USA (Xu et al. 2017), 6.8% in Sweden (Strömberg and Karlsson 2013), 10–15% in Athens, Greece (Zarkadoula et al. 2007) or 17% in Porto, Portugal (Perrotta et al. 2014). Nevertheless, the actual eco-driving training effect also depends on the age and experience of a bus driver as found in the case of Lisbon, Portugal (Rolim et al. 2014). Consequently, varying driver behaviour from different bus drivers also adds uncertainty on energy use and fuel cost and eventually, the cost of transport service.

Therefore, more understanding is needed on the influence of both passenger load and driving cycle on energy use and fuel cost concerning conventional bi-articulated buses as well as in comparison to other types of buses. Here, quantified differences are valuable to inform decision makers in the transformation process of bus transport systems before they select a new type of bus as potential replacement of older buses. As of yet, only one study by (Dreier et al. 2018) contributed to enhance understanding concerning the comparison of conventional bi-articulated buses to other types of buses. The study analysed, among other aspects, the energy use during operation, but did not explicitly quantify the influence of passenger load or driving cycles on it. These two parameters, in combination with fluctuating fuel prices, affect the fuel cost and cost of transport service, and thus are of interest to entities and companies involved in the operation of bus transport systems.

In summary, this study contributes to the scientific literature by providing deeper understanding about the influence of passenger load, driving cycle and fuel price on fuel cost and cost of transport service for different types of buses such as a conventional bi-articulated bus, a hybrid-electric two-axle bus, a hybrid-electric articulated bus and a plug-in hybrid-electric two-axle bus. Furthermore, it explores consequences of this understanding that may affect the choice of bus replacements.

Methodology and input data

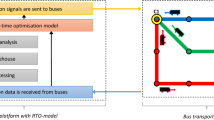
The consecutive steps of the applied bottom-up analysis are shown in Fig. 1. First, the energy use of the four city buses was simulated for different passenger loads and driving cycles for the operation phase, also called Tank-to-Wheel (TTW) analysis. Then, the energy use estimations were used together with data on fuel prices and the lower heating value of the fuel to calculate the fuel cost as well as to quantify uncertainty. The importance of fuel cost and uncertainty was then evaluated concerning the cost of transport service for each bus. The implications of the analysis results were then analysed by modelling different scenarios for the operation of one BRT route, in which the currently operated conventional bi-articulated bus fleet was partly and completely replaced by the other types of buses. The scenarios were evaluated concerning the cost of transport service and service quality. Following this brief overview, the next sub-sections describe more in detail the methods and input data that were applied and used in this study, respectively.

Fig. 1

Consecutive steps of the bottom-up analysis

Energy use estimation method

The energy use of the buses was estimated using the software tool Advanced Vehicle Simulator (ADVISOR). The latest free and open-source version of ADVISOR was used (Wipke et al. 1999; Markel et al. 2002). ADVISOR allows the user to model a road vehicle and its driving on a route to analyse the vehicle’s performance. To run the simulations, the buses were modelled by inserting technical data (see Tables 1 and 2 and the electronic supplementary material). Then, the driving on the BRT route was modelled by using two inputs: (1) the elevation profile data set that represents the topology of the BRT route, loaded as road gradient versus distance in ADVISOR, and (2) the driving cycle data set that represents the driving of a bus, loaded as speed versus time in ADVISOR. After this, the simulations were run and energy use results were obtained. The estimations of the energy use and fuel cost are presented in two functional units: ‘distance’ in kilometres (km) and ‘passenger-distance’ in passenger-kilometres (pkm). The term ‘pkm’ refers to the accumulated distance travelled by all passengers carried in a bus when driving a distance of one kilometre.

Table 1 Technical specifications of the buses

Table 2 Total weight of buses at different occupancy rates

Concerning the uncertainty and validation of ADVISOR, the software tool uses a deterministic modelling approach of vehicles including an open-source code written in MATLAB/Simulink (The MathWorks Inc. 2015) and open input data. Thus, open-source code and open data make the functional principle and assumptions transparent and address endogenous and exogenous uncertainties, respectively. Furthermore, (Wipke and Cuddy 1996) carried out a sensitivity analysis of key parameters to quantify endogenous uncertainty of ADVISOR, e.g. for conventional and hybrid-electric vehicles. Their results suggest, for instance, a fairly linear relationship of mass changes on the fuel economy. These insights are relevant, since ADVISOR has got a scaling function that dimensions the components of default vehicle models according to the specific adjustments made through inserting of new input data for parameters. Thereby, ADVISOR possess the flexibility to analyse a wide range of different types of vehicles. As a result of the open-source code and flexibility, ADVISOR has been used in many scientific studies, e.g. for conventional, hybrid-electric, plug-in hybrid-electric, battery-electric and fuel cell buses, as summarised for the studies by (Khanipour et al. 2007; Lajunen 2012a, b, 2014a, b; He et al. 2014; Melo et al. 2014; Mirmohammadi and Rashtbarzadeh 2014; Ribau et al. 2014; Correa et al. 2017; Wang et al. 2017). In regards to the types of buses analysed in this study, the ADVISOR models of the four buses were already used in a previous study (Dreier et al. 2018) and showed representative energy use estimations when compared to real-world fuel consumption data from the bus fleet in Curitiba, Brazil. Furthermore, the energy use estimation of this present study are also validated against real-world data from Curitiba as later shown in the results and discussion section. Thus, the bus models used in ADVISOR are empirically validated against real-world data. Besides, a few relative recent studies exist that explicitly measured the accuracy of ADVISOR and found a discrepancy of 3–8% for a wide range of different vehicles (Ma et al. 2011, 2012).

City buses

The BRT system, in which mainly conventional bi-articulated buses (ConvBi) are operated at present, is part of the bus transport system in Curitiba. Despite this predominance of the conventional powertrain technology, a few (i.e. 30) hybrid-electric two-axle buses are actually operated in the city. However, those drive on regular bus routes rather than in the BRT system. Further, two new types of buses were also tested on regular bus routes for a test phase of six months in 2016 (Volvo Bus Corporation 2016a, b; URBS 2017a), namely a hybrid-electric articulated bus (HybAr) and a plug-in hybrid-electric two-axle bus (PlugTw). While a conventional bi-articulated bus only employs an internal combustion engine, both hybrid-electric and plug-in hybrid-electric buses, employ, in addition to an internal combustion engine, also an electric motor. The powertrains of these hybrid-electric and plug-in hybrid-electric buses are configured in parallel with a power split option, i.e. the electric motor runs either alone or simultaneously with the internal combustion engine.

The liquid fuel considered in the simulations was a biodiesel blend consisting of 93% petroleum diesel and 7% biodiesel. This fuel blend was a result of the blending mandate in Brazil in 2015, that required a mandatory minimum share of 7% biodiesel blended into petroleum diesel (Executive Power 2014). The fuel properties were calculated based on the volumetric shares of petroleum diesel and biodiesel using data from Ref. (Canakci and van Gerpen 2003). This gave a fuel density of 0.856 kg/L and lower heating value (LHV) of 42.27 MJ/kg or 36.17 MJ/L. The fuel properties were kept constant in all simulations and hence, the potential effect of fuel quality variation on the energy use, e.g. as shown by (Farkas et al. 2014), was outside the scope of the analysis. In the case of the plug-in hybrid-electric two-axle bus (PlugTw), electrical energy was considered, too.

Most of the buses do not have any air conditioning in Curitiba, because of the relative mild climate in the South Region of Brazil. Therefore, the buses were simulated in ADVISOR without air conditioning to consider the same standard of thermal comfort to the passengers. An overview of the technical specifications of the buses used as input data in ADVISOR is provided in Table 1. Additional data is provided in the electronic supplementary material.

Energy management strategies

Both hybrid-electric buses (HybTw, HybAr) always drove with all-electric drive until a speed of 20 km/h (power split: only electric motor) in the simulations. When this speed was exceeded, the internal combustion engine started to run in parallel with the electric motor to provide additional torque and power. Regenerative braking was always sufficient to recharge the energy storage system (ESS) to reach the initial State-of-Charge (SOC) before operation start. SOC refers to the ratio of available capacity to the nominal capacity of an ESS (full: SOC = 100%; empty: SOC = 0%). Thus, the SOC fluctuated due to discharging during all-electric drive and recharging during regenerative braking throughout the operation. Consequently, the net electrical energy use was zero when driving in this so-called charge-sustaining (CS) mode for the hybrid-electric buses (HybTw, HybAr).

In contrast, the plug-in hybrid-electric two-axle bus (PlugTw) has got a larger ESS with a usable capacity $UsableCapacity$ of 8.5 kWh (Volvo Group 2015). The usable capacity represents a range within the nominal capacity that is bounded by two limits, namely a high SOC ($SOC_{high} = 74.5{\text{\% }}$) and a low SOC ($SOC_{low} = 30{\text{\% }}$). The upper bound at $SOC_{high}$ is set to stop the charging process to reduce the charging time, because it increases over-proportional above this SOC (Hõimoja et al. 2012; Ke et al. 2016). The simulations started with a SOC equal to $SOC_{high}$. The lower bound at $SOC_{low}$ is set to avoid a potential damage of the ESS and consequently, shorter lifetime (Rosenkranz 2003). Since, regenerative braking was insufficient to recover enough energy in form of electrical energy to drive frequently and over relative long distances in all-electric drive at speeds above 20 km/h in the simulations, the ESS depleted over time. As a result, the initial SOC could not be sustained, which made it necessary to set a threshold ($SOC_{threshold} = 35{\text{\% }})$ to consider a prevention of a potential lower depletion than $SOC_{low}$. When this threshold was reached, this so-called charge-depleting (CD) mode stopped and the CS mode was used as in the case of both hybrid-electric buses (Fig. 2). The distance, that can be driven in CD mode, is the all-electric range (AER) of a bus.

Fig. 2

Energy management strategies and State-of-Charge (SOC) progress in the energy storage system (ESS) of a plug-in hybrid-electric bus over the driven distance. CD Charge-depleting, CS Charge-sustaining, AER All-electric range

For the estimation of the energy use per distance of the PlugTw bus at a certain passenger load, the operation was divided into the two distance sections for each driving cycle $j$: (1) the distance driven in CD mode that is $AER_{j}$ (in km) and (2) the distance driven in CS mode that is the difference between the total distance $D_{j}$ (in km) of driving cycle $j$ and $AER_{j}$. The distances $D_{j}$ of all driving cycles were always longer than the possible $AER_{j}$ of the PlugTw bus (data is provided in the electronic supplementary material). Therefore, the total energy use of net electrical energy $TE_{elec,j}$ (in MJ) could be also directly calculated by the used electrical energy between $SOC_{high}$ and $SOC_{threshold}$:

$$TE_{elec,j} = \left( {SOC_{high} - SOC_{threshold} } \right)/\left( {SOC_{high} - SOC_{low} } \right) \cdot UsableCapacity \cdot 3.6MJ/kWh = 27 {\text{MJ}}$$

(1)

Then, the energy use per distance in CD mode $E_{elec,j}$ (in MJ/km) was calculated by relating $TE_{elec,j}$ to $AER_{j}$:

$$E_{elec,j} = TE_{elec,j} /AER_{j}$$

(2)

And the mean value of $E_{elec,j}$ (in MJ/km) was calculated considering equal importance of each driving cycle $j$:

$$E_{elec} = \mathop \sum \limits_{j}^{N} E_{elec,j} /N$$

(3)

Similarly, the total energy use of the biodiesel blend $TE_{BB,j}$ (in MJ/km) was the amount of energy to drive the remaining distance $\left( {D_{j} - AER_{j} } \right)$ in CS mode. Thus, the energy use per distance in CS mode $E_{BB,j}$ (in MJ/km) was calculated by:

$$E_{BB,j} = TE_{BB,j} /\left( {D_{j} - AER_{j} } \right)$$

(4)

And the mean value of $E_{BB,j}$ (in MJ/km) was calculated considering again equal importance of each driving cycle $j$:

$$E_{BB} = \mathop \sum \limits_{j}^{N} E_{BB,j} /N$$

(5)

The sum of both external energy sources to drive first in CD mode (i.e. use of electrical energy) and then, followed by CS mode (i.e. use of biodiesel blend) gave the energy use per distance of the PlugTw bus:

$$E_{j} = \left( {E_{elec,j} \cdot AER_{j} + E_{BB,j} \cdot \left( {D_{j} - AER_{j} } \right)} \right)/D_{j}$$

(6)

And the mean value of $E_{j}$ (in MJ/km) was calculated considering again equal importance of each driving cycle $j$:

$$E = \mathop \sum \limits_{j}^{N} E_{j} /N$$

(7)

Note: In the case of the buses ConvBi, HybTw and HybAr, only the biodiesel blend was used as an external energy source and therefore: $E_{j} = E_{BB,j}$.

Passenger load

For the purpose of the simulations, six occupancy rates were considered in 20%-increments from 0 to 100% to obtain energy use estimations that cover the whole range of passenger loads, i.e. from an empty bus at 0% to a full bus at 100%. Later, the buses are compared to each other according to the actual number of passengers that they carry. Table 2 provides the total weights of the buses for each of the six occupancy rates. The total weight of a bus $m_{b}$ (in tonnes) was calculated with:

$$m_{b} = m_{b,PassengerLoad} + m_{b,KerbWeight}$$

(8)

where $m_{b,PassengerLoad}$ is the passenger load (in tonnes) and $m_{b,KerbWeight}$ is the kerb weight of the bus (in tonnes). The passenger load was estimated by assuming the average weight of one passenger $m_{Passenger}$ (67 kg, 0.067 tonnes) and considering the occupancy rate $OR$ (in %) of the passenger carrying capacity of a bus $PCC_{b}$ (in passengers) from Table 1:

$$m_{b,PassengerLoad} = m_{Passenger} \cdot OR \cdot PCC_{b}$$

(9)

With the aid of Eqs. (8) and (9), the kerb weight of a bus (including the bus driver) was estimated by assuming that the permitted gross vehicle weight $GVW_{b}$ (in tonne) represents the total weight of a bus at maximal passenger load (i.e. $OR = 100\%$) given by:

$$m_{b,KerbWeight} = GVW_{b} - m_{Passenger} \cdot 100\% \cdot PCC_{b}$$

(10)

Values for $GVW_{b}$ were retrieved from the following references: ConvBi: (Volvo Bus Corporation 2015a); HybTw: (Volvo Bus Corporation 2015c); HybAr: (Volvo Bus Corporation 2016c); PlugTw: (Volvo Bus Corporation 2015g).

Driving cycles and elevation profile

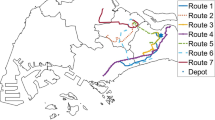
The BRT route in the analysis has a one-way distance of 10 km with 19 bus stops (Fig. 3a), which is BRT route ‘503’ in Curitiba. Due to the fact that standardised driving cycles can strongly differ from the characteristics of real-world operation, e.g. as found by (Zhang et al. 2014; Wang et al. 2015; Xu et al. 2015; Yay et al. 2016), local real-world driving cycles were used in the simulations. Additionally, the elevation profile was considered to include the slightly hilly topology of the BRT route (Fig. 3b). This was important to consider in the simulations as road gradient changes also affect the energy demand of a vehicle (Prati et al. 2014).

Fig. 3

Source: (URBS 2015a)

BRT route ‘503’ in Curitiba: a routing, b elevation profile, c driving cycles of eleven conventional bi-articulated buses.

Eleven data sets from the real-world operation of conventional bi-articulated buses on the BRT route were provided by the public transport authority in Curitiba—URBS Urbanization of Curitiba S/A (URBS 2015a). The buses drove from bus stop ‘Tubo Praça Carlos Gomes’ (north) to bus stop ‘Terminal Boqueirão’ (south) according to their everyday operation time table during the week in the morning. The data sets of the eleven driving cycles (i.e. speed vs. time) were collected with an average frequency of 0.1 Hz. Since the software tool ADVISOR requires a second-by-second data series for speed vs time, linear interpolation was used to generate accordingly the data format of the driving cycles for the simulations. The driving cycles differ slightly in their characteristics due to different bus drivers that drove in different traffic and operation situations in terms of traffic lights, dwell times of passengers, et cetera (see Table 3 and Fig. 3c). The buses were only little influenced by other vehicles, because they drove on exclusive bus lanes aligned in the centre of the road as typical for BRT routes in Curitiba. Furthermore, the bus stops in Curitiba’s BRT system have off-board fare collection and platform-level boarding that both allow shorter dwell times. As a result, the buses could drive at a speed above 20 km/h for more than half of their operation time and reached a maximum speed of 55–65 km/h (Fig. 3c). For more details about the local traffic and operation conditions, see the field trip study by (Dreier 2015).

Table 3 Characteristics of the driving cycles

In summary, a total of 264 simulations were run in ADVISOR to estimate the energy use of the four types of buses, six passenger loads and eleven driving cycles.

Fuel cost and uncertainty estimation methods

The currency US Dollar (USD) is used as monetary unit in this study. The local currency Brazilian Real (BRL) was converted to USD using the average currency exchange rate of 0.2833 USD/BRL over the period from 1st Jan 2014 to 31st Dec 2017 (X-rates 2018). The average value was used to have a constant factor between BRL and USD. This allowed a systematic conversion without introducing random uncertainty that could have been potentially caused by the fluctuation of the exchange rate. The fuel prices were retrieved from Ref. (ANEEL 2018; ANP 2018). The historical trends from 1st Jan 2014 to 31st Dec 2017 are shown in Fig. 4 and the corresponding descriptive statistics are provided in Table 4. Obviously, the fuel prices of both the biodiesel blend and electrical energy gradually increased over this period in Brazil. The mean fuel prices of the biodiesel blend and electrical energy amount to (0.913 ± 0.052) USD/L and (0.160 ± 0.029) USD/kWh, respectively. A brief remark on the values of skewness and kurtosis: although both values are within a range of ± 2 indicating normality of the distributions, an additional observation of histograms in Past 3.x (Hammer et al. 2001) showed that both fuel prices are not normally distributed. Therefore, Chebyshev’s inequality was used to interpret the findings in the results and discussion section to derive more general conclusions concerning the uncertainty and probability distribution. The difference between a normal distribution and Chebyshev’s inequality concerns the spread of data. Normally distributed data follows the empirical rule that 68%, 95% and 99.7% of the data is within the width of one, two and three standard deviations from the mean, respectively. In contrast, Chebyshev’s inequality is more conservative in stating the coverage of expected values following the rule $1 - 1/k^{2}$, where $k$ is the number of standard deviations. Chebyshev’s inequality does not state any useful insight for one standard deviation $k = 1$, but for example for $k$ values of $k = \sqrt 2 : 1 - 1/\sqrt 2^{2} = 1 - 0.5 = 50\%$, i.e. 50% of the expected values are covered by $\sqrt 2$ standard deviations from the mean; or $k = 2: 1 - 1/2^{2} = 1 - 0.25 = 75\%$; or $k = 3: 1 - 1/3^{2} = 1 - 0.111 = 88.9\%$.

Fig. 4

Sources: ANEEL (2018), ANP (2018)

Fuel prices of the biodiesel blend and electrical energy in Brazil from 1st Jan 2014 to 31st Dec 2017.

Table 4 Descriptive statistics for the fuel prices of the biodiesel blend and electrical energy in Brazil from 1st Jan 2014 to 31st Dec 2017.

The fuel cost $FuelCost$ (in USD/km) was calculated based on the energy use estimation and fuel price/s. In the case of the buses ConvBi, HybTw and HybAr, their fuel costs could be estimated straightforward as they only consumed the biodiesel blend (i.e. $E_{elec} = 0)$. In the case of PlugTw, both the biodiesel blend and net electrical energy use had to be taken into account:

$$FuelCost = \left( {P_{BB} \cdot TE_{BB} + P_{elec} \cdot TE_{elec} } \right)/D$$

(11)

where $TE_{BB}$ (in MJ) and $TE_{elec}$ (in MJ) are the mean values for the total energy use of biodiesel blend and electrical energy, respectively, considering all driving cycles $j$ from the set of driving cycles $\left( {N = 11} \right)$:

$$TE_{BB} = \mathop \sum \limits_{j}^{N} E_{{BB,j}} \cdot \left( {D_{j} - AER_{j} } \right)/N$$

(12)

$$TE_{elec} = \mathop \sum \limits_{j}^{N} E_{{elec,j}} \cdot AER_{j} /N$$

(13)

Since small differences were recorded between the driven distances in the set of driving cycles due to minor measurement deviations, a mean distance $D$ (in km) was calculated:

$$D = \mathop \sum \limits_{j}^{N} D_{j} /N$$

(14)

And lastly, $P_{BB}$ (in USD/MJ) and $P_{elec}$ (in USD/MJ) are the mean values of the fuel prices of the biodiesel blend and electrical energy, respectively, considering all months $i$ from the set of months $M$ over the period 1st Jan 2014 to 31st Dec 2017 $\left( {M = 48} \right)$:

$$P_{BB} = \mathop \sum \limits_{i}^{M} P_{BB,i} /M$$

(15)

$$P_{elec} = \mathop \sum \limits_{i}^{M} P_{elec,i} /M$$

(16)

Uncertainty

Real-world operation is a dynamic process, in which each bus is slightly differently affected by varying bus driver behaviour due to different traffic situations such as traffic lights, bus stops, dwell times, intersections, etc. Hence, the driving cycles collected from real-world operation vary and cause variations of the energy use. In addition, fluctuating fuel prices of the biodiesel blend and electrical energy can influence fuel cost. Therefore, an uncertainty analysis was carried out to quantify the combined standard uncertainty of both varying bus driver behaviour and fluctuating fuel prices. The combined standard uncertainty $u_{c} \left( y \right)$ of an output estimate $y$ that is calculated with a function $f$ that has non-linear combinations of input estimates $x_{k}$ and their associated standard uncertainties $u\left( {x_{k} } \right)$ is given by (JCGM 2008):

$$u_{c} \left( y \right) = \sqrt {\mathop \sum \limits_{k = 1}^{N} \left( {\frac{\partial f}{{\partial x_{k} }}} \right)^{2} \cdot u^{2} \left( {x_{k} } \right) + 2\mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l = k + 1}^{N - 1} \frac{\partial f}{{\partial x_{k} }}\frac{\partial f}{{\partial x_{l} }} \cdot u\left( {x_{k} ,x_{l} } \right)}$$

(17)

The correlation coefficient $r\left( {x_{k} ,x_{l} } \right)$ estimates the degree of correlation between the variables $x_{k}$ and $x_{l}$:

$$r\left( {x_{k} ,x_{l} } \right) = u\left( {x_{k} ,x_{l} } \right)/\left( {u\left( {x_{k} } \right) \cdot u\left( {x_{l} } \right)} \right) \leftrightarrow u\left( {x_{k} ,x_{l} } \right) = u\left( {x_{k} } \right) \cdot u\left( {x_{l} } \right) \cdot r\left( {x_{k} ,x_{l} } \right)$$

(18)

where $u\left( {x_{k} ,x_{l} } \right)$ is the covariance associated with $x_{k}$ and $x_{l}$. Then, Eq. (17) becomes with the aid of Eq. (18):

$$u_{c} \left( y \right) = \sqrt {\mathop \sum \limits_{k = 1}^{N} \left( {\frac{\partial f}{{\partial x_{k} }}} \right)^{2} \cdot u^{2} \left( {x_{k} } \right) + 2\mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l = k + 1}^{N - 1} \frac{\partial f}{{\partial x_{k} }}\frac{\partial f}{{\partial x_{l} }} \cdot u\left( {x_{k} } \right) \cdot u\left( {x_{l} } \right) \cdot r\left( {x_{k} ,x_{l} } \right)}$$

(19)

The fuel cost function in Eq. (11) has got five input estimates $P_{BB}$, $TE_{BB}$, $P_{elec}$, $TE_{elec}$ and $D$. Testing for linear correlation revealed statistical significance between the fuel prices of the biodiesel blend $P_{BB}$ and electrical energy $P_{elec}$. Consequently, this correlation was considered with a determined correlation coefficient of $r\left( {P_{BB} ,P_{elec} } \right) = 0.923$. Other correlations between any of the five input estimates did not exist, because, for instance, $TE_{elec,j}$ always amounted to 27 MJ due to the fact that the distance of each driving cycle $D_{j}$ was always longer than the $AER_{j}$ of PlugTw. Furthermore, this constant value of $TE_{elec,j}$ implies that there cannot exist any correlation to $TE_{BB,j}$. Besides, both $TE_{elec,j}$ and $TE_{elec,j}$ were neither influenced by $P_{BB}$ nor by $P_{elec}$, because only the biodiesel blend was consumed in Curitiba at the time when the driving cycles were collected. Hence, no possibility existed for any bus driver to make a fuel choice that would have potentially affected his/her behaviour and thus, the driving cycle. Lastly, the distances of the driving cycles $D_{j}$ have a standard deviation of 40 meters due to minor measurement deviations and therefore, someone might presume that $TE_{BB}$ was larger for those driving cycles with longer distances. However, testing for correlation between $D_{j}$ and $TE_{BB}$ for all buses, passenger loads and driving cycles gave mostly values for the correlation coefficient $r$ between 0.1 and 0.2. This, in turn, gave values for the coefficient of determination $r^{2}$ between 0.01 and 0.04, i.e. only 1–4% of the occurring variation between $TE_{BB}$ and $D$ can be statistically explained through the linear correlation. This demonstrates the insignificance of this correlation and hence, independence was considered between $TE_{BB}$ and $D$. Based on these explanations, the applied Eq. (19) to estimate the combined standard uncertainty of the fuel cost (11) is then written as:

$$u_{c} \left( {FuelCost} \right) = \sqrt {\begin{array}{*{20}c} {\left( {TE_{BB} /D} \right)^{2} \cdot u\left( {P_{BB} } \right)^{2} + \left( {P_{BB} /D} \right)^{2} \cdot u\left( {TE_{BB} } \right)^{2} + \left( {TE_{elec} /D} \right)^{2} \cdot u\left( {P_{elec} } \right)^{2} + \left( {P_{elec} /D} \right)^{2} \cdot u\left( {TE_{elec} } \right)^{2} } \\ { + \left( {P_{BB} \cdot TE_{BB} + P_{elec} \cdot TE_{elec} } \right)^{2} /D^{4} \cdot u\left( D \right)^{2} + 2 \cdot TE_{BB} /D \cdot TE_{elec} /D \cdot u\left( {P_{BB} } \right) \cdot u\left( {P_{elec} } \right) \cdot r\left( {P_{BB} ,P_{elec} } \right)} \\ \end{array} }$$

(20)

Additionally, the coefficient of variation $C_{v}$ of the fuel cost was calculated to estimate the dispersion of the fuel cost distribution around the estimated mean:

$$C_{v} \left( {FuelCost} \right) = u_{c} \left( {FuelCost} \right)/FuelCost$$

(21)

Cost data

The provision and operation of a bus transport systems comes along with a variety of different cost components that eventually must pay off through the revenues generated from selling of tickets to the passengers. The public transport authority URBS in Curitiba published an extensive amount of information online (URBS 2017b) together with a description of their applied methodology (URBS 2018b) how they determine the fare for the passengers based on the cost of the transport service ($CTS$) related to the driven distance by the buses (Table 5). Thus, $CTS$ represents the cost to operate a bus in a profitable manner. Cost data was available for the two currently operated buses, i.e. the conventional bi-articulated bus (ConvBi) in the BRT system and hybrid-electric two-axle bus (HybTw) on regular bus routes. In contrast, since no reliable data has been published for the cost components of the hybrid-electric articulated bus (HybAr) and the plug-in hybrid-electric two-axle bus (PlugTw), some assumption had to be made (see footnotes of Table 5 for more information). Overall, the $CTS$ of a bus transport system consists of the operating cost of the bus fleet, personnel cost of the bus transport system, administration cost of the bus transport system, amortisation of buses and facilities, profitability requirements for a fair return on the investments made by bus operators, taxes and another small cost addition. The cost information for the $CTS$ (in USD/km) in Table 5 were used as input data in the scenario analysis as presented next.

Table 5 Cost of transport service (CTS) for buses in Curitiba

Scenario analysis model

The operation of the BRT route is in accordance with a time table in Curitiba at present. The number of buses that leave the bus stop ‘Tubo Praça Carlos Gomes’ is shown in an aggregated form as sum of buses by hourly time slices in Fig. 5. The figure shows the current situation, in which conventional bi-articulated buses are exclusively operated (baseline scenario). As the aggregation is made by hourly time slices and taking into account that the time for one roundtrip amounts to approximately 1 h (URBS 2016), then the actual number of buses that simultaneously drive on the BRT route are the same as the number of buses shown for each time slice in Fig. 5. Furthermore, the figure indicates that more buses are operated during peak hours such as in the morning and evening from Monday to Friday (URBS 2018c). These are the times when the residents of Curitiba commute between home and work and vice versa and thus, more buses are needed to transport the larger ridership. On the weekend, the distribution of buses is rather constant, while more buses operate on Saturday than on Sunday. A commonly applied measure to evaluate the transport service is the headway, i.e. the inverse of the frequency of buses. The headway states the time between buses (in minutes/bus) leaving a bus stop or in other word the waiting time for passengers at a bus stop. Therefore, a short headway is desirable as it indicates more convenience for the passengers. The headway $Headway_{d,ts}$ on day $d$ during time slice $ts$ (in minutes/bus) is therefore calculated by:

$$Headway_{d,ts} = t_{d,ts} /\mathop \sum \limits_{b} n_{d,ts,b}$$

(22)

where $t_{d,ts}$ is the duration on day $d$ of time slice $ts$ and $n_{d,ts,b}$ is the number of buses operating simultaneously on day $d$ during time slice $ts$ of bus type $b$ (in buses/hour). As all times slices were chosen in 1-h intervals, $t_{d,ts}$ always amounts to 60 min in this study. Then, the average headway $AverageHeadway$ over several days and time slices of operation (e.g. 1 week) is calculated as follows:

Fig. 5

Source: URBS (2018c)

Number of buses per time slice that leave bus stop ‘Tubo Praça Carlos Gomes’ on BRT route ‘503’ in Curitiba according to the time table.

$$AverageHeadway = \left.\mathop \sum \limits_{d} \mathop \sum \limits_{ts} t_{d,ts} \right/\mathop \sum \limits_{d} \mathop \sum \limits_{ts} \mathop \sum \limits_{b} n_{d,ts,b}$$

(23)

A couple of different scenarios were developed in this study to evaluate how the use of buses other than the conventional bi-articulated bus as in the baseline scenario would differ concerning the cost of transport service evaluated by the weekly cost of transport service $WeeklyCTS$ (in USD/week) in Eq. (25) and service quality quantified by the $AverageHeadway$ (in minutes/bus) in Eq. (23). The compilation of the new bus fleet in each scenario was determined by using a techno-economic optimisation model formulated in Eqs. (23)–(29). Variables and parameters are listed in Table 6. This optimisation model ensured an objective and data-driven decision making concerning how many buses of which bus type $b$ should be operated on day $d$ during time slice $ts$. The objective function aims at minimising the $WeeklyCTS$:

$$minimise\; WeeklyCTS$$

(24)

where $WeeklyCTS$ was calculated by:

$$WeeklyCTS = \mathop \sum \limits_{d} \mathop \sum \limits_{ts} \mathop \sum \limits_{b} n_{d,ts,b} \cdot RD \cdot CTS_{b}$$

(25)

where $n_{d,ts,b}$ is again the number of buses operated on day $d$ during time slice $ts$ of bus type $b$ (in buses/hour); $RD$ is the roundtrip distance of the BRT route $(2 \cdot 10\,{\text{km}})$; and $CTS_{b}$ (in USD/km) is the cost of transport service of bus type $b$ (Table 5). The optimisation was subject to two constraints. The first constraint ensured the provision of sufficient transport service considering the current ridership. This prevented an undersizing of the new bus fleet consisting of buses other than ConvBi, because a one-by-one substitution of ConvBi by any of the other three options (HybTw, HybAr or PlugTw) would result in a lower aggregated passenger carrying capacity, since their passenger carrying capacities are smaller. The underlying assumption of this constraint is that the current ridership does not exceed the current aggregated passenger carrying capacity in the baseline scenario. This seems to be reasonable, because otherwise this would imply that already an undersizing of the bus fleet exists at present. Thus, the first constraint required to achieve at least the same aggregated passenger carrying capacity $AggPCC_{d,ts}$ (in passengers/hour) as the one in the baseline scenario $BL\_AggPCC_{d,ts}$ (in passengers/hour):

$$AggPCC_{d,ts} \ge BL\_AggPCC_{d,ts}$$

(26)

where $AggPCC_{d,ts}$ is the sum of the number of buses operated on day $d$ during time slice $ts$ times the respective passenger carrying capacity of bus type $b$$PCC_{b}$ (in passengers/bus):

Table 6 Variables and parameters in the optimisation model

$$AggPCC_{d,ts} = \mathop \sum \limits_{b} n_{d,ts,b} \cdot PCC_{b}$$

(27)

The second constraint set minimum $MinTarget_{d,ts,b}$ (dimensionless) and maximum targets $MaxTarget_{d,ts,b}$ (dimensionless) for minimum and maximum shares of a particular bus type $b$ that shall be operated on day $d$ during time slice $ts$:

$$n_{d,ts,b} \ge MinTarget_{d,ts,b} \cdot \mathop \sum \limits_{b} n_{d,ts,b}$$

(28)

$$n_{d,ts,b} \le MaxTarget_{d,ts,b} \cdot \mathop \sum \limits_{b} n_{d,ts,b}$$

(29)

Note: This optimisation model focuses exclusively on the choice of buses considering technology and cost, and does not include any management for the charging schedule for buses of the type PlugTw.

Table 7 provides an overview of all scenarios. Each scenario considers a technology change aiming at an introduction of hybrid-electric and/or plug-in hybrid-electric buses on the BRT route. The scenarios were run using the values for $CTS$ as input data from Table 5.

Table 7 Overview of scenarios

Results and discussion

The results build consecutively upon each other starting with the energy use estimations and their validation followed by the fuel cost and uncertainty estimations and lastly, the scenario analysis results.

Comparison of energy use

The descriptive statistics of the energy use estimations for the buses are provided in Table 8 and visualised in Fig. 6. Assessment for normality using the Shapiro–Wilk test in Past 3.x (Hammer et al. 2001) as well as considering the observation that the values for both skewness and kurtosis are within a range of ± 2 indicate together that the energy use estimations are normally distributed for all buses at all passenger loads. This, by implication, means a normal distribution for bus driver behaviour in the sample of the driving cycles from Curitiba.

Table 8 Descriptive statistics of the energy use estimations at different occupancy rates (OR)

Fig. 6

Energy use of the buses a per distance and b per passenger-distance

The energy use per distance increases gradually with increasing passenger load for all buses as shown in Fig. 6a. The following ranges represent the energy use per distance estimations from 0 to 100% passenger load. The highest values are estimated for the conventional bi-articulated bus (ConvBi) amounting to (24.89–36.50) MJ/km, which is not surprising as it is the heaviest bus in the comparison as well as uses only the energy-inefficient internal combustion engine. A lower energy use is found for the two hybrid-electric buses amounting to (11.51–14.20) MJ/km for HybTw and (13.45–16.91) MJ/km for HybAr. The least energy is used by PlugTw amounting to a value range of (6.24–10.33) MJ/km. The simulations show that PlugTw uses 63% less energy in CD mode than in CS mode. This difference indicates a significant energy efficiency improvement when using all-electric drive (i.e. only the electric motor is used for propulsion) compared to parallel operation of internal combustion engine and electric motor. Based on this, it is desirable that a bus driver avoids aggressive driving to allow a longer operation in CD mode to benefit the most from this energy efficiency advantage. However, the simulations also show that differences exist between the driving cycles as well as sensitivities of the buses to this uncertainty. In this respect, ConvBi has the smallest coefficient of variance ($C_{v}$) out of all buses, i.e. the smallest value dispersion around the mean. The $C_{v}$ of ConvBi’s energy use amounts to 4–5%. This means that ConvBi is the least influenced by varying bus driver behaviour. The influence of bus driver behaviour gains in importance as the degree of electrification increases in the powertrain, e.g. hybrid-electric buses (HybTw, HybAr) have a $C_{v}$ of 8–9% and the plug-in hybrid-electric bus (PlugTw) has a $C_{v}$ of 13–16%. Therefore, it is crucial to pay attention to the bus driver behaviour for buses with advanced powertrain technologies. In this respect, PlugTw is the most sensitive bus as indicated by having the highest $C_{v}$. Another observation for PlugTw is a decreasing $C_{v}$ with increasing passenger load, i.e. from a $C_{v} = 16\%$ at a passenger load of 0% to a $C_{v} = 13\%$ at a passenger load of 100%. This opposite trend is explained by the fact that more energy is needed at higher passenger load. As a result, the CD mode becomes shorter, while the CS mode becomes longer. Thus, the share of CS mode to CD mode increases and hence, the energy use increases due to more combustion of the biodiesel blend in the less energy-efficient internal combustion engine rather than using electrical energy in the more energy-efficient electric motor. As a result, PlugTw’s operation approximates to the operation of a hybrid-electric two-axle bus such as HybTw, leading to a similar uncertainty concerning energy use variations due to bus driver behaviour.

The estimations for energy use per passenger-distance follow strong regressive trends for all buses, because the denominator (i.e. passenger-distance in pkm) influences more the ratio MJ/pkm than the nominator (i.e. energy use in MJ), see Fig. 6b. On one hand, this means, the energy use per passenger-distance increases drastically when approaching zero passengers, which corresponds to the operation of an empty bus. On the other hand, this means that energy use per passenger-distance decreases as the passenger load increases, which confirms the importance of utilising the passenger carrying capacity in a bus. For instance, if ConvBi is operated, many passengers should be transported to benefit effectively from its large passenger carrying capacity in terms of energy use per passenger-distance.

Validation of the energy use

For the validation of the energy use estimations, the value range from 0 to 100% passenger load for each bus is compared to real-world data from Curitiba (Table 9). In the case that no real-world data is available, other scientific studies are used for comparison. The local public transport authority URBS in Curitiba has published real-world data for the fuel cost of all currently operated types of buses on their website in Ref. (URBS 2017b). However, this data had to be converted from the fuel cost to the actual energy use first to allow a direct comparison. Therefore, the actual energy use of the buses was calculated backwards starting at the original data of fuel cost given in BRL/km to fuel cost in USD/km to energy use in L/km and finally, to energy use in MJ/km. The conversion from BRL to USD was done by using the same average currency exchange rate of 0.2833 USD/BRL as stated in methodology section. Furthermore, as earlier shown in Fig. 4, the fuel price of the biodiesel blend varied over time and as a result, the fuel price considered by (URBS 2017b) amounted to 0.726 USD/L (original value: 2.5621 BRL/L), whereas the fuel price used in this study amounts to 0.802 USD/L (Table 4). For this reason, a normalisation between both fuel prices was necessary to allow an unbiased comparison. The normalisation was done by multiplying the fuel cost data (URBS 2017b) with a factor of 1.105 that had been obtained from the ratio between the two fuel prices 0.802 USD/L and 0.726 USD/L. Lastly, the lower heating value (LHV) for the considered biodiesel blend of 36.17 MJ/L (from methodology section) was used for the conversion from litre (L) to megajoule (MJ).

Table 9 Validation of energy use estimations

The comparison of energy use estimations and real-world data from Curitiba (Table 9) shows valid estimations for the conventional bi-articulated bus (ConvBi) and hybrid-electric two-axle bus (HybTw). Since the real-world data value for HybTw is at the upper limit of the energy use estimations at 100% passenger load obtained from the simulations, it should be noted that the current operation of this type of bus happens on regular bus routes in Curitiba that are not segregated from the other traffic rather than on BRT routes having exclusive bus lanes. This most likely explains the higher estimated energy use of HybTw due to interaction with other traffic affecting the driving cycle, e.g. it was shown by (Hu et al. 2012) that 10% more fuel is needed to drive on regular routes than on exclusive bus lanes for the operation during peak hours.

Although demonstration tests were carried out for the operation of both the hybrid-electric articulated bus (HybAr) and plug-in hybrid-electric two-axle bus (PlugTw) in Curitiba, no real-world energy use data has been published online, yet. Therefore, comparisons to other available information are made. For instance, the energy use of a hybrid-electric articulated bus amounted to 15.88 MJ/km in the case of Zhengzhou in China (Grütter 2014), 17.18 MJ/km in Ghent in Belgium (CIVITAS Initiative 2013) or 31.83 MJ/km in Seattle in the USA (Chandler and Walkowicz 2006). The original data of the former three studies were converted to MJ/km considering as a fuel petroleum diesel with an LHV of 36.40 MJ/L based on the fuel properties stated in Ref. (Canakci and van Gerpen 2003). While the findings by (Grütter 2014) and (CIVITAS Initiative 2013) are close to the estimations in this study, the estimation by (Chandler and Walkowicz 2006) is considerable higher. A closer look into this reference also indicates a much higher fuel consumption for a conventional articulated bus than in the case of Curitiba. Reasons for this divergence could be different driving cycles, passenger loads, and/or energy efficiencies in the powertrain components, because the technology analysed by (Chandler and Walkowicz 2006) was from 2005.

Lastly, the validation of the energy use estimations for the simulated plug-in hybrid-electric two-axle bus (PlugTw) is made by distinguishing the operation between charge-depleting (CD) mode and charge-sustaining (CS) mode. The energy use during CD mode is compared to a real-world test of a battery-electric two-axle bus in Curitiba that was tested in 2015 (URBS 2015b). PlugTw uses in the CD mode (3.99–5.57 MJ/km) a comparable amount of electrical energy per distance as the tested battery-electric bus (4.68 MJ/km) in Curitiba. Concerning the CS mode, PlugTw uses the same energy management strategies as HybTw, while having a similar gross vehicle weight and hence, the energy use during CS mode is again similar to the real-world data for the hybrid-electric two-axle buses in Curitiba.

Overall, the energy use estimations could be empirically validated through the comparison to real-world data from Curitiba or in the case of HybAr to data from other cases. All simulated buses possess representative values for the energy use and hence, further use of the estimations seems to be justified.

Comparison of the influence of fuel cost and uncertainty on the cost of transport service

The fuel cost and uncertainty estimations are provided in Table 10. The trends of the cost of transport service ($CTS$) and uncertainties are shown in Fig. 7 (after adding federal and municipal taxes to the $CTS$ such as in Table 5). The error bars in this figure indicate the probability distribution corresponding to Chebyshev’s inequality for $k = \sqrt 2$, $k = 2$, $k = 3$ that cover 50, 75 and 88.9% of the expected fuel cost values around the mean, respectively. As the generated amount of data could be used to discuss various different cases, the discussions had to be limited and are only presented for the case of 80% passenger load in the following. This passenger load was chosen as an example as it represents the case that buses are quite occupied, but yet, some passenger variation is possible, e.g. 60% passenger load at operation start, then reaching a peak of 100% passenger load in the middle of the BRT route and eventually, arriving at the end station again with 60% passenger load and thus, having 80% passenger load on average.

Table 10 Fuel cost and uncertainty estimations

Fig. 7

Cost of transport service of the buses. Error bars indicate Chebyshev’s inequality for $k = \sqrt 2$, $k = 2$, $k = 3$ that cover 50%, 75% and 88.9% of the expected fuel cost values around the mean, respectively

The contribution of the fuel cost to $CTS$ decreases with increasing degree of electrification in the powertrain in a bus. While the fuel cost contribute 19.7% to the $CTS$ for the conventional bus ConvBi, it is less for the two hybrid-electric buses (10.9% for HybTw, 9.7% for HybAr) and the least for the plug-in hybrid-electric bus PlugTw (8.1%). The reason for this decreasing trend is the result of the much lower energy use of both hybrid-electric and plug-in hybrid-electric buses compared to the conventional bus. This observation becomes particularly important concerning the combined standard uncertainty of varying bus driver behaviour that influence directly the energy use as well as fluctuating fuel prices of the biodiesel blend and electrical energy. As a result, the coefficient of variation ($C_{v}$) is consistently higher for all buses by approx. 2–3%-points when accounting both varying bus driver behaviour and fluctuating fuel prices compared to only accounting varying bus driver behaviour. For instance, while the $C_{v}$ value at 80% passenger load for the energy use of ConvBi amounted to 4.8%, it increases for the fuel cost to 7.9%. Similarly, the $C_{v}$ values increase for the hybrid-electric buses HybTw and HybAr from 8.9% to 8.5% for energy use to 11.0% and 10.6% for fuel cost as well as for the plug-in hybrid-electric bus (PlugTw) from 13.7% to 15.6%. The largest increase in uncertainty is found for ConvBi (+ 3.1%-points for $C_{v}$) due to its much higher energy use compared to the other buses. Noteworthy, although PlugTw uses two different energy sources, namely the biodiesel blend and electrical energy, this bus is only slightly more influenced by accounting the additional uncertainty from fuel price fluctuations. The reason for this rather small increase is that PlugTw consumes considerable less energy than any other bus in this study and hence, its fuel cost is less impacted by fuel price uncertainties than the other buses. So, the energy-efficient operation in charge-depleting (CD) mode does not only save energy, but also mitigates the effect of fuel price fluctuations on the actual fuel cost for PlugTw.

Next, Chebyshev’s inequality is used to make statements about the probability distribution and to quantify the extent of deviation for expected fuel cost values from the estimated mean at 80% passenger load. For example, in the case of $k = 3$, three times the combined standard uncertainty ($3 \cdot u_{c}$) must be considered to cover 88.9% of the expected values. Similarly, three times the coefficient of variation ($3 \cdot C_{v}$) can be used to express the deviation in percentage. For instance, ConvBi has got a value for $3 \cdot C_{v}$ of 24%, which is much lower than for HybTw (33%), HybAr (32%) and PlugTw (47%). While these numbers show that a rather large dispersion of expected values around the mean must be considered for a coverage of 88.9%, they also show that the estimated combined standard uncertainty increases with increasing degree of electrification in the powertrain, i.e. the relative dispersion is the smallest for ConvBi, whereas it is the largest PlugTw. Hence, fuel cost and uncertainty pose opposite trends, because the fuel cost is the highest for ConvBi, whereas it is the lowest for PlugTw, and the uncertainty is the lowest for ConvBi, whereas it is the highest for PlugTw. Additionally, the estimation of the two hybrid-electric buses HybTw and HybAr are situated in-between the values for ConvBi and PlugTw and therefore, they represent trade-off options concerning fuel cost and uncertainty.

Evaluation of replacement scenarios

This scenario analysis assesses potential replacement scenarios, in which hybrid-electric and plug-in hybrid-electric buses are introduced and replace the currently operated conventional bi-articulated buses (i.e. the baseline scenario ScBaseline), considering the actual time table of the BRT route in Curitiba. The evaluation is done based on the weekly cost of transport service ($WeeklyCTS$), while taking into account the service quality in terms of average headway ($AverageHeadway$). The $WeeklyCTS$ are rounded to thousands of USD. The complete output from the optimisation model is provided in the electronic supplementary material. A summary of the key findings is provided in Table 11. The average bus fleet composition states the share between the four types of buses on average, i.e. the average share of the buses of type $b$ over all days $d$ and time slices $ts$.

Table 11 Results of the scenario analysis

The $WeeklyCTS$ of the baseline scenario ScBaseline amounts to 61,000 USD/week, while achieving an $AverageHeadway$ of 11.0 min/bus. In contrast, if 50% of the conventional bi-articulated buses (ConvBi) are replaced, then the $WeeklyCTS$ increases by 29%, while, however, also achieving an improved transport service with an $AverageHeadway$ of 8.1 min/bus, i.e. 26% less waiting time for passengers at a bus stop until the next bus leaves. Although, most buses are still of the conventional type (46.4%), there is a considerable share of 40.0% hybrid-electric articulated buses (HybAr) that is complemented by 12.0% hybrid-electric two-axle buses (HybTw). The remainder (1.6%) are plug-in hybrid-electric two-axle buses (PlugTw), which is an interesting finding as it show that this bus can compete with HybTw, despite higher cost of transport service $CTS$ per distance (PlugTw: 3.716 USD/km; HybTw: 3.049 USD/km). This highlights that the replacement of buses is not only a question of $CTS$, but also of the actual passenger carrying capacity of a bus. In this respect, PlugTw’s passenger carrying capacity amounts to 96 passengers, which is more than for HybTw (PCC: 79). As a result, fewer buses of type PlugTw can provide the necessary transport service on the BRT route in a more cost-effective way than using more buses of the type HybTw. If all ConvBi are replaced such as in the scenario ScConv0, then the $WeeklyCTS$ amounts to 100,000 USD/week (64% more than in ScBaseline), while having an $AverageHeadway$ of 6.4% (42% less than in ScBaseline). The bus fleet in this scenario consists of mostly HybAr (88.2%), followed by similar shares of HybTw (6.5%) and PlugTw (5.3%). Since the shares of HybTw and PlugTw are quite similar, this finding again confirms that PlugTw represents a competitive techno-economic option to HybTw when aiming at a minimisation of the $WeeklyCTS$.

The next scenario ScHybrid100 considers only hybrid-electric buses for the replacement to illustrate how buses of this type would influence the $WeeklyCTS$ and service quality on the BRT route. In this scenario, the ConvBi fleet is almost completely replaced by a share of 93.5% HybAr, while being complemented by a small share of 6.5% HybTw. This gives the same $WeeklyCTS$ as well as same $AverageHeadway$ as previously found in the scenario ScConv0. The difference between the ScConv0 and ScHybrid100 scenario is though that the share of 5.3% PlugTw in the ScConv0 is completely replaced by HybAr, while the share of 6.5% HybTw remains the same.

The next scenario promotes more electrification of the BRT route by requiring a minimum share of 25% plug-in hybrid-electric two-axle buses (PlugTw), i.e. the scenario ScPlug25. Comparing the findings of ScPlug25 to the previous two scenarios ScConv0 and ScHybrid100 shows that the set target leads to a further increase by 10,000 USD/week amounting to $WeeklyCTS$ of 110,000 USD/week (80% more than in ScBaseline), while the $AverageHeadway$ decreases from 6.4 min/bus to 5.7 min/bus (48% less than in ScBaseline). In regards to the bus fleet composition, the target of 25% PlugTw is actually exceeded and reaches a share of 40.9%. This finding reinforces the previous observation that PlugTw can compete with HybTw, despite its higher $CTS$. The remainder (59.1%) buses in the bus fleet are HybAr buses. Since HybAr did not reach a share of 75%, PlugTw represents also a viable techno-economic option compared to HybAr buses under the given circumstances. A further increase of the PlugTw buses as in the next two scenarios ScPlug50 (at least 50% PlugTw) and ScPlug100 (all buses PlugTW) shows that the $WeeklyCTS$ increase gradually to 113,000 USD/week (85% more than in ScBaseline) and 147,000 USD/week (139% more than in ScBaseline), respectively. Besides, the $AverageHeadway$ is reduced to 5.5 min/bus in ScPlug50 (50% less than in ScBaseline) and 4.0 min/bus in ScPlug100 (64% less than in ScBaseline). The 50% of PlugTw buses are complemented by the same share of HybAr buses in the scenario ScPlug50.

Based on the scenario analysis, there exists obviously a trade-off between cost ($WeeklyCTS$) and service quality ($AverageHeadway$) when replacing large conventional bi-articulated buses (ConvBi) by smaller but technologically more advanced buses (HybTw, HybAr and PlugTw). The $WeeklyCTS$ increases between 64% and 139% in the case of a complete replacement of all conventional bi-articulated buses in the bus fleet by advanced buses. The optimisation model demonstrated that HybAr is the most preferred bus to replace ConvBi.

In addition to changes in cost and service quality, other side effects should be mentioned. For example, the findings by (Kim et al. 2011) for the case of Seoul in South Korea showed that advanced buses can positively influence the perception of the city’s residents on public buses. And thus, the operation of more advanced buses such as hybrid-electric and plug-in hybrid-electric buses could also potentially contribute to a more positive perception of Curitiba’s residents on the public bus transport service. Furthermore, as it was shown in the analysis, the choice of a bus is influenced by both $CTS$ and passenger carrying capacity. The applied optimisation model demonstrated that the plug-in hybrid-electric bus PlugTw represents a viable option that can compete with the two hybrid-electric buses HybTw and HybAr. Additionally, the scenario analysis showed that the $AverageHeadway$ could be reduced by up to 64% compared to the baseline scenario. In this regards, a comprehensive study by (Hensher and Li 2012a, b) analysed 46 BRT systems globally (including Curitiba) and found statistical significance that the shorter the headway is, the more passenger trips are made. Thus, in addition to the commonly discussed aspect of cost, also convenience of the transport service must be considered to attract more paying passengers that can potentially increase the revenues.

Conclusions

This paper analysed the influence of passenger load, driving cycle, fuel price and four different types of buses on the cost of transport service for one BRT route in Curitiba, Brazil. The energy use was estimated for a conventional bi-articulated bus (ConvBi), a hybrid-electric two-axle bus (HybTw), a hybrid-electric articulated bus (HybAr) and a plug-in hybrid-electric two-axle bus (PlugTw) considering different passenger loads and driving cycles. The energy use estimations could be empirically validated through comparison to real-world data from Curitiba as well as data from other cases. Then, the fuel cost and uncertainties were estimated. Based on this and additional cost data, replacement scenarios for the currently operated conventional bi-articulated bus fleet were determined using a techno-economic optimisation model aiming at minimising the weekly cost of transport service. The study’s conclusions are tied to the two research questions (i) and (ii) from the introductory section in the following.

• i) How do passenger load, driving cycle and fuel price influence the fuel cost and cost of transport service of different types of buses?

  The passenger load influences the energy of the buses considerably in the simulations, which is stated by the following ranges covering 0% to 100% passenger load. The comparison between the buses shows that ConvBi uses the largest amount of energy (24.89–36.50) MJ/km, followed by HybAr (13.45–16.91) MJ/km, HybTw (11.51–14.20) MJ/km and PlugTw (6.24–10.33) MJ/km. The plug-in hybrid-electric bus PlugTw is the most sensitive bus to varying bus driver behaviour in this study. The coefficient of variation ($C_{v}$) of PlugTw amounts to 13–16% with the highest value at passenger load of 0%. In comparison, the conventional bus ConvBi is the least influenced by this uncertainty as stated by an estimated $C_{v}$ of 4–5%. The $C_{v}$ values amount to 8–9% for the two hybrid-electric buses and therefore, these buses are situated in-between ConvBi and PlugTw. Obviously, a trade-off exists between energy efficiency and sensitivity to varying bus driver behaviour. Besides, when relating the energy use to passenger-distance, the importance of utilising the passenger carrying capacity of a bus becomes obvious as the values of all buses decrease drastically with increasing number of passengers.

  The fuel cost contribute to a large extent to the cost of transport service ($CTS$) for a bus, although the importance differs between the four types of buses. For example in the case of a passenger load of 80%: While the fuel cost represent 19.7% of the $CTS$ for the conventional bus ConvBi, the importance decreases as the energy use decreases leading to contributions of 10.9% for HybTw, 9.7% for HybAr and 8.1% for PlugTw. Meanwhile, the combined standard uncertainty increases by 2–3%-points as fluctuating fuel prices add another uncertainty to the existing varying bus driver behaviour. The uncertainty analysis further shows that the probability distribution corresponding to Chebyshev’s inequality results in a large dispersion of expected fuel cost around the estimated mean. For statements aiming at a 88.9% coverage ($k = 3:$ giving $3 \cdot u_{c}$, or $3 \cdot C_{v}$) of the expected fuel cost values, the deviations expressed in percentage amount to 24% for ConvBi, 33% for HybTw, 32% for HybAr and 47% for PlugTw. The relative dispersion is the smallest for ConvBi, whereas it is the largest PlugTw. Hence, fuel cost and uncertainty pose opposite trends, because the fuel cost is the highest for ConvBi, whereas it is the lowest for PlugTw, and the uncertainty is the lowest for ConvBi, whereas it is the highest for PlugTw. Therefore, a trade-off also exists between fuel cost and combined standard uncertainty of varying bus driver behaviour and fluctuating fuel prices.

  Based on these findings, a bus operator ought to consider carefully the uncertainty of a bus concerning fuel cost and potential impact on the economic planning before the bus is acquired. The answer to which type of bus to choose for the replacement of conventional bi-articulated buses (ConvBi) operated on the BRT was done based on the actual time table of the BRT route in Curitiba and is answered next.

• ii) How do replacements of the currently operated conventional bi-articulated buses by other types of buses influence the cost of transport service and service quality for the operation of a BRT route?

  The scenario analysis for a passenger load of 80% demonstrates that a complete replacement of the currently operated conventional bi-articulated buses comes along with an increase of at least 64% and up to 139% for the weekly cost of transport service ($WeeklyCTS$) for the BRT route. The reason for this drastic increase is due to the fact that a direct one-by-one substitution of ConvBi by any of the three buses is impossible, since the passenger carrying capacities of HybTw, HybAr and PlugTw are much smaller. Hence, more buses are actually needed to provide the same aggregated passenger carrying capacity to transport the ridership on the BRT route. Nevertheless, the type of bus to choose for the replacement of ConvBi is not only a question of $CTS$, but also of the passenger carrying capacity. In this respect, the optimisation model demonstrated that HybAr is the most preferred option to replace ConvBi. Moreover, it was also found that PlugTw represents a techno-economic viable option that can compete against both HybTw and HybAr.

  While the $WeeklyCTS$ increases in every replacement scenario, the service quality is also improved as more buses operate at the same time on the BRT route. This leads to a reduction of the average headway $AverageHeadway$ from 11.0 min/bus as in baseline scenario to 4.0 min/bus if all ConvBi are replaced by PlugTw. This, by implication, means that passengers need to wait 64% less until the next bus leaves the bus stop. Less waiting time gives more convenience for the passengers using the BRT route, which in turn could attract more paying passengers, e.g. considering the study by (Hensher and Li 2012a, b) who found that a short headway increases the number of passenger trips. In this respect, the replacement of conventional bi-articulated buses by more smaller sized buses, such as those that were analysed, could improve the factor of convenience. Meanwhile, hybrid-electric and plug-in hybrid-electric buses employ more technologically advanced powertrains compared to the conventional powertrain as in ConvBi. Considering the findings by (Kim et al. 2011) that advanced buses influence positively the perception of the residents in a city on public buses, the operation of more advanced buses such as hybrid-electric and plug-in hybrid-electric buses could potentially also influence positively the perception of the residents of Curitiba on the public bus transport system.

  In conclusion, the findings of the techno-economic analysis for the potential replacement of the currently operated conventional bi-articulated buses demonstrated the possibility to improve the service quality of the BRT route, but only at the corresponding cost increase.

Following the conclusions, some indications for future work are given concerning other aspects that can complement the analysis of this study. For instance, more research work on bi-articulated buses would be needed about their energetic and environmental life-cycle. While this study already provides extensive data about the Tank-to-Wheel stage in the life-cycle of this bus, more research on other life-cycle stages such as production and recycling would be useful to assess replacement scenarios based on the whole life-cycle. In this way, a multifaceted life-cycle assessment would be possible considering jointly energy, environment and economic aspects.

Appendix

See Tables 12, 13 and 14.

Table 12 Glossary

Table 13 Abbreviations

Table 14 Symbols and units