Abstract
Assessing and predicting car type choices are important for policy analysis. Car type choice models are often based on aggregate alternatives. This is due to the fact that analysts typically do not observe choices at the detailed level that they are made. In this paper, we use registry data of all new car purchases in Sweden for two years where cars are observed by their brand, model and fuel type. However, the choices are made at a more detailed level. Hence, an aggregate (observed) alternative can correspond to several disaggregate (detailed) alternatives. We present an extensive empirical study analyzing estimation results, in-sample and out-of-sample fit as well as prediction performance of five model specifications. These models use different aggregation methods from the literature. We propose a specification of a two-level nested logit model that captures correlation between aggregate and disaggregate alternatives. The nest specific scale parameters are defined as parameterized exponential functions to keep the number of parameters reasonable. The results show that the in-sample and out-of-sample fit as well as the prediction performance differ. The best model accounts for the heterogeneity over disaggregate alternatives as well as the correlation between both disaggregate and aggregate alternatives. It outperforms the commonly used aggregation method of simply including a size measure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Models that analyze and forecast car type choice are of interest to policy makers due to the high contribution of car usage in energy consumption and greenhouse gas emissions. For this reason, car type choices have been extensively studied during the previous decades. For example, Jong et al. (2004) and Potoglou and Kanaroglou (2008) provide reviews of the related literature. These models can be used to evaluate policies that aim at influencing the composition of the car fleet towards energy and emissions efficient alternatives. For instance, Hugosson et al. (2016), Hensher and Plastrier (1985), Mannering (1983) and Page et al. (2000) analyze policies in Sweden, Australia, the United States and the United Kingdom. In order to design effective policies, consumer valuations of important attributes like fuel efficiency are necessary. However, studies on such consumer valuations are not conclusive. Brownstone et al. (2015) suggest that discrepancy in the results may be partially due to the practice of aggregation of alternatives.
Car type choice models are often based on aggregate alternatives. This is due to the fact that analysts typically do not observe choices at the detailed level that they are made. In this paper, we use registry data from Sweden where cars are characterized by their brand, model and fuel type. However, the choices are made at a more detailed level considering e.g. the version of the model. Hence, an aggregate (observed) alternative can correspond to several disaggregate (detailed) alternatives. The associated modeling challenge resides in how to accurately model the true choice set of disaggregate alternatives while estimating models using observations of aggregate alternatives.
The objective of this paper is to empirically analyze different aggregation methods and compare estimation results, in-sample fit, out-of-sample fit and prediction results. We use two years of registry data from Sweden that contains all new car purchases in 2006 and 2007. For the same 2 years, we also have detailed information on all car alternatives available in the Swedish market. This rich data set allows us to perform an extensive empirical study where we can account for the characteristics of disaggregate alternatives in different manners. We also analyze correlation between disaggregate and aggregate alternatives.
Early studies which address aggregation of alternatives in choice models are mainly situated in the context of residential location choice. Lerman (1977) includes a size measure which represents the number of disaggregate alternatives (house units) within an aggregate alternative (neighborhood) into the utility function to correct for the aggregation problem. His method, often used in the literature, is based on a multinomial logit assumption on the choice of disaggregate alternatives if the parameter associated with the size measure equals one. McFadden (1978), also in the residential location choice context, discusses that perceived similarities between disaggregate alternatives may violate the multinomial logit assumption, and therefore, he proposes nested logit models. This nested logit model has not been frequently used in the literature, probably due to the lack of data on disaggregate alternatives. Instead, several studies use an approximation that is valid when the number of disaggregate alternatives that correspond to each aggregate alternative is large, also proposed by McFadden (1978).
Daly (1982) discusses algorithmic challenges associated with maximum likelihood estimation of models that make use of aggregation methods. He proposes an algorithm that allows to simultaneously estimate all model parameters which was a challenge at the time when that paper was published. Since then, there have been extensive developments on non-linear optimization algorithms, along with an exponential increase in computational power, which allows us to simultaneously estimate the parameters of the models in this paper.
There have also been efforts to model other spatial choices at the level of disaggregate alternatives. In this setting, one particular challenge is to construct the universal choice set and impute the attributes of non-chosen alternatives, see e.g., Bayer et al. (2004) and the recent work of Zolfaghari et al. (2016). This paper focuses on another issue related to the fact that choice observations are recorded at an aggregate level. In our case, the universal choice sets are known along with the attributes of the alternatives.
Several studies emphasize that using aggregate alternatives without correcting the model accordingly may lead to biased parameter estimates (e.g. Parsons and Needelman 1992; Haener et al. 2004). Brownstone et al. (2015) compare McFadden’s (1978) approach to Brownstone and Li’s (2017), where the choice probability of an aggregate alternative is defined as the sum of the choice probabilities of the disaggregate alternatives. Their results show that aggregation affects the point estimates and associated standard errors of the models. In a car type choice application using Danish registry data, Mabit (2011) includes the measurement for the size into the model. The parameter for this variable becomes positive and significant, explaining the influence of the supply side in the car type choice, which is usually not considered in the related literature. Spiller (2012) shows that the elasticity of demand for gasoline changes significantly under different assumptions of aggregation. Train and Winston (2007) estimates a mixed logit model for vehicle choice, which handles unobserved heterogeneity and correlation at an aggregate level, yet not accounting for the same issues related to, and typically propagated from, a more disaggregate level of choice. Mabit (2014) also estimates a mixed logit model for vehicle choice and includes the measure of the size.
This paper makes several contributions to the literature. The rich data set allows us to conduct an extensive empirical study where we do not only analyze estimation results and in-sample fit but also assess out-of-sample fit and prediction results. The aggregation methodology is based on the work by Brownstone and Li (2017) and McFadden (1978) and we define different choice models for disaggregate alternatives that we estimate using observations of choices reported at an aggregate level. These models range from multinomial logit to different nested logit structures accounting for correlation between disaggregate and aggregate alternatives. We propose a two-level nested logit model where the nest specific scale parameters are given by parameterized exponential functions. This model has the best results in terms of in-sample, out-of-sample and prediction results.
The remainder of the paper is structured as follows. In Sect. 2 we present the data sources and some descriptive statistics. We present aggregation methodology in Sect. 3 and the different choice models in Sect. 4. The empirical results are reported in Sect. 5 and finally, Sect. 6 concludes.
Data
In this paper, we use two different data sources covering two years of interest, namely 2006 and 2007. The first data source is the Swedish car registry that contains all passenger cars in the Swedish fleet. The second data source contains detailed information about all car types available on the Swedish market during the two years. In this section, we start by describing the registry data followed by the data on alternatives and finally, we present how we merge the two data sources.
Swedish car registry data
The car registry data contains all passenger cars in Sweden that are owned privately or by a company. We focus on new car purchases done by persons (not companies). We hence need to extract these observations from the registry and exclude imports. We use three attributes that should all be equal to the same year in order to identify new cars: model year, production year and first registration date. Combining these attributes is important since, in a given year, the registry contains older cars that are purchased and registered for the first time. This definition of new cars results in 107,717 observations of new cars in 2006 and 116,566 in 2007. These numbers are slightly lower than the official car sales statistics because of the previously described definition of new cars.
In 2007, Sweden introduced a purchase subsidy of 1000 euros for clean cars. At that time, a clean car was defined as one meeting the Euro 4 (2005) standard and emitting less than 120 g/km of \(\text {CO}_2\). Moreover, diesel cars had to be equipped with a particle filter. Given this context, we present descriptive statistics on the fuel type of new cars in Table 1. The percentage of new petrol cars decreased by 20% in 2007 compared to 2007, mainly in favor of diesel cars that increased by 15% and ethanol cars that increased by 5%.
Data on new car alternatives
In order to model new car purchases, we need data on alternatives and important attributes that are missing in the car registry data, such as price, fuel consumption and \(\text {CO}_2\) emissions. For this purpose, we use a data source provided by a consultant company Ynnor AB. This data contains detailed information on all new cars available in the Swedish market in 2006 and 2007, down to version level (for example, Volvo S40 diesel 2.0 D Bas DPF).
Similar to the registry data, we present descriptive statistics on the number and percentage of car alternatives by fuel type in Table 2. We note that there is an important increase in the number of clean car versions offered in 2007 compared to 2006. Indeed, there are 7 more petrol versions, 14 more diesel versions, and 28 more ethanol versions. We also note that the number of petrol car versions increased by 169 while its total share decreased by 3% and the percentage of petrol car purchases (Table 1) decreased by 20%.
Data matching
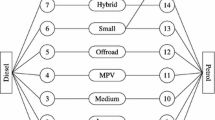
The two data sources that we describe in Sects. 2.1 and 2.2 do not define cars at the same level of detail. On the one hand, we have the registry data that define a car by its brand, model and fuel type (for example, Volvo S40 diesel). On the other hand, we have the data on alternatives that define cars at a detailed version level (for example Volvo S40 diesel 2.0 Bass DPF). Figure 1 illustrates the matching issue.
Henceforth, we use aggregate alternatives to refer to the level of detail of the registry data (observations) and disaggregate alternatives the level of detail of the choice sets. It is important to account for these different levels of details because certain attributes, such as price, can vary over disaggregate alternatives corresponding to a same aggregate one. We illustrate this fact in Fig. 2 using the data from 2006. The figure presents a histogram showing the distribution of the price coefficient of variation (CV) over aggregate alternatives. The CV is the ratio of the standard deviation to the mean. We compute the CV for the price for each aggregate alternative. The figure shows that 25% of the aggregate alternatives in the 2006 data have a low CV while an important share has substantially higher values.
After matching the two data sources, we have 103,155 observations for 2006 and 112,964 observations for 2007. These values are slightly lower than the total number of new cars in the registry because of data issues. These observations correspond to 398 and 485 aggregate alternatives for 2006 and 2007, respectively. The number of disaggregate alternatives is 2320 and 2679, in 2006 and 2007, respectively.
Aggregation methodology
The aggregation methodology is motivated by the fact that only aggregate alternatives are observed on the demand side, and each such aggregate alternative corresponds to possibly many disaggregate alternatives. Thus, the data describes choices at an aggregate level, yet the actual cars that are available to consumers are described with their attributes at the disaggregate level. In this section, we describe how we make use of this data when estimating random utility models. The method of aggregation presented here is consistent with the model proposed by Brownstone and Li (2017) for broad choice data. It is also consistent with the approach in McFadden (1978).
It is assumed that an individual n chooses a disaggregate alternative \(l\in C\), from a universal choice set. However, we observe that individual n chooses an aggregate alternative \(i\in A\), where the elements of A represent a partition of C. That is, each aggregate alternative i corresponds to a set of disaggregate alternatives, \(L_i\), such that \(L_i \subset C\), \(\bigcup _i L_{i}=C\) and \(L_i\cap L_j=\emptyset\) if \(i \ne j\). Each \(L_i\) is obtained by grouping elements of C based on some main characteristics such as make, model, and fuel-type. Therefore, each \(L_i\) consists of disaggregate alternatives which share some main characteristics but differ in others, e.g. weight and body type. We note that the choice sets can be individual specific although we do not index the choice sets by n in order to be consistent with our application.
Since we have information regarding attributes at the more detailed level of disaggregate alternatives l, and we assume that individuals make choices from the universal choice set C, we wish to utilize this information to estimate a choice model P(l|C) specified at the disaggregate level. However, our observations of choices are at the aggregate level of i. Hence, for an aggregate alternative i we define L(i|A) as the likelihood, or probability, of observing the aggregate choice i, given that behavior is described by the disaggregate choice model \(P(l|C;\beta )\) where \(\beta\) is a vector of parameters. Observing a choice i means that the individual has chosen one of the alternatives in \(L_i\), and the probability of this occurring is given by
The model parameters \(\beta\) can be estimated by maximum likelihood and the log-likelihood function over the sample \(n=1,\ldots ,N\) is
where \(y_{ni}=1\) if person n chose i and zero otherwise. In the following section we describe the choice models \(P(l|C;\beta )\). In order to make the notation lighter, we omit \(\beta\) and henceforth write P(l|C).
Choice models
The objective of this article is to empirically analyze different ways to model aggregation and assess the in-sample and out-of-sample fit as well as prediction performance. In this section, we present five discrete choice models that account for aggregation and correlation across alternatives in different manners. In the following two subsections we present multinomial logit (MNL) and nested logit (NL) models. In this case, the NL models capture correlation across disaggregate alternatives and hence present alternative ways to model aggregation compared to MNL. In Sect. 4.3 we present a two-level NL model that is designed to capture the correlation across both disaggregate and aggregate alternatives. We keep the presentation brief since these models are not new to the literature. The only novelty that we introduce is that we specify scale parameters in one of the NL models as an exponential function. The same trick is used by Mai et al. (2015) to allow scale parameters to vary while avoiding the estimation of a large number of parameters.
Multinomial logit
If the probability of choosing a disaggregate alternative is a multinomial logit model
then we can write the likelihood of observing an aggregate choice i using (1) as
Here \(m_i\) denotes the number of alternatives in \(L_i\), and \({\bar{V}}_i\) denotes the mean of \(V_l\) over \(l\in L_i\). The above reformulation displays the idea that the utility of the aggregate alternative can be seen as a combination of the average utility that the aggregate choice provides plus a size factor \(\ln (m_i)\) and finally a measure of the heterogeneity of the disaggregate alternatives within the aggregate (McFadden 1978).
Nested logit models
The disaggregate alternatives are grouped into aggregate alternatives because they share certain observed characteristics. Since they are similar, they may also share unobserved characteristics. In this case, the independence from irrelevant alternatives property of the MNL model does not hold. McFadden (1978) proposes to model the correlation between utilities of disaggregate alternatives using a nested logit model where there is one nest per aggregate alternative. This nesting structure is illustrated in Fig. 3.
The probability of choosing \(l\in C\) is \(P(l|C)= P(l|i)L(i|A)\) and can be written as
where \(\lambda _i\) are nest specific scale parameters (sometimes called logsum parameters). We combine (1) and (5) to write the likelihood of observing an aggregate choice i
Comparing (6) and the MNL model (4), we note that the correlation of disaggregate alternatives affects the probability of observing an aggregate choice through the scale parameters. The latter are interacting with both the size factor \(\ln (m_i)\) and the measure of heterogeneity. In the results Sect. 5 we present estimation and prediction results for three models that are different versions of 6. We present these three versions in the following.
We call the first model NL without Heterogeneity (NLwH) which results from the assumption that the deterministic utilities of disaggregate alternatives are equal, i.e. \(V_l={\bar{V}}_i\), \(l\in L_i\). In other words, there is no heterogeneity, and the corresponding term in (6) equals zero. Moreover, we assume that the scale parameters are equal for all nests \(\lambda _i=\lambda ~\forall i\in A\). In this case, (6) simplifies to
Even though the underlying assumptions may seem restrictive, we include this model because it is used in the literature, for example, when there is no data on disaggregate utilities (Lerman 1977; Mabit 2011).
In the second model Nested Logit (NL), we include the term capturing the heterogeneity in disaggregate utilities, but we keep the assumption that the scale parameters are equal for all nests \(\lambda _i=\lambda ~\forall i\in A\). Accordingly, (6) becomes
Finally, in the third model Nested Logit with Nest Specific Scale Parameters (NLP), we allow the scale parameters to be nest specific which hence corresponds to (6). Since the number of aggregate alternatives can be large (in our application 398), we reduce the number of scale parameters to estimate by assuming that they follow a parameterized exponential function (a similar idea is used in Mai et al. 2015). In our case, we use one parameter \(\alpha\) and the number of disaggregate alternatives \(m_i\), \(\lambda _i=e^{-\alpha m_i}\). The probability of observing aggregate alternative i is hence
where \(\lambda _i=e^{-\alpha m_i}\).
Modeling correlation between aggregate alternatives
In the previous section, we define nested logit models that can capture the correlation between disaggregate alternatives. In this section, we present a two-level nested logit model that is designed to capture the correlation between aggregate alternatives as well. Such multi-level nested structures are known as network MEV models (Daly and Bierlaire 2006; Mai et al. 2017).
We illustrate the nesting structure in Fig. 4. The bottom level nests correspond to aggregate alternatives \(i\in A\), which in turn are grouped in upper level nests, in our case, according to brand. Let \(B_k\) denote aggregate alternatives that share the same brand \(k\in K\). Then the probability of choosing disaggregate alternative \(l\in C\) can be written as \(P(l|C)= P(l|i)P(i|k)P(k|C)\), or equivalently,
where \(I_{i}=\ln \sum _{l \in L_i}e^{V_{l}/\lambda _i}\), \(I_{k}=\ln \sum _{i \in B_k}e^{\lambda _i/\lambda _{k} I_{i}}\), \(\lambda _k=e^{-\gamma \sum _{i\in B_k} m_i}\) and \(\lambda _i=\lambda _k e^{-\alpha m_i}\). We note that we we use a parametrized exponential function for the different scales. The model is consistent with random utility maximizing behavior if \(\lambda _k<1\), and \(\lambda _i<\lambda _k\) for all i and k. This is the case if \(\alpha\) and \(\gamma\) are positive. Using (1) we can write the likelihood of observing an aggregate alternative as
Empirical results
In this section, we present estimation results and assess forecasting performance. We start by presenting the model specifications and the corresponding estimation results. We then present a cross-validation study to assess out-of-sample fit followed by forecasting results where we compared predicted market shares to actual ones.
Estimation results
We use the same linear-in-parameters utility specifications for all the models P(l|C) that we present in Sect. 4. Since the choice models are defined for the disaggregate alternatives, but only aggregate ones are observed, it is important to consider issues related to the identification of parameters. With this issue in mind, we have chosen to include a series of constants for brand, fuel type and body type while avoiding a full set of alternative specific constants that would not be identifiable. We also include a number of explanatory variables: price, tax, tank volume and weight divided by power (Table 3).
We estimate the parameters by maximum likelihood using MATLAB and a Quasi-Newton method for the non-linear optimization problem. Table 4 reports the parameter estimates and t-test values with respect to zero. We start by analyzing the parameter estimates. A Volvo station-wagon petrol car is used as reference alternative, and the corresponding constants are fixed to zero. Cars of this type have the highest market share in Sweden. According to expectation, and with few exceptions, the estimated constants for other brands, body types and fuel types are negative. The positive constants are associated with brands and fuel types having few observations, namely, luxury brands (Bentley, Ferrari, and Lamborghini) and E85 fuel type. The parameter estimates associated with explanatory variables are significant and have their expected signs. The tax parameter associated with diesel cars is positive but we note it should be interpreted together with the general tax parameter and the sum of the two remain negative. Hence, there is a higher sensitivity to paying tax for alternative fuel vehicles (AFV) than petrol ones while it is the other way around for diesel cars. We also note that the parameter estimates are highly significant, except for some luxury cars with small market shares.
We now turn our attention to the scale parameters. The scale parameter estimate \(\widehat{\lambda }\) of the NL model without (NLwH) and with heterogeneity (NL) are significantly different from one (t test 8.07 and 19.19 respectively). This is consistent with the finding in Mabit (2011). The scale parameters of models NLP and NL2 are less straightforward to analyze since they are given by an exponential function that depends on \(\widehat{\alpha }\) and \(\widehat{\gamma }\). For the NLP model, Fig. 5 shows a plot of \(\widehat{\lambda }_i=e^{\widehat{\alpha } m_i}\) for actual values of \(m_i\). We note that, as expected, \(\widehat{\lambda }_i\) decreases with the number of alternatives and is always less than 1. The lowest value 0.87 is close to \(\widehat{\lambda }\) of the NL model. We provide similar plots for the two-level nested logit model (NL2) in Fig. 6. The plot on the left shows the values of scale parameters for the upper nest, \(\widehat{\lambda }_k=e^{-\widehat{\gamma } \sum _{i\in B_k} m_i}\) as a function of the number of disaggregate alternatives (\(\sum _{i\in B_k} m_i\)). According to expectation it is a decreasing function. The right-hand plot shows \(\widehat{\lambda }_i=\widehat{\lambda }_k e^{-\widehat{\alpha } m_i}\) as a function of \(m_i\). There are several possible values for a given value of \(m_i\) since it depends on the upper nest through \(\widehat{\lambda }_k\). In both Figs. 5 and 6, \(\widehat{\lambda }\) is a decreasing function showing the correlation among disaggregate alternatives increases with the number of disaggregate alternatives. This finding is consistent with Haener et al. (2004).
Table 5 reports ratios of some parameters divided by price. The ratio values are similar in all models except for NL2 where they are higher. This can be explained by the difference in scale parameters as NL2 captures correlation between aggregate alternatives.
We can compare the in-sample fit (final log-likelihood value) of some of the models. It is not meaningful to compare NLwH with the others because it is not a restricted version of them, nor can any of the other models be formulated as a restriction of it. This can clearly be seen from the final log-likelihood values since the value is higher for MNL compared to NLwH while the latter has one more degree of freedom. We can, however, statistically compare MNL, NL, NLP and NL2 using a likelihood ratio test. The NL2 has a significantly better fit than the other three models showing that there is a significant correlation between aggregate and disaggregate alternatives and that this correlation is not the same across nests. Moreover, NLP has a significantly better fit than NL, but NL has significantly better fit than MNL. In the following section, we present a cross-validation study with the purpose to compare the out-of-sample fit of the five models.
Cross-validation study
We use the same data as in the previous section, namely the 103,155 observations from 2006. We repeatedly and randomly divide the data into two sets, one that is used for estimation and the other one to compute predicted choice probabilities. The latter are aggregated into a function, in our case predicted log-likelihood. We use two methods to define these sets of observations: random sampling (Monte Carlo) and tenfold. The sample sizes of the random sampling method are 82,524 (estimation) and 20,631 (prediction) which correspond to a 80%/20% division of the full set. We do 20 cross-validation iterations using this method and report the average predicted log-likelihood values in the first row of Table 6.
In the case of the tenfold method, the data is partitioned into 10 equally sized subsets (10,315 observations). These sets are used one by one to compute predicted log-likelihood values. The remaining 9 subsets are used for estimation. The second row of Table 6 reports the predicted log-likelihood averaged over the 10 iterations. Similar to in-sample fit, a higher value means better performance. Since the sample sizes and methods are different, the values in the two rows cannot be compared. Instead, we focus on the ordering of the models and note that it is the same for the two methods. The NL2 model has the best out-of-sample fit followed by NLP, NL, MNL, and NLwH.
Prediction results
In Sect. 2 we present data from two years: 2006 and 2007. The estimation and cross-validation results in the previous sections concerned only the observations from 2006. In this section, we use the models estimated on the 2006 data to predict brand market shares in 2007 after a clean car purchase subsidy of 1000 euros was introduced. We report the actual and predicted market shares in Table 7 as well as the root mean squared error of prediction (RMSE) for each model.
The results show that NL2 provides the most accurate forecasts according to the RMSE performance measure and the second-best model is NLP. These two models have the same ordering according to in-sample and out-of-sample fit as well. NL and NLwH have similar performance, and the MNL model has the worst prediction performance (although it has better in-sample and out-of-sample fit than NLwH). We note that all the models under predict the market share of Volvo. This may be due to brand loyalty in the Swedish market that the models do not capture. Furthermore, all the models except NL2 over predict the market share of BMW which could be explained by the fact that the number of disaggregate alternatives corresponding to this brand increased by 133% from 2006 to 2007. NL2 has brand specific nests and has more accurate substitution patterns between brands.
Conclusion
In this paper, we presented an extensive empirical analysis of aggregation methods for discrete choice models in a new car choice application. We used registry data covering all new car purchases in the Swedish market in 2006 and 2007 as well as detailed data on car alternatives available on the market in those years. In this context, the observations are at an aggregate level while actual alternatives are disaggregate.
We presented several different models of aggregation from the literature (McFadden 1978; Brownstone and Li 2017) as well as a new model specification where we allow scale parameters to vary over nests while keeping the number of parameters to estimate low. More precisely, we model scale parameter values with a parameterized exponential function.
We compared estimation results, in-sample, and out-of-sample fit as well prediction performance of five different models for the choice of disaggregate alternatives. The results showed that a two-level nested logit model that accounts for heterogeneity and correlation between disaggregate and aggregate alternatives with nest-specific scale parameters has the best performance in all aspects. The results also showed that the commonly used model where aggregation is only captured through a “size measure” has the worst out-of-sample fit and two other models have better prediction performance. Their findings are different from Haener et al. (2004). They report that accounting for heterogeneity did not improve the results compared to only including a size measure. They, however, focus on in-sample results and state that assessing prediction performance is an important topic for future research.
The findings of this paper suggest that it is important to account for correlation and heterogeneity between disaggregate alternatives when choice observations are at aggregate levels. We hope that the paper can stimulate more research in this direction, for example, modeling more complex substitution patterns and unobserved heterogeneity using logit mixture models. A key issue in that context is related to parameter identification.
References
Bayer, P., McMillan, R., Rueben, K.: An equilibrium model of sorting in an urban housing market. Technical report, National Bureau of Economic Research (2004)
Brownstone, D., Li, P.: A model for broad choice data. J. Choice Model. (2017). http://dx.doi.org/10.1016/j.jocm.2017.09.001
Brownstone, D., Bunch, D., Wong, T.: Aggregation bias in discrete choice models with an application to household vehicle choice. In: International Choice Modelling Conference, Austin, Texas, 10–13 May 2015
Daly, A.: Estimating choice models containing attraction variables. Transp. Res. B Methodol. 16(1), 5–15 (1982)
Daly, A., Bierlaire, M.: A general and operational representation of generalised extreme value models. Transp. Res. B Methodol. 40(4), 285–305 (2006)
De Jong, G., Fox, J., Pieters, M., Daly, A.J., Smit, R.: A comparison of car ownership models. Transp. Rev. 24(4), 379–408 (2004)
Haener, M.K., Boxall, P., Adamowicz, W.L., Kuhnke, D.: Aggregation bias in recreation site choice models: resolving the resolution problem. Land Econ. 80(4), 561–574 (2004)
Hensher, D.A., Plastrier, V.L.: Towards a dynamic discrete-choice model of household automobile fleet size and composition. Transp. Res. B Methodol. 19(6), 481–495 (1985)
Hugosson, M.B., Algers, S., Habibi, S., Sundbergh, P.: Evaluation of the swedish car fleet model using recent applications. Transp. Policy 49, 30–40 (2016)
Lerman, S.R.: Location, housing, automobile ownership, and mode to work: a joint choice model. Transp. Res. Rec. 610, 6–11 (1977)
Mabit, S.L.: Vehicle type choice and differentiated registration taxes. In: 39th European Transport Conference. Glasgow, Scotland, UK (2011)
Mabit, S.L.: Vehicle type choice under the influence of a tax reform and rising fuel prices. Transp. Res. A Policy Practice 64, 32–42 (2014)
Mai, T., Fosgerau, M., Frejinger, E.: A nested recursive logit model for route choice analysis. Transp. Res. B Methodol. 75, 100–112 (2015)
Mai, T., Frejinger, E., Fosgerau, M., Bastin, F.: A dynamic programming approach for quickly estimating large network-based MEV models. Transp. Res. B Methodol. 98, 179–197 (2017)
Mannering, F.L.: An econometric analysis of vihicle use in multivehicle households. Transp. Res. A Gen. 17(3), 183–189 (1983)
McFadden, D.: Modelling the choice of residential location. In: Karlqvist, A., Lundqvist, L., Snickars, F., Weibull, J. (eds.) Spatial Interaction Theory and Residential Location, pp. 75–96. North-Holland, Amsterdam (1978)
Page, M., Whelan, G., Daly, A.: Modelling The Factors which Influence New Car Purchasing. In: European Transport Conference. Homerton College, Cambridge (2000)
Parsons, G.R., Needelman, M.S.: Site aggregation in a random utility model of recreation. Land Econ. 68(4), 418–433 (1992)
Potoglou, D., Kanaroglou, P.S.: Disaggregate demand analyses for conventional and alternative fueled automobiles: a review. Int. J. Sustain. Transp. 2(4), 234–259 (2008)
Spiller, E.: Household vehicle bundle choice and gasoline demand: a discrete-continuous approach (2012). http://dx.doi.org/10.2139/ssrn.2129396
Train, K.E., Winston, C.: Vehicle choice behavior and the declining market share of us automakers. Int. Econ. Rev. 48(4), 1469–1496 (2007)
Zolfaghari, A., Polak, J., Sivakumar, A.: Choice set imputation in atomistic spatial choice models. Transp. Res. Rec. J. Transp. Res. Board 2564, 138–146 (2016)
Acknowledgements
We are grateful to Yu Shen, who started the work on merging the two data sources during his master’s thesis. We would also like to thank Anders Karlström and Staffan Algers for their valuable comments and also Mohammad-Reza Yahya for assisting us with the registry data. Finally, we are thankful to Ynnor for providing data on car alternatives.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Habibi, S., Frejinger, E. & Sundberg, M. An empirical study on aggregation of alternatives and its influence on prediction in car type choice models. Transportation 46, 563–582 (2019). https://doi.org/10.1007/s11116-017-9828-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-017-9828-5