Abstract
In order to reliably predict and assess effects of congestion charges and other congestion mitigating measures, a transportation model including dynamic assignment and departure time choice is important. This paper presents a transport model that incorporates departure time choice for analysis of road users’ temporal adjustments and uses a mesoscopic traffic simulation model to capture the dynamic nature of congestion. Departure time choice modelling relies heavily on car users’ preferred times of travel and without knowledge of these no meaningful conclusions can be drawn from application of the model. This paper shows how preferred times of travel can be consistently derived from field observations and conditional probabilities of departure times using a reverse engineering approach. It is also shown how aggregation of origin–destination pairs with similar preferred departure time profiles can solve the problem of negative solutions resulting from the reverse engineering equation. The method is shown to work well for large-scale applications and results are given for the network of Stockholm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Urban sprawl as well as inadequate supply of public transport and infrastructure promotes high demand for individual car travel during certain periods of time, which in urban areas often leads to congestion accompanied by long travel times and pollution. Several congestion-mitigating measures have been applied in different cities, such as public transport and road investments, time-dependent charges, traveller information etc. Dependable estimates of social benefit are important for correct choice of mitigating measure. However, reliably predicting the social benefits of congestion mitigating measures requires advanced transportation modelling methods that take into account various travel choice dimensions such as mode, departure time and route choice and that are able to calculate accurately the resulting travel times for the travellers.
Congestion is a highly dynamic phenomenon and the time gains from mitigating measures experienced by the user depend both on where and when the user travels. For example, reduced queuing at a bottleneck can alleviate congestion on road links upstream and reduce travel time for users not even passing the bottleneck. Furthermore, time-dependent congestion charging systems aim at moving traffic from the peak hour to the peak shoulders. This change of departure time is typically encouraged by so-called shoulder pricing: the charge increases in steps until the most congested point in time is reached and then decreases in steps after the peak. For example, a charging scheme with shoulder pricing was introduced in Stockholm in 2006.Footnote 1
Conventional transportation models, which lack departure time choice and use static assignment, are unable to capture the effects described above. Static assignment was used in the design of congestion charging schemes both in London using the AREAL model (ROCOL 2000) and Stockholm using the SAMPERS model (Beser and Algers 2001). Some models combine the static traffic assignment with a time-of-day model describing the choice between broad departure time intervals, such as peak and off-peak. Recent research has shown that, even though static models are good enough for designing the charging system, they severely underestimate the reduction in queuing time resulting from congestion charging (Engelson and van Amelsfort 2011; Eliasson et al. 2013) and thereby also severely underestimate the social benefits of the charges (Börjesson and Kristoffersson 2014). Another branch of research [see e.g. May and Milne (2000)], analyses impacts of congestion charging using more advanced (sometimes dynamic) assignment models coupled with a simple demand elasticity algorithm, which does not differentiate between trip suppression, mode or departure time changes.
Two of the most important changes to conventional models are thus to extend the demand model with departure time choice and replace the static equilibrium assignment with dynamic traffic assignment (DTA). This would more precisely represent the complex demand/supply-interactions in congested urban areas and thereby substantially improve estimates of social benefits of congestion mitigating measures.
Since state-of-the-art departure time choice models use disutility associated with deviation from a preferred time of travel, they require estimates of when the traveller would depart/arrive in the uncongested situation. Hence, departure time choice modelling relies heavily on car users’ preferred times of travel and without knowledge of these no meaningful conclusions can be drawn from application of the model. The aim of this paper is to derive preferred departure times (PDTs) of car users in a large urban network using reverse engineering. Reverse engineering can replace time and money-consuming travel surveys and ensure that the result of the departure time choice model is consistent with the observed spatial–temporal travel pattern. Another aim of the paper is to find explanatory factors that can be used to aggregate origin–destination (OD) pairs into different groups with similar PDT profiles.
Vickrey (1969), Abkowitz (1981) and Small (1982) laid the theoretical basis for departure time choice modelling. Their model formulations use information about travellers’ preferred departure/arrival time (PDT/PAT), since travellers are assumed to trade-off travel time and monetary cost against schedule delay.Footnote 2 Preferred times of travel are thus introduced to acknowledge the scheduling cost travellers face when being unable to start a planned activity on time. Travellers choose a departure time with (different level of) knowledge about the trip, such as the travel time at a different time-of-day and a perception about the trip’s travel time variability. Travellers may therefore respond to congestion or congestion charging by changing departure time to avoid long travel times, high charges or add a head start to account for travel time variability.
PDT/PAT is the optimal departure/arrival time in an uncongested situation, given trip duration and time constraints at the origin and destination. Application of a departure time choice model in planning practice is hindered by the difficulty in revealing the PDT/PAT. In data collection conducted for estimation of a departure time choice model, the respondents can be asked to state their preferred time of travel, but what the respondent had in mind when answering this question is not clear due to the hypothetical nature of PDT.
Previous work has often assumed a simplified distribution, such as all travellers in a market segment having the same PDT (Ben-Akiva and Abou-Zeid 2007) or that the PAT-distribution is uniform between 8.00 a.m. and 9.00 a.m. for commuters (De Palma and Marchal 2002). Without calibration of PDT’s, using, for instance, only a simplified exogenous assumption, the predictive capability of the transport model is uncertain.
There are very few studies that try to capture detailed information on preferred times of travel for large-scale departure time choice models. One such study is Polak and Han (1999), in which a relationship between preferred arrival time (PAT), actual arrival time (AAT) and socio-economic variables was established for the London area. The attractiveness of that method is its simplicity. Due to inconsistency between the departure time choice model and the derived relationship, however, the result when the model is applied may deviate considerably from observed departure times.
In this paper, schedule delay is defined with respect to departure time, i.e. deviation from PDT. In an uncongested situation there is no difference defining scheduling costs around PDT or PAT, since a shift from PDT then corresponds to a similar shift from PAT. Given congestion, the definitions differ and scheduling cost should be defined at the end where the traveller has the most crucial time constraint. The stated preference data collected for estimation of the departure time and mode switch model used in this paper indicate time constraints at both origin and destination (Börjesson 2006). In this paper we show that even commuting trips with fixed working hours (the fixed trip purpose) do not only have time constraints at destination, but also at origin, probably due to the timing of fixed trips being early in the morning and scheduling costs are known to increase for early morning departures (Tseng and Verhoef 2008). Defining scheduling costs with respect to PDT has advantages from an implementation point of view. It can also be argued that it is more adequate to define scheduling costs around PDT since PDT is what the traveller can control.
An advantage of using PAT is that disutility of travel time variability (TTV) can naturally be taken into account. Fosgerau and Karlström (2010) show that defining scheduling costs around PAT and given schedule delay parameters, the expected scheduling cost can be expressed as a constant factor times the standard deviation of travel time. This unifies the scheduling and mean–variance approaches commonly used for describing the importance of timing of an activity and disutility of travel time variability per se. The property is lost when defining scheduling cost around PDT, but can be accounted for by including both scheduling delays and TTV as variables in the utility function of the departure time choice model, which is the case in this paper.
In Teekamp et al. (2002) the reverse engineering approach is utilized for the first time in order to find preferred departure times from observed ones. The authors stress that the actual departure times (ADTs), which are the times possible to observe, cannot be assumed to be equal to the PDTs in a congested area. To avoid time- and money-consuming surveys, they propose the combined use of a departure time choice model and data observed from the field in order to estimate PDT profiles.
The reverse engineering approach is investigated further in van Berkum and van Amelsfort (2003). The authors apply reverse engineering to a network with two origins and two destinations. They note the importance of reaching equilibrium in assignment for the success of the reverse engineering approach. Berkum and van Amelsfort (2003) point out two directions for further research: either to apply maximum likelihood estimation instead of the inverse of the P-matrix or to extend the existing methodology to large-scale networks. The method is applied to the large-scale network of Utrecht in Bezembinder and Brandt (2004). However, Bezembinder and Brandt (2004) use only one common profile for base year departure time fractions for all OD pairs and thereby estimate only one PDT profile. Furthermore, they use a multinomial logit model even though departure time periods are highly correlated. The scheduling parameters are adopted from Small (1982) and their applicability to the Utrecht area is uncertain. Also, PDT fractions are estimated only for a sub-selection of the OD pairs—those for which the probability matrix is diagonal dominant. Bezembinder and Brandt (2004) point out several directions for future research, among others (1) to use separate departure time fractions and thereby PDT profiles for e.g. different purposes and types of OD relations, (2) to adapt parameters to local conditions and (3) to replace MNL by a more advanced choice model. In this paper we address all these three directions for future research and show results for the Stockholm network. Regarding point (1) we also evaluate along which dimensions (purposes, distances, origin areas etc.) PDT profiles are best estimated.
This paper continues in the next section with a description of the applied reverse engineering methodology. “The Stockholm application” Section contains an overview of the large-scale dynamic model for Stockholm. Resulting PDT profiles are given in “Results” Section and Conclusions” Section concludes.
Methodology
Reverse engineering is applied to departure time choice modelling in order to derive PDTs for the base year situation. The PDTs can then be used in application of the model to future charging scenarios, assuming that transport network costs change but the PDTs of the users stay approximately the same. Two major forms of input data are needed to derive PDTs for the base year using reverse engineering:
-
1.
Conditional probabilities to start in each departure time interval given a PDT interval
-
2.
An OD matrix stating the demand in each departure time interval, which has been adjusted to observed link flows and possibly other characteristics of the reference situation.Footnote 3
The equation system
Reverse engineering of PDTs relies on the fact that observed trips in a certain time interval are built up of trips from a set of PDT intervals, for which the road user has decided to actually depart in the considered time interval. Assuming that the users’ PDT lies in one of the time intervals \(y = 1, \ldots ,Y\) and that users depart in one of the time intervals \(t = 1, \ldots ,Y\), we obtain for each trip purpose and OD pair (6).
In (6), \(q^{t}\) is the expected number of trips actually starting in time interval \(t\), \(v^{y}\) is the number of trips that have PDT in time interval \(y\), \(P^{ty}\) is the conditional probability of starting in \(t\) given that the users’ PDT interval is \(y\) and \(Y\) is the number of time intervals in the model. (6) can be written in a more compact format as \(Pv = q\), where \(P\) is a square matrix of probabilities with column sums that equal one. If \(P\) is non-singular, then a unique solution vector \(\nu\) exists and, for each OD-pair, the number of trips in each PDT interval can be estimated by solving the equation system. Note that measured flow may be different from expected flow and that the calibrated demand matrix may contain errors. When applying reverse engineering in practice it is therefore likely that there are errors in the right-hand vector \(q\). Furthermore, deficits in the departure time choice model result in a badly conditioned \(P\) matrix, which may give large errors in \(\nu\) for small errors in \(q\). Even if the PDTs resulting from the reversal engineering approach are consistent with flow counts and departure time models in the baseline situation, there still is a problem of potentially wrong response forecast if there are substantial errors in PDTs. Moreover, if we allow for a negative number of PDT trips, then it would be very difficult to interpret the results of the model. The negative solutions indicate that OD pair level is too detailed for PDT estimation to hold.
Negative solutions
A realistic solution to the reverse engineering problem must fulfil the condition \(v^{y} \ge 0\), otherwise there will be a negative number of trips preferring to start in one or more of the time intervals.
A square, non-singular matrix \(A\) which gives a non-negative solution \(x\) to the equation system \(Ax = b\) for any positive right-hand-side vector \(b\) is called an inverse-positive matrix and has the property that \(A ^{ - 1} \ge 0\) (all entries in \(A^{ - 1}\) are greater than or equal to zero).
Since \(PP^{ - 1} = I\), simple reasoning implies that the positive matrix \(P\) cannot be inverse-positive. Indeed, the product of the second row in \(P\) with the first column in \(P^{ - 1}\) must equal zero, which means that there must be at least one negative element in \(P^{ - 1}\) since it is non-singular. One can thus not rely on a positive solution for any positive right-hand-side vector \(q\).
To solve the problem of negative solutions, a constraint \(v^{y} \ge 0\) could be imposed on (6). This results, however, in zero number of trips in PDT intervals for many of the OD pairs, which is unrealistic given actual demand in all time intervals and large zones.
Grouping of OD pairs
Negative solutions arise because of errors both in the probability matrix \((P)\) and the number of trips to actually depart \((q)\). The proposed solution to the problem is to group OD pairs and estimate PDT profiles at the aggregate level. Aggregation reduces the impact of errors and inconsistencies between different data sources and thus leads to fewer or no negative solutions (Fig. 3). The reliability of the entries in the \(P\) matrix depends on the explanatory power of the departure time choice model. At disaggregate level the reliability may be low. Undertaking reverse engineering simultaneously for several OD pairs reduces the impact of unexplained variance in the departure time choice model.
Aggregation of OD pairs is also beneficial from another point of view. Travellers differ in their preferred departure times, but it is likely that similarities exist, for example for trips with the same trip purpose and trips with nearby origins and destinations. The behavioural explanatory power of the PDT profiles is thus likely to be higher if the profiles are estimated for groups of OD pairs with similar PDT patterns.
Technically, the estimation is made by finding a weight \(w_{G}^{y}\) for each PDT interval \(y\) and group \(G\), which is to be multiplied by the total number of observed trips, \(n^{\omega }\), for OD pair \(\omega\) in order to get the PDT-demand for that OD pair: \(v_{{}}^{\omega y} = w_{G}^{y} n^{\omega }\). The share of trips in a PDT interval is thus assumed to be the same for all OD pairs in a group, but the actual number of trips differs. The weights are found by solving for each trip purpose and group of OD pairs \((G)\) an over-determined equation system (2).
Here \(N_{G}\) denotes number of OD pairs in group \(G\). Remember that the observed number of trips in each interval does not need to coincide with the expected number of trips. Therefore (2) does not need to be fulfilled exactly. The least squares solution to (2) is also the solution to the minimization problem:
for each trip purpose \((k)\) and group \((G)\). The weights \(w_{G}^{y}\) can thus be estimated by finding the solution to the minimization problem (6).
Evaluation measures
In order to assess the results of reverse engineering when it is applied to departure time choice modelling, some evaluation measures are needed. The measures used in this paper and the effects they capture are described below.
One aim of this paper is to find explanatory factors by which OD pairs can be aggregated into groups with common PDT profiles. The PDT profiles should differ between groups in order to explain differences in the data material regarding departure time preferences. A goodness-of-fit measure, the \({\rm X}^{2}\)-statistic (6), is used in order to compare explanatory factors.
Here \(\varOmega\) denotes number of groups, \(o^{yG}\) is number of trips in PDT interval \(y\) for group \(G\) after aggregation over all OD pairs in a group, and \(e^{yG}\) is the expected number of trips in PDT-interval \(y\) for group \(G\). A high value on the \({\rm X}^{2}\)-statistic implies large differences between the groups of the corresponding explanatory factor. Therefore, the chosen explanatory factor should be the one with highest \({\rm X}^{2}\)-value.
An evaluation measure to assess differences in peaking is also needed. If the ADT profile is less peaked than the PDT profile this indicates that travellers have spread out because of high travel costs during peak hour, so-called peak spreading. A measure of peakiness is the peak-hour-to-peak-period ratio (PHPPR), which is the percent of total demand that occurs during peak hour. The PHPPR measure is used for example in Cain et al. (2001). (5) shows the PHPPR formula for actual departure time profiles (ADT profiles). In order to calculate PHPPR for PDT profiles \(q\) is replaced by \(v\). The PHPPR for preferred and actual profiles can be compared in order to evaluate peak spreading effects.
The Stockholm application
The PDT profiles estimated in this paper are to be used in SILVESTER (SImuLation of choice betWEen Starting TimEs and Routes), which is a dynamic transport model for the Stockholm Area (Kristoffersson and Engelson 2009a). Also, the conditional probabilities used in reverse engineering are the probabilities of the SILVESTER departure time choice model. For the reader to understand the context this section starts with a description of the SILVESTER modelling system.
Description of the SILVESTER modelling system
The main application area of SILVESTER is comparison of different time-dependent congestion charging schemes and forecasts of impacts on travel times and traffic flows within the morning peak period (6.30–9.30 a.m.). The model may also be used to evaluate the impact of other congestion mitigating measures and institutional constraints such as fixed working hours.
In SILVESTER, the morning peak period is divided into twelve 15-min time intervals, and a mixed logit (also known as EClogit) departure time choice model allocates trips to each interval depending on their attractiveness. The attractiveness of a time interval is determined by its corresponding travel time, travel distance, travel time variability, monetary cost and how close it is to the PDT interval of the traveller. To account for correlation between time intervals, departure time choice has in previous literature often been modelled using the ordered generalized extreme value model (OGEV) or the multinomial probit model (MNP). Mixed logit, however, is a flexible model that can approximate both the OGEV model and the MNP model.Footnote 4 The mixed logit model used in SILVESTER was estimated based on data from a stated preference and revealed preference survey of 1044 car users in Stockholm (Börjesson 2008; Börjesson 2009). It distinguishes between three trip purposes: business trips (short: business), work trips with fixed working schedule and school trips (short: fixed), and work trips with flexible schedule and other trips (short: flexible).
There are fifteen alternatives in the choice model for the three trip purposes: to start in time period 1–12 (6.30–9.30 a.m.), start earlier than 6.30 a.m., start later than 9.30 a.m. or switch to public transport, except that for business trips the public transport alternative is not available.Footnote 5 The utility function is given by (6).
Here \(t\) is index of time period,Footnote 6 \(k\) is index of trip purpose, \(y\) is index of preferred time period, \(\omega\) is index of OD pair, \(d\) is index of draw from parameter distribution, \(SDE\) and \(SDL\) are schedule delay early and late respectively, \(M\) is monetary cost, \(T\) is travel time, \(\sigma\) is standard deviation of travel time, \(\varepsilon\) is a Gumbel-distributed error term, \(C_{p}\) is an alternative specific constant for public transport, and \(\delta\) is the share of the car users who also have a public transport monthly card.Footnote 7 The parameters labelled \(\beta\) are heterogeneous in the population, whereas parameters labelled \(b\) are constants. The model formulation thus includes \(SDE\) and \(SDL\). Preferred departure \(y\) is located between 6.30 and 9.30 a.m. Schedule delays are calculated between the centres of the corresponding time intervals, except for the periods before 6.30 a.m.and after 9.30 a.m. where \(t\) is taken as 6.22.5 and 9.37.5 correspondingly.
The fact that users are heterogeneous is taken into account by allowing the monetary cost and schedule delay parameters to be specified as distributions instead of constants, which is possible in a mixed logit framework. Thus, within and across trip purposes users have different values of time, values of schedule delay early and values of schedule delay late. The fact that adjacent time periods are in many respects more similar than time periods far from one another is accounted for by including correlation between the distributions for schedule delay early and schedule delay late parameters.
In SILVESTER, iterations towards a general equilibrium between supply and demand are performed. The origin–destination car travel times, travel distances and charges are calculated with the mesoscopic dynamic traffic assignment model CONTRAM (Taylor 2003), whereas the demand for each time interval and public transport alternative is calculated with the mixed logit discrete choice model described above. Standard deviations of car travel times are calculated using a separate travel time variability model based on Eliasson (2007) and public transport travel times are taken from skimming the transit network of another regional model for Stockholm County (the public transport travel times are assumed to be constant during the simulation period). Figure 1 shows a schematic picture of the iterative procedure in SILVESTER.
The network of Stockholm used in the SILVESTER application has 315 zones and 5850 links. To render calculations more effective and save run-time the number of OD pairs in the OD-matrix has with care been reduced from 90770 to 35120. The network covers an area of about 20 × 30 km, including central Stockholm. The area covered is depicted in Fig. 2, which also shows the subdivision of the network into inner city (I), north (N) and south (S). Area I coincides with the area inside of the congestion charging cordon, which is approximately a circle with a radius of 3 km.Footnote 8
The base year OD matrix with observed flows in each departure time interval emanates from a static regional model for Stockholm, which is part of the SAMPERS system (Beser and Algers 2001), and its corresponding OD matrix for the peak hour between 7.00 and 8.00 AM. This OD matrix was first divided into 15-min time periods and then extended to the time span 6.30–9.30 a.m. using general traffic flow profiles on a set of important roads. The CONTRAM OD matrix has then been calibrated over the years against traffic counts and travel time measurements using the software COMEST, which is a complementary tool to the assignment model (Taylor 2003).
The base year CONTRAM OD matrix (time-dependent with 15-min time periods) has been segmented in this paper such that it coincides with the trip purposes of SILVESTER. This implies that the time-dependent OD matrix has been split into three time-dependent OD matrices: for flexible, fixed and business trips respectively. This segmentation was done based on a Stockholm travel behaviour survey from 2004 (Trivector Traffic 2006). Table 1 shows that the trip purpose shares differ depending on starting time in the morning.
Implementation of reverse engineering in SILVESTER
In the application of reverse engineering to the Stockholm case, the base case is the situation without congestion charging. The conditional probabilities are calculated by applying the departure time choice model described above to this base case.
As mentioned earlier there are twelve PDT intervals in SILVESTER, each 15 min long. Thus \(Y = 12\) in the reverse engineering equation. Moreover, there are 35120 OD pairs and three trip purposes so \(\omega = 1, \ldots ,35120\) and \(k = 1,2,3\). None of the probability matrices (corresponding to a certain OD pair and trip purpose) resulting from the SILVESTER departure time choice model is a singular matrix. We have thus not experienced the problem discussed in van Berkum and van Amelsfort (2003) that a solution to (1) may not exist because of singularity of \(P\). A PDT profile can thus be estimated for each OD pair and trip purpose combination. The PDT solution is not, however, guaranteed to be non-negative (see “Negative solutions” Section). For each trip purpose, Table 2 gives the percentage of OD pairs with a PDT solution that contains one or more negative elements.
Further investigation indicates that the condition numbersFootnote 9 of the probability matrices \(P\) are generally higher for OD pairs with negative solutions (unweighted mean condition number is 3.4) than for OD pairs without negative solutions (unweighted mean condition number is 2.1). For each OD-pair \(\omega\), the condition number of matrix \(P^{\omega }\) is the maximum ratio of the relative error in v to the relative error in q. Although the condition numbers are not very high in the average (the condition number is always greater than 1), there might be still many OD-pairs with high condition number.
As noted in “Grouping of OD pairs” Section, aggregation of OD pairs into groups can mitigate the problem of negative solutions appearing in the PDT profiles. In SILVESTER, PDT profiles for groups of OD pairs are estimated by solving a minimization problem (3). Figure 3 shows the effect of random aggregation of OD pairs into groups. The larger the groups are, the smaller is the share of negative solutions. The percentage of OD pairs with one or more negative components in the PDT-solution decreases approximately as fast as \(27.4/x\), where \(x\) is number of OD pairs in each group (see the trend curve in Fig. 3). Results are free from negative solutions for groups larger than 100 OD pairs.
Random aggregation, however, is not preferable. In order to enhance the explanatory power of the model, it is desirable to aggregate OD pairs according to some factor that would reasonably explain the differences between the estimated group PDT profiles. Moreover, a significant difference between the profiles makes it more likely that the employed factor captures essential parts of population heterogeneity as regards preferred departure times.
Grouping OD pairs according to some explanatory factor requires aggregation over larger groups than random aggregation to fulfil the requirement for no negative solutions. In SILVESTER it was possible to find solutions that fulfilled both needs. Subdivisions into different OD pair groups were tried for each trip purpose (flexible, fixed and business). The subdivisions are based on the explanatory factors trip distance, average income of inhabitants in origin zone, geographic location of origin and geographic location of destination (Table 3).
Table 4 shows the value on the \({\rm X}^{2}\)-statistic for each explanatory factor and trip purpose. For each trip purpose, values in bold represent the highest \({\rm X}^{2}\)-values. The results show that “trip distance” is the best explanatory factor for the trip purpose flexible, whereas for fixed and business, differences between OD pair groups are best captured by “geographic location of origin”. The explanatory factor “geographic location of destination” also gets high values. This is most likely explained by the fact that most trips have origin and destination within the same geographical area (North, Inner City or South) and that correlation between origin and destination is high. Furthermore, the areas differ a lot regarding type of workplaces available, with blue-collar workplaces being in a majority in the South, white-collar in the inner city and a mixture of both in the North. These differences in types of workplaces have a substantial impact on work-starting times and thus also on departure times from home.
Apart from negative solutions another issue in previous reverse engineering applications has been the run-time of the estimation of PDT profiles. In this application, calculating a PDT profile for each OD pair and trip purpose combination using the software Matlab and a 3.21 GB RAM computer takes only 1.5 min in total, so run-time is not an issue in our case.
Results
Explanatory factors and resulting PDT profiles
For the trip purpose fixed, the grouping based on geographic location of origin resulted in the highest value of the \({\rm X}^{2}\)-statistic (Table 4). The PDT profiles are shown in Fig. 4. The shares of PDT trips for the early time periods (6.30–7.45 a.m.) are largest for trips with origin located in the southern parts of Stockholm, followed by trips with origin in the northern parts and then trips with origin in the inner city. Correspondingly, for late PDT intervals (7.45–9.30 a.m.) trips that originate from the inner city show the largest shares, trips with origin in the northern parts of Stockholm are in-between and trips originating in the southern parts result in the smallest shares.
The reason for the results shown in Fig. 4 is most likely historical differences between the northern and southern parts of the city. By tradition, types of occupation differ between the inhabitants in these two areas. The shares of blue-collar jobs are larger in the southern population than in the northern, and these occupations typically start early. The reason for trips with origin in the inner city preferring to travel latest is probably that, just as in the northern suburbs, the share of blue-collar jobs is low and in addition the trip distance is short, since many also have their destination in the inner city. Note also that the build-up of the morning peak is not captured for fixed trips. This would require starting the simulation period earlier than 6.30 a.m..
The sudden jump in PDT trips between the time periods 7.45–8.00 a.m. and 8.00–8.15 a.m. exists also in the ADT profile, which can be seen in Fig. 8. The reason for the jump is most likely twofold: first, 8.00 a.m. is the starting time of schools and many workplaces, which has a major impact on departure times; second, stating their departure times travellers might round off to the nearest half an hour. The segmentation of the baseline observed OD matrix into trip purposes has been done with purpose shares from a travel behaviour survey (Trivector Traffic 2006) where the purpose shares depend on time period, e.g. the share of fixed trips is higher in the beginning of the morning period than in the end (Table 1). There might be some round off error in these shares that should have been smoothed, but it is very difficult to separate these from the real impact of fixed school and working start times, wherefore observed ADT profiles are left unsmoothed.
For business trips the grouping based on geographic location of origin also gives the highest \({\rm X}^{2}\)-value (Table 4). The resulting PDT profiles are shown in Fig. 5.
For business trips the share of travellers preferring to start early (6.30–8.00 AM) is largest for trips with origin in the inner city and smallest for trips with origin in the southern parts of Stockholm, with the northern part in-between. The order is the other way around for the later part of the morning (8.00–9.30 AM). The likely reason for business trips from South and North starting later than business trips from the inner city is that, in the first two cases, a fairly long private trip often precedes the business trip. Similar to fixed trips, Fig. 5 shows a sudden jump between the time periods 7.45–8.00 a.m. and 8.00–8.15 a.m. in the PDT profiles for business trips. The jump is likely due to the common work start time of 8.00 a.m.. There might also be some impact of round-off error when users state their departure times. The business segment is however much smaller than the others, representing only 6–16% of trips depending on departure time interval (Table 1).
For the trip purpose flexible Table 4 shows that, among the tested explanatory factors, “trip distance” is the one that results in groups that differ most in their departure time preferences. However, on inspection it is found that the PDT profiles of the first two groups are rather similar. These groups are therefore combined into a single one. Figure 6 shows the resulting PDT profiles using the explanatory factor “trip distance” with two groups: trips shorter than 15 km and trips longer than or equal to 15 km.
From Fig. 6 one can see that those travelling long distances prefer to start earlier than those travelling short distances (except for the very first time period). The likely explanation is that even though these trips are flexible, it is still preferable from a cooperation point of view to be at work during the same hours. In order to achieve this, long-distance trips must start earlier than short-distance trips.
Comparison of PDT and ADT profiles
Figures 7 and 8 compare PDT and ADT profiles in order to evaluate differences between preferred and actual trip profiles and whether the results indicate that peak spreading has occurred or not. The result is shown both aggregated over trip purpose (Fig. 7) and for each trip purpose (Fig. 8).
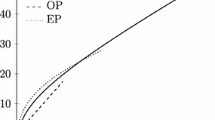
From Fig. 7 one can see that the resulting PDT and ADT profiles aggregated over all OD pairs and trip purposes differ in both level of “peakiness” and when the peak occurs: The PDT profile is more peaked and the peak occurs later than in the ADT case. The total PDT demand for all trips is 285,462 trips preferring to start during the analysed period. Since the total ADT demand is 267,507 trips, this means that about 6% of the PDT-trips switch to public transport or to a time interval outside the analysed period because of congestion.
From Fig. 8 one can see that the differences between the PDT- and ADT-profiles are dependent on trip purpose. Flexible is the largest segment and is also the one most similar to the overall profiles.
In this paper, peak hour is defined as the hour with most demand. Table 5 shows when the PDT and ADT peak hours occur for all trips and for the three trip purposes. Table 5 also shows that peak hour for the ADT profile occurs either at the same time or earlier than peak hour for the corresponding PDT profile. This indicates that travellers who change departure time switch to an earlier time period rather than a later one. The times at which the peak hours occur differ a lot between trip purposes. The peak is earliest for fixed trips, followed by flexible trips and latest for business trips. One should note that the time when the peak hour occurs for the different trip segments depends on more than trip flexibility; the segments differ in socio-economic characteristics (e.g. type of occupation), which has a major impact on when they prefer to undertake their trips. Flexible trips occur later than fixed trips because travellers in this segment start work later.
The peak-hour-to-peak-period ratio—PHPPR (5), which is the percentage of trips that occur during peak hour, can be used as a measure to evaluate peak spreading. The PHPPR for PDT and ADT profiles are compared in Table 5.
The PDT profiles are either more than or equally as peaked as the ADT profiles, i.e. many travellers have similar preferred departure times, but when they realize their trips they spread out to avoid congestion. Note that the situation analysed here is the one without congestion charges, which means that peak spreading occurs due to congestion—not due to an extra high charge during peak hour.
It is not possible to validate the PDT profiles directly since they are not directly observable. Instead we validate them indirectly by evaluating how they work in practice when applying them to the situation with and without the Stockholm charging scheme. The Stockholm congestion charging trial was carefully monitored and detailed data exist on the situation before and after introduction of the charges. Kristoffersson and Engelson (2009b) show that SILVESTER—based on the PDT profiles estimated in this paper—gives accurate predictions of traffic in the uncharged situation, see Fig. 9. Moreover, SILVESTER accurately predicts the changes that occur due to charging: flow on 59 validation links (see Fig. 2) spread out over the network are predicted to reduce on average 12% compared to measurements that showed on average 11% reduction. The travel time prolongation (how much longer travel time is compared to free-flow time) in the situation with congestion charges was measured to be 0.86 times the travel time prolongation before introduction of charges at 11 routes in the network. SILVESTER predicted this figure to be 0.87. Thus, using the PDT profiles estimated in this paper results in a model with good predictive capability.
Conclusions
Travellers in a congested road network face not only long car travel times; congestion also has an impact on the choice of when to depart from home. Departure time choice is in general modelled as a trade-off between generalized travel cost and schedule delay. The idea is that some users will accept departing somewhat early or late to work (or leisure activity) because their travel time, travel time variability and (if applicable) time-dependent congestion charges are reduced. The willingness to trade schedule delay against reduced travel costs increases with user schedule flexibility, for example if the user has flexible working hours. This is captured in the present paper by dividing trips into three trip purpose segments: flexible, fixed and business trips. Also, letting the schedule delay parameters of the utility functions be distributions rather than just constants captures heterogeneity within each trip purpose. This is captured in the present paper by using a mixed logit model rather than a simple MNL model. Furthermore, the mixed logit model is estimated on local conditions rather than using standard parameter values.
In order to calculate schedule delay, one must know the users’ preferred time of travel. Preferred times of travel are, however, not observable directly from the field in a congested city, since users have already adapted to the congested situation. The reverse engineering approach is a method in which observed (actual) times of travel from the field are used together with the departure time choice model in order to find the underlying preferred times of travel by “going backwards”.
The contributions of the present paper are in both methodology and application of reverse engineering in the departure time choice context. A methodological problem with the reverse engineering approach is that ill-conditioned probability matrices combined with errors in the observed number of trips may result in large errors in the preferred departure time profiles. For some OD-pairs and time intervals the method may even provide a negative number of preferred departures although the number of realised departures is non-negative in all time intervals. In the present paper, aggregation of OD pairs into groups is used as a method to solve this problem, since aggregation alleviates the impact of errors on the PDT profiles. Explanatory factors, by which OD pairs are aggregated into groups that are assumed to share a common PDT profile, capture similarities between PDT profiles of different OD pairs. Earlier papers have derived a single PDT profile for all OD pairs. In this paper we derive eight different PDT profiles, which provide enough aggregation to mitigate the impacts of errors on the PDT pattern but still allows for differences among trip purposes and OD pairs. Although the PDT profiles cannot be verified by direct observation, the difference between them can be explained by socio-economic and historical circumstances.
The reverse engineering results show that the differences between preferred and actual profiles are larger for flexible and business trips than for fixed trips. Flexible and business trips thus change departure time because of congestion to a greater extent than fixed trips. Not only do fixed trips have stronger time restrictions at work, they also seem to have strong time restrictions at the origin. The reason for this is not evident, but a tentative explanation is that fixed trips occur earlier in the morning, which has been shown to increase schedule disutility (Tseng and Verhoef 2008). Fixed trips are in general also more rigid, following a certain time schedule and less open to changes in timing of the trip. One should remember that the segments differ not only in trip flexibility, but also in socio-economic characteristics.
For both fixed and business trips aggregation of OD pairs is made based on geographic location of origin. Other groupings were also tried but showed less clear differences in their resulting PDT profiles. Which kind of grouping one should use is dependent on the specific city for which the model is calibrated. In the Stockholm case there are historical socio-economic reasons why the shares of fixed and business trips depend on where the origin is located. For flexible trips aggregation of OD pairs is made based on trip distance. The results indicate that travellers undertaking long trips prefer to start earlier than travellers undertaking short trips. A possible explanation for this pattern is that it is more beneficial to be at work when colleagues are there, even though working hours are flexible.
To sum up, this paper shows that it is possible to use the reverse engineering approach to derive preferred times of travel in a large network (Stockholm). The method is easy to use and consistent with observed times of travel in the specific city for which the model is calibrated. It is also consistent with the applied departure time choice model. We verify the reverse engineering method by calculating measures of peakiness and by applying the model to the Stockholm congestion charging scheme and validating the outcome against measurements. The measure of peakiness change as expected in the congested situation (ADT) compared to the uncongested situation (PDT), with more peaked PDT profiles compared to ADT which spread out due to congestion. The result thus indicates peak spreading due to congestion. The actual departure times are mostly shifted backwards compared to the preferred ones, which means that in order to avoid congestion car-users change their departures earlier rather than later. This is in line with previous research. Moreover, when adding congestion charges to the model, the flow reduction over the cordon and the travel time reduction on selected routes are in line with measured effects at introduction of congestion charging in Stockholm (Kristoffersson and Engelson 2009b, 2011).
Notes
Delay should here not be interpreted in the traffic engineering sense, where delay is defined as extra travel time in addition to travel time in free-flow conditions. Shifting departure time from ones preferred departure time implies a schedule delay, but does not necessarily result in a longer travel time. On the contrary, the reason to shift departure time may be to reduce travel time.
See e.g. Antoniou et al. (2006) for an example of a dynamic matrix adjustment procedure.
For an overview of models used for departure time choice see e.g. de Jong et al. (2003).
The public transport alternative was removed for business trips since in the collected stated choice data almost no business traveller chose public transport.
The time period index \(t = 0\) denotes departure times before 06:30, \(t = 1, \ldots ,12\) denotes departure times in the twelve quarters from 06:30–09:30 respectively and \(t = 13\) departure times after 09:30.
In the estimation, \(\delta\) was a dummy variable equal to 1 if the driver had a public transport monthly card and 0 otherwise.
For a more thorough description of the SILVESTER modelling system see Kristoffersson and Engelson (2009a).
The condition number of a matrix measures the sensitivity of the solution of a system of linear equations to errors in the data, and is calculated as the ratio of the largest singular value of the matrix to the smallest.
References
Abkowitz, M.: An analysis of the commuter departure time decision. Transportation 10(3), 283–297 (1981)
Antoniou, C., Ben-Akiva, M., Koutsopoulos, H.: Dynamic traffic demand prediction using conventional and emerging data sources. IEEE Proc. Intell. Transp. Syst. 153(1), 97–104 (2006)
Ben-Akiva, M., Abou-Zeid, M. 2007. “Methodological issues in modeling time-of-travel preferences.” In 11th World Conference on Transportation Research. Berkeley, California, USA
Beser, M., Algers, S. SAMPERS—The New Swedish National Travel Demand Forecasting Tool. In National Transport Models: Recent Developments and Prospects, 101–18, (2001)
Bezembinder, E., Brandt, F. “Application of an integrated static and dynamic traffic modelling system for large scale detailed networks.” In Proceedings of the 32nd European Transport Conference. Strasbourg, France (2004)
Börjesson, M. “Issues in urban travel demand modelling: ict implications and trip timing choice.” Doctoral Thesis, KTH, Stockholm (2006)
Börjesson, M.: Joint RP-SP data in a mixed logit analysis of trip timing decisions. Transp. Res. Part E 44(6), 1025–1038 (2008)
Börjesson, M.: Modelling the preference for scheduled and unexpected delays. J. Choice Model. 2(1), 29–50 (2009)
Börjesson, M., Eliasson, J., Beser-Hugosson, M., Brundell-Freij, K.: The Stockholm congestion charges—5 years on effects, acceptability and lessons learnt. Transp. Policy 20, 1–12 (2012)
Börjesson, M., Kristoffersson, I.: Assessing the welfare effects of congestion charges in a real world setting. Transp. Res. Part E 70, 339–355 (2014)
Cain, A., Burris, M., Pendyala, R.: Impact of variable pricing on temporal distribution of travel demand. Transp. Res. Rec. 1747, 36–43 (2001)
De Jong, G., Daly, A., Pieters, M., Vellay, C., Bradley, M., Hofman, F.: A model for time of day and mode choice using error components logit. Transp. Res. Part E 39(3), 245–268 (2003)
De Palma, A., Marchal, F.: Real cases applications of the fully dynamic metropolis tool-box: an advocacy for large-scale mesoscopic transportation systems. Netw. Spat. Econ. 2(4), 347–369 (2002)
Eliasson, J. “The relationship between travel time variability and road congestion.” In Proceedings of the 11th World Conference on Transport Research, Berkely, California (2007)
Eliasson, J., Börjesson, M., van Amelsfort, D., Brundell-Freij, K., Engelson, L.: Accuracy of congestion pricing forecasts. Transp. Res. Part A 52, 34–46 (2013)
Eliasson, J., Hultkrantz, L., Nerhagen, L., Rosqvist, L.: The Stockholm congestion-charging trial 2006: overview of effects. Transp. Res. Part A 43(3), 240–250 (2009)
Engelson, L., van Amelsfort, D 2011 “The role of volume-delay functions in forecast and evaluation of congestion charging schemes, application to Stockholm.” In Proceedings of the Kuhmo Nectar Conference. Stockholm (2011)
Fosgerau, M., Karlström, A.: The Value of Reliability. Transp. Res. Part B 44(1), 38–49 (2010)
Kristoffersson, I., Engelson, L.: A dynamic transportation model for the stockholm area: implementation issues regarding departure time choice and OD-pair reduction. Netw. Spat. Econ. 9(4), 551–573 (2009a)
Kristoffersson, I., Engelson, L.: “Valideringsrapport—Hur Väl Kan Trafikmodellen SILVESTER Återskapa Stockholmsförsökets Effekter? (Validation Report—How Good Is the SILVESTER Transport Model at Predicting the Effects of the Stockholm Trial?).” Technical Report, CTR, KTH. ISSN 1653-4484. ISBN 13: 978-91-85539-44-4. http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1050165&dswid=629 (2009b)
Kristoffersson, I., Engelson, L 2011. “Alternative road pricing schemes and their equity effects: results of simulations for Stockholm.” In Proceedings of the TRB 90th Annual Meeting, Washington, D.C
May, A., Milne, D.: Effects of alternative road pricing systems on network performance. Transp. Res. Part A 34(6), 407–436 (2000)
Polak, J, Han, X. “PATSI—Preferred arrival times synthesised by imputation.” Report to the DETR, Centre for Transport Studies, Imperial College London (1999)
ROCOL.: “Road charging options for London, a technical assessment. Annex E—behvioural modelling and model parameters.” London: HMSO. http://webarchive.nationalarchives.gov.uk/20100528142817/http://www.gos.gov.uk/497417/docs/204399/rocol_ch8_annexes_121k.pdf (2000)
Small, K.: The scheduling of consumer activities: work trips. Am. Econ. Rev. 72(3), 467–479 (1982)
Taylor, N.: The CONTRAM dynamic traffic assignment model. Netw. Spat. Econ. 3(3), 297–322 (2003)
Teekamp, R., E Bezembinder, D van Amelsfort, van Berkum, E. “Estimation of preferred departure times and changes in departure time patterns.” In Proceedings of the TRB 81th Annual Meeting, Washington, D.C. (2002)
Trivector Traffic A., B.: “Förändrade Resvanor I Stockholms Län (Changes in travel behaviour in Stockholm County).” Report 2006:67. http://www.stockholmsforsoket.se/upload/Rapporter/Resvanor/Under/Förändrade_resvanor_i_stockholms_län_060830.pdf (2006)
Tseng, Y.-Y., Verhoef, E.: Value of time by time of day: a stated-preference study. Transp. Res. Part B 42(7–8), 607–618 (2008)
Van Berkum, E., van Amelsfort D. “A reverse engineering approach to determine preferred time of travel patterns.” In Proceedings of the 31st European Transport Conference, Strasbourg, (2003)
Vickrey, W.: Congestion theory and transport investment. Am. Econ. Rev. 59(2), 251–260 (1969)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kristoffersson, I., Engelson, L. Estimating preferred departure times of road users in a large urban network. Transportation 45, 767–787 (2018). https://doi.org/10.1007/s11116-016-9750-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-016-9750-2