Abstract
Understanding travellers’ response is essential to address policy questions arising from spatial and transport planning sectors. This paper demonstrates the usefulness of the multi-state supernetwork approach to investigate the effects of land-use transport scenarios on individuals’ travel patterns. In particular, it illustrates that multi-state supernetworks are capable of representing activity-travel patterns at a high level of detail, including the choice of mode, route, parking and activity location. Multi-faceted activity-travel preferences can be accommodated in supernetworks. Using a micro-simulation approach, the adaptation of individuals’ travel patterns to policies can be readily captured. The illustration concerns hypothetical land-use and transport scenarios for the city of Rotterdam (The Netherlands), focusing on accessibility changes, modal substitution and shift in the use of transport and location facilities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cities throughout the world are struggling with the challenge of improving the efficiency of their transport systems, which heavily depend on private motor vehicles. Considerable efforts in current spatial and transport planning are devoted to designing future cities that enable mobility while reducing car dependency and increasing the share of energy-efficient transport modes. Predicting the impacts of competing policies is not an easy task due to the overwhelming data dependency and multitude of concurrent changes (Wegener 2004). Spatial development determines the need for spatial interaction, and thus transport, which in turn has impacts on land use patterns. They together shape individuals’ activity-travel behavior. In that sense, the models used to support travel demand management need to integrate them to capture the underlying effects (Waddell 2011). This notion has been widely accepted in contemporary activity-based travel demand models.
Activity-based models acknowledge the fact that the travel needs of a population are determined by their need to participate in activities spread out in time and space (Chapin 1971; Bhat and Koppelman 1999; McNally 2000). The explicit modeling of activities and the consequent trip chaining allows a thorough analysis of individuals’ response to land-use and transport policies. The responses can be viewed as a series of location and travel choices concerning how to implement activity programs. Thus, effects of the policies emerge from the activity-travel scheduling process, which should take into account travel and location preferences from the demand side and locations of facilities/services and transport from the supply side (Shiftan and Ben-Akiva 2011). A variety of policy-sensitive systems have been developed along this line of logic, which include platforms principally based on (1) computational process models, such as TASHA (Miller and Roorda 2003), ALBATROSS (Arentze and Timmermans, 2004a) and ADAPTS (Auld and Mohammadian, 2009); (2) utility-maximization, such as DAS (Bowman and Ben-Akiva 2001), CEMDAP (Bhat et al. 2004) and FAMOS (Pendyala et al. 2005); and (3) constraints-based approaches, such as CARLA(Jones et al. 1983) and several GIS-based systems (Miller 1999), etc.
Although these activity-based models represent an important step forward compared to the classical aggregate trip-based approaches, few of these systems can capture multi-modal trip chaining in the context of full activity-travel patterns. The use of private vehicles (PV) such as car and bike is often separated from the use of public transport (PT) as parking choice is not explicitly modeled. This model limitation causes insensitivity to parking and transit-related policies, e.g. park and ride (P+R), as well as policies to synchronize transport networks. These policies are attracting increasing attention and are regarded as feasible instruments to improve the capacity of the existing transport system. In addition, most of them adopt a hierarchical structure, where decisions are made in sequence from activity pattern via tours to trips, to derive the activity-travel schedule of an individual. In hierarchical approaches, capturing the impact of lower-level choice facets (e.g., route choice) on the higher-level ones (e.g., activity location choice) generally requires a reduction of the level of detail in the lower-level choice facets. Consequently, reduction of information may be the result in predicting the effects of land use policies on combined activity location and travel choice. Overall, a mechanism that can simultaneously model the choice of mode, route, parking and activity location at a sufficient level of detail is lacking in these approaches.
The multi-state supernetwork approach (Arentze and Timmermans 2004b) is a promising way to model the high dimensionality of choice behavior. This approach was extended and further developed by Liao et al. (2010, 2011, 2012, 2013a, b). Networks of passenger transport (both PV and PT) and locations of facilities/services together with activity programs of individuals are integrated into the structure of multi-state supernetworks. Different choice facets mentioned above are modeled as a unified “path choice” (Nagurney and Dong 2002) through the supernetworks, and the optimal (least generalized cost) path can be used to predict how individuals make choices to implement their activity programs. Thus, this approach can be applied to predict changes in travel choice made due to adaptations to the land-use and transport system. Since the choice facets in a supernetwork are fully represented, the approach is highly policy-sensitive.
The purpose of this paper is to demonstrate how the multi-state supernetwork approach can be applied to analyse the likely effects of a set of integrated land-use transport scenarios on individuals’ travel patterns. The approach is applied for the city of Rotterdam (The Netherlands), where several policy scenarios are considered by the municipality concerning transit improvement (including P+R), parking price, and land-use redevelopment. To that end, a synthetic population of a broader area, i.e. Den Haag-Rotterdam–Dordrecht corridor, together with activity programs, are extracted from Dutch national travel-diary surveys. Individuals’ travel preferences regarding multi-modal trips and activity locations are based on estimation results from stated and revealed data.
The remainder of this paper is organized as follows. In “Multi-state supernetwork” section, we discuss the basic concepts of the multi-state supernetwork approach and how it is tailored to analyse policy scenarios on individuals’ travel patterns and accessibility (welfare). Next, we describe the study area and scenarios. Then, the application results are discussed in “Application” section. Finally, the paper is completed with conclusions and future research.
Multi-state supernetwork
Basics for supernetwork representation
Network extension techniques have long been applied to solve transport-related problems. Dafermos (1972) first demonstrated an abstract traffic network to model multi-class users through the expansion of a road network. Later, road network and transit network have been integrated into a hyper-network (Sheffi and Daganzo 1978) or supernetwork (Sheffi 1985) to model mode and route choice simultaneously. Several studies (Nguyen and Pallottino 1989; Carlier et al. 2003; Lozano and Storchi 2002) also modelled multi-modal trip scheduling and equilibrium based on a higher network extension, in which transfer links are added at any location where an individual can switch between any transport modes. Meanwhile, Nagurney et al. (2003) introduced transaction links to model virtual travel, i.e. commuting versus telecommuting. The logic behind these supernetwork models is that a higher-order of choice dimension can be additionally modeled by adding a dimension of network extension.
Nevertheless, all the above supernetwork models treated travel only on a trip-based level. Arentze and Timmermans (2004b) extended the supernetworks to an activity-based level and proposed a multi-state supernetwork framework for multi-modal and multi-activity travel planning. This approach has been further developed for activity-travel scheduling with a more efficient representation (Liao et al. 2010) and an approach constructing the personalized transport networks (Liao et al. 2011). The essence of this approach is that an integrated land-use transport network is extended to represent the choice space of implementing an activity program. The basics for the representation are given as follows:
-
1.
Daily activity program including a list of out-of-home activities during the day, available private vehicles, and (in-)complete sequencing between activities;
-
2.
Activity state which activities in the activity program have already been conducted;
-
3.
Vehicle state where the private vehicles are (in use or parked at particular locations);
-
4.
Activity-vehicle state the combination of activity and vehicle state. When an individual is conducting an activity, the private vehicles must be parked;
Meanwhile, a node denotes a real location in space, for example, home, an activity location or a parking location. Links are defined in terms of three categories:
-
1.
Travel links connecting different nodes representing the movement of the individual—the individual stays in the same activity-vehicle state;
-
2.
Transition links connecting the same nodes of different vehicle states—the individual stays in the same location (i.e., parking/picking-up a private vehicle for changes of vehicle states or boarding/alighting PT for changes of mode states);
-
3.
Transaction links connecting the same nodes of different activity states representing the implementation of activities—the individual stays at the same location.
Based on the notion that only a small set of the locations/facilities is of interest to an individual’s activity program, a reduced integrated multi-modal network is firstly constructed by location choice models (Liao et al. 2011). As the fixed locations are given, flexible locations are selected in terms of the attractiveness of alternatives and the travel disutility to associated fixed locations. Note that a reduced choice set rather than only one location is selected for one activity or parking. To describe the reduced integrated network in a compact way, it is further divided into PV networks (PVN) for every type of private vehicle (e.g., the networks for car and bike etc.) and a single PT network (PTN) for pedestrian and PT. Parking locations are inside both PVN and PTN, but activity locations are only inside PTN. The travel links are inside PVN and PTN, transition links of alighting/boarding are always in PTN. Different nodes/locations in PVN and PTN are connected by PVN and PTN connections respectively, which potentially include a series of travel links. In particular, there is only one transport mode in PVN, i.e. the private vehicle. PTN is organized in the form of time-expanded network structure (Pyrga et al. 2008) for accommodating timetable-based PT. Thus, PTN connections may include link components of walking for access and egress, waiting, boarding/alighting, and in-vehicle.
There is a clear distinction between PVN and PTN in that a private vehicle is always being in use in a PVN, while it is always being parked at a parking location in a PTN. Thus, a transition link from PVN to PTN always represents parking, and it denotes picking-up from PTN to PVN. We use a pentagon and a hexagon to denote PVN and PTN respectively, and the angles to denote locations for the purpose of illustration. These locations are connected by other locations and links inside the PVN and PTN, which are not shown. Figure 1a displays the transition links of parking and picking-up a private vehicle (undirected links are bi-directed), in which the private vehicle can be parked at either P 1 or P 2. Likewise, transaction links are illustrated in Fig. 1b, in which one activity can be conducted at either L 1 or L 2, activity state 0 means the activity is not conducted yet, and 1 means the opposite. Figure 1c is a combination of Fig. 1a and b, in which each network unit is attached with a specific activity-vehicle state.
According to the above definitions, a multi-state supernetwork is constructed specifically for each (simulated) individual to represent all choice options given the activity program. This is done in two steps. Firstly, a copy of the PVN or PTN is created for each possible activity-vehicle state. Secondly, the network copies are interconnected by transition links (between PVNs and PTNs) and transaction links (between PTNs and PTNs). Figure 2 is an example of a multi-state supernetwork for an individual. In this example, the activity program includes two activities (A 1 & A 2) and two private vehicles (car and bike). P 1 & P 2 and P 3 & P 4 are the optional parking locations for car and bike respectively. Network copies in columns P i (i = 1, 2, 3, 4) represent a state where the private vehicle is parked at a particular location, whereas columns P 0 and P 5 represent a state where car and bike are in use, respectively. On the other hand, network copies within rows correspond to a particular activity state. s 1 & s 2 represents the activity states for A 1 & A 2. For example, the first row shows travel options where both activities A 1 and A 2 have not yet been conducted. H and H′ denote being at home at the start and end of the activity program, respectively. The path indicated by bold links show an example activity-travel pattern where the individual leaves home by car to conduct A 1 at a particular location with parking at P 2, returns home and switches to bike to conduct A 2 at another location with parking at P 4, and finally returns home.
As shown in Fig. 2, activity locations and the (multi-modal) transport system are organically integrated via a multi-state supernetwork. In general, a personalized multi-state supernetwork represents the choice space with regard to an individual’s activity program. It can be proven that every possible path from H to H′ is a feasible fully detailed activity-travel pattern. Every link in the path represents a particular choice of mode, route, parking/boarding location or activity location. The next sub-section discusses how the multi-state supernetworks are applied to assess policy scenarios.
Application for assessing scenarios
As every link and state is explicitly represented in a personalized multi-state supernetwork, each link can be defined in a state-dependent and personalized way as follows:
where \(disU_{isml}\) denotes the disutility (costs) on link l for individual i in activity state s and mode m, \(\varvec{X}_{{\varvec{isml}}}\) is a vector of attributes, \(\varvec{\beta}_{{\varvec{ism}}}\) is an attribute-vector of weights, and \(\epsilon_{isml}\) is an error term. By defining a disutility rather than a utility for each link, a standard shortest-path routine can be used to identify the most preferred path. Attributes may be time-dependent. For instance, travel time on a PTN or a PVN connection may vary with the time of day depending on congestion. On the other hand, the weight vector \(\varvec{\beta}_{{\varvec{ism}}}\) represents preferences of the individual that are stable over time. To capture time-dependence, Eq. 1 is extended as:
where t is the arrival time at link l.
Since the personalized parameters \(\varvec{\beta}_{{\varvec{ism}}}\) are incorporated in the supernetwork, a path from H to H′ with the least disutility is the optimal or the most preferred activity-travel pattern for the individual. If the activity program is typical to the individual, the least disutility can be considered as an indicator of personal accessibility, taking accessibility in the broadest possible sense as the utility the individual derives from his or her daily activities given the available location and transport facilities (Kwan et al. 2003). Formally, the personal activity-based accessibility index is defined as:
where \(p_{{{\text{H}} \to {\text{H}}^{{\prime }} }}\) and \(PATH\) denote a path from H to H′ and the path space respectively. This value can be obtained by applying a standard (or time-dependent) shortest path algorithm.
By aggregating across a population, a measure of accessibility can be derived for a study area in a straightforward way as:
where Acc and POP denotes the accessibility and the population for a particular scenario in the study area. It is worth noting that Eq. 4 does not take into account a dynamic equilibrium of travel times on links resulting from the collective implementation of individuals’ activity programs. Instead, Eq. 4 assumes that travel time profiles are given based on proper estimates of equilibrium travel times (in a scenario considered).
In addition to accessibility, mobility indicators can be derived from the model. Since the optimal paths contain every detail of the choice of route, mode and location, specific usage aspects of a multimodal network can be evaluated. Thus, apart from usual travel demand measures, such as total distance travelled by car (VMT) and modal split, indicators such as average waiting time for PT, use of P+R and other particular facilities etc. can be derived as well. As all travel choices are made explicitly and micro-simulation is used, the model can also provide information about the underlying activities and individual characteristics.
The model needs input of integrated land-use transport scenarios from the supply side and synthesized population and daily activity programs with travel preferences from the demand side. Once receiving the input, the multi-state supernetwork approach generates the PVNs and PTN for each individual specifically. We adopt a different model specification from Liao et al. (2011) for the activity location choice model, which will be discussed in “Data”section. The model for parking location choice remains the same as Liao et al. (2012). Given the arrival time at the entry node of a PVN connection, the shortest travel time path is sought in a time-dependent road network to the exit node. Similarly, given the arrival time at the entry node of a PTN connection, the least-cost path is sought in a time-expanded PT network to the exit node. After executing the multi-state supernetwork module for POP at a scenario, the aggregate effects are compared with the results of other scenarios. Figure 3 shows the flowchart of applying the multi-state supernetwork approach for analysing plan scenarios.
Data
The multi-state supernetwork approach is applied to the city of Rotterdam (The Netherlands) to analyse several hypothetical policy scenarios. In this section, we describe the study area, the input data and policy scenarios of the case study.
Study area
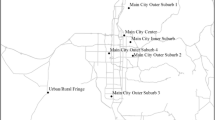
Although Rotterdam city is the targeted area, a broader area should be taken into account given the interactions that exist with Den Haag (on the North-Western side) and Dordrecht (on the South-Eastern side). According to MON (Dutch one-day travel survey) from year 2004 to 2008, around 90 % of all the fixed activities of Rotterdam residents including work/business, education and chauffeuring are conducted inside the Den Haag-Rotterdam–Dordrecht region. In addition, around 50 % of the people living in Rotterdam city have a work activity outside and 16.4 % living outside have the work activity inside Rotterdam. Therefore, we select the long corridor i.e. Den Haag-Rotterdam–Dordrecht (Fig. 4) as the study area. In Fig. 4, grey, grey (bold) and black (bold) lines denote local, regional and national roads respectively, the dashed lines differentiate three parts with the Rotterdam region in the middle and Den Hague and Dordrecht regions in the flanks, and the dashed circle determines the border of Rotterdam city. The study area is divided into four areas, which will be used to track where individuals come from. (Area 2 excludes Area 4.)
The synthetic population is extracted from the MON database (years from 2004 to 2008 are merged to obtain a large enough sample size). Individuals of 12 years or older living in the corridor and having at least one trip on the observed day are selected. In total, there are 21,117 individuals in the corridor, around 4000 of which live in Rotterdam. The sample takes up around 1 % of the real population. To correct for sampling bias, person and trip-based weighting factors provided with the MON are used.
As implied by the approach, the activity programs are taken out from the MON as well as the residential locations and transport mode availability conditions. Since the focus of this paper is on individuals’ location and travel choice, the sequencing of activities of an activity program is assumed fixed, although the supernetwork approach is capable to model activity sequencing as well. With the fixed sequencing, most activities automatically fall within opening hours of the relevant facilities. Thus, we do not consider time window constraints at activity locations. Activities are classified as fixed or flexible depending on whether the activity can be conducted only at one fixed location or a location choice is involved. The classification is based on activity type. Table 1 shows the classification of activities and relative frequencies in the activity programs with fixed labelled as 1 and flexible as 0. For fixed activities, the activity locations remain the same as given in the travel survey. For flexible activities, an activity location choice model (discussed below) will be applied to select the location alternatives that individuals would consider. Table 2 shows the distribution of number of trips per person. On average, each person has 2.46 activities, 1.57 home-based tours and 4.11 trips in the daily activity program.
Table 3 displays the distribution of possession of private vehicles per person. In this application, we consider only two types of private vehicles, i.e. car and bike. We assume that every person has a bike and that car owners in this simulation remain unchanged from the MON. Furthermore, car-passenger is also considered as a mode choice for the same individuals that traveled as car passengers in the MON. We further assume that car passengers do not pay parking and fuel cost.
Available locations for activities are determined based on the BAG (2011) database (Dutch building geo-data). With this dataset, the floor space and function can be identified for each individual building in the study area. The functions are mapped into the activities in Table 1. Floor space is used as an indication for attractiveness. In BAG, one building represents a small geographical area. In MON, however, trip destinations are indicated in terms of 4-digit postcode areas, which comprise a larger area (In total, there are 389 4-digit postcodes in the corridor). To keep consistency, we use the 4-digit postcode area as an indication for locations of flexible activities. The revealed choices of flexible activity locations in MON are used to estimate preference parameters for the activity location choice model. On the other hand, for a fixed activity, the more detailed 5-digit postcode area is used as an indication for activity location. The 4-digit fixed locations in the MON are assigned to a 5-digit postcode subarea by Monte-Carlo simulation taking into account the spatial distribution of the floor space in the 4-digit postcode area. This manner of location assignment is also applied to allocate the residential locations of the households.
The timetables of public transport in the study area are taken into account, including buses, trams, stop trains and intercity trains. The data are provided by the Dutch PT route planner (OV9292) for the year of 2010. In the time-expanded PTN, we assume a margin of at least one minute for transfers at a same PT stop and four minutes for transfers between different neighbouring PT stops. In the base scenario, the PT system includes 1576 stops/stations and 177,147 basic connections. In the expanded graph, there are 533,241 nodes and 1026,371 links. The fares for PT bus/tram, stop train and intercity train are assumed as 0.12, 0.14 and 0.15 €/min respectively.
The road network data are obtained from a national database (NWB). The data from 2003 are updated to 2010 by appending the major road changes that took place during that period. In total, there are 72,513 nodes and 205,072 links. In this database, three road types are distinguished, namely local, regional and national roads. The local roads are further differentiated in urban and non-urban local roads based on overlaying a map of the city centers of Den Haag, Rotterdam and Dordrecht. The dataset does not include information about travel speed. Estimates of average car speeds are defined by time of the day as shown in Fig. 5. Average speeds for bike are assumed by rule of thumb as 14 (urban), 16 (non-urban) and 17 (regional) km/h and for walking as 5 (urban) and 6 (non-urban) km/h, respectively. Average car fuel consumption is assumed as 0.17, 0.15, 0.125 and 0.105 €/km for the four types of roads, respectively.
Parking locations are characterized by parking facility type and parking cost. Potential parking locations are activity locations, P+Rs (park and ride facilities) and THs (transport hubs, like train stations). Estimated parking cost is dependent on the parking location and the parking duration based on the following model:
where t and \(y_{{P_{k} }}\) are the parking duration and the parking fee at a parking location \(P_{k}\), respectively. \(a_{{P_{k} }}\) and \(b_{{P_{k} }}\) are parameters for the constant and variable costs. They are expressed in € and €/h, respectively.
As for bike, we assume that parking is possible everywhere and always free of charge. Thus, in the model, \(a_{{P_{k} }} = b_{{P_{k} }} = 0\) for every \(P_{k}\). Bike and ride (B+R) are explicitly considered in the application. It is assumed that all the train stations are B+R locations (dots in Fig. 6a). Park and ride is also taken into account for car. Nine P+R facilities located at the border of Rotterdam (in Fig. 6b) are especially designed to alleviate the car traffic in Rotterdam city center. In addition, ten train stations in the corridor are identified as P+R locations (Fig. 6b). Only two P+R facilities in the north-west of Rotterdam charge parking cost; others do not charge as long as the drivers take PT.
Following the parking tariff zoning system, parking costs at activity locations take on one of four possible levels: L1, high tariff parking in Rotterdam and Den Haag centers (the darkest area in Fig. 6c); L2, medium tariff parking cost (the second darkest area); L3, low parking tariff (the third darkest area) and L4, free parking. Capacity constraints are not considered in the current application. In the base scenario, \(a_{{P_{k} }}\) and \(b_{{P_{k} }}\) are set according to actual tariff structures, which are 0.6 and 2.4 (L1), 0.5 and 1.2 (L2) and 0.4 and 0.6 (L3). For example, Eq. 5 is written as \(y_{{P_{k} }} = 0.6 + 2.4 \times {\text{hours}}\) for L1 zones.
Disutility functions are used to define link costs that represent individuals’ preferences for travel and location options. We adopt the parameter estimations obtained from a series of large-scale choice experiments that have specifically been conducted for this purpose of defining the link costs for supernetworks (Arentze and Molin 2013). A large representative nation-wide sample of individuals participated in the experiments (2746 respondents) and efficient designs were used to develop the choice tasks. A Multinomial Logit model is used to estimate activity-travel preferences. Preferences related to time, cost and service-quality attributes are estimated mode and trip stage specific. Table 4 show the parameter setting for individuals’ preferences related to travel components. The parameters represent population averages. These parameters are adapted to disutility settings (i.e., changing the sign of each parameter) to keep it consistent with the multi-state supernetwork approach. This model does not take into account observed (effects of socio-demographic and context variables) and unobserved (error terms) heterogeneity across individuals and trips.
In the location choice model used to estimate utility parameters of locations, every flexible activity is surrounded by two fixed activities. Departing and retuning home are also considered as fixed activities in this selection process. Different flexible activities may be surrounded and thus associated with the same pair of fixed activities. For each pair of surrounding fixed activities, the utility function in the flexible activity location choice model is specified as:
where \(disU_{{f_{n} }}\) is the choice-related disutility of conducting flexible activity \(f\) at location \(n\), \(\alpha_{{f_{n} }}\) is the base disutility, \(aDist_{{f_{n} }}\) is the travel distance from the former fixed activity location to n, \(size_{{f_{n} }}\) is floor-space size for \(f_{n}\), and \(\beta_{iAD}^{*}\) and \(\beta_{is}^{*}\) are parameters for distance and size respectively. As this equation shows, each 4-digit postcode area has a specific value of constant \(\alpha_{{f_{n} }}\). These parameters (Table 5) for the location choice model are estimated based on observed location choices in the MON using likelihood estimation.
In the application, activity location choice-sets are defined for each person and flexible activity. The selected location alternatives for that person and activity have the least disutility in the study area according to Eq. 6. For each activity program and person, at most 20 parking locations are selected for car and 10 for bike. Other parameters are set as: bike acceptance distance \(d_{ib}^{A}\) = 5 km, bike limit distance \(d_{ib}^{L}\) = 15 km, car acceptance distance \(d_{ic}^{A}\) = 15 km and car limit distance \(d_{ic}^{A}\) = +∞ (see Liao et al. 2012).
Scenarios
The following policy scenario elements originating from different departments of the Rotterdam municipality are considered:
E1 increase of train-service frequency (called the PHS program). This program involves an increase of the frequency of trains connecting the large cities in the corridor, which is part of a larger program aiming at concentrating spatial developments around the railway stations and improving transfer options in the south-wing of the Randstad. In this scenario, the frequencies of inter-city (fast) and stop-(slow) train connections are increased from 6 to 8 and 4 to 6 per hour respectively. After increasing the frequencies, the basic PT connections increase from 177,147 to 179,076. In addition, \(\beta_{iCT}^{TRAINm}\), the constant for using train as the main mode, is reduced to 0.75. This reduction is a rough estimate of an increase in preference of using the train when higher service frequency allows more flexible choice of trip departure time. 0.75 is set by rule of thumb; therefore, we ran a sensitivity analysis on this parameter as shown below.
E2 upgrade of Rotterdam Stadion station. Rotterdam Stadion station is now a stop train station only used for special events taking place on weekends in the football stadion. This scenario involves an upgrade of this station to an inter-city station to facilitate mobility in the southern part of Rotterdam. It involves two other developments simultaneously: (i) a P+R facility is developed near the station; and (ii) Rotterdam Blaak station, about 2.5 km to the north of Stadion station, is downgraded from an intercity to a local station.
E3 introduction of a new tram line. To further coordinate with the upgrade of Rotterdam Station station, a new tram line is introduced connecting the east and the west of Rotterdam city, which goes through the station. This tram runs once every 8 min on average.
E4 increase of parking prices at activity locations. To reduce the car traffic in the city centers of Den Haag, Rotterdam and Dordrecht, parking prices are doubled compared to the base scenario. Thus, in the scenario <\(a_{{P_{k} }}\), \(b_{{P_{k} }}\)> are set as <1.2, 4.8> , <1.0, 2.4> and <0.8, 1.2> for the L1, L2 and L3 respectively in Fig. 6c. The increase in parking cost is supposed to promote the use of P+R and B+R facilities.
E5 land-use development pattern 1: scattered. In many 4-digit postcode areas scattered around the city area (shadow areas in Fig. 7a), the floor space for four types of flexible activities are moderately increased (5–10 % more). Thus, the attractiveness of these areas for conducting these activities is increased correspondingly.
E6 land-use development pattern 2: city center. In this scenario, land-use developments are concentrated in the city center of Rotterdam (shadow areas in Fig. 7b). Floor space is more strongly increased in the city center (35 % more) since the city center originally bears the largest floor space for all the flexible activities.
E7 land-use development pattern 3: transport node-oriented. In this scenario, the land-use development is concentrated around three big transport hubs. Again, the increase (25 % more) concerns floor space for all the flexible activities. Note that the city center in the north part is also a big transport node.
The land-use—transport scenarios considered in the application are formed by combining the above scenario elements. The scenario combination is dependent on the planning timeline and purpose so that assessing the exhaustive combinations is not necessary. According to the planning timeline, the three transport scenario elements are supposed to be implemented sequentially and prior to land use policies (the latter four). Therefore, we run the scenarios in a cumulative way from scenario element (1)–(4). For example, the first scenario only includes the first scenario element, and the second includes the first two elements, and so on. Since the three land use development patterns are mutually exclusive, each of them is separately added to the fourth scenario. Note that all these seven scenarios are compared with the base scenario of no change. Hence, there are eight running scenarios in total.
We use eight labels to sequentially denote the scenarios: (1) Base, the base scenario; (2) Freq, equaling to Base plus E1; (3) UpStad, Freq plus E2; (4) Tram, UpStad plus E3; (5) ParkP, Tram plus E4; (6) Scat, ParkP plus E5; (7) Cent, ParkP plus E6; and (8) TNode, ParkP plus E7.
Application
In this section, we present the results of the application, which follows the steps discussed in “Application for assessing scenarios” subsection (Fig. 3). Key indicators of accessibility and VMT as well as more detailed aspects of individual travel patterns are compared among the eight scenarios. The application is executed with C++ in Windows® environment. The computation time is around 2.25 h per scenario on a standard PC (Intel® Core™2 Duo CPU E8400@ 3.00 GHz 3.00G RAM).
Several indicators predicted under the base scenario are compared with MON in the year of 2004, and the results show the validity of the model. The average trip length and travel time in the model are 9.2 km and 25.2 min respectively, while in MON they are 9.4 km and 22.1 min. It implies that the predicted flexible activity locations are basically accurate. Moreover, the model predicts that 36 and 142 individuals choose P+R and B+R respectively, while in MON the numbers are 41 and 127. One point should be mentioned that some biases exist in the mode share of walk and bike for the whole corridor. The model predicts that the shares are 29.8 and 13.2 % for walk and bike respectively, while in MON they are 22.3 and 19.7 %, while other mode shares are on the same level. It is mainly because of the space resolution that flexible activity locations are indicated by the centroids of the 4-digit postcode areas and these areas are much larger in suburban area than in the urban area. Therefore, more individuals would prefer walking to cycling in the model based on the travel preferences when both trip ends are in the same (large) postcode area; whereas, they would prefer cycling in reality. This explanation is well-reflected in the mode distribution for Rotterdam city only, where the 4-digit postcode areas are smaller and the predicted mode distribution is consistent with the MON. (The respective mode distribution for the corridor and Rotterdam is shown below.) Since such biases only occur for trips within a same 4-digit postcode area, the overall validity of the model is not affected.
Results
As aforementioned, a broader corridor is selected as the study area to take into account the spatial interactions between Rotterdam and surrounding cities. For the accessibility and travel demand indicators, the results of the analysis are shown for two areas separately, i.e. the Corridor and Rotterdam.
Figure 8 illustrates the indicator of accessibility under different scenarios of the corridor and Rotterdam respectively. The left side hand refers to the total disutility of the people living in the corridor, while the right hand side refers to the total disutility of the people living in Rotterdam city only. Thus, they are at a different scale (the same applies to Fig. 9). As expected, the increase in train-connection frequency leads to an increase in accessibility. Upgrading Rotterdam Stadion station (and downgrading Blaak stadion) hardly has any influence on accessibility. However, when the new tram line is additionally implemented, we do see a small positive effect on accessibility. Doubling parking cost obviously reduces accessibility in this broad meaning of disutility since people need to pay more or switch to less efficient transport modes or locations. The model predicts a relatively drastic increase of disutility particularly for people living outside Rotterdam. On the other hand, the land use developments, according to the model, bring about a relatively strong increase in accessibility (decrease in total disutility). The increase is strongest for the city center pattern and weakest for the scattered pattern.
Figure 9 shows the effects on the indicator of VMT. Like the effects on accessibility, the transport-system changes do not have substantial impacts on VMT for both the corridor and Rotterdam. On the other hand, the increase in parking cost leads to a relatively strong decrease in VMT; the effect is stronger for people living in Rotterdam. Surprisingly, the scattered land use development pattern, in contrast to other patterns, does not reduce the VMT. On the level of the Corridor, the VMT even increases. The likely explanation is that the locations that become more attractive are mostly situated outside the center so that people drive longer to the locations. The city center pattern has the most favorable effect in terms of reducing VMT. This may be because it increases the attractiveness of public transport use as parking costs are high and public transport services are of the highest order.
Figures 10 and 11 display the average PT travel time (including waiting time) and PT waiting time per trip involving PT respectively. On average, people living in Rotterdam spend less time on PT travel and waiting. Note that, according to these predictions, higher parking cost (scenario ParkP) does not only suppress the use of car, but also reduces the time spent on PT trips. Probably, this has to do with a simultaneous shift towards using P+R, which increases the number of relatively short PT trips. Since the leg traveled by public transport is relatively short, a shift to P+R leads to a decrease in average time spent on PT. On the other hand, the land-use developments attract people from further distances as the locations become more attractive, resulting in an increasing average travel time of both car-trips and PT trips. (In the following figures, for ease of presentation, we do not differentiate between the three land use development patterns in the way in Figs. 8, 9.)
Figure 12a and b show the distribution of transport modes across trips (c-ride represents the mode as car passenger). The share of c-ride is little changed over the scenarios. Since there is no parking and fuel cost and potentially less travel time involved in c-ride, c-ride tends to be more preferable than other transport modes for the same travel links. As observed, the mode shares are quite stable across the transport-system changes. However, they change dramatically after the increase in parking prices. As expected, the increase in parking costs in urban and highly developed area reduces car use. However, unexpectedly, car trips are not primarily substituted by PT but by bike. Furthermore, the parking cost increase leads to a substantial grow in use of P+R. A noticeable part of walk mode and to a lesser extent also car use is replaced by PT use in the land-use development scenarios. The use of B+R appears to respond only marginally to the various scenarios.
The multi-state supernetwork approach also allows tracing the use of particular facilities and who use them. Figure 13 shows the number of P+R users broken down by area of origin (see Fig. 4 for an explanation of area codes). P+R users are defined as individuals who use a P+R at least one time on a trip or a day. As the majority of the synthesized population comes from Den Hague region (Area 1) and the outer Rotterdam region (Area 2), more people choose P+R from these two areas. It is observed that the transport-node oriented land-use development (TNode) results in the strongest increase in P+R users compared with the other land use scenarios (Scat and Cent). This is plausible since it is easier to combine PT and car when activities are conducted at big transport nodes. Furthermore, an increase in parking costs also renders people living in Rotterdam to use P+R more often inside Rotterdam, even though the P+R locations are primarily developed for people living outside.
In Fig. 14, the y-axis represents the number of trips with P+R use broken down by trip purpose. The figure shows the four activities that occupy the highest shares of P+R use. Obviously, the work and shopping activities have the highest shares. Note that when a car is parked at a P+R facility, the multi-state supernetwork approach allows an individual to conduct multiple activities, which is in line with reality. It implies that the land use developments do not have as strong an effect on P+R use as the increase in parking cost does. However, the figure does show a tendency of a decrease of P+R trips for work after the land use development—from scenario ParkP to Scat, which is contradictory at the first glance. Inspection of particular cases shows that some individuals use P+R for the combined activities of work and shopping in scenario ParkP; whereas, in scenario Scat, they drive directly to the working location, and after working choose a new P+R facility and a new shopping location.
In Fig. 15, the y-axis represents the share of P+R trips by parking price level at the destination. Figure 15 should be looked up with Fig. 12a for absolute numbers. As it appears, most P+R trips have destinations in the zones around the city center (L2 zones). This effect is intensified by the parking-price and land use policies since L2 zone is associated with better trade-off among PT connection, parking cost and facility attractiveness.
Figure 16 shows the effects of the scenarios on the use of Rotterdam Stadion station for accessing (boarding) or egressing (alighting). The y-axis represents the percentage of trips where the Stadion station is used for these purposes of all trips (including non PT trips). As expected, the station is more often used by people living in Rotterdam. The new tram line appears to lead to a substantial increase in the use of the station as intended by the planners. The land-use development scenarios also lead to an increase. The increase is particularly strong in the scattered land-use development scenario. A likely explanation is that in this particular scenario people living or working in the south part of Rotterdam travel more often to locations where they need to travel by train.
As mentioned in E1 (“Scenarios” section) \(\beta_{iCT}^{TRAINm}\) = 0.75 is set by rule of thumb. Since this setting is somewhat arbitrary, we have run the simulation with other values decreasing from 1.0 to 0.7 with steps of −0.05. The effect differences are marginal while the effect trend is the same. Hence, the results are not affected by changing this setting within a reasonable margin of uncertainty.
Interpretation
As illustrated by this application, the supernetwork model can provide detailed information on the effects of integrated pricing, location and transport planning scenarios on travel patterns. According to the above results, transport-system improvements have relatively small effects on the indicators considered since these changes take place only on a small scale. Nevertheless, they do increase accessibility and reduce VMT especially when the upgrade of the station is facilitated with the new tram line. In combination with transport-system changes, on the other hand, land use policies generate clear-cut changes in travel patterns. Interestingly, the analysis indicates that city-center oriented development has particularly favorable effects on accessibility and public transport use, in part, because the city center is also a big transport node.
However, it is unwise to focus on a single effect since there are many interactions between factors. For instance, while the scattered development scenario attracts more usage of Rotterdam Stadion station, it also results in an increase of VMT; and while the transport-node oriented development leads to the highest P+R use, the city-center oriented development results in the highest share of PT use. Obviously, for plan decision making also other factors should be taken into account. For example, the city-center oriented development may have the best effects on accessibility and VMT, but may also need the largest investment costs in land use development. All in all, the multi-state supernetwork application provides rich information for urban and transport planners.
Conclusions and future research
Recently, the multi-state supernetwork approach has found increasing attention in transportation research. Most previous work has been theoretical in nature. The purpose of the present paper has been to illustrate the application of this approach in policy assessment. The application illustrates what type of results the modeling approach can generate, to demonstrate its suitability for evaluating transport-land use scenarios. A set of cumulative land-use transport scenarios has been evaluated. The output provides the basis for analyzing response behavior in more detail than in competing approaches. The results exhibit the interplay between transport and land-use policies, and reveal accessibility change, modal substitution and shift in the use of facilities under different scenarios. Thus, this study showed that the supernetwork modeling approach can provide detailed and rich information especially for the integrated planning of land-use and a multi-modal transportation system taking into account the complete activity programs of individuals.
Several problems remain for future research. First, travel preferences of individuals were estimated on an average level, whereas effects of socio-demographic variables and unobserved heterogeneity should be taken into account (by drawing from appropriate distributions of parameters). Second, the multi-state supernetworks were constructed separately for each individual. The mode of car-passenger was modeled in the application without taking into account the car-drivers simultaneously, which might result in bias on modal split. For this matter, joint travel choice should be modeled explicitly like other choices. Lastly, in the application we did not take into account that more attractive locations could generate more traffic, which may cause congestion and hence, delays for car drivers and therefore increased costs. A similar limitation is the ignorance of capacity constraints of the P+R parking locations. The interaction among the individuals can be potentially solved by embedding external activity-travel pattern assignment models. These issues should be addressed in further developing the approach to further improve the use of the model for policy assessments.
References
Arentze, T.A., Molin, E.J.E.: Travelers’ preferences in multimodal networks: design and results of a comprehensive series of choice experiments. In: Proceedings of the 92st Annual Meeting of the Transportation Research Board, Washington, DC (2013)
Arentze, T.A., Timmermans, H.J.P.: A learning-based transportation oriented simulation system. Transp. Res. Part B 38(7), 613–633 (2004a)
Arentze, T.A., Timmermans, H.J.P.: A multi-state supernetwork approach to modelling multi-activity multi-modal trip chains. Int. J. Geogr. Inf. Sci. 18, 631–651 (2004b)
Auld, J., Mohammadian, A.: Framework for the development of the agent-based dynamic activity planning and travel scheduling (ADAPTS) model. J. Transp. Lett. 1(3), 245–255 (2009)
Bhat, C.R., Koppelman, F.S.: Activity-Based Modeling of Travel Demand. In: Hall, R.W. (ed.) The Handbook of Transportation Science, p. 3561. Kluwer Academic Publishers, Norwell Massachusetts (1999)
Bhat, C.R., Guo, J.Y., Srinivasan, S., Sivakumar, A.: A comprehensive econometric micro-simulator for daily activity-travel patterns (CEMDAP). Transp. Res. Rec. 1894(1), 57–66 (2004)
Bowman, J.L., Ben-Akiva, M.: Activity-based disaggregate travel demand model system with activity schedules. Transp. Res. A 35(1), 1–28 (2001)
Carlier, K., Fiorenzo-Catalano, S., Lindvel, C., Bovy, P.: A supernetwork approach towards multimodal travel modelling. In: Proceedings of the 82nd Annual Meeting of the Transportation Research Board, Washington, DC (2003)
Chapin, F.S.: Free-time activities and the quality of urban life. J. Am. Inst. Plan. 37, 411–417 (1971)
Dafermos, S.: The traffic assignment problem for multimodal networks. Transp. Sci. 6, 73–87 (1972)
Jones, P.M., Dix, M.C., Clarke, M.I., Heggie, I.G.: Understanding Travel Behavior. Gower, Aldershot (1983)
Kwan, M.-P., Murray, A.T., Okelly, M.E., Tiefelsdorf, M.: Recent advances in accessibility research: Representation, methodology and applications. J. Geogr. Syst. 5(1), 129–138 (2003)
Liao, F., Arentze, T.A., Timmermans, H.J.P.: Supernetwork approach for multi-modal and multi-activity travel planning. Transp. Res. Rec. 2175, 38–46 (2010)
Liao, F., Arentze, T.A., Timmermans, H.J.P.: Constructing personalized transportation network in multi-state supernetworks: A heuristic approach. Int. J. Geogr. Inf. Sci. 25(11), 1885–1903 (2011)
Liao, F., Arentze, T.A., Timmermans, H.J.P.: A supernetwork approach for modeling traveler response to park-and-ride. J. Transp. Res. Rec. 2323, 10–17 (2012)
Liao, F., Arentze, T.A., Timmermans, H.J.P.: Multi-state supernetwork framework for two-person joint travel problem. Transportation 40(4), 813–826 (2013a)
Liao, F., Arentze, T.A., Timmermans, H.J.P.: Incorporating space–time constraints and activity-travel time profiles in a multi-state supernetwork approach to individual activity-travel scheduling. Transp. Res. Part B 55, 41–58 (2013b)
Lozano, A., Storchi, G.: Shortest viable hyperpath in multimodal networks. Transp. Res. Part B 36, 853–874 (2002)
McNally, M.G.: The activity-based approach. In: Hensher, D.A., Button, K.J. (eds.) Handbook of Transport Modelling, pp. 53–70. Pergamon, Amsterdam (2000)
Miller, E., Roorda, M.: A prototype model of household activity-travel scheduling. Transp. Res. Rec. 1831, 98–105 (2003)
Miller, H.J.: Measuring space–time accessibility benefits within transportation networks: Basic theory and computational procedures. Geogr. Anal. 31(1), 1–26 (1999)
Nagurney, A., Dong, J.: Urban location and transportation in the information age: A multiclass, multicriteria network equilibrium perspective. Environ. Plan. B 29, 53–74 (2002)
Nagurney, A., Dong, J., Mokhtarian, P.L.: A space-time network for telecommuting versus commuting decision-making. Reg. Sci. 82, 451–473 (2003)
Nguyen, S., Pallottino, S.: Hyperpaths and shortest hyperpaths. In: Simeone B. (ed.) Combinatorial Optimization. Lecture Notes in Mathematics, vol. 1403, pp. 258–271. Springer, Berlin (1989)
Pendyala, R.M., Kitamura, R., Kikuchi, A., Yamamoto, T., Fujji, S.: FAMOS: Florida activity mobility simulator. In: Proceedings of the 84th Annual Meeting of the Transportation Research Board, Washington, DC (2005)
Pyrga, E., Schulz, F., Wagner, D., Zaroliagis, C.: Efficient models for timetable information in public transportation systems. ACM J. Exp. Algorithmics 12, 1–39 (2008)
Sheffi, Y.: Urban Transportation Networks Equilibrium Analysis with Mathematical Programming Methods. Prentice-Hall, Englewood Cliffs, New Jersey (1985)
Sheffi, Y., Daganzo, C.F.: Hypernetworks and supply–demand equilibrium obtained with disaggregate demand models. Transp. Res. Rec. 673, 113–121 (1978)
Shiftan, Y., Ben-Akiva, M.: A practical policy-sensitive, activity-based, travel-demand model. Ann. Reg. Sci. 47, 517–541 (2011)
Waddell, P.: Integrated land use and transportation planning and modelling: Addressing challenges in research and practice. Transp. Rev. 31(2), 209–229 (2011)
Wegener M.: Overview of land-use transport models. Transport Geography and Spatial Systems. Handbook 5 of the Handbook in Transport, pp. 127–146. Pergamon/Elsevier Science, Kidlington (2004)
Acknowledgments
This study is supported by Dutch Science foundation (NWO). We also acknowledge Rotterdam municipality for the involvement in generating the policy scenarios.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liao, F., Arentze, T., Molin, E. et al. Effects of land-use transport scenarios on travel patterns: a multi-state supernetwork application. Transportation 44, 1–25 (2017). https://doi.org/10.1007/s11116-015-9616-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-015-9616-z