Introduction

The purpose of this paper is twofold. First, we use stable population theory and Fisher’s reproductive value to develop the concept of the stationary population equivalent (SPE), a model of population change under assumed unchanging regimes of mortality, fertility, and international migration. The advantage of the SPE model is that it incorporates age-specific schedules of immigration and emigration, while avoiding the pitfalls of some earlier approaches. This paper considers what we believe to be an appropriate model for analyzing the impact of international migration on population change. In particular, the SPE model examines population change in the absence of the effect of population momentum, an effect that can seriously distort population dynamics in many populations that had significantly higher fertility in the recent past. Population momentum has been examined primarily for populations with moderately high fertility. It has been noted by Keyfitz and others that a high fertility population would continue to grow for some time even if fertility rates were reduced immediately to the replacement level (Keyfitz, 1971b). Preston, Heuveline, and Guillot (2001, p. 163) point out that population momentum—the tendency for populations to increase or decrease even if replacement-fertility levels prevail immediately—is a function of differences between a population’s actual and stationary age structure.

Second, we apply the SPE model to the population of Germany, a country characterized by modest levels of international migration into and out of the national population and below replacement fertility. The paper investigates the impact of changes in fertility and migration on the hypothetical future population (the SPE), comparing results to similar data from population projections of the Statistisches Bundesamt, Germany’s Federal Statistical Office. The results of the SPE model for Germany provide a measure of the magnitude of population decline in the eventual German population due to below replacement fertility, and the extent to which positive net immigration counteracts this decline.

This paper develops a stationary population equivalent model. It owes several key features to the pioneering work of Nathan Keyfitz. Prior work on this model was in collaboration with Roger Avery (Edmonston & Avery, 1988). Previous discussion of earlier work appears in Edmonston and Lee (1989) and Edmonston (1990).

Background

When recent changes in fertility and international migration create differences between the current age schedule and the eventual stable age structure implied by current rates, then current crude vital rates may give distorted indications of the long-run demographic consequences of current conditions (Preston et al., 2001: Chapter 7). This situation is particularly appropriate for the current German population, when public policy debate focuses on consequences of low fertility levels and modest net immigration, yet the eventual demographic situation is not clear from observation of current rates.

Previous solutions to this demographic situation have generally involved the stationary population model (Coale, 1972) or the stable population model (Espenshade, 1975; Espenshade & Campbell, 1977; Keyfitz, 1968, 1969, 1971a, b, 1977). Work presented in this paper on the SPE model overcomes several limitations in past work and offers a succinct quantitative framework for demographic analysis of the impact of migration on population growth.

The earliest work on this demographic situation considered intrinsic vital rates (Dublin & Lotka, 1925), along with the intrinsic rate of natural increase. If age-specific fertility and mortality rates continue unchanged for a long time period in a population closed to migration, the population will eventually attain an unchanging stable age structure with unchanging vital rates and population increase. In other words, there are a rate of growth and associated vital rates that are “intrinsic” to a set of current fertility and mortality rates.

Further work by Coale, Espenshade, and Keyfitz advanced substantially the generality and application of the intrinsic rate calculations. But while intrinsic rate calculations offer valuable insight, they have several limitations. First, the standard intrinsic rate procedures do not include international migration (they assume a closed population for the calculations), and are not, therefore, germane to questions of long-term growth of the German population. Both Keyfitz (1968) and Sivamurthy (1982) showed that international migration could be included in stable population modes, although there are disadvantages (described later in this paper) to their approach. Second, the measure of size for the stable population model, the stable population equivalent (Keyfitz, 1968, p. 57), is complicated in calculation and interpretation. Third, the stable population equivalent measure is time-dependent because, if the stable population model holds, the measure will grow by the intrinsic rate of growth (or, the “true” rate of natural increase in Lotka’s formulation; it is defined below).

Stationary population equivalent model overview

This paper proposes the use of the stationary population equivalent (SPE) model, as an alternative to earlier procedures, for the situation of analyzing the long-term consequences of current vital rates and international migration. Work in this paper develops from prior work on the U.S. population reported in Coale (1972) and Keely and Kraly (1978). In particular, this paper presents a formal model, proposed earlier by Edmonston and Avery (1988), and offers analysis of the German population.

The stable population model assumes constant fertility and mortality rates holding indefinitely. As a result, the stable model provides measures of an unchanging stable age structure and unchanging vital rates in order to offer a contrasting picture for interpreting the current situation. The stationary population equivalent model differs. With a stationary population, mortality is assumed to remain constant, fertility is assumed to continue at the replacement level (the net reproduction rate equals one, in other words), and the current age structure is maintained.

There are several advantages to the SPE approach. The SPE model provides an unambiguous single population size for interpretation, a size that holds for all years under analysis and not just the current year. The population size calculated for this proposed stationary population model is referred to as the stationary population equivalent (SPE). Comparisons of SPEs at different times or under different conditions give fairly simple and clear measures of population size differences. Finally, changes in mortality or migration conditions indicate changes in population size that are unaffected by momentum or peculiarities in the current age structure, two problems that pose particular troubles for standard stable population analysis.

The SPE measure could be calculated for the German population annually to determine if the eventual population size would be growing or declining (independent of momentum in the current age structure). Here we report results for 2000. Further, the SPE calculation provides measures of the proportion of change in SPE due to mortality, fertility above or below replacement, and international migration. The effect of changes in mortality can be assessed by comparing the SPEs under different conditions. The influence of fertility can be noted by comparing the number of births assumed by the model (which, assuming the net reproduction rate, equals one) to actual fertility. Increased immigration makes the SPE larger, while increased emigration makes the SPE smaller. The long-run impact of international migration can, therefore, also be assessed in the SPE model.

Stationary population equivalent approach

Stationary population equivalent model

The interrelationship of age structure, fertility, mortality, and international migration can all be treated by a single theory. This section develops the theory that allows us to compare the demographic effects of mortality, fertility, immigration, and emigration changes on Germany’s population growth. We begin by describing the concept of Fisher’s reproductive value, then discuss the basic idea of a stable population age distribution (including migration), and finally derive the stationary population equivalent.

Fisher’s reproductive value

In work on the genetic aspects of population, Fisher (1930, p. 27–29) proposed the concept of the reproductive value. He proposed that the newborn female has a probability of living from birth to age a of l a and the chance of bearing a daughter between age a and a+da of m a da. So, over her lifetime, the woman would bear R 0 expected number of females:

$$ R_0 = \int_\alpha ^\beta {\,l_a m_a {\text{d}}a} $$
(1)

where α and β are the beginning and ending years of childbearing. R 0 is the ratio of the number of females in the next generation compared to the initial generation, and is called the net reproduction rate (NRR).

Fisher’s work discounts the future at the rate of interest of r, the intrinsic rate of natural increase for the population. The value of 1 female child, discounted back a years at an annual rate of r, compounded continuously, is e -ra. Since the birth of a single female equals 1, the present value of the female through the ages of reproduction is:

$$ 1 = \int_\alpha ^\beta {\;e^{ - ra} l_a m_a {\text{d}}a} $$
(2)

which is, one observes, the characteristic equation used by Lotka (1939, p. 35) to derive the intrinsic rate of natural increase implied by a population’s net maternity function, l a m a . In Fisher’s formulation, Eq. 2 can be seen as the “loan” of a life repaid over the reproductive years, where the debt is fully repaid when age β is reached.

For a woman aged x, her expected births during an interval a to a + da are [l a /l x ]m a . Discounting the births as in Eq. 2, the reproductive value of a woman at age x, V x , is:

$$ V_x = \int_x^\beta {e^{ - r(a - x)} \frac{{l_a }} {{l_x }}m_a {\text{d}}a} $$
(3)

Note that V 0 = 1 and when x > β, V x  = 0. V x represents the prospective number of females that would be born, under prevailing mortality conditions and fertility regimes, discounted at the intrinsic rate of natural increase.

Equations 2 and 3 hold for the general case of stable population assumptions. For a stationary population, we assume replacement-level fertility, NRR = 1, by multiplying the observed fertility rates times 1/NRR. Stationarity can be achieved by many different changes of fertility schedules. Multiplying the observed rates by 1/NRR has the attraction that it adjusts the observed age-specific rates to produce rates that are consistent, other factors held constant, with zero long-term growth. This produces a stationary population, where r = 0 and the exponential expression becomes 1. Equation 3 becomes:

$$ V_x = \int_x^\beta {\frac{{l_a }} {{l_x }}\frac{{m_a }} {{{\text{NRR}}}}{\text{d}}a} $$
(4)

for the reproductive value of the population. Equation 4 is used later in this section for defining the reproductive value, V x , in the SPE calculation. It should be noted that Eq. 4 and derivations based on Eq. 4 below apply if the V x values are at the replacement level, and that the age structure of fertility and mortality used in calculating V x are the same as the current population. If this were not assumed to be the case, then the adjustment for NRR = 1 would not be appropriate.

Stable population

Our next task is to see how the population at time t depends on the reproductive value. For an initial stable age distribution that matches the intrinsic rate of growth, r, the future population at time t, P t , can be written:

$$ P_t = \frac{1} {b} \cdot Q \cdot e^{rt} $$
(5)

where b is the intrinsic birth rate and Q is a constant representing the number of births at time zero of an equivalent stable population (Keyfitz, 1971a, p. 64).

Following Keyfitz’s (1971a, p. 64) exposition of Lotka’s (1939, p. 85) stable population work, Q in Eq. 5 can be expressed as:

$$ Q = \frac{1} {K}\int_0^\infty {e^{ - rt} } \int_0^\infty {P_a \frac{{l_{a + t} }} {{l_a }}m_{a + t} {\text{d}}a{\kern 1pt} \;{\text{d}}t} $$
(6)

for a stable population, where K equals the mean age of childbearing. A computation formula for K is given below in Eq. 19. By changing the order of integration and substituting V x for the expression in Eq. 3:

$$ Q = \frac{1} {K}\int_0^\beta {P_x V_x {\text{d}}x} $$
(7)

Now, Eq. 5 can be written as:

$$ P_t = \frac{1} {K} \cdot \frac{1} {b} \cdot e^{rt} \int_0^\beta {P_x V_x {\text{d}}x} $$
(8)

Stationary population equivalent

If r equals 0, which is assumed under conditions of stationarity, Eq. 8 can be further simplified. Then e rt becomes 1 and P becomes independent of time. Moreover, 1/b then equals life expectancy at birth, e 0, so Eq. 8 can be restated as:

$$ P_0 = \frac{{e_0 }} {K}\int_0^\beta {P_x V_x {\text{d}}x} $$
(9)

P 0 is the aggregate population size, at the initial year, of the present mortality and fertility schedules, and of the current age distribution for stationary population assumptions. We refer to P 0 as the stationary population equivalent (SPE) for females.

Our final task is to rewrite Eq. 9 to express the function in terms of both sexes. Note, first of all, that the initial male population has no influence on a female-dominant calculation. Rather, for a female-dominant model, it suffices to include the sex ratio at birth and the life expectancy at birth, for both sexes. It helps to consider that e 0/K is the number of generations in the population, and the number of generations in the population for both sexes, N, can be written:

$$ N = \frac{{e_0^{\text{f}} }} {K} + \frac{{e_0^{\text{m}} }} {K} \cdot \frac{{1 - s}} {s} = \frac{1} {K}\left( {e_0^{\text{f}} + e_0^{\text{m}} \cdot \frac{{1 - s}} {s}} \right) $$
(10)

where the superscripts f and m represent females and males, respectively. Note that s is the proportion of births that are female and, hence, (1−s)/s is the sex ratio at birth. Finally, the stationary population equivalent (SPE) for the population, P, for both sexes is:

$$ {\text{SPE}}(P) = N \cdot \int_0^\beta {P_x V_x {\text{d}}x} $$
(11)

Equation (11) can be rewritten for immigrants and emigrants. Assuming fertility and mortality conditions for immigrants (I) and emigrants (E) that are the same as the resident population, we replace the age distribution of the population (P) under study by the age distribution of migrants to derive an SPE for the migrant groups:

$$ {\text{SPE}}(I)\, = \,N \cdot \int_0^\beta {I_x V_x {\text{d}}x} $$
(12)

where I x is the age distribution of immigrants.

$$ {\text{SPE}}(E)\, = \,N \cdot \int_0^\beta {E_x V_x {\text{d}}x} $$
(13)

where E x is the age distribution of emigrants.

The overall SPE for a population, including the initial population by age and sex and international migrants, also by age and sex, equals:

$$ {\text{SPE}}\, = \,{\text{SPE}}(P)\, + \,{\text{SPE}}(I)\, - \,{\text{SPE}}(E) $$
(14)

where we have three SPE-type calculations, one for the initial population, one for the immigrants, and one for the emigrants. If a population has no international migration, Eq. 14 reduces to a standard aggregate population reproductive value, shown in Eq. 11. Also, note that the model might include, in fact, different fertility and mortality schedules for migrants; in this case, Eqs. 12 and 13 would involve different N and V x values for immigrants and emigrants.

Alternatively, we could study the overall effect of change in the three SPE-type calculations. The SPE does not change, year to year, as long as the model conditions remain the same: constant mortality, replacement level fertility, and no migration. Any change in the demographic conditions, however, produces a corresponding change in the SPE. For example, each birth below replacement decreases the SPE by N. Immigrants add to and emigrants subtract from the SPE by the amounts SPE(I) or SPE(E) in Eqs. 12 and 13, respectively. The overall effect of international migration at time t, called OE(t), can be written as:

$$ {\text{OE}}(t)\, = \,N \cdot \left[ {B_t \, - \,B_t^r \, + \,\int_0^\beta {I_{t,x} V_x {\text{d}}x\; - \;\int_0^\beta {E_{t,x} V_x {\text{d}}x} } } \right] $$
(15)

where B(t) is the actual number of female births in year t, B r(t) is the number of female births needed for replacement (at a net reproduction rate equal to one) for year t, and I t,x and E t,x are the number of immigrants and emigrants by age x in year t, respectively.

It is useful to consider three possible situations in which combinations of changes in births and international migration might affect the overall stationary population equivalent model. The first situation is where replacement-level fertility prevails in the absence of international migration. The second involves replacement-level immigration in the presence of observed below replacement births. The third situation pertains to increases in current fertility levels to “fill-the-gap” in the presence of current immigration. These calculations are used in later analysis of Germany’s population dynamics. Various other calculations, based on Eq. 15, might be made to examine population dynamics in other populations.

1. Replacement-level births

If there were zero international migration, the number of replacement-level births is:

$$ B_t^r \, = \,\int_\alpha ^\beta {\frac{{P_x m_x }} {{{\text{NRR}}}}{\text{d}}x\,} = \,B_t \bullet \frac{1} {{{\text{NRR}}}} $$
(16)

or, more simply, the number of replacement-level births equals the observed number of births times 1/NRR.

2. Replacement-level immigration

Given current fertility levels, how many immigrants are required annually to maintain the stationary population equivalent? Replacement-level immigration requires that the overall effect of fertility and international on the stationary population equivalent be zero. If current fertility and emigration levels prevail, the number of required replacement-level immigrants, I r, is:

$$ I^r\,=\,\frac{{N \bullet \int_0^\beta {P_x V_x dx}\,\; - } \;N \bullet \int_0^\beta {E_x V_x {\text{d}}x}}{{{{N \bullet \int_0^\beta {I_x V_x {\text{d}}x} } \mathord{\left/ {\vphantom {{N \bullet \int_0^\beta {I_x V_x {\text{d}}x} } {I_ \bullet }}} \right. \kern-\nulldelimiterspace} {I_ \bullet }}}} $$
(17)

where P x is the female population by age, E x is the emigrant population by age, I x is the immigrant population by age, and I is the total number of immigrants.

3. Fill-the-gap births

A third possible situation involves the question of how much current fertility would need to increase to maintain the stationary population equivalent in the presence of current international migration levels. Recalling Eq. 15 for the overall effect of international migration on the SPE calculation, we set Eq. 15 to zero in order to derive the “fill-the-gap” number of births, B fg:

$$ B_t^{{\text{fg}}} = B_t^r - \frac{{\int_0^\beta {I_{t,x} V_x {\text{d}}x\; - \;\int_0^\beta {E_{t,x} V_x {\text{d}}x} } }} {N} $$
(18)

Equation (18) assumes that there is no change in mortality. If fertility remains at replacement levels and mortality decreases, however, this would increase the SPE value.

Data requirements and calculations

There are some data requirements for calculating the SPE measures. For a population closed to migration, the SPE calculation requires female mortality rates (using the person-years column, L x , of the life table), female fertility rates (called F x ), the female population by age (called P x ), and three constants: the proportion of births that are female (called S), and life expectancies at birth for males and females (called e m0 and e f0 ). If the population is open to international migration, then the SPE calculation requires either net immigration by age and sex or immigration and emigration by age and sex.

Knowing the life tables L x values and the age-specific fertility rates, F x , the mean age of childbearing, K, is:

$$ K\, = \,\frac{{\sum\limits_{x = 15}^{45} {(x\, + \,2.5) \cdot L_x \cdot F_x } }} {{\sum\limits_{x = 15}^{45} {L_x \cdot F_x } }} $$
(19)

The number of generations in the population—knowing K, life expectancies at birth for both sexes, and the proportion of births that are female—is obtained using Eq. 10.

The reproductive value of a woman at age x, is calculated with the following computational formula:

$$ V_x \, = \,5 \bullet \frac{{F_x }} {{2 \cdot {\text{NRR}}}}\, + \,\sum\limits_{y = x + 5}^{45} {5 \bullet \frac{{L_y }} {{L_x }}} \cdot \frac{{F_y }} {{{\text{NRR}}}} $$
(20)

Note that one might consider an improved estimate of F x /(2•NRR) with [F x /(2•NRR)][L x+5/L x ]1/4 to take mortality changes by age into account. But the refinement in the mortality term that would result, in the maximum change for these German data, is an adjustment of 0.99692. We include the mortality adjustment in this analysis but it makes a negligible difference compared to the results that would be obtained using Eq. 20. The mortality adjustment, however, should be included in analysis of high mortality populations.

Knowing the population by age, P x , the SPE calculation yields:

$$ {\text{SPE}}(P)\, = \,N \cdot \sum\limits_{x = 1}^{45} {P_x V_x } $$
(21)

for the final computation of the stationary population equivalent. For the stationary population equivalent calculations for immigrants and emigrants, P x uses immigrants or emigrants by age.

Other approaches

In contrast to the stationary population equivalent approach presented above, four other approaches have been proposed. This section summarizes these other approaches and notes their comparative features.

The first approach has been carefully presented in an important series of papers by Keyfitz (1968, 1969, 1971a, b, 1977). Keyfitz’s work derives from stable population theory and expresses population change in terms of the stable population. This approach, therefore, is not independent of the momentum of the current population and, compared to the proposed SPE measure, it is difficult to distinguish future growth due to momentum and growth due to the intrinsic vital rates. Keyfitz’s work pays particular attention to the single year effect of international migration and gives a convenient model for calculating the amount of emigration needed to balance above replacement fertility. The SPE measure can, if desired, also incorporate analysis of immigration on a year-to-year basis, while the Keyfitz model does not provide for analysis of the effect of continuing immigration. Much of the work on the stationary population equivalent model in this paper develops from Keyfitz’s work.

Sivamurthy (1982) has proposed a second approach, closely resembling the stable population method of Keyfitz. In Sivamurthy’s work on the Australian population, he develops a stable population model that incorporates a constant vector of immigrants with a fixed age structure. Like Keyfitz’s approach, Sivamurthy’s method does not separate future growth due to momentum from growth due to intrinsic vital rates, including immigration. Sivamurthy’s work purposes useful methods, however, for modeling immigration with standard Leslie matrix population projections (Leslie, 1945).

A third approach derives from the work of Coale (1972) and related work by Keely and Kraly (1978). This approach begins with a life table population, and treats each immigrant as an elimination of a death in the population. Positive net immigration generates an increase in life expectancy in the stationary population model, which, because replacement fertility is assumed, requires fewer births in the population. This approach results in the calculation of the eventual stationary population size adjusted for the momentum in the current age structure and the continuation of current net immigration. We make use of Coale’s notion of a life table adjusted for immigration in later sections of this paper, where we calculate a stationary population equivalent age structure, assuming that a net immigrant has the same effect as eliminating a death.

The fourth approach develops from the work of Espenshade (1975) and Espenshade and Campbell (1977). The Espenshade model assumes constant mortality and fertility for a stationary population. If fertility is below replacement, the Espenshade model calculates the continued stream of migrants—fixed in number and age structure—required to balance the fertility deficiency. Note, in comparison, that Coale’s and Keely and Kraly’s approach uses a constant ratio of immigrants to current population whereas Espenshade’s model requires a constant number of immigrants. Finally, Espenshade, Bouvier, and Arthur (1982) contribute an important theoretical piece on the role of migration in population growth: they demonstrate that a stationary population will eventually be reached, under the assumptions of the Espenshade model, where the eventual size and age structure depend only on the fertility, mortality, and number and age composition of migrants. The Espenshade, Bouvier, and Arthur (1982) results are, in a sense, a special instance of stable population theory generalized to include migration.

A key difference between the four approaches described above and the proposed SPE measure is the manner for projecting future international migration. The Keyfitz model deals with the impact of one-time migration on a stable population and does not, therefore, consider continued migration. Sivamurthy’s approach assumes immigrants to be a constant proportion of the total population and with a fixed age structure. The third approach, taken by Coale and by Keely and Kraly, describes migrants as a balancing of births and implicitly assumes migration to be constant. This approach is clearly appropriate for emigration and potentially sensible for modeling that portion of immigration generated by relatives of past immigrants. It is not clear in the long run, though, that immigration levels will be proportionately related to current population size. In the short run, at least for the analysis in this paper, Germany’s immigration levels are related to an annual number rather than as a proportion of the current population size. Our approach can incorporate the Coale and the Keely and Kraly procedures by assuming that migration changes the life table used for the V(x) and e 0 calculations. In calculations with adjusted life tables, an immigrant is a reduction of a death and an emigrant adds a death. The fourth model, by Espenshade, involves a constant number and age structure of immigrants. We find it particularly useful to adapt our SPE model to handle immigration in the fashion advocated by Espenshade, although the SPE model is not limited to this particular framework for immigration. As shown in later sections, our model reflects the annual flows on international migration that might be imposed by Germany’s future immigration policy.

Stationary population equivalent for Germany

The stationary population equivalent (SPE) model is particularly attractive for analysis of Germany’s population growth for several reasons. First, current German population policy debate has strong interest in the long-term consequences of the annual volume of international immigration on population growth. Although emigration is obviously of interest to policy makers, it is less susceptible to policy measures than immigration. Second, fertility levels in Germany have been relatively unchanging at below replacement levels for more than a decade. This means, if continued, that the German population will eventually suffer negative rates of natural increase. Any possible German population will, given negative rates of natural increase, derive solely from the offsetting contribution of positive net international migration. Finally, there is negative momentum in the current German age structure. With below replacement fertility and even with modest net immigration, as demonstrated below, the German population will decline in the future. As a result, the present observed levels of German population growth are a poor indicator of long-term growth. And, given the negative momentum built into the current age structure, projections of growth in the near future are deficient measures of the interrelated dynamics of fertility, mortality, and international migration.

In order to evaluate better the effect of international migration on the German population, we use the SPE model as an indication of population size and rate of change. This allows the analysis to balance fertility and mortality with estimates of immigration and emigration to assess the impact of each of these factors on the long-run population size of Germany. Our specific interest is to estimate the amount of decline in the stationary population equivalent implied by various levels of these rates, and to analyze the contribution of immigration and emigration necessary to prevent a decline in Germany’s population. Subsequent analysis, derived from the work outlined in this paper, could describe growth goals other than this paper’s assumed target of zero growth.

The results reported here, in a methodological sense, are a replication of the most recent population projection of the Statistisches Bundesamt, Germany’s Federal Statistical Office, for the period 2001–2050 (Statistisches Bundesamt, 2003). Germany’s projections include the initial national population, age-specific rates of fertility, mortality, and international migration under a series of reasonable assumptions about the levels and patterns of these components. The SPE model offers an alternative method for understanding the future German population under various demographic alternatives. This paper, therefore, contrasts the use of population projections with an explicit population model for addressing debate on the future implications of fertility, immigration, and emigration for Germany’s national population structure.

Population data

All population data for this paper are for the 2000 calendar year. This year, 2000, is selected in order to make comparisons of the SPE results with the Statistisches Bundesamt’s most recent population projections.

The stationary population equivalent model requires information about fertility, mortality, and international migration. The fertility schedule affects the calculation of the reproductive value, V x , and the number of generations in the stationary population, N, through its determination of the mean length of a generation. Fertility also appears in the proportion of births that are female, S.

The mortality schedule also influences the reproductive value of the population, as well as affecting the number of generations in the population. Finally, the immigration and emigration schedules alter the reproductive value calculation because immigration affects the “birth” of a new individual—albeit not necessarily at age 0—and emigration acts as the “death” of an existing person.

Basic population data for 2000 are shown in Tables 1 and 2. In the sections below, we comment on data sources and adjustments to the data.

Table 1 Population by age and sex, life table L(x) and life expectancy by sex, and total fertility rate and age-specific fertility rates, Germany, 2000
Full size table
Table 2 Age and sex compositon of immigrants and emigrants, and total annual number of immigrants and emigrants, Germany, 2000
Full size table

Population by age and sex

The observed population data, by age and sex, are for 30 June 2000 and taken from Heilig (2000). The 2000 age–sex data from Heilig (2000) are consistent with the Statistisches Bundesamt’s (2003) population data for 2001 and are very similar to 2000 population estimates presented in the United Nations Population Division (2001a, 2001b) tables for Germany. Heilig’s estimates show a 2000 population total of 82,221,000. The Statistisches Bundesamt reports a population of 82,440,000 for 2001. The United Nations’ estimates show a total population of 82,017,000 in 2000, or 204,000 fewer people than the Heilig estimate.

Mortality

Deaths by age and sex for 2000 are taken from Heilig (2000). Age-specific mortality rates were tabulated by sex, and the probability of dying between x and x + n, n q x , were estimated by procedures developed by Chiang (1968). Chiang’s method requires knowing the fraction of the interval, from x to x + n, lived by those dying in the interval, called n a x . The formula then for n q x in terms of the age-specific mortality rates, n m x is:

$$ {}_nq{}_x\, = \,\frac{{n_x \cdot m_x }} {{1 + (1 - {}_na_x ) \cdot n_x m_x }} $$
(22)

for an abridged life table. Based on empirical investigations, Chiang found that n a x varies little by sex or geographic location for similar mortality levels. The life table uses n a x values published in Namboodiri and Suchindran (1987, p. 26) for ages 0–84; for ages 85–99, we assume that the value of .48 for the 80–84 age group was the same for older groups. The survivorship function, l x , was derived from the n q x values by standard life table methods. The L x values for males and females are shown in columns 4 and 5 of Table 1. The life expectancy at birth, for these life tables for Germany in 2000, is 74.7 years for males and 80.7 years for females. These values are the same as baseline life expectancy values published by the Statistisches Bundesamt in their population projections.

Fertility

We reviewed data for previous years on the sex ratio at birth in Germany. While there are some minor annual variations, we used a sex ratio at birth of 1.053 for this work. The sex ratio at birth has a trivial impact on the results and modest changes in the sex ratio could be ignored. Age-specific fertility rates are taken from Heilig (2000). The age-specific fertility rates were multiplied times the female population by age to obtain the number of births by age of mother. Our estimates of the number of births by age of mother are adjusted to match the total fertility rate of 1.4 published by the Statistisches Bundesamt for 2001. The age-specific fertility rates used in this analysis are shown in column 6 of Table 1.

We assume that the fertility rates for immigrants and emigrants are the same as those for the resident German population because we lack information on fertility by nativity, and on fertility for emigrants. If data were available on the actual fertility of immigrants and emigrants, these additional data could be incorporated. If the fertility of immigrants is higher than the resident population—as it is in some immigrant-receiving countries—then this would increase the reproductive value for immigration, reducing the number of immigrants required to offset below replacement fertility. If immigrant fertility exceeds the resident population’s childbearing levels, then a smaller number of immigrants could maintain a constant SPE level.

Immigration and emigration

Immigrants and emigrants by age and sex are derived from unpublished Statistisches Bundesamt data on immigrants and emigrants by sex and seven age groups (0–14, 15–19, 20–29, 30–39, 40–49, 50–59, and 60 years of age and older). Heilig’s (2000) data on the age–sex percentage distribution for immigrants and emigrants for Germany in 2000 were used to interpolate five-year age data that, when summed, matched the Statistisches Bundesamt’s information for ages 0–14 and 60 years of age and older. Five-year age group data for ages 20–59 were derived by Karup–King interpolation formulas (Shryock & Siegel, 1976, Table C-4), applied to the Statistisches Bundesamt’s data. Based on trends from the 1990 to 2000 period, we assume annual current international migration levels of 700,000 immigrants, 500,000 emigrants, and 200,000 net immigrants. For comparison, the Statistisches Bundesamt’s medium-level net immigration projections assume 280,000 initially in 2001, decreasing to 200,000 in 2030, and remaining at 200,000 thereafter. Table 2 presents data on the age–sex composition of immigrants and emigrants, and the annual numbers of immigrants and emigrants for the SPE analysis.

Germany’s 2000 stationary population equivalent

Table 3 displays basic aspects of the SPE analysis for Germany in 2000. This table reports the SPE assuming replacement fertility and no net international migration or, in other words, a closed population with long-term zero population growth. The second column shows the reproductive value of women, assuming constant replacement fertility. While the total of reproductive values by age is 1.0, by definition, the total for column 2 reports instead the overall reproductive value (1.0) times the number of generations (N), including the adjustment to add males. Column 3 reports the contribution of each cohort of women to the final stationary population, including males. Column 3 derives from the reproductive values times the number of generations for both sexes times the observed 2000 female population by age.

Table 3 Stationary population equivalent (SPE) calculation, Germany, 2000
Full size table

The reproductive values, V x , begin at 1.0 at the instant of birth, rise slightly in the early years of life to offset childhood mortality, then decrease almost linearly after puberty. This is the expected pattern for V x by age for low mortality and low fertility populations (Keyfitz, 1968, p. 55). Note that the reproductive values drop to about one-half by age 25 and reach essentially zero by age 40. The total contribution of each cohort to the SPE, shown in column 3, reflects in part the fertility and migration history for Germany. The peak contribution stems from the 10 to 14 age group, which has the highest reproductive value. There is little contribution to the SPE from older women in the childbearing years, reflecting that reproduction diminishes substantially after age 40. Also shown in Table 3 is the calculation for the mean age of childbearing (K = 28.6) and the net reproduction rate (NRR = 0.674).

The number of generations equals 5.8, reflecting a mean length of a generation of 28.6 years and the life expectancies, by sex, shown earlier. The number, 5.8, means each additional female birth adds 5.8 persons to the population: herself, her daughter, her granddaughter, and 2.8 males, for instance.

The following sections report three SPE calculations. First, the assumption of a closed German population, with no international migration, is explored. This calculation indicates how much current fertility is below the replacement level, in the absence of migration. Second, a calculation is made for the German population with current 2000 levels of migration. This shows the long-term consequences of the current demographic rates, including migration. Third, an assumption is made that international migration alone offsets below replacement fertility, and the calculation indicates the level of net immigration needed to balance completely 2000 below replacement fertility.

No international migration assumption

The German SPE value in 2000, assuming no international migration, is 66.0 million. Given below replacement fertility (the net reproduction rate equals 0.67 in 2000) and current mortality levels, there were 374,000 births rather than the 555,000 births necessary for long-term fertility replacement. The SPE calculation displayed in Table 3 reveals, therefore, a deficit of 181,000 births, or 33% below replacement.

Columns 4 and 5 of Table 3 show the eventual stationary age distribution for females and males, respectively. This is the long-term age–sex structure for the German population if the NRR were equal to 1.0 and if there were no international migration. These age data are useful for comparing alternative SPE calculations to the current age distributions.

Table 4 displays the ratio of the stationary population (from Table 3) to the observed 2000 population. The model constrains the current and stationary populations to have the same reproductive potential; thus, the actual and stationary female populations below 30 years of age must be roughly equal. Three features are readily apparent. First, there is negative population momentum in the current age structure of the German population. The overall ratio of .802 (shown at the bottom of Table 4) indicates that, even with replacement level fertility, the population would decrease approximately 16.2 million, or 20%. This negative momentum occurs because the current age structure has relatively few people in the childbearing years. Negative population momentum occurs in other European populations where a history of several decades of low fertility has produced smaller numbers of children than parents (Lutz, O’Neill, & Scherbov, 2003). When there are smaller cohorts in younger ages, there is a tendency for the population to decline, even if fertility were to be at replacement level. Second, there is a noticeable increase in the population under age 10 in the stationary age distribution. And third, the stationary population exhibits slightly more elderly in ages 80–95, 40% more in ages 95–99, and about twice as many over 100 years.

Table 4 Ratio of stationary population to current population, by age, Germany 2000
Full size table

What is the effect of current low fertility on Germany’s stationary population equivalent? Table 5 shows calculations for the change in the SPE due to the observed 2000 fertility rates as well as for the SPE of migrants. Note that the actual SPE calculations are for females, but the contribution shows results for the total population, including females and males. Because the observed fertility rates are below the replacement level, the net contribution of births is a reduction of the SPE by 1,008,000. In the absence of migration and with 2000 fertility levels persisting, the SPE for Germany would decrease from the 2000 base of 66.0 million by about 1.0 million annually, or about 1.5% per year. If below replacement fertility levels of NRR = 0.67 were to persist for 10 years and if mortality remained constant, for example, Germany’s stationary population equivalent would decrease to 66.0−(10*1.0) = 56.0 million in 2010, in the absence of net immigration.

Table 5 Changes in stationary population equivalent (SPE) due to births and international migration, Germany, 2000
Full size table

2000 international migration assumptions

How much does current international migration counterbalance Germany’s fertility deficit? This question has a direct answer using the SPE model. Using the age structure of immigrants and emigrants and following the procedures outlined above, the SPE of migrants can be calculated for a level of net immigration of 200,000. As shown in Table 5, immigration increases Germany’s SPE level by 819,000, while emigration reduces the SPE by 461,000. The calculations indicate that each immigrant results in an increase of 1.17 and each emigrant produces a decrease of 0.92 in the SPE. The impacts of immigration and emigration on the SPE are different because the age distributions of the two flows differ. The age composition of immigrants is slightly younger, as reflected in the slightly higher effect on the SPE value. If immigration is at 700,000 and emigration at 500,000 (or 287,000 female immigrants and 185,000 female emigrants), then the net contribution of international migration adds about 358,000 to the SPE for Germany. The offsetting contribution of observed fertility, however, results in an overall effect of −650,000 to the SPE, as shown in the last column of Table 5. The long-term stationary population equivalent decreases annually by about 650,000, or about 1.0% each year that the current combination of mortality, fertility, and migration levels persists.

With current net immigration of about 200,000 annually, fertility levels are still too low to replace the population in the long run. Approximately 490,000 annual births are required, in conjunction with present migration, for long-run replacement of the population for this SPE model. With net immigration of 200,000, current annual births of 374,000 births fall about 116,000 births, or 24%, short of the required replacement level. Net immigration offsets about 34% of the overall below replacement fertility deficit. But there remains a considerable shortfall from the perspective of a long-term stationary population.

A related approach for examining the effect of migration on Germany’s population dynamics is to display survival values, by age and sex, adjusted for migration. These adjusted values are shown in Table 6. Note that the probability of an age group surviving exceeds 1.0 for ages 0–40, due to net immigration. Under 2000 mortality and international migration, therefore, the survival of age groups over time yields very similar-sized groups from infancy to the early retirement years.

Table 6 Calculation of life table survival values adjusted for international migration, Germany, 2000
Full size table

Repeating the earlier exercise, the revised life tables in Table 6 lead to the results shown in Table 7. Table 7 presents the stationary population that would result if the current level of migration were to continue indefinitely, and if fertility were raised to yield replacement level fertility. A stationary population under these conditions would be older and larger—with an SPE of 81.3 million—than the population shown in Tables 3 and 4 (a population with no migration and replacement level fertility). Such a population—with net immigration of 200,000 annually and a net reproduction rate of 0.779 (16% higher than currently)—would have a long-term stationary population equivalent than would be only 1% smaller than presently observed. The differences between Tables 3 and 4 and Table 7 represent the effect of the years lived by the assumed continuing stream of net immigrants in Germany.

Table 7 Current and stationary population equivalent (SPE), by age and sex, for current international migration levels, and ratio of SPE to current population, Germany, 2000
Full size table

Replacement level international migration assumption

Given the current fertility levels, how many immigrants, assuming the present age structure of migrants, are needed for a stationary population? We can make several possible calculations using the SPE model. For example, we know from the previous section that levels of 700,000 immigrants and 500,000 emigrants balance about one-third of the losses from below replacement fertility. In fact, annual net immigration of 755,000 is required to maintain the current SPE of 81.3 million for Germany. This level of 755,000 net immigration implies, for instance, 1,255,000 immigrants and 500,000 emigrants, assuming that 500,000 residents leave Germany annually. This level of immigration is considerably higher than the current immigration levels and considerably above the medium-level net immigration assumption of 200,000 in the Statistics Bundesamt’s current population projections.

Alternatively, we could search for a continuing migration rate that, when added to the life table, would produce a NRR equal to 1 with current fertility rates. Such a life table would also require a net level of immigration of 755,000, or 1,255,000 immigrants, if emigration were 500,000. Both calculations yield similar results and equivalent figures for the required level of net immigration.

Stationary population age structure

Table 8 summarizes several possible stationary age distributions, compared to the 2000 age distribution shown in column 2 of the table. Column 3 shows a stationary population with replacement fertility but no migration (this population is detailed in Tables 3 and 4). Column 4 displays a replacement fertility population consistent with current migration levels. Finally, column 5 presents a stationary population with approximately current fertility, but with 1,255,000 annual immigrants to offset fertility deficits.

Table 8 Comparison of current population to stationary population equivalent (SPE), for several possible demographic conditions, Germany, 2000
Full size table

All stationary populations presented in Table 8 are older populations than the current German population. These alternative future populations have markedly fewer individuals in the 20–50 age group and greatly more elderly.

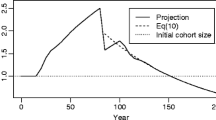
Differences also exist between alternative stationary populations (Fig. 1 shows the three stationary populations along with the 2000 population). As a rule, the greater the reliance placed on international migration to maintain a stationary population—and this may seem counterintuitive—the older the German population becomes. Comparing columns 3 and 5 of Table 6, for example, indicates that the high immigration population (column 5) produces an age structure with about one-fifth more people in the elderly years (26% of the population are 65 years of age and older), compared to the stationary population with no immigration (see column 3, where 21% are 65 years of age and older).

Fig. 1
figure 1

Female age distribution for current and various stationary population equivalents, Germany, 2000

Full size image

Comparisons of SPE to Statistics Germany’s projections

As published, Germany’s (Statistisches Bundesamt, 2003) projections are an exemplary presentation of national population projections. The official projections present varying assumptions for three facets for the national forecasts: (1) three alternative patterns for a fixed number of international migrants by age and sex, (2) three varying mortality levels measured by survivorship increasing from 2003 to 2050, and (3) fertility increasing slightly to a total fertility rate of 1.4 in 2010 continuing at that level thereafter. The official projections do not include estimates for the 16 German Länder, but these subnational estimates are outside our concern with national data.

German government projections describe nine series (three mortality series by three migration series) that they believe cover the plausible range of possibilities of future fertility, mortality, and migration for Germany. The German projection that resembles our SPE analysis is projection variant 5, which assumes modest mortality improvements, net immigration of 200,000 per year, and a total fertility rate of 1.4 in 2010 and after. German population projections assume, for all variants, that there is initially net immigration of 80,000 ethnic Germans, decreasing to zero net immigration of ethnic Germans in 2030. Thus, population projection variant 5 assumes initially a total net immigration of 280,000 (80,000 ethnic Germans, referred to as “Deutsche” in the projections, and 200,000 non-German immigrants, referred to as “Ausländer” in the projections). In 2030 and after, total net immigration is 200,000.

But, because our SPE calculation acknowledges that fertility must increase to the replacement level (with an SPE total population size equal to 81.3 million), it comes as no surprise that projection variant 5 shows that the German population peaks at about 83.1 million in 2010 and decreases to about 75.1 million in 2050.

Projection number 4 in the German analysis includes a total fertility rate equal to 1.4 in 2010 and after, mortality improvements, and a lower level of net immigration of 100,000 annually, including an additional 80,000 net immigration of ethnic Germans in the initial years of the projection. From our SPE analysis, we know that 100,000 net immigrants is considerably too low, by about 655,000 immigrants, to maintain the 2000 SPE of 81.3 million. In projection variant 4, the German population steadily declines to 68.5 million in 2050.

Projection variant 6 assumes a higher level of net immigration of 300,000 per year (including, as in all series, an additional 80,000 net immigrants of ethnic Germans in the initial years) in addition to moderate mortality improvements and a total fertility rate of 1.4 in 2010 and after. Again, the net immigration levels, according to our SPE analysis, are too low, by about 455,000 immigrants, to maintain 2000 SPE population size levels. Projection variant reaches the largest German population size of about 83.9 million in 2020 and then declines to 80.0 million in 2050.

This paper assumes that mortality remains constant for the SPE calculations. If life expectancy increases by about one-fifth of a year per year, which is a reasonable assumption for current mortality improvements in Europe, this would add about 170,000 to the SPE each year by increasing N, the number of generations in the population for both sexes. In thinking about the possible effects of below replacement fertility and the contribution of international migration, it is worth noting that likely future mortality improvements may play a role in maintaining a constant SPE level.

Replacement-level births

We can use the SPE model to make calculations about the number of births needed to maintain Germany’s current SPE population of 81.3 million, assuming different levels of net immigration. Table 9 shows the births needed to maintain current SPE levels under the assumption that net immigration is zero, 100,000, 200,000, 300,000, and 755,387. The last figure of 755,387 is selected because, from earlier work, we know that it is the replacement-level net immigration, given current fertility levels.

Table 9 Comparison of births needed to maintain current stationary population equivalent for various levels of net immigration, Germany, 2000
Full size table

Under the range of net immigration assumptions for the Statistisches Bundesamt’s population projections, there remains an annual deficit of 95,000 to 137,000 births, or 26% to 37% more births needed than at present, depending upon the assumed level of net immigration, in order to main the long-term SPE population of 81.3 million. If net immigration were zero, current births would need to increase by 158,000, or 42%. If net immigration were 755,000, then the SPE population size would be maintained without the need for additional births.

Replacement-level net immigration

Germany’s population projections do not assume higher alternative fertility levels, including possible replacement-level fertility, as they are presumably thought to be implausible. There are, therefore, no official projections for comparison to our SPE analysis with replacement-level fertility. We can, however, make assumptions about a range of possible alternative fertility rates (adjusting current age-specific fertility rates to produce alternative assumed levels of the total fertility rate) in order to explore the implications for replacement-level net immigration.

If Germany’s total fertility rate were different than 1.4—say, 1.0, 1.2, 1.6, 1.8, 2.0, or 2.1—this implies changes in the annual number of births and in the net reproduction rate, as shown in Table 10. The total fertility rate of 2.1 (actually, 2.0759) is selected in order to obtain a net reproduction rate of 1.0, replacement-level fertility.

Table 10 Comparison of replacement-level net immigration needed to maintain current stationary population equivalent levels for various assumed levels of total fertility rate, Germany, 2000
Full size table

Different assumptions about current fertility have consequences for the net immigration level needed to maintain Germany’s current SPE population level of 81.3 million. Lower fertility levels require higher levels of net immigration: if the total fertility rate were to be 1.0, it would require almost 900,000 net immigrants annually to maintain German’s current SPE population size. On the other hand, total fertility rates above 1.4 reduce the required levels of net immigration. If Germany’s total fertility rate were in the range of 1.8–2.0, for instance, then the current SPE population level of 81.3 million could be maintained with net immigration of about 32,000 to 346,000—in the range roughly of Statistisches Bundesamt’s low to high assumptions for net immigration.

The United Nations’ Population Division (2000) has studied the question of whether replacement immigration can address declining and aging populations. The U.N. study used a population projection framework for the analysis of eight countries, including Germany. For Germany, maintaining a constant population of 81.7 million (the 1995 base population for Germany in the U.N. study) would require 279,000 net immigrants annually between 2000 and 2025, and 408,000 net immigrants annually thereafter until 2050. The U.N. analysis assumes the same age–sex composition for immigrants for all countries and is, therefore, not directly comparable to the results provided here. It appears that the U.N. study assumes a younger age structure for immigrants than actually occurs in Germany. As a result, the U.N. study reports replacement-level immigrant levels that are considerable below those in this analysis.

Immigration age and sex composition

As a final exploration of the uses of the SPE approach for understanding Germany’s population projections, we investigate the sensitivity of Germany’s population dynamics to assumptions about the age and sex composition of immigrants. As noted earlier in discussion of Table 2, males comprise 59% of Germany’s immigrants and 63% of its emigrants. This is rather different than major immigrant-receiving counties—such as Australia, Canada, and the United States—where females typically comprise one-half or more of immigrants. Besides the proportion female, the age distribution of female immigrants has a critical effect on population change. Other factors being equal, the immigration of younger females has the greatest potential contribution to a population’s SPE size. Males and older females have virtually no effect on a population’s stationary population equivalent.

We examine the influence of alternative age–sex immigration composition by assuming that Germany’s immigration has the age–sex distribution of those in Canada (Statistics Canada, 1995, Table 4–16) or the United States (U.S. Census Bureau, 1996, Table C-2). The age–sex composition in these two countries is distinctive. Canada’s immigration selection is based on an annual quota for overall immigration and a point-based preference system that, in part, gives higher preference to educated and skilled immigrants aged 21–44 years (Smith & Edmonston, 1997, Appendix 2-A). U.S. immigration includes several categories for employment-based immigration, but reserves the largest share for family-based admission (Smith & Edmonston, 1997, pp. 40–46).

As shown in panel A of Table 11, more than one-half of the immigrants in Canada and the United States are female, compared to 41% in Germany. Although Canada has more immigrants aged 20–44 years than the United States (56% for Canada and 50% for the United States), as expected given the Canadian preference system, Germany’s immigrants are even more concentrated in this age group, with 70% aged 20–44 years. The SPE population calculation is predominantly affected by the proportion of females who are younger females: the United States has the highest proportion (34%), Canada ranks second (29%), and Germany’s immigrant composition ranks third (27%).

Table 11 Effect of different patterns of immigration age–sex composition on current stationary population equivalent (SPE), Germany, 2000
Full size table

Panel B displays results for the assumption that 700,000 immigrants (and 500,000 emigrants) enter Germany each year under three different assumptions about the age–sex composition of the immigrants. Each immigrant, on average, increases Germany’s SPE population by 1.17, assuming the age–sex immigrant composition of Germany. Under the assumption of Canada’s age–sex immigrant composition, each immigrant increases it by 1.34. And, under the assumption of the U.S. age–sex immigrant composition, it raises it by 1.61. The larger effects for Canada and the United States occur because their immigrants include more females, especially younger females.

The larger SPE effects of immigration based on either the immigrant composition of Canada or the United States means that fewer immigrants would be needed to maintain Germany’s SPE population level of 81.3 million (with a total fertility rate of 1.4), as shown in Table 11’s panel C. Instead of 1,255,000 immigrants needed under current German age–sex immigrant composition, this figures decreases to 1,090,000 if immigrants were similar to Canada and to 910,000 if they were similar to those in the United States. Immigration still needs to increase, of course, from current levels of 700,000 in order to maintain Germany’s SPE population level. But substantially fewer immigrants would be needed if Germany’s immigrant composition were to include more young females.

Different age–sex composition of immigrants affects how many births are needed to “fill the gap” between current births and net immigration of 200,000. If each average immigrant makes a greater contribution to maintaining current SPE population levels (by including more younger females), then the number of births needed to fill the gap between current and required births would diminish. As noted earlier and shown in Table 11’s panel D, Germany’s births need to increase 31% in order to maintain current SPE levels, assuming net immigration of 200,000. If, however, the immigrant age–sex composition included a greater proportion of younger females, the required increase in births would be less: a 25% increase assuming Canada’s immigrant composition and a 17% increase assuming the composition of U.S. immigration.

In summary, it is relatively straightforward to compare SPE analysis and standard population projections. SPE analysis complements the interpretation of population projections in three ways. First, the results from the SPE analysis indicate the demographic conditions (fertility, mortality, and migration) that are associated with an unchanging SPE. Second, it may be useful to display SPE values as part of the presentation of population projections: the SPE measure offers a quantitative indication of population change in the midst of often complex shifts in the age distribution, vital rates, and migration. And third, the SPE model offers a potentially attractive method for making such calculations as replacement-level net immigration that assist the interpretation of population projection results.

Policy implications and conclusions

Germany faces serious demographic challenges as its population ages and, as is likely, declines. Fertility rates are well below the level needed to maintain a constant population, although German rates are higher than in several other European countries, such as Italy and Spain (Kohler, Billari, & Ortega, 2002; Lutz et al., 2003). Germany’s population had a median age of 40 years in 2000, close behind Japan, which has the oldest population in the world with a median age of 41 years. Germany’s population is expected to age significantly in the next few decades, reaching a median age of 48 years in 2045 (Enquete Commission on Demographic Change, 1999, pp. 54–55). These demographic figures make Germany, along with other European countries and Japan, likely victims of a pension time bomb (Bräuninger, Gräf, Gruber, Neuhaus, & Schneider, 2002).

Germany’s population is likely to increase slightly from 82.2 million in 2000 to about 83.1 million in 2010 before declining steadily thereafter to 75.1 million in 2050 (Statistisches Bundesamt, 2003). Germany’s population is forecast to decrease by about 9% over the next five decades. A falling and aging population will increase the ratio of retirees to workers and pose difficult demographic problems for Germany.

Although the determinants of population aging are well-known (Preston, Himes, & Eggers, 1989), there is considerable debate about possible German policies measures to deal with consequences such as pension reform (Bräuninger et al., 2002; Enquete Commission on Demographic Change, 1999) or to change the demographic factors causing population aging. Two broad potential determinants are being discussed in Germany and other European countries. There are no short-term options, however, because whatever is done will take decades to change. One possibility is to consider family policies that might increase the number of births. Changes to the tax system and employment practices, for example, might remove obstacles to women having children and pursuing a career at the same time. More active family policies, such as providing financial incentives for more children, are possible. Governments need to tread cautiously, however, because having children is one of the more private decisions and incentives to have more births risks seemingly too coercive in liberal democratic societies.

A second option, and one that is debated considerably in Germany at the moment, is to increase immigration (Independent Commission on Migration to Germany, 2001). Increasing levels of international migration in Germany is also controversial, but it makes good demographic and economic sense. Immigration levels in the range of 100,000 to 300,000, as have prevailed in recent years (Lederer, Rau, & Rühl, 1999) increase the working-age population and, at least in the short run, improve the ratio of retirees to workers, for example.

The various population models considered here provide results consistent with formal analyses and Germany’s population projections. The stationary population equivalent (SPE) model finds, under current mortality and fertility conditions, that an annual level of about 755,000 net immigrants is required to maintain a stationary population in Germany. As long as the net reproduction rate remains at about 0.67, as it has for some time, recent levels of net immigration are inadequate to counterbalance eventual population decline. With 500,000 emigrants (the anticipated levels in Germany’s population projections), Germany requires about 1,255,000 immigrants annually to maintain the current SPE of 81.3 million. This is more than twice the level assumed in Germany’s medium-level population projections.

These results should be provocative in light of current public debate about Germany’s immigration policies and Germany’s important European role as a recipient of East European populations. For example, greatly increased numbers of immigrants can be accommodated within the demographic realm of Germany’s stationary population—there is room for more than 500,000 additional annual immigrants (above the current level of about 700,000 immigrants), without exceeding the long-term SPE goal of 81.3 million.

We would be amiss if we did not emphasize that demographic calculations about the effect of immigration on population size are only one part of the complex policy issue of immigration. Aspects of multiculturalism, employment, regional distribution of the population, health and welfare care for the elderly, and humanitarianism for refugees are, obviously, also important considerations. But, nevertheless, how immigration affects Germany’s growth and size is one crucial issue, and the calculations reported in this paper offer a distinctive demographic perspective for current debate.