Abstract
Despite decades of research, there is no consensus as to the core correlates of national-level voter turnout. We argue that this is, in part, due to the lack of comprehensive, systematic empirical analysis. This paper conducts such an analysis. We identify 44 articles on turnout from 1986 to 2017. These articles include over 127 potential predictors of voter turnout, and we collect data on seventy of these variables. Using extreme bounds analysis, we run over 15 million regressions to determine which of these 70 variables are robustly associated with voter turnout in 579 elections in 80 democracies from 1945 to 2014. Overall, 22 variables are robustly associated with voter turnout, including compulsory voting, concurrent elections, competitive elections, inflation, previous turnout, and economic globalization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A common challenge in the study of comparative politics is balancing theoretical and empirical comprehensiveness with substantive importance. Consider voter turnout. If we ask what the most statistically significant and substantively important predictors of national-level voter turnout in democratic elections are, even after more than 50 years of comparative voter turnout research, there are few certainties beyond the fact that compulsory voting increases turnout. For example, several studies including Radcliff and Davis (2000) find larger district magnitudes increase turnout while others like Tavits (2008) find either no significant relationship or even a negative one (Fumagalli & Narciso, 2012).
One possible reason for these sorts of contradictory findings is that a topic has not received enough research attention for a consensus to emerge. This is not the case for voter turnout; it is one of the most studied topics in the discipline. Indeed, Cancela and Geys (2016, p. 264) suggest “turnout scholarship witnessed a veritable explosion” in the last 15 years. A second possibility is that we lack a thorough understanding of the underlying explanatory factors. Again, this does not seem to be the case here given the profusion of turnout meta-analyses. A recent meta-analysis of 130 journal articles identifies over a hundred explanatory factors (Stockemer, 2017). Geys’s (2006) earlier meta-analysis of 83 studies focuses on fourteen correlates but identifies several dozen more; and more recently Cancela and Geys (2016) examine 102 studies and identify several dozen correlates. Therefore, although there are myriad possible factors driving voter turnout, it has been difficult to reach solid empirical conclusions. A third possibility is that the world’s contextual heterogeneity explains why some variables behave differently in certain contexts, driving contradictory findings. Although empirical conflicts can definitely arise from contextual differences, they do not tell the whole story. For if a goal of comparative politics is reaching solid and generalizable conclusions across contexts, it is important to systematically approach competing explanations for comparable outcomes while recognizing important contextual differences. The comparable outcome we explore here is national-level voter turnout.
In the national-level voter turnout literature, it is uncommon to claim that one empirical model trumps others (Temple, 2000). However, there are developed techniques to systematically evaluate the proposed factors for a political outcome including meta-analyses and extreme bounds analyses. Given the sizable, established literature on voter turnout, this paper’s contribution is synthesizing the recent literature and evaluating its proposed correlates of national-level voter turnout using an extreme bounds analysis.
Extreme bounds analysis (EBA) has been used in a wide variety of contexts to evaluate factors driving a number of political and economic outcomes (Leamer, 1983; Levine & Renelt, 1992; Sala-i-Martin, 1997). For example, it has been used to evaluate over 50 predictors of economic growth (Levine & Renelt, 1992), 20 possible factors contributing to human rights violations (Hafner-Burton, 2005), 59 predictors of democracy (Gassebner, Lamla, & Vreeland, 2013), 59 electoral integrity predictors (Frank & Martínez i Coma, 2017), 43 covariates of life expectancy and infant mortality (Carmignani et al., 2014), 53 determinants of health care expenditures (Hartwig & Sturm, 2014), and 23 factors behind the diffusion of coups (Miller, Joseph, & Ohl, 2018). While many proposed proxies in these areas are statistically significant when considered in isolation, when tested with other predictors such findings are often fragile (Leamer, 1983). Extreme bounds analysis allows us to systematically evaluate what factors are robust to different model specifications. Hence, a primary EBA goal is to show that the “assumed model specification is largely inconsequential for statistical inference” (Gassebner, Gutmann, & Voigt, 2016, p. 295). Another goal is to reconcile the literature’s several (sometimes contradictory) findings.
To collect possible predictors of national-level electoral turnout, we analyze 44 articles on voter turnout published between 1986 and 2017 in leading political science journals. We identified 127 unique independent variables that may affect turnout, and we were able to collect data and run models using seventy of these variables in 579 elections in 80 democracies from 1945 to 2014. We then run over two million regressions with different combinations of these seventy predictors. Each variable was included in up to 41,660 models with various combinations of other variables. If a variable is a significant predictor across models, then we can conclude that its statistical significance is unlikely to be an artefact of model specification. To determine robust turnout predictors, we used the two most common EBA decision criteria proposed by Leamer (1983) and Sala-i-Martin (1997), and we find 7 and 22 variables respectively are robust according to these 2 sets of criteria across 2 model specifications.Footnote 1 The first series of models includes country fixed effects to control for unobserved country-level factors; the second series of models includes random effects which allows for the inclusion of sluggish or stationary country-level factors the literature suggests affects turnout. We also run a number of further sensitivity analyses excluding a lagged dependent variable, using a dependent variable with a different denominator (voting age population rather than registered voters), and running models on eight election subsamples.
This research is theoretically significant because we still lack a systematic and parsimonious explanation of voter turnout that can address the current inconclusive and sometimes contradictory nature of the literature’s empirical results. The aim of this paper is, therefore, threefold: (1) to shed light on the dozens of factors that can affect turnout; (2) assess the empirical robustness of the different explanatory factors; and (3) provide insight on which controls may be worth including in future work on voter turnout.Footnote 2 We proceed as follows. The next section briefly summarizes the current voter turnout literature. The third section examines meta-analysis’s strengths and weaknesses and describes how extreme bounds analysis compliments it. The research design section discusses our election sample, the dependent and independent variables, and several estimation considerations. Our main results are then presented and are followed by a series of further analyses. We then conclude with a discussion of our main findings and areas for future research.
What Do We Know About Voter Turnout?
The first national-level turnout studies explain variations in voter turnout by focusing on a selected sample of lower house elections in OECD countries. For example, Jackman (1987) analyzes 19 democracies, Jackman and Miller (1995) analyze 23, and Blais and Carty (1990) and Powell (1986) include 20. Normally, these studies focus on a series of factors such as “socio-economic environment, the constitutional setting, and the party system,” (Blais & Dobrzynska, 1998, p. 241).
Recent years have seen a proliferation of potential theoretical factors shaping turnout as well as an expansion of coverage. For instance, voter turnout is depressed with the size of a political community (Remmer, 2010), economic globalization (Steiner, 2010), corruption (Stockemer, LaMontagne, & Scruggs, 2013), and ethnic diversity (Martínez i Coma & Nai, 2017). Terrorism, in turn, increases the electorates’ attention on national politics and, consequently, turnout increases (Robbins, Hunter, & Murray, 2013). Similarly, while previous studies focused mostly on economically developed democracies, Blais and Dobrzynska (1998) were the first to have a truly global collection of democratic elections. More recent analyses focus on other regions including Latin America (Fornos, Timothy Power, & Garand, 2004), post-Cold War Eastern Europe (Kostadinova, 2003), Africa (Kuenzi & Lambright, 2007), and Muslim-majority countries (Stockemer & Khazaei, 2014).
These works share a number of similarities including the use of three general types of independent variables: socioeconomic, institutional, and political (Geys, 2006; Blais & Dobrzyinska, 1998). Socioeconomic variables include factors like economic growth and urbanization. Institutional variables capture the institutional arrangements under which the election take place (e.g., electoral formula). Finally, political variables account for specific electoral outcomes (e.g., the margin of victory).Footnote 3
The literature’s limitations appear when comparing their results. For example, one of the most cited studies by Blais and Dobrzyinska (1998) find that turnout is significantly affected by economic development, literacy rates, population size and density, compulsory voting laws, minimum voting ages, the electoral system, the number of political parties seeking seats, and the election’s competitiveness. Endersby and Krieckhaus (2008) reach similar empirical conclusions but suggest that context is important. Along the same lines, Martínez i Coma (2016) confirms some of Blais and Dobrzyinska’s (1998) findings but not others—notably those relating to electoral systems and economic development.
Furthermore, and more important for the purpose of this paper, a consensus does not yet exist on the robustness of these variables and, consequently, on what variables should be considered for a core model of cross-national aggregate voter turnout. For example, of the eight socio-economic factors used in the three articles mentioned above, only one variable is considered in all three—population.Footnote 4 Put simply, comparative studies provide mixed evidence for the robustness of particular factors affecting voter turnout. In summary, after over 50 years of research the literature still has not coalesced around a core model of turnout; different sets of variables are used in different analysis.Footnote 5 The literature, “draw[s] on relatively small samples, differing sets of observations, divergent operationalizations of turnout, and a wide array of theoretical models, the literature has mainly converged around relatively commonsensical observations” (Remmer, 2010, p. 277).
Why a Meta-analysis is Not Enough
One popular means of evaluating a literature’s lessons is a meta-analysis, which basically assesses whether (or not) an independent variable affects a dependent variable.Footnote 6 A meta-analysis, or an “analysis of analyses” (Glass, 1976, p. 3), normally employs two procedures: “vote-counting” and “combined tests.” The former counts the number of times a given coefficient is significant and in the expected direction. In such cases, it is counted as a ‘success’; otherwise, it is considered an anomaly. The higher the success rate, the more likely it is that we are to be observing a real association between the variables. A combined test is “based on the summation of the actual test statistics provided in each study” (Geys, 2006, p. 640).Footnote 7
Such meta-analyses have been done in the voter turnout literature. For example, Geys (2006, p. 641) identifies twelve significant socio-economic, political, and institutional factors affecting turnout, while highlighting that none are “omnipresent in the literature.”Footnote 8 This is “partly due to the lack of a firm theoretical model at the basis of variable selection,” and he argues for the “construction of a ‘core’ model of turnout” (Geys, 2006, pp. 641, 653). Along similar lines, Stockemer’s (2017, p. 712) meta-analysis of 135 studies from 2004 to 2013 identifies over 100 potentially salient variables, thoroughly analyzes 10 of them, and concludes “no variable is omnipresent or appears in most studies. Rather, different variables are used in various contexts.” The divergence pointed out by Stockemer (2017) explains the different results from his and Geys’ (2006) meta-analysis. They assess the “success” or robustness of 18 variables, 5 of those common in both works. Even for those five common variables,Footnote 9 when comparing the studies’ success rates, there are three common results: compulsory voting and population size impact turnout while income inequality does not. They diverge on the impact of election closeness and PR system because Geys (2006) finds they affect turnout, while Stockemer (2017) does not. Unsurprisingly then, Stockemer (2017, p. 712) acknowledges that the “literature is far from establishing a core turnout model.”
Meta-analysis’s main limitation is not procedural but conceptual. In the end, even the most exhaustive meta-analyses like those above are circumscribed by their samples. This implies that we are unsure about the robustness of such results, given that most researchers’ robustness checks are ad hoc. “They identify a set of competing explanations and see if their empirical results hold once they control for some variables that might be consistent with those explanations” (Hegre & Sambanis, 2006, p. 509). In other words, given all possible variable combinations, we cannot be sure that the selected model and the results presented are the ‘right’ ones. Usually, sensitivity (or robustness) checks estimate a series of regressions with alternative specifications. However, the number of possible alternative specifications is, of course, substantially higher. For example, without assuming any initial knowledge of variable selection, 5 variables lead to 32 possible model specifications, 6 variables have 64 combinations, 7 variables have 5040, 8 have 40,320, etcetera. The number of permutations increases exponentially as the number of variables increases; therefore, any particular study is likely showing a tiny proportion of the possible combinations. Hence, even the most demanding and detailed meta-analysis will only cover a tiny percentage of the multiple possible combinations that may affect voter turnout.
The standard regression framework on which meta-analyses rely has two other limitations. First, a particular variable’s statistical significance may be sensitive to the inclusion/exclusion of other variables. As Leamer (1983, p. 38) concludes, “an inference is not believable if it is fragile, if it can be reversed by minor changes in assumptions.” Second, even when theories point to particular mechanisms, they are not “refined enough to inform the choice of the empirical measure to be used to proxy for such factors/mechanisms” (Carmignani et al., 2014, p. 516). For example, should we use GDP per capita (as four studies considered in this paper do) as a proxy, the log of GDP per capita (two studies), or the log of GDP at purchaser’s price parity (two studies)? Should we use one measure or two? How would results change, for example, if instead of using Laakso and Taagepera’s (1979) effective number of parties, one decides to use the disaggregated number of parties or the number of parties weighted by their vote share?
Why Extreme Bounds Analysis?
By contrast, one of extreme bounds analysis’ key characteristics is that it estimates all possible combinations of a set of predictors showing how slight changes in the included variables affect estimation results. Therefore, rather than focusing on a specific set of variables, by considering all possible variable combinations, EBA can suggest which predictors are systematically robust. What EBA cannot do as well as meta-analysis is theoretically and empirically highlight the relationship between a particular outcome and explanatory variable, including possible mediation and moderation by other factors.
An extreme bounds analysis estimates a set of regressions with the following functional form:
where Y is the dependent variable (in our case, voter turnout), I is a vector of core variables included in all models, M is the variable of interest, Z is a set of controls, and u is the error term (Levine & Renelt, 1992). I is the set of variables always included—the “base” or “core” variables—because the literature suggests a well-established relationship with the dependent variable. What is the I vector of variables for electoral turnout? Unfortunately, as we show below, less than those that one, a priori, may think.
EBA repeatedly estimates the equation with a different set of Z controls in each regression. Since every regression produces a coefficient for all included variables, all the regressions create a distribution of such coefficients. In order to decide whether the coefficients are robust, researchers have relied on two main criteria. The first by Leamer (1983) suggests that a variable should be considered robustly related to the outcome variable if, and only if, the lower and upper extremes of a variable’s coefficients have the same sign.Footnote 10 Specifically, the extreme upper (lower) bound is defined by the maximum (minimum) value of the variable of interest plus (minus) two standard deviations. If the variable of interest remains of the same sign at both upper and lower bounds, then such relation among the variables is said to be “robust.” When the variable of interest does not keep the same sign at both upper and lower bounds, then such relation among the variables is said to be “fragile.” In short, only after running all possible regressions including all variables and only if all estimates are in the same direction, are results considered robust. Sala-i-Martin (1997) finds Leamer’s standard to be overly restrictive in most cases because it is likely that if enough model specifications are analyzed, and assuming that the distribution of β has both some positive and negative support, it is likely that the signs of the coefficients will change at least once. In fact, following Leamer’s criteria if a single regression produces a coefficient of the opposite sign large enough to shift one of the bounds, then the variable is considered not robust. Sala-i-Martin (1997) proposes to look at the entire distribution of coefficients and conclude a variable is robustly related to the outcome variable when a large percentage—say 90–95%—of the coefficient’s distribution is either above or below zero.
These criteria, then, can lead to different substantive conclusions. In the extreme, if enough regressions are run and the distribution of the estimators have some “positive and some negative support, then one is bound to find one regression for which the estimated coefficient changes signs” (Sala-i-Martin, 1997, p. 179). Indeed, by following Leamer’s approach, we may conclude that the knowledge about many social phenomena is scarce and thereby make a consequential Type-II error. In contrast, as Plümper and Traunmüller (2020, p. 149) recently show, Leamer’s EBA has “an extremely low probability of producing false positives” while, Sala-i-Martin is “more likely to suffer from identifying false positives than the inferential rule it replaced” (Plümper & Traunmüller, 2020, p. 149). Previous works have, in the main, relied on Sala-i-Martin’s rather than Leamer’s approach.Footnote 11 However, both criteria are informative, so we follow Hafner-Burton (2005) and report results according to both criteria. As is clear below, there are substantive differences in what is considered robust predictors of turnout using these different criteria, and we compare our results using both criteria.
Research Design
In the turnout literature, there has been a thorough discussion of how to best operationalize the phenomenon of interest. The two main options are the number of votes cast as a percentage of the voting age population (VAP) or the voting registered population (VRP). There are arguments for both. For example, Blais and Dobrzynska (1998) use the latter and argue that VAP is not adjusted for the alien population, which artificially downplays turnout. Endersby and Krieckhaus (2008, p. 602), by contrast, recommend VAP because if registration is not automatic, and registration and voting are correlated, “then the ratio of voters to registered voters is a biased measure of citizen’s motivation to vote.” Among our 44 studies, 16 use VAP, 18 use VRP, 5 use both, 4 use other definitionsFootnote 12 and 1 (Siaroff & Merer, 2002) does not provide a definition. In this article, we primarily use VRP, but we also use VAP measures in a series of robustness checks.Footnote 13 If after applying the same analysis on two related but different dependent variables, the results of the independent variables are similar, this would be a clear signal of a variable’s strength. Turnout data are from International IDEA (2017). According to IDEA, their data comes from the national election management bodies (EMBs) and national statistical bureaus. EMBs provide data from their official reports and web portals. IDEA’s population data comes from secondary sources. In order to be included in the dataset, the election has been held after 1945; must have been for national political office in an independent nation state; there must more than one party contesting the election; and the franchise must be universal.Footnote 14
In our data, the VAP and VRP turnout measures correlate at 0.68. Consistent with the literature we limit our sample to lower house elections in democracies (defined as a Polity value of six and above in the year before the observed election). Overall, our sample includes 579 elections in 80 democratic countries from 1945 to 2014.
Independent Variables
In order to identify the most common predictors of voter turnout, we rely on Geys (2006), Geys and Cancela (2016), and Stockemer (2017) meta-analyses of 83, 185, and 130 works, respectively. For our analysis, we included all English language, national-level, comparative, peer-reviewed journal articles focused on voter turnout published between 1980 and 2017. We therefore exclude case studies, studies focusing on local, regional, or provincial elections, book-length studies, and studies not in English. We focus on the national level because local dynamics are likely distinct from those at the national level. Furthermore, logistically it also makes sense to exclude works where the underlying data are not comparable to other cases: for example, exploring the effects of Norwegian school referendums (Kaniovski & Miller, 2006) on voter turnout in non-Norwegian countries is not possible. This decision implies that some factors, like campaign expenditures, cannot be examined given the almost total lack of available data outside the US. The 44 included studies are listed in the Appendix.Footnote 15
As mentioned above, turnout predictors are usually organized into three groups: socio-economic, institutional, and political; and we follow this approach when organizing 127 independent variables derived from the 42 articles we examine.Footnote 16 We find 41 socio-economic factors, 48 institutional factors, and 38 political factors. Such a large number of independent variables reinforce the diversity of empirical approaches in the literature and the need to clearly determine what robustly affects turnout (and what does not).
Tables 1, 2 and 3 summarizes each group of variables. The first column presents the number of times a variable is used in the literature; the second column includes the variable name or concept; the third column show the ways in which the variable has been measured (if available); the fourth column present the directional effect in turnout—sub-divided in four sub-columns, one accounting for each possible result. When the variable had a positive impact for turnout, it is labelled as ‘positive’, ‘negative’ when the contrary; ‘NS’ suggests a non-significant result, while ‘mixed’ captures those results when the results vary depending on the model.
Table 1 includes 48 institutional factors. The most frequent factor is compulsory voting, which is measured in three different ways. Twenty-eight studies find that compulsory voting has a positive and significant effect while five find it not significant. Two other variables—the number of political parties and proportional representation (PR)—are the next frequent (19 times each). This illustrates the literature’s differences in measurement; the former is operationalized in 10 different ways, the latter in two. We have created a straightforward measure of agreement among studies by dividing the most frequent result by the number of studies that use such measure and multiplying it by 100. The higher the percentage, the more established the finding.Footnote 17 For compulsory voting, the degree of agreement is over 84%. Other variables are less established. For example, the agreement on the impact of the number of parties or the impact of proportional representation electoral systems is unclear, with about 53% agreement. Regarding the former, while 10 cases find that higher number of parties, lead to lower turnout, 8 do not find it significant. Likewise, 10 studies show that countries under proportional representation systems show higher turnout while 7 find it not significant. Table 2’s socio-economic variables include two sub-groups, socioeconomic characteristics and geographical dummies. First, the indicators gathering relevant socio-economic characteristics of a given society, such as size of population, GDP, GDP growth, and urbanization. Twenty-two studies include GDP as an independent variable. Eight find that GDP has a positive impact on turnout, while seven show a non-significant relationship, three report a negative influence, and four show mixed results. Results are not much better for the rest of such variables. Second, there are geographical dummies for specific countries or regions. Most notable about these variables is that including a variable for Switzerland and/or for the US almost always are negatively related to turnout. There are two patterns worth mentioning when discussing Table 3’s political variables. First, not many political variables appear in the articles we examined. This is surprising given the fundamentally political nature of turning out to vote. An exception is “closeness/competitiveness” that appears in 21 studies (almost half of our sample). Furthermore, the level of agreement for this variable is below 50%. Second, we only find a high level of agreement for the previous election turnout level (though such variable only appears in five studies).
In sum, three important findings arise from this initial literature review. First, out of 127 distinct variables, less than half (44%) appear more than once. Even the most frequently used indicator, compulsory voting, was included in less than 75% of the examined studies. Second, among the 55 variables that appear in more than 1 article, over half (57%) are measured in more than one way. Third, it seems more generally that turnout studies face a paradox—while voting is mainly a political act, the most common empirically tested arguments in the literature are of institutional or socioeconomic mechanisms. Only recently have some articles examined the impact of terrorist attacks (Robbins et al., 2013), corruption (Stockemer et al., 2013) or electoral dynamics (Martínez i Coma & Trinh, 2017) on turnout.
Table 4 condenses this information and also offers an overview of the distribution of the 70 variables for which we have data. These results strongly suggest that a standard model of turnout does not yet exist, and few factors—especially institutional and socioeconomic—have a consistently established effect on voter turnout.
Estimation Considerations
Including all 127 predictors discussed above in our empirical models is not possible due to data availability—several variables are available for only a short span of time, specific region (i.e., Europe) or a clear set of countries (i.e., OECD members).Footnote 18 The final line in Table 4 describes the distribution of the seventy variables we include, and Appendix Tables A2, A3 and A4 present these variables’ summary statistics, operationalization, and sources.
Given the absence of a commonly accepted model of voter turnout, in our selection of core variables we rely on several theoretical assumptions consistent with the literature and empirical regularities to include five variables in all of our models. From an institutional perspective, compulsory voting has been found to affect turnout. 84% of our 44 studies find that compulsory voting increases turnout, which is likely the literature’s most commonly accepted finding. The electoral system is also a recurrent variable of study under the (challenged) assumption that voter turnout is usually higher in proportional representation systems (Blais & Carty, 1990). We also include two socio-economic factors—per capita gross national income and population (both logged to control for outliers). The former accounts for the literature’s finding that economic development fosters turnout while the latter controls for the relationship between community size (an element assessed both by Geys, 2006 and Stockemer, 2017) and turnout. Finally, we include the level of turnout in the previous election because the literature suggests that turnout may be habit forming and has its own inertia (Geys, 2006).Footnote 19 While we acknowledge that more core variables could be included, we believe our core turnout predictors are consistent with the literature we survey.
Given that several variables measure similar concepts and/or that the measurement of such variables may be related, multicollinearity may be a risk when including such a large number of predictors. Levine and Renelt (1992, p. 945)Footnote 20 rely on three common strategies to reduce this risk: (1) they limit the total number of explanatory variables to eight at most; (2) they limit the number of Z controls to seven; (3) and they further restrict their Z variables by excluding variables that a priori may measure the same phenomenon. Similarly, Hartwig and Sturm (2014) drop some variables when they are highly correlated. To avoid artificially inflating our estimates, we have followed their first and third strategies (we limit the total number of core and independent variables to eight and we exclude multiple measures of the same underlying phenomena).Footnote 21Footnote 22
The final estimation consideration is what type of model to run. The most commonly used method in the 44 reviewed studies was ordinary least squares (OLS) with robust standard errors clustered by country (15 articles). Regression models with fixed effects and random effects were used in several (6 articles and 7 articles respectively) of the 44 articles examined in the literature review above.Footnote 23 Nevertheless, there are reasons to expect with eight predictors that there is the real risk of unobserved variable bias and risk of unmeasured unit-effects. Furthermore, like most of the literature we are interested in the reasons for differences in turnout both between and within countries. There is an ongoing methodological debate about which is appropriate for time-series cross-section data such as ours that is outside the scope of this article.Footnote 24 Therefore, we estimate two series of models. The first series of OLS models with fixed effects focuses on time-varying explanations for turnout. Our I vector includes 5 variables, and the Z vector has 53 variables. The second series of models use random effects and clustered standard errors by country to include time-invariant variables. A random effects approach relies on the strong assumption that the included predictors are uncorrelated with country-specific intercepts (i.e., unobserved factors), but it does allow for time-invariant factors’ effects on turnout to be estimated. Our I vector for the random effects models includes 5 variables, and the Z vector has 65 variables. In both series of models, continuous independent variables are standardized in order to aid the comparability of coefficients and a number of continuous predictors were log-transformed to reduce the effects of extreme values.Footnote 25
Results
After running 1,170,324 regressions with fixed effects, the 5 core variables, and 22,096 unique combinations of 53 independent variables, nine variables are robust according to Sala-i-Martin’s criteria [the area under the general cumulative density function (CDF) that are on either side of zero is less than 0.05].Footnote 26 One variable (economic globalization) also meets Leamer’s (1985) more demanding criteria. Table 5 summarizes the results for the variables our fixed effects analysis suggests are robustly associated with voter turnout.Footnote 27 The nine robust predictors are evenly split between institutional, socio-economic, and political factors. The three institutional variables are proportional representation, concurrent elections, and the number of years since universal suffrage was introduced—the first two increase turnout, while the last decreases turnout. As for socioeconomic conditions, economic globalization decreases turnout and inflation, and spending decentralization increases it. Among the three political factors (competitiveness, a dummy for elections before 1995, and a time trend variable), the most interesting result is that higher levels of competitiveness (measured as the difference between the first and the second party’s vote share) decreases turnout. Only one (proportional representation) of the core five variables was found to be robust. Finally, it is notable that several variables our analysis finds significant have been largely overlooked by the existing literature. For instance, economic globalization and spending decentralization were each included in only 1 of the 44 articles we analyze, yet they are both robust predictors in these and other models discussed below.
Our fixed effects model results suggest that 9 out of the 53 time-varying variables we measure are robustly associated with national-level turnout. However, as mentioned above these models exclude 12 time-invariant or sluggishly changing variables that previous research has found important. Therefore, we run an additional 2.9 million regressions with random effects that allow us to capture important variation in turnout across countries and regions. Our findings (summarized in Table 6) suggest that seven variables meet Leamer’s robustness criterion and 14 variables meet Sala-i-Martin’s.Footnote 28 Seven are location dummies—Eastern Europe, Latin America, and Switzerland dummies depress national-level voter turnout while Norway, New Zealand, Oceania, and Sweden dummies have the opposite effect. From the socio-economic indicators, higher ethnic fractionalization and levels of inequality are robustly associated with lower electoral turnout while inflation increases turnout. Additionally, the lagged dependent variable is a robust turnout predictor (unlike in the fixed effects models). Finally, two institutional factors (concurrent elections and compulsory voting) are also robustly associated with higher turnout.
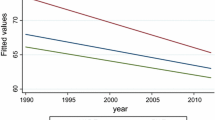
The results for these two institutional variables (concurrent elections and compulsory voting) are also interesting because they highlight the different substantive conclusions that would be reached depending on which robustness threshold is chosen. Both variables are significant using Sala-i-Martin’s criterion but not Leamer’s. Let us explore for a bit why this is the case. In almost three million regressions using random effects, the concurrent election variable never has an estimated coefficient below zero (the smallest is 0.04). This is why this variable’s CDF never includes negative values and therefore why Sala-i-Martin would consider this variable a robust predictor of turnout. At the same time, because of concurrent election’s average standard deviation (7.01) is similar in size to its average coefficient (7.89), its lower extreme bound (two standard deviations below the mean) is less than zero and therefore not robust for Leamer. The story behind compulsory voting’s results is different because (out of 2.9 million random effects models) 9775 models (0.003%) do indeed produce a negative coefficient for this variable. Is there something systematically different about these 9775 models that lead to such a counter-intuitive result? Several things stand out.Footnote 29 First, the inclusion of several variables substantially reduce the sample size. Union density is in 9430 (96%) of these 9775 models, followed by human development index (6616, 68%) and the Oceania dummy (1500, 15%). Second, democracies with union density data are relatively rare (17 of 80) leading to the possibility that outliers can have undue effects on estimated coefficients. This might help explain why the average number of observations (40) in these 9775 models are significantly lower than for the other 2.9 million models including compulsory voting (360).Footnote 30 Figure 1 provides a striking visual of this difference in sample size. It is worth noting that (as in all articles using EBA that we are aware of) our regressions include varying sample sizes due to data availability. This is one of EBA’s main strengths—if a variable significantly affects turnout across a range of samples, this is a clear signal of the robustness of the estimated relationship.
Turning now to other ways our results are consistent (or not) with the previous work summarized in Tables 1, 2 and 3, we reach several main conclusions. First, the mixed results for two of our core variables (population and GNI) is consistent with the literature. Take population. Table 2 suggests that population size has an inconclusive effect on turnout—seven studies find a negative effect and another seven find no significant effect. Our fixed effects and random effects results also suggest that population and economic development have no robust effect on turnout. Similarly, we do not find significant effects for several common socioeconomic variables including economic growth (nine studies) and literacy (seven studies). Regarding institutional variables, we do not find robust results for the number of parties, the different electoral formulae, the magnitude of the electoral district, the level of disproportionality, and the legal voting age, among others.Footnote 31 By contrast, our results suggest that economic globalization (one study) and inflation (two studies) affect turnout while receiving nowhere near as much attention as a number of institutional and political factors (e.g., 19 articles include the number of political parties in their models). It is also notable that (regardless of the criteria we rely upon and excluding geographical dummies) the most robust turnout predictors are political while (as we saw above) previous research focuses more on institutional and socioeconomic factors.
Finally, it is worth highlighting our models’ average substantive effects. Figure 2 summarizes the coefficient distributions for Table 5’s robust predictors. Each square represents a variable’s average estimated impact on national-level voter turnout, and the bars on either side of these coefficients represent Leamer’s upper and lower extreme bounds. Holding all else equal, concurrent elections increase turnout 7.9% over elections without candidates competing for executive office. Proportional representative election systems are associated with higher levels (5.2%) of voter turnout than states without this electoral system. The variables that (on average) depressed turnout the most in the fixed effects models are the time trend (which estimated a lowering of average turnout by 6.9% from 1945 to 2014) and economic globalization (− 4.3% average effect across its observed range).
Robust predictors of voter turnout, mean coefficients and extreme bounds. Note Results from fixed effects models reported in Table 5. Table A7 includes complete results. *Identifies core variables in all fixed effects models. The only core variable found to be (Sala-i-Martin) robust is proportional representation. Population is a core variable but not included in figure due to the disproportionate size of its extreme bounds
Further Analyses
Our empirical results taken from over four million regressions using fixed and random effects provide compelling evidence for the robustness of a number of predictors of national-level voter turnout. These results, however, vary more in the variables the models included than their model specifications themselves, which lead to several potential limitations. First, we run our main models using fixed and random effects rather than the literature’s most common model specification—OLS regression using robust standard errors clustered by country. Second, they include a lagged dependent variable, which some (e.g., Achen, 2001) argue depress predictors’ statistical significance. Third, we focus on registered voter turnout, while the literature also suggests turnout as a percentage of voting age population could lead to different results. Fourth, these seventy factors may work differently in different types of countries (e.g., developed/developing, Western/non-Western), and fifth there may be over-time variation that is not captured by our time trend variables. We, therefore, re-run all or part of our analyses with fourteen additional model or sample variations. Figure 3 summarizes the results from these additional 11.8 million models for the variables included in Tables 5 and 6.Footnote 32
Further analyses checks, coefficient and extreme bounds plots. Note Y-axis abbreviations represent distinct model series. Horizontal lines represent extreme bounds (+/− two standard deviations). All models (except those marked VTA) are limited to democracies. VTFE registered voters with fixed effects and lagged dependent variable (DV), VTRE registered voters with random effects and lagged DV, VTNLFE registered voters with fixed effects and no lagged DV, VTNLRE registered voters with random effects and no lagged DV, VT registered voter turnout, robust standard errors clustered by country, and lagged DV, VTNL registered voter turnout, robust standard errors clustered by country, and lagged DV, VAP voting aged population voter turnout, robust standard errors clustered by country, and lagged DV, VTA registered voter turnout, robust standard errors clustered by country, lagged DV and including all countries. Population’s extreme bounds for VTFE and VTNLFE models excluded due to their disproportionate size (− 3666.2 and 3681.1 for VTFE)
Using robust standard errors First, we run 2,433,115 models using robust clustered standard errors the core 5 variables, and 65 alternating M and Z variables. 11 and 20 variables were significant using either Leamer or Sala-i-Martin’s criteria. Fourteen of these 20 (70%) variables were also significant in either the fixed effects or random effects models. Six variables (boycott, a fifth or sixth election dummy, GNI growth, quality of democracy, union density, and unionization) were robust in these new models but not in our main models, although four of these six (fifth or sixth election, quality of democracy, union density, and unionization) would be considered robust in either the fixed or random effects models if we use a 0.1 level rather than 0.95. Thus, our first set of further analyses suggest that the majority of our results using fixed effects and random effects hold if we use robust standard errors clustered by country.Footnote 33
Removing the lagged dependent variable Next, we run an additional 4,228,480 regressions identical to the three series of models described above except that we lagged turnout. We included it above because the literature suggests today’s turnout is systematically related to previous turnout. However, as Achen (2001) explains, lagged dependent variables may suppress the explanatory power of relatively time-invariant independent variables, such as compulsory voting or population size. The results for models without a lagged dependent variable do vary in a few ways, a few variables lose robustness, while more than double are now found to be robust. Specifically, in the fixed effects models without a lagged dependent variable, concurrent elections now meet the Leamer robustness criteria while suffrage is no longer significant at either level. Otherwise, the other 54 variables in these fixed effects models (96%) have substantively identical results. Turning to the random effects models, economic globalization, the time trend, the 1945–1994 dummy, and competitiveness are now significant and in the same direction as the fixed effects models. Our population variable is also now significant, while the second election dummy loses significance. Overall, 57 of 69 variables (83%) have substantively identical results. Finally, in the models with robust standard errors and no lagged dependent variable concurrent elections and the second election loses significance without lagged dependent variable while population gains significance. Here, 58 of 69 variables (84%) have substantively similar results. Overall, these three series of models without lagged dependent variables produce quite substantively similar results as those models with a lagged term.
Changing denominators Next, we re-estimate the lagged dependent variables and clustered standard errors models using a different dependent variable denominator (voting aged population instead of registered voters). The literature summarized above splits almost evenly in its use of these denominators. Given that these variables’ correlation coefficient is 0.67, results may significantly vary depending on which denominator used. Overall, we find 51 of 70 (73%) variables’ robustness unchanged. Twelve of seventy variables are robust according to both criteria. Four are geographical dummies (Sweden, Switzerland, Easter Europe, and Latin America/Caribbean), and the others are now familiar (compulsory voting, concurrent election, ethnic fractionalization, inflation, previous turnout, second election, fifth or sixth election, time trend, and union density). Eight variables are no longer robust (boycott, GNI growth, the Latin American and Oceania dummies, quality of democracy, spending decentralization, unionization, and years 1945–1994), while 11 are now considered robust (the Asia, Norway, and USA dummies, economic globalization, female suffrage, plurality system, radios per capita, third election dummy, legislative seats, share of voters aged 30 to 69, and violence) in this series of over 2.3 million models.
Splitting samples Different samples of countries may also have systematically different correlates of national-level voter turnout (Stockemer, 2015). Therefore, we ran an additional 2,647,887 analyses breaking up our sample into different groups—democracies and all states, Western and non-Western states, established and newer democracies, and above and below median income states.Footnote 34 Our results (see Appendix) suggest that while we limit our main analysis to democratic states, turnout drivers are overwhelmingly similar in non-democracies.Footnote 35 Indeed, 64 of 70 variables’ robustness does not substantively change in models including anocracies and autocracies (i.e., states with a Polity score of less than six). Of the six variables with changes, four are robust in all-states models and not in democracy-only models (Asia, revenue decentralization, urban population, and violence), while two are no longer robust (boycott, and the 1945–1994 dummy). The vast majority (12 of 15) of variables in Western and non-Western democracies did not significantly change from the original models. For those that did change, boycotts, per capita GNI, and spending decentralization were robustly associated with turnout in Western states but not in non-Western states. The results for the latter are likely to be at least partly driven by increased data availability in Western states. The most notable differences in these series of split sample models were found between countries that had more or less than two decades since democratization. Take, for example, the Eastern Europe dummy that is robust in the main models, it robustly decreases expected turnout in established democracies but not in the new democracies. Relatedly, once the analysis is performed in newer democracies, regional differences fade away—a result consistent with previous studies (e.g., Kostadinova & Powers, 2007).Footnote 36 Additionally, the original findings hold for a number of variables by countries with above the median income than below it. Of the 22 robust predictors described above, the richer country models had 9 significant predictors while the poor states had 4. Specifically, compulsory voting increases turnout in rich states but not poor states. So too did ethnic fractionalization, economic growth, spending decentralization and inflation. Poorer states’ national voter turnout was robustly associated with boycotts (as in Western states) and concurrent elections while rich states’ turnout was not.
Variation over time Finally, there may be over-time variation that is not captured by the time-trend variables in our original analyses. We therefore ran two additional series of models, one with a linear time trend and a time squared variable in all models and the second with time, time squared, and time cubed. Substantive results for the other variables were virtually identical to our main model, and the time trend variable and time cubed variables are robust in their respective model series.
Take as a whole, the results of over 15 million regressions of national-level voter turnout on 70 unique variables using 16 distinct model (or sample) variations suggest that there are indeed a recurring series of country-level factors shaping national-level voter turnout. Some of these factors are consistent with a wide swath of the turnout literature (e.g., institutional factors like compulsory voting or concurrent elections) while others have only been included in one or two studies (e.g., socio-economic factors like economic globalization and inflation). The implications of our findings are twofold. First, our results suggest that there is room for theoretical reassessments of several frequently used institutional variables (e.g., electoral formulae or the number of parties). Second, our results provide a comprehensive evidence base for future turnout research.
Discussion and Conclusion
In this article we establish which social, institutional, and political factors driving national-level voter turnout are empirically robust using a wide vary of model specifications. This has three implications. First, it sheds light on what national political, institutional, or socio-economic factors are significantly associated with turnout. Second, it provides fodder for further inductive theory development. Third, our results suggest a set of potentially useful control variables for future turnout studies. Below, we develop these three points further.
First, robust results are essential to discriminate among the dozens of proposed mechanisms driving national-level voter turnout. When over a hundred factors potentially affecting turnout, it is hard to determine what robustly shapes turnout. We collect 127 literature-derived factors and empirically analyze 70 of them. We find that some of the literature’s results are highly sensitive to small changes in model specification while others are not. Overall, we find that compulsory voting, competitive elections, concurrent elections, economic globalization, inflation, previous turnout, proportional representation, spending decentralization, and some geographical dummies are robust predictors of turnout. Similar to other empirical assessments (e.g., Gassebner et al., 2013’s study of the emergence and survival of democracy) our results are humbling but provide an empirical foundation for future research.
Second, from a theory-building perspective, fragile results are important because they force us to reassess both the theoretical underpinnings of our hypotheses as well as “reconsider whether it is theoretically reasonable to expect robustness across the various sample populations being considered” (Hafner-Burton, 2005, p. 696). Furthermore, reassessing the theories that generate our hypotheses requires taking into account other possible causes that have not received much attention in previous studies. For example, several economic factors (e.g., economic globalization and inflation) are robust in our models but have yet to receive much theoretical attention in the turnout literature.
We conclude by highlighting a number of possible areas for future research. For example, our data contain several different measures for the same concept. For practical reasons, we have relied on the most commonly used measures. A logical next step would be to use other sources and operationalizations and compare results. Relatedly, including all or some of the remaining 57 variables included in Tables 1, 2 and 3 but not analyzed in this paper is a possibility. Furthermore, like previous studies (e.g., Hegre & Sambanis, 2006), we did not include any interaction effects in our models. Including theoretically informed interactions may provide for a more comprehensive analysis of the interplay of different explanatory factors and the way they may mediate or moderation certain relationships. Certainly, then, our analysis is limited and, by no means, definitive, but it is the largest systematic evaluation of factors shaping national-level voter turnout to date.
Notes
Using extreme bounds analysis, we examine the most robust factors correlated with turnout. Like previous studies using this methodology, we do not estimate a structural model, theorize the relationship between different variables, establish specific causal mechanisms, or improve turnout measurements.
Existing meta-analyses present contradictory results. In fact, Stockemer (2017, p. 15) states “the fact that the influence of many factors … on turnout is inconclusive demands more contextual analysis.” While we agree with the need for context bound analysis, our research shows that even at the most general level there are common voter turnout correlates in democratic countries.
Such categorizations are neither exhaustive nor exclusive; rather they can be seen as a useful theoretical heuristic.
The other variables are population density, gross domestic (or national) product per capita, gross domestic product, literacy rate, life expectancy, and ethnic diversity.
Even when studies include the same variables, there is no consensus on how to measure some concepts. See below for a broader measurement discussion.
In discussing meta-analyses, we are not referring to quantitative analysis of a variable’s average treatment effect because this literature’s focus is on a broad spectrum of possible causes rather than any one particular cause.
The variables that only Geys (2006) considers are: population concentration, population stability, population homogeneity (ethnic diversity), previous turnout, campaign expenditures, political fragmentation, proportional representation electoral system, concurrent elections, and registration requirements. The variables that only Stockhemer (2017) considers are district magnitude, effective number of parties, important elections, education, and literacy rate.
A criterion used by Levine and Renelt (1992).
Such definitions measure turnout as “the total votes cast divided by the size of the electorate” (Blais & Carty, 1990, p. 169); “the average turnout of each country” (Colomer, 1991, p. 319); the proportion of the eligible electorate voting (Radcliff, 1992, p. 445); and “the percentage of eligible voters that turned out at the respective country's national election” (Stockemer, 2015, p. 87).
This debate is not new. In the United States, McDonald and Popkin (2001) proposed another measure, but no cross-national data for this measure exists. More recently, Stockemer (2016) created VEP for 500 elections in 116 countries. Given our focus here, we rely on the established measures.
Despite all the efforts, IDEA’s data are not perfect. For example, when two elections were held in a single year, IDEA does not report which election is captured. We thank a reviewer for highlighting this fact.
Appendix Table A1 lists the 285 studies that were excluded and the reasons for exclusion.
For example, see Geys (2006) and Blais and Drobzinska (1998).
This points us to a degree of agreement about a specific covariate. We define 70% or more as a “high level of agreement.” When comparing the common variables from Geys (2006) and Stockemer (2017), only compulsory voting shows a high level of agreement (84%), followed by income inequality (60%), PR (53%), vote closeness (47%) and population size (44%).
Over 80% of excluded variables appear in only one study.
We are aware of Achen’s (2001) warning regarding the inclusion of a lagged dependent variable. Our further analyses below address this concern.
This article examines economic growth and over 50 independent variables.
The third strategy to avoid multicollinearity is included in our design by default because we rely only on the most frequent source and variable operationalization.
We also lag time-varying independent variables to reduce the risks of endogeneity or reverse causality.
Models took an average of 12.5 days to run 2,433,115 regressions using Stata 16.1 on an Amazon Web Service Elastic Compute Cloud c3.large instance running 2019 Windows Server Edition.
There are two possible sources of variation: (1) substantively important results to small changes in the variables included and (2) how fragile the inferences are to small changes in operationalization. Given that some variables appear nineteen times but are operationalized in ten different ways, we focus on the first source of variation. Even in this case, 70 variables in the random effects models lead to over 2 million regressions. We leave for future research the analysis of different operationalizations.
Sala-i-Martin (1997, pp. 179–180) looks at both normal and generalized CDFs. Histograms of the 1.2 million estimated coefficients (available on request) suggest most coefficients are not normally distributed, so we use the generalized CDF.
Table A7 summarizes results for all 58 variables.
Complete results available in Table A8.
Table A15 includes the variables included in these 9775 models.
Negative coefficient model average sample size: 40 (s.d. 33.8); all models: 360 (s.d. 179.3).
It is important to note that all of these variables also had mixed results in the literature.
Appendix Tables A7 to A18 includes more detailed results for these analyses.
70% of variables in fixed effects models and 83% of random effects variables.
States that had Polity2 scores of six or greater for 20 years or more are considered “established”.
We follow Kostelka (2017) in believing that the differences here require an in-depth exploration of alternative explanations of voter turnout.
References
Achen, C. (2001). Why lagged dependent variables can suppress the explanatory power of other independent variables. Presented at the annual meeting of the American Political Science Association.
Bell, A., Fairbrother, M., & Jones, K. (2019). Fixed and random effects models: Making an informed choice. Quality and Quantity, 53, 1051–1074.
Bell, A., & Jones, K. (2015). Explaining fixed effects: Random effects modeling of time-series cross-sectional and panel data. Political Science Research and Methods, 3(3), 133–153.
Blais, A., & Carty, R. (1990). Does proportional representation foster voter turnout? European Journal of Political Research, 18(2), 167–181.
Blais, A., & Dobrzynska, A. (1998). Turnout in electoral democracies. European Journal of Political Research, 33(2), 239–261.
Cancela, J., & Geys, B. (2016). Explaining voter turnout: A meta-analysis of national and subnational elections. Electoral Studies, 42, 264–275.
Carmignani, F., Shankar, S., Tan, E., & Tang, K. (2014). Identifying covariates of population health using extreme bound analysis. European Journal of Health Economics, 15, 515–531.
Clark, T. S., & Linzer, D. A. (2015). Should I use fixed or random effects? Political Science Research and Methods, 3(2), 399–408.
Colomer, J. M. (1991). Benefits and costs of voting. Electoral Studies, 10(4), 313–326.
Dieleman, J. L., & Templin, T. (2014). Random-effects, fixed effects and the within-between specification for clustered data in observational health studies: A simulation study. PLoS ONE, 9(10), 1–17.
Endersby, J. W., & Krieckhaus, J. T. (2008). Turnout around the globe: The influence of electoral institutions on national voter participation, 1972–2000. Electoral Studies, 27(4), 601–610.
Fornos, C., Timothy Power, T., & Garand, J. (2004). Explaining voter turnout in Latin America, 1980 to 2000. Comparative Political Studies, 37(8), 909–940.
Frank, R., & Martínez i Coma, F. (2017). How election dynamics shape perceptions of electoral integrity. Electoral Studies, 48, 143–165.
Fumagalli, E., & Narciso, G. (2012). Political institutions, voter turnout, and policy outcomes. European Journal of Political Economy, 28(2), 162–173.
Gassebner, M., Gutmann, J., & Voigt, S. (2016). When to expect a coup d’état? An extreme bounds analysis of coup determinants. Public Choice, 169(3–4), 293–313.
Gassebner, M., Lamla, M., & Vreeland, J. (2013). Extreme bounds of democracy. Journal of Conflict Resolution, 57(2), 171–197.
Geys, B. (2006). Voter turnout: A review of aggregate-level research. Electoral Studies, 25(4), 637–663.
Glass, G. (1976). Primary, secondary and meta-analysis of research. Educational Researcher, 5, 3–8.
Hafner-Burton, E. (2005). Right or robust? The sensitive nature of repression to globalization. Journal of Peace Research, 42(6), 679–698.
Hartwig, J., & Sturm, J. (2014). Robust determinants of health care expenditure growth. Applied Economics, 46(36), 4455–4474.
Hegre, H., & Sambanis, N. (2006). Sensitivity analysis of empirical results on civil war onset. Journal of Conflict Resolution, 50(4), 508–535.
Imai, K., & Kim, I. S. (2019). When should we use unit fixed effects regression models for causal inference with longitudinal data? American Journal of Political Science, 63(2), 467–490.
International IDEA. (2017). Voter turnout database. Stockholm: International Institute for Democracy and Electoral Assistance.
Jackman, R. (1987). Political institutions and voter turnout in the industrialized democracies. American Political Science Review, 81(2), 405–424.
Jackman, R., & Miller, R. (1995). Voter turnout in the industrial democracies during the 1980s. Comparative Political Studies, 27(4), 467–492.
Kaniovski, S., & Miller, D. C. (2006). Community size, heterogeneity, and voter turnouts. Public Choice, 129, 399–415.
Kostadinova, T. (2003). Voter turnout dynamics in post-communist Europe. European Journal of Political Research, 42(6), 741–759.
Kostadinova, T., & Powers, T. J. (2007). Does democratization depress participation? Voter turnout in the Latin American and Eastern European transitional democracies. Political Research Quarterly, 60(3), 363–377.
Kostelka, F. (2017). Does democratic consolidation lead to a decline in voter turnout? Global evidence since 1939. American Political Science Review, 111(4), 653–667.
Kuenzi, M., & Lambright, G. (2007). Voter turnout in Africa’s multiparty regimes. Comparative Political Studies, 40(6), 665–690.
Laakso, M., & Taagepera, R. (1979). ‘Effective’ number of parties: A measure with application to West Europe. Comparative Political Studies, 12(1), 3–27.
Leamer, E. (1983). Let’s take the con out of econometrics. American Economic Review, 73(1), 31–43.
Leamer, E. (1985). Sensitivity analysis would help. American Economic Review, 75(3), 308–313.
Levine, R., & Renelt, D. (1992). A sensitivity analysis of cross-country growth regressions. American Economic Review, 82(4), 942–963.
Martínez i Coma, F. (2016). Turnout determinants in democracies and in non-democracies. Electoral Studies, 41, 50–59.
Martínez i Coma, F., & Nai, A. (2017). Ethnic diversity decreases turnout. Comparative evidence from over 650 elections around the world. Electoral Studies, 49, 75–95.
Martínez i Coma, F., & Trinh, M. (2017). How electoral integrity affects voter turnout in democracies. Australian Journal of Political Science, 52(1), 53–74.
Martínez I Coma, F., & Morgenbesser, L. (2020). Election turnout in authoritarian regimes. Electoral Studies, 68, 102222.
McDonald, M., & Popkin, S. (2001). The myth of the vanishing voter. American Political Science Review, 95(4), 963–974.
McNeish, D., & Kelley, K. (2019). Fixed effects models versus mixed effects models for clustered data: Reviewing the approaches, disentangling the differences and making recommendations. Psychological Methods, 24(1), 20–35.
Miller, M., Joseph, M., & Ohl, D. (2018). Are coups really contagious? An extreme bounds analysis of political diffusion. Journal of Conflict Resolution, 62(2), 410–441.
Plümper, T., & Traunmüller, R. (2020). The sensitivity of sensitivity analysis. Political Science Research and Methods, 8(1), 149–159.
Powell, B. (1986). American voter turnout in comparative perspective. American Political Science Review, 80(1), 17–40.
Radcliff, B. (1992). The welfare state, turnout and the economy: A comparative analysis. American Political Science Review, 86(2), 444–454.
Radcliff, B., & Davis, P. (2000). Labor organization and electoral participation in industrial democracies. American Journal of Political Science, 44(1), 132–141.
Remmer, K. (2010). Political scale and electoral turnout: Evidence from the less industrialized world. Comparative Political Studies, 43(3), 275–303.
Robbins, J., Hunter, L., & Murray, G. (2013). Voters versus terrorists: Analyzing the effect of terrorist events on voter turnout. Journal of Peace Research, 50(4), 495–508.
Sala-i-Martin, X. (1997). I just ran two million regressions. American Economic Review, 87(2), 178–183.
Siaroff, A., & Merer, J. (2002). Parliamentary election turnout in Europe since 1990. Political Studies, 50(5), 916–927.
Smets, K., & Van Ham, C. (2013). The embarrassment of riches? A meta-analysis of individual-level research on voter turnout. Electoral Studies, 32(2), 344–359.
Steiner, N. (2010). Economic globalization and voter turnout in established democracies. Electoral Studies, 29(3), 444–459.
Stockemer, D. (2015). District magnitude and electoral turnout: A macro-level global analysis. Acta Politica, 50(1), 82–100.
Stockemer, D. (2017). What affects voter turnout? A review article/meta-analysis of aggregate research. Government and Opposition, 52(4), 698–722.
Stockemer, D., LaMontagne, B., & Scruggs, L. (2013). Bribes and ballots: The impact of corruption on voter turnout in democracies. International Political Science Review, 34(1), 74–90.
Stockemer, D., & Khazael, S. (2014). Electoral turnout in Muslim-majority states: A macro-level panel analysis. Politics and Religion, 7, 79–99.
Tavits, M. (2008). Direct presidential elections and turnout in parliamentary contests. Political Research Quarterly, 62(1), 42–54.
Temple, J. (2000). Growth regressions and what the textbooks don’t tell you. Bulletin of Economic Research, 52(3), 181–205.
Acknowledgements
We would like to thank Ignacio Lago, Ciaran O'Faircheallaigh, participants of the 2017 Australian Society of Quantitative Political Science Conference, the 2018 Doctores Miembro and former Post-Doctoral Fellows of Juan March Institute Conference, the Editor, and the anonymous peer reviewers for their valuable comments and suggestions. Replication materials are available at: https://dataverse.harvard.edu/dataverse/richardwfrank. All remaining errors are our own.
Funding
The authors acknowledge support for this research from the Australian Research Council’s Discovery Project Scheme (DP150102398, DP190101978).
Author information
Authors and Affiliations
Contributions
The authors are listed alphabetically and contributed equally.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frank, R.W., Martínez i Coma, F. Correlates of Voter Turnout. Polit Behav 45, 607–633 (2023). https://doi.org/10.1007/s11109-021-09720-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11109-021-09720-y