Abstract
The effects of pH on nutrient availability are not solely caused by to the effects on reaction with soils but are an interaction between these effects and the effects on rate of uptake by plants. Some effects are specific to particular ions, but an important aspect is that plant roots and soil particles both have variable charge surfaces. This influences availability, but in opposite directions. Sulfate is an example of this interplay. Its sorption by soil decreases markedly with increasing pH and thus “soil availability” increases. However, plant uptake also decreases with increasing pH thus “plant availability” decreases. For phosphate, the plant effect is stronger than the soil effect and uptake decreases with increasing pH. In contrast, effects of increasing pH on molybdate adsorption are so large that they dominate the overall effect. Sorption of cations, such as zinc or copper, increases with increasing pH but uptake rate also increases. The net effect is a small decrease in availability with increasing pH. Boron is an exception; there are small effects of pH on sorption; and it is the uncharged boric acid molecules that are taken up by plant roots. Their uptake is not affected by charge and uptake is proportional to the concentration of uncharged boric acid molecules. We argue that emphasis on the effects of pH on reactions with soil has led to a distorted picture of the effects of pH on nutrient availability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
“Soil pH is considered to be the “master variable” of soil chemistry due to its profound impact on countless chemical reactions involving essential plant nutrients” (Penn and Camberato 2019). This is the opening statement of a paper which the authors consider as presenting the classic understanding of the effects of pH on P uptake. We quote it here because it illustrates a common attitude. It emphasises the effects on soil chemistry but scarcely considers the effects of pH on the rate of uptake of nutrients by plant roots. This is a fault that is not limited to that paper.
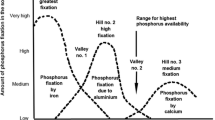
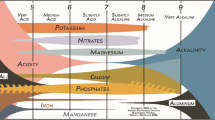
In an accompanying paper (Hartemink and Barrow 2023), we discussed a conceptual soil pH-nutrient availability diagram that purported to show how the availability of major and minor nutrients was affected by the pH. The diagram has been published in textbooks and soil extension material and continues to be used as a teaching tool. We argued that the diagram was simplistic. One of the aspects to which it plays insufficient attention was the effect of pH on the uptake of nutrients by plant roots. Here we show that these effects can be large. The relevant information is somewhat scattered; in this article we attempt to bring plant and soil information together to give an overall picture of the effects of pH on availability of both anions and cations.
Penn and Camberato (2019) write that ligand exchange is “not dependent on surface charge”. Here we start by explaining that surface charge, or more appropriately surface electric potential, is an important influence on the effects of pH on reaction of ions with soil.
Variable charge
It is not elements that react with soils; it is ions, and ions bear charge. We therefore need to understand the charge carried by soil particles.
Soil scientists have long understood that clay minerals bear a negative charge that is caused by isomorphic substitution. These are known as permanent charges. However, clay minerals are rather unusual crystals in that the faces do not have atoms with unsatisfied bonds. For the surface of most crystals, and for the edges of clay minerals, atoms do have unsatisfied bonds. The classical example is silver chloride which takes up either silver or chloride ions depending on which is the present in excess and therefore has either positive or negative charge. These ions are therefore the charge determining, or we can also say the potential determining, ions. For oxides, and the edges of clay minerals, the unsatisfied bonds result in links to water molecules. These gain or lose protons depending on the pH and thus the charge, and also the potential, varies with pH. In shorthand, they are variable-charge substances. During the 1960s, the importance of variable charge components in soil began to be realised and several groups studied the reaction with oxides such as goethite (α-FeOOH). The relevance to soil science was brought to general attention by the work of van Raij and Peech (1972) who showed that some highly-weathered tropical soils behaved as variable charge materials. They drew a distinction between tropical soils, which they regarded as variable charge soils, and temperate soils which they regarded as fixed charge soils. However, this is too simple. It disregards one of the most obvious properties of soils: their colour.
Soil colour, though easily observed, is a complicated property depending partly on organic matter and partly on the oxides present. Iron oxides are an important contributor to soil colour with goethite tending to be dominant in cooler damper soils and providing yellow–brown colours, and haematite tending to be important in hotter, drier soils and providing reddish colours. The important interpretation of this is that variable charge materials are present in just about all soils; their presence is important in determining the effects of pH on reaction with nutrients and interpreting pH.
Interpreting measured pH
Although we speak of “soil pH”, the term is, strictly speaking, nonsense; pH is a property of liquids not of solids. What we measure is the pH of a solution in contact with a soil; the answer we obtain depends on the solution we use and on the net charge carried by the soil. Although there are exceptions, as shown by van Raij and Peech (1972), most soils bear a net negative charge at their native pH – partly from fixed charge and partly from variable charge. For such soils, increasing the electrolyte concentration decreases the pH (Fig. 1). As a mnemonic, we can think of increasing electrolyte cations displacing more protons from the surface. Further, the magnitude of the effect depends on the magnitude of the negative charge; as Fig. 1 shows, the greater the pH difference from the point of zero salt effect, the greater the effect on pH. Commonly, soil pH is measured after mixing soil with water. This decreases the electrolyte concentration in solution and results in a higher measured pH than would be appropriate for the soil solution.
The movement of water towards plant roots brings more calcium to the root surface than is taken up by the plants (Barber et al. 1963). This means that calcium ions accumulate near the root surface and this, in turn, means that the pH close to the root surface is lower than that in the bulk soil. This is one reason why many scientists choose to measure pH in 0.01 M calcium chloride solution. (Other reasons are that measurements are much more stable and are not affected by the solution soil ratio.) There are two consequences. One is that when interpreting measured pH, values obtained using water will be higher than those experienced at the root surface. The other is that, to avoid ambiguity, we should add a subscript to indicate the method of measurement such as pHH2O or pHCaCl2.
The effects of pH on adsorption of anions
Studies using model systems
There have been many studies of the effects of pH on adsorption of both cations and anions on oxides, especially on goethite.
The effects of pH on adsorption of anions by goethite seemed puzzlingly diverse – until Hingston et al. (1972) showed that that there was either a peak in adsorption or a change in the slope near the pK for dissociation of the relevant acid (Fig. 2). It was realised later that this was an important clue in understanding the nature of the reaction. The challenge was to describe these observations in a consistent way.
Effect of pH on adsorption of some anions by goethite. (Drawn from the data of Hingston et al. (1972))
The separation of charge at the surface of charged particles gives rise to an electric potential difference. This is large at the surface and declines to zero in the bulk solution. These changes in potential have been included in several models. All the models allocate the ions to mean planes of reaction, but the models differ in the number of planes and in the way the reaction is portrayed. Figure 3 demonstrates the assumptions of the 4-plane model. In more-detailed models (Hiemstra and van Riemsdijk 1996) the charge conveyed to the surface by a phosphate molecule is distributed between the s and b planes. In the simplification of the 4-plane model this distribution is simulated by assuming it can be represented as a mean. If the charge distribution is different, the position of this assumed plane changes. Consequently, the way the potential changes with pH also changes. This contrasts with the 2-plane model – also called “the constant capacitance model”. In this model the charge due to reaction is allocated to the s plane. There is no opportunity for it to be changed for molecules of different size.
The models have been compared in terms of their ability to describe observations by Barrow and Bowden (1987). Goldberg and Glaubig (1985, 1986a, b) used the constant capacitance model to describe the effects of pH on boron adsorption at one initial concentration of boron. Goldberg et al. (2002) used it to describe the effects of pH on molybdate adsorption at one initial concentration. However, Barrow and Bowden (1987) found that this model did not describe the data well when pH and the concentration of adsorbate were both varied. It only worked well when presented with a limited data set, such as the effect of pH on adsorption at one initial concentration of adsorbate.
Because the number of postulated planes is limited, the change in electric potential with change in pH is constrained. It explains the effects of pH on adsorption by more than one separate reaction. That is, it adds curves that are individually of an inappropriate shape to give a resulting curve that is close to the required shape. It is more effective, and realistic to assume that the adsorbed ions do not experience the same potential as the hydroxyl ions that are linked to the metal atoms of the oxide but rather that their mean centre of charge is located at some little distance. They therefore experience a different change in potential with change in pH, the magnitude of which depends on where this plane is sited. This is an effective simplification and allows the effects of pH to be described and understood in a consistent way.
Bowden et al. (1977) proposed that reaction depended not on the concentration of the reactant but on a surface activity function (ais).
Where α is the proportion of the reactant present as the appropriate ion, γ is the activity coefficient, c is the total concentration, ki is the binding constant, zi is the valency (including sign), ψ is the electric potential in the plane of adsorption, F is the Faraday, R is the gas constant, and T the absolute temperature.
The binding constants of different ions are related to the appropriate dissociation constant of the relevant acid (Fig. 4). This can be interpreted as showing that ions that have a strong affinity for protons also have a strong affinity for the electrophilic metal ions of the oxide surface.
Relevance to particular ions
An ion can dominate the reaction even though it is a minor constituent if its binding constant is large enough. Consider the monovalent and the divalent phosphate ions ((H2PO4− and HPO42−). The first and second pK values for phosphoric acid are about 2 and about 7. From Fig. 4, the binding constant for the divalent ion will be about 105 times that for the monovalent ion. Then, even at pH 4, when there are about 103 monovalent ions for every divalent ion, the product of αk will be 100 times more favourable for the divalent ion. This explains why a minor constituent can dominate adsorption.
Molybdate, for which the two dissociation constants are close together, fits nicely into the relationship shown in Fig. 4. It therefore provides an exception to the “one ion” rule; both monovalent and divalent ions appear to be important in the reaction (see below).
Factors affecting the value for the potential
The value of the potential depends on several factors. One is the size of the ion. Fluoride ions are about the same size as hydroxyl ions and are therefore located at the surface and experience a large change in potential with pH; for phosphate ions, the mean centre of charge is further from the surface and the change in potential with pH is smaller.
Another important factor is the nature of the solution surrounding the particles. Increasing its ionic strength compresses the diffuse double layer and decreases the rate at which the potential changes with pH. This is an important reason why it is difficult to make a simple statement about the effects of pH on adsorption.
Adsorption of ions changes the charge on the reacting particle. This also changes the electric potential. Equation (1) is therefore a “chicken and egg” equation: you need to know the potential in order to calculate the adsorption, and you need to know the adsorption in order to calculate the potential. This problem can be overcome by reiteration. This feedback effect, in which increasing adsorption changes the nature of the surface, means that the Langmuir equation, though often used, is invalid in this context.
Application to some reactants
Let us now consider how Eq. (1) explains the effects of pH on some reactants starting with, arguably, the most important: phosphate. At pH values appropriate for soils, phosphate mostly forms bidentate links to oxides, and these are in equilibrium with divalent phosphate ions in solution. For phosphoric acid, the pK2 is about 7 – with the exact value depending on the ionic strength of the solution. At pH values but well below 7, the concentration of the divalent phosphate ions increases 10-fold for unit increase in pH. This increase in α is opposed by decreasing value of the exponential term. This is large because zi equals 2. The outcome is that in dilute solutions of NaCl there is a large decrease in adsorption by goethite with increasing pH (Fig. 5). In more-concentrated solutions, the decrease is smaller (Fig. 5). As the pH is increased towards 7, the rate of increase in the concentration of the divalent phosphate ions decreases; when the pH equals the pK2, half of the ions are divalent and further increases in pH can produce no more than a doubling. The exponential term therefore dominates and there is a sharp decrease in adsorption – and an inflection point.
Effect of pH and NaCl concentration on adsorption of phosphate from solutions with the same initial phosphate concentration. Lines are from the fitted four-plane model. Drawn from the data of Barrow et al. (1980)
When the effects of NaCl concentration and of pH are measured for soil, rather than for an oxide, extreme values for pH do not occur in fertile soils; the steep decrease in sorption above pH 7 is not well represented (Fig. 6). Overall, the effects of pH are smaller. When CaCl2 is used as background electrolyte rather than NaCl, there is only a small decrease in sorption with increasing pH after one day of reaction (Fig. 6). With increasing time of reaction, the effects becoming increasingly U-shaped because reaction is faster at high and at low pH. This will be considered furtherlbelow. It suffices to note here, that the above shows that when phosphate sorption is measured using a soil and a background electrolyte containing calcium, the observations do not support the general position that phosphate sorption is very strong at low pH.
The effects of pH on selenite adsorption are analogous to those on phosphate, with the proviso that the relevant dissociation constant is slightly higher (Fig. 2). Its inflection point is therefore at a higher pH (Figs. 2 and 6).
Boric acid is very weak with the pK at about 9 – again with the exact value depending on the ionic strength of the solution. At low pH there is only a very small proportion present as the monovalent borate ion but the fraction present increases tenfold for each unit increase in pH. Because zi equals 1, the effect of the exponential term is smaller and, in contrast to phosphate, adsorption increases with increasing pH (Fig. 6) with the increase being most marked at high NaCl concentrations. This effect of salt concentration is not consistent with the model used by Goldberg and Glaubig (1985, 1986a, b). They postulated that uncharged boric acid molecules reacted with uncharged sites on the surface of oxides. If this were the case there could be no effect of salt concentration.
Amongst the anions, molybdate has the perhaps best-known effect of pH on adsorption, with a sharp decrease between pH 4 and pH 6 (Fig. 7). For molybdic acid, the first and second dissociations are close together with pK values of about 3.8 and 4.1 in 0.0 1 M CaCl2. This means that the monovalent ion (HMoO4−) is only present over a limited pH range. Mckenzie (1983) found that the 4 plane model closely described effects of pH for goethite if the concentration of both monovalent and divalent ions were considered (Figs. 4 and 8). However, he was unable to successfully fit the model to oxides with a low point of zero charge for which adsorption was measured at low pH. He thought this was probably due to the tendency of molybdate to form polymers. An example of the kind of reaction thought to be involved is:
Effect of pH and time on sorption of phosphate by a soil. The equation used to relate sorption of phosphate (S) to concentration of phosphate in solution (c) and to time (t) was: S = a cb1tb2. The graph shows the values of atb2 at the indicated times and thus of sorption at unit concentration. Drawn from the data of Barrow et al. (2020)
Observed and modelled effect of pH on molybdate sorption by goethite. Drawn from the data of Mckenzie (1983)
From the law of mass action, formation of this polymer is proportional to the seventh power of the molybdate concentration and the eighth power of the hydrogen ion concentration. It only occurs at low pH and at high molybdate concentration – outside the range of values normally occurring in soils.
Sulfur sometimes seems like a schizophrenic nutrient; it has two personalities; in some soils it acts as a specifically sorbed anion; in others sulfur supply is governed by mineralisation of organic sulfur. In Australia, soils that sorb sulfate strongly are found in high rainfall areas and are derived from basic rocks. Examples occur on the north coast of New South Wales, in south-eastern Victoria, and in south-western Western Australia (Barrow et al 1969). Sulfate sorption is marked on Andisols (Camps Arbestain et al. 2001). These soils have elevated contents of short-range ordered minerals and/or insoluble Al–humus compounds. It is also marked and on highly weathered soils such as Oxisols (Couto et al. 1979).
Sulfuric acid is fully dissociated at soil pH values. The decrease in electric potential with increasing pH is the only effect of pH on its sorption; it therefore decreases markedly with increasing pH (Fig. 9a).
Comparison of the effect of pH on sorption of phosphate by soils derived from basic rocks (part a) with the effect of pH on uptake of sulfate by barley roots (part b). For part a, sorption is the total amount sorbed at a solution of 20 mg l−1, that is the amount sorbed as a result sorption experiment plus the amount already present as measured by sulfate displaced by a calcium phosphate solution. (Part a drawn using the data of Barrow et al. (1969)). Part b drawn using the data of Vange et al. (1974))
The effects of pH on adsorption of cations
The behaviour of cations is remarkably consistent with the change from little adsorption to complete adsorption over a small pH range (Fig. 10). In solution, metal ions tend to be surrounded by six water molecules arranged in an octahedron. We might write such an ion as: M(H2O)62+. Such ions can be considered as multi-protic acids because the water molecules may lose protons. The first step gives MOH(H2O)5+, more simply written as MOH+. Each metal may therefore be considered to have a dissociation constant (pKa).
Effect of on the adsorption of nine metals ions by goethite after reaction periods of two hours and eight hours. (Drawn from the data of Fischer et al. (2007))
The order in which the metals are adsorbed with increasing pH is determined by the fitted value of ki of Eq. (1): when the value of ki is large, the surface activity function (Eq. 1) is large enough to permit adsorption at low pH. Once adsorption is initiated, the increasing value of the exponential term with increasing pH means that adsorption rapidly increases.
For goethite the values of ki are closely correlated with the values for pKa (Fig. 11). The relationship is similar to that for anions (Fig. 4), but different in sign. It was explained by Fischer et al. (2007) as showing that metals that have a large affinity for hydroxyl ions in solution also have a large affinity for hydroxyl ions of the oxide surfaces.
Part a, relationship between the log of the binding constant for reaction of metals with goethite and the dissociation constant. Part b, relationship between the diffusion coefficient for the slow continuing reaction and the ionic radius. (Drawn from the data of Fischer et al. (2007))
Summarising the importance of potential
In the foregoing sections, we have shown how interaction between the electric potential of the surfaces and the dissociation behaviour of the ions gives a consistent explanation of diverse effects of pH. This contrasts with the concepts of Penn and Camberato (2019) who used the term “ligand exchange” to describe specific adsorption and considered that it is “not dependent on surface charge”.
Effects of rate of reaction
Chemists tend to think in terms of equilibrium, but farmers and agricultural scientists know that nutrients react with soils for a very long time and as a result become less effective. We are aware of only one study on the effects of pH on rate of reaction. Figure 7 shows that for phosphate the continuing reaction is fastest at low and at high pH and slowest at medium pH. This means that the effects of pH on sorption become increasingly U-shaped: a further indication of how difficult it is to make a simple statement about the effects of pH on phosphate sorption.
Metals also continue to react with goethite and, as a result, the sorption curves move to lower pH values (Fig. 10). However, the rate at which they react differs. This can be seen by comparing the curves for copper and lead; after two hours reaction time they are similar but after eight weeks the curve for copper has moved further to the left. For most of the metals the rate of reaction is related to ion size: large ions move slower (Fig. 11). It was suggested that aluminium and chromium react as Al(OH)2+ and Cr(OH)2+ and that the behaviour of nickel was consistent with surface oxidation to the trivalent form followed by movement as Ni(OH)2+.
Effects of pH on decomposition of organic matter
Decomposition of organic matter is accelerated by increasing pH (Fig. 12). Supply of both nitrogen and sulfur are therefore increased. This is consistent with the effects of low pH in decreasing the activity of microbes leading to accumulation of organic matter (Malik et al. 2018).
Effect of pH on mineralisation of carbon, sulfur and nitrogen from a soil. (Drawn from the date of Barrow (1965))
Oxides are not soils
Studies using oxides such as goethite have several advantages: it is possible to investigate a large range of pH from as low as pH 2 as high as pH 12; the substrate is uniform and, subject to some limitations, results can be compared between laboratories; the substrate is free of contamination from, for example, native phosphate present in soil; and the surface is well-characterised and its behaviour with change of pH is known. These advantages can become disadvantages if applied too literally as models of reaction with soils: for most soils, the range of pH values is much smaller; the particle surfaces are not uniform and not well-characterised; and the aluminium present in solutions at low pH can complex fluoride and so decrease adsorption (Barrow and Ellis 1986a, b).
However, a major difference is that the change in electric potential with change in pH is much steeper for pure compounds such as goethite than for soils. Consequently the effects of pH for soils are much smaller. This has been illustrated earlier for phosphate. For cations, Barrow and Whelan (1998) compared the effects of pH on sorption in terms of the concentration of ions required to produce equal sorption. They found that for goethite, unit increase in pH decreased the required concentration of zinc 35 fold and of cadmium 11 fold. For soil, the equivalent values were 10-fold for zinc and 4-fold for cadmium.
Effects of pH on nutrient uptake by plants
The surfaces of plant roots also bear variable charge. Lu et al. (2020) measured zeta potentials of plant roots and showed that, as the pH increased, the surfaces became increasingly negative. This means that the concentration of cations near the surface will decrease, and the concentration of anions increase. There are also specific effects of pH on the uptake mechanisms. The overall effects of pH on the availability of nutrients to plants are a combination of the effects of pH on sorption by soils and the effects of pH on plant uptake. In most cases the overall effects are smaller than would follow from soil sorption alone. We now consider individual nutrients.
Phosphorus
Soil scientists have tended to emphasise the effects of pH on sorption of phosphate. However, when we consider the effects of pH on availability, the factors that are important are the effect of pH on the rate of desorption and the effects of pH on the rate of uptake by plant roots. These can be measured by obtaining response curves to phosphate over several pH values and using a modified form of the Mitscherlich equation (Barrow et al. 2020):
where Y is the yield; x is the P applied; and m, c, and d are parameters. The parameter m indicates the maximum yield to which the data trend; the parameter c indicates the slope of the response curve; and the parameter d indicates the P desorbed from the soil plus that from the seed. The parameter c can be regarded as a measure of the effectiveness of the fertiliser; the larger its value, the smaller the amount of fertiliser needed for a given response.
There is a U-shaped relationship between desorption and pH, with the least desorption in the middle pH range (Barrow 2017). There is also a U-shaped between pH and the parameter d – which largely reflects effects of pH on rate of desorption as induced by plant roots (Fig. 13). Thus, the rate of desorption and the rate of sorption (Fig. 8) are similarly affected by pH; both are slowest in the mid pH range.
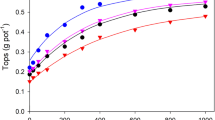
Effect of pH on response to phosphate. Mustard (Brassica campestris), lucerne (Medicago sativa) and rice (Oryza sativa) were grown in a pot trial with 10 different amounts of phosphate a and pH(cacl2) ranging from 3.99 to 7.26. The yield at each pH were described by \(Y = m[1- \mathrm{exp}(-c(x + d)]\) where y is the yield; x is the P applied; and m, c, and d are parameters. In part a, response curves for mustard at two pH values are extrapolated to illustrate the values of the parameter d. Part b shows the effects of pH on the uptake of P at a P application of 400 mg pot−1 and part c shows the effects of pH on parameter d. (Drawn from data of Barrow et al. (2020))
Phosphate uptake by plant roots increases as the pH decreases. When this was first observed, the rate of phosphate uptake was noted as closely matching the proportion of phosphate present as the monovalent H2PO4− ion and it was thought to show that this was the ion taken up by roots (Vange et al. 1974). Subsequently Rausch and Bucher (2002) concluded that the mechanism of phosphate uptake involves H+/Pi cotransport. We are not overly concerned with the mechanism here; the important message is that there is a large effect of pH, so large that it dominates – at least above pH of about 5.
The outcome is that phosphate fertiliser is least effective near pH 7 (Fig. 13); it is necessary to apply more of it to achieve the same yield as at lower pH. It is most effective near pH 5; at lower pH, aluminium toxicity decreases the responses. The behaviour of aluminium is thus consistent other cations; its solubility decreases as the pH increases.
Boron
Oertli and Grgurevic (1975) concluded that boron uptake by roots involves passive diffusion into the roots of undissociated (and therefore uncharged) boric acid molecules. It therefore differs fundamentally from most other nutrients, the uptake of which involves ionised forms and active transport. Most of the results of Oertli and Grgurevic (1975) were for fairly high pH values. If we extrapolate to the lower pH values of interest for uptake from soil, effects would be small. This is consistent with the results of Peterson and Newman (1976). They found little effect on boron uptake between pH 4.7 and pH 6.3, but a 2.5-fold decrease at pH 7.4.
Molybdenum
Uptake of molybdate occurs via phosphate binding/ transporting sites at the plasma membrane of root cells (Heuwinkel et al. 1992). This means that, like phosphate, uptake will be slowest at high pH. However, the effects of pH on sorption are so large that they dominate, and availability increases with increasing pH. These effects have been known for a long time. Lewis and Watson (1942) reported that acidic fertilisers applied to the soil decreased teart disease in cattle. This disease is caused by excess molybdenum in the diet. On the other hand, Anderson and Moye (1952) showed that clover growth could be improved either by applying lime or by applying molybdenum, a classic example of a negative interaction.
Sulfur
Sorption of sulfate decreases with increasing pH (Fig. 9), and mineralisation of organic sulfur also increases with increasing pH (Fig. 12). On the other hand, uptake of sulfate by barley roots decreases with increasing pH (Fig. 12). The effect is like that of pH on phosphate uptake even though uptake seems to involve a different pathway (Vange et al. 1974). This is another example in which the effects of pH on plant uptake are opposite to the effects of pH on soil chemistry. As far as we are aware the outcome has not yet been measured.
Nitrogen
Nitrogen mineralisation increases linearly with increasing pH (Fig. 12). The uptake of ammonium ions decreases with decreasing pH (Henry and Raper 1989, Vessey et al. 1990). This would be expected to make effects of pH even more marked.
Exchangeable cations: potassium, magnesium, and calcium
Two of these elements provide further examples for which the effects of pH on soil chemistry are opposite to the effects on plant physiology. As the pH is increased, the increased negative charge on soil particles will mean that a smaller proportion of the cations is present in the solution phase and the rate of movement to plant roots by diffusion will decrease. However, uptake of potassium involves export of protons (Maathuis and Sanders 1996) and a similar mechanism would probably apply to magnesium. Uptake of potassium is therefore favoured by high pH (Harper and Balke 1981) as is uptake of magnesium (Maas and Ogata 1971). Again, as far as we are aware, the outcome from the two opposing effects has not yet been measured.
For calcium, there is usually such a high concentration in the soil solution that movement to plant roots is by mass flow rather than by diffusion and the effects of pH on surface charge would be expected to be less important. The mechanism of calcium uptake also differs; it is thought that it is taken up through plasma membrane channels expressed in roots and transported to the shoot in a mainly apoplastic way (Thor 2019). This suggests it would be little affected by pH. Further, pH is often adjusted by adding calcium carbonate, so the effects of pH and calcium concentration are confounded.
Zinc and other specifically sorbed cations
Uptake of metal ions from solution by plants is increased by increasing pH. This has been shown for zinc by Chaudhry and Loneragan (1972), for manganese by Robson and Loneragan (1970), and for cadmium by Hatch et al. (1988). This opposes the effects of pH on metal sorption. As noted earlier, for soil, if the pH was increased by one unit, the solution concentration required to give the same sorption of zinc was decreased 10-fold and of cadmium 4-fold. For uptake of zinc and cobalt, the effects of pH a much smaller (Barrow and Whelan 1998). The slope of the response curves (Fig. 14a, b) is a measure of the relative effectiveness at each pH. There was a logarithmic relationship between the slopes and pH (Fig. 14c). The slopes were such that the effectiveness of zinc changed in proportion to pH−0.12 and cobalt in proportion to pH−0.14.
Effect of pH on the uptake of zinc and cobalt from soil by subterranean clover (Trifolium subterranean). Parts a and b show the uptake plots. In part c, the slopes of the lines are plotted against pH. (Drawn from the data of Barrow and Whelan (1998))
A qualification
The relatively few measurements that have been made of the effects of pH or nutrient availability have utilised plants which, for want of a better name, we might think of as “ordinary” plants. By this is meant plants that have only small effects on the pH of their rhizosphere. Little attention has yet been allocated to plants that have large effects on their rhizosphere. This includes plants with modified structures such as cluster roots. These occur in several plant families, especially the Proteaceae, but are perhaps best known in white lupin (Lupinus albus). Such plants “make their own pH” and so might be less affected by bulk soil pH.
Conclusions
Effects of pH on availability of nutrients are complicated and diverse, but they do follow principles that we are beginning to understand. Nevertheless, too often, theories have been advanced based on observations with model substances, or with soils, without regard to the effects of pH on uptake by plant roots. In some cases, these can be overwhelmingly important. Too seldom have theories been tested by actually measuring the effects of pH on uptake of nutrients by plants growing in soil.
Data availability
No new data were generated during the preparation of this manuscript.
References
Anderson AJ, Moye DV (1952) Lime and molybdenum in clover development on acid soils. Aust J Agric Res 3:95–110
Barber SA, Walker JM, Vasey EH (1963) Mechanisms for movement of plant nutrients from soil and fertilizer to plant root. J Agric Food Chem 11:204–207
Barrow NJ (1965) Further investigations of the use of lime on established pastures. Aust J Exp Agric Animal Husb 5:442–449
Barrow NJ (1989) Testing a mechanistic model 10 the effects of pH and electrolyte concentration on borate sorption by a soil. J Soil Sci 40:427–436
Barrow NJ (2017) The effects of pH on phosphate uptake from the soil. Plant Soil 410:401–410. https://doi.org/10.1007/s11104-016-3008-9
Barrow NJ (2020) Comparing the two theories about the nature of soil phosphate. Europ J Soil Sci. https://doi.org/10.1111/ejss.13027
Barrow NJ, Bowden JW (1987) A comparison of models for describing the adsorption of anions on a variable charge mineral surface. J Colloid Interface Sci 119:36–50
Barrow NJ, Ellis AS (1986a) Testing a mechanistic model 5 the points of zero salt effect for phosphate retention, for zinc retention and for acid/alkali titration. J Soil Sci 37:303–310
Barrow NJ, Ellis AS (1986b) Testing a mechanistic model 3 the effects of pH on fluoride retention by a soil. J Soil Sci 37:287–293
Barrow NJ, Whelan BR (1989) testing a mechanistic model 7 the effects of pH and of electrolyte on the reaction of selenite and selenate with a soil. J Soil Sci 40:17–28
Barrow NJ, Whelan BR (1998) Comparing the effects of pH on the sorption of metals by soil, by goethite, and on uptake by plants. Europ J Soil Sci 49:683–692
Barrow NJ, Spencer K, Mcarthur WM (1969) Effects of rainfall and parent material on the ability of soils to adsorb sulfate. Soil Sci 108:120–126
Barrow NJ, Bowden JW, Posner AM, Quirk JP (1980) Describing the effects of electrolyte on adsorption of phosphate by a variable charge surface. Aust J Soil Res 18:395–404
Barrow NJ, Debnath A, Sen A (2020) Measurement of the effects of pH on phosphate availability. Plant Soil 454:217–224. https://doi.org/10.1007/s11104-020-04647-5
Bowden JW, Posner AM, Quirk JP (1977) Ionic adsorption on variable charge mineral surfaces. Theoretical charge development and titration curves. Aust J Soil Res 15:121–136
Camps Arbestain M, Barreal ME, Macı́as F (2001) Sulfate sorption in nonvolcanic Andisols and Andic soils from Galicia, NW Spain. Geoderma 104:75–93
Chaudhry PM, Loneragan JF (1972) Zinc absorption by wheat seedlings. Ii. Inhibition by hydrogen ions and by micronutrient cations. Soil Sci Soc Amer Proc 36:327–331
Couto W, Lathwell DJ, Bouldin DR (1979) Sulfate sorption by two Oxisols and an Alfisol of the tropics. Soil Sci 127:108–116
Fischer L, Brümmer GW, Barrow NJ (2007) Observations and modelling of the reactions of ten metals with goethite: adsorption and diffusion processes. Europ J Soil Sci 58:1304–1315
Goldberg S, Glaubig RA (1985) Boron adsorption on aluminium and iron oxide minerals. Soil Sci Soc Amer J 49:1314–1319
Goldberg S, Glaubig RA (1986a) Boron adsorption on California soils. Soil Sci Soc Amer J 50:1173–1176
Goldberg S, Glaubig RA (1986b) boron adsorption and silicone release by the clay minerals kaolinite, montmorillonite, and illite. Soil Sci Soc Amer J 50:1442–1448
Goldberg S, Lesch SM, Suarez DL (2002) Predicting molybdenum adsorption by soils using soil chemical parameters in the constant capacitance model. Soil Sci Soc Am J 66:1836–1842
Hartemink AE, Barrow NJ (2023) Soil pH – nutrient relationships: the diagram. Plant Soil. https://doi.org/10.1007/s11104-022-05861-z
Hatch DJ, Jones LHP, Burau RG (1988) The effect of pH on the uptake of cadmium by four plant species grown in flowing solution culture. Plant Soil 105:121–126
Henry LT, Raper CD Jr (1989) Effects of root-zone acidity on utilization of nitrate and ammonium in tobacco plants. J Plant Nutr 12:811–826. https://doi.org/10.1080/01904168909363995.Pmid:11537085
Heuwinkel H, Kirkby EA, le Bot J, Marschner H (1992) Phosphorus deficiency enhances molybdenum uptake by tomato plants. J Plant Nutr 15:549–568. https://doi.org/10.1080/01904169209364340
Hiemstra T, Van Riemsdijk WH (1996) A surface structural approach to ion adsorption: the charge distribution (CD) model. J Colloid Interface Sci 179:488–508
Hingston FJ, Posner AM, Quirk JP (1972) Anion adsorption by goethite and gibbsite. I. The role of the proton in determining adsorption envelopes. J Soil Sci 23:177–192
Harper JR, Balke NE (1981) Characterization of the inhibition of K+ absorption in oat roots by salicylic acid. Plant Physiol 68:1349–1353
Lewis AH, Watson SJ (1942) Teart pastures. Agric Gt Brit 49:82–84
Lu HL, Nkoh JN, Baquy MA, Dong G, Li JY (2020) Plants alter surface charge and functional groups of their roots to adapt to acidic soil conditions. Environ Pollut 267:115590. https://doi.org/10.1016/j.envpol.2020.115590. (ISSN 0269-7491)
Maas EV, Ogata G (1971) Absorption of magnesium and chloride by excised corn roots. Plant Physiol 47:357–360
Maathuis FJM, Sanders D (1996) Mechanisms of potassium absorption by higher plant roots. Physiol Plant 96:158–168
Malik AA, Puissant J, Buckeridge KM et al (2018) Land use driven change in soil pH affects microbial carbon cycling processes. Nat Commun. https://doi.org/10.1038/s41467-018-05980-1
Mckenzie R (1983) The Adsorption of molybdenum on oxide surfaces. Aus J Soil Res 21:503–513
Oertli JJ, Grgurevic E (1975) Effect of pH on the absorption of boron by excised barley roots. Agron J 67:278–280
Penn CJ, Camberto JJ (2019) A critical review on soil chemical processes that control how soil pH affects phosphorus availability to plants. Agriculture 9:120–138
Peterson LA, Newman RC (1975) Influence of soil pH on the availability of added boron. Soil Sci Soc Amer J 40:280–282. https://doi.org/10.2136/sssaj1976.03615995004000020023x
Rausch C, Bucher M (2002) Molecular mechanisms of phosphate transport in plants. Planta 216:23–37. https://doi.org/10.1007/s00425-002-0921-3
Robson AD, Loneragan JF (1970) Sensitivity of annual Medicago species to manganese toxicity as affected by calcium and pH. Aust J Agric Res 21:223–232
Thor K (2019) Calcium – nutrient and messenger. Front Plant Sci. https://doi.org/10.3389/fpls.2019.00440
van Raij B, Peech M (1972) Electrochemical properties of some oxisols and alfisols of the tropics. Soil Sci Soc Amer J 36:587–593
Vange MS, Holmern K, Nissen P (1974) Multiphasic uptake of sulfate by barley roots i effects of analogues, phosphate, and pH. Physiol Plant 31:292–301
Vessey JK, Henry LT, Chaillou S, Raper CD Jr (1990) Root-zone acidity affects relative uptake of nitrate and ammonium from mixed nitrogen sources. J Plant Nutr 13:95–116. https://doi.org/10.1080/01904169009364061.Pmid:11538113
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Contributions
Both authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
We have no relevant financial or non-financial interests to disclose.
Additional information
Responsible Editor: Peter J. Gregory.
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barrow, N.J., Hartemink, A.E. The effects of pH on nutrient availability depend on both soils and plants. Plant Soil 487, 21–37 (2023). https://doi.org/10.1007/s11104-023-05960-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11104-023-05960-5