Abstract
Aims
The sub-Antarctic cushion plant, Azorella selago, is usually hemispherical when small but frequently crescent-shaped when larger. Spatial variation in wind speed and in air-borne seed and sediment deposition is examined to determine if wind scouring and deposition patterns could contribute to the development of non-hemispherical shapes in cushion plants.
Methods
Computational fluid dynamic analyses were conducted for hemispherical and crescent-shaped cushion plants parameterizing models with data from A. selago habitats on Marion Island. Numerical data were contextualized with field observations to arrive at a conceptual model for shape development.
Results
Airflow modelling showed that both wind scouring and seed deposition of the commonly co-occurring grass Agrostis magellanica are greater on the windward side of the plant. By contrast, heavier sediment particles are predominantly deposited on the leeward side of plants, leading to burial of lee-side A. selago stems. This sediment accumulation may initiate the development of the crescent-shape in hemispherical plants by increasing stem mortality on the plant’s leeward edge. Once developed, the crescent-shape is probably self-reinforcing because it generates greater air recirculation (and lower air velocities) which enhances further deposition and establishment of A. magellanica grasses in the lee of the crescent. The conceptual model consists therefore of three stages namely, (1) negligible air recirculation, (2) sediment deposition and grass establishment, and (3) differential cushion growth.
Conclusion
This conceptual model of plant shape development may explain the occurrence and orientation of crescent-shaped cushion plants and highlights how predicted changes in wind patterns may affect vegetation patterns.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Strong and prevailing winds can have considerable effects on the growth and survival patterns of individual plants. The impacts of wind on plants can be direct, by altering a plant’s microclimate (e.g. affecting temperature or humidity gradients around leaves) or through mechanical damage to leaves and stems (de Langre 2008; Grace 1977; Wilson 1959). However, the impacts of wind can also be indirect, acting through the entrainment, transport and deposition of particles (Grace 1977), leading to, for example, erosion around plant’s roots, wind-scouring of leaves and stem burial e.g. (Baumeister and Callaway 2006; Kullman 2005; van Gardingen et al. 1991). While the direct and indirect impacts of wind on the growth and survival of trees and some crops has been relatively well studied (de Langre 2008; Ennos 1997), wind impacts on other growth forms are more poorly understood. Indeed, even though the compact and hemispherical cushion growth form is considered an adaptation to windy conditions (Hauri 1912) (see also (Hauri and Schröter 1914) and (Spomer 1964)), there has been surprisingly little research examining the impact of wind on cushion plants (e.g. (Ashton and Gill 1965; Fitzgerald and Kirkpatrick 2017; Lynch and Kirkpatrick 1995; Whitehead 1951)).
Cushion plants are often common in cold and exposed areas ((Aubert et al. 2014; Hauri and Schröter 1914; Körner 2003)), with the cushion growth form being genetically fixed (i.e. obligate) for many species, but facultative for others i.e. only adopted in windy habitats; (Hauri 1912; Spomer 1964). The cushion growth form may also reflect responses to other stressors, such as higher ultraviolet radiations and lower temperatures, which are also prevalent at higher altitudes (Ruffier-Lanche 1964; Ruthsatz 1978). In these abiotically-stressful environments individual cushion plants of the same species can exhibit a range of different shapes, particularly as they grow larger (Huntley 1972; Pyšek and Liška 1991), despite a circular circumference (i.e. a hemispherical shape) being optimal for heat and moisture retention (Gauslaa 1984), see also (Zotz et al. 2000). Various mechanisms have been suggested to cause unequal growth and/or mortality on different sides of cushion plants, thereby resulting in the development of non-hemispherical shapes in larger individuals. For example, the presence of rocks and other plants can cause irregular growth of cushions (Pyšek and Liška 1991), while cushions established on inclines may grow perpendicular to the slope (Selkirk-Bell and Selkirk 2013; Taylor 1955a). Turf exfoliation by needle ice formation (in colder areas) and salt-spray deposition (in coastal areas) could also contribute to unequal mortality of cushion plant stems and the development of crescent-shaped cushions (Boelhouwers et al. 2003; Huntley 1971).
Airflow patterns may also affect the shape of cushion plants (Boelhouwers et al. 2003; Pyšek and Liška 1991; Whitehead 1951), as wind strength (i.e. air flow velocity) influences the height, growth rate and compactness of some cushion-forming species (Lynch and Kirkpatrick 1995) (see also (Fitzgerald and Kirkpatrick 2017; Huntley 1972; Ralph 1978; Ternetz 1902; Whinam et al. 2014)). The interaction between cushion plant shape and airflow is probably important in exposed sites because plant survival may be strongly linked to the shape of individuals. For example, plants with a more irregular shape offer greater resistance to airflow, and therefore have a greater chance of sustaining wind damage (including breaking of branches and erosion of soil under the plant; (Whitehead 1951), see also (Cerfonteyn et al. 2011)). As a result, the factors that determine cushion shape probably also affect the survival of individual plants. However, contrasting observations have been made about cushion plants sustaining wind-related damage predominantly on their windward or leeward sides, see e.g. (Ashton and Gill 1965; Huntley 1971; Whinam et al. 2014).
Furthermore, because many cushion plant species are nurse plants facilitating the presence of other species, the survival and longevity of cushion plants can considerably alter plant community richness and composition (Badano and Marquet 2008; Badano and Cavieres 2006). For example, at high altitudes in the Andes, cushion plants increase local species richness by 22–243% (Badano and Cavieres 2006) and the biomass of other species by up to 54% (Badano et al. 2007). Therefore, the pattern of airflow over individual cushion plants may have community-level consequences, directly by providing sheltered establishment sites and indirectly by affecting the survival of the cushion plants and all the species that depend on them. However, apart from a few basic observational studies, see also e.g. (Courtin and Bliss 1971; Wilson 1959), airflow around cushion plants has yet to be studied in detail.
Due to the differences in the height of origin, mass, density and smoothness of plant seeds and sediment particles, their deposition patterns can differ considerably. In particular, soil sediment particles typically have a relatively high density and are entrained into the airflow from the soil surface (Zhang and Miao 2003). As a result, sediment particles usually travel close to the ground and for relatively short distances. Wind movement of sediments is well understood, with most sediments accumulating in areas of low shear stress (i.e. regions of decreased velocity) (Durán and Herrmann 2006; Pye and Tsoar 1990; Zhang and Miao 2003). In vegetated areas wind-transported sediments often accumulate on the lee of plants with non-porous canopies or bases that divert airflow (Pye and Tsoar 1990) or within plants that slow airflow due to a porous canopy (Ravi et al. 2008). Indeed, some species are able to initiate dune (nebkha) formation by causing sand deposition in their lee (Cooke and Warren 1973).
Here we use computational fluid dynamics techniques to model airflow around cushion plants to predict spatial variation in the direct physical force of the wind and in the accumulation of air-borne seeds, and to understand if these impacts of wind could affect the directional growth and, as a result, the shape of cushion plants. Based on these results, and combined with field observations, we propose a conceptual model of cushion plant shape development in windy environments. In particular we focus on Azorella selago (Apiaceae) which is a dominant species across much of the sub-Antarctic (Frenot et al. 1993). The size, shape and compactness of this species are representative of many other cushion plants (Aubert et al. 2014; Rauh 1939), and it is therefore an appropriate model species for this study.
Materials and methods
Study species
A. selago (Apiaceae) forms compact cushions with a thin surface layer of photosynthesizing leaves overlying a dense core of live stems, decomposing leaves and fine mineral material soil (Fig. 1). Due to their dense nature, cushion plants were modelled as non-porous obstructions to airflow, see e.g.(Hager and Faggi 1990). On sub-Antarctic Marion Island (46°54’S, 32°45′E), A. selago is the most widespread vascular plant species, and has a median maximum diameter of 0.4–1.2 m and a height of 0.05–0.20 m, (Huntley 1972; le Roux and McGeoch 2004; Phiri et al. 2009) (see also (Chown and Froneman 2008) for a complete review of the island’s climate, geology and ecology).
Azorella selago plants on Marion Island with (a) hemispherical shape and (b) crescent shape. A 15 cm length ruler is provided for scale. The grass Agrostis magellanica is visible on both cushion plants (see also Fig. 2)
Cushion shape varies between individuals, with smaller plants usually being hemispherical and larger plants having more irregular shapes (Haussmann et al. 2009). Indeed, larger cushions may often have a crescent shape, with their convex edges facing in the direction of the prevailing wind, i.e. the tails of the crescent point away from the prevailing wind; (Huntley 1972). As a result, we modelled the airflow over two different plant shapes, corresponding to the size and form of a medium-sized hemispherical cushion and a larger crescent-shaped cushion (sizes based on data from (le Roux and McGeoch 2004); see Table 1).
The grass A. magellanica (Poaceae) is the second most widespread vascular plant on Marion Island (Fig. 2; (Huntley 1971)) and grows both rooted in the soil and epiphytically on A. selago (i.e. rooted within the cushion plant’s humus-like core) (Huntley 1972).
At mid and high altitudes (> 100 m a.s.l.) A. magellanica is strongly facilitated by A. selago, having higher abundance, cover, biomass and reproductive effort when growing on A. selago relative to the adjacent substrate (le Roux and McGeoch 2010). High densities of epiphytic A. magellanica are thought to have a negative impact on A. selago due to the strong shading of the cushion plant’s leaves (le Roux et al. 2005), see also (Schöb et al. 2014). At higher altitudes the abundance of A. magellanica is thought to be limited by strong winds (le Roux et al. 2005; Taylor 1955b) see also (Pammenter et al. 1986) and low temperatures (Huntley 1970).
Study site: Fellfield habitats on eastern Marion Island
Fellfield habitats cover the majority of Marion Island between 100 and 500 m a.s.l. (Smith et al. 2001). This vegetation type is characterised by the dominance of A. selago (up to 30% cover), low total plant cover (usually <30%), high rock cover and poorly-developed mineral soils (Huntley 1971) (Fig. 3).
The climate in these habitats is cold (mean annual temperature = 6.4 °C), oceanic (seasonal temperature range = 4.1 °C) and wet (mean annual precipitation = 1975 mm, mean humidity exceeding 80%) (data from the meteorological station on the eastern side of the island at sea level; (le Roux 2008; le Roux and McGeoch 2008; Smith 2002)). As is typical for the sub-Antarctic region, the island is very windy, experiencing gale force winds (> 15 m/s) on more than 100 days per year (Schulze 1971). The dominant winds on the eastern side of the island are north-westerlies (60% of observations) and south-westerlies (20%), which are also the strongest winds, averaging >10 m/s and 7 m/s respectively (le Roux 2008). Average wind speed at sea level on the island is 8 m/s, although this is probably stronger at higher altitudes, particularly under neutrally stable atmospheric conditions, (Garratt 1994); see also le Roux et al. 2018–2019 unpublished data, (Berg et al. 2011).
Modelling airflow using computational fluid dynamics
Previous studies of airflow around plants have almost exclusively considered trees and grasses (de Langre 2008). Similarly, amongst studies not examining plants, few researchers have documented the patterns of airflow over hemispheres or crescents (Cao and Tamura 2020; Kim and Baik 2003; Savory and Toy 1985; Tavakol et al. 2015; Tavakol et al. 2010). However, the airflow around spherical and cylindrical obstructions is well described (Achenbach 1974; Achenbach 1972; Breuer 2000; Breuer 1998; Constantinescu and Squires 2004; Dehbi and Martin 2011; Hoffman 2006; Lyotard et al. 2007; Norberg 1987; Raithby and Eckert 1968; Tiwari et al. 2020), and provides a framework to interpret flow around cushion plants. Indeed, it has been consistently observed that as free-stream air approaches a non-porous bluff (i.e. not streamlined) obstacle, like a sphere or a cylinder, shear forces on the object’s surface cause the velocity of the air particles to decrease, creating a narrow boundary layer over the object’s surface [i.e. a layer separating the free-stream air and the still air on the obstacle’s surface; (Greeley and Iversen 1985; White 2016). As air flows over the crest of a cylinder (or around the circumference of a sphere) it attains its highest velocity, and the boundary layer remains relatively thin (Anderson Jr 2015; Pye and Tsoar 1990). However, as air particles move into the lee of the obstruction (i.e. downstream of the maximum flow velocity), the boundary layer may separate from the surface of the obstruction due to an adverse pressure gradient [i.e. diminishing of the shear stress, hampering airflow attachment to the plant surface; (Greeley and Iversen 1985; Houghton and Carpenter 1993; White 2016). As a result, a wake forms between the boundary layer and the obstruction, where recirculation occurs (i.e. airflow counter to the free-stream airflow direction), turbulent eddies form and mean air flow velocity is low (Bakić and Perić 2005; Pye and Tsoar 1990). Downstream of the obstruction the boundary layer rejoins the surface at the reattachment point, beyond which recirculation is minimal (Pye and Tsoar 1990).
We investigated these patterns of airflow around hemispherical and crescent-shaped cushion plants growing on a flat surface using computational fluid dynamics (CFD), a mathematical modelling tool that solves fluid flow problems using numerical algorithms (Versteeg and Malalasekera 2007). CFD models are based on the three laws of conservation of mass, momentum and energy, from which a system of partial differential equations governing the flow of fluids and entrained particles are derived. These equations are algebraically transformed and solved iteratively. StarCD software (CD-Adapco, London, UK) was used to conduct the airflow analysis over hemispherical and crescent-shaped cushion plant (version 3.24), and to perform Eulerian two phase flow simulations for particle tracks (version 4.06). Complete model specifications, wind tunnel validation and results are provided in (Combrinck 2009) and verified (Meas et al. n.d.).
In addition to mean airflow patterns, turbulence in atmospheric flow is also well described by the three conservation laws on which CFD modelling is based (see above). However, due to current computational resource limitations, the fine-scale patterns of airflow speed and direction need to be resolved using additional turbulence modelling. A comparison of turbulence models by Combrinck (Combrinck 2009), based on wind tunnel tests of air flowing over a hemispherical model, concluded that the k-ε turbulence model (k = turbulence kinetic energy, ε = turbulence kinetic energy dissipation rate) with wall functions can adequately resolve the bulk flow features examined here such as velocity and pressure increase and decrease (Meas et al. n.d.; Versteeg and Malalasekera 2007).
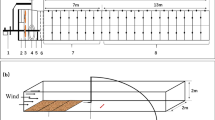
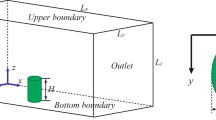
CFD modelling requires the definition of a computational domain and the specification of boundary conditions (Fig. 4). The domain consists of: a free stream velocity inlet with an atmospheric profile (as discussed in section 2.4.1), a pressure outlet, sides and top defined as symmetry planes and no-slip walls with defined surface roughness (discussed in section 2.4.2) to represent the hemisphere or crescent and floor surrounding the cushion.
The computational domain for the hemisphere had a length, width and height of 4 m, 4.5 m and 1.5 m respectively (Table 2). Given the dimensions of the hemisphere (Table 1), the aerodynamic blockage of the hemisphere in the domain was 0.5%, in line with good practice requiring blockage of <10% (preventing the boundaries of the domain from influencing the solution). Similarly, the dimensions of the crescent shape computational domain are 5 × 3.5 × 1 m, equating to a blockage percentage of 3.5%. The cell numbers (i.e. the number of units into which the computational domain was divided for calculations) for the hemispherical and crescent shapes were 923,181 and 778,973 respectively. The spatial resolution was constructed for both grid independent and y+ values associated with the high Reynolds number turbulence model strategy (i.e. y+ between 30 and 300). Grid independence ensure that the number of units into which the computational domain was divided was sufficiently small to obtain a good mathematical resolution of the results. Smaller resolutions provide more accurate results, however this comes at the cost of computational time. Part of the verification process of flow modelling is obtaining a grid size that is small enough to obtain a good results within reasonable CPU (central processing unit) time. Another part of verification process was ensuring that the cell size at the walls was appropriate for the turbulence model used. The parameter y+ is a dimensionless wall distance which is an indication of the cell sizes in the near wall region.
The computational model has to capture the flow physics correctly; this is dependent on the regime of the flow and the solution methodology implemented. The flow was hence defined as incompressible (since the Mach number for air is well below 0.3) with standard atmospheric conditions for the pressure. The simulations were solved in the steady state domain with single precision. The AMG (Algebraic Multigrid) solution method was employed in conjunction with the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) solution algorithm. Discretisation of the domain was done using a central differencing scheme with a blending factor of 0.9. Relaxation factors were employed for the momentum, pressure and turbulent viscosity at values of 0.7, 0.3 and 0.7 respectively. Models were run to convergence where the residual values were both lower than 1e-6 and stabilised to a near constant value. The hemispherical model converged after 4535 iterations and the crescent shape after 2268.
Parameterizing the airflow models
First, to simulate airflow over cushion plants, models were parameterized based on the characteristics of A. selago cushion plants and on the physical conditions on the eastern side of sub-Antarctic Marion Island in fellfield habitats where the species is the dominant vascular plant. Model parameterization was completed by determining the airflow velocity profile within fellfield habitats, and the surface roughness of A. selago cushions and the surrounding surface.
Airflow velocity profile
The vertical airflow velocity profile experienced by A. selago cushions was measured in two fellfield sites, Skua-Ridge and Tafelberg, on the eastern side of Marion Island. Wind speed was recorded at three heights (0.20, 0.47 and 1.40 m above the soil surface) using WSD100 anemometers with ±5% accuracy and a XR5SE data logger (Pace Scientific, Mooresville, USA; Fig. 5).
Data were obtained on Skua-Ridge on three different days measuring one sample per minute for three hours. On Tafelberg this was repeated also on three separate days taking four samples per minute for 1.5 h. Airflow velocity increased strongly with height (Table 3), and a logarithmic relationship fitted the data well (R2 = 0.98–0.99, p < 0.001) for both sites after log-transformation.
As a result, the airflow velocity profile was modelled by:
where u* is the friction velocity, κ is the von Kármán constant (= 0.41), z is the height above the soil surface and z0 the roughness length (following (Petersen et al. 1998). The final parameter, ψ, is a stability-dependent function that is positive in unstable conditions, negative in stable conditions and zero for neutral stability (Kim and Baik 2003; Petersen et al. 1998; Yang et al. 2008). To achieve a logarithmic vertical airflow profile (such a observed in the result shown in?) with a mean velocity of 8 m/s at 1.5 m height (i.e. the mean speed recorded at the island’s meteorological station (le Roux and McGeoch 2008)) over a surface with z0 = 0.0057, we set u* = 0.138 and ψ = −18. This vertical airflow velocity profile was then used in all simulations.
Surface roughness parameters
Both Skua Ridge and Tafelberg are pre-glacial lava flows dominated by smooth basalt rocks. The sediment size in the immediate surface area around A. selago can display a high degree of variation (e.g. Fig. 6).
The diameter of surface particles around A. selago cushions at a fellfield site on the eastern side of Marion Island ranged between 2.0 and 313.2 mm (Haussmann et al. 2009). The mean particle size (5.7 mm diameter) was therefore used as an estimate of ground surface roughness. The surface roughness of fellfield A. selago cushions was estimated as 1.5 mm (pers. obs.; MLC), reflecting the average deviation of the height of the leaf surface.
The model for surface roughness in StarCD version 3.24 is based on the sand grain experiments of Nikuradse (H. Schlichting 1968). The modified Law-of-the-Wall equation is used to model fully rough walls at high Reynolds numbers:
The generic values for the constants A, B, C, D and Cμ are 8.5, 0, 1, 0 and 0.09 respectively. κ is the von Kármán constant (= 0.41). The parameter y0 represents the roughness height; this was specified in the model as 5.7 mm and 1.5 mm for the ground and plant area respectively.
Modelling seed deposition
The deposition of solid particles on cushion plants was modelled using a Eulerian two phase flow model, where Phase 1 represents the continuous fluid (i.e. the airflow) and Phase 2 the dispersed particles (i.e. seeds) (CD-Adapco Group 2008). The two phases (a gas and a solid) behave differently in the proximity of an obstruction due to their different physical properties and densities. In particular, while the trajectory of an air particle is deflected by an object (guided around the curvatures), a solid particle is more likely to impact with the obstruction (due to the greater momentum of heavier particles; (CD-Adapco Group 2008)). In contrast to sediment particles, seeds are lighter (equivalent to airborne contaminants in CFD modelling; (CD-Adapco Group 2008)) and are released into the airstream above the ground surface (e.g. inflorescences at 0.05–0.4 m in fellfield; le Roux et al. unpublished data).
Seed particles in the model were parameterized based on the aerodynamic characteristics of the seeds of the common grass Agrostis magellanica. The seeds appear to be dispersed within their spikelets, which have an irregular shape and numerous sharp points, which are likely to enhance seed adherence to surfaces. As a result, the seeds (and the spikelets) are likely to be deposited on first impact, while smoother sediment particles are more likely to be deflected and only settle in low airflow velocity conditions, see also (Beyers and Waechter 2008; Grace 1977). Therefore, air-borne seeds and sediment are expected to have different deposition patterns due to differences in their mass, shape and the height at which they are entrained into the airstream. As sediment deposition has been modelled extensively in other studies, seed deposition was the focus of this study.
The mean drag coefficient of A. magellanica seeds was determined using a gravitational drop test (Combrinck 2009; C.T. Crowe et al. 2001), where the mean time taken for seeds to fall 4.15 m was determined. A. magellanica inflorescences were collected from the eastern side of the island, and dried at room temperature. Individual spikelets (n = 150) were separated from the inflorescence, weighed (mean ± S.E. = 0.29 ± 0.09 mg) and measured (mean ± S.E. maximum diameter = 3.26 ± 0.09 mm). For calculations the assumption was made that seeds instantly reached terminal velocity [see (Grace 1977), data analysed in Matlab version R2007b, details in (Combrinck 2009)]. The average time of first arrival (3.33 s) was used, excluding seeds which fell more slowly due to collisions with the container wall during descent. Four equations were used to model the drag coefficient of the seeds (Clift and Gauvin 1970; Flemmer and Banks 1986; Perry and Chilton 1973; Schiller and Naumann 1933), of which the Flemmer and Banks correlation (Flemmer and Banks 1986) had the smallest difference between the numerical and experimental drag coefficient. As a result, the drag coefficient calculated by this method (Cd = 0.681) was considered most suitable for this application, within the range of values reported by e.g. (Greene and Quesada 2005).
In the CFD simulations the deposition of seeds on A. selago plants was modelled by releasing particles at the air inlet of the computational domain (Fig. 4) with a volume fraction of 0.01% in the dispersed phase (Phase 2). The seeds were assumed to be spherical particles with a diameter of 3 mm. The virtual mass was left per default value of 0.5. The drag coefficient was specified as 0.681.
Results
Airflow patterns
Results are displayed through contour plots of velocity magnitude (using side and top views at various slices through the computational domain), velocity vector plots (to highlight regions of recirculation and reattachment), air particle tracks (to show the path of a particle though the domain), pressure contours on the hemisphere or crescent and velocity profiles extracted at specified points (Figs. 8 and 9). Figure 7 facilitate explanation of the flow results obtained from the CFD analysis. In each image the flow direction is indicated along with the orientation from which it is shown (i.e. top view or front view and x-y-z axis orientation). This convention is used consistently throughout the manuscript.
Vertical velocity profiles were obtained at the midsection of the hemisphere and crescent shape, this extended from the ground level to the top boundary of the domain (Fig. 8). The data from four sample lines were extracted; directly in front, at the apex, directly behind and 0.4 m behind the object. The results are displayed in (Fig. 9); this is used in subsequent paragraphs to describe the behaviour of the airflow.
In the analyses of the hemisphere the airflow decelerated at the leading edge (from Fig. 9 velocities were 1.2 m/s, 4.17 m/s and 6.18 m/s directly in front of the hemisphere at heights of 40 mm, 80 mm and 120 mm respectively, in comparison with free stream velocities of 6.88 m/s, 7.12 m/s and 7.26 m/s at similar heights) of the cushion plant. This created a region of high pressure approximately 21.67 Pa higher than the reference atmospheric pressure; 101,350 Pa. The flow was deflected equally over and around the plant (Figs. 10 and 11). As a result, faster air flow (maximum velocity was 10 mm above the apex of the plant at 9.42 m/s) and lower pressure following Bernoulli’s principal (35.11 Pa lower than the reference pressure) occurred over the top and around the sides of the plant (Fig. 12). This suggests that wind scouring would be greatest on these portions of the cushions’ windward aspect. In the lee of the hemispherical cushion plant airflow velocity was slower in two narrow zones, separated by a broader region of airflow at the midsection of the domain (from Fig. 9 the flow directly behind the plant was 1.75 m/s, 3. 89 m/s and 6.38 m/s at heights of 40 mm, 80 mm and 120 mm respectively, in comparison with free stream velocities of 6.88 m/s, 7.12 m/s and 7.26 m/s). This pattern of three trailing zones of airflow velocity suggests the establishment of a horseshoe vortex in the lee of hemispherical plants (Fig. 13), which regularly sheds vortices (i.e. turbulent eddy features comprising recirculating air) in two distinct areas. Therefore, under average wind speed conditions, two lines of eddies form behind hemispherical cushion plants.
On the windward side of hemispherical cushions airflow closely followed the contours of the plant (e.g. Figure 13). However, in the plant’s lee, airflow separated from the plant’s surface and started to recirculate, forming a wake (Figs. 14 and 15). Airflow only became more regular (and recirculation reduced) well beyond the trailing edge of the plant, with the distance to airflow reattachment varying with distance from the center of the plant (Fig. 16). The distance to airflow reattachment was greater further from the mid-plane of the cushion (i.e. stronger recirculation occurring further from the center of the cushion within the two trailing zones of lower airflow velocity). As a result, recirculation was reduced behind the center of the plant relative to its edges (Fig. 17). Recirculation was strongest close to the ground but weaker higher above the ground surface (Combrinck 2009).
Airflow patterns were similar on the windward sides of the crescent and the hemispherical cushion plants, with a deceleration of air velocity (from Fig. 9 velocities were 3.36 m/s, 5.54 m/s and 6.45 m/s directly in front of the hemisphere at heights of 40 mm, 80 mm and 120 mm respectively, in comparison with free stream velocities of 6.88 m/s, 7.12 m/s and 7.26 m/s at similar heights) in front of the crescent cushion due to the obstruction of the airflow (Fig. 18). This resulted in a zone of high pressure (14.76 Pa higher than the reference atmospheric pressure; 101,350 Pa) along the leading edge of the plant (Fig. 19). On the sides and the top of the plant the airflow accelerated and a distinct area of low pressure was formed (maximum velocity of 9.35 m/s was reached approximately 15 mm above the plant apex at a pressure of 33.6 Pa lower than reference pressure) (Fig. 19). On the leeward side of the plant the airflow showed three areas of differing velocities, with the lowest velocity in the center, bordered by two trailing zones of slightly accelerated airflow (Fig. 20). There is a distinct region of near zero velocity flow directly behind the plant the extends to approximately 90 mm above ground level (Fig. 9). The low velocity flow extends to 120 mm above ground level where the velocity is 3.45 m/s, the free stream in comparison at that height would have been 7.26 m/s. While the two outer zones (faster airflow, Fig. 20) weaken rapidly with increasing height, the central zone of slower mean airflow weakened more slowly. The central zone of airflow therefore represents a single vortex street being shed in the wake of the crescent (Fig. 21), contrasting with the horseshoe vortex observed behind hemispherical cushion plants.
Recirculation patterns in the lee of the crescent cushion were more pronounced, and of a different form, than those behind the hemispherical plant (Figs. 22 and 23). The ground level airflow around the crescent was pulled into the recirculation zone behind the plant, and then directed upwards (Fig. 24). Additionally, in contrast to the hemispherical plants, the distance to airflow reattachment was further from the center of the plant than from the edges of the cushion (Fig. 25) illustrating the persistence of turbulence due to the vortex street in the lee of the plant.
Seed deposition
The flow patterns between the continuous phase (Phase 1, airflow modelled as a gas) and the dispersed phase (Phase 2, seeds modelled as solid particles) is distinctly different (Fig. 26). The recirculation patterns behind the hemispherical and crescent shapes are also less complex for Phase 2 than observed for Phase 1 in the previous section.
An air particle is deflected over and around the sides of the object, guiding it along the curvatures and forming unique patterns such as the horseshoe vortex behind the hemisphere. The entrained solid particle has a greater mass and will be propelled by its momentum in the air stream. An entrained seed approaching an obstacle will behave in a number of ways; it may impact with the object on the windward side or it may be carried upwards or around the sides of the object with the air stream. It was previously explained that seed are likely to deposit on the plant at first impact due to their irregular shape and numerous sharp points. Therefore, seeds that impact on the windward side is not expected to be displaced to other regions of the plant. In the second instance where the seed was lifted over and deflected around the plant the momentum imposed on the seed by the increase of the airflow in this region will likely carry it away from the plant. A portion of the seeds lifted and deflected, that is not displaced by momentum, will be further entrained by the airflow and trapped in the recirculation region. It is expected that these seeds will be deposited on the lower regions of the leeward side of the plant where it is sheltered from the elements thus facilitating germination.
Simulations suggest that most seeds would be deposited in the upper middle region of the windward side of cushion plants (red region in Figs. 27 and 28), suggesting that the friction drag forces of the air on the seeds particles were insufficient to lift a significant portion of the seeds over and around the plant. However, in the regions closer to the ground a portion of the seeds were carried upwards and deposition in the region indicated in red. Accelerated airflow on the sides and the top of the plants increased the momentum and kinetic energy of the seeds, causing them to deflect from the plant in the direction of the resultant residual forces. Therefore, few particles were deposited on the leeward side of the plant through the mechanism of recirculation in the flow field. However, because light particle recirculation extended to a height of 39 mm (Fig. 29) for hemispherical cushion and to 81 mm (Fig. 30) for crescent plants (both plants having similar heights; Table 1), a greater proportion of particles were deposited on the leeward side of the crescent-shaped plants than on the leeward side of the hemispherical plants.
The mathematical simulation of airflow around different shapes of cushion plants provided a clear indication of the potential impacts of wind on these plants. Numerical analyses indicated some similarities in airflow velocity patterns around hemispherical and crescent-shaped plants. For example, air velocity was always fastest on the top and sides of the plants, with the highest air pressure on their windward sides (suggesting the greatest mechanical stress due to airflow on these portions of the plant). Similarly, seed deposition was consistently predicted to be greatest in the middle of the plants’ windward aspects. However, recirculation patterns differed considerably between the two cushion forms, with the periodic formation of eddies along both sides of the hemispherical plants (i.e. shedding of horseshoe vortices), and a more pronounced single vortex loop being shed behind the crescent cushions.
From a computational fluid dynamics perspective, airflow over a hemisphere or crescent on flat ground is challenging, since it necessitates the analysis of flow over two different surfaces (a flat plane and a curved surface) each with a unique surface roughness. Nonetheless, our results are in agreement with studies of flow around similar (but less complex) shapes. For example, in turbulent flow the separation point on a sphere has been reported to occur at 120° (Bakić 2004; Bakić and Perić 2005; Constantinescu and Squires 2004), which closely matches our results. Similarly, both forms of flow recirculation and vortex shedding are well documented (Bakić 2004; Bakić and Perić 2005; Constantinescu and Squires 2004). Additionally, from a biological perspective, the windward deposition of seeds against cushion plants predicted by the CFD model also matches field observations [e.g. (Bullock and Moy 2004), although see (Aguiar and Sala 1994). In this study variability in airflow speed (i.e. gusting) was not considered, but it is known that changes in airflow velocity can affect the presence of a turbulent wake with recirculation (and the extent of the wake) (Bakić and Perić 2005). Similarly, an increase in the turbulence intensity in the free stream airflow causes the position of the separation point to move further downstream (i.e. later separation of the boundary layer), decreases the recirculation zone, and increases mixing processes and particle entrainment (Bakić 2004). As a result, under gusting conditions the extent of the recirculation zone behind cushion plants is likely to be more variable and, on average, probably smaller.
Conceptual model
Based on our results and on published data about A. selago, A. magellanica and sediment accumulation patterns, we propose a conceptual model for the development of crescent-shaped cushion plants. Our model makes two assumptions about differences in the growth of A. selago stems and the survival of A. magellanica grasses in exposed and sheltered conditions. First, we assume that direct wind damage through cooling, drying and scouring is minimal to intact cushion plants [although this is not true once a plant has started to lose its surface integrity; e.g. (Copson 1984). This is a reasonable assumption given that the species’ compact morphology reduces heat and water loss (e.g. xerophytic leaves) and minimizes physical damage to the leaves (Huntley 1971; Schenck 1905; Ternetz 1902). Field observations support this assumption since there is a similar proportion of dead stems (and gaps due to the loss of stems) on the windward and leeward sides of hemispherical cushions [although see also (le Roux et al. 2005; Whinam et al. 2014).
Second, the model assumes that A. magellanica seedlings suffer higher mortality when exposed to strong winds than when they grow in more sheltered microsites. Indeed, the fine-scale distribution of mature A. magellanica on A. selago supports this assumption, with much higher cover of larger individuals of the grass on the cushion’s leeward side (see also (Ashton and Gill 1965; le Roux et al. 2005)), despite A. magellanica seedlings occurring on all aspects of cushion plants (PCLR, pers. obs.). This suggests that despite potentially far greater seed deposition on the exposed portions of the cushion plant and the ability for A. magellanica seeds to germinate on any part of a cushion, grasses are much more likely to survive in the lee of the hemispherical cushion where airflow velocity is much lower than the windward side. The distribution of the grass across topographic gradients also supports this assumption, with A. magellanica exhibiting higher densities in more wind-sheltered positions than in wind-exposed locations ((le Roux and McGeoch 2010), see also (Pammenter et al. 1986)).
We summarize the process of crescent-shape cushion development into three stages, considering the deposition of seeds (irregularly shaped, with low mass and density) and sediment (smoother and denser than seeds, always being entrained from the soil surface) as two separate processes (Fig. 31):
-
1)
Negligible air recirculation. Airflow around a small, hemispherical cushion plant is relatively slow (due to the plant’s low height) and there is little flow recirculation in its lee (and therefore negligible deposition of sediment). A. magellanica seeds are mainly deposited on the windward side of the cushion. While these seeds may germinate, they are unable to establish on the windward aspect of the cushion due to the strong scouring, cooling and drying effects of the direct wind.
-
2)
Sediment deposition and grass establishment. As the cushion grows taller, airflow recirculation intensifies, leading to sediment deposition on the lee of the cushion. With stronger recirculation some A. magellanica seeds are also deposited on the lee of the cushion plant (although the majority are still deposited on the windward side of the plant) (see also (Aguiar and Sala 1994)). The seeds deposited on the cushion’s leeward aspect are more likely to establish due to the lower air velocities on that side of the plant. Additionally, the fine sediment that has accumulated in the lee of the plant may enhance seed trapping and survival (Chambers et al. 1991). As a result, A. magellanica biomass increases on the lee of the cushion. This causes the development of a positive feedback loop, with greater grass volume slowing airflow in the lee of the cushion even further, leading to increased deposition of sediment and seeds [(Pye and Tsoar 1990; Ravi et al. 2008), see also (Cooke and Warren 1973)].
-
3)
Differential cushion growth. Due to shading (from grass growth) and burial (from sediment deposition; which also reduces incoming light) the cushion stems on the leeward side suffer disproportionately higher mortality [see also (Ashton and Gill 1965; Hauri and Schröter 1914) for other cushion plant species, (le Roux et al. 2005; Schöb et al. 2014). However, stem growth on the other sides of the cushion is unaffected, and as a consequence, the cushion develops a crescent shape. The change to the plant’s shape in turn affects the plants aerodynamic characteristics, further enhancing air recirculation, leading to greater sediment and seed accumulation in the lee of the cushion. The intensification of recirculation on the sheltered side of the cushion plant also increases the wind protection for A. magellanica, favouring its continued growth and maintaining the positive feedback to crescent-shape development.
In areas lacking A. magellanica (or other epiphytes) the same stages of cushion shape development are likely to occur, because sediment deposition alone can still cause differential stem mortality on the wind- and leeward sides of A. selago cushions. Similarly, in the absence of wind-borne sediments, greater A. magellanica growth on the leeward sides of cushion plants may also be likely to be sufficient by itself to cause the development of crescent-shaped cushions. However, in the absence of either A. magellanica or sufficient wind-blown soil, the development of the crescent-shape is less likely to occur because there will be no positive feedback between grass growth and sediment trapping. As a result, our model may be applicable to the development of cushion plant shape in many windy environments, provided that adequate wind-borne sediment or seeds are present.
Our conceptual model is most appropriately applied to areas with sparse populations of A. selago with minimal other features that can act as wind disturbances (e.g. grey lava regions where the substrate is relatively flat). In black lava regions the substrate is more uneven and the ruggedness of the lava itself shapes the cushions (i.e. cushion plants, especially smaller individuals, grow between and around the taller shards of lava). Additionally, in dense or aggregated A. selago populations there may also be downstream wind flow impacts on cushion plants from upstream individuals too. However, A. selago plants generally do not have aggregate distributions locally [particularly for plants with diameters <15 cm; (Nyakatya 2006)], and there is typically a relatively even spacing between cushions (this likely reflects that the species root system extends far beyond individual cushion’s canopies (Frenot et al. 1998)). Therefore, while there is potential for upstream plants to affect the wind flow experienced by downstream plants, where the plants are uniformly or randomly spaced, there is some distance so that there will be some stabilization of flow between individuals. Nearest neighbour data for A. selago [e.g. (le Roux and McGeoch 2004)] indicates that the distance to plants’ nearest neighbours average 0.66–0.90 m (data from three different sites on Marion Island), and therefore, based on our CFD results (see e.g. Figure 9f which illustrates velocity profiles 0.4 m behind cushion plant), the wind conditions experienced by A. selago plants growing at typical densities will be minimally affected by upstream disturbances by other individuals.
Other mechanisms causing the development of crescent-shaped A. selago cushions have also been proposed. For example, it has been suggested that crescent-shaped cushions may develop due to leeward turf exfoliation by needle ice (Boelhouwers et al. 2003). This hypothesis posits that needle ice is disproportionately common in exposed soil on the leeward side of cushions (because air movement can inhibit needle ice formation), and therefore effects greater damage to the margin of the plant that is most sheltered from the wind. Upon damage to cushion stems (and the resultant loss of plant compactness) the organic soil underlying the plant is vulnerable to further needle ice formation and additional damage to stems. This hypothesis may be complementary with our model, because a greater proportion of fine sediments and enhanced moisture conditions (due to lower wind-driven evaporation) in the lee of the cushion is likely to favour needle-ice formation [(Pérez 1987), see also e.g. (Holness 2004)]. Indeed, the low plant cover observed in the exposed soil in the center of some crescent-shaped cushions may reflect regular needle-ice formation and active frost-heave processes [see e.g. (Boelhouwers et al. 2003)]. However, it seems unlikely that turf exfoliation alone would be able to initiate the leeward degradation of A. selago cushions [following e.g. (Butler et al. 2004; Pérez 1992)], given the compact nature of the cushions and their buffering impact on cushion and soil temperatures (Arroyo et al. 2003; Chown and Crafford 1992; Nyakatya and McGeoch 2007). Additionally, needle ice is very rarely observed on intact cushion plants (Cavieres et al. 2007; Pérez 1987). In coastal areas, greater deposition of salt-spray on the windward side of cushion plants could also drive the development of the crescent shape, as suggested by (Huntley 1971), although salt-deposition alone seems unlikely to drive asymmetrical growth or stem mortality given the abundance of A. selago in the coastal areas of Marion Island (Gremmen 1981). Therefore, while other mechanisms could also play a role in the development of crescent-shaped A. selago cushions, we suggest that wind-driven sediment and seed deposition initiates the change in plant shape. These mechanisms could also be the cause of other patterns of directionality observed in A. selago on Marion Island. For example, because A. magellanica cover is highest on the sheltered leeward side of the cushion plants, it may indirectly drive higher densities of arthropods on the sheltered sides of A. selago cushions [the grass is thought to provide an extra food resource to the arthropods; (Hugo et al. 2004).
Discussion
Our “leeward-deposition” model of cushion plant shape development generates some testable predictions. For example, on substrates with more turbulent airflow there should be less sediment accumulation on the leeward side of cushion plants. This results from a negative relationship between flow turbulence and the extent of recirculation in the lee of a sphere (Bakić 2004). In consequence, a testable prediction from our model is that cushions will have less pronounced crescent shapes in habitats where airflow is more turbulent. Considering, for example, Marion Island, we would therefore predict less pronounced development of crescent-shapes in plants in fellfield areas with higher surface roughness (e.g. boulders and ridges or, more generally, post-glacial lava flows; increasing turbulence in the airflow) than in areas of lower surface roughness (i.e. relatively smooth soil surface; pre-glacial lava flows where glacial scouring has smoothed the landscape). Similarly, because substrates differ in their probability of entrainment by airflow (based on differences in particle density and size), sediment accumulation rates behind cushions are likely to vary between substrate types. As a result, our model predicts more pronounced crescent shapes for cushions growing in areas with small particles of low density (e.g. ash fields) than on substrates composed of larger, denser particles (e.g. scoria) provided the airflow is not too turbulent (i.e. subject to first prediction).
At the scale of individual plants, the model predicts that the mortality of leeward stems will expose humus that had developed in that portion of the cushion plant. Therefore, we expect the soil in the hollow of crescent-shaped cushions to have higher organic matter content than the surrounding mineral soils (at least in the upper surface layers). Furthermore, the sizes of sediment particles present in the hollow of crescent-shaped cushions should represent a subset of the available particles present in the surrounding soil, with an over-representation of particles that are light enough to be entrained by the prevailing winds. This prediction provides a strong test to distinguish between our model and the leeward turf exfoliation model (Boelhouwers et al. 2003), because needle ice-driven turf exfoliation is likely to favour the movement of fine particles away from the crescent by loosening the soil surface [although this may only be pronounced during times of soil dryness; (Pérez 1992), leaving a heavier subset of particles present in the surrounding soil. Finally, the model also predicts that if cushions that are exposed to the prevailing wind are subsequently experimentally sheltered, the A. magellanica seeds which were deposited on the windward side of the cushion will have higher establishment success. Furthermore, after wind sheltering is imposed, crescent-shape development is expected to slow considerably relative to plants still exposed to the prevailing wind [although to verify this would require long-term monitoring due to the slow growth of A. selago; (le Roux and McGeoch 2004).
Conclusion
Cushion plants are an important vegetation component of many windy environments (Aubert et al. 2014). Due their slow growth rates and constrained growth forms, cushion plants may be sensitive to the direct (e.g. changes in temperature) and indirect (e.g. altered biotic interactions) effects of climate change [e.g. (le Roux et al. 2005). Our results suggest that cushion plants may also be sensitive to changes in wind patterns [see, e.g., (Bergstrom et al. 2015). While weakening winds are likely to favour the growth of competitors, rapid changes in wind conditions, as have occurred in the past at high latitudes in the southern hemisphere (Buizert et al. 2018), could affect cushion survival. If the prevailing wind direction changes after a cushion has developed directionality (i.e. its crescent-shape), cushions will experience increased stem mortality in different areas (because different portions of the plants will now comprise its wind- and leeward sides). For example, on Marion Island the decrease in wind speed variability over the last half century (le Roux and McGeoch 2008) may have strengthened the development of the crescent-shape in A. selago cushions. By contrast, the shift in mean wind direction on the island (Rouault et al. 2005) could have caused a change in the directionality of young cushions. Indeed, if the directionality of cushion plant growth is relatively stable after the development of the crescent shape, the directionality of different cohorts of crescent-shaped cushions may be a guide to past wind patterns.
References
Achenbach E (1972) Experiments on the flow past spheres at very high Reynolds numbers. J Fluid Mech 54:565–575. https://doi.org/10.1017/S0022112072000874
Achenbach E (1974) Vortex shedding from spheres. J Fluid Mech 62:209–221. https://doi.org/10.1017/S0022112074000644
Aguiar MR, Sala OE (1994) Competition, facilitation, seed distribution and the origin of patches in a Patagonian steppe. Oikos 70:26–34
Anderson JD Jr (2015) Introduction to flight, 8th edn. McGraw Hill, USA
Arroyo MTK, Cavieres LA, Peñaloza A, Arroyo-Kalin MA (2003) Positive associations between the cushion plant Azorella monantha (Apiaceae) and alpine plant species in the Chilean Patagonian Andes. Plant Ecol 169:121–129. https://doi.org/10.1023/A:1026281405115
Ashton DH, Gill AM (1965) Pattern and process in a Macquarie Island feldmark. Proc R Soc Vic 79:235–245
Aubert S, Boucher F, Lavergne S, Renaud J, Choler P (2014) 1914–2014: a revised worldwide catalogue of cushion plants 100 years after Hauri and Schröter. Alp Bot 124:59–70. https://doi.org/10.1007/s00035-014-0127-x
Badano EI, Cavieres LA (2006) Impacts of ecosystem engineers on community attributes: effects of cushion plants at different elevations of the Chilean Andes. Divers Distrib 12:388–396. https://doi.org/10.1111/j.1366-9516.2006.00248.x
Badano E, Marquet P (2008) Ecosystem engineering affects ecosystem functioning in high-Andean landscapes. Oecologia 155:821–829. https://doi.org/10.1007/s00442-007-0953-2
Badano EI, Villarroel E, Bustamante RO, Marquet PA, Cavieres LA (2007) Ecosystem engineering facilitates invasions by exotic plants in high-Andean ecosystems. J Ecol 95:682–688. https://doi.org/10.1111/j.1365-2745.2007.01262.x
Bakić V (2004) Experimental investigation of a flow around a sphere. Therm Sci 8:63–81
Bakić V, Perić M (2005) Visualization of flow around sphere for Reynolds number between 22 000 and 400 000. Thermophys Aeromechanics 12:307–314
Baumeister D, Callaway RM (2006) Facilitation by Pinus flexilis during succession: a hierarchy of mechanisms benefits other plant species. Ecology 87:1816–1830. https://doi.org/10.1890/0012-9658(2006)87[1816:FBPFDS]2.0.CO;2
Berg J, Mann J, Bechmann A, Courtney MS, Jørgensen HE (2011) The Bolund experiment, part I: flow over a steep. Three-Dimensional Hill Bound-Layer Meteorol 141:219–243. https://doi.org/10.1007/s10546-011-9636-y
Bergstrom DM, Bricher PK, Raymond B, Terauds A, Doley D, McGeoch MA, Whinam J, Glen M, Yuan ZQ, Kiefer K, Shaw JD, Bramely-Alves J, Rudman T, Mohammed C, Lucieer A, Visoiu M, van Vuuren BJ, Ball MC (2015) Rapid collapse of a sub-Antarctic alpine ecosystem: the role of climate and pathogens. J Appl Ecol 52:774–783. https://doi.org/10.1111/1365-2664.12436
Beyers M, Waechter B (2008) Modeling transient snowdrift development around complex three-dimensional structures. J Wind Eng Ind Aerodyn 96:1603–1615. https://doi.org/10.1016/j.jweia.2008.02.032
Boelhouwers J, Holness S, Sumner P (2003) The maritime sub-Antarctic: a distinct periglacial environment. Geomorphology 52:39–55. https://doi.org/10.1016/S0169-555X(02)00247-7
Breuer M (1998) Numerical and modeling influences on large eddy simulations for the flow past a circular cylinder. Int. J. Heat Fluid Flow 19:512–521. https://doi.org/10.1016/S0142-727X(98)10015-2
Breuer M (2000) A challenging test case for large eddy simulation: high Reynolds number circular cylinder flow. Int. J. Heat Fluid Flow 21:648–654. https://doi.org/10.1016/S0142-727X(00)00056-4
Buizert C, Sigl M, Severi M, Markle BR, Wettstein JJ, McConnell JR, Pedro JB, Sodemann H, Goto-Azuma K, Kawamura K, Fujita S, Motoyama H, Hirabayashi M, Uemura R, Stenni B, Parrenin F, He F, Fudge TJ, Steig EJ (2018) Abrupt ice-age shifts in southern westerly winds and Antarctic climate forced from the north. Nature 563:681–685. https://doi.org/10.1038/s41586-018-0727-5
Bullock JA, Moy IL (2004) Plants as seed traps: inter-specific interference with dispersal. Acta Oecol 25:35–41. https://doi.org/10.1016/j.actao.2003.10.005
Butler DR, Malanson GP, Resler LM (2004) Turf-banked terrace treads and risers, turf exfoliation and possible relationships with advancing treeline. Catena 58:259–274. https://doi.org/10.1016/j.catena.2004.05.003
Cao Y, Tamura T (2020) Large-eddy simulation study of Reynolds number effects on the flow around a wall-mounted hemisphere in a boundary layer. Phys Fluids 32:025109
Cavieres LA, Badano EI, Sierra-Almeida A, Molina-Montenegro MA (2007) Microclimatic modifications of cushion plants and their consequences for seedling survival of native and non-native herbaceous species in the high Andes of Central Chile. Arct Antarct Alp Res 39:229–236. https://doi.org/10.1657/1523-0430(2007)39[229:MMOCPA]2.0.CO;2
CD-Adapco Group, 2008. StarCD methodology manual v4.06. CD-Adapco group (http://www.cd-adapco.com/), London, UK
Cerfonteyn ME, le Roux PC, Van Vuuren BJ, Born C (2011) Cryptic spatial aggregation of the cushion plant Azorella selago (Apiaceae) revealed by a multilocus molecular approach suggests frequent intraspecific facilitation under sub-Antarctic conditions. Am J Bot 98:909–914. https://doi.org/10.3732/ajb.1000460
Chambers JC, Macmahon JA, Haefner JH (1991) Seed entrapment in alpine ecosystems - effects of soil particle-size and diaspore morphology. Ecology 72:1668–1677
Chown SL, Crafford JE (1992) Microhabitat temperatures at Marion Island (46o54’ S 37o45’ E). South Afr J Antarct Res 22:51–58
Chown SL, Froneman PW (2008) The Prince Edward islands: Land-Sea interactions in a changing ecosystem. African SunMedia, Stellenbosch
Clift R, Gauvin WH (1970) The motion of particles in turbulent gas streams. Proc Chemeca 70(1):14–28
Combrinck ML (2009) A computational fluid dynamic analysis of airflow over a keystone plant species, Azorella selago on sub-Antarctic Marion Island (MScEng thesis). Stellenbosch University, Stellenbosch
Constantinescu G, Squires K (2004) Numerical investigations of flow over a sphere in the subcritical and supercritical regimes. Phys Fluids 16:1449–1466. https://doi.org/10.1063/1.1688325
Cooke RU, Warren A (1973) Geomorphology in deserts. University of California Press, Berkeley
Copson GR (1984) An annotated atlas of the vascular flora of Macquarie Island, ANARE research notes 18. Australian National Antarctic Research Expeditions. Kingston, Tasmania
Courtin GM, Bliss LC (1971) A hydrostatic lysimeter to measure evapotranspiration under remote field conditions. Arct Alp Res 3:81–89
C.T. Crowe, Elger, D.F., Roberson, J.A., 2001. Engineering fluid mechanics, 7th ed. Wiley and Sons
de Langre E (2008) Effects of wind on plants. Annu Rev Fluid Mech 40:141–168. https://doi.org/10.1146/annurev.fluid.40.111406.102135
Dehbi A, Martin S (2011) CFD simulation of particle deposition on an array of spheres using an Euler/Lagrange approach. Nucl Eng Des 241:3121–3129. https://doi.org/10.1016/j.nucengdes.2011.05.031
Durán O, Herrmann HJ (2006) Vegetation against dune mobility. Phys Rev Lett 97:188001(4). https://doi.org/10.1103/PhysRevLett.97.188001
Ennos AR (1997) Wind as an ecological factor. Trends Ecol Evol 12:108–111. https://doi.org/10.1016/S0169-5347(96)10066-5
Fitzgerald NB, Kirkpatrick JB (2017) Wind distortion in alpine and subantarctic plants is constant among life forms but does not necessarily reflect prevailing wind direction. Arct Antarct Alp Res 49:521–535. https://doi.org/10.1657/aaar0016-054
Flemmer RLC, Banks CL (1986) On the drag coefficient of a sphere. Powder Technol 48:217–221
Frenot Y, Gloaguen J-C, Picot G, Bougère J, Benjamin D (1993) Azorella selago hook. Used to estimate glacier fluctuations and climatic history in the Kerguelen Islands over the last two centuries. Oecologia 95:140–144. https://doi.org/10.1007/BF00649517
Frenot Y, Gloaguen J-C, Cannavacciuolo M, Bellido A (1998) Primary succession on glacier forelands in the sub-Antarctic Kerguelen Islands. J Veg Sci 9:75–84
Garratt J (1994) Review: the atmospheric boundary layer. Earth-Sci Rev 37:89–134. https://doi.org/10.1016/0012-8252(94)90026-4
Gauslaa Y (1984) Heat resistance and energy budget in different Scandinavian plants. Holarct Ecol 7:5–78. https://doi.org/10.1111/j.1600-0587.1984.tb01098.x
Grace J (1977) Plant response to wind. Academic Press, London
Greeley R, Iversen JD (1985) Wind as a geological process on earth, Mars, Venus and titan, Cambridge planetary science series. Cambridge University Press, Cambridge
Greene DF, Quesada M (2005) Seed size, dispersal, and aerodynamic constraints within the Bombacaceae. Am J Bot 92:998–1005. https://doi.org/10.3732/ajb.92.6.998
Gremmen NJM (1981) The vegetation of the sub-Antarctic islands, Marion and Prince Edward. Junk, The Hague
Hager J, Faggi AM (1990) Observaciones sobre distribución y microclima de cojines enanos de la Isla de Creta y del noroeste de la Patagonia. Parodiana 6:109–127
Hauri H (1912) Anabasis aretioïdes Moq. and Coss., eine Polsterpflanze der algerischen Sahara: Mit einem Anhang, die Kenntnis der angiospermen Polsterpflanzen überhaupt betreffend. Beih Zum Bot Cent 28:323–421
Hauri H, Schröter C (1914) Versuch einer Übersicht der siphonogamen Polsterpflanzen. Bot Jahrb Für Syst Pflanzengesch Pflanzengeogr. 50(Suppl):618–656
Haussmann NS, McGeoch MA, Boelhouwers JC (2009) Interactions between a cushion plant (Azorella selago) and surface sediment transport on sub-Antarctic Marion Island. Geomorphology 107:139–148. https://doi.org/10.1016/j.geomorph.2008.12.002
Hoffman J (2006) Simulation of turbulent flow past bluff bodies on coarse meshes using general Galerkin methods: drag crisis and turbulent Euler solutions. Comput Mech 38:390–402. https://doi.org/10.1007/s00466-006-0053-x
Holness SD (2004) Sediment movement rates and processes on cinder cones in the maritime Subantarctic (Marion Island). Earth Surf Process Landf 29:91–103. https://doi.org/10.1002/esp.1015
Houghton EL, Carpenter PW (1993) Aerodynamics for engineering students, 4th, edn. edn. Arnold, London
Hugo EA, McGeoch MA, Marshall DJ, Chown SL (2004) Fine scale variation in microarthropod communities inhabiting the keystone species Azorella selago on Marion Island. Polar Biol 27:466–473. https://doi.org/10.1007/s00300-004-0614-4
Huntley BJ (1970) Altitudinal distribution and phenology of Marion Island vascular plants. Tydskr. Vir Natuurwetenskap 10:255–262
Huntley BJ (1971) Vegetation. In: van Zinderen Bakker EM, Winterbottom JM, Dyer RA (eds) Marion and Prince Edward Islands: Report on the South African Biological and Geological Expeditions, 1965–1966. A.A. Balkema, Cape Town, pp 98–160
Huntley BJ (1972) Notes on the ecology of Azorella selago Hook. f. J South Afr Bot 38:103–113
Kim J-J, Baik J-J (2003) Effects of inflow turbulence intensity on flow and pollutant dispersion in an urban street canyon. J Wind Eng Ind Aerodyn 91:309–329. https://doi.org/10.1016/S0167-6105(02)00395-1
Körner C (2003) Alpine plant life: functional plant ecology of high mountain ecosystems, 2nd, ed. edn. Springer-Verlag, Heidelberg
Kullman L (2005) Wind-conditioned 20th century decline of birch treeline vegetation in the Swedish Scandes. Arctic 58:286–294
le Roux, P.C., 2008. Climate change and vascular plant species interactions on sub-Antarctic Marion Island (PhD thesis). Stellenbosch University, Stellenbosch
le Roux PC, McGeoch MA (2004) The use of size as an estimator of age in the subantarctic cushion plant, Azorella selago (Apiaceae). Arct Antarct Alp Res 36:509–517. https://doi.org/10.1657/1523-0430(2004)36[509:TUOSAA]2.0.CO;2
le Roux PC, McGeoch MA (2008) Changes in climate extremes, variability and signature on sub-Antarctic Marion Island. Clim Chang 86:309–329. https://doi.org/10.1007/s10584-007-9259-y
le Roux PC, McGeoch MA (2010) Interaction intensity and importance along two stress gradients: adding shape to the stress-gradient hypothesis. Oecologia 162:733–745. https://doi.org/10.1007/s00442-009-1484-9
le Roux PC, McGeoch MA, Nyakatya MJ, Chown SL (2005) Effects of a short-term climate change experiment on a sub-Antarctic keystone plant species. Glob Change Biol 11:1628–1639. https://doi.org/10.1111/j.1365-2486.2005.001022.x
Lynch AJJ, Kirkpatrick JB (1995) Pattern and process in alpine vegetation and landforms at hill one, southern range. Tasmania Aust J Bot 43:537–554. https://doi.org/10.1071/BT9950537
Lyotard N, Shew WL, Bocquet L, Pinton J-F (2007) Polymer and surface roughness effects on the drag crisis for falling spheres. Eur Phys J B 60:469–476. https://doi.org/10.1140/epjb/e2008-00018-0
Meas, M.R., Bruwer, J.F., Harms, T.M., Combrinck, M.L., n.d. Simulating turbulent air flow past a hemispherical body. RD J South Afr Inst Mech Eng 6
Norberg C (1987) Effects of Reynolds number and low-intensity free-stream turbulence on the flow around a circular cylinder. Publication number 87/2. Department of Applied Thermodynamics and Fluid Mechanics, Chalmer University of Technology, Gothenburg, Sweden
Nyakatya, M.J., 2006. Patterns of variability in Azorella selago hook. (Apiaceae) on sub-Antarctic Marion Island: climate change implications. University of Stellenbosch
Nyakatya M, McGeoch MA (2007) The microclimate associated with a keystone plant species (Azorella selago hook. (Apiaceae)) on Marion Island. Polar Biol 31:139–151
Pammenter NW, Drennan PM, Smith VR (1986) Physiological and anatomical aspects of photosynthesis of two Agrostis species at a sub-Antarctic island. New Phytol 102:143–160. https://doi.org/10.1111/j.1469-8137.1986.tb00806.x
Pérez FL (1987) Needle-ice activity and the distribution of stem-rosette species in a Venezuelan páramo. Arct Alp Res 19:135–153
Pérez FL (1992) Processes of turf exfoliation (Rasenabschalung) in the high Venezuelan Andes. Z Für Geomorphol 36:81–106
Perry RH, Chilton CH (1973) Chemical engineers’ handbook, 5th, edn. edn. McGraw-Hill Kogakusha, Tokyo
Petersen EL, Mortensen NG, Landberg L, Højstrup J, Frank HP (1998) Wind power meteorology. Part I: climate and turbulence. Wind Energy 1:2–22. https://doi.org/10.1002/(SICI)1099-1824(199809)1:1<2::AID-WE15>3.0.CO;2-Y
Phiri EE, McGeoch MA, Chown SL (2009) Spatial variation in structural damage to a keystone plant species in the sub-Antarctic: interactions between Azorella selago and invasive house mice. Antarct Sci 21:189–196. https://doi.org/10.1017/S0954102008001569
Pye K, Tsoar H (1990) Aeolian sand and sand dunes. Unwin Hyman, London
Pyšek P, Liška J (1991) Colonization of Sibbaldia tetrandra cushions on alpine scree in the Pamiro-Alai Mountains, Central Asia. Arct Alp Res 23:263–272
Raithby GD, Eckert ERG (1968) The effect of support position and turbulence intensity on the flow near the surface of a sphere. Wärme- Stoffübertrag 1:87–94. https://doi.org/10.1007/BF00750790
Ralph CP (1978) Observations on Azorella compacta (Umbelliferae), a tropical Andean cushion plant. Biotropica 10:62–67
Rauh W (1939) Über polsterförmigen Wuchs, ein Beitrag zur Kenntnis der Wuchsformen der höheren Pflanzen. Nova Acta Leopoldina 7:267–508
Ravi S, D’Odorico P, Wang L, Collins S (2008) Form and function of grass ring patterns in arid grasslands: the role of abiotic controls. Oecologia 158:545–555. https://doi.org/10.1007/s00442-008-1164-1
Rouault M, Mélice J-L, Reason CJC, Lutjeharms JRE (2005) Climate variability at Marion Island, Southern Ocean, since 1960. J Geophys Res-Oceans 110:C05007.1–C05007.9. https://doi.org/10.1029/2004JC002492
Ruffier-Lanche R (1964) Les plantes en coussinet. Bull Société Amat Jard Alp 4:3–13
Ruthsatz B (1978) Las plantas en cojín de los semi-desiertos andinos del Noroeste Argentino. Darwiniana 21:491–539
Savory E, Toy N (1985) The flow regime in the turbulent near wake of a hemisphere. Exp Fluids 4:181–188. https://doi.org/10.1007/BF00717812
Schenck H (1905) Vergleichende Darstellung der Pflanzengeographie des Subantarktischen Inseln : insbesondere über Flora und Vegetation von Kerguelen. In: Chun C (ed) Deutsche Tiefsee-Expedition 1898–1899, Band II. Teil I. Gustav Fischer, Jena, pp 1–178
Schiller L, Naumann Z (1933) A drag coefficient correlation. Z Vereines Dtsch Ingenieure 77:318–320
H. Schlichting, 1968. Boundary-layer theory, 3rd ed. McGraw-Hill
Schöb C, Michalet R, Cavieres LA, Pugnaire FI, Brooker RW, Butterfield BJ, Cook BJ, Kikvidze Z, Lortie CJ, Xiao S, Al Hayek P, Anthelme F, Cranston BH, García M-C, Le Bagousse-Pinguet Y, Reid AM, le Roux PC, Lingua E, Nyakatya MJ, Touzard B, Zhao L, Callaway RM (2014) A global analysis of bi-directional interactions in alpine plant communities shows facilitators experiencing strong reciprocal fitness costs. New Phytol 202:95–105
Schulze BR (1971) The climate of Marion Island. In: van Zinderen Bakker EM, Winterbottom JM, Dyer RA (eds) Marion and Prince Edward Islands: Report on the South African Biological and Geological Expeditions, 1965–1966. A.A. Balkema, Cape Town, pp 16–31
Selkirk-Bell JM, Selkirk PM (2013) Vegetation-banked terraces on Subantarctic Macquarie Island: a reappraisal. Arct Antarct Alp Res 45:261–274. https://doi.org/10.1657/1938-4246-45.2.261
Smith VR (2002) Climate change in the sub-Antarctic: an illustration from Marion Island. Clim Chang 52:345–357. https://doi.org/10.1023/A:1013718617277
Smith VR, Steenkamp M, Gremmen NJM (2001) Terrestrial habitats on sub-Antarctic Marion Island: their vegetation, edaphic attributes, distribution and response to climate change. South Afr J Bot 67:641–654
Spomer GG (1964) Physiological ecology studies of alpine cushion plants. Physiol Plant 17:717–724
Tavakol MM, Yaghoubi M, Masoudi Motlagh M (2010) Air flow aerodynamic on a wall-mounted hemisphere for various turbulent boundary layers. Exp Thermal Fluid Sci 34:538–553. https://doi.org/10.1016/j.expthermflusci.2009.11.007
Tavakol MM, Abouali O, Yaghoubi M (2015) Large eddy simulation of turbulent flow around a wall mounted hemisphere. Appl Math Model 39:3596–3618. https://doi.org/10.1016/j.apm.2014.11.055
Taylor BW (1955a) Terrace formation on Macquarie Island. J Ecol 43:133–137
Taylor BW (1955b) The flora, vegetation and soils of Macquarie Island, Australian national Antarctic research expeditions reports: series B, volume II. Antarctic division, Department of External Affairs, Melbourne
Ternetz C (1902) Morphologie und anatomie de Azorella selago hook. F. Bot Ztg 60:1–19
Tiwari SS, Pal E, Bale S, Minocha N, Patwardhan AW, Nandakumar K, Joshi JB (2020) Flow past a single stationary sphere, 1. Exp Numerical Techniques Powder Technol 365:115–148. https://doi.org/10.1016/j.powtec.2019.01.037
van Gardingen PR, Grace J, Jeffree CE (1991) Abrasive damage by wind to the needle surfaces of Picea sitchensis (bong.) Carr. And Pinus sylvestris L. Plant Cell Environ 14:185–193. https://doi.org/10.1111/j.1365-3040.1991.tb01335.x
Versteeg H, Malalasekera W (2007) An introduction to computational fluid dynamics: the finite volume method, 2nd, edition. edn. Pearson Prentice Hall, United Kingdom
Whinam J, Abdul-Rahman JA, Visoiu M, di Folco MBF, Kirkpatrick JB (2014) Spatial and temporal variation in damage and dieback in a threatened subantarctic cushion species. Aust J Bot 62:10–21. https://doi.org/10.1071/bt13207
White FM (2016) Fluid mechanics, 8th edn. McGraw Hill, USA
Whitehead FH (1951) Ecology of the Altipiano of Monte Maiella. Italy J Ecol 39:330–355
Wilson JW (1959) Notes on wind and its effects in Arctic-Alpine vegetation. J Ecol 47:415. https://doi.org/10.2307/2257374
Yang W, Quan Y, Jin X, Tamura Y, Gu M (2008) Influences of equilibrium atmosphere boundary layer and turbulence parameter on wind loads of low-rise buildings. J Wind Eng Ind Aerodyn 96:2080–2092. https://doi.org/10.1016/j.jweia.2008.02.014
Zhang QH, Miao TD (2003) Aeolian sand ripples around plants. Phys Rev E 67:051304(4). https://doi.org/10.1103/PhysRevE.67.051304
Zotz G, Schweikert A, Jetz W, Westerman H (2000) Water relations and carbon gain are closely related to cushion size in the moss Grimmia pulvinata. New Phytol 148:59–67. https://doi.org/10.1046/j.1469-8137.2000.00745.x
Acknowledgements
The South African National Research Foundation (NRF) and the South African National Antarctic Program (SANAP; unique grant number 110726) are thanked for their financial and logistic support. PCLR was additionally supported by the DST-NRF Center of Excellence for Invasion Biology. We thank C. Hui, J. Lee and E. Phiri for thoughtful comment on earlier drafts of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Jeffrey Walck
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Combrinck, M.L., Harms, T.M., McGeoch, M.A. et al. Wind and seed: a conceptual model of shape-formation in the cushion plant Azorella Selago. Plant Soil 455, 339–366 (2020). https://doi.org/10.1007/s11104-020-04665-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11104-020-04665-3