Introduction

In the UK, the most common type of peatland is blanket bog, which covers approximately 15,700 km2 (Baird et al. 2009). Around a quarter of these peatlands have been drained by ditches (Joint Nature Conservation Committee 2011), but efforts are now being made to restore them by ditch blocking (Parry et al. 2014). In England alone, at least 6% of blanket peatland ditches have recently been dammed or infilled (Joint Nature Conservation Committee 2011). Ditch-drained peatlands are often net emitters of carbon dioxide (CO2) (Baird et al. 2009; Lindsay 2010; Reed et al. 2013) and it is commonly assumed that ditch blocking will help re-start a peatland’s carbon-sink function, but there is also concern that such benefits from blocking will be off-set, in part, by a post-blocking spike in methane (CH4) emissions (Joosten et al. 2006; Baird et al. 2009). There is also debate over how long such CH4 increases might last.

Intact peatlands are usually net carbon (C) sinks; for a peatland to form, this must have been true during much of its developmental history. Peatland drainage may change the C balance of a peatland in a number of ways. With lower (deeper) water tables, a larger proportion of the peat profile will be exposed to oxic conditions and higher rates of decomposition. If, after ditch construction, depth-integrated peat decomposition exceeds net C uptake via photosynthesis, the peatland will become a source of atmospheric C. However, changes in water-table position may also lead to changes in the species composition and vigour of the peatland vegetation, which in turn will affect photosynthetic uptake of C. In a study of a raised bog in SW Scotland, for example, Belyea and Clymo (2001) found that net annual litter production showed a quartic (hump-backed) relationship with water-table depth, with highest rates of litter production recorded for intermediate water-table depths (20–30 cm below the surface) and lowest rates for shallow (0–5 cm) and deep (> 45 cm) water tables. This relationship suggests that the response of overall peat C balance to drainage could be non-linear, and that minor drainage might not lead to a transition from a C sink to a C source in all cases. This also creates some uncertainty regarding the outcome of ditch blocking, which, as noted above, is being widely implemented in expectation of restoring the C balance of drained blanket bogs (Bain et al. 2011; Parry et al. 2014).

There are two components to consider when investigating the effects of ditch blocking on the greenhouse gas (GHG) balance of peatlands: (a) the inter- or between- ditch areas and (b) the dammed or blocked ditches themselves. In this paper we deal with the latter. To our knowledge there are only two studies that consider the GHG balance within blocked ditches in blanket bogs: Green et al. (2014) and Cooper et al. (2014). Green et al. (2014) undertook a series of laboratory mesocosm experiments to investigate how different methods of blocking affect GHG uptake and release from drainage ditches. They found that CH4 emissions and GHG balance expressed in terms of CO2 equivalents – CO2-e – were affected by the method of (laboratory-simulated) ditch blocking. Mesocosms representing dammed ditches with no infill or that had been colonised by a mat of Sphagnum mosses had a lower CO2 efflux than (a) mesocosms representing ditches that had been dammed and partially infilled with peat, and (b) mesocosms simulating ditches that had been blocked with bales of heather (cut and compacted Calluna vulgaris (L.) Hull.). However, as noted in Green et al. (2014), these outcomes need confirming at the field scale; there is a limit to what mesocosm studies can reveal about field conditions. Cooper et al. (2014) showed that within-ditch CH4 fluxes can be very high, supporting the hypothesis proposed by Joosten et al. (2006) that there would be a CH4 spike post-blocking, but this finding was based on a transect study at a single location, and lacked treatment replication (i.e., only one blocked ditch and one unblocked ditch were investigated). In addition there is debate on whether blocked ditches become net C accumulators and are radiatively cooling or, because of a spike in CH4 emissions, become radiatively warming (Baird et al. 2009). Cooper et al. (2014) did not measure CO2 fluxes, so the CO2-e effect of blocking at their site could not be quantified. Nevertheless, they did demonstrate that sedges (Eriophorum spp.) can rapidly colonise blocked ditches and become important sources of atmospheric CH4. It is clear that both studies (Cooper et al. 2014 and Green et al. 2014) have limitations, which need to be addressed to provide a more comprehensive assessment of how CH4 emissions, CO2 exchanges, and the overall CO2-e balance respond to ditch blocking. To address this research gap we conducted a fully-replicated field trial on a drained blanket bog in north Wales, UK. The site was chosen to be representative of UK blanket bogs more widely and comprised a series of 12 drainage ditches. Four ditches were left open to act as controls, while the remaining eight were subjected to two types of blocking (see “Materials and methods”). From these ditches we measured and modelled both CH4 and CO2 fluxes for a period of four years after ditch blocking, from which we were able to determine the overall C gas / GHG balance.

Materials and methods

Field site and experimental setup

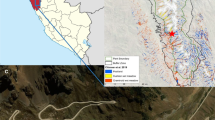
The study was carried out on an area of blanket bog in the Migneint in the Upper Conwy catchment, north Wales, UK (latitude 52.97°N, longitude 3.84°W). The site description below follows closely that of Green et al. (2016), Holden et al. (2017) and Green et al. (2017). The study site was a ~2 ha area of hillslope located approximately 500 m above sea level, drained by a set of parallel ditches running approximately downslope from a drainage divide at the hillslope crest (Fig. 1). It is not known exactly when the ditches were constructed, but it was at least 30 years before the experiment started. The ditches had a mean spacing of 16 m (range 11 to 26 m), a mean slope of 4.5° (range 3.9 to 5.1°), and a mean length of 99 m (range 84 to 107 m). They were shallow (c. 50–70 cm deep) and in some cases overgrown by vegetation, although all were hydrologically functional at the start of the experiment. Analysis of LiDAR elevation data from the study site suggests that some localised peat subsidence has occurred in the vicinity of the ditches since their construction (Williamson et al. 2017). Measured peat depth in the study area ranges from around 0.5 m to 2 m, and vegetation at the site comprises a typical blanket mire assemblage including Calluna vulgaris, Eriophorum vaginatum L. and Sphagnum spp. An important consideration for this study was the wider representativeness of the site. To compare the site with other blanket bogs, we characterised the physical and chemical properties of the peat in the experimental area. Based on published data, our study site is similar to other UK blanket bogs (see Green and Baird 2017). The bulk density of the peat at the site (0.06–0.18 g cm−3) is within the published range from other sites (e.g., Coggins et al. 2006; Finnegan et al. 2014; Holden et al. 2011), as is pH (H2O) (3.31–4.07) (e.g., Adamson et al. 2001; Clark et al. 2005), the C/N quotient (18.8–63.7) (e.g., Clark et al. 2005), and loss-on-ignition (90.1–99.9%) (Adamson et al. 2001; Clark et al. 2005; Crowe et al. 2008; Finnegan et al. 2014). As noted above, our study ditches were orientated in a predominantly downslope direction. Blanket peat ditches investigated in other studies such as Holden et al. (2011) and Wilson et al. (2010) have been mostly cross-slope, but both types of configuration are common in the UK (Holden et al. 2017).

Fig. 1
figure 1

Schematic of the experimental area. The alphabetical notation indicates the treatment applied (C = control (open), D = dammed, R = reprofiled). Altitude is in meters

Full size image

Four of the 12 study ditches were left open as controls, four were dammed with peat (i.e., dams were constructed at intervals of a few metres along the length of the ditch – ‘dammed’) and four were partially infilled with peat and dammed (‘reprofiled’) (see Holden et al. 2017; Parry et al. 2014). To avoid systematic bias, the assignment of the ditches to different treatments (Fig. 1) took account of their measured pre-blocking discharge rate and position on the hillslope. Ditch blocking was carried out in February 2011. Measurements then continued for 48 months between March 2011 and March 2015, henceforth denoted as Years 1–4.

Meteorological conditions at the site were measured using a Davis Instruments Vantage Pro 2 automatic weather station (AWS) (Davis Instruments Corp., Hayward, California). With the exception of rainfall, the meteorological variables were measured every 2.5–75 s and their 60-min averages logged. We used the AWS measurements of solar irradiance (I, W m−2), air temperature (T air , °C), and soil temperature at a depth of 5 cm (Tsoil,5, °C) to model both CO2 and CH4 fluxes (see “Time-integrated fluxes” below, this section). Meteorological conditions were highly variable over the study period, with annual mean air temperature being 7.8 °C (Year 1 – March 2011 to February 2012), 6.5 °C (Year 2), 6.9 °C (Year 3) and 7.6 °C (Year 4). In the same period, the rainfall for each successive year was 2255, 2409, 1786 and 1936 mm. For details, see Green et al. (2017).

The open ditches at the site frequently contained flowing water, but during extended rain-free periods they would dry up, and water tables would drop below ditch base level. Ditches like those at the study site, that have been established for many years, can have vegetated or partially-vegetated bases but still function effectively in conveying water off a peatland (Holden et al. 2008). It is not always clear how water levels relative to the peatland surface within ditches will change after ditch blocking. In dammed ditches, deep pools (of variable depth, but up to ~80 cm) form behind many of the dams, while the stretches of ditch between pools are drier and vegetated. As a result of their slope, these ditches can have areas just downstream of a dam that are also relatively dry, and these areas may not function much differently from an open ditch. In reprofiled ditches, the ditch base is raised by the peat infill. Pools are also present, separated by vegetated lengths of ditch, but these pools are typically shallower (variable but up to ~40 cm deep) than those in the dammed ditches. The area downstream of the dams in these ditches may actually be drier (in terms of water-table depths below the peat surface) than the open ditches because of their raised base (caused by the infilling). However, much depends on how the overall wetness of the peatland changes in response to ditch blocking.

For a comprehensive GHG balance assessment, each of these situations needs to be considered. In this study, within-ditch CH4 and CO2 exchanges were measured using flux chambers (see “Flux chamber measurements” below) (Denmead 2008). N2O was also initially measured; however, within-chamber concentrations were mostly below detection limits so N2O fluxes were assumed to be negligible. In the dammed and reprofiled ditches measurements were made in the between-pool vegetated area (denoted DV (dammed-vegetated) and RV (reprofiled-vegetated), respectively) and in the pools using floating chambers (DP (dammed-pool) and RP (reprofiled-pool), respectively). In the control (open) ditches two collars were positioned within the ditch channel, one in areas dominated by Sphagnum (control-Sphagnum – CS) and one in areas with a mix of plant species (control-vegetated – CV).

Flux chamber measurements

Twenty-four collars were installed within the ditches, two per ditch, and four per treatment (i.e., CS, CV, DP, DV, RP, RV) (Fig. 1). The flux chambers comprised cylindrical acrylic chambers with an outside diameter (o.d.) of 30 cm, a wall thickness of 3 mm and a height of 33.3 cm. Except for the floating chambers used in the pools, they were placed on permanently-installed polyvinyl chloride (PVC) collars when being used for a flux measurement. The collars had an o.d. of 31.5 cm and wall thickness of 8 mm, enclosing an area of 702 cm2. The collars were 20 cm long with half that length inserted below the ground surface. They were fitted with gutters on their upper rim into which water was poured and the chamber fitted to form a gas-tight seal during flux measurements. Drainage holes with a diameter of 10 mm were drilled into the sides of the collars at ground level to ensure water did not accumulate in them and create an artificial pool. During flux measurements these holes were plugged with rubber bungs. The shallow depth of the collars meant water could flow between the peat enclosed in the collar and that outside the collar to equalise any differences in water-table level between the two. Permanent collars can affect the vegetation within them. Although we did not formally measured the vegetation outside of the collars, we did not notice any consistent differences between within-collar vegetation and that outside (see “Environmental/ecological conditions” section).

Flux chamber measurements were conducted every three to six weeks, with the higher frequency during the growing season. During winter months some measurement visits were not possible because the access roads to the site were blocked by snow. During gas flux measurements, small electric fans were used within the chambers to ensure mixing of the chamber gas. Each chamber was also drilled and fitted with an acrylic tube. On the inside of the chamber, an air bag was attached to the tube; this arrangement allowed the equalisation of atmospheric pressure between the inside and outside of the chamber. Temperature and pressure within the chambers during flux measurements were measured using a Commeter C4141 probe (pressure accuracy of ~ ± 0.5 hPa and precision of ~ 0.2 hPa; temperature accuracy of ~ ± 0.5 °C and precision of 0.2 °C; Comet Systems, Rožnov pod Radhoštěm, Czech Republic).

Three types of measurement were conducted using the flux chambers as follows:

  1. (a)

    Between March 2011 and November 2012, CH4 flux measurements lasted for 21 min, and 25 mL samples of chamber gas were taken 1, 6, 11, 16, and 21 min after chamber closure. The samples were taken from a port in the chamber fitted with a gas-tight septum using a needle and syringe. During these measurements the chamber was shrouded with a reflective cover to reduce rises of within-chamber temperature. Each gas sample extraction was preceded by triplicate purges of the syringe after septum penetration. Gas samples were transferred in the field into either 22-mL pre-evacuated vials (Perkin Elmer, Cambridge, UK) or 12 mL pre-evacuated Labco Exetainers (Labco Limited, Lampeter, UK). The samples in the former were measured for their CH4 content using a Perkin Elmer Clarus 500 gas chromatograph (GC) system (Waltham, Massachusetts, USA) fitted with a flame ionisation detector (FID), while the samples in the Exetainers were measured for their CH4 content using an Agilent Varian 450 GC (Santa Clara, California, USA), also fitted with a FID. Standard analytical grade reference span gases (Cryoservice, Worcester, UK) were used to calibrate the GCs, and were inserted at regular intervals into the GC sample runs to check for instrument drift.

  2. (b)

    In the same period as (a), CO2 fluxes were estimated with separate chamber measurements. To measure CO2 fluxes under ambient light conditions – which represent the net balance between CO2 uptake by photosynthesis and loss by plant and soil respiration – short (2–3 min) measurement periods were used with un-shrouded chambers. Within-chamber temperature rises during such measurement periods were small (always less than 0.2°C). CO2 concentrations were measured using an on-line infra-red gas analyser (IRGA; EGM-4 portable IRGA, PP Systems, Amesbury, Massachusetts, USA). During each light-chamber measurement period, photosynthetically active radiation (PAR) was measured using a PAR meter (SKP 215 PAR Quantum sensor, Skye Instruments Ltd., Llandrindod Wells, Wales, UK). PAR measurements were taken next to the chamber. Tests showed that the acrylic walls of the chamber typically reduced PAR within the chamber by less than 2%, allowing us to estimate within-chamber PAR during flux measurements. To measure respiration, the light chamber measurements were followed immediately by dark chamber measurements. Upon completion of the light measurements, the chamber was lifted from the collar or pool, and the chamber concentration of CO2 allowed to return to ambient levels. A shroud was then placed on the chamber which was re-attached to the collar (or placed on the pool) and the dark measurements taken. The time between the end of a light measurement period and beginning of a dark measurement period was typically two minutes.

  3. (c)

    From February 2013, we used an on-line Los Gatos Research Ultra-portable GHG Analyzer (UGHGA; Model 915–0011; Los Gatos Research, Mountain View, California) to measure CH4 and CO2 concentrations simultaneously, so that it was no longer necessary to conduct separate sets of CH4 and CO2 measurements. The UGHGA measures gas concentrations using off-axis integrated cavity output spectroscopy—ICOS (Baer et al. 2002). All chamber measurement periods using the UGHGA were 2–5 min in duration and comprised paired light-dark measurement periods as described in (b) above.

In total, greenhouse gas fluxes at the site were measured using 912 dark chamber placements (measurement periods) for CH4 fluxes and 600 dark and 600 light chamber placements for CO2. Initially, we also measured N2O, but the concentration was mostly below detection limits. Therefore, N2O fluxes were assumed to be negligible and are not considered further.

The chambers were used to measure ‘steady’ gas fluxes, where steady has been defined by Green and Baird (2012) as the combination of diffusion through the soil, diffusion through plant tissue, and steady ebullition (bubbling). Episodic ebullition was not separately measured during the study (e.g., using inverted funnels – see Stamp et al. 2013).

Flux chamber measurement calculations

Changes in [CO2] and [CH4] (square brackets denote concentration) during a chamber measurement period can be used to estimate flux between the peatland and the atmosphere using (Denmead 2008):

$$ {f}_g=\frac{1}{A}\frac{dg_m}{dt} $$
(1)

where f g is the gas flux density at the peatland surface (mg m−2 day−1), A is the inside area of the collar (m2), g m is the mass of the gas in the chamber (mg), and t is time (days).

We applied Eq. (1) to our chamber data by first converting ppm gas concentrations into masses using the ideal gas equation. Ordinary least squares regression (using the LINEST function in Excel 2010) was used to estimate dg m /dt by fitting a line through the g m vs time data. The regression fit was only accepted if r2 ≥ 0.7 and p < 0.05. Fluxes for data sets that did not meet these criteria were rejected, with one exception: if [gas] variations during a measurement period were within a threshold error range of the instrument being used to measure [gas], the flux was assumed to be zero. For [CO2] measured using both the IRGA and UGHGA, the threshold error was 3 ppm. For CH4 it was 0.3 ppm for the GC-FID and 0.03 ppm for the UGHGA. If this additional criterion had not been used, the flux estimates would have been biased to higher values because all zero and close-to-zero fluxes would have failed the regression criteria and been excluded from our estimates. Clear episodic ebullition events were also excluded from the dataset.

Environmental/ecological conditions

The AWS (see “Field site and experimental setup” section) was used to provide information on overall conditions across the study area. In addition, we measured water tables and soil temperatures adjacent to the collars. The vegetation within the collars was also determined.

Water tables were measured at the control-vegetated (CV), dammed-vegetated (DV), and reprofiled-vegetated (RV) collars using manually-monitored dipwells. We did not measure water levels in the pools because the hydrological status and regime in these was clearly different from all other treatments (they were permanently ponded). In addition, we had a series of dipwells across the site fitted with automatic water-level recorders set to log every 120 min (see Holden et al. 2017), and this network of automatic wells included the CS (control-Sphagnum) treatment. The dipwells were made from 32 mm o.d. × 100 cm PVC pipe with a 3.5 mm wall thickness. The pipes were perforated with 8-mm diameter holes drilled at 10 cm intervals along four lines running lengthwise along the pipe, with holes in each line offset from those in neighbouring lines by 5 cm. All dipwells were tested for their response time by measuring the recovery of water levels after a rapid withdrawal of water. The time for 90% recovery ranged from a few seconds to 120 min. Where we refer to water-table depths (see “Results”), the ground surface is the reference point, and positive depths refer to water tables below the surface. Thus, for example, a water-table depth of 4 cm means the water table resided 4 cm below the peat surface. A depth of −4 cm means the surface was inundated to a depth of 4 cm. Hydrologically, it is interesting to consider absolute changes in water levels (Holden et al. 2017). However, ecologically, it is more important to consider water-table position relative to the peat surface because this controls a range of processes including plant growth and rates of decay; hence, our focus on water-table depth in this paper.

Peat temperature next to each collar and at a depth of 10 cm was also measured prior to each flux measurement using a digital thermometer (Hanna Instruments HI98501, Leighton Buzzard, UK). As noted above (see “Field site and experimental setup” section), we logged soil temperature at a depth of 5 cm at 60 min intervals at the AWS.

Where data were collected manually (i.e., the temperature at each collar and water tables at the CV, DV, and RV collars), we constructed a higher-frequency dataset for use in some of our CO2 and CH4 flux models (see “Time-integrated fluxes” section), by relating the manual collar readings to automatic readings (temperature from the AWS and water-tables from nearby auto wells) using bivariate regression.

Photographs of each collar (or area of pool where a floating chamber was placed) were taken during every flux measurement period. Two photographs from each collar – from April and August – were analysed for nested frequency of different plant functional types (PFTs). This measurement involved placing a 100-cell grid over the photograph and recording the presence/absence of all sedges (mainly Eriophorum spp.), Sphagnum spp. and ericoid shrubs in each cell, which provides a quantitative measure of plant abundance that can be used as a predictor of gaseous exchanges between a peatland and the atmosphere. More details of the method can be found in Green and Baird (2017).

Time-integrated fluxes

Fluxes estimated from chamber measurements represent a snapshot in time. In order to compare annual emissions of CH4 and net ecosystem CO2 exchange (NEE) from each treatment, the measured chamber fluxes need to be time-integrated.

CH4 fluxes may be integrated with respect to time using interpolation between measurements or by developing models that relate fluxes to a suite of environmental and ecological variables (Green and Baird 2017). If some of these variables are measured at a higher frequency than flux chamber measurements, the models in which they are used can, in turn, be run or applied to simulate CH4 emissions at those higher frequencies. The high-frequency flux estimates thus obtained can then be summed to give an annual flux estimate. We used both approaches here: linear interpolation between measurements and simple linear models (see Green and Baird 2017 for details). We explored the use of non-linear models but these proved worse than the linear models. In the analysis, each collar / chamber location was treated separately; i.e., for each location and each year of the study we estimated a separate flux of CH4. In the linear models the candidate explanatory variables were air temperature, soil temperature at 10 cm depth (modelled at each collar from the 5 cm depth AWS readings), a temperature sum index that ‘tracks’ the summer growth curve of peatland vegetation (Alm et al. 1997; Green and Baird 2017), water-table depth, and a measure of the abundance of the three PFTs within the area enclosed by the collars/chambers. Further details on our methods may be found in Green and Baird (2017). Except for PFTs, all of these variables were measured or estimated at hourly or two-hourly intervals. The models were run at hourly time intervals and the hourly fluxes summed to give annualised fluxes. To obtain hourly water tables from the two-hourly modelled values (see “Flux chamber measurements” section), linear interpolation was used. The plant abundance data were obviously not available at hourly intervals, but were entered for each hour and updated twice per year (see “Environmental/ecological conditions” section).

The training data used to construct the CH4 models were based on data collected from Years 2, 3 and 4. Hence, any apparent statistical differences (see “Statistical analysis” section) in fluxes between Year 1 and the other years should be treated with some caution. Our fits of the CH4 flux model yielded r2 > 0.5 in 21 of the 24 collars. For the three collars deemed unsatisfactory (i.e., r2 < 0.5) we used interpolation to estimate the annual budget. Hence, when we refer to ‘modelled’ CH4 fluxes in the paper, this includes interpolation for three of the collars.

Net CO2 exchange between the soil and atmosphere varies substantially according to PAR, which in turn varies according to cloud cover, hour of day, and day of year (season). NEE can be divided into two components: gross photosynthesis or primary production, GPP (mg CO2 m−2 day−1), and ecosystem respiration, ER (units as for GPP):

$$ NEE= ER+ GPP $$
(2)

so that

$$ GPP= NEE- ER $$
(3)

We use the convention that an uptake of CO2 by the ecosystem is denoted as a negative value and a loss is positive. Therefore GPP has a negative value (indicating uptake) and ER a positive value, so that, in Eq. (2), NEE will be negative (net uptake) when the absolute magnitude of GPP exceeds that of ER.

From Eq. (3) it can be seen that GPP may be obtained from a combination of light and dark chamber measurements. As with CH4, CO2 exchanges were modelled on a per collar/chamber basis, with separate models used for GPP and ER. GPP was modelled using:

$$ GPP=\frac{Q\times I}{k+I}\times {X}_1\times {X}_2\times \dots \times {X}_n $$
(4)

where Q may be thought of as an asymptotic limit of GPP, I is irradiance (W m−2; or photon flux density (PFD) mol m−2 s−1), and k is the half saturation constant (units as for irradiance) (e.g., Tuittila et al. 1999). The quotient on the right-hand side of Eq. (4) (the first multiplicative term) produces a rectangular hyperbola, while the variables to the right of the quotient are environmental or ecological factors such as sedge abundance, water-table depth, and air or soil temperature. The two parameters in Eq. (4) (Q and k) may be optimised to maximise the fit between GPP and I and any X variables that are included. Model error was estimated as the sum of the squared differences between the modelled and observed GPP values, and the Solver numerical optimisation tool in Microsoft Excel 2010 was used for model fitting. The multiplicative variables (X1, X2 etc) considered in the model were the same as the candidate variables used in the linear CH4 flux models.

PAR measurements during chamber measurements were converted to I for use in Eq. (4). This meant that the model could then be applied directly using the hourly AWS data to integrate CO2 fluxes over the 48-month duration of the experiments.

As with CH4 fluxes and GPP, we modelled ER on a per collar/chamber basis. We used a linear regression model in which the same candidate variables used in the GPP models were considered. We also tried fitting alternative non-linear models or mixed linear / non-linear models to our data but, as with the CH4 modelling, these did not perform as well as the linear models. Our models of GPP and ER yielded r2 > 0.5 in 21 and 20 of 24 the collars, respectively. Any model with an r2 < 0.5 was deemed unsatisfactory (although we recognise that this threshold is somewhat arbitrary).

Statistical analyses

The CH4, GPP and ER models were used to generate time-integrated fluxes for each study year between March 2011 and March 2015 (Years 1–4). Using Eq. (2) we could obtain NEE from the time-integrated fluxes of GPP and ER. For each type of flux – i.e., CH4, GPP, ER, and NEE – a repeated-measures ANOVA was used to assess the differences between treatments (i.e., CS, CV, DP, DV, RP, RV) and time (i.e., between study years). All tests were performed using IBM SPSS Statistics version 23. ANOVA assumptions were checked and the data transformed where necessary. Where Mauchly’s test indicated a violation of the sphericity assumption, changes were made to the degrees of freedom using a Greenhouse Geisser correction to reduce the chances of a Type I error. Where p ≤ 0.05, Tukey’s HSD (honest significant difference) test was used to identity which treatments or times were significantly different from each other. We conducted separate statistical analysis on the modelled and interpolated annualised CH4 fluxes following the recommendation of Green and Baird (2017). For all of the collars we were able to estimate annual CH4 fluxes for the experimental period. However, for GPP and ER this was not possible because some of the models failed to reach the threshold for acceptance. Therefore, the number of satisfactory annual NEE estimates was less than four for some treatments (CV = 4, CS = 2; DV = 4; DP = 3; RV = 4, and RP = 3).

The combined radiative forcing effect of CH4 emissions and NEE was calculated using carbon dioxide equivalents (CO2-e). We used CO2-e values for CH4 given for a 100-year time frame – 28 – in the 2013 Intergovernmental Panel on Climate Change (IPCC) assessment (Myhre et al. 2013). An alternative to the IPCC approach would be to use the concepts of sustained-flux global warming potential (for gas emissions) and sustained-flux global cooling potential (for gas uptake) as presented by Neubauer and Megonigal (2015). A repeated-measures ANOVA was used to assess the differences in CO2-e exchanges between treatments and time and followed the same protocols as used in the ANOVA used for the separate CH4 and CO2 flux data.

To help interpret any differences in CH4 and CO2 fluxes between the treatments and study years we analysed a subset of the within-collar vegetation data and the collar-adjacent water tables. For the vegetation data we focused on the nested frequency of the sedges (expressed as a percentage), given their apparent importance as emitters of CH4 (Cooper et al. 2014). Sedges can greatly increase CH4 emissions because they act as conduits between the peat and the atmosphere, with the CH4 moving through the aerenchyma, by-passing methanotrophic bacteria in the zone above the water table (e.g., Frenzel and Rudolph 1998; Greenup et al. 2000). Furthermore, sedges are also thought to decrease in cover over time after restoration (i.e., rewetting, Lindsay 2010). As with the CH4 and CO2 fluxes, we analysed the sedge abundance data using a repeated-measures ANOVA.

As noted above (“Flux chamber measurements” section) we did not measure the depth of ponding in the pools; we measured water tables only next to those collars located away from the dams. We compared water-table depths from Cv (control vegetated), CS (control Sphagnum), Dv (dammed vegetated, and RV (reprofiled vegetated) – using repeated-measures ANOVA. Annual, time-weighted water-table depths between the treatments were analysed (Holden et al. 2017).

Results

Water tables

The ANOVA indicated a significant effect of drainage/blocking treatment (p = 0.029) on water-table depths, with control (open) ditch water tables (CV = −2.5 cm and CS = −4.9 cm) being significantly higher, relative to the ground surface, than the water tables in the reprofiled ditches (9.4 cm below the ground surface) (Table 1). It is important to put these results into context. Immediately upstream of each dam, where pools formed, the dammed and reprofiled ditches were, obviously, wetter than any part of the control (open) ditches. What these results compare is the water-table depth in the non-pooled parts of the blocked ditches with the control ditches. There was no significant difference in non-pooled water tables between the control ditches and the dammed ditches (p = 0.160). The means are different, but, because of high variability, the confidence intervals show considerable overlap (Table 1). The significant difference between the control (open) ditches and the reprofiled ditches (p = 0.038) may be explained by the effect of infilling. After infilling, absolute water-table position (relative to a fixed datum) increased in the reprofiled ditches (data not shown). However, because the peat surface was raised in the reprofiled ditches, water-table depths relative to the peatland surface were greater (deeper) than in the control ditch. The ANOVA also showed that there was no significant effect of year on water-table depths (p = 0.065).

Table 1 Mean annual weighted water-table depths (cm) for each treatment by year (negative values indicate water levels above the ground surface)
Full size table

Sedge abundance

The repeated-measures ANOVA comparing sedge abundance between the different treatments suggested there was a treatment effect (p = 0.038), where CS = RP = DP < DV = CV = RV (Fig. 2). The observed differences were as expected and reflect the choice of collar location noted above (see “Field site and experimental setup” section). The mean sedge abundance for CS, RP and DP on average was 29% lower than DV, CV and RV. There was a significant difference between years (p = 0.001), with Year 1 (8.2%) < Year 2 (20.2%) = Year 3 (27.1%) = Year 4 (27.8%); but no interaction effect between time after blocking and treatment (p = 0.113).

Fig. 2
figure 2

Nested frequency (%) of sedges (mainly Eriophorum vaginatum) from collars within the ditches (n = 4) for the different treatments over the study period (Years 1–4), where C = control, D = dammed, R = reprofiled, V = vegetated, S = Sphagnum and P = pool. Error bars show standard deviation

Full size image

Explanatory variables in the CH4, GPP and ER flux models

The most common explanatory variable for GPP, in addition to PAR which was in every GPP model, was air temperature, while for ER air temperature, the temperature sum index and PFT (abundance of either sedge or Sphagnum) were all important (Table 2). In comparison, the most common explanatory variables (in order of importance) in the CH4 models were temperature (soil and/or air), the temperature sum index (tracking the peatland vegetation growing season), sedge abundance and water-table depth (Table 2). A notable feature of the models is the variation in the importance of the candidate explanatory variables between different collars, even within the same treatment type.

Table 2 Environmental variables included within CH4, GPP and ER models. All GPP models include irradiance. ‘X’ denotes inclusion of a variable
Full size table

CO2 fluxes

GPP showed significant (p = 0.007) variation between treatments, and was lower (i.e., less negative in Fig. 3 and Table 3) in DP, CS, and RP than in RV, with CV and DV not significantly different from either statistical sub-set. There were also significant differences between years after blocking (p = 0.001), with Year 4 having a higher GPP (i.e., more negative in Fig. 3) than Years 1–3. For ER, there was also significant variation between treatments (p = 0.008), with CS and RP significantly lower than RV. However, neither group was significantly different from any of the other treatments. There was no evidence of ER significantly changing over time (p = 0.251). Despite the differences between treatments for GPP and ER, there was no significant difference in NEE between treatments (p = 0.102). However, NEE in Year 4 was significantly lower (i.e., greater uptake of CO2) than all other years (p = 0.039). This was a feature of all treatments and vegetation types and was not related to the ditch blocked sites developing into CO2 sinks (vs open ditch sites remaining sources).

Fig. 3
figure 3

Mean annual GPP, ER and NEE (g CO2 m−2 d−1) for the different treatments over the study period (Years 1–4), where C = control, D = dammed, R = reprofiled, V = vegetated, S = Sphagnum and P = pool. Error bars show standard deviation. n = 4 for CV, DV and RV, n = 3 for DP and RP, and n = 2 for CS. Note that negative values are used to indicate uptake by the soil/ecosystem; so a more negative value represents a higher uptake

Full size image
Table 3 Summary of the annual fluxes disaggregated by treatment (four years amalgamated) (standard deviation in parentheses)
Full size table

CH4 fluxes

Fluxes of CH4 show an annual cycle, with both the average magnitude and variability of fluxes increasing in the summer (Fig. 4) (although the increase in variability may be partly an artefact of higher frequency of monitoring during the growing season). Fluxes of CH4 from the different treatments show considerable overlap. Figure 4 suggests that there is some separation between the control (CS and CV) and the dammed (DP and DV) treatments but there is also overlap between these two at the lower end of the range of fluxes (see below). Some very high fluxes were measured, particularly from floating chambers. Such fluxes can only be explained by steady ebullition, which was evident in some of the pools as a sustained passage of small bubbles through the water profile. Despite these very high values, the majority of the fluxes were below 100 mg CH4 m−2 d−1 (89% – all collars combined), although there is the suggestion that the reprofiled ditches produced more fluxes above this apparent threshold in the data. However, there was no strong statistical evidence of a difference between treatments in the percentage of individual fluxes above 100 mg CH4 m−2 d−1 (p = 0.053).

Fig. 4
figure 4

Steady CH4 flux (mg CH4 m−2 d−1) from the ditches. Each plot mark represents a single CH4 flux from a single collar. All data are for the post-blocking period. Δ denotes Sphagnum collars, + vegetated collars, and o pools. Negative fluxes are not displayed (due to logarithmic scale), of which there are four values (ranging from −1.8 to −24.4 mg CH4 m−2 d−1). The frequency of sampling was the same for each year of the study. However, there was a greater number of failed chamber tests in Year 1 compared to years 2–4

Full size image

The ANOVA comparing annualised CH4 fluxes (Fig. 5 and Table 3) suggests there was no treatment effect; i.e., there was no significant difference between the collar groups (modelled integration: p = 0.641; interpolated integration: p = 0.238). Our dataset does not suggest that restoration from a drained state increases CH4 emissions. There was some indication of a significant effect of time when using the modelled integration (p = 0.021), with fluxes in Year 1 (14.8 g CH4 m−2 y−1) being higher than in Year 2 (7.5 g CH4 m−2 y−1), Year 3 (5.2 g CH4 m−2 y−1), and Year 4 (7.9 g CH4 m−2 y−1). However, this may be an artefact of the modelling process and the fact that the model training set was mostly from Years 2–4 (see “Materials and methods” and “Time-integrated fluxes” sections). There is no evidence when using interpolation of annual CH4 emissions being different over time (p = 0.100).

Fig. 5
figure 5

Mean annual steady CH4 flux (g CH4 m−2 y−1) for all collar locations over the study period (Years 1–4) for a modelled integration and b interpolated integration, where C = control, D = dammed, R = reprofiled, V = vegetated, S = Sphagnum and P = pool. Error bars show standard deviation (n = 4)

Full size image

These statistical results may at first seem somewhat at odds with the modelled and interpolated fluxes in Fig. 5, which appear to suggest that there are some large variations between groupings. For example, the mean fluxes from CS were lower (mostly net uptake) than the fluxes recorded by the floating chambers (DP and RP). However, the lack of a significant difference is readily explained by the CH4 emissions being very variable spatially (Figs. 4 and 5). Generally, there was less variation in fluxes over time than there was spatially; that is, there was some coherence in the data: collar locations with high fluxes in Year 1 tended to have high fluxes in the succeeding years while locations with low fluxes in a particular year also had low fluxes in the other years.

Net CO2-e balance

Net CO2-e balance based on a 100 year time-frame was calculated for all chambers for which satisfactory models of GPP, ER and CH4 flux could be developed (Fig. 6 and Table 3). There is a wide scatter in CO2-e values, with little obvious separation according to collar type, although a CO2-e balance could not be calculated for four of the 24 collars. There was no significant difference between treatments (p = 0.065 for interpolated integration of CH4 fluxes and 0.095 for modelled CH4 fluxes). From this somewhat limited dataset there is the suggestion of a trend from net emissions towards net uptake over the four year period (p = 0.027 for interpolated integration of CH4 fluxes and 0.019 for modelled fluxes), with Year 1 = Year 2 = Year 3 > Year 4. In Year 1, 10 of the 20 collars showed a net radiative warming effect (positive CO2-e value), whereas by Year 4 only five were in this category (modelled CH4 integration). Nevertheless, there was considerable inter-annual variability, with the mean CO2-e across all of the collars declining from 462 to 34 CO2-e m−2 y−1 between Years 1 and 2, increasing to 93 CO2-e m−2 y−1 in Year 3, and thereafter declining substantially to −439 CO2-e m−2 y−1. It is notable that these means are affected quite strongly by one outlier from the RV treatment that had a large negative net CO2-e balance values in Years 2–4. If this outlier is removed, the inter-annual variability narrows, with the mean CO2-e across all of the collars declining from 534 to 182 CO2-e m−2 y−1 between Years 1 and 2, increasing to 268 CO2-e m−2 y−1 in Year 3, and thereafter declining substantially to −260 CO2-e m−2 y−1.

Fig. 6
figure 6

Net CO2-e balance (Years 1-4) based on: a annual CH4 fluxes estimated by linear models and b annual CH4 fluxes estimated by interpolation, where C = control, D = dammed, R = reprofiled, V = vegetated, S = Sphagnum and P = pool. Error bars represent standard deviation (n = 4 for CV, DV and RV, n = 3 for DP and RP, and n = 2 for CS)

Full size image

Discussion

Given the significant differences in water-table depths and sedge abundance between treatments, we expected clear treatment effects on CH4 fluxes, NEE and overall GHG balance. In particular we expected fluxes from the pooled areas of the blocked ditches (DP and RP) to differ from the other treatments, because they had different hydrological regimes and, compared to three of the other four treatments, significantly lower sedge abundances. The lack of significant differences in fluxes between the treatments may be explained in part by the high spatial variability within the treatments. Additionally, while the flux models showed that water tables and sedge abundance can be important explanatory variables, the combination and relative importance of these variables varied within as well as between treatments (Table 2). For example, for the RV (reprofiled-vegetated) treatments, every ER flux model was different (RV.1: T air , RV.2: T air , T soil , and sedge abundance; RV.3: T air , T soil , ETI, and sedge abundance, RV.4: T soil and sedge abundance) (see Table 2). Notably, too, water table was not included in any of the CO2 models, although it was important in the CH4 models (except in the pooled areas where it was not measured; see further discussion below and “Flux chamber measurements” section).

There are few studies that directly consider GHG emissions from within ditches in blanket bogs. Cooper et al. (2014) estimated mean annual CH4 fluxes of 197 g CH4 m−2 y−1 for infilled ditches that had been colonised by E. vaginatum, compared to 10.3 g CH4 m−2 y−1 for unvegetated within-ditch sites. CH4 fluxes from the dammed and reprofiled ditches at our site were closer to the latter (Table 3). An apparently important difference between our study and that of Cooper et al. (2014) is the method of blocking. Blocking of ditches with heather bales, as was the case at the site studied by Cooper et al. (2014), is no longer widely used, partly because of concerns over the stability of the bales over time. In their laboratory study Green et al. (2014) showed that heather bales provide a source of labile substrate, and that they can decay readily to produce free-phase CO2 and DOC: their mesocosms representing ditches blocked with heather bales had a NEE of 4676 ± 632 mg CO2 m−2 day−1 and pore-water DOC concentrations of more than 100 mg L−1, with both NEE and [DOC] being higher than in any other mesocosm treatment (no infill, peat infill). However, while such rapid decomposition of the heather bales might be expected to produce substrate for methanogens, Green et al. (2014) did not find significant differences in CH4 emissions between their heather bale mesocosms and those representing re-profiling and damming, which suggests that the very high fluxes observed by Cooper et al. (2014) are related more to the presence and productivity of E. vaginatum than the decay of the heather.

Very few studies have been done on GHG fluxes from open and blocked ditches in other types of peatland (e.g., raised bogs). Waddington and Day (2007) reported growing-season CH4 fluxes, which can be assumed to be the same as annual fluxes, of 14.6 g CH4 m−2 y−1 from open ditches on a boreal cutover raised bog in Québec, Canada, which are comparable with values were reported by Roulet and Moore (1995) from open drainage ditches in a boreal forested bog (14.8 g CH4 m−2 y−1). Hyvonen et al. (2013) investigated the GHG emission from drainage ditches in an abandoned boreal peatland previously used for extraction in Finland, and report estimated annual emissions of 0.33 g CH4 m−2 y−1. In contrast, Huotari et al. (2013) estimated annual within-ditch fluxes of 53.3 g CH4 m−2 y−1 for a drained boreal bog in Finland. These values bracket those found for our control (open) ditches, which ranged from 0.8 to 6.1 g CH4 m−2 y−1 (modelled integration). Waddington and Day (2007) also examined CH4 fluxes from restored ditches. In their study, they compared ditches that had been infilled with a mixture of peat and cut (i.e., dead) vegetation with ditches that were left open. Like us, they did not find significant differences between the two treatments. However, in terms of the overall restoration landscape (i.e., including inter-ditch areas), blocked ditches were hotspots of CH4 emissions. Waddington and Day (2007) found that the infill of the restored ditches slumped towards the end of the first growing season post-restoration, so that water started to pool in them; in effect the restored ditches became shallow versions of the open (unrestored) ditches. The slumping of the infill and pooling of water in the restored ditches may have explained a three-year increase in average growing-season fluxes from 11 to 474 mg CH4 m−2 d−1. Plant cover did not change in the ditches during this time, so was probably not a factor in the increases, although decay of the vegetation used as infill could have contributed to the increase, in combination with a loss of an aerobic zone at the top of the peat infill. Different pictures seem to emerge from different sites, and CH4 emissions from both open and blocked ditches appear to depend on a range of factors that vary in their relative importance between sites, but also within sites. This is clearly evident with our models constructed to estimate CH4 (Table 2), which vary from collar to collar. For example, for the DV (dammed-vegetated) treatment, each collar had a different CH4 model (DV.1: T soil , water table and sedge abundance; DV.2: T air , T soil , ETI and sedge abundance; DV.3: T air , T soil , ETI, water table and sedge abundance; and DV.4: Tsoil). In addition, relatively small changes in driving variables, such as peat water content or the composition of the peatland vegetation, may cause substantial changes in the microbial community of peat soils, altering the balance between methanogenesis and methanotrophy, and, therefore, the emissions of CH4 to the atmosphere (Freitag et al. 2010; Robroek et al. 2015).

We found evidence of significant temporal changes in the variables we measured, but these changes showed little consistency between variables. Sedge abundance was significantly lower in Year 1 than in Years 2–4, NEE lower in Year 4 than in Years 1–3, and CH4 (modelled) emissions higher in Year 1 than Years 2–4. The CH4 results seem to be contradictory to the sedge results. It is well documented that sedge abundance is often directly correlated with CH4 emissions and net CO2 uptake (see Frenzel and Rudolph 1998; Greenup et al. 2000; Green and Baird 2012). However, it is possible that the apparent difference in CH4 fluxes between years is an artefact of the integration method. Because of a relatively high number of failed CH4 tests in the first year (see Fig. 4), the modelled CH4 fluxes were trained mainly on data from Years 2–4. This may have had the effect of causing Year 1 fluxes to apparently differ from those in Years 2–4. The interpolated fluxes were not subject to the same potential bias and did not show any between-year differences. Additionally, CH4 emissions at the site, and perhaps in blanket bogs more generally, may be driven by a complex array of factors, as reflected by the CH4 models (Table 2).

In general, it is clear that the GHG balance of blanket bog ditches does not follow a simple trajectory in response to damming or reprofiling. In contrast to Cooper et al. (2014), our results show that blocked ditches do not necessarily show a spike in CH4 emissions or high net CO2-e fluxes. Thus, restored ditches may be ‘carbon-neutral’ even in the immediate post-blocking period, which should be considered when evaluating the wider ecohydrological benefits of ditch blocking.

Finally, it is important to consider the effect of our experimental design on our findings. Our flux data showed high spatial variability, and this, combined with the small (spatial) sample size, will have affected the outcomes (the power) of our statistical tests. Despite our study involving over 900 gas flux measurements, we recommend greater spatial replication in future studies of blanket bogs. An additional aspect of our experimental design, as shown by Holden et al. (2017), is that the treatments were not wholly hydrologically isolated from each other, partly because the ditches were not aligned exactly with the maximum slope (Fig. 1). Therefore, a reprofiled ditch next to an open ditch (Fig. 1) could have been drier than if it was in a larger area where all ditches had been blocked using the reprofiling method. Such hydrological effects could have influenced the gas flux results and should be borne in mind as a possible confounding factor in our analysis. Nevertheless, hydrologically-large differences were observed between treatments. The pools that formed behind the dams in the reprofiled treatment gave clearly wetter conditions than in the control or open ditches. Additionally, the infilling of the reprofiled ditches is likely to have had a greater hydrological effect than interactions between treatments and can explain why water-table depths were greater in the reprofiled ditches away from the dams than in the open ditches.

Conclusions

In conclusion, we have not found evidence of consistent differences between blocking treatments in terms of CH4 emissions or net GHG balance from shallow ditches on a sloping blanket bog. To date, we cannot identify any net GHG balance benefit from ditch blocking of blanket bog at our study site, which had downslope-orientated drainage ditches. Differences in sedge abundance and water-table depth were not related to differences in CH4, NEE and GHG balance between treatments, and this is likely to be related to micro-scale differences within the site. On the other hand, ditch blocking does not appear to lead to any undesirable outcomes in terms of C balance in that the theorised spike in CH4 fluxes post-ditch blocking was not evident. Lastly, we note that this study concerns within-ditch fluxes only; it does not deal with the effect of ditch-blocking on the area between ditches; those effects will be presented in a later publication.