Introduction

Increasing plant water and nutrient use efficiencies is a major challenge that must be met in order to respond to the rising demand for sufficient food supply of an ever growing human population. Plant productivity is governed by many environmental factors such as radiation interception and water and nutrient availability in soils. Thus, a fundamental understanding of the key processes determining plant growth is necessary in order to improve cropping systems and cultivars for resource limited environments (de Dorlodot et al. 2007). Understanding the impact of roots and rhizosphere traits on plant resource efficiency is important, in particular in the light of sustainable production with reduced fertilizer input, potential shortages and increasing costs of fertilizers and climate change with increasing frequency of droughts. In this context, root architecture is a fundamental aspect of plant productivity (Lynch 1995) and thus needs to be accurately considered when describing root processes.

Existing root system models can be divided into pure root growth models, which focus on describing the root system’s morphology, and more holistic models, which include several root–environment interaction processes, e.g. water and nutrient uptake.

The first descriptive three-dimensional root system models were presented by Diggle (1988) (RootMap) and Pagès et al. (1989). These models described a herringbone topology and defined root properties for every topological order in the root system. Based on these ideas, Lynch et al. (1997) and Spek (1997) developed new root growth models (SimRoot and ArtRoot) with a strong focus on visualisation. Pagès et al. (2004) presented a root system model in which the different types of roots composing the root system topology are not strictly related to the topological order (Root Typ).

These dynamic three-dimensional root growth models have provided a basis to couple root growth to plant and soil interaction models in order to simulate environmental processes such as water and nutrient uptake. A root system model developed for such a process oriented analysis was presented by Fitter et al. (1991) to study the exploration efficiency of root systems in dependence of root architecture. It could be demonstrated that both root topology and link lengths strongly influence nutrient uptake efficiency (Fitter and Strickland 1991). Dunbabin et al. (2006, 2002) predicted water and nutrient uptake, in the presence of exudates (Dunbabin et al. 2006), by integrating RootMap into a simulation environment. Dunbabin et al. (2004) analysed the effect of different root system architectures on nitrate uptake efficiency. Walk et al. (2006) used SimRoot to assess the trade off effects of different root system morphologies on phosphorus acquisition. Based on the model of Pagès et al. (1989), a model of water conduction within roots has been proposed by Doussan et al. (1998) and combined with a model for water transport in soil (Doussan et al. 2006). Clausnitzer and Hopmans (1994) developed a new root growth model and analysed water flow in the soil root zone which was further extended by Somma et al. (1998) for nutrient uptake. Javaux et al. (2008) combined the model of Somma et al. (1998) and the model of Doussan et al. (1998) to comprehensively describe water flow between the soil and plant root domain. Roose and Fowler (2004) derived sink terms for nutrient and water uptake from a continuous root system growth model which can be solved analytically.

Beside the effects of root growth dynamics and architectural traits on the soil (water and nutrient uptake), a major challenge of root modelling is the dynamic interactions of soil properties on the root growth and architecture itself. Water availability, nutrient concentration as well as mechanical impedance have been shown to strongly influence plant root traits (e.g. Hodge 2004; Eapen et al. 2005; Bengough et al. 2006). Integrating root plasticity in response to the growth environment into root architecture models remains a major challenge for an accurate model based analysis of plant growth strategies in different environments (Tsutsumi et al. 2003). Root responses to resource heterogeneity in the soil are subject to ongoing empirical research concerning phytohormone mediated signalling pathways and species specific morphological and physiological reactions (e.g. Forde and Lorenzo 2001; Callaway et al. 2003; Hodge 2004; Zhang et al. 2007; Peret et al. 2009). This requires a flexible modelling approach for continuous incorporation of new knowledge.

Processes and interactions in the soil–plant–atmosphere continuum are often described by partial differential equations. The most important equations are the Richards equation for water flow (Jury and Horton 2004) and the convection diffusion equation for solute transport in soil (Barber 1995). With increasing computational power, it is now possible to solve these equations numerically in three dimensions using finite difference, finite volume or finite element methods. The complexity of the root–soil system, however, requires an accurate and detailed description not only of each subsystem (e.g. root growth, root architecture, water and solute transport), but also of their mutual linkage and influence. Thus, a modelling approach with a modular structure would be most appropriate to join developments in modelling the individual components of the rhizosphere. The powerful numerical solvers available today (e.g.: Comsol Multiphysics, FlexPDE), combined with techniques such as operator splitting, yield a detailed description of the single subsystems and subsequently enable these to be joined into a comprehensive system analysis.

This study presents such a modular approach for root growth, root architecture and root–soil interactions based on L-Systems. L-Systems are often used in plant architecture modelling (Prusinkiewicz 2004) and have also been applied to root systems (Prusinkiewicz 1998). We provide an implementation of our L-system based root growth and architecture model in Matlab and the integration of the root system description into a plant–soil interaction model. This approach considers the plasticity of root growth and branching strategies as influenced by local soil properties. From the root system architecture model, parameters such as density distributions can be derived and used in soil models. Matlab makes it is easy to link the model to existing simulation codes (e.g.: Java, C, Fortran) or to apply external numerical solvers. The new approach is exemplified in a simulation study of maize root growth and phosphate uptake in a pot experiment. The effects of different sink terms derived from the modelled root architecture and the role of gravitropism and chemotropism is demonstrated. Our main objective is to provide a mathematically sound and publicly accessible dynamic root growth model with a focus on a modular approach to integrate various types of interactions between root architecture and the soil environment.

Model description

Introduction to L-Systems

L-Systems are rewriting systems based on strings where each character stands for a specific entity (Prusinkiewicz and Lindenmayer 1990). Every character of an initial string ω is replaced according to its corresponding production rule. This is performed iteratively n times to achieve an L-System of the n th generation which can be interpreted graphically. For example the initiator ω and the production rule for the character X,

$$ \begin{array}{lll} \omega &=& {X}, \\ X &\rightarrow& F \ [ \ + \ X \ ] \ [ \ - X \ ] \ F \ X, \end{array} $$
(1)

produce Fig. 1. In this example X denotes the tips and F represents the segment that has been produced. The characters +, −, [ and ] are used for the graphical interpretation using turtle graphics. In Appendix we briefly describe turtle graphics and provide a list of turtle commands.

Fig. 1
figure 1

The 2nd–5th generation of an L-System (reproduced from Prusinkiewicz and Lindenmayer 1990)

Full size image

L-Systems provide a compact description for branched geometries. However, in root growth simulations, we need to describe continuous growth in time. For this reason, we use parametric L-Systems, which include a special parameter t denoting the local age of an L-System character. Additionally, every production rule is applied for a certain time step Δt. We indicate this by writing the time step as a superscript of the L-System character. For example, a character that is replaced after a predetermined time t end by a successive L-System string N s (delay rule D Δt) is given by

$$ D^{\Delta t}(t) \rightarrow \begin{cases} \begin{array}{ll} t+\Delta t \geq t_{end}&: N_s^{t+\Delta t-t_{end}} \\ \textrm{otherwise} &: D(t+\Delta t), \end{array}\end{cases} \label{ruleD} $$
(2)

where the parameter t is the local age and t end is the time at which the character is replaced, Δt is the time which passes during the application of the rule. If the local time is longer than t end the character is replaced by its successor N s . The production rule of N s is applied with the time t + Δt − t end , which is the corresponding time overlap. Otherwise, the local time is increased to t + Δt, which is the new local time of the character D.

The production rules have to be designed such that the result does not depend on the discretisation of the overall simulation time. The delay rule utilises two different kinds of parameters. The local age t changes when the production rule is applied, while t end and N s are predetermined initial values. We use a syntax in which local parameters are given in front of the semicolon and initial parameters are given after the semicolon, i.e., D(t): = D(t ; t end , N).

The following sections describe the basic production rules of the L-System model for root growth. A major concern is that all production rules are based on biological mechanisms. Our production rule for elongation of individual roots is based on the continuous root growth model of Roose et al. (2001). If required, it can be replaced by other models.

Axial growth

We first present a production rule for the growth of a single root without branching according to a continuous growth function λ(t). In our application, λ(t) is chosen for every root type i. Root elongation follows a negative exponential function (following Pagès et al. 2004).

$$ \lambda_{i}(t) = k_i \left( 1-e^{-\frac{r_i}{k_i}t} \right), \label{eqn:length} $$
(3)

where k i is the maximal length of the root and r i is initial growth speed. In the simplest case, the root type corresponds to the topological order of the root within the root system.

The production rule G Δt for the growth of a single root is given by

$$ \begin{array}{lll} & &{\kern-6pt}G^{\Delta t}(t,l){\kern6pt}\\& &\rightarrow \begin{array}{ll} l\!+\!\Delta x < \lambda(t\!+\!\Delta t) &: R \ F_{\Delta x} \ G^{\Delta t}(t,l\!+\!\Delta x) \\ \textrm{otherwise} &: G(t\!+\!\Delta t, l). \end{array}\end{array} \label{ruleG}\\ $$
(4)

The parameter t represents the local age of the root tip, l is an approximation of the actual root length λ(t), Δt is the time step and Δx is the spatial discretisation. The character R denotes a rotation that describes root deflection and the character F Δx denotes a segment of the root with length Δx. The choice of the rotation R describing the root tip deflection will be addressed in Section “Tropisms and root tip deflection”. The first expression of Eq. 4 produces segments R F Δx until the predetermined length λ(t) is approximated. This is done recursively, thus, in one step numerous segments can be produced. Otherwise the local time is increased to t + Δt. In this way the root axis is described by segments with length Δx. The growth function λ(t) and the discretisation along the root Δx are initial values, thus G(t,l) : = G(t,l; λ, Δx).

In this section, we have described a production rule for the growth of an individual root. In the next section, we present an L-System rule for lateral branching and summarise the root parameters that are needed for a single root with branches.

Lateral branching

In a root system, every root of a certain order produces lateral branches. A root is therefore divided into three zones: the basal- and apical zones near the base and the tip of the root, respectively, where no branches are produced, and the branching zone where new roots of successive order are created. The self similar structure of the root system is used in the model description.

Growth of basal and apical zones as well as the growth between the branches, are described with the section growth rule S Δt given by Eq. 5, which is a generalisation of the axial growth rule given by Eq. 4. In our implementation, new branches can lie at an arbitrary position that is independent of the discretisation Δx. Thus, Eq. 4 needs to be modified such that it can produce segments of length Δx or less:

$$ \begin{array}{lll} & &{\kern-6pt} S^{\Delta t}(t,l) \\& &{\kern6pt}\rightarrow\left\{ \begin{array}{ll} A \ \& \ (l\!+\!\Delta x<l_s) &\!:\! R \ F_{\Delta x} \ S^{\Delta t}(t,l\!+\!\Delta x) \\ A \ \& \ (l\!+\!\Delta x \geq l_s) &\!:\!R \ F_{l_s-l} \ N_s^{t\!+\!\Delta t - (t_{end}-t_0)} \\ \textrm{otherwise} &\!:\! S(t\!+\!\Delta t, l), \end{array}\right.\end{array} \label{ruleS}\\ $$
(5)
$$ A := \lambda(t_0)+l+\Delta x \le \lambda(t_0+t+\Delta t), $$

where t 0 and t end are the times at which the growth starts and ends; λ(t 0) and λ(t end ) are the respective positions on the root axis and l s : = λ(t end ) − λ(t 0) is the length of the section. The successive L-System string N s represents the next section.

The first expression of the rule corresponds to the first expression of Eq. 4 with the additional constraint that growth does not exceed length l s . The second expression describes the case if the length exceeds l s . In that case, a segment with the remaining length \(F_{l_s-l}\) is produced and the successor, N s is applied with the correct time overlap t + Δt − (t end  − t 0). Otherwise, local time is increased. The following parameters and initial values are needed: S(t,l) : = S Δt(t,l; t 0, t end , N s ,λ,Δx). In this way, a section is described by a number of segments with lengths equal to or less than Δx. Using the section growth rule, the basal zone is succeeded by the branching zone which is then succeeded by the apical zone.

Within the branching zone, a predetermined number of branches are created. The spacing between the branches is determined by the section growth rule. The rule allows that branches can occur at any point along the root axis and not only at segment edges with fixed segment length. When new branches are created, they begin to grow as soon as the apical zone has reached its required length. The branching zone produces L-System strings N b , which represent branches of the next topological order; these are then followed by a successive L-System string N s , which represents the apical zone. The production rule for branching B Δt is given by

$$ B^{\Delta t}(c)\rightarrow\left\{ \begin{array}{lll} c\!&<&\!n\!:\! D^{\Delta t}(0;d_c,N_{b}) \\ && \quad S^{\Delta t}(0,0;t_{0,c},t_{end,c}, B(c\!+\!1),\lambda,\Delta x) \\ c\!&=&\!n\!:\! D^{\Delta t}(0;d_c,N_{b}) \\ && \quad S^{\Delta t}(0,0;t_{0,c},t_{end,c}, N_s,\lambda,\Delta x). \end{array} \right.\label{ruleB} $$
(6)

The parameter c counts how many branches have already been produced and n denotes the maximal number of branches. The first expression of the rule describes that if c < n, then a new lateral branch N b is produced with the corresponding time delay d c ; D is given in Eq. 2. This time delay is necessary because the new branch can only start growing when the apical zone has reached its required length. Furthermore, a section with the length of the space between the branches is created with times t 0,c and t end,c. S is given in Eq. 5, and is followed by the branching rule with increased counter c. The second expression states that after the last branch is created, the final section is followed by the successive string N s , which produces the apical zone. All parameters and initial values of the branching rule are given by \(B^{\Delta t}(c; N_{b}, \!N_s, n, \{t_{0,i}\}, \{t_{end,i}\}, \{d_i\}, \lambda,\! \Delta x)\), where i = 1 ...c.

When a new branch is created, first the turtle state, position, heading, width and colour is stored. The local root tip axis performs a radial rotation by a uniform random angle β between − π and π. Then the tip axially rotates by a predetermined angle α (following Pagès et al. 1989), see Fig. 2. The new branch is created with a new local axis and, finally, the original turtle state is retrieved. Thus, the string N b has the following structure:

$$ N_b = [ \ R_{\beta} \ R_{\alpha} \ b \ ], $$
(7)

where b describes the new branch. The production rule of the character b sets up the basal, apical and branching zone and the delays d. The local times t 0 and t end , which are needed for rule (6), are calculated from the growth function λ(t) i , which is given by Eq. 3 and is determined by the parameters r i and k i for every root type i.

Fig. 2
figure 2

The change of root tip heading due to the rotations R α and R β

Full size image

We summarise the required model parameters needed for a root type in Table 1. All parameters are given by their mean value with a standard deviation. For roots with no lateral branches the parameters l b , l n , and n are not needed.

Table 1 Parameters for a root with lateral branches
Full size table

Root systems

In order to describe different kinds of root systems like tap root systems or fibrous root systems, an adequate initial L-System string must be created. In the case of a tap root system, the initial string consists of a single root tip of a zero order root. In the case of fibrous root systems, the initial string is created as follows: We start with a root collar using a predefined number of root tips n 0. We assume that the roots initially grow away from the stem in a conical way. The initial angle is determined by assuming an even distribution of roots on a cone’s base with radius r 0 and height 1 cm. The cone’s tip is positioned at the centre of the root collar. Thus, the initial parameters of the L-System model are the number of initial roots n 0, and the cone’s radius r 0. To achieve uniform distribution of the roots on the cone’s base, the initial axial insertion angles α and initial radial insertion angle β must be chosen as follows,

$$ \alpha = \arctan(\sqrt{X} \ r_0), $$
(8)

with random X uniformly distributed between 0 and 1. Random β is uniformly distributed between − π and π.

To include effects that arise from gravitation and soil heterogeneities, more mechanisms have to be included, which are discussed in the following section.

Tropisms and root tip deflection

The previous explanation shows that the root system is described by a large number of segments of length less than or equal to Δx. In front of every segment F Δx is a rotation R which is created when the root axis grows, see Eqs. 4 and 5. In the model, we specify R by two rotations (following Diggle 1988). The root tip axis rotates radially by an angle β and then axially by an angle α, see Fig. 2. In reality, the direction of root growth is influenced by mechanical as well as plant physiological properties. We include this in the model by specifying different ways to choose α and β. In this way, we can simulate root tip response to mechanical soil heterogeneities as well as various types of tropisms like gravitropism, hydrotropism or chemotropism. The specific growth behaviour can be chosen for every root type.

To choose the angles α and β in relation to global parameters, the root tip position \(\boldsymbol{x}_p\) and local axis given by \(\boldsymbol{h}_x\), \(\boldsymbol{h}_y\), and \(\boldsymbol{h}_z\) are needed. Therefore, an additional set of parameters is introduced for L-System characters describing root tips. If a root tip is replaced by any production rule

$$ \textrm{tip} \rightarrow \underbrace{ \dots R F_{\Delta x} }_{\textrm{transformation } T} \textrm{tip}, \label{eqn:global} $$
(9)

the set of parameters is updated corresponding to the transformation T.

A simple approach to model the effect of soil particles on the direction of root growth is to modify the growth direction of the root tip randomly. In this case we do not consider the positions of the soil particles explicitly but merely describe their influence on growth by random variation of the growth direction. Therefore, we choose a random radial angle β uniformly distributed from − π to π and a random axial angle α that is normally distributed with mean 0 and standard deviation σ dx . The standard deviation σ dx is dependent on the length of the next segment dx. It can be calculated from a global parameter σ that controls how strong the root’s direction changes per 1 cm growth. The standard deviation σ dx is calculated from σ using Gaussian error propagation where the number of trials is 1 / dx (segments per cm). The standard deviation σ dx is given by

$$ \sigma_{dx}=\sqrt{dx} \ \sigma. \label{eqn:gauss} $$
(10)

In this way, the expected change of the root axis does not depend on the spatial resolution. The root axis is described by segments. The segments lengths dx are equal to or less than the spatial discretisation Δx i , whereby the spatial discretisation can be chosen for every root type i.

Tropisms

An easy way to implement gravitropism is to randomly calculate several rotations and pick out the rotation that leads to a downward movement of the root tip. Therefore, we introduce the parameter N denoting the number of trials to find the optimal angles α and β for the rotation R in order to achieve a downward movement. The angle α is a normally distributed random number with mean 0 and standard deviation σ dx , the angle β is uniformly distributed from − π to π. Figure 3 demonstrates how the choice of parameters N and σ influences a fibrous root system, whereby σ describes the expected change of root tip heading per 1 cm root growth and N controls the trend to grow downwards. The parameter N can be a real number. N=1.5 means that the number of trials can be either one or two.

Fig. 3
figure 3

The influence of the parameters N and σ on the extent of gravitropism in a fibrous root system (n 0 = 30, r 0 = 5)

Full size image

This approach has two main advantages: Firstly, the effect of gravitropism does not depend on the spatial resolution along the root axis. Secondly, the objective function can be freely chosen; thus, different tropisms can be realised using this concept. In the following we give some examples of objective functions to be minimised:

$$ \begin{array}{ll} \textrm{Gravitropism}\!\!\! \!\!\!& f = {(\boldsymbol{h}_x)}_3\\ \textrm{Plagiotropism}\!\!\!\! \!\!& f = |{(\boldsymbol{h}_x)}_3| \\ \textrm{Chemotropism, Hydrotropism,}\!\!\!\!\!\! & \\ \textrm{Thermotropism}\!\! \!\!\!\!& f\!=\! - s(\boldsymbol{x}_p \!+\! dx \ \boldsymbol{h}_x)\\ \end{array} \label{equ:tropism} $$
(11)

The point \(\boldsymbol{x}_p\) denotes the position of the root tip, see Eq. 9. The root tip heading \(\boldsymbol{h}_x\) is the direction of growth of the local axis after applying the rotation R(α, β), see Fig. 2. The scalar field \(s(\boldsymbol{x})\) contains nutrient concentration, water content, pressure head or temperature. The value \({(\boldsymbol{h}_x)}_3\) denotes the z-coordinate of the vector \(\boldsymbol{h}_x\). Minimising the z-component \((\boldsymbol{h}_x)_3\) yields a vector \(\boldsymbol{h}_x\) pointing preferably downwards (with a negative z-component) and therefore describing gravitropism. Plagiotropism is obtained by minimising the absolute value \(|(\boldsymbol{h}_x)_3|\), which leads to larger values of \(|(\boldsymbol{h}_x)_1|\) and \(|(\boldsymbol{h}_x)_2|\) and therefore, horizontal growth. Chemotropism is described by maximising \(s(\boldsymbol{x}_p + dx \ \boldsymbol{h}_x)\); thus, we multiply by ( − 1) to obtain a minimisation problem. Objective functions can be freely combined (e.g.: by linear combination). In this way, different kinds of tropisms can be realised for each root type.

Root tip deflection

In many experiments like pot or rhizobox experiments, root growth is spatially bounded (Doussan et al. 2006). We can bound our root growth simulations by an arbitrary geometry which is given implicitly by a signed distance function. The signed distance function determines how close a given point is to a boundary and returns a negative value if the point is outside the boundary. Additionally, this provides a way to include obstacles in our model.

The following algorithm takes the spatial boundaries into account. In a first step, the rotation angles α and β are derived as described in Section “Tropisms”. If the new root tip position does not lie within the geometric boundaries, then a new pair (α, β) is chosen as follows: First, only β is chosen uniformly random between − π and π while α is left unchanged. If, after a maximal number of trials n β , no new valid pair α and β has been found, α is increased for a small fixed angle dα and the procedure for finding an angle β is started again. This simple approach leads to a realistic root behaviour at the boundaries, where thigmotropism can be observed.

Coupling to a soil model

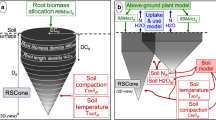
In many applications, it is important to couple a root growth model to soil models because they mutually affect each other (Pierret et al. 2007). For example, root growth influences the nutrient distribution and water content of soil, while root growth itself is dependent on these parameters. Coupling of the models is achieved by operator splitting, i.e. by calculating both models alternately with a sufficiently small time step Δt. The interaction between root growth and soil properties is illustrated in Fig. 4.

Fig. 4
figure 4

Plant and soil interaction by coupling the root growth model with a soil model

Full size image

In our model, the dynamic root growth can be influenced by soil properties in different ways: firstly, by specific tropisms (e.g.: chemotropism, hydrotropism), secondly, by the influence of soil properties on the root elongation rate and thirdly, by changing branching strategies. These three mechanisms describe the key root responses to soil properties (Hodge 2004; Fitter and Stickland 1991). The soil properties are the dynamic output of a soil model. The interaction is implemented in the model as follows.

  • A specific tropism can be chosen which depends on soil properties (e.g. water content, nutrient concentration or temperature). Depending on which plant and soil interaction model is described, combinations of different tropisms such as hydrotropism, chemotropism or thermotropism can be considered, see Eq. 11.

  • The root growth function λ(t) can be related to soil properties, which alters the roots’ elongation rate.

  • The branching strategy can depend on soil properties. In this way the density of lateral branches can vary or the root type of the branches can change.

The root growth model supplies the time dependent three-dimensional geometry of the root system and resulting global parameters such as total length, surface or spatial distributions, see right part of Fig. 4. Generally it is computationally too expensive to directly use the explicit three-dimensional geometry even for the static case. For this reason, density distributions are used to create a sink term in the plant and soil interaction model, which is often described by partial differential equations and numerically solved by the finite element method (Doussan et al. 2006; Javaux et al. 2008). The development of a suitable sink term is crucial and several upscaling techniques are available (Roose and Schnepf 2008). However, these methods often use simplifying assumptions, e.g. that roots are evenly distributed, that soil is homogeneous or that roots are functionally equivalent. Therefore, in general, sink terms need an accurate validation on an experimental basis.

We emphasise that the Matlab code for the root growth model is freely available.Footnote 1 Every production rule has a Matlab file with a corresponding name. This allows to adapt existing production rules and to easily extend the model for new production rules.

The case of phosphate uptake

In the following, we introduce a simple phosphate uptake model to which the root growth model can be coupled. Neglecting convection, we describe the solute transport by the diffusion equation (Barber 1995):

$$ (\theta+b)\frac{\partial c}{\partial t} = \nabla \cdot (D_l f \theta \nabla c) - f(s,t) \label{eqn:from} $$
(12)

where c is the phosphate concentration, t is the time, f(s) is a sink term for phosphate uptake by roots, s is the root surface area per volume of soil, D l is the diffusion coefficient in water, f is the impedance factor, θ is the volumetric water content and b is the buffer power.

For simplicity, and since the aim of this paper is to demonstrate the coupling of the L-System root growth- to a soil model, we assumed that the volumetric sink term is given by

$$ f(s) = s \ \frac{F_m c}{K_m +c}, \label{eqn:sst} $$
(13)

where F m is the maximal influx into the root and K m is the Michaelis Menten constant. This simple sink term will often overestimate uptake. Firstly, root uptake capacity may decrease with root age. Assuming an exponential decrease, the sink term (13) is modified such that

$$ f(s,t) = s \ \frac{F_m c}{K_m +c} \exp(-k \ t_{age}), $$
(14)

where k is the capacity decay constant and t age is the average root surface age. Secondly, in the case of sparingly soluble nutrients such as phosphate, depletion zones around the root limit uptake. Roose and Fowler (2004) presented a sink term for nutrient uptake which considers the creation of depletion zones around individual roots. These three cases will be analysed in our simulations.

At the boundaries representing a pot we apply a no-flux condition:

$$ \nabla c \cdot \boldsymbol{n}= 0, $$
(15)

where the unit normal \(\boldsymbol{n}\) is pointing inside the pot. The initial phosphate concentration is given by

$$ c(\boldsymbol{x},0) = c_0. \label{eqn:to} $$
(16)

Results

We first present the results of the root growth model only, exemplified for maize. We compared our L-System root growth model with the continuous model of Roose et al. (2001) where no stochastic processes are included. Then we simulate the interaction between root system and soil, exemplified for phosphate uptake. We investigated spatial properties of a maize root system confined in a pot and analysed the effect of chemotropism and gravitropism on phosphate uptake by coupling the root growth model to a soil model. Finally, sink terms with different complexities were derived from the simulated root architecture and their effect on phosphate uptake was analysed.

Root growth and architecture

The continuous root growth model of Roose et al. (2001), that is based on a population growth model, was used as a benchmark problem. For model comparison, we parametrised the L-System model such that it had exactly the same behaviour but neglected root mortality. The total root length of every root order over 100 days is given in Fig. 5. The dynamic behaviour of the L-System model is exactly the same as in the growth model given by Roose et al. (2001).

Fig. 5
figure 5

Total root length of each order of a maize root system with 25 initial roots

Full size image

Next we added spatial parameters determining the angle between branch and successive branch \(\delta_0=63^{\circ}\), δ s,0 = 15, \(\delta_1=68^{\circ}\) and δ s,1 = 3 (Shibusawa 1994). To create a more realistic three-dimensional representation of the root system, we added a standard deviation of 10% to all root system parameters (except for δ). We also included gravitropism, choosing N 0,1 = 1.5, N 2 = 0 and \(\sigma_0=20^{\circ}\) cm − 1, \(\sigma_{1,2}=40^{\circ}\) cm − 1, see Section “Tropisms and root tip deflection”. The fibrous root system was created with 25 initial roots, n 0 = 25, starting to grow into a cone with base radius, r 0 = 5, at the same time, see Section “Root systems”. The resulting root system after 25 days is presented in Fig. 6a. This three-dimensional representation of the 25 days old root system was analysed for root length fraction and root surface densities, see Fig. 6b, c. Figure 6c shows the mean root surface area density in volume elements of 1 cm3 along the y-axis. Such densities can be the basis for coupling root growth to a soil model.

Fig. 6
figure 6

Analysis of a simulated maize root system

Full size image

Phosphate uptake from a pot

Having obtained the root architectural traits from our root system model, these results were integrated into a soil model to analyse phosphate uptake. The soil model is given by Eqs. 12–16. The root system grew in a pot with a bottom radius of 3 cm, a top radius of 5 cm and a height of 10 cm. Model parameters were taken from literature and represent typical values for phosphate uptake from soil by maize (Tinker and Nye 2000; Föhse et al. 1991). The initial concentration c 0 was assumed to be 10 − 4 μmol cm − 3, impedance factor f = 0.3, water content θ = 0.4, buffer power b = 100, diffusion coefficient for phosphate \(D_l=10^{-5}\) cm2 s − 1, maximal influx F m was assumed to be 2.76 ·10 − 7 μmol cm − 2 s − 1 and the Michaelis Menten constant \(K_m = 4 \cdot 10^{-4}\) μmol cm − 3.

The phosphate uptake was dependent on the root surface area s per volume of soil. In every time step Δt of 1 day the values of s were determined from the root growth in volume elements of 0.125 cm3. The overall simulation time was 50 days. We used the finite difference method to obtain a numerical solution of the solute transport model.

The first set of simulations studied the effect of different tropisms on phosphate uptake. Chemotropism was included as described in Section “Tropisms” with N 0,1 = 5, \(\sigma_0\!\!=\!\!20^{\circ}\), \(\sigma_1\!\!=\!\!40^{\circ}\). Gravitropism was considered with the same parameters as in Fig. 6a. Uptake was calculated with the simple sink term given in Eq. 13. In order to create a suitable root system for the pot size, initial root system parameters were n 0 = 5 and r 0 = 2. The resulting root systems are shown in Fig. 7a, and c. The nutrient concentrations in the pot are given in Fig. 7b, d. The root system including chemotropism was more evenly distributed due to initially homogeneous phosphate concentration. This results in even depletion of the soil in the pot. The root system with pronounced gravitropism had a higher root density at the bottom of the pot. Hence the soil was less depleted at the top than at the bottom.

Fig. 7
figure 7

Maize growing in a pot with different tropisms: Root distribution (a) and corresponding phosphate concentration (b) in the case of chemotropism (N 0,1 = 5, \(\sigma_0\!=\!20^{\circ}\), \(\sigma_1\!=\!40^{\circ}\)). Root distribution (c) and corresponding phosphate concentration (d) in the case of gravitropism (N 0,1 = 1.5, \(\sigma_0\!=\!20^{\circ}\), \(\sigma_1\!=\!40^{\circ}\))

Full size image

The cumulative phosphate uptake by the two root systems is given in Fig. 8. The root system including chemotropism had an 82% higher cumulative uptake after 50 days under the chosen sets of model assumptions. This result is in agreement with Jackson and Caldwell (1996) who estimated an increase in phosphate uptake due to root proliferation in nutrient rich patches up to 70%.

Fig. 8
figure 8

Cumulative phosphate uptake from a pot as effected by chemotropism and gravitropism due to the simple sink term given in Eq. 13

Full size image

The second set of simulations studied the effect of the different sink terms described in Section “Coupling to a soil model” on phosphate uptake in the case of chemotropism. The resulting cumulative phosphate uptake is shown in Fig. 9. As expected, the simple sink term yielded the largest uptake. When root uptake capacity decreased with age, cumulative uptake was 88% of the first case. We chose the capacity decay constant k to be 0.5 days − 1 such that uptake approaches 0 after 10 days (Ernst et al. 1989). When the individual depletion zones around roots were considered using the model by Roose and Fowler (2004), uptake was 79% of the first case. This indicates that the consideration of individual depletion zones is important, in particular for sparingly mobile nutrients.

Fig. 9
figure 9

Cumulative phosphate uptake from a pot as effected by chemotropism comparing three different sink terms described in Section “Coupling to a soil model”

Full size image

Discussion

L-Systems are a common tool in plant architecture modelling (Prusinkiewicz and Lindenmayer 1990). They have also been used for root architecture modelling, although mainly in the context of visualisation (Prusinkiewicz 1998). We realised an interface in our L-System model which enables coupling the three-dimensional root growth model to any arbitrary soil model. Furthermore, the modular implementation in Matlab allows to define new production rules as required. Most dynamic root system models are based on simple production rules that include emergence of new main axes, growth of the axes and branching (Doussan et al. 2003). L-System formalism is most suitable to describe such production rules. We explicitly stated our production rules and provided the corresponding Matlab files to increase reproducibility.

The way tropisms were implemented in our model differs from previous implementations. The most common approach is to compute the new growth direction by adding vectors denoting the initial growth direction, mechanical constraints and gravitropism (Pagès et al. 1989). Tsutsumi et al. (2003) compute the new growth direction in their two-dimensional model based on differences of elongation rates at the elongation points (located opposite to each other just behind the root tip). In our implementation, the new direction was computed by random minimisation of an objective function. Tropisms were realised by choosing appropriate objective functions. The advantages of this approach are that tropisms can be easily described, see Eq. 11, and that results do not depend on the spatial resolution.

We used a maize root architecture to demonstrate basic features of the proposed model. Maize root lengths found in literature strongly vary depending on maize cultivar and environmental conditions. The presented results lie well in this range and do for example quantitatively correspond to the nitrate inefficient maize breed Wu312 described in Peng et al. (2010).

Root water and nutrient uptake based on three-dimensional root architecture models is commonly included in soil models via sink terms (e.g. Clausnitzer and Hopmans 1994; Somma et al. 1998; Dunbabin et al. 2002, 2006; Doussan et al. 2006; Javaux et al. 2008). Those sink terms depend on root length or root surface densities. The spatial resolution of the soil model for which the densities are computed is often 1 cm3. In our simulations we used half the edge length, i.e. the grid size was 0.125 cm3. However, in our model, the spatial resolution can be freely chosen by the user depending on the scale of the problem. Ge et al. (2000) use the SimRoot model (Lynch et al. 1997) to simulate phosphate acquisition efficiency in dependence on gravitropism. Contrary to our model, this root architecture model is not coupled to a dynamic soil model. It uses the diffusion length of phosphate in soil, \(L=2\sqrt{D_e t}\), where D e is the effective diffusion coefficient, in order to estimate the depletion volume for a root system. No other mechanisms such as root responses to phosphate concentration are considered. This approach provides an estimate for the potential phosphate uptake under the assumption that diffusion is the dominant mechanism in the soil. Somma et al. (1998) base their sink term for nutrient uptake on the root surface density and the local averaged nutrient concentration. Depletion around individual roots is neglected. We used a similar approach in the ‘simple’ and ‘age dependent’ sink term but also provided an example where individual depletion zones were taken into account. In our example water transport was neglected. However, our L-System model was designed in such a way that it can be coupled to models including water transport, e.g. based on the Richards equation as used by Somma et al. (1998). This would enable to study hydrotropism. Advances with regards to additional rhizosphere traits have been made by Dunbabin et al. (2006) by simulating the effects of phospholipid surfactants on water and nutrient uptake. In our example, we did not consider exudation. However, due to the flexibility of our approach, the root growth model can easily be coupled to soil models including exudation. The sink term for nutrient uptake in Dunbabin et al. (2002, 2006) is based on plant demand as well as nutrient concentration at the root surface according to the Baldwin, Nye and Tinker equation. Thus, depletion around individual roots is approximated with a steady rate solution. This is a similar approach like our sink term which considered individual depletion zones based on an approximate analytic solution to the dynamic model (Roose et al. 2001).

In this work we exemplified the coupling of the root system to a soil model with a model for phosphate uptake by a maize root system from a pot. We considered root response via chemotropism as described in Section “The case of phosphate uptake” and via root responses to barriers as described in Section “Root tip deflection”. We compared three different sink terms for nutrient uptake that were based on the root growth model. We showed that neglecting the development of depletion zones around individual roots is likely to overestimate uptake, in particular for nutrients with low mobility such as phosphate. The comparison of the different sink terms indicated that it may be difficult to distinguish between age and depletion effects experimentally in soil. Furthermore, we showed that chemotropism strongly increased phosphate uptake from a pot which is in good agreement with Jackson and Caldwell (1996). As demonstrated by Ge et al. (2000), this is due to overlapping depletion zones in the case of gravitropism.

A comparison to measurement results from literature on phosphorus uptake of maize in pot experiments required consideration of the soil volume, as well as the growing duration of the maize crop. We converted the results from literature using the pot volume of 509.5 cm3 as taken for our simulation. Data range from 28.74 to 51.66 μmol after 32 days (El Dessougi et al. 2003), and 33.90 to 83.31 μmol after 45 days (Mujeeb et al. 2008) phosphate root uptake depending on fertilization level and fertilizer type. These amounts are higher, but in a similar order of magnitude, as compared to our model outputs. A lower uptake is anticipated considering that we described a low phosphate scenario.

The main benefit of our approach in Matlab is that the L-System model can be easily coupled to arbitrary soil models. Thereby various rhizosphere traits such as nutrient and water uptake and exudation can be modelled in response to root system development and vice versa. The possibility to let the root system grow in a confined environment will be useful for comparison to experimental data from pot or rhizotron experiments.

Conclusions

We presented a new dynamic root architecture model based on L-Systems. The objective of this new model was to realistically represent a three-dimensional root system that was subsequently coupled to a soil model in order to describe the dynamic interactions of both the root system with soil processes (water, solute transport) as well as local soil properties with the rooting pattern (root plasticity, tropism). L-systems provide a compact description of dynamic root system models. Our implementation of the model into Matlab makes it accessible to a wider public and encourages its development with new features. Furthermore it facilitates coupling to different soil models.

We exemplified the proposed root growth model and its interaction with a soil model by simulating phosphate uptake of a maize plant in a confined growth environment (pot experiment). This example demonstrated that our approach provides a convenient tool to create feedback loops between root system and soil. Thus it is possible to analyse both root effects on soil processes via a sink term derived from the architecture model as well as soil property impacts on the root architecture dynamics via tropisms. We implemented chemotropism and were able to clearly reveal substantial effects of root architecture and its interaction with the soil environment on plant nutrient use. Chemotropism increased phosphate uptake by as much as 82% compared to a root system governed by gravitropism only. We compared three different sink terms and analysed their effect on calculated phosphate uptake and found that considering individual depletion zones around each root reduces calculated uptake significantly.

In contrast to existing root growth models, our model can be freely coupled to any soil model and new sink terms can be easily implemented as required. With this approach, we hope to facilitate model development and increase reproducibility of simulation studies.