Abstract
This paper explores the connective ‘because’, based on the idea that ‘C because A’ implies the acceptance/truth of the antecedent A as well as of the consequent C, and additionally that the antecedent makes a difference for the consequent. To capture this idea of difference-making a ‘relevantized’ version of the Ramsey Test for conditionals is employed that takes the antecedent to be relevant to the consequent in the following sense: a conditional is true/accepted in a state \(\sigma \) just in case (i) the consequent is true/accepted when \(\sigma \) is revised by the antecedent and (ii) the consequent fails to be true/accepted when \(\sigma \) is revised by the antecedent’s negation. To extend this to a semantics for ‘because’, we add that (iii) the antecedent and (iv) the consequent are accepted/true in the state \(\sigma \). We get metaphysical or doxastic interpretations of these clauses, depending on what we mean by a model and a state. We introduce several semantics known from suppositional conditionals, which we reinterpret for difference-making conditionals and ‘because’. We present a minimal logic for ‘because’ sentences and show how it can be extended in ways that parallel the hierarchy of extensions of the logic of suppositional conditionals. We establish correspondence results between axioms for ‘because’ and properties of states, and prove that the specified logics are sound with respect to the semantics.
Similar content being viewed by others
1 Introduction: conditionals and ‘because’
Many philosophers felt that there is a close connection between the connective ‘if’ on the one hand and the connectives ‘since’ and ‘because’ on the other. Frege (1892, p. 48), Ramsey (1931, p. 317), Goodman (1947, p. 114), Ryle (1950, pp. 339–340), von Kutschera (1974, pp. 265–268), Pizzi (1980, pp. 75–77), McCall (1983, p. 315) and Blau (2008, p. 164–171) have all voiced their opinions about this idea. For example, it has been argued that ‘because A, C’ implies the conditional ‘if A, then C’, and also the might counterfactual ‘if \(\lnot A\), it might have been the case that \(\lnot C\)’, or even the stronger ‘if \(\lnot A\), it would have been the case that \(\lnot C\)’. There is even a terminological encoding of the similarity of ‘if’ and ‘since’. Goodman called ‘since’ sentences factual conditionals, because their assertion presupposes that the antecedent is (believed to be) a fact. This label makes equally good sense for ‘because’. In this article, we will in fact assume that ‘since’ and ‘because’ are synonymous, and we will mostly talk about ‘because’. We take it that ‘because’ sentences do not necessarily express causal relations, but may express reason relations or explanatory relations in a broader sense.
Given the above-mentioned long tradition of philosophical notes on the relation between ‘because’ and ‘if’, it is a striking and surprising fact that although philosophy, logic, linguistics and psychology have produced a vast literature on the logic of ‘if’ sentences (i.e., on conditional logic), these investigations have not been used to get more insights on ‘because’. Indeed, very little work has been done on the logic of sentences featuring ‘because’.
In this paper, we want to make up for this discrepancy by proposing a logic for ‘because’. We will not, however, use any of the bridges suggested by the philosophers mentioned above. We will follow our own route linking ‘because’ to existing work in conditional logic. We argue that there is a missing link between the suppositional conditionals that are typically the subject of conditional logics and ‘because’ sentences. This missing link are difference-making conditionals. On the one hand, difference-making conditionals are like suppositional conditionals in that they allow for various truth or acceptance values of the antecedent (which is not true for ‘because’). In fact, we think that many conditionals uttered in ordinary discourse are intended as difference-making conditionals, and we’ll give some examples for this claim. On the other hand, difference-making conditionals are like ‘because’ sentences in that they highlight that their antecedent is relevant for their consequent (which is not true for ‘if’ in its suppositional interpretation). That is, supposing the antecedent to be true has the effect of ‘raising’ the truth value or acceptance value of the consequent. This is consonant with the idea that ‘because’ sentences express explanations, that their antecedents name reasons for their consequents. In our approach, difference-making conditionals are stronger than suppositional conditionals, and ‘because’ sentences are in turn stronger than difference-making conditionals.
The plan of the paper is as follows. We first recapitulate some of the most popular logics for suppositional conditionals. We base our subsequent considerations on a minimal core logic and show how it can be extended to some of the most well-known logics for suppositional conditionals. Second, we argue that most of the usual principles for suppositional conditionals fail for ‘because’. Then we introduce several semantics known from suppositional conditionals, which we reinterpret for difference-making conditionals and for ‘because’. In a fourth step, we present our minimal logic for ‘because’ sentences and show how it can be extended in ways that parallel the extensions of the minimal logic of suppositional conditionals. We prove these logics to be sound with respect to the semantics. We then compare our account with related work. In this first and major part of the paper, we argue on the one hand from a number of natural language examples that certain principles should fail for reasoning with ‘because’. On the other hand, we argue from a semantic interpretation of ‘because’ that it should follow certain principles. At the end of our paper, we confront our analysis with a number of examples known to be problematic for models of causal reasoning. Some of them turn out to be problematic for our analysis of ‘because’ sentences, too, others don’t.
2 The logic of suppositional conditionals
We will be using several object languages in this paper. All of them feature the usual truth-functional propositional operators \(\lnot \), \(\wedge \), \(\vee \),  and \(\equiv \). We define the logical constants \(\top \) (verum) and \(\bot \) (falsum) in the obvious way: \(\top \) designates an arbitrary classical propositional tautology, for example \(p \vee \lnot p\), and \(\bot \) designates \(\lnot \top \). We use \(\vdash \) to denote classical consequence. We say that a sentence is factual if it is only composed of the above vocabulary, i.e., factual sentences are the sentences of classical propositional logic.
and \(\equiv \). We define the logical constants \(\top \) (verum) and \(\bot \) (falsum) in the obvious way: \(\top \) designates an arbitrary classical propositional tautology, for example \(p \vee \lnot p\), and \(\bot \) designates \(\lnot \top \). We use \(\vdash \) to denote classical consequence. We say that a sentence is factual if it is only composed of the above vocabulary, i.e., factual sentences are the sentences of classical propositional logic.
Our object languages also feature conditional connectives of three different kinds: the suppositional conditional >, the difference-making conditional \(\gg \) (both read ‘if ..., [then] ...’) and the ‘because’ connective  . \(A \not > B\) is short for the negation of the statement \(A > B\), and similarly for the other conditionals. The semantics for these conditionals will be presented in Sect. 4. In this section, we are concerned with the most important inference principles known from suppositional conditional reasoning. They should be read as follows: If the antecedent conditionals hold, the consequent conditionals hold as well.Footnote 1
. \(A \not > B\) is short for the negation of the statement \(A > B\), and similarly for the other conditionals. The semantics for these conditionals will be presented in Sect. 4. In this section, we are concerned with the most important inference principles known from suppositional conditional reasoning. They should be read as follows: If the antecedent conditionals hold, the consequent conditionals hold as well.Footnote 1
The most prominent principles of suppositional conditionals > are:
-
If \(\vdash A \equiv B\), then: if \(A>C\) then \(B>C\). LLE
-
If \(\vdash B \supset C\), then: if \(A>B\) then \(A>C\). RW
-
\(A>A\). ID
-
If \(A>B\) and \(A>C\), then \(A>B\wedge C\). AND
-
If \(A>C\) and \(A>B\), then \(A\wedge B>C\). CM
-
If \(A\wedge B>C\) and \(A>B\), then \(A>C\). CUT
-
If \(A>C\) and \(B>C\), then \(A\vee B>C\). OR
-
If \(A\vee B>C\), then \(A>C\) or \(B>C\). DR
-
If \(A>C\) and \(A\not >\lnot B\), then \(A\wedge B>C\). RM
LLE is Left Logical Equivalence, RW is Right Weakening, ID is Identity (also known as Reflexivity), AND is also known Conjunction in the Consequent, CM is Cautious Monotonicity, CUT is a kind of reverse version of CM, OR is also known as Disjunction in the Antecedent, DR is Disjunctive Rationality and RM is Rational Monotonicity.
The four principles LLE–AND determine the System B for basic reasoning.Footnote 2 The six principles LLE–CUT determine the System C for cumulative reasoning, the seven principles LLE–OR determine the System P for preferential reasoning.Footnote 3 System P has often been considered to be the conservative core of reasoning with conditionals.Footnote 4 The eight principles LLE–DR determine the System D for disjunctively rational reasoning, the nine principles LLE–RM determine the System R for rational reasoning.Footnote 5
It should be noted that in the presence of Right Logical Equivalence
-
If \(\vdash B \equiv C\), then: if \(A > B\) then \(A > C\). RLE
RW is equivalent to any of the following two conditions:
-
If \(A > B\), then \(A > B \vee C\). DW
-
If \(A > B \wedge C\), then \(A > C\). CW
DW stands for Disjunctive Weakening, CW for Conjunctive Weakening. In fact, we can always replace RW by RLE + DW (Raidl, 2021b, p. 88) or by RLE + CW.
We define the inner necessity \({{\,\mathrm{\boxdot }\,}}A\) and the outer necessity \({{\,\mathrm{\square }\,}}A\) in the following wayFootnote 6:
-
\({{\,\mathrm{\boxdot }\,}}A \,= \ (\top > A)\).
-
\({{\,\mathrm{\square }\,}}A \,= \ (\lnot A > \bot )\).
We let  and
and  denote the inner and outer possibility of A, respectively. In a possible worlds account (see Sect. 4 below), the inner necessity can be interpreted as expressing what is true in the closest possible world(s) and the outer necessity can be thought of as a metaphysical necessity. In a belief revision account (see Sect. 4), the inner necessity can be interpreted as a belief operator (provided we assume that revising by the tautology does not change the agent’s beliefs), and the outer necessity is a doxastic necessity.
denote the inner and outer possibility of A, respectively. In a possible worlds account (see Sect. 4 below), the inner necessity can be interpreted as expressing what is true in the closest possible world(s) and the outer necessity can be thought of as a metaphysical necessity. In a belief revision account (see Sect. 4), the inner necessity can be interpreted as a belief operator (provided we assume that revising by the tautology does not change the agent’s beliefs), and the outer necessity is a doxastic necessity.
The weakest logic that we will consider here, let us call it \({{\,\mathrm{\textbf{B}}\,}}^+\), is \({{\,\mathrm{\textbf{B}}\,}}\) augmented by the following principles:
-
\(\lnot {{\,\mathrm{\boxdot }\,}}\bot \). CONS
-
If \(A>C\), then
 . INC
. INC -
If \({{\,\mathrm{\boxdot }\,}}A\) and \({{\,\mathrm{\boxdot }\,}}C\), then \(A > C\). CPRES
CONS is a Consistency condition, INC is similar to the belief revision principle of Inclusion and CPRES to the belief revision principle of Cautious Preservation.Footnote 7 The last is not to be confused with the (in)famous principle of Preservation
-
If
 , then \(A > C\). PRES
, then \(A > C\). PRES
We do not necessarily assume PRES. And we do not require the following principle of Strong Consistency, which strengthens CONS:
-
If \(A > \bot \), then \(A\vdash \bot \). SCONS
In most systems \({{\,\mathrm{\square }\,}}A\) implies \({{\,\mathrm{\boxdot }\,}}A\). It suffices to apply RW and INC. It is easy to verify that given ID, LLE and RW, we can derive INC, CPRES, PRES from OR, CM, RM, respectively. Furthermore, PRES implies CPRES in the presence of CONS. CONS says that the inner modality (and the outer modality) is consistent. In terms of beliefs, this means that the prior beliefs (and the doxastic necessities) are consistent. In terms of closest worlds, it means that there are always closest possible worlds (and thus always accessible worlds).
We call \(\textbf{B}'\) the system obtained from \(\textbf{B}\) by adding INC and CPRES, and \(\textbf{B}_{\tiny \text{ AGM }}\) the system obtained from \(\textbf{B}\) by adding INC and PRES. We call \(\textbf{BN}\), \(\textbf{PN}\), \(\textbf{DN}\) and \(\textbf{RN}\), the strengthenings of the systems \(\textbf{B}\), \(\textbf{P}\), \(\textbf{D}\) and \(\textbf{R}\) by the principle CONS (Fig. 1).Footnote 8 Thus our system \({{\,\mathrm{\textbf{B}}\,}}^+\) can equivalently be written as \({{\,\mathrm{\textbf{BN}}\,}}+\ \textrm{INC} +\ \textrm{CPRES}\), or as \({{\,\mathrm{\textbf{B}}\,}}'\textbf{N}\). \({{\,\mathrm{\textbf{RN}}\,}}\) can be seen as the non-nested fragment of the Lewisean System \(\textsf{VN} = \textsf{V} + \text{ CONS }\), analysed in Raidl (2019). A hierarchy including \(\textbf{P}\), \({{\,\mathrm{\textbf{D}}\,}}\), \({{\,\mathrm{\textbf{R}}\,}}\), \({{\,\mathrm{\textbf{PN}}\,}}\), \({{\,\mathrm{\textbf{DN}}\,}}\), \({{\,\mathrm{\textbf{RN}}\,}}\), or rather their extensions with unrestricted embeddings and nestings of conditionals, is analysed in Raidl (2021a, ch. 7).
Hierarchy of systems: On the left: the system B for basic reasoning, C for cumulative reasoning, \(\textbf{B}_{\tiny \text{ AGM }}\) for basic reasoning according the AGM theory, P for preferential reasoning, D for disjunctive rational reasoning, R for rational reasoning, and \(\textbf{B}'\) the system obtained from B by adding Inclusion (INC) and Cautious Preservation (CPRES). On the right: the strengthenings of these systems by Consistency (CONS) are denoted by adding the letter N. The basic system considered here is B\(^+\) = B\('\)N
3 Almost all traditional principles for suppositional conditionals fail for ‘because’
It will turn out that only two of the principles for suppositional conditionals remain valid in our modeling of ‘because’, namely LLE and AND. We discuss here a few examples that illustrate how some of the principles can come to fail.Footnote 9 In Sect. 4.3 below we will formalize these examples.
Against Right Weakening. It makes perfect sense to say ‘Because you pay an extra fee (p), your letter will be delivered (q) by express (r)’, since the extra fee will buy you a special service.Footnote 10 But it sounds odd to say ‘Because you pay an extra fee, your letter will be delivered’, since the letter would be delivered anyway, even if you did not pay the extra fee.
Rott (2022a) has argued that it is the hallmark of difference-making conditionals that they do not satisfy Right Weakening. Just as it is the most striking feature of the conditionals modeled by conditional logics in the wake of Stalnaker and Lewis that they don’t validate ‘Left Strengthening’ (also known as Strengthening the Antecedent), it is the most striking feature of difference-making conditionals that they invalidate Right Weakening (or Weakening the Consequent).
Against Cautious Monotony. A research project with two postdoc positions is about to start. I believe that Pam and Quinn will work on the project (p and q), and that the project will be successful (r). I know that Pam is an excellent and dedicated researcher, and if she is missing, the project might fail. On the other hand, I know that Quinn is neither the greatest researcher and nor terribly interested in the topic of the project. But Quinn likes Pam a lot, and if Pam is not in, it is not sure that Quinn will be in. So I think ‘Because Pam works on the project, Quinn will work on it, too’, and I also think ‘Because Pam works on the project, the project will be successful’. It sounds strange, however, to say ‘Because Pam and Quinn work on the project, the project will be successful’, since should one of them not be in the project, it will most likely be Quinn who is missing—remember he is not keen on the topic—and the project will be a success anyway because of Pam’s work.
Against Cut. Another research project with two postdoc positions is about to start. There have been many highly qualified applicants. I believe that Peter and Quiana will work on this project (p and q), and that the project will be successful (r). I know that Peter is not the greatest researcher but an exceptionally nice person, and that Quiana is brilliant but the topic of the project is not her favourite one. However, Quiana likes Peter a lot, and if Peter is not in, it is very unlikely that Quiana will be in. Peter and Quiana form a very good team, but if one of them is missing, this will be Quiana and the project is likely to fail (it is Quiana’s contribution that is crucial for the success of the project). So I think ‘Because Peter works on the project, Quiana will work on it, too’, and I also think ‘Because Peter and Quiana work on the project, the project will be successful’. It sounds strange, however, to say ‘Because Peter works on the project, the project will be successful’, since should Peter not be in the project, it will be successful anyway, as there are many competent applicants for this project.
Against OR. Pam and Quinn live in a village with two pubs. They both prefer the Irish pub to the Spanish pub, but they don’t avoid the latter altogether. I know that they will go out tonight and they want to meet in a pub, but it is not quite clear in which pub. I believe that Pam will go to the Irish pub (p), that Quinn will go to the Irish pub (q), and that they will meet each other (r). It makes sense to say ‘Because Pam goes to the Irish pub, they will meet’, since if Pam does not go to the Irish pub (and goes to the Spanish pub instead), they will most likely miss each other. Similarly for ‘Because Quinn goes to the Irish pub, they will meet’. But it sounds odd to say ‘Because Pam goes to the Irish pub or Quinn goes to the Irish pub, they will meet’, since if neither of them goes to the Irish pub, they will meet each other anyway in the Spanish pub.Footnote 11
4 Semantics
In the debate about conditionals there is a controversy whether conditionals have truth values or only acceptance values. We want to provide a semantics that is flexible enough to accommodate both positions. The most general models of this kind are multi-state models in which the states may either be doxastic states or wordly states. Each state is represented by a set of possible worlds and some choice function over this set.Footnote 12 More traditional possible-worlds models of the Stalnaker-Lewis kind are special cases of multi-state models: they can be identified with models having a multitude of states each of which is associated to a single world which is the “most plausible” world for that state. This then is the distinguished world of the state, and the “plausibility” of the other worlds is reinterpreted as their comparative closeness or similarity to the distinguished world. Such models can be understood as non-doxastic ones, and they provide truth conditions for conditionals at world-state pairs. In the following we will consider truth conditions and acceptance conditions in parallel.
In this paper, we do not want to commit ourselves to the view that sentences with conditionals or ‘because’ as the main connective express propositions. So we consider only flat (non-embedded) conditionals with a factual antecedent A and a factual consequent C. We refrain from insisting that it makes sense to embed conditionals in complex sentences.Footnote 13 For this reason, we can work with very simple single-state models with only a single state.
4.1 Models, satisfaction, validity
A model is a triple \(M = \langle W, \sigma , v\rangle \), where W is a set of possible worlds, v is a valuation function over worlds and propositional variables extended to all factual sentences in the classical Boolean way,Footnote 14 and \(\sigma \) is a choice function over W which assigns to each subset V of W a (possibly empty) subset of V. Thus the following property is satisfied:
-
(id) \(\sigma (V) \subseteq V\).
Since we assume (id), we will also call these models (id)-models.
Our guiding idea is to think of \(\sigma \) as a plausibility function representing our dispositions to restrict attention to certain possible worlds, given certain suppositions. Intuitively, for a subset V of W, \(\sigma \) selects the most plausible elements of V; these are then given by \(\sigma (V)\). An agent whose dispositions are represented by \(\sigma \) and who makes the supposition that V restricts attention to the worlds in \(\sigma (V)\) for her further reasoning. This allows for both a doxastic interpretation and a metaphysical interpretation of M and \(\sigma \). In the doxastic interpretation, M represents an agent’s doxastic state, and \(\sigma (V)\) can be understood as the strongest believed proposition after (hypothetically) revising her beliefs by V. \(\sigma (W)\) can be identified with the strongest proposition currently believed to be true by the agent. In the metaphysical interpretation, M represents a possible-worlds scenario, and \(\sigma (V)\) can be understood as the set of V-worlds that are closest to the actual world. \(\sigma (W)\) then is the set containing only the world that is closest to the actual world, viz., the actual world itself.
If A is a factual sentence, we write  for the A-worlds \(\{w\in W: v(w,A)=1\}\) and drop the subscript if there is no danger of confusion. Factual sentences A are satisfied in worlds as usual: \(w {{\,\mathrm{\vDash }\,}}A\) iff
for the A-worlds \(\{w\in W: v(w,A)=1\}\) and drop the subscript if there is no danger of confusion. Factual sentences A are satisfied in worlds as usual: \(w {{\,\mathrm{\vDash }\,}}A\) iff  . For two factual sentences A and C, the satisfaction of a suppositional conditional \(A>C\) in a model \(M = \langle W, \sigma , v\rangle \) is defined by
. For two factual sentences A and C, the satisfaction of a suppositional conditional \(A>C\) in a model \(M = \langle W, \sigma , v\rangle \) is defined by
-
\(M \;{{\,\mathrm{\vDash }\,}}\, A > C\) iff
 .
.
We also allow negated conditionals and define \(M \,{{\,\mathrm{\vDash }\,}}A \not > C\) as \(M \,{{\,\mathrm{\nvDash }\,}}\, (A > C)\). Let \(X_1, \dots , X_n\) be a (possibly empty) sequence of conditionals or negated conditionals, and let Y be a conditional or a negated conditional or a disjunction ‘\(Y_1\) or \(Y_2\)’ of conditionals. The inference from \(X_1, \dots , X_n\) to Y is valid in a model iff whenever \(\sigma \) satisfies \(X_1, \dots , X_n\), it also satisfies Y (or respectively, it also satisfies \(Y_1\) or satisfies \(Y_2\)).Footnote 15 The inference is valid in a class of models iff it is valid in all models of that class.
Our basic semantics, which we call 0-semantics, has the following additional properties:
- (cons):
-
\(\sigma (W) \ne \emptyset \) .
- (inc):
-
If \(\sigma (V) \subseteq U\), then
 .
. - (cpres):
-
If \(\sigma (W) \subseteq V \cap U\), then \(\sigma (V) \subseteq U\).
We will shortly see that the properties (id), (cons), (inc) and (cpres) correspond to the principles ID, CONS, INC and CPRES, respectively. We will not generally impose the stronger principles
- (scons):
-
If \(\sigma (V) = \emptyset \), then \(V = \emptyset \).
- (pres):
-
If \(\sigma (W) \subseteq U\) and
 , then \(\sigma (V) \subseteq U\).
, then \(\sigma (V) \subseteq U\).
We can now formulate properties corresponding to the principles OR, CM, DR and RM, and just as we extended our minimal logic \({{\,\mathrm{\textbf{B}}\,}}^+\) by the additional principles, we can strengthen our semantics by the corresponding properties:
- (or):
-
\(\sigma (U \cup V) \subseteq \sigma (U) \cup \sigma (V)\).
- (cm):
-
If \(\sigma (U) \subseteq V\), then \(\sigma (U \cap V) \subseteq \sigma (U)\).
- (dr):
-
If \(\sigma (U \cup V) \subseteq T\), then \(\sigma (U) \subseteq T\) or \(\sigma (V) \subseteq T\).
- (rm):
-
If
 , then \(\sigma (U \cap V) \subseteq \sigma (U)\).
, then \(\sigma (U \cap V) \subseteq \sigma (U)\).
The (id)-semantics with (cons), (or), (cm) and (rm) was called consistent Lewisean semantics by Raidl (2019). The weaker (id)-semantics with just (or) and (cm), or the additional (dr) were analysed in Raidl (2021a, ch. 7).
Lemma 1
Every (id)-model validates the principles LLE, RW, AND and ID.
Theorem 1
If a model has the property (cons), (inc), (cpres), (pres), (cm), (or), (dr) or (rm), respectively, it validates the corresponding principle (CONS), (INC), (CPRES), (PRES), (CM), (OR), (DR) or (RM).
We can thus conclude that our 0-semantics validates \({{\,\mathrm{\textbf{B}}\,}}^+\), and that if it has a collection of properties from the above list then it validates the corresponding collection of principles.Footnote 16
We can properly reproduce the Lewisean account, restricted to the flat language, in our models. Lewis’ assumption that the possible worlds can be arranged in nested plausibility spheres is encoded by (id), (or), (cm) and (rm)—call this a Lewisean model. A centered model is a model where \(\sigma (W)\) is a singleton \(\{w_{\sigma }\}\). The world \(w_{\sigma }\) can be thought of as the ‘center’ of the state \(\sigma \) and thus of the Lewisean spheres. Intuitively (and in accordance with Lewis), for all \(V\subseteq W\), \(\sigma (V)\) is the set of V-worlds that are closest or most similar to the world \(w_\sigma \). The move from models to centered models marks a transition from a doxastic interpretation to a metaphysical interpretation of our models. Conditionals can then be interpreted as having truth values—and not just acceptance values—in possible worlds models.
4.2 Suppositional conditionals, difference-making conditionals and ‘because’
We extend the language \({{\,\mathrm{\mathcal {L}}\,}}_>\) so as to feature not only > but also the connectives \(\gg \) and  . As before, we only consider flat conditionals.Footnote 17 Conditionals (with factual antecedent A and factual consequent C) are satisfied in a model \(M = \langle W, \sigma , v\rangle \), and the defining conditions are the followingFootnote 18:
. As before, we only consider flat conditionals.Footnote 17 Conditionals (with factual antecedent A and factual consequent C) are satisfied in a model \(M = \langle W, \sigma , v\rangle \), and the defining conditions are the followingFootnote 18:
Suppositional conditionals:
-
(RT) \(M \;{{\,\mathrm{\vDash }\,}}\, A > C\) iff
 .
.
Difference-making conditionals:
-
(RRT) \(M \;{{\,\mathrm{\vDash }\,}}\, A \gg C\) iff
 and
and  .
.
‘Because’:
-
(RTB)
 iff
iff  and
and  and
and  .
.
A few comments are in order. We have repeated clause (RT) that is reminiscent of the famous Ramsey testFootnote 19 and encodes the suppositional conditional > (or Lewisean conditional). ‘\(M \,{{\,\mathrm{\vDash }\,}}A > C\)’ may generally be read as ‘\(A > C\) holds in M’. According to (RT), the condition for this is that C is true in all worlds from  . In the doxastic interpretation, (RT) requires that C is believed after supposing A and minimally altering one’s beliefs in accordance with that supposition. In this interpretation, ‘\(A>C\) holds in M’ means that \(A > C\) is accepted by the agent whose doxastic state is represented by \(\sigma \). In the metaphysical interpretation, on the other hand, (RT) requires that C is true in the A-worlds that are closest or most similar to the world in \(\sigma (W)\). In this interpretation, ‘\(A>C\) holds in M’ means that \(A >C\) is true in the world in \(\sigma (W)\).
. In the doxastic interpretation, (RT) requires that C is believed after supposing A and minimally altering one’s beliefs in accordance with that supposition. In this interpretation, ‘\(A>C\) holds in M’ means that \(A > C\) is accepted by the agent whose doxastic state is represented by \(\sigma \). In the metaphysical interpretation, on the other hand, (RT) requires that C is true in the A-worlds that are closest or most similar to the world in \(\sigma (W)\). In this interpretation, ‘\(A>C\) holds in M’ means that \(A >C\) is true in the world in \(\sigma (W)\).
In most accounts, (RT) yields that whenever A and C are (believed to be) true in M, then the conditional ‘If A then C’ holds in M—regardless of whether A is in any way (considered to be) relevant for C or whether there is any substantive connection between A and C.Footnote 20 In many contexts, this inference, called conjunctive sufficiency or conjunction conditionalization, is counter-intuitive and should be blocked. Thus (RT) does not take into account a fundamental feature of conditionals as used in natural language: typically, such conditionals do express that the antecedent is relevant to the consequent.Footnote 21
Taking up this idea, (RRT) is reminiscent of the Relevant Ramsey test of Rott (2022a) and encodes the difference-making conditional. Such a conditional \(A\gg B\) holds in a model M just in case (i) B is true at all worlds in  , (ii) but not at all worlds in
, (ii) but not at all worlds in  . Roughly speaking, supposing A makes a difference to the metaphysical or doxastic status of the consequent. The idea of incorporating relevance into the interpretation of conditionals was the basis of Rott (1986), who introduced RRT in a belief-revision interpretation.Footnote 22 Difference-making conditionals express that the antecedent is a “sufficient reason” for the consequent in the sense of Spohn (1983), a notion that was suggested to be applied to conditionals in Spohn (2013, 2015). The logic of such conditionals was analysed by Raidl (2021b, 2021c).
. Roughly speaking, supposing A makes a difference to the metaphysical or doxastic status of the consequent. The idea of incorporating relevance into the interpretation of conditionals was the basis of Rott (1986), who introduced RRT in a belief-revision interpretation.Footnote 22 Difference-making conditionals express that the antecedent is a “sufficient reason” for the consequent in the sense of Spohn (1983), a notion that was suggested to be applied to conditionals in Spohn (2013, 2015). The logic of such conditionals was analysed by Raidl (2021b, 2021c).
The conditions of (RTB) for a ‘because’ sentence  to hold are those of (RRT), namely (i) and (ii), extended by the requirement (iii) of the truth or acceptance of the antecedent and (iv) of the consequent. It is a kind of Ramsey test for ‘because’ sentences. We formally represent ‘because’ by the symbol
to hold are those of (RRT), namely (i) and (ii), extended by the requirement (iii) of the truth or acceptance of the antecedent and (iv) of the consequent. It is a kind of Ramsey test for ‘because’ sentences. We formally represent ‘because’ by the symbol  in this paper.
in this paper.
Overall, (RRT) and (RTB) stepwise strengthen the original Ramsey test (RT). For a conditional to hold in \(\sigma \), (RT) imposes (i) that the consequent is true in the most plausible antecedent worlds, (RRT) adds (ii) that the consequent fails to be true in at least one of the most plausible non-antecedent worlds. (RTB) further adds (iii) that the antecedent is (believed to be) true in the state and that (iv) the consequent is (believed to be) true in the state.
Validity is defined as before. In Sect. 5, we will derive principles of reasoning with ‘because’ from the properties of the choice functions \(\sigma \).
Although widely taken for granted, the semantic postulate of Preservation (pres) and its conditional analogue (PRES) have repeatedly been criticised in belief revision theory and conditional logic alike.Footnote 23 There is no similar discussion of the weaker cousin—Cautious Preservation (CPRES)—nor of Inclusion (INC) for suppositional conditionals. In fact, the semantic conditions (inc) and (cpres) are unavoidable, if we model \(\sigma (V)\) as the minimal V-worlds according to an order relation. They are also unavoidable if we accept the highly entrenched laws of conditional reasoning OR and CM. For this reason, we prefer not to endorse (pres) generally, but do not quarrel with (inc) and (cpres).
In fact, one can show that we need not adopt Preservation at all. In the language  (without > and \(\gg \)), it makes no difference whether the models do or do not satisfy (pres).
(without > and \(\gg \)), it makes no difference whether the models do or do not satisfy (pres).
Lemma 2
For every model M satisfying (id), (cons) and (cpres), and violating (pres), there is a (pres) model \(M'\) with the same worlds and the same valuation which agrees with M on all  -sentences.
-sentences.
Corollary 1
Let C be a class of models satisfying (id), (cons) and (cpres), and \(C'\) the restriction of C to those that satisfy (pres). Then C and \(C'\) have the same  logic.
logic.
Our choice of 0-semantics as the minimal semantics for the modelling of ‘because’ is rooted in our assumption that actual belief is consistent (cons) and our endorsement of (inc) and (cpres), which are weak standard requirements in both doxastic or metaphysical interpretations of conditionals.
4.3 Formalizing the counterexamples
We here briefly formalize the examples from Sect. 3 and illustrate why the principles mentioned there are invalid. For this we use a system of spheres in the style of Grove (1988). In the center of such a system, we find the possible worlds compatible with the agent’s beliefs. These are the most plausible worlds. Should the agent learn, however, that none of these possible worlds is the actual one, she has a first fallback position with the ring of possible worlds around the center. Should she learn that none of these is the actual world either, her next fallback position is the next ring. And so on. Systems of spheres interpreted in this way are essentially equivalent to a total plausibility preordering of W, where w is more plausible than v, in symbols \(w < v\), iff there is a sphere that contains w but doesn’t contain v. Since all possible worlds are comparable in terms of plausibility, it should be noted that this representation makes the conditional > rather strong, and the related hypothetical belief revision is close to the standard AGM belief revision mechanism. But this causes no problems for the argument, since if a principle is invalid for a strong semantics, it is invalid for any weaker semantics. Thus to show that the principles RW, CM, CUT and OR are invalid in our ground semantics, it suffices to show that they are invalid in a stronger semantics for ‘because’.
Against Right Weakening. Recall our example: It is fine to say ‘Because you pay an extra fee (p), your letter will be delivered (q) by express (r)’, formalized as  . But it sounds odd to say ‘Because you pay an extra fee, your letter will be delivered’, formalized as
. But it sounds odd to say ‘Because you pay an extra fee, your letter will be delivered’, formalized as  . Figure 2 gives a diagram representing this situation.
. Figure 2 gives a diagram representing this situation.
The figure is to be read as follows. The most plausible worlds are all in the inner circle. Each of them make p, q and r true. That is, we believe p, q and r. We also believe \(q \wedge r\) given p, since the most plausible p-worlds (in the inner circle) are \(q \wedge r\)-worlds. And we don’t believe \(q \wedge r\) given \(\lnot p\), since some of the most plausible \(\lnot p\)-worlds (like the one designated by the red spot and in the second circle) is not an r-world. That is, we accept the suppositional conditional ‘if you hadn’t payed the extra fee, your letter might not have been delivered by express’. However, we also accept the suppositional conditional ‘if you hadn’t payed the extra fee, your letter would have been delivered’, since the most plausible \(\lnot p\)-worlds (in the second circle but outside the p-area) are in fact q-worlds. And thus we reject ‘if you hadn’t payed the extra fee, your letter might not have been delivered’. This is why we reject ‘your letter will be delivered, because you pay the extra fee’. We won’t repeat such a detailed analysis for the following illustrations.
Against Cautious Monotony. Our example was that we accept ‘Because Pam works on the project (p), Quinn will work on it, too (q)’, formalized as  . We also accept ‘Because Pam works on the project (p), the project will be successful (r)’, formalized as
. We also accept ‘Because Pam works on the project (p), the project will be successful (r)’, formalized as  . But in the situation described, we would reject ‘Because Pam and Quinn work on the project, the project will be successful’, formalized as
. But in the situation described, we would reject ‘Because Pam and Quinn work on the project, the project will be successful’, formalized as  . The reason was that we think that Quinn is not competent and is not interested in the project, but wants to work with Pam. Figure 3 depicts this situation. We accept \(\lnot (\lnot p > q)\) and \(\lnot (\lnot p > r)\), but we reject \(\lnot (\lnot (p \wedge q) > r)\), since we accept \(\lnot (p \wedge q) > r\).
. The reason was that we think that Quinn is not competent and is not interested in the project, but wants to work with Pam. Figure 3 depicts this situation. We accept \(\lnot (\lnot p > q)\) and \(\lnot (\lnot p > r)\), but we reject \(\lnot (\lnot (p \wedge q) > r)\), since we accept \(\lnot (p \wedge q) > r\).
Against Cut. We accept ‘Because Peter works on the project (p), Quiana will work on it, too (q)’, formalized as  , and we also accept ‘Because Peter and Quiana work on the project, the project will be successful (r)’, formalized as
, and we also accept ‘Because Peter and Quiana work on the project, the project will be successful (r)’, formalized as  . But we reject ‘Because Peter works on the project, the project will be successful’, formalized as
. But we reject ‘Because Peter works on the project, the project will be successful’, formalized as  . The project will be successful due to Quiana, and Quiana will work on the project because Peter works on it, but Peter will make no contribution to the project. Figure 4 presents a diagram illustrating this situation. We accept \(\lnot (\lnot p > q)\) and \(\lnot (\lnot (p \wedge q) > r)\), but we reject \(\lnot (\lnot p > r)\), since we accept \(\lnot p > r\).
. The project will be successful due to Quiana, and Quiana will work on the project because Peter works on it, but Peter will make no contribution to the project. Figure 4 presents a diagram illustrating this situation. We accept \(\lnot (\lnot p > q)\) and \(\lnot (\lnot (p \wedge q) > r)\), but we reject \(\lnot (\lnot p > r)\), since we accept \(\lnot p > r\).
Against OR. In our example we accepted ‘Because Pam goes to the Irish pub, they will meet’ ( ), and ‘Because Quinn goes to the Irish pub, they will meet’ (
), and ‘Because Quinn goes to the Irish pub, they will meet’ ( ), but we would reject ‘Because Pam goes to the Irish pub or Quinn goes to the Irish pub, they will meet’ (
), but we would reject ‘Because Pam goes to the Irish pub or Quinn goes to the Irish pub, they will meet’ ( ), This situation is depicted in Fig. 5. We accept \(\lnot (\lnot p > r)\) and \(\lnot (\lnot q > r)\), but we reject \(\lnot (\lnot (p \vee q) > r)\), since we accept \((\lnot p \wedge \lnot q) > r\).
), This situation is depicted in Fig. 5. We accept \(\lnot (\lnot p > r)\) and \(\lnot (\lnot q > r)\), but we reject \(\lnot (\lnot (p \vee q) > r)\), since we accept \((\lnot p \wedge \lnot q) > r\).
5 Logics for ‘because’
5.1 Translation and backtranslation
Now we will concentrate on two sublanguages. The first language \({{\,\mathrm{\mathcal {L}}\,}}_>\) has just > as a non-classical connective. The other one,  , has
, has  and \({{\,\mathrm{\boxdot }\,}}\) as non-classical connectives. We correspondingly denote the restricted semantic relations by \({{\,\mathrm{\vDash }\,}}_>\) and
and \({{\,\mathrm{\boxdot }\,}}\) as non-classical connectives. We correspondingly denote the restricted semantic relations by \({{\,\mathrm{\vDash }\,}}_>\) and  . We want to find the logic for
. We want to find the logic for  , and for this we will use two translations between the languages and our knowledge about the logic for the suppositional conditional >. We need \({{\,\mathrm{\boxdot }\,}}\) in the language for ‘because’ for the following reason:
, and for this we will use two translations between the languages and our knowledge about the logic for the suppositional conditional >. We need \({{\,\mathrm{\boxdot }\,}}\) in the language for ‘because’ for the following reason:
Lemma 3
\({{\,\mathrm{\boxdot }\,}}\) is not definable in terms of  .
.
The relation between the two languages is given by:
Lemma 4
In all models we have (1), in all 0-models we have (2), and assuming additionally (pres) we have (3) and (4):
-
(1)
 iff \(M {{\,\mathrm{\vDash }\,}}_> \top > A\).
iff \(M {{\,\mathrm{\vDash }\,}}_> \top > A\). -
(2)
 iff \(M {{\,\mathrm{\vDash }\,}}_> (\top> A) \wedge (\top> C) \wedge (\lnot A \not > C)\).
iff \(M {{\,\mathrm{\vDash }\,}}_> (\top> A) \wedge (\top> C) \wedge (\lnot A \not > C)\). -
(3)
 iff \(M {{\,\mathrm{\vDash }\,}}_> (\top> C) \wedge (\lnot A \not > C)\).
iff \(M {{\,\mathrm{\vDash }\,}}_> (\top> C) \wedge (\lnot A \not > C)\). -
(4)
\(M {{\,\mathrm{\vDash }\,}}_> A > C\) iff
 .
.
The meanings of some particular ‘because’ conditionals in the doxastic interpretation are collected in Table 1.
5.2 Systems for ‘because’
We are finally in a position to list the central principles of our systems for because.
-
If \(\vdash A\), then \({{\,\mathrm{\boxdot }\,}}A\). N
-
If \({{\,\mathrm{\boxdot }\,}}(A \supset B)\) and \({{\,\mathrm{\boxdot }\,}}A\), then \({{\,\mathrm{\boxdot }\,}}B\). K
-
Not \({{\,\mathrm{\boxdot }\,}}\bot \). D
-
If \(\vdash A \equiv B\), then: if
 then
then  . LLE
. LLE -
If \(\vdash A \equiv B\), then: if
 then
then  . RLE
. RLE -
If
 , then \({{\,\mathrm{\boxdot }\,}}A\). BA
, then \({{\,\mathrm{\boxdot }\,}}A\). BA -
If
 , then \({{\,\mathrm{\boxdot }\,}}B\). BC
, then \({{\,\mathrm{\boxdot }\,}}B\). BC -
 . NTC
. NTC -
If
 , then
, then  . VDW
. VDW -
If
 and \({{\,\mathrm{\boxdot }\,}}B\), then
and \({{\,\mathrm{\boxdot }\,}}B\), then  . CW*
. CW* -
If
 , then
, then  or
or  . AND*
. AND* -
If
 and \({{\,\mathrm{\boxdot }\,}}B\), then
and \({{\,\mathrm{\boxdot }\,}}B\), then  or
or  . CUT*
. CUT* -
If
 , then
, then  or
or  . OR*
. OR* -
If
 and \({{\,\mathrm{\boxdot }\,}}B\), then
and \({{\,\mathrm{\boxdot }\,}}B\), then  or
or  . CM*
. CM* -
If
 and
and  , then
, then  . DR*
. DR* -
If
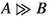 and
and  , then
, then  . RM*
. RM*
The core of the logic is given by the first eleven principles from N to AND*. We denote this logic by \({{\,\mathrm{\textbf{BEC}}\,}}\). Extensions are given by adding any (combination) of the remaining principles CUT*, OR*, CM*, DR* or RM*.
The starred labels may strike the reader as surprising. The principles with starred labels are best understood as obtained by backtranslating the original principles for > and sometimes applying some further logical simplifications involving other principles. The first three principles (N)–(D) are standard assumptions for a belief modality. It follows that belief is monotone,Footnote 24 closed under conjunction and consistent. LLE and RLE are Left Logical Equivalence and Right Logical Equivalence. But in \({{\,\mathrm{\textbf{BEC}}\,}}\) the stronger RW is invalid. The reader might ask why we endorse LLE (and relatedly RLE). After all, ‘because’ might be hyperintensional, just as ‘if’ has been suggested to be hyperintentional, for instance by Fine (2012). We realize that this is an interesting topic for future research, but in this paper we take LLE and RLE as simplifying assumptions and assume ‘because’ to be an intensional connective.Footnote 25 BA and BC are our fundamental assumptions that the explanans (antecedent) and the explanandum (consequent) of an explanation are believed. NTC stands for No Tautological Consequent and says that there is no relevant antecedent for the tautology. It corresponds to the principle CN \(A > \top \), but in the language of  it is expressed by the negation of CN. CW* is obtained as a backtranslation from CW, and thus in a way corresponds to RW. VDW stands for Very Weak Disjunctive Weakening and says that one can always weaken an explanatory conditional by introducing the antecedent as additional disjunct in the consequent. AND* is obtained as a backtranslation of AND. Both VDW and AND* constitute weak replacements for Right Weakening which is invalid for ‘because’.
it is expressed by the negation of CN. CW* is obtained as a backtranslation from CW, and thus in a way corresponds to RW. VDW stands for Very Weak Disjunctive Weakening and says that one can always weaken an explanatory conditional by introducing the antecedent as additional disjunct in the consequent. AND* is obtained as a backtranslation of AND. Both VDW and AND* constitute weak replacements for Right Weakening which is invalid for ‘because’.
CUT* and CM* are more complex. CUT* says that if A is a reason for C but not for the belief B, then the material implication \(B \supset A\) is a reason for C. CM* says that if A is neither a reason for C nor for the belief B, then the material conditional \(B \supset A\) is not a reason for C either. Taken together, CUT* and CM* imply that if A is not a reason for the belief B then: A is a reason for C if and only if the weaker \(B \supset A\) is already a reason for C. OR*, DR* and RM* are rather simple. OR* says that if neither A nor B is a reason for C, then they cannot jointly be a reason for C. DR* says that reasons can be conjunctively conjoined in the antecedents of factive conditionals with the same consequent. While Rational Monotonicity for suppositional conditionals is a rather complicated principle involving a negated conditional in the antecedent (a so-called non-Horn principle), its counterpart RM* for  is rather simple and intuitive: If B because A, and C because A or B, then C because A. In general, the counterparts of Horn principles frequently become non-Horn, and vice versa.
is rather simple and intuitive: If B because A, and C because A or B, then C because A. In general, the counterparts of Horn principles frequently become non-Horn, and vice versa.
Note that due to CW* and RLE, the conjunction of the three principles BA, BC and VDW can equivalently be expressed as a single more compact principle.
-
 iff \({{\,\mathrm{\boxdot }\,}}A\) and \({{\,\mathrm{\boxdot }\,}}B\) and
iff \({{\,\mathrm{\boxdot }\,}}A\) and \({{\,\mathrm{\boxdot }\,}}B\) and  B
B
B together with CW* is the proper axiom of the logic of ‘because’ in the sense of Raidl (2021b). Together with LLE and RLE they form a minimal core for the logic of ‘because’.
Theorem 2
The above principles from \({{\,\mathrm{\textbf{BEC}}\,}}\) are valid in our 0-semantics. And if the semantics validates CUT, OR, CM, DR, RM in \({{\,\mathrm{\mathcal {L}}\,}}_>\), then it validates CUT*, OR*, CM*, DR*, RM* in  .
.
One can in fact prove a stronger result: the principles of \({{\,\mathrm{\textbf{BEC}}\,}}\) determine the 0-semantics. And the reverse of the second statement holds, too.Footnote 26
5.3 Further derivable principles and validities
The following lemma lists further interesting principles.
Lemma 5
The following principles are derivable in BEC:
-
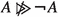 . AT
. AT -
 . NTA
. NTA
If we additionally assume OR*, we can also derive:
-
If
 and \({{\,\mathrm{\boxdot }\,}}C\), then
and \({{\,\mathrm{\boxdot }\,}}C\), then 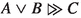 . COND*
. COND*
AT stands for Aristotle’s Thesis. It is a fundamental principle of connexive logic and says that a sentence cannot explain its negation. NTA stands for No Tautological Antecedent and says that tautologies are not relevant for anything. NTA and NTC taken together tell us that tautologies do not enter into relevance relations. COND* says that if \(A\vee B\) is not a reason for a belief C, then A cannot be a reason for \(B \vee C\). It is a problematic principle that will be discussed in Sect. 7.
6 Comparison with other work
We believe that the systems introduced and discussed in this paper constitute the first systematic study of logics for ‘because’. Our semantics closely links the meaning of ‘because’ to the meaning of ‘if’. As a consequence, our logics for ‘because’ are closely related and comparable to the standard systems of conditional logic that have been studied over the last 50 years. To the best of our knowledge, there has so far been no comparable work on the logic of ‘because’ or ‘since’.
There are nonetheless some works that may be compared to our approach. Some works aim at a logic of ‘because’ rather directly; some works offer alternatives to the account of difference-making conditionals; some works address similar problems in a probabilistic framework. We briefly comment on each of these approaches in turn.
6.1 Work on ‘because’
Burks (1951) developed an early proposal for a kind of causal conditional called ‘causal implication’ and a kind of counterfactual called ‘counterfactual implication’, assuming the latter to be definable from the former by adding that the antecedent is false. Burks’s implication is supposed to express causal sufficiency which he analyzes with the help of a strict implication, with the necessity behaving like a normal Kripke necessity. As a consequence, his causal implication validates rather undesirable laws, such as Strengthening the Antecedent, (weak) Transitivity, Contraposition and the paradoxes of strict implication. We hope to have made it clear that these principles cannot hold for the natural-language connective ‘because’.
Urchs (1994) investigates principles for a precausal connective, listing good principles that should be valid and bad principles that should be invalid. There are some axiomatic similarities to our account, since he rejects symmetry as well as asymmetry as general principles, and also rejects Contraposition and Strengthening the Antecedent. His connective is factive. However, he endorses Conjunctive Weakening. The latter fails, however, for ‘because’, since Right Weakening fails.
Schnieder’s (2011) paper on “A logic for ‘because’ ” is very different from, and can hardly be compared to, the work in conditional logic. He motivates the axioms for his logic based on a particular kind of ‘because’—the noncausal ‘because’ appearing in the literature on grounding. A similarity with our account are Schnieder’s truth axioms, according to which ‘because’ implies the truth of the antecedent as well as of the consequent, and thus his grounding ‘because’ is factive. But his approach differs from ours significantly. On the one hand, Schnieder’s axiomatic system is rather weak. In particular, ‘because’ is treated as hyperintensional, so that equivalent sentences cannot be substituted in the scope of ‘because’ and LLE and RLE become invalid. On the other hand, Schnieder’s system is rather strong, since his ‘because’ is required to be asymmetric and transitive. In contrast, our ‘because’ invalidates asymmetry and transitivity. Concerning transitivity, this is just as it should be in a general analysis of ‘because’. From the premises ‘Because Hinckley fired at Reagan, agent McCarthy threw himself in front of Reagan’ and ‘Because Agent McCarthy threw himself in front of Reagan, Reagan survived March 30, 1981’ it does not follow that ‘Because Hinckley fired at Reagan, Reagan survived March 30, 1981.’ Concerning asymmetry, we say more in Sect. 7.
Andreas and Günther (2019) offer a formal analysis of ‘because’ that has some similarities to our doxastic interpretation. Like Rott (2022a), they pick up on an idea contained in Rott (1986) and emphasize that ‘because’ is factive and not strictly asymmetric. However, they use a variant of the Ramsey Test, contracting first to ensure that any beliefs about the antecedent and about the consequent (or their negations) get eliminated, and then expanding by the antecedent. Andreas and Günter do not offer a logic for ‘because’, but such an analysis might be given if the properties of the contraction operation with respect to the antecedent and the consequent were analyzed in detail.
6.2 Alternatives to difference-making conditionals
Fariñas del Cerro and Herzig (1996) frame their work in the context of belief change theories. They use the formula ‘\(A \leadsto C\)’ to express that ‘C depends on A’. After non-trivial adaptations to our framework are made, this is equivalent to \({{\,\mathrm{\boxdot }\,}}C\) and \(\lnot A \not > C\).Footnote 27 If we assume PRES (and CONS), this in turn is equivalent to our definition of  (see part 3 of Lemma 4). Thus the formula \(A \leadsto C\) seems to express exactly the same content as our ‘C, because A’.
(see part 3 of Lemma 4). Thus the formula \(A \leadsto C\) seems to express exactly the same content as our ‘C, because A’.
However, the equivalence only holds in a rather strong semantics, and differences emerge as soon as we drop PRES or admit incomparabilities.Footnote 28 Consider the example given in Fig. 6 with a language having only two propositional variables p and q. The example violates Preservation, since we have \(\top > q\) and \(\top \not > p\), but \(\lnot p \not > q\). In such a context, Fariñas and Herzig’s analysis (FH) of dependency and our analysis (RTB) of ‘because’ diverge: we have \(p\leadsto q\) but not  .Footnote 29 It is intuitively clear that an agent would not accept ‘q, because p’ in this situation because she does not believe that the antecedent p is true. ‘Because’ is factive in the antecedent. If we want to be able to do without full comparability (or without Preservation) and retain factivity, we must add, as we did, that the antecedent is believed as a defining condition for ‘because’.
.Footnote 29 It is intuitively clear that an agent would not accept ‘q, because p’ in this situation because she does not believe that the antecedent p is true. ‘Because’ is factive in the antecedent. If we want to be able to do without full comparability (or without Preservation) and retain factivity, we must add, as we did, that the antecedent is believed as a defining condition for ‘because’.
A further difference to Fariñas and Herzig is that their semantics is rather strong. In our terminology, they consider models for the logic \(\textbf{RN} + \text{ SCONS }\). SCONS allows them to treat the outer modality as validity or logical truth. This, however goes against the now standard precaution to distinguish metaphysical or doxastic necessity from the stronger logical necessity. For this reason, we consider SCONS as a dubious axiom.
We already mentioned that Spohn’s notion of sufficient reason has essentially the same structure as the difference-making conditional. And Spohn’s account can be captured by a semantics with the conditional logic \(\textbf{RN}\) (Raidl 2019). As a consequence, our strongest doxastic analysis of ‘C, because A’ captures essentially the same idea as A being a sufficient reason for C joined with having the reason A.Footnote 30
A structurally different account is the ‘evidential conditional’ studied by Crupi and Iacona (2022a) in the framework of a possible world semantics. Their evidential conditional can be defined from a Lewisean suppositional conditional > by putting \(A \vartriangleright B\) iff \(A > B\) and \(\lnot B > \lnot A\). The evidential conditional thus has Contraposition built into it, which is invalid for our ‘because’. Further differences are that the evidential conditional validates AND, CM, OR and even Supraclassicality, as well as the so-called paradoxes of strict implication, i.e., Necessary Consequent and Impossible Antecedent (Raidl, Iacona and Crupi 2022). The evidential conditional is not factual. The only similarity to difference making and our ‘because’ is that Right Weakening is violated—this violation being the ‘hallmark of relevance’. One may very well, however, base a definition for ‘because’ on \(\vartriangleright \) by adding that the antecedent and the consequent are (believed to be) true; the logic of such a connective remains yet to be explored. Rott (2022b), however, raises serious doubts as to whether Contraposition is suitable for capturing the idea of evidence or support.
6.3 Probabilistic accounts
The study of a logic of conditionals that incorporates relevance in a probabilistic framework has only begun very recently, with the analysis of ‘evidential conditionals’ by Douven (2016, Ch. 5), Crupi and Iacona (2022b) and van Rooij and Schulz (2022).
Douven’s account of an evidential conditional \(A \Rightarrow C\) is a refinement of the combination of probabilistic relevance \(P(C|A) > P(C)\) and high conditional probability \(P(C|A)>t\) for an appropriate threshold t. Whereas high conditional probability is known to invalidate AND (cf. Hawthorne and Makinson 2007), probabilistic relevance is known to validate symmetry. Like our ‘because’, Douven’s evidential conditional violates RW, and it also invalidates AND, CM, CUT and OR. In addition, it is not factive.
Crupi and Iacona’s probabilistic evidential conditional, although having a slightly different logic from their possible-worlds based account, also violates RW and validates AND, but it in addition validates CM, OR and Contraposition. It is also not factive.
According to van Rooij and Schulz (2022), a relevance-based conditional \(A \Rightarrow C\) holds when the causal power of A for C is high, i.e., \(\frac{P(C|A)-P(C|\lnot A)}{1-P(C|\lnot A)} > t\) for an appropriate threshold t. If \(P(C|\lnot A) = 0\) we obtain high conditional probability. If we disregard the subtraction in the denominator and set t to 0, we obtain probabilistic relevance, since \(P(C|A) > P(C|\lnot A)\) iff \(P(C|A) > P(C)\).Footnote 31 So far the logic for this notion of causal power has not been determined. Note, however, that AND will fail, and that this connective, too, will not be factive.
7 Problem cases
So far we have argued that certain first principles should hold for reasoning with ‘because’. We have built a formal framework for these natural ideas and outlined the logic for ‘because’ that flows naturally from our premises. In this section, we confront our analysis with a number of examples that are known to be pose problems for models of causal reasoning. A word of caution is in order, though: problematic examples for causation are not necessarily problematic when transferred to the discussion of ‘because’ sentences. While a causal relation can always be expressed by a ‘because’ sentence, it must be borne in mind that ‘because’ sentences can be used to express non-causal explanatory relations, too. And thus, not every ‘because’ sentence expresses a causal relation.
Unless stated otherwise, we will make the simplifying assumption that the selection function \(\sigma \) is based on a plausibility order <. That is, there is a strict transitive relation < over \(W' \subseteq W\) such that \(\sigma (V) = \min _< (V \cap W')\), where \(\min _< X = \{y \in X:\) there is no \(x \in X\) such that \(x < y\}\). Here \(x<y\) is read as ‘x is more(!) plausible than y’.
Reflexivity.Footnote 32 On our account,  holds if and only if A is a belief the negation of which is possible. So ‘A, because A’ is a contingent sentence that may, but need not be true. In conditional logic many people think that Reflexivity should be axiomatic. This is in stark contrast to causation and explanation. It seems that A cannot possibly ever cause or explain itself. Not everyone agrees: Halpern (2016, p. 17), for instance, holds that reflexivity is a natural property of his ‘affects’ relation. Another possible reaction to this problem is to say that ‘A, because A’ is a limiting case in our formalization that can and should be dealt with just according to what one’s best theory tells us.
holds if and only if A is a belief the negation of which is possible. So ‘A, because A’ is a contingent sentence that may, but need not be true. In conditional logic many people think that Reflexivity should be axiomatic. This is in stark contrast to causation and explanation. It seems that A cannot possibly ever cause or explain itself. Not everyone agrees: Halpern (2016, p. 17), for instance, holds that reflexivity is a natural property of his ‘affects’ relation. Another possible reaction to this problem is to say that ‘A, because A’ is a limiting case in our formalization that can and should be dealt with just according to what one’s best theory tells us.
Asymmetry. Since causation is asymmetric, one may be inclined to think that because should be asymmetric as well. This inference, however, would only be admissible if all ‘because’ sentences could be rephrased in terms of causing. As already mentioned, we think that this is not the case. We can always express the fact that p causes q by the sentence ‘q because p’; but not every such ‘because’ sentence expresses a causal relation. Other than for causation, asymmetry is not always to be expected for explanation. Sometimes an effect may be regarded as a reason for, or an explanation of, the (fact that we infer the) cause, as for example in an inference to the best explanation. And this, too, can be expressed by ‘because’ sentences. We can say both ‘Because Carol is at home, her apartment is lit’ (which may track a causal relation) and ‘Carol is at home, because her apartment is lit’ (which may be seen as tracking a converse ‘is evidence for’ relation).Footnote 33 Our account makes room for such symmetric explanations, thus violating asymmetry. Yet it does not fall into the other extreme of validating symmetry, contrary to the probabilistic concept of dependency or relevance.
The problem, on our account, is rather that symmetric explanations are abundant. Consider a situation in which you believe, with good justification, that Pam and Quentin, a married couple, are at Frieda’s party. However, you are not entirely sure, because you know that they have also been invited by Ben. You think it is not impossible that either (i) they both went to Ben’s party ( ) or that they split and (ii) Pam went to Frieda and Quentin went to Ben (
) or that they split and (ii) Pam went to Frieda and Quentin went to Ben ( ) or (iii) Quentin went to Frieda and Pam went to Ben (
) or (iii) Quentin went to Frieda and Pam went to Ben ( ). Actually, you think that if they aren’t both at Frieda’s party, each of the three possibilities (i), (ii) and (iii) is equally plausible. In this case, our analysis then commits us to accepting both ‘Pam went to Frieda’s party because Quentin went’ (
). Actually, you think that if they aren’t both at Frieda’s party, each of the three possibilities (i), (ii) and (iii) is equally plausible. In this case, our analysis then commits us to accepting both ‘Pam went to Frieda’s party because Quentin went’ ( ) and ‘Quentin went to Frieda’s party because Pam went’ (
) and ‘Quentin went to Frieda’s party because Pam went’ ( ); see part (1) of Fig. 7. This may seem strange. But perhaps it is an adequate result. They are a married couple after all, and both of them being at Ben’s party is just as plausible as only one of them being there. So p and q seem to explain each other. Parts (2) and (3) of Fig. 7 show how alternative plausibility orderings give rise to other acceptance and rejection patterns of ‘because’ sentences.
); see part (1) of Fig. 7. This may seem strange. But perhaps it is an adequate result. They are a married couple after all, and both of them being at Ben’s party is just as plausible as only one of them being there. So p and q seem to explain each other. Parts (2) and (3) of Fig. 7 show how alternative plausibility orderings give rise to other acceptance and rejection patterns of ‘because’ sentences.
Sufficient reasons.Footnote 34 Consider a situation in which a reasoner accepts the sentence (i) ‘Peter went to the party because he was invited to the party and he wanted to get drunk.’ If we suppose that the ‘because’ clause specifies sufficient reasons for the main clause, it may seem that, on our analysis, the reasoner is committed to accepting also the reverse, (ii) ‘Peter was invited to the party and wanted to get drunk because he went to the party.’ If the reasons given in (i) are considered as sufficient, then supposing that Peter didn’t go to the party will result in giving up the reasons. Now it looks as if we are caught with a counter-intuitive result regarding the acceptance of (ii). The two reasons mentioned are only sufficient in the context of the particular situation at hand—which is captured, in our model, by the selection function. In order to see whether sentence (ii) is acceptable, we have to look at the situation carefully. There are situations in which (ii) is indeed acceptable, namely when the counterfactual assumption that Peter didn’t go to the party would lead the reasoner to abandon the conjunction ‘Peter was invited to the party and he wanted to get drunk’. But this need not be the case. If, for example, the reasoner is very sure for independent reasons that Peter was invited and wanted to get drunk, then the counterfactual assumption of his absence would make her rather believe that Peter was sick, had an accident or faced some other strong impediment that prevented him from coming. So the acceptability of (ii) depends on whether Peter’s presence is evidence for his being invited (i) and desiring to get drunk (d).
Now one may object: The example can be strengthened by appending to the conjunction in the ‘because’ clause of (i) and the main clause of (ii) that none of the potential impediments is present: that Peter isn’t sick, doesn’t have an accident, etc (\(q_1\wedge \dots \wedge q_n\)). By using such an extended conjunction, the speaker takes care to specify ‘fully sufficient reasons’ for Peter’s going to the party (p). In our model, it makes sense then to render the extended ‘fully sufficient’ form of (i) as the modal (i\(^f\))  , and the question is whether (i\(^f\)) entails that (ii\(^f\))
, and the question is whether (i\(^f\)) entails that (ii\(^f\))  . To this we reply that, first, extending the natural-language sentence (i) in such a way would result in a rather long and unnatural ‘because’ sentence, one that would hardly ever be uttered in normal conversations.Footnote 35 But second, it is true that our analysis predicts that (ii\(^f\)) be accepted if (i\(^f\)) is accepted, \(i, d, q_1, \ldots , q_n, p\) are believed and the side condition \(\lnot \Box p\) is accepted, too. Given that the reasoner believes that all parts of the fully specified conjunctive sufficient reason are true, the fact that Peter goes to the party is evidence for this sufficient reason (unless Peter goes to the Party necessarily). Correspondingly, according to our analysis, ‘because’ comes out symmetric for all truly sufficient reasons in the above modal sense. We do not think that this is a counterintuitive result. A problem will arise, however, in the case of (presumed) overdetermination—another problem to which we now turn.
. To this we reply that, first, extending the natural-language sentence (i) in such a way would result in a rather long and unnatural ‘because’ sentence, one that would hardly ever be uttered in normal conversations.Footnote 35 But second, it is true that our analysis predicts that (ii\(^f\)) be accepted if (i\(^f\)) is accepted, \(i, d, q_1, \ldots , q_n, p\) are believed and the side condition \(\lnot \Box p\) is accepted, too. Given that the reasoner believes that all parts of the fully specified conjunctive sufficient reason are true, the fact that Peter goes to the party is evidence for this sufficient reason (unless Peter goes to the Party necessarily). Correspondingly, according to our analysis, ‘because’ comes out symmetric for all truly sufficient reasons in the above modal sense. We do not think that this is a counterintuitive result. A problem will arise, however, in the case of (presumed) overdetermination—another problem to which we now turn.
Plausibility orderings for the worlds pqr,  ,
,  ,
,  , .... Implausible worlds are not represented. In (1)
, .... Implausible worlds are not represented. In (1)  ,
,  ,
,  . In (2)
. In (2)  ,
,  ,
,  . In (3)
. In (3)  ,
,  ,
,  . In (4)
. In (4)  ,
,  ,
,  . In all cases
. In all cases  . (1) treats overdetermination but is problematic for productive preemption. (2) explains non-productive preemption. (3)–(4) explain productive preemption
. (1) treats overdetermination but is problematic for productive preemption. (2) explains non-productive preemption. (3)–(4) explain productive preemption
Overdetermination.Footnote 36 Overdetermination is known to be a problem for many causal theories. Consider a firing squad of two soldiers (Pam and Quinn), and assume that one shot is sufficient for the delinquent’s (Ron’s) death (r). Pam and Quinn actually fire a shot (pq). What does our model say? This depends on the plausibilities of possible worlds. The situation suggests that we think that Ron dies (r) and that both fire, and it is more plausible that both Pam and Quinn fire than only one of them (see (1) in Fig. 8). The world  and those with
and those with  are all implausible. Assuming this, our model says that neither ‘Ron dies because Pam fires’ nor ‘Ron dies because Quinn fires’ holds (
are all implausible. Assuming this, our model says that neither ‘Ron dies because Pam fires’ nor ‘Ron dies because Quinn fires’ holds ( ,
,  ). ‘Ron dies because Pam and Quinn fire’ does not hold either, according to the model, but ‘Ron dies because Pam or Quinn fires’ does hold (
). ‘Ron dies because Pam and Quinn fire’ does not hold either, according to the model, but ‘Ron dies because Pam or Quinn fires’ does hold ( ,
,  ). We think that this is a satisfying result. It is not that Ron died because Pam shot at him—he would have died even if Pam had refrained from shooting. Similarly for Quinn Ron died because at least one member of the squad shot at him. Our analysis produces a disjunctive explanation and excludes the single-factor explanations (and the conjunctive explanation, too).Footnote 37
). We think that this is a satisfying result. It is not that Ron died because Pam shot at him—he would have died even if Pam had refrained from shooting. Similarly for Quinn Ron died because at least one member of the squad shot at him. Our analysis produces a disjunctive explanation and excludes the single-factor explanations (and the conjunctive explanation, too).Footnote 37
We think that the above plausibility order gets the conjunctive and the disjunctive reading right—the shooting of all soldiers doesn’t make a difference, but the shooting of at least one of them does. Yet, many contributors to the causal and legal literature agree that every single shot is a cause and thus provides an explanation. Our diagnosis is that such overdetermining causes do not provide an explanation, since one soldier’s refraining from shooting doesn’t make a difference. If this is correct, then we have a deviation here from the thesis mentioned above that a causal relation can always be expressed by a ‘because’ sentence.
Preemption. Preemption is also known from the causal literature. An event (p) may cause some effect (r), while another (slightly later) event (q) is merely a preempted potential cause, since the first already caused the effect. Usually, if ‘because’ is read as expressing (productive) causing, one would like to affirm ‘r because p’ but not ‘r because q’.
Let us consider the well-known case of late preemption (with new names) from Hall (2004). Both Pam and Quentin throw a stone at a glass bottle (pq). The bottle breaks (r). Pam throws just a fraction of a second earlier, so that it is her stone that actually hits the glass bottle and causes its shattering. Quentin’s throw is a preempted potential cause. In our simple model which does not have time in it, a possible representation is again part (1) of Fig. 8. Then our model says that both ‘The bottle shatters because Pam throws’ and ‘The bottle shatters because Quentin throws’ are false or unacceptable, but that ‘The bottle shatters because Pam or Quentin throws’ is true or acceptable. This is counterintuitive in one (perhaps the preferred!) reading of ‘because’. Indeed, one reading of ‘because’ is the causal reading in the production sense, using Hall’s terminology. And in this sense we expect ‘The bottle shatters because Pam throws a stone at it’ to hold but we would reject the same claim for Quentin.
This diagnosis cannot be reproduced if ‘because’ is interpreted along the lines suggested in this paper. Our connective  can only represent causal relations in the dependence sense—which we think is an admissible interpretation. If Pam had refrained from throwing a stone at the bottle, it would still have shattered. So the shattering of the bottle does not depend on Pam’s throwing, just as it doesn’t depend on Quentin’s throwing. Although the situation represented by part (1) of Fig. 8 does not allow for a productive causal reading of ‘because’ it allows for a dependence reading.Footnote 38
can only represent causal relations in the dependence sense—which we think is an admissible interpretation. If Pam had refrained from throwing a stone at the bottle, it would still have shattered. So the shattering of the bottle does not depend on Pam’s throwing, just as it doesn’t depend on Quentin’s throwing. Although the situation represented by part (1) of Fig. 8 does not allow for a productive causal reading of ‘because’ it allows for a dependence reading.Footnote 38
This failure to model the productive reading in the preemptive case is due to the fact that the asymmetry of the example is not represented in the model. There are however at least two ways of getting an asymmetric model in which the disjunction (\(p\vee q\)) as well as one of the disjuncts (p) explain, but the other disjunct (q) doesn’t.
The first option is essentially to assume that p is believed but q is not, and that  and
and  are equally plausible (or incomparable) in terms of plausibility. Part (4) of Fig. 8 depicts this situation. In the bottle example, this means that we believe that Pam (and thus someone) throws, but we don’t believe that Quentin throws. After all, he throws after Pam, so that he might refrain from throwing if Pam does not throw. The second option is essentially to assume that
are equally plausible (or incomparable) in terms of plausibility. Part (4) of Fig. 8 depicts this situation. In the bottle example, this means that we believe that Pam (and thus someone) throws, but we don’t believe that Quentin throws. After all, he throws after Pam, so that he might refrain from throwing if Pam does not throw. The second option is essentially to assume that  is not less plausible than
is not less plausible than  , but keeping the belief of both q and p (and r). Part (3) of Fig. 8 depicts this situation. In the bottle example, this means that we believe that both throw, and we think that if Pam hadn’t thrown, Quentin might not have thrown either. In both options, the disjunction explains (
, but keeping the belief of both q and p (and r). Part (3) of Fig. 8 depicts this situation. In the bottle example, this means that we believe that both throw, and we think that if Pam hadn’t thrown, Quentin might not have thrown either. In both options, the disjunction explains ( ), and one of the disjuncts explains the shattering of the bottle (
), and one of the disjuncts explains the shattering of the bottle ( , but
, but  ).
).
Both option (3) and option (4) of Fig. 8 represent situations with patterns of ‘because’ sentences that match the production sense of causation. However, it is debatable whether they represent our plausibilistic intuitions about the situation.
‘Conditionalization’. The principle of Conditionalization for suppositional conditionals (COND: If \(A \wedge B>C\), then \(A>(B\supset C)\)) gets transformed for factual difference-making conditionals into the following principle (COND*): If  and \({{\,\mathrm{\boxdot }\,}}C\), then
and \({{\,\mathrm{\boxdot }\,}}C\), then  (see Lemma 5). This is a very surprising principle. Consider the following example concerning a much desired job. Sam accepts ‘Bob gets the job or Carol gets the job because Ann makes the decision’, since he knows that Bob and Carol are Ann’s protégés. Actually, Sam believes that Carol will get the job. It seems strange, to say the least, that Sam is justified to infer from these premises that ‘Carol gets the job because Ann makes the decision or Bob gets the job.’ After all, Bob getting the job would exclude Carol’s getting it! But this is what our analysis licenses. We acknowledge that this inference presents a serious challenge to our analysis. We may, however, note that ‘Carol gets the job because Ann makes the decision or Bob gets the job’ does not imply ‘Carol gets the job because Bob gets the job.’ Moreover, (COND*) requires (OR*) or the corresponding semantic principle (or), and we can do without that principle in our weakest semantics (see Fig. 1).
(see Lemma 5). This is a very surprising principle. Consider the following example concerning a much desired job. Sam accepts ‘Bob gets the job or Carol gets the job because Ann makes the decision’, since he knows that Bob and Carol are Ann’s protégés. Actually, Sam believes that Carol will get the job. It seems strange, to say the least, that Sam is justified to infer from these premises that ‘Carol gets the job because Ann makes the decision or Bob gets the job.’ After all, Bob getting the job would exclude Carol’s getting it! But this is what our analysis licenses. We acknowledge that this inference presents a serious challenge to our analysis. We may, however, note that ‘Carol gets the job because Ann makes the decision or Bob gets the job’ does not imply ‘Carol gets the job because Bob gets the job.’ Moreover, (COND*) requires (OR*) or the corresponding semantic principle (or), and we can do without that principle in our weakest semantics (see Fig. 1).
In sum, we think that some of the six problem cases reviewed in this section turned out to be problematic for our analysis. Others are not so problematic. We do not claim that our approach solves all the problems. The main goal of this paper has been to give an axiomatic characterization of an analysis of ‘because’ that is plausible prima facie. In this section, we have indicated some (real and potential) problems that we see in our account, with the idea of paving the way for a discussion between the modal logic and the causation communities. But our main contribution clearly lies in the development of a formal system (or actually, of formal systems) that can be put to such tests in the first place. Our systems are in a situation akin to that of the early conditional logics that were known to be plagued by problems of a similar caliber (like the problem of Simplification of Disjunctive Antecedents) and were yet given a chance to grow and develop.
8 Conclusion
Different kinds of conditionals validate different sets of inference patterns. For natural-language conditionals, as opposed to material (or strict) conditionals, strengthening the antecedent is invalid. This has been one of the most important messages of conditional logic ever since the times of Goodman, Adams, Stalnaker and Lewis. For difference-making conditionals, as opposed to conditionals normally studied in the field of conditional logic, the dual pattern of weakening the consequent (RW) is invalid, too. What raises the doxastic status of C does not necessarily raise the doxastic status of \(B\vee C\). Many other well-known patterns get lost as well, and conditionals appear to behave rather irregularly if the relevance idea is heeded. Still there is a logic of difference-making conditionals as captured by the Relevant Ramsey Test and there is a logic for ‘because’ as captured by the Ramsey Test for ‘because’. We used the latter to provide a semantics for ‘because’.
To the best of our knowledge, we have presented in this paper the first logics for ‘because’ that can be compared, in status and elaboration, to the more orthodox logics for suppositional conditionals that have been dominant in the discussion for 50 years. We have shown how they relate to each other. For every conditional logic \(\textbf{L}_>\) (starting with \({{\,\mathrm{\textbf{B}}\,}}^+\)) there is a corresponding companion ‘because’ logic  such that they are valid in the same sets of models, the first with respect to the Ramsey Test (RT), the second with respect to the Ramsey Test for ‘because’ (RTB). Difference-making conditionals defined by the Relevant Ramsey Test (RRT) can be viewed as a missing link.
such that they are valid in the same sets of models, the first with respect to the Ramsey Test (RT), the second with respect to the Ramsey Test for ‘because’ (RTB). Difference-making conditionals defined by the Relevant Ramsey Test (RRT) can be viewed as a missing link.
Our analysis is not fully exhaustive yet and can be extended. We restrict ourselves to mentioning the technical aspects here. First, we have disregarded Boolean combinations of conditionals as well as nested conditionals. Correspondingly, we have disregarded multistate models and possible worlds semantics with multistates. Second, our validity results here constitute only one direction of the correspondence result. The other direction requires one to argue on the level of frames (instead of models). Third, although we obtain more general soundness results from our validity results, the related completeness part requires a proof of the full correspondence result and a property known as canonicity. This can also be done indirectly by backsimulating the suppositional conditional logic in the logic for ‘because’ (cf. Raidl 2021b). The logics arising from our principles for ‘because’ are in fact not only sound, but also complete for their corresponding semantics. This is shown by Raidl (2022).
It is, of course, a very good question to ask how far an analysis of ‘because’ can go if it is confined to modal logic broadly construed.Footnote 39 We have not answered this question. But we believe we have provided a solid logical basis for attacking it, by showing what follows from our analysis (the validities) and discussing what the limits of this analysis are (its invalidities and potential counter-examples).
Data availability
Not applicable.
Code availability
Not applicable.
Notes
The verb ‘to hold’ is used in this paper with the intention that it can be understood both in terms of acceptance and in terms of truth.
\(\textbf{N}\) stands for Lewis’ (1973, p. 120–21) ‘normality’ which corresponds to adding CONS.
Our examples are similar to the examples for difference-making conditionals given in Rott (2022a). It is proven there (Observation 5.4) that for all inference schemes except for Right Weakening, counterexamples are possible only if the difference-making conditionals involved are factual ones, in the sense that their antecedents and consequents are believed to be true.
A reviewer has pointed out that ‘by express’ is not a proposition. We presuppose here that the above sentence is equivalent to ‘Because you pay an extra fee (p), your letter will be delivered (q) and it will be delivered by express (r)’.
To enforce a non-exclusive reading of ‘or’, we may consider ‘Because at least one of Pam and Quinn goes to the Irish pub, they will meet’. To our ears, this sentence sounds odd for the same reasons.
Since W is only needed to define the domain of the selection function \(\sigma \), we will frequently identify states with selection functions.
On the other hand, we do not want to exclude an interpretation of conditionals that takes them as expressing propositions. See below on the ‘metaphysical’ interpretation.
A valuation is a function \(v: W \times {{\,\mathrm{\mathcal {L}}\,}}\longrightarrow \{0,1\}\). \(v(w,A)=1\) means that A is true in w. Otherwise A is false in w.
When we generalize this approach to multi-state models, satisfaction in a model is satisfaction in all states of the model, and we need to generalize validity locally by inserting ‘for all states \(\sigma \) in the model’ in front of ‘whenever \(\sigma \)’.
Although our flat language can express the suppositional ‘if’, the difference-making ‘if’ and ‘because’, this does not mean that it expresses beliefs about the relevant connections. But it could be extended accordingly. For a fully general account of nested and embedded conditionals and ‘because’, see Raidl (2022).
For multi-state semantics, the same adjustment needs to made here as in footnote 15.
See for example Stalnaker (1968, pp. 100–103).
In the metaphysical setting, this is due to centering, in the doxastic one, it is due to (cpres).
The notion of relevance used here is a doxastic one and different from the one tracked by relevance logic.
The idea of difference-making conditionals was first formulated (but not worked out) by von Kutschera (1974, p. 266).
For arguments against Preservation in belief revision, see Cross (1990), Rabinowicz (1996), Bradley (2012), Shear and Fitelson (2019) and Cantwell and Rott (2019). Arguments against the stronger principle of Rational Monotonicity were put forward by Stalnaker (1994), Lin and Kelly (2012), Genin (2019), Genin and Kelly (2019), Kelly and Lin (2021), Genin and Huber (2021), and Boylan and Schultheis (2021).
If \(\vdash A \supset B\) and \({{\,\mathrm{\boxdot }\,}}A\), then \({{\,\mathrm{\boxdot }\,}}B\).
We thank an anonymous reviewer for raising this point. Fine’s particular argument against LLE for counterfactuals cannot be transferred to our analysis of ‘because’, since we reject some of his principles (for example RW).
For these results and completeness proofs for the full language of these logics, see Raidl (2022, Theorem 1–5).
Incomparabilities arise if we define \(\sigma (V) = \min _< (V \cap W')\), where < is an irreflexive and transitive relation on \(W' \subseteq W\), but < is not modular. A relation < is modular iff for any x, y, z, if \(x<y\) then \(x<z\) or \(z<y\).
Provided we maintain condition (iii) of Sect. 4.2,
 .
.Indeed, by INC, \(A > C\) implies the belief that \(A \supset C\) and this together with the belief that A implies the belief that C.
We neglect the case \(P(\lnot A)=0\), in which \(P(C|\lnot A)\) is undefined and \(P(C|A) > P(C)\) is false.
The problem of reflexivity was raised by Vera Hoffmann-Kolss in discussion.
One might call the latter an evidential ‘because’. However, we won’t use this term in order to avoid confusion with the sense of ‘evidential’ in the ‘evidential conditionals’ of Douven and Crupi and Iacona discussed above.
We are grateful to an anonymous reviewer for pressing us on the problem of sufficient reasons and confronting us with the example discussed in this paragraph. The notion of ‘sufficient reason’ used here is, however, different from Spohn’s notion that we mentioned earlier.
Notice, by the way, that the modal sufficient-reasons statement
 does not imply the ‘because’ statement
does not imply the ‘because’ statement  . And the reverse does not hold either.
. And the reverse does not hold either.The problems of overdetermination and preemption were brought up by Jonathan Schaffer in discussion.
Halpern’s (2016, p. 29) more sophisticated analysis of overdetermination rests on a modified Lewisean analysis and can handle overdeterminers as proper causes. Halpern is ready to allow ‘discunctive causes’ here.
We reach a similar conclusion if we use part (2) of Fig. 8.
We thank a referee for raising this question.
References
Adams, E. W. (1975). The logic of conditionals. Reidel.
Alchourrón, C. E., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50(2), 510–530.
Andreas, H., & Günther, M. (2019). On the Ramsey test analysis of ‘because’. Erkenntnis, 84(6), 1229–1262.
Blau, U. (2008). Die Logik der Unbestimmtheiten und Paradoxien. Synchron Wissenschaftsverlag der Autoren.
Boylan, D., & Schultheis, G. (2021). How strong is a counterfactual? Journal of Philosophy, 118(7), 373–404.
Bradley, R. (2012). Restricting preservation: A response to Hill. Mind, 121(481), 147–159.
Burgess, J. P. (1981). Quick completeness proofs for some logics of conditionals. Notre Dame Journal of Formal Logic, 22, 76–84.
Burks, A. W. (1951). The logic of causal propositions. Mind, 60(239), 363–382.
Cantwell, J., & Rott, H. (2019). Probability, coherent belief and coherent belief changes. Annals of Mathematics and Artificial Intelligence, 87, 259–291.
Cross, C. B. (1990). Belief revision, nonmonotonic reasoning, and the Ramsey test. In H. E. Kyburg, R. P. Loui, & G. N. Carlson (Eds.), Knowledge Representation and Defeasible Reasoning Knowledge representation and defeasible reasoning (pp. 223–244). Kluwer.
Crupi, V., & Iacona, A. (2022). The evidential conditional. Erkenntnis, 87(6), 2897–2921.
Crupi, V., & Iacona, A. (2022). Three ways of being non-material. Studia Logica, 110(1), 47–93.
Douven, I. (2016). The epistemology of indicative conditionals: Formal and empirical approaches. Cambridge University Press.
Fariñas del Cerro, L., & Herzig, A. (1996). Belief change and dependence. In Y. Shoham (Ed.), Proceedings of the Sixth Conference on Theoretical Aspects of Rationality and Knowledge (pp. 147–161). Morgan Kaufmann.
Fine, K. (2012). Counterfactuals without possible worlds Counterfactuals without possible worlds. The Journal of Philosophy, 109(3), 221–246.
Frege, G. (1892). Über Sinn und Bedeutung. Zeitschrift für Philosophie und philosophische Kritik, 100, 25–50.
Freund, M. (1993). Injective models and disjunctive relations. Journal of Logic and Computation, 3(3), 231–247.
Genin, K. (2019). Full & partial belief. In R. Pettigrew & J. Weisberg (Eds.), The open handbook of formal epistemology (pp. 437–498). PhilPapers Foundation.
Genin, K., & Huber, F. (2021). Formal Representations of Belief Formal representations of belief. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy Spring 2021 ed. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/spr2021/entries/formal-belief/
Genin, K., & Kelly, K. (2019). Theory choice, theory change, and inductive truth-conduciveness. Studia Logica, 107, 949–989.
Goodman, N. (1947). The problem of counterfactual conditionals. Journal of Philosophy, 44, 113–128.
Grove, A. (1988). Two modellings for theory change. Journal of Philosophical Logic, 17(2), 157–170.
Hall, N. (2004). Two concepts of causation. In J. Collins, N. Hall, & L. A. Paul (Eds.), Causation and counterfactuals (pp. 225–276). MIT Press.
Halpern, J. Y. (2003). Reasoning about uncertainty. MIT Press.
Halpern, J. Y. (2016). Actual causality. MIT Press.
Hawthorne, J., & Makinson, D. (2007). The quantitative/qualitative watershed for rules of uncertain inference. Studia Logica, 86(2), 247–297.
Kelly, K. T., & Lin, H. (2021). Beliefs, probabilities, and their coherent correspondence. In I. Douven (Ed.), Lotteries, knowledge and rational belief: Essays on the lottery paradox (pp. 185–222). Cambridge University Press.
Kraus, S., Lehmann, D., & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167–207.
Lewis, D. (1973). Counterfactuals Counterfactuals. Blackwell.
Lin, H., & Kelly, K. T. (2012). Propositional reasoning that tracks probabilistic reasoning. Journal of Philosophical Logic, 41(6), 957–981.
Makinson, D. (1989). General theory of cumulative inference. In M. Reinfrank, J. de Kleer, M. L. Ginsberg, & E. Sandewall (eds.), Non-monotonic Reasoning: Proceedings of the 2nd International Workshop 1988 (Vol. 346, pp. 1–18). Berlin: Springer.
McCall, S. (1983). If, since and because: A study in conditional connection. Logique et Analyse, 26(103–104), 309–321.
Pearl, J. (1989). Probabilistic semantics for nonmonotonic reasoning: a survey. In R. J. Brachman, H. J. Levesque, & R. Reiter (eds.), Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning (pp. 505–516). Morgan Kaufmann.
Pizzi, C. (1980). ‘Since’, ‘even if’, ‘as if’. In M. L. Dallachiara (Ed.), Italian studies in the philosophy of science (Vol. 47, pp. 73–87). Reidel.
Rabinowicz, W. (1996). Stable revision, or is preservation worth preserving? In A. Fuhrmann & H. Rott (Eds.), Logic, action, and information: Essays on logic in philosophy and artificial intelligence (pp. 101–128). Berlinde Gruyter.
Raidl, E. (2019). Completeness for counter-doxa conditionals—using ranking semantics. The Review of Symbolic Logic, 12(4), 1–31.
Raidl, E. (2021a). Conditional(s). University of Konstanz. Habilitation Thesis.
Raidl, E. (2021b). Definable conditionals. Topoi, 40, 87–105.
Raidl, E. (2021c). Three conditionals: Contraposition, difference-making and dependency. In M. Blicha & I. Sedlar (Eds.), The Logica Yearbook 2020 (pp. 201–217). College Publications.
Raidl, E. (2022). ‘Because’ and ‘if’: Logics for ‘because’. Manuscript
Raidl, E., Iacona, A., & Crupi, V. (2022). The logic of the evidential conditional. Review of Symbolic Logic, 15(3), 758–770.
Ramsey, F. P. (1931). General propositions and causality. In J. B. Braithwaite (Ed.), The foundations of mathematics and other logical essays (pp. 237–255). Kegan Paul.
Rott, H. (1986). Ifs, though and because. Erkenntnis, 25(3), 345–370.
Rott, H. (2022a). Difference-making conditionals and the relevant Ramsey test. Review of Symbolic Logic, 15(1), 133–164.
Rott, H. (2022b). Evidential support and contraposition. Erkenntnis. Published online 10 November 2022
Ryle, G. (1950). If’, ‘so’, and ‘because. In M. Black (Ed.), Philosophical analysis (pp. 323–340). Cornell University Press.
Schnieder, B. (2011). A logic for ‘because’. Review of Symbolic Logic, 4, 445–465.
Shear, T., & Fitelson, B. (2019). Two approaches to belief revision. Erkenntnis, 84(3), 487–518.
Spohn, W. (1983). Deterministic and probabilistic reasons and causes. Erkenntnis, 19(1), 371–396.
Spohn, W. (2013). A ranking-theoretic approach to conditionals. Cognitive Science, 37(6), 1074–1106.
Spohn, W. (2015). Conditionals: A unifying ranking-theoretic perspective. Philosophers’ Imprint, 15(1), 1–30.
Stalnaker, R. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory (Vol. 2, pp. 98–112). Blackwell.
Stalnaker, R. (1994). What is a nonmonotonic consequence relation? Fundamenta Informaticae, 21, 7–21.
Urchs, M. (1994). On the logic of event-causation: Jaśkowski-style systems of causal logic. Studia Logica, 53(4), 551–578.
van Rooij, R., & Schulz, K. (2022). Causal relevance of conditionals: Semantics or pragmatics? Linguistics Vanguard, 8(4), 363–370.
Veltman, F. (1985). Logics for conditionals. University of Amsterdam. PhD Thesis.
von Kutschera, F. (1974). Indicative conditionals. Theoretical Linguistics, 1, 257–269.
Acknowledgements
We thank the participants of the virtual conference ‘Difference-Making and Explanatory Relevance’ organized by Stephan Krämer’s Emmy Noether group, audiences at the hybrid conference EENPS 2021, the ‘Logic and Interactive Rationality’ seminar at the Universiteit van Amsterdam, GAP.11 at the Humboldt-Universität zu Berlin, and in particular Vera Hoffmann-Kolss, Jonathan Schaffer and two referees of this journal for very helpful comments on earlier versions of this paper.
Funding
Open Access funding enabled and organized by Projekt DEAL. Parts of this work were funded by the German Excellence Strategy, EXCNumber 2064/1, and the Baden-Württemberg Foundation (Eric Raidl), as well as the Deutsche Forschungsgemeinschaft, project number RO 1219/12-1 (Hans Rott).
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work and are listed in alphabetical order. They approved the version to be published and agree to be accountable for all aspects of the work.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose. The authors have no conflict of interest to declare that are relevant to the content of this article.
Consent for publication
Not applicable.
Ethical approval
Not applicable.
Appendix: Proofs
Appendix: Proofs
Proof of Theorem 1:
The proof is similar as for set-selection semantics, see Raidl (2021b, Theorems 2, 9, and remark after Theorem 12), or Raidl (2021a, Theorem 5.3). \(\square \)
Proof of Lemma 2:
For simplicity, but without loss of generality, suppose that all subsets in M are representable by sentences. Suppose M is a model which does not satisfy (pres). Hence (by representability) there are sentences A, C such that  , \({{\,\mathrm{\boxdot }\,}}C\) and \(A \not > C\). Since we assume (cpres), this means that \(\lnot {{\,\mathrm{\boxdot }\,}}A\), and hence
, \({{\,\mathrm{\boxdot }\,}}C\) and \(A \not > C\). Since we assume (cpres), this means that \(\lnot {{\,\mathrm{\boxdot }\,}}A\), and hence  . Call such a pair (A, C), where
. Call such a pair (A, C), where  and \(A \not > C\) a (pres)-violator. We define a new model \(M'\) from M, with the same worlds and the same valuation but with the new state \(\sigma '\), where
and \(A \not > C\) a (pres)-violator. We define a new model \(M'\) from M, with the same worlds and the same valuation but with the new state \(\sigma '\), where
-
1.
 , if there is C such that (A, C) is a (pres)-violator,
, if there is C such that (A, C) is a (pres)-violator, -
2.
 , otherwise.
, otherwise.
Remark (\(\dag \)): \(\sigma '(W)=\sigma (W)\), since \({{\,\mathrm{\boxdot }\,}}\top \) by (id), and hence there is no (pres)-violator \((\top , C)\). Let us first show that \(M'\) now satisfies (pres), i.e., validates PRES.
Case 1. When \({{\,\mathrm{\boxdot }\,}}A\) in M, there can be no (pres)-violator, since \({{\,\mathrm{\boxdot }\,}}A\) contradicts  . Hence
. Hence  . Thus \(\sigma '\) satisfies (pres) for these A, due to (cpres).
. Thus \(\sigma '\) satisfies (pres) for these A, due to (cpres).
Case 2. Similarly when \({{\,\mathrm{\boxdot }\,}}\lnot A\)
Case 3. Let A such that \(\lnot {{\,\mathrm{\boxdot }\,}}A\) and \(\lnot {{\,\mathrm{\boxdot }\,}}\lnot A\). Thus  and
and  in M. Suppose (A, C) is a (pres)-violator in M. Hence \({{\,\mathrm{\boxdot }\,}}C\), but \(A \not >C\) in M. Now
in M. Suppose (A, C) is a (pres)-violator in M. Hence \({{\,\mathrm{\boxdot }\,}}C\), but \(A \not >C\) in M. Now  by definition, and \(\sigma '(W)= \sigma (W)\) by (\(\dag \)). Since \({{\,\mathrm{\boxdot }\,}}C\), that is
by definition, and \(\sigma '(W)= \sigma (W)\) by (\(\dag \)). Since \({{\,\mathrm{\boxdot }\,}}C\), that is  , we obtain
, we obtain  . Thus (pres)-violators have been deleted.
. Thus (pres)-violators have been deleted.
The satisfaction of the same  sentences is proven by induction over the complexity of the formula. Only \({{\,\mathrm{\boxdot }\,}}\) and
sentences is proven by induction over the complexity of the formula. Only \({{\,\mathrm{\boxdot }\,}}\) and  sentences need to be checked. We have \({{\,\mathrm{\boxdot }\,}}A\) in \(\sigma \) iff \({{\,\mathrm{\boxdot }\,}}A\) in \(\sigma '\), since we have
sentences need to be checked. We have \({{\,\mathrm{\boxdot }\,}}A\) in \(\sigma \) iff \({{\,\mathrm{\boxdot }\,}}A\) in \(\sigma '\), since we have  , due to the fact that \({{\,\mathrm{\boxdot }\,}}\top \), and hence we are in case 1 here. Consider
, due to the fact that \({{\,\mathrm{\boxdot }\,}}\top \), and hence we are in case 1 here. Consider  :
:
Case 1. Suppose \({{\,\mathrm{\boxdot }\,}}A\). Since \({{\,\mathrm{\boxdot }\,}}A\), we have  by definition of \(\sigma '\). Since \({{\,\mathrm{\boxdot }\,}}\lnot \lnot A\), we also have
by definition of \(\sigma '\). Since \({{\,\mathrm{\boxdot }\,}}\lnot \lnot A\), we also have  from case 2. By definition:
from case 2. By definition:  iff
iff  ,
,  ,
,  . But since \(\sigma '(V)= \sigma (V)\) for
. But since \(\sigma '(V)= \sigma (V)\) for  , we obtain that the previous holds iff
, we obtain that the previous holds iff  .
.
Case 2. Similarly.
Case 3. Let A such that \(\lnot {{\,\mathrm{\boxdot }\,}}A\) and \(\lnot {{\,\mathrm{\boxdot }\,}}\lnot A\). Then  and
and  in \(\sigma \). Since \(\sigma '(W)= \sigma (W)\),
in \(\sigma \). Since \(\sigma '(W)= \sigma (W)\),  and
and  in \(\sigma '\). Thus
in \(\sigma '\). Thus  and
and  . \(\square \)
. \(\square \)
Proof of Corollary 1:
Since \(C' \subseteq C\), everything that is valid in C is valid in \(C'\). Conversely, suppose \(\alpha \) is valid in \(C'\), and suppose for reductio that it is not in C. Hence there is a model M in C such that \(\alpha \) does not hold in M. But since we showed that M can be transformed into a (pres) model \(M'\) satisfying the same  sentences, \(\alpha \) would not hold in \(M'\). Yet \(M'\) is from \(C'\). This contradicts that \(\alpha \) is valid in \(C'\). \(\square \)
sentences, \(\alpha \) would not hold in \(M'\). Yet \(M'\) is from \(C'\). This contradicts that \(\alpha \) is valid in \(C'\). \(\square \)
Proof of Lemma 3:
It suffices to find two models that agree on  , but disagree on \({{\,\mathrm{\boxdot }\,}}\). Consider the language with two propositional variables p and q. Let \(W =\{v, w, \ldots \}\) be a set of worlds and V some valuation such that \(w \in [p \wedge q]\) and \(v \in [\lnot p \wedge q]\). We define \(M_1\) by
, but disagree on \({{\,\mathrm{\boxdot }\,}}\). Consider the language with two propositional variables p and q. Let \(W =\{v, w, \ldots \}\) be a set of worlds and V some valuation such that \(w \in [p \wedge q]\) and \(v \in [\lnot p \wedge q]\). We define \(M_1\) by  and \(M_2\) by
and \(M_2\) by  , with \(M_1\) and \(M_2\) having the same worlds W and the same valuation v. (Both models satisfy our basic assumptions (id), (inc) and (cpres).)
, with \(M_1\) and \(M_2\) having the same worlds W and the same valuation v. (Both models satisfy our basic assumptions (id), (inc) and (cpres).)
We have \(M_1 {{\,\mathrm{\vDash }\,}}{{\,\mathrm{\boxdot }\,}}p\), but \(M_2 {{\,\mathrm{\nvDash }\,}}{{\,\mathrm{\boxdot }\,}}p\): Indeed,  , but
, but  . Yet, \(M_1\) and \(M_2\) satisfy the same
. Yet, \(M_1\) and \(M_2\) satisfy the same  -sentences, viz., no sentences of the form
-sentences, viz., no sentences of the form  at all: Suppose for reductio that \(M_1\) satisfies some such sentence, i.e.,
at all: Suppose for reductio that \(M_1\) satisfies some such sentence, i.e.,  . By (RTB), this implies
. By (RTB), this implies  , i.e.,
, i.e.,  . But then
. But then  , so
, so  , which contradicts
, which contradicts  , by (RTB) again. A similar argument can be made for \(M_2\). Thus the two models agree on
, by (RTB) again. A similar argument can be made for \(M_2\). Thus the two models agree on  but disagree on \({{\,\mathrm{\boxdot }\,}}\).
but disagree on \({{\,\mathrm{\boxdot }\,}}\).
\(\square \)
Proof of Lemma 4:
(1) follows from the syntactic definition of \({{\,\mathrm{\boxdot }\,}}\), (2) follows from the semantic definition of  and assuming (cpres). (3) By (pres), \(\top > C\) together with \(\lnot A \not >C\) implies \(\top > A\). Finally, let us prove (4), assuming (pres). Suppose \({{\,\mathrm{\boxdot }\,}}(A \supset C)\) and
and assuming (cpres). (3) By (pres), \(\top > C\) together with \(\lnot A \not >C\) implies \(\top > A\). Finally, let us prove (4), assuming (pres). Suppose \({{\,\mathrm{\boxdot }\,}}(A \supset C)\) and  . Thus, by (1) and (3), which uses (pres), we have \(\top > (A \supset C)\) and either (i) \(\top \not > \lnot A \vee C\) or (ii) \(\lnot \lnot A > \lnot A \vee C\). But (i) is incompatible with \(\top > (A \supset C)\), due to RLE. Thus only (ii) remains. But (ii) implies \(A > C\), by LLE, ID, AND and RW, and so we have the left-hand side of (4). Conversely, \(\top > (A \supset C)\) follows from \(A > C\), by (inc). The latter also implies (ii), by LLE and RW. As we have seen, this is the right-hand side of (4). \(\square \)
. Thus, by (1) and (3), which uses (pres), we have \(\top > (A \supset C)\) and either (i) \(\top \not > \lnot A \vee C\) or (ii) \(\lnot \lnot A > \lnot A \vee C\). But (i) is incompatible with \(\top > (A \supset C)\), due to RLE. Thus only (ii) remains. But (ii) implies \(A > C\), by LLE, ID, AND and RW, and so we have the left-hand side of (4). Conversely, \(\top > (A \supset C)\) follows from \(A > C\), by (inc). The latter also implies (ii), by LLE and RW. As we have seen, this is the right-hand side of (4). \(\square \)
Proof of Theorem 2:
We use parts (1) and (2) of Lemma 4. In what follow A, B, C are all factual.
N. Suppose \(\vdash A\). Then \(\vdash \top \supset A\). By ID, we have \(\top > \top \). Thus by RW we have \(\top > A\). That is \({{\,\mathrm{\boxdot }\,}}A\).
K. Suppose \({{\,\mathrm{\boxdot }\,}}(A \supset B)\) and \({{\,\mathrm{\boxdot }\,}}A\). Thus \(\top > (A \supset B)\) and \(\top > A\). Hence \(\top > B\) by AND and RW. That is \({{\,\mathrm{\boxdot }\,}}B\).
D. We need to prove \(\lnot {{\,\mathrm{\boxdot }\,}}\bot \). That is \(\lnot (\top > \bot )\). But this is the axiom Cons.
LLE. Suppose that \(\vdash A \equiv B\) and assume that  . That is, either \(\top \not >A\), or \(\top \not > C\) or \(\lnot A > C\). Thus \(\top \not > B\) or \(\top \not > C\) or \(\lnot B > C\) by RLE and LLE. This is the translation of
. That is, either \(\top \not >A\), or \(\top \not > C\) or \(\lnot A > C\). Thus \(\top \not > B\) or \(\top \not > C\) or \(\lnot B > C\) by RLE and LLE. This is the translation of  .
.
RLE. Suppose that \(\vdash B \equiv C\) and  . That is, either \(\top \not >A\) or \(\top \not > B\) or \(\lnot A > B\). Thus \(\top \not >A\) or \(\top \not >C\) or \(\lnot A > C\) by RLE. This is the translation of
. That is, either \(\top \not >A\) or \(\top \not > B\) or \(\lnot A > B\). Thus \(\top \not >A\) or \(\top \not >C\) or \(\lnot A > C\) by RLE. This is the translation of  .
.
BA. Suppose  . Then \(\top > A\), that is, \({{\,\mathrm{\boxdot }\,}}A\).
. Then \(\top > A\), that is, \({{\,\mathrm{\boxdot }\,}}A\).
BC. Suppose  . Then \(\top >B\), that is \({{\,\mathrm{\boxdot }\,}}B\).
. Then \(\top >B\), that is \({{\,\mathrm{\boxdot }\,}}B\).
VDW. Suppose  . Thus \(\top > A\) and \(\top > B\) and \(\lnot A \not > B\). If we had, \(\lnot A > A \vee B\), we would have \(\lnot A > B\) by ID, AND and RW. This contradicts our assumption. Thus we must have \(\lnot A \not > A \vee B\). But from \(\top > B\) we obtain \(\top > A \vee B\) by RW. And \(\top > A\) by assumption. Thus
. Thus \(\top > A\) and \(\top > B\) and \(\lnot A \not > B\). If we had, \(\lnot A > A \vee B\), we would have \(\lnot A > B\) by ID, AND and RW. This contradicts our assumption. Thus we must have \(\lnot A \not > A \vee B\). But from \(\top > B\) we obtain \(\top > A \vee B\) by RW. And \(\top > A\) by assumption. Thus  .
.
CW*. Suppose that \({{\,\mathrm{\boxdot }\,}}B\) and  . That is, \(\top > B\), and \(\top \not >A\) or \(\top \not > B\wedge C\) or \(\lnot A > B\wedge C\). If the second disjunct holds, then \(\top \not > C\), by AND. If the third disjunct holds, then \(\lnot A > C\), by RW. Thus overall, we get \(\top \not > A\) or \(\top \not >C\) or \(\lnot A > C\). This is the translation of
. That is, \(\top > B\), and \(\top \not >A\) or \(\top \not > B\wedge C\) or \(\lnot A > B\wedge C\). If the second disjunct holds, then \(\top \not > C\), by AND. If the third disjunct holds, then \(\lnot A > C\), by RW. Thus overall, we get \(\top \not > A\) or \(\top \not >C\) or \(\lnot A > C\). This is the translation of  .
.
AND*. Suppose that  and
and  . That is, first, either \(\top \not > A\) or \(\top \not > B\) or \(\lnot A > B\), and second, either \(\top \not >A\) or \(\top \not > C\) or \(\lnot A > C\). If, on the one hand, \(\top \not > B\) then \(\top \not > B\wedge C\), by RW. The same holds when \(\top \not > C\). If, on the other hand, \(\lnot A > B\) and \(\lnot A > C\), then \(\lnot A > B\wedge C\), by AND. Thus overall, we get \(\top \not >A\) or \(\top \not >B \wedge C\) or \(\lnot A > B \wedge C\). This is the translation of
. That is, first, either \(\top \not > A\) or \(\top \not > B\) or \(\lnot A > B\), and second, either \(\top \not >A\) or \(\top \not > C\) or \(\lnot A > C\). If, on the one hand, \(\top \not > B\) then \(\top \not > B\wedge C\), by RW. The same holds when \(\top \not > C\). If, on the other hand, \(\lnot A > B\) and \(\lnot A > C\), then \(\lnot A > B\wedge C\), by AND. Thus overall, we get \(\top \not >A\) or \(\top \not >B \wedge C\) or \(\lnot A > B \wedge C\). This is the translation of  .
.
NTC. Suppose for reductio that  . That is, \(\top > A\), \(\top > \top \) and \(\lnot A \not > \top \) by the translation. The latter contradicts ID + RW.
. That is, \(\top > A\), \(\top > \top \) and \(\lnot A \not > \top \) by the translation. The latter contradicts ID + RW.
In the following, we assume CUT for CUT*, OR for OR*, CM for CM*, DR for DR* and RM for RM*.
CUT*. Suppose  and \({{\,\mathrm{\boxdot }\,}}B\), and also
and \({{\,\mathrm{\boxdot }\,}}B\), and also  . Then first we have \(\lnot A \not >C\), \(\top > A\), \(\top >C\) and \(\top > B\). We can already say that from these we obtain the belief parts \(\top > (B \supset C)\) and \(\top > C\) of the conclusion
. Then first we have \(\lnot A \not >C\), \(\top > A\), \(\top >C\) and \(\top > B\). We can already say that from these we obtain the belief parts \(\top > (B \supset C)\) and \(\top > C\) of the conclusion  that we want to establish. It thus suffices to establish \(\lnot (B \supset A) \not > C\). By
that we want to establish. It thus suffices to establish \(\lnot (B \supset A) \not > C\). By  , we also have \(\lnot A > B\) or \(\top \not >A\) or \(\top \not > B\). But the last two are excluded by what we already know. Hence \(\lnot A > B\). Suppose now for reductio that \(\lnot (B \supset A) > C\). Then \((\lnot A \wedge B) > C\), by LLE. Hence and since we previously established \(\lnot A > B\), we obtain \(\lnot A > C\), by CUT. This contradicts \(\lnot A \not >C\). Thus the reductio assumption is false, and we have proven
, we also have \(\lnot A > B\) or \(\top \not >A\) or \(\top \not > B\). But the last two are excluded by what we already know. Hence \(\lnot A > B\). Suppose now for reductio that \(\lnot (B \supset A) > C\). Then \((\lnot A \wedge B) > C\), by LLE. Hence and since we previously established \(\lnot A > B\), we obtain \(\lnot A > C\), by CUT. This contradicts \(\lnot A \not >C\). Thus the reductio assumption is false, and we have proven  .
.
OR*. Suppose that  and
and  . That is, first, either \(\top \not > A\) or \(\top \not > C\) or \(\lnot A > C\), and second, either \(\top \not > B\) or \(\top \not > C\) or \(\lnot B > C\). That is, either \(\top \not >A\) or \(\top \not >B\), or \(\top \not > C\) or both \(\lnot A > C\) and \(\lnot B > C\). If \(\top \not > A\) or \(\top \not >B\), we obtain \(\top \not > A \wedge B\), by RW. This implies
. That is, first, either \(\top \not > A\) or \(\top \not > C\) or \(\lnot A > C\), and second, either \(\top \not > B\) or \(\top \not > C\) or \(\lnot B > C\). That is, either \(\top \not >A\) or \(\top \not >B\), or \(\top \not > C\) or both \(\lnot A > C\) and \(\lnot B > C\). If \(\top \not > A\) or \(\top \not >B\), we obtain \(\top \not > A \wedge B\), by RW. This implies  . If \(\top \not > C\), then
. If \(\top \not > C\), then  , too. If both \(\lnot A > C\) and \(\lnot B > C\), then \(\lnot A \vee \lnot B> C\), by OR, and thus \(\lnot (A \wedge B)> C\) by LLE. So again,
, too. If both \(\lnot A > C\) and \(\lnot B > C\), then \(\lnot A \vee \lnot B> C\), by OR, and thus \(\lnot (A \wedge B)> C\) by LLE. So again,  .
.
CM*. Suppose that \({{\,\mathrm{\boxdot }\,}}B\),  and
and  . That is, (i) \(\top > B\), (ii) either \(\top \not > A\) or \(\top \not > B\) or \(\lnot A > B\), and (iii) \(\top \not > A\) or \(\top \not > C\) or \(\lnot A > C\). Due to (i), (ii) delivers \(\top \not > A\) or \(\lnot A > B\). Now we consider the three cases of (iii) in turn. If \(\top \not > A\), then we obtain from (i) that
. That is, (i) \(\top > B\), (ii) either \(\top \not > A\) or \(\top \not > B\) or \(\lnot A > B\), and (iii) \(\top \not > A\) or \(\top \not > C\) or \(\lnot A > C\). Due to (i), (ii) delivers \(\top \not > A\) or \(\lnot A > B\). Now we consider the three cases of (iii) in turn. If \(\top \not > A\), then we obtain from (i) that  , by AND and RW. Hence
, by AND and RW. Hence  . If \(\top \not > C\), then
. If \(\top \not > C\), then  , too. If \(\lnot A > C\), we can use the previously established \(\top \not > A\) or \(\lnot A > B\). The case \(\top \not > A\) was already treated. The second possibility leads to \(\lnot A \wedge B> C\), by CM. Thus
, too. If \(\lnot A > C\), we can use the previously established \(\top \not > A\) or \(\lnot A > B\). The case \(\top \not > A\) was already treated. The second possibility leads to \(\lnot A \wedge B> C\), by CM. Thus  , by LLE. So again,
, by LLE. So again,  .
.
DR*. Suppose  and
and  . Thus on the one hand \(\top > A\), \(\top > C\) and \(\lnot A \not > C\). On the other hand \(\top > B\), \(\top > C\) and \(\lnot B \not > C\). From \(\lnot A\not >C\) and \(\lnot B\not > C\), we obtain \((\lnot A \vee \lnot B) \not >C\) by DR. That is \(\lnot (A \wedge B) \not > C\) by LLE. And from \(\top > A\) and \(\top > B\), we obtain \(\top > (A \wedge B)\) by AND. Hence, since we also have \(\top > C\), this establishes
. Thus on the one hand \(\top > A\), \(\top > C\) and \(\lnot A \not > C\). On the other hand \(\top > B\), \(\top > C\) and \(\lnot B \not > C\). From \(\lnot A\not >C\) and \(\lnot B\not > C\), we obtain \((\lnot A \vee \lnot B) \not >C\) by DR. That is \(\lnot (A \wedge B) \not > C\) by LLE. And from \(\top > A\) and \(\top > B\), we obtain \(\top > (A \wedge B)\) by AND. Hence, since we also have \(\top > C\), this establishes  .
.
RM*. Suppose that  and
and  . That is, (i) \(\top > A\) and \(\top > B\) and \(\lnot A \not > B\), and, since \(\top > A\), using AND, RW and CONS, (ii) either \(\top \not > C\) or \(\lnot A > C\). If, on the one hand, \(\top \not > C\), then
. That is, (i) \(\top > A\) and \(\top > B\) and \(\lnot A \not > B\), and, since \(\top > A\), using AND, RW and CONS, (ii) either \(\top \not > C\) or \(\lnot A > C\). If, on the one hand, \(\top \not > C\), then  . If, on the other hand, \(\lnot A > C\), we can use \(\lnot A \not > B\), that is \(\lnot A \not > \lnot \lnot B\) by RW, to obtain \(\lnot A \wedge \lnot B> C\) by RM. Thus \(\lnot (A\vee B)>C\) by LLE. So again,
. If, on the other hand, \(\lnot A > C\), we can use \(\lnot A \not > B\), that is \(\lnot A \not > \lnot \lnot B\) by RW, to obtain \(\lnot A \wedge \lnot B> C\) by RM. Thus \(\lnot (A\vee B)>C\) by LLE. So again,  . \(\square \)
. \(\square \)
Proof of Lemma 5:
AT.  follows from BA, BC, N, K and D.
follows from BA, BC, N, K and D.
NTA. Suppose for reductio that  . Then by VDW
. Then by VDW  , and by RLE
, and by RLE  , contradicting NTC.
, contradicting NTC.
COND*. Suppose  and \({{\,\mathrm{\boxdot }\,}}C\). From the former we get with LLE that
and \({{\,\mathrm{\boxdot }\,}}C\). From the former we get with LLE that  . So by OR*, either
. So by OR*, either  or
or  . But the latter is impossible, by VDW, NTC and RLE. So we have the former, from which we get, by CW* and RLE, that
. But the latter is impossible, by VDW, NTC and RLE. So we have the former, from which we get, by CW* and RLE, that  , as desired. \(\square \)
, as desired. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Raidl, E., Rott, H. Towards a logic for ‘because’. Philos Stud (2023). https://doi.org/10.1007/s11098-023-01998-4
Accepted:
Published:
DOI: https://doi.org/10.1007/s11098-023-01998-4




 . INC
. INC , then
, then 
 .
. .
. , then
, then  , then
, then  .
. and
and  .
. iff
iff  and
and  and
and  .
.
 , but not
, but not 

 and
and  , but not
, but not 

 and
and  , but not
, but not 

 and
and  , but not
, but not 
 iff
iff  iff
iff  iff
iff  .
. then
then  . LLE
. LLE then
then  . RLE
. RLE , then
, then  , then
, then  . NTC
. NTC , then
, then  . VDW
. VDW and
and  . CW*
. CW* , then
, then  or
or  . AND*
. AND* and
and  or
or  . CUT*
. CUT* , then
, then  or
or  . OR*
. OR* and
and  or
or  . CM*
. CM* and
and  , then
, then  . DR*
. DR*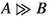 and
and  , then
, then  . RM*
. RM* iff
iff  B
B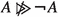 . AT
. AT . NTA
. NTA and
and 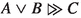 . COND*
. COND*
 ’, at which p is false and q is true, is neither more plausible nor less plausible than any of the other worlds. World pq is more plausible than world
’, at which p is false and q is true, is neither more plausible nor less plausible than any of the other worlds. World pq is more plausible than world 

 ,
,  and
and  . In (1), we have
. In (1), we have  and
and  , a violation of Asymmetry. In (2),
, a violation of Asymmetry. In (2),  and
and  , and in (3),
, and in (3),  and
and  , a violation of Symmetry
, a violation of Symmetry
 .
. does not imply the ‘because’ statement
does not imply the ‘because’ statement  . And the reverse does not hold either.
. And the reverse does not hold either. , if there is C such that (A, C) is a (pres)-violator,
, if there is C such that (A, C) is a (pres)-violator, , otherwise.
, otherwise.