Abstract
Objects appear to fall into different sorts, each with their own criteria for identity. This raises the question of whether sorts overlap. Abstractionists about numbers—those who think natural numbers are objects characterized by abstraction principles—face an acute version of this problem. Many abstraction principles appear to characterize the natural numbers. If each abstraction principle determines its own sort, then there is no single subject-matter of arithmetic—there are too many numbers. That is, unless objects can belong to more than one sort. But if there are multi-sorted objects, there should be cross-sortal identity principles for identifying objects across sorts. The going cross-sortal identity principle, ECIA2 of (Cook and Ebert 2005), solves the problem of too many numbers. But, I argue, it does so at a high cost. I therefore propose a novel cross-sortal identity principle, based on embeddings of the induced models of abstracts developed by Walsh (2012). The new criterion matches ECIA2’s success, but offers interestingly different answers to the more controversial identifications made by ECIA2.
Similar content being viewed by others
Notes
The alternando: for any proportions a, b, c, and d, a : b : : c : d iff a : c : : b : d
Aristotle’s answer is that there is a nameless higher sort, to which numbers and lines both belong. It is because the various proportions derive from things in this higher sort that the common property holds of them for a common reason.
Though standard, this terminology can mislead: abstracts in this sense need not be abstract, in the sense of “not concrete”.
I’m using “sort” here to mean much the same as “kind”. I shall not engage how this interacts with, e.g., Wright’s discussion of which concepts are “sortal” in (Wright 1999).
A similar observation was made by Parsons (1965, pp. 184–5, 191, 195).
Frege’s own program, as realized in the Grundgesetze (Frege 1964, 2013), presumed the abstraction principle BLV would determine special abstracts called extensions, among which would be the natural numbers. It is easy to think that BLV is doubly defective: it is inconsistent, and extensions are enough like sets to fall prey to Benacerraf’s challenge. But the second defect is contested. See Benacerraf (1981), Weiner (1984), and Blanchette (1994, p. 101), the last of which argues “Frege was in a position to argue that the claims of ordinary arithmetic were logically equivalent with their Fregean surrogates, and hence that the grounds of the latter sufficed to ground the former”.
In as much as cardinality is to be understood in terms of bijectability. But see, for example, (Mancosu 2015).
Frege’s Theorem was mentioned by Parsons (1965, p. 194), and emphasized by Wright (1983). The latter initiated the neo-Fregean program, which argues more than just the abstractionist point. It also avers that HP is analytic; by Frege’s Theorem, so (arguably) is arithmetic, resulting in endorsement of Frege’s logicism as well as his realism. I’ve been using “neo-Fregean” to mean those who more-or-less uphold this souped-up abstractionism. The terminology of “abstractionism”, “neo-Fregeanism”, and “neo-logicism” is not standardized, so the distinctions I draw may cut across others’ use of the terms.
Wright remarks that Benacerraf’s problem besets singular terms at large, from the non-controversially objectual like persons and rabbits (Wright 1983, pp. 124–5, 127), to the very sets that drive Benacerraf’s argument (Wright 1983, pp. 125–6)—and not just singular terms for natural numbers.
For a recent discussion of the relation between structuralism and referential indeterminacy, see (Hodesdon 2014). For a more general discussion of responses to Benacerraf’s problem(s), see (Leng 2009). It is an interesting question the extent to which neo-Fregean abstractionism, with its own talk of implicit definition, counts as an algebraic approach.
Here “distinct” means involving numerically distinct abstraction operators. We take as given that extensionally distinct equivalence relations will have different abstraction operators. So, it can happen that \(@_1\) and \(@_2\) are distinct operators, even if both satisfy (1) for the same equivalence E. (I will at times use \(AP_1\), \(@_1\), and \(E_1\) instead of \(AP_{@_1}\), \(@_1\), and \(E_{@_1}\); context should lead the reader to make the obvious identifications.)
This “Good Company Problem” arising from the work of Heck (1997) should not be confused with another due to Boolos (1997) and so named by Clark (2004). The Boolos/Clark problem is that the conception of cardinality forwarded by neo-Fregeans seems incompatible with the conception put foward by the esteemed company of set theorists.
This is to be distinguished from Dedekind finite. See (Heck 1998, p. 434) for how Frege does it; there are of course equivalent ways.
This motivation is made explicit in (Mancosu 2015, p. 402–3). A similar motivation is given by Cook and Ebert (2005, p. 125), who call the problem “the C-R problem”, partly to pun on “Caesar problem” and partly to reference the question of how to identify real numbers as a subset of the complex numbers.
Of course cross-sortal identity criteria bear on much more than just variants of HP. For example, suppose the abstractionist, while not committed to identifying numbers with extensions, wants to identify them anyway? Such a gratuitous realist would need a very finely calibrated criterion for cross-sortal identity. This paper will not address cross-sortal principles as they bear on these thorny issues.
Linnebo (2005, pp. 217–219) argues that to be is to be of a sort F, and that maximal sorts cannot overlap. Though this is consistent with every sort being maximal, it does not require it.
Similar principles are mentioned by Fine (2002, pp. 166, 170) and Linnebo (2009a, pp. 379–80). I have simplified Cook’s and Ebert’s version of \(ECIA_2\) by omitting the restricted quantifiers in its statement in (Cook and Ebert 2005).
Cook and Ebert propose a constraint on cross-sortal identity principles, the Principle of Uniform Identity (PUI), which causes trouble for identifying cardinals with ordinal extensions (Cook and Ebert 2005). But trouble is even closer to home: Mancosu (2015, p. 404–5) raises a problem for PUI that can be applied to the case of “Good Company” as follows. If the HP- and FHP-abstracts are identified for finite concepts, then \((\exists X)(\#X = \#_f X)\). That’s a version of the antecedent of PUI. Its consequent would be \((\forall X)(\# X = \#_f X)\), whence \(\# V = \#_f V = \#_f N = \# N\)—so the universe is countable.
For example, the theory \(D2^*\) of (Shapiro 1991, pp. 67, 108).
All of the following principles can be varied in many ways; one can, for instance, insert an infinite cardinality where I’ve put a finite one. I’ve omitted these for the sake of brevity.
Additionally, the concerns listed below are not exhaustive, since some concerns with \(ECIA_2\) might arise outside the context of coarsenings of HP. For example, one can generate a consistent theory of extensions with the principle NewV (see (Boolos 1989) and the discussion in (Cook and Ebert 2005) and (Shapiro and Weir 1999)):
$$\begin{aligned} (\forall X)(\forall Y)(\S X = \S Y \leftrightarrow X \approx Y \approx V \vee X = Y) \end{aligned}$$(10)where V is the universal concept.
Now \(ECIA_2\) declares that each equivalence-type can be represented by an abstract at most once. However, there are interpretations of \(\S\) that are not isomorphic (this is shown in (Jané and Uzquiano 2004); see also (Walsh and Ebels-Duggan 2015, Sect. 5.2) and (Ebels-Duggan 2019, Lemma 53).)
If the operators \(\S _1\) and \(\S _2\) both satisfy NewV, \(ECIA_2\) requires that the ranges of \(\S _1\) and \(\S _2\) be not just isomorphic, but pointwise identical. But which isomorphism type should be represented? No answer is given, and that \(ECIA_2\) forces this question might be regarded in itself as overreach.
See (Linnebo 2009b) for an alternate development of this thought.
It is also quite close to the thought that the natural numbers should be characterized as ordinals, rather than (or in addition to) as cardinals. But one needn’t go so far to have the “counts up” worry, since to “count up” is to arrange one’s cardinal assessments—answers to “how many” questions—in an ordinal sequence. So something could be part of a counting sequence without being, fundamentally, an ordinal, since to be part of such a sequence is to be a cardinally that can be ordinally arranged.
One could be more democratic and require only that a majority, or a plurality, of such functions assign x to y. We’ll not explore this route here.
Notice it won’t be enough to use isomorphisms that preserve locally defined relations between abstracts. For example, one might think to define a relation that respects < on the natural numbers, and identify abstracts that respect this relation. The problem is that every infinite subset of the natural numbers is <-isomorphic. So identifying abstracts by this kind of isomorphism would mean the collapse of distinctions between any finite HP-abstracts—plainly an undesirable situation.
The construction in Definition 1 differs from that of (Walsh 2012) and (Walsh and Ebels-Duggan 2015) in that the i-ary second-order domain in the original construction is given by \(S_i[M] \cap P(U^i)\) rather than \(Field^i(U)\). This change is made because if \(U\subsetneq \mathrm {rng}(@_j)\), it can happen that there are \(U'\subseteq U\) but no \(@_j U'\in U\), so the operator \(@_j\) would not be total. See the discussion of false atoms on page 29 for more of relevance to this point.
Note also that in general the structure \({\mathcal {M}}_j(U)\) does not satisfy the comprehension axioms for second-order logic, or the abstraction principle \(AP_j\). The primary reason that Field(U) is the monadic second-order domain is to ensure the abstraction operator \(@_j\) is total in \({\mathcal {M}}_j(U)\). However, there are others: this restriction, in conjunction with certain restrictions on U (see Definition 3), combine to ensure that the concepts of our model coordinate correctly with the abstracts of those concepts.
Equivalently, (19) could be given by \((\forall X\in Field(U))(e@_jX = @_k (eX))\).
This holds even if we replaced “\(Field(\mathrm {rng}(\#^i))\)” with “\(P(\mathrm {rng}(\#^i))\)” in (18).
It can happen that nearly all objects in an induced structure are false atoms, as in the case where the following principle, \(OVER(\omega )\), is satisfied in a ground model of size \(\aleph _\omega\):
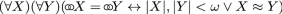 (21)
(21)This principle groups together all of the finite sets, but discriminates infinite sets by cardinality. Observe that
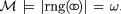 . The induced structure
. The induced structure  not only has false atoms, but also the only abstract that acts like an abstract in the induced structure does so because of the false atoms.
not only has false atoms, but also the only abstract that acts like an abstract in the induced structure does so because of the false atoms.It is important to note, however, that a model is not ungrounded simply in virtue of being “small”. One might think that U was defective for inducing a suitable model because it was not infinite, even though every model of HP is. The defect, however, was not size but the “visible gap” U left in the abstract-concept correspondence, a gap generated by omitting part of an initial segment of an HP-model. For notice that \(U' = \{0,1,2\}\) is also of size 3, but its induced model is grounded. No abstract in the model is a false atom, and every subset of a represented concept is also represented by an abstract.
One might then ask why grounded models should not include abstracts for all subsets of the inducing set U: if one can reason from a size-2 concept down to a singleton, why not reason from a size-2 up to the universal concept (for the induced model)? This is a good and difficult question, but two considerations suggest reasoning “upward” is not as safe as reasoning “downward”. First, as Heck (1997, p. 596) remarks, Cantor’s recognition of infinite numbers was a “conceptual leap” that is easy to overlook. Someone naive of Cantor’s paradise could well conceive herself in a universe with infinitely many objects—among them numbers, and so abstracts—and yet not recognize that there is an infinite number. Second, the same goes for someone who lives in Cantor’s paradise: in modern set theory, formulas defining collections that are “too large” do not determine sets. In light of this it is worth remarking that grounded induced models arise, in general, from initial segments of the universe of abstracts. Thus one can generate a grounded set (in the sense of Definition 3) from a given set of abstracts S by:
$$\begin{aligned} U = \{x\in \mathrm {rng}(@)\mid (\exists s\in S)(\exists X, Y)(x= @ X, s= @ Y, X\subseteq Y \}. \end{aligned}$$(Note that a set so generated might have false atoms.) A corollary for \(\$\)-extensions (as on page 8) is that each initial segment \(V_\alpha\) of a well-founded universe will be \(\$\)-grounded.
Note that this does not imply \(U = \{x\in \mathrm {rng}(@)\mid (\exists Y\subseteq U)(x = @ Y)\}\).
It conflicts with the PUI of (Cook and Ebert 2005), but as shown in footnote \(^{18}\), there are reasons to be wary of this principle.
The difficult case is the one in which \(@_1 X \ll @_2 Y\) and \(@_3 Z \ll @_2 Y\); here one uses (25) to show that if \(\Gamma _1 (U_1)\preceq \Gamma _3(U_3)\) for \(\Gamma _i:{\mathcal {M}}_i(U_i)\hookrightarrow {\mathcal {M}}_2\) then by Lemmata 1 and 2 , the natural embedding e exists and \(e(@_1 X)= @_3 Z\).
It is worth noting that as stated, SI cannot be applied generally, since the relation \(\ll \gg\) is not reflexive for all collections of abstracts. To wit, any collection U of abstracts @ with non-trivial automorphisms renders SI(@, @) false. To apply generally, then, SI must at least prohibit the axioms \(SI(@_i, @_j)\) where \(i=j\). This isn’t a concern in T(HP) since (as follows from Lemmata 1 and 2) automorphisms for the abstracts of HP-coarsenings are unique.
One might wonder why one cannot use Theorem 2 here, on the expectation that \(U_\omega\), or \(U_{\omega ^+}\), maximally \(\#\)-respects \(E_@\) for each Good Companion \(AP_@\). But it is not clear this latter claim is true. For it is consistent (if ZF is consistent) that there are \(2^{\aleph _0}\) many concepts that are infinite but Dedekind finite (see (Tarski 1965; Rubin and Rubin 1974; Truss 1974)). In such a case, if U contains all and only the Dedekind finite abstracts, then U is suitable though \(U \not \preceq U_\omega\).
References
Antonelli, G. A. (2010). Notions of invariance for abstraction principles. Philosophia Mathematica, 18(3), 276–292.
Benacerraf, P. (1965). What numbers could not be. The Philosophical Review, 74(1), 47–73.
Benacerraf, P. (1973). Mathematical truth. Journal of Philosophy, 70(19), 661–679.
Benacerraf, P. (1981). Frege: The Last Logicist. Midwest Studies in Philosophy, 6, 17–35. Reprinted in Demopoulos (1995).
Blanchette, P. A. (1994). Frege’s reduction. History and Philosophy of Logic, 15, 85–103.
Boolos, G. (1989). Iteration again. Philosophical Topics, 17, 5–21.
Boolos, G. (1997). Is Hume’s Principle analytic? In R. K. Heck (Ed.), Language, thought, and logic: Essays in honour of Michael Dummett (pp. 245–261). Oxford: Oxford University Press. Originally edited under the name “Richard G. Heck, Jr.”
Boyer, C. B. (1968). A history of mathematics. New York: Wiley.
Clark, P. (2004). Frege, neo-logicism and applied mathematics. Vienna Circle Institute Yearbook, 11, 169–183.
Clarke-Doane, J. (2017). What is the Benacerraf problem? In F. Pataut (Ed.), New perspectives on the philosophy of Paul Benacerraf: Truth, Objects, Infinity. Cham: Springer.
Cook, R. T., & Ebert, P. (2005). Abstraction and identity. Dialectica, 59(2), 121–139.
Dedekind, R. (1963). Essays on the theory of numbers. New York: Dover Publications Inc.
Descartes, R. (1954). The Geometry of René Descartes. New York: Dover. (Trans. by David Eugene Smith and Marcia L. Latham).
Ebels-Duggan, S. C. (2019). Abstraction Principles and the Classification of Second-Order Equivalence Relations. Notre Dame Journal of Formal Logic, 60(1), 77–117.
Field, H. (1989). Realism, mathematics and modality. London: Blackwell.
Fine, K. (2002). The limits of abstraction. Oxford: The Clarendon Press.
Frege, G. (1964). The Basic Laws of Arithmetic: Exposition of the System. : University of California Press. Translated and edited by Montgomery Furth.
Frege, G. (2013). Basic Laws of Arithmetic. Oxford: Oxford University Press. Translated by Philip A. Ebert and Marcus Rossberg.
Hale, B., & Wright, C. (2001). To bury Caesar. The reason’s proper study (pp. 335–396). Oxford: Clarendon Press.
Heathcote, A. (2014). On the exhaustion of mathematical entities by structures. Axiomathes, 24(2), 167–180.
Heck, R. K. (1997). Finitude and Hume’s Principle. Journal of Philosophical Logic, 26(6), 589–617. Originally published under the name “Richard G. Heck, Jr”.
Heck, R. K. (1998). The finite and the infinite in Frege’s Grundgesetze der Arithmetik. In M. Schirn (Ed.), The philosophy of mathematics today (pp. 429–466). Oxford: Clarendon Press. Originally published under the name “Richard G. Heck, Jr”.
Heck, R. K. (2011). Frege’s Theorem. Oxford: Oxford University Press. Originally published under the name “Richard G. Heck, Jr”.d.
Hodesdon, K. (2014). Mathematical representation: Playing a role. Philosophical Studies, 168(3), 769–782.
Jané, I., & Uzquiano, G. (2004). Well and non-well-founded Fregean extensions. Journal of Philosophical Logic, 33, 437–465.
Kouri, T. (2015). A reply to Heathcote’s: On the exhaustion of mathematical entities by structures. Axiomathes, 25(3), 345–357.
Ladyman, J., Linnebo, O., & Pettigrew, R. (2012). Identity and discernibility in philosophy and logic. The Review of Symbolic Logic, 5(1), 162–186.
Leitgeb, H., & Ladyman, J. (2008). Criteria of identity and structuralist ontology. Philosophia Mathematica, 16(3), 388–396.
Leng, M. (2009). “Algebraic” approaches to mathematics. In O. Bueno & Ø. Linnebo (Eds.), New waves in the philosophy of mathematics (pp. 117–134). New York: Palmgrave.
Linnebo, Ø. (2005). To be is to be an F. Dialectica, 59(2), 201–222.
Linnebo, Ø. (2009a). Bad company tamed. Synthese, 170(3), 371–391.
Linnebo, Ø. (2009b). Frege’s Context Principle and reference to natural numbers. In S. Lindström, E. Palmgran, K. Seberberg, & V. Stoltenberg-Hansen (Eds.), Logicism, intuitionism, and formalism: What has become of them? (Vol. 341, pp. 47–68). Dordrecht: Springer.
Linnebo, Ø., & Pettigrew, R. (2014). Two types of abstraction for structuralism. The Philosophical Quarterly, 64(255), 267–283.
Maddy, P. (1990). Realism in mathematics. Oxford: Clarendon Press.
Mancosu, P. (2015). In good company? On Hume’s Principle and the assignment of numbers to infinite concepts. Review of Symbolic Logic, 8(2), 370–410.
Parsons, C. (1965). Frege’s theory of number. In M. Black (Ed.), Philosophy in America (pp. 180–203). Ithaca: Cornell University Press.
Parsons, C. (2008). Mathematical thought and its objects. Cambridge: Harvard University Press.
Potter, M. (2000). Reason’s Nearest Kin: Philosophies of Arithmetic from Kant to Carnap. Oxford: Oxford University Press.
Resnik, M. D. (1997). Mathematics as a science of patterns. Oxford: Clarendon.
Rubin, A. L., & Rubin, J. E. (1974). The cardinality of the set of Dedekind finite cardinals in Fraenkel-Mostowski models. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 20(31–33), 517–528.
Schiemer, G., & Wigglesworth, J. (2019). The structuralist thesis reconsidered. The British Journal for the Philosophy of Science, 70(4), 1201–1226.
Shapiro, S. (1991). Foundations without foundationalism: A case for second-order logic volume 17 of Oxford logic guides. New York: The Clarendon Press.
Shapiro, S. (2000). Philosophy of mathematics: Structure and ontology. Oxford: Oxford University Press.
Shapiro, S. (2008). Identity, indiscernibility, and ante rem structuralism: The tale of \(i\) and \(-i\). Philosophia Mathematica, 16(3), 285–309.
Shapiro, S., & Weir, A. (1999). New V, ZF, and abstraction. Philosophia Mathematica, 7, 293–321.
Tarski, A. (1965). On the existence of large sets of Dedekind finite cardinals. Notices of the American Mathematical Society, 12, 719.
Truss, J. (1974). Classes of Dedekind finite cardinals. Fundamenta Mathematicae, 84(3), 187–208.
Walsh, S. (2012). Comparing Hume’s Principle, Basic Law V and Peano Arithmetic. Annals of Pure and Applied Logic, 163, 1679–1709.
Walsh, S., & Ebels-Duggan, S. (2015). Relative categoricity and abstraction principles. The Review of Symbolic Logic, 8(3), 572–606.
Weiner, J. (1984). The philosopher behind the last logicist. Philosophical Quarterly, 34(136), 242–264.
Wigglesworth, J. (2018). Non-eliminative structuralism, Fregean abstraction, and non-rigid structures. Erkenntnis. https://doi.org/10.1007/s10670-018-0096-3.
Wright, C. (1983). Frege’s conception of numbers as objects volume 2 of scots philosophical monographs. Aberdeen: Aberdeen University Press.
Wright, C. (1999). Is Hume’s Principle analytic? Notre Dame Journal of Formal Logic, 40(1), 6–30.
Acknowledgements
The author would like to thank an anonymous reviewer for this journal, the audience at the 2018 ASL North American Meeting, Michael Glanzberg, Jc Beall, Sean Walsh, Patricia Blanchette, Josiah Lopez-Wild, Conor Jones, Matthias Schirn, and Teresa Kouri Kissel for discussion of this project, as well as Emily Moorman and Maria Galaviz Huerta, who also proofread the original manuscript (all errors are mine, of course). Ms. Galaviz Huerta worked under a Summer Undergraduate Research Assistantship Grant generously provided by the Northwestern University Office of Undergraduate Research. Thanks also to Andrew Hull and especially Joe Karbowski for enlightening discussion of Aristotle. They are not at all responsible for any of the liberties I’ve taken with Aristotle’s text.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ebels-Duggan, S.C. Identifying finite cardinal abstracts. Philos Stud 178, 1603–1630 (2021). https://doi.org/10.1007/s11098-020-01503-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-020-01503-1




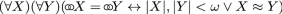
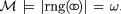 . The induced structure
. The induced structure 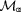 not only has false atoms, but also the only abstract that acts like an abstract in the induced structure does so because of the false atoms.
not only has false atoms, but also the only abstract that acts like an abstract in the induced structure does so because of the false atoms.