Abstract
Core principles of mereology have been questioned by appealing to time travel scenarios. This paper questions the methodology of employing time travel scenarios to argue against mereology. We show some time travel scenarios are structurally equivalent to more standard ones not involving time travel; and that the three main theories about persistence through time (i.e., endurantism, perdurantism, and stage theory) can each solve both the time travel scenario as well as the structurally similar classical scenario. Time travel scenarios that are not similar to more standard arguments are instead problematic because they are open to different, incompatible interpretations. We conclude that compared to the classical arguments against mereological principles, time travel scenarios do not add anything new.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mereology is the study of the part–whole relation and the relations between parts within a whole. Taking identity and the notion of proper parthood (‘<’) as primitive, we can define improper parthood and overlap as follows
-
Parthood
\(x \le y =_{df} x <y \vee x = y\)
-
Overlap
\(x \circ y =_{df} \exists z (z \le x \wedge z \le y)\)
The axioms of minimal mereologyFootnote 1 (MM) describe the proper parthood relation as a transitive, asymmetric and weakly supplemented relation, i.e. a relation that satisfies the following axioms
-
TR
\(\forall x \forall y \forall z ((x<y \wedge y<z) \rightarrow x <z)\)
-
AS
\(\forall x \forall y (x<y \rightarrow y \not < x)\)
-
WS
\(\forall x \forall y (x <y \rightarrow \exists z (z \le y \wedge \lnot z \circ x ))\)
From these axioms we can derive irreflexivity
-
IR
\(x \not < x\)
Recently, some have argued that some or all of these axioms are inconsistent with objects that are multilocated after time travel (Barker and Dowe 2003; Effingham and Robson 2007; Effingham 2010; Gilmore 2009; Kearns 2011). These arguments typically run by showing that time travel scenarios imply a reductio which forces one to either abandon at least one of the above principles, or deny the possibility of multilocation after time travel. We reproduce this kind of argument in the version provided by Shieva Kleinschmidt (2011) (Argument 1 of Sect. 2). We then formalise it in a first-order modal framework which helps us capturing its key steps from the point of view an endurantist ontology of objects in time.
A time travel scenario is either structurally identical to a scenario not involving time travel, or it is not. In Sects. 2 and 3 we focus on the first disjunct, while Sect. 4 is devoted to the argumentative value of time travel scenarios that have no mundane counterpart. In particular, we show that the time travel scenario of Kleinschmidt has the same deductive structure as a mereological puzzle not involving time travel (Argument 2 of Sect. 2). It is then easy to show that these arguments stand or fall together. Indeed, the only way to make one of the arguments substantially different is to operate a ‘modal shortcut’ on Argument 1 (the time travel scenario). This is only possible by interpreting the notion of time travel in its strongest possible sense; i.e., as a proper ‘loop’ of the four-dimensional block universe on itself. In that case, however, not only minimal mereology is then up for grabs but so is the whole ‘logical structure’ of the world, as already pointed out by Lewis (1976) and formally proven by Yanofsky (2003).
In Sect. 3 we consider Arguments 1 and 2 from the perspective of an endurantist, a perdurantist, and a stage theorist. From an endurantist point of view Arguments 1 and 2 are both sound (Sect. 3.1). Therefore, in order to avoid the reductio, some of its assumptions should be discarded. This can be done in several ways, and we illustrate the most relevant strategies that can be found in the philosophical literature. We show that Arguments 1 and 2 are instead not sound from the point of view of a perdurantist (Sect. 3.2) or of a stage theorist (Sect. 3.3). This is essentially due to the fact that these theories do not validate the necessity of difference, a key principle involved in the reductio, nor the stronger unrestricted Leibniz’s Law.
Having considered time travel scenarios that are structurally identical to arguments that do not involve time travel, we then consider in Sect. 4 the argumentative value of time travel scenarios that are not structurally similar to time-travel-free arguments. We argue that they have no added argumentative value because the plausibility of such scenarios depends on background assumptions that are themselves up for debate. We claim that in this sense time travel scenarios function like Rorschach tests: they show what one wants to see, whether this is the invalidity of some mereological principle, or the impossibility of time travel and multilocation. As long as we lack a commonly agreed upon metaphysical theory of persistence and the metaphysics of time travel, it is best not to use time travel scenarios as philosophical arguments for or against mereological principles.
2 The puzzle
Kleinschmidt (2011) provides the following argument against multilocation after time travel.
Argument 1
Meet Clifford. Clifford is a handsome dog statue who was lovingly made from smaller statues. He has Kibble, a statue of a biscuit, as a proper part that makes up his torso. Kibble also has statues among its proper parts, including Odie, a solid dog-statue who makes up most of Kibble. Clifford is an outside dog, and after 20 years of sitting in the sun three things happened: (i) he melted a bit, making Clifford a solid, continuous mass. Unfortunately this has resulted in Clifford no longer having any statues as proper parts; none of them could remain after melting together. But Clifford survived, since most of the same matter stuck around. (ii) Next, all of the atoms that once made up Clifford were slowly replaced by new ones. But this change happened a little bit at a time. (iii) Like a raisin in the sun, Clifford shrank quite a bit, and many of his atoms left for good. Over the course of 20 years, Clifford came to be about a third of his original size. But again, the change was quite slow, and Clifford was resilient. One day, God looked down and said, “Clifford, you’ve been a good boy. I’m going to let you go on an adventure. I’m going to let you travel back in time to just before you were created.” Perhaps Clifford was helped to move discontinuously, or perhaps spacetime was simply looped, providing a path to the past a dog-statue could follow. But one way or another, Clifford ended up sitting on a shelf, visiting this earlier time and occupying exactly the region that had been occupied by Odie. Then an artist came along and saw him and said, “I know just what to do with you!” The artist used Clifford to make up most of Kibble, just like Odie. In fact, Odie and Clifford didn’t share just these properties, they shared all of their properties: they’re one and the same dog-statue! So Clifford was located within Kibble, which was located within Clifford.
When we started describing the case we noted that Odie was a proper part of Kibble, which was a proper part of Clifford. Finding out that Odie is actually a time traveller shouldn’t change the parthood relations we say he stands in at that time (especially if we think that time-travellers don’t bloat: i.e., we think Odie is, in fact, wholly located at the small region within Clifford). So we ought to claim that Clifford/Odie is a proper part of Kibble, which is a proper part of Clifford. However, this is clearly problematic. It is in obvious conflict with the Transitivity of Proper Parthood. (Kleinschmidt 2011, pp. 256–257)
So multilocation as the result of time travelling is inconsistent with MM, in particular with the transitivity of proper parthood. Kleinschmidt (2011, p. 272) argues that the conclusion to draw from scenarios like the above is that multilocation is impossible,Footnote 2 while others instead take it that the problem lies with MM (Donnelly 2010; Gilmore 2009). How do we decide which conclusion to draw? What might help is to see whether time travel is essential to the arguments. If it is essential, then one might want to avoid these philosophical conundrums by simply denying the possibility of time travel. Unfortunately, we argue that time travel is not essential to these arguments. More precisely, we think time travel puzzles are structurally equivalent to classical puzzles concerning the interplay between persistence through time and mereological change. This is still progress because it means we can use solutions to the classical cases to dissolve the more exotic time travel situations.
Before making the equivalence between the puzzles more precise, consider Argument 2, i.e. a slightly modified version of Argument 1 where no time travel is involved.Footnote 3
Argument 2
Clifford has Kibble and Odie as proper parts, as in the previous case. As time goes by, Clifford gradually loses atoms and shrinks to the size of Odie. Twenty years later an artist comes, recollects the atoms Clifford has lost in his lifetime and makes a statue with the shrunken Clifford as a proper part at the place where Odie was. Again, Odie and Clifford share all their properties, they are one and the same. Again, Clifford/Odie is inside Kibble which is inside Clifford. Although no time travel is involved, MM and in particular the transitivity of proper parthood seems violated here too.
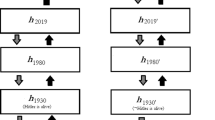
Argument 2 is adapted from Van Inwagen (1981) and has been widely debated. Is it structurally different from Argument 1? To assess this we need to take a closer look to their formal structure. In order to reason about objects and their properties over time we need (at least) a first-order modal language that contains (a) Boolean operators \(\lnot \phi\) (‘it is not the case that \(\phi\)’), \(\psi \rightarrow \phi\) (‘if \(\psi\) then \(\phi\)’), \(\phi \wedge \psi\) (‘\(\phi\) and \(\psi\)’) and \(\phi \vee \psi\) (‘\(\phi\) or \(\psi\)’); (b) quantifiers \(\forall x \phi\) (‘for all x it is the case that \(\phi\)’) and \(\exists x \phi\) (‘for some x it is the case that \(\phi\)’) and (c) temporal operators \(\Box \phi\) (‘it has always been the case that \(\phi\)’) and \(\diamond \phi\) (‘it has been the case at least once that \(\phi\)’).Footnote 4 Also, notice that both arguments presuppose reidentification of objects through different contexts: the ‘later’ Odie (\(\mathbf {o}_{\mathbf {t3}}\)) is identified with the ‘former’ Clifford (\(\mathbf {c}_{\mathbf {t1}}\)), and the ‘later’ Clifford (\(\mathbf {c}_{\mathbf {t3}}\)) is identified with the ‘former’ Clifford as well (see also Fig. 1). To properly express these reidentifications we endow our language with predicate abstraction as in (Fitting and Mendelsohn 1998): for any formula \(\phi\) we introduce \(\langle \lambda x. \phi (x) \rangle (t)\), which intuitively says ‘the object denoted by t enjoys the property expressed by \(\phi (x)\)’, where x is a place holder filled by the object denoted by t. The use of predicate abstraction allows us to make certain scope differences explicit.Footnote 5
In order to show, for reductio, that some object is a proper part of itself, both arguments employ Leibniz’s Law: if two variables denote the same object then they are substitutable in the same formulas salva veritate. The latter is however restricted to a non modal (non intensional) context, i.e. we have
-
RLL
\(x = y \rightarrow (\phi \rightarrow \phi [x/y])\) where \(\phi\) does not contain any modal operator
The second principle used by both arguments is a non-standard version of the Necessity of Difference principle, usually formulated as (ND) \(x \not = y \rightarrow \Box (x \not = y)\), i.e. if the values assigned to x and y are distinct then these values are necessarily distinct. By contraposition, if the value assigned to x is possibly identical to the value assigned to y, then x and y are assigned the same value (i.e., denote the same object). Here, Arguments 1 and 2 exploit the fact that if some object at some point in time, e.g. the later Clifford, has the property of ‘being identical to some former object’, e.g. the former Clifford, then the two objects are identical tout court. This is expressed by the following principle
-
ND*
\(\langle \lambda w. \diamond (w=y) \rangle (x) \rightarrow x = y\)
Both RLL and ND* are valid principles for varying domain Kripke models. Indeed they both follow from the validity of the more general
-
LL
\(x = y \rightarrow (\phi \rightarrow \phi [x/y])\) where \(\phi\) is any formula
i.e. the unrestricted Leibniz’s Law (see Fitting and Mendelsohn 1998, Ch. 4, Ch. 9, Ch. 10).Footnote 6,Footnote 7
Let \(\mathbf {o}_{\mathbf {t1}}\) denote the individual referred to as Odie at the initial moment \(t_{1}\) of our story. Analogously, \(\mathbf {o}_{\mathbf {t3}}\) denotes the individual referred to as Odie at the later moment \(t_{3}\), and \(\mathbf {c}_{\mathbf {t1}}\) (resp. \(\mathbf {c}_{\mathbf {t3}}\)) the former (resp. the later) Clifford. The reductio contained in both arguments depends on the truth of the three following assumptions under some valuation v of the variables, where \(\phi [x/\mathbf {o}_{\mathbf {t3}}, y/\mathbf {c}_{\mathbf {t1}}, z/\mathbf {c}_{\mathbf {t3}}]\) indicates that v assigns value \(\mathbf {o}_{\mathbf {t3}}\) to x, \(\mathbf {c}_{\mathbf {t1}}\) to y and \(\mathbf {c}_{\mathbf {t3}}\) to z.
Under the valuation v, A.1 says of\(\mathbf {o}_{\mathbf {t3}}\) that it has the property of being ‘identical at some previous point’ with the value of y, i.e. \(\mathbf {c}_{\mathbf {t1}}\). More colloquially A.1 says that, going back in time, the later Odie (\(\mathbf {o}_{\mathbf {t3}}\)) is ‘reidentified’ with the former Clifford. Analogously A.2 says that the later Clifford (\(\mathbf {c}_{\mathbf {t3}}\)) is ‘reidentified’ back in time with the former Clifford. A.3 expresses the fact that the later Odie is a proper part of the later Clifford, which is assumed by both arguments.Footnote 8
The following reductio is common to Arguments 1 and 2. In order to not overload our derivation we write e.g. \(\mathbf {o}_{\mathbf {t3}}= \mathbf {c}_{\mathbf {t1}}\) instead of \(x = y [x/\mathbf {o}_{\mathbf {t3}}, y/\mathbf {c}_{\mathbf {t1}}, z/\mathbf {c}_{\mathbf {t3}}]\). We beg the reader to forgive this abuse of notation.
1. | \(\langle \lambda w. \diamond (w=\mathbf {c}_{\mathbf {t1}})\rangle \mathbf {o}_{\mathbf {t3}}\) | |
2. | \(\langle \lambda w. \diamond (w = \mathbf {c}_{\mathbf {t1}})\rangle \mathbf {c}_{\mathbf {t3}}\) | |
3. | \(\mathbf {c}_{\mathbf {t3}}\not < \mathbf {c}_{\mathbf {t3}}\) | by IR |
4. | \(\mathbf {o}_{\mathbf {t3}}= \mathbf {c}_{\mathbf {t1}}\) | from 1 by ND* |
5. | \(\mathbf {c}_{\mathbf {t1}}= \mathbf {c}_{\mathbf {t3}}\) | from 2 by ND* |
6. | \(\mathbf {o}_{\mathbf {t3}}= \mathbf {c}_{\mathbf {t3}}\) | from 4 and 5 by transitivity of identity |
7. | \(\mathbf {o}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\) | |
8. | \(\mathbf {o}_{\mathbf {t3}}= \mathbf {c}_{\mathbf {t3}}\rightarrow (\mathbf {o}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\rightarrow \mathbf {c}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}})\) | RLL |
9. | \(\mathbf {o}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\rightarrow \mathbf {c}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\) | from 6 and 8 by MP |
10. | \(\mathbf {c}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\) | from 7 and 9 by MP |
11. | \(\bot\) | from 3 and 10 |
Insofar as ND* and RLL are accepted as sound, the reductio seems compelling. We claim that this is the general structure of both Arguments 1 and 2, for the key assumptions are the same. This is obvious for A.3: Odie is a proper part of Clifford in both scenarios. Also, in both scenarios Odie is at some point in time identical with the former Clifford and the latter Clifford is at some point in time identical with the former Clifford, i.e. A.1 and A.2, respectively.Footnote 9
The temporal structure for Argument 2
The only difference lies in the fact that Argument 2 presupposes an intuitive temporal structure as that depicted in Fig. 1 whereas Argument 1 holds that the two points of valuation \(t_{1}\) and \(t_{3}\) are located ‘at the same time’ as in Fig. 2, where \(t_{1} \sim t_{3}\) indicates the simultaneity of \(t_{1}\) and \(t_{3}\). This however has no impact on our reductio. Indeed, structures like the one outlined in Figs. 1 and 2 give rise to modally equivalent models. If so, both arguments stand or fall together. And a solution to either argument should be a solution to both if it is to be a satisfactory solution. But this suggests that time travel does not create new or additional complications with respect to the standard case presented by, for example, van Inwagen.
The temporal structure for Argument 1
If the time travel scenario were to create new or additional problems for MM then some solutions to Argument 2 should not be applicable to Argument 1. In order to show this, one should argue that the reductio presented above is not sound (by blocking some step of the derivation). In addition, one should claim that Argument 1 is based on some other assumption(s), to the effect that it is more compelling than Argument 2. And, consequently, that our reconstruction above is incorrect as a reconstruction of Argument 1. This is possible, it seems, only by ‘shortcutting’ the above derivation and claiming that Argument 1 directly assumes 4 and 5 with no ‘modal detour’ via ND*. In that case time travel scenarios as the one represented in Fig. 2 assume not only \(t_{1} \sim t_{3}\), but instead the stronger \(t_{1} = t_{3}\). However, it is easy to see that as soon as one makes this move the argument from time travel against MM does not pose a special problem to mereology, but rather a problem to the logic of identity. For if we assume \(x=y\) and \(y=z\) there is no room left for ascribing (not just mereological relations but) any n-place relation such that, at one and the same time, x stands in that relation but z does not, because doing so would lead to a contradiction via RLL (and a fortiori via LL).
For example, besides any mereological relations that hold between Clifford and Odie (= Clifford) there is the non-mereological relation of being one third the size of holding between Clifford and Odie. (Remember, Clifford shrinks to a third its original size before time travelling.) This relation seems irreflexive: nothing is—at one and the same time—one third its own size. But since Odie is the time traveling Clifford, we are forced to choose between RLL and the irreflexivity of being one third the size of. Giving up the latter merely postpones the main issue, which is that RLL in relation to time travel results in puzzles and conundrums. For example, Clifford is, say, 12 feet tall, but Odie is not 12 feet tall (but 4). But by RLL, Clifford is and is not 12 feet tall—contradiction. Major logical problems with looping scenarios as that of Fig. 2 were signaled, among others, already by Lewis (1976). Based on a diagonalization argument, Yanofsky (2003) provides a fully formal set-theoretic proof of the fact that loops of this kind entail a contradiction.
So the challenge we pose is this: if an argument from time travel should add a novel reason for abandoning a principle of minimal mereology, then that argument should differ from classical arguments against minimal mereology in such a way that solutions to those classical arguments do not apply. In the next section we show how three theories about the persistence of objects relate to Arguments 1 and 2. For each theory we show that it can answer both arguments in a uniform manner. This means that time travel scenarios that are structurally similar to classical arguments against minimal mereology do not have any added argumentative value relative to the classical case. In Sect. 4 we consider instead time travel scenarios that are not similar to any classical argument against minimal mereology. We argue that in those cases we still have no additional or new argument against minimal mereology because any interpretation of such a scenario would have to employ principles that the defender of minimal mereology need not accept.
3 Three theories of persistence
To affirm that Clifford at the earlier moment is ‘the same’ as Clifford at a later moment is to say that Clifford persists. But how do we identify objects through time? There are roughly three distinct theories available and they each provide different answers to Arguments 1 and 2. They go under the name of ‘endurantism’, ‘perdurantism’, and ‘stage theory’ (also known as ‘sequentialism’ or ‘exdurantism’). According to endurantism objects can be extended in space but not in time. They persist through time by being wholly present at every moment in which they exist. Perdurantism instead holds that objects are extended in space as well as in time and that an object’s temporal parts are thus analogous to its spatial parts.Footnote 10 Finally, the stage theorist treats objects as three-dimensional (like the endurantism) but denies that objects persist through time. Instead objects are instantaneous stages that are connected by a temporal counterpart relation. So endurantism differs from the other two in that the former is the only theory that allows for strict identity over time. The perdurantist is alone in holding that objects are four-dimensional entities with both spatial and temporal parts, and the stage theorists is unique since it is the only one who thinks persistence has to be analysed in terms of a counterpart relation.
We now discuss how each theory can deal with the above two puzzles.
3.1 Endurantism
The metaphysical position of the endurantist corresponds to standard Kripke semantics with possibilist quantification. Therefore she accepts LL and ND*. To avoid contradicting LL, endurantists hold that having a property, or standing in a relation, is relative to a time. This relativisation to time can be accomplished in two ways: one can hold that an object a has at t the property F; or, alternatively, that an object a has the property F at t. Applying these ideas to mereology means that, for example, the handle and the cup stand at t in a proper parthood relation (alternatively, that they stand in a proper parthood relation at t).
Let’s see how this pertains to the mereological case, starting with Argument 2. The endurantist will say that Odie stands, at \(t_1\), in a proper parthood relation to Clifford. As time passes, Clifford shrinks such that at \(t_3\) all proper parts that Clifford had at \(t_1\) are gone except for Odie. So it seems that at \(t_3\) Odie = Clifford. But since identity holds necessarilyFootnote 11 (i.e., that identity over time is strict), we get that Odie = Clifford at all times.Footnote 12 Hence at \(t_1\) it is both the case that Odie is a proper part of Clifford, and that Odie = Clifford—contradiction. Making mereological relations time-relative is thus insufficient to solve Argument 2 and—as the reader may verify—neither will it solve Argument 1. The endurantist should thus find an alternative way out of our reductio of Sect. 2.
Direct routes are (1) denying transitivity of identity (Geach 1968), (2) accepting mereological essentialism by rejecting A.2 (Chisholm 1973), or (3) accepting the Doctrine of Potential Parts by rejecting A.3.Footnote 13 Denying the transitivity of identity amounts to a denial of RLL because transitivity follows from RLL together with the reflexivity of =. So denying the transitivity of = solves both Arguments 1 and 2 at the cost of denying RLL (and a fortiori LL). The second option also solves both Arguments 1 and 2 for the simple reason that the small Clifford that travels back in time does not have the same parts that the larger Clifford has, hence they are not the same. Finally, the Doctrine of Potential Parts says that objects such as my hands are merely potential objects and it is only by detaching them from the rest of me that they become actual objects. In our case this results in a denial of A.3 because at the moments we would say that Odie is a proper part of Clifford, Odie is attached to Clifford and thus merely a potential object. Whereas after Clifford shrank to a third its size, Odie is an actual object but—crucially—it can then not be said to be a proper part of Clifford. So there is no time at which it is the case that both Odie and Clifford exist as actual objects and that they stand in a proper parthood relation.Footnote 14
We have sketched how the standard endurantistic responses to Argument 2 extend to Argument 1. We do not wish to assess the relative strength of these responses here since our goal is only to show that arguments which employ time travel do not create novel problems for minimal mereology but are merely variations on more classical puzzles.
3.2 Perdurantism
The perdurantist holds that an object persists through time by having temporal parts at each moment of time it exists. This means an object has both spatial and temporal parts.Footnote 15 The perdurantist does not accept standard Kripke semantics for quantified modal logic but instead holds a substantial interpretation where objects are identified with functions from possible worlds to individuals in the domain (Belardinelli 2006, chap. 34). The substantial interpretation does not validate the necessity of difference principle: two different objects can coincide by sharing a temporal part at some point in time while being different at other points in time. As a consequence the reductio is blocked since 4 and 5 cannot be derived. To convince the reader that Arguments 1 and 2 are equally unproblematic on the perdurantist account we show how a perdurantist would model either argument, starting with Argument 2.
Consider Fig. 2, where \(\mathbf {o}_{\mathbf {t1}}, \mathbf {c}_{\mathbf {t1}}, \mathbf {o}_{\mathbf {t2}}\) etc. are now not considered as ‘complete’ individuals but merely as simple elements of the domain, corresponding to ‘temporal parts’ of some object. Each four-dimensional object is instead modelled as a function \(\mathbf {f}\) from points in time to elements of the domain. Following our story, we can coherently describe the persisting Odie as the function \(\mathbf {o}\) such that \(\mathbf {o}(t_{1})=\mathbf {c}_{\mathbf {t1}}\), \(\mathbf {o}(t_{2})=\mathbf {c}_{\mathbf {t2}}\) and \(\mathbf {o}(t_{3})=\mathbf {o}_{\mathbf {t3}}\). The spatiotemporal object called Clifford is instead the function \(\mathbf {c}\) such that \(\mathbf {c}(t_{1})=\mathbf {c}_{\mathbf {t1}}\), \(\mathbf {c}(t_{2})=\mathbf {c}_{\mathbf {t2}}\) and \(\mathbf {c}(t_{3})=\mathbf {c}_{\mathbf {t3}}\). In other words, the metaphysical interpretation perdurantists give of this situation is that Clifford and Odie are spatiotemporal worms that share temporal parts at \(t_1\) and \(t_2\).
Consider now \(t_{3}\) as our reference point. Here it is true of \(\mathbf {o}\) that it is ‘possibly identical with \(\mathbf {c}\) in the past’, since \(\mathbf {o}\) and \(\mathbf {c}\) temporally overlap at \(t_{1}\) and \(t_{2}\). (They both have \(\mathbf {c}_{\mathbf {t2}}\) as a temporal part.) It is also trivially true of \(\mathbf {c}\) that it is ‘possibly identical with \(\mathbf {c}\) in the past’, since \(\mathbf {c}\) overlaps with itself at every point. At \(t_{3}\) it is also true that \(\mathbf {o}\) is a proper part of \(\mathbf {c}\) since it is the case that \(\mathbf {o}_{\mathbf {t3}}<\mathbf {c}_{\mathbf {t3}}\). By consequence the conditions previously expressed by A.1 to A.3 are satisfied at \(t_{3}\). By assuming that the axioms of MM hold at every point for the elements of our domain (e.g. \(\mathbf {c}_{\mathbf {t3}}\not < \mathbf {c}_{\mathbf {t3}}\) at \(t_{3}\)) we derive also that irreflexivity holds and \(\mathbf {c}\) is not a proper part of \(\mathbf {c}\) at \(t_{3}\).
Therefore the assumptions 1, 2, 3 and 7 of our derivation are satisfied by this interpretation. However, it is not the case that \(\mathbf {o}\) is identical with \(\mathbf {c}\), since \(\mathbf {c}_{\mathbf {t3}}\ne \mathbf {o}_{\mathbf {t3}}\). This is because the necessity of difference, and, more generally, Leibniz’s Law is invalid under the substantial interpretation when applied to elements of the domain, i.e. the temporal (proper) parts of the four-dimensional worms. Therefore steps 4 to 6 of our reductio (and steps analogous to them) are not sound in this framework. The same reasoning holds for Argument 2, where \(t_3\) of Fig. 2 provides the very same counterexample to our reductio. The fact that Odie travelled back in time makes no significant difference. Once again, things are more complicated in case of a proper loop, i.e. if \(t_{1} = t_{3}\). In this case there is no way of providing an interpretation satisfying assumptions 1, 2, 3 and 7 altogether. However, once again, this problem is not specific to mereology.
3.3 Stage theory
Stage theory has been defended in one form or another by Hawley (2001), Sider (2001), and Varzi (2003). The stage theorist rejects the principle of necessity of difference for reasons similar to those of the perdurantist. Recall, the stage theorist holds that objects do not persist through time but are related to other objects by means of counterpart relations. So two distinct objects can have a single counterpart at another point in time, and a single object can have multiple counterparts at a single future or past point in time. Here again, the steps leading to 4 and 5 are blocked. (We do not give a full model since the stage theorist denies the same steps in the argument as the perdurantist, although the former needs the additional machinery of counterpart semantics.Footnote 16)
Yet, one may hold that for the stage theorist Argument 1 is more problematic than Argument 2 because in the latter argument Clifford and Odie are objects existing at distinct times, whereas in the former they exist ‘at the same time’ and could be regarded, maybe, as one and the same object. The ‘could be regarded as’-clause is crucial. The combination of time travel and stage theory demands a choice with respect to the relation between the time traveller and its past self when both exist in the same moment in time. Are they related by a counterpart relation, or by identity? It seems to us that the stage theorist will say that they are related by counterpart relations, because the stage theorist holds that, strictly speaking, objects do not persist and can thus not have incompatible properties at different times. Since the time traveler may have properties incompatible with the properties of its past self, the relation holding between them would thus not be identity. The stage theorist will thus say that objects like Clifford and Odie stand in a counterpart relation even when Odie is a time traveller. Hence Arguments 1 and 2 are equally (un)problematic for the stage theorist who accepts MM.
4 Time travel scenarios as Rorschach tests
Time travel thus plays no essential role in the arguments against certain mereological principles because these arguments are structurally equivalent to arguments that do not employ time travel. Moreover, solutions to the more mundane argument also work for the time travel variant. Our desired conclusion is that time travel scenarios do not count as additional arguments for or against certain mereological principles but simply illustrate some consequences of certain combinations of principles. We take it that our conclusion may be challenged by devising a fancy time travel scenario that has no obvious time-travel–free counterpart. To cover that possibility we here discuss the general structure of time travel scenarios that could be used to invalidate a principle of minimal mereology. We show that these arguments are dead-ends because their plausibility depends on background principles that the other party may simply reject.
We focus on AS, but what we say extends straightforwardly to the other cases. For AS to be invalid one should show that it is possible for the antecedent to be satisfied while the consequent is not. So for a scenario to be a plausible counterexample to AS it should be such that it is plausible to say that for some objects x and y we have at a single moment in time (1) \(x <y\) and (2) \(x = y\), from which it follows by LL that (3) \(y <x\).Footnote 17 In time travel scenarios the first two conditions are commonly satisfied by having an enduring object travel back in time such that it becomes a proper part of itself.Footnote 18 Then, because \(x = y\) and \(x <y\), one concludes via LL that \(y <x\)—thereby invalidating AS. Granting that \(x = y\), it is crucial that \(x <y\) is made plausible. In the time travel scenarios we are aware of the claim that \(x <y\) is made plausible by triggering our intuitions about spatial inclusion. For example, Odie is taken to be a proper part of Clifford because the former’s exact location is a proper subregion of the latter’s exact location. More generally, the idea is that proper spatial inclusion is sufficient for proper parthood: if x is exactly located in a proper subregion of the exact location of y, then x is a proper part of y.Footnote 19
To conclude that AS fails one should then also hold that it is possible for something to be, at one and the same time, exactly located at a proper subregion of its exact location. Notice that this is an additional claim because one might hold that time travel and multilocation are co-possible, and claim that whenever an object is multilocated at one and the same time the intersection of their regions is empty. On such a view it is never the case that an object is at one and the same time exactly located at a subregion of its exact location. But that also means that we cannot then use the proper spatial inclusion model to make it plausible that something is a proper part of itself.
So the philosopher who is using the spatial inclusion model to show that the combination of time travel and multilocation invalidates AS also needs to hold that something can be, at one and the same time, exactly located at a proper subregion of its exact location. However, it is not clear why one should accept this claim. In the Odie/Clifford case, for example, one might say instead that Odie/Clifford is multilocated, such that the exact location of Clifford is not exactly dog-shaped but instead has an Odie-sized hole in it where Odie is exactly located. The intersection of Odie’s region with Clifford’s region would then be empty. But in that case we have no reason to believe that Odie is a proper part of Clifford; Clifford/Odie is just a single multilocated object that stands in no mereological relation to itself (other than such reflexive relations as overlap and improper parthood).
This may, however, come across as fishy. Surely, one might say, we would take Odie to be a proper part of Clifford if we weren’t told that Odie = Clifford, the time travelling dog-statue. Hence we should do justice to that intuition and thus hold that Odie is a proper part of Clifford and instead deny that proper parthood is asymmetric. However, this response backfires immediately. Surely, we could say, we would take Odie and Clifford to be numerically distinct objects if we weren’t told that Odie = Clifford, the time travelling dog-statue. (We would take them to be numerically distinct because one is smaller than the other.) Hence we should do justice to that intuition and thus hold that Odie and Clifford are numerically distinct and deny that multilocation (or time travel) is possible. Or, alternatively, we could follow Kleinschmidt (2011, p. 274, fn.20) in holding that since Odie = Clifford, the one is not a proper part of the other.Footnote 20
The problem is a general one: when describing a time travel scenario with the aim to provide a counterexample to some mereological principle, there will be principles in the background concerning location and spatial inclusion that are themselves up for debate. Time travel scenarios thus function like Rorschach tests: those who think time travel and multilocation are co-possible will deny any mereological principle that conflicts with it, whereas those who think our evidence for these mereological principles is stronger than any evidence for the co-possibility of time travel and multilocation will instead hold on to these mereological principles. A time travel scenario does not provide a new argument for or against either view but only makes the differences between different packages starker.
5 Conclusions
Core principles of mereology may be invalid under certain interpretations of time travel scenarios. Such scenarios are, however, either structurally identical to more classical scenarios that do not involve time travel, or they are not. In the first case, the time travel scenario does not add any argumentative value but merely rephrases a more classical argument. In the latter case the time travel scenario still has no added argumentative value because the interpretation of the scenario, as well as the assumptions needed to derive the desired conclusion, are at least as controversial as the mereological principle targeted. Hence time travel scenarios should not be used as arguments for or against mereological principles.
Notes
The term ‘minimal mereology’ is from Casati and Varzi (1999, p. 39).
Parsons (2007) also prefers this conclusion.
One might say that there is time travel involved in our case, but of the ordinary boring kind that we all partake in: travelling into the future. We use ‘time travel’, as it is commonly done in the metaphysics of time, as denoting traveling back in time.
We choose to use modal operators to represent the argument because this gives a rather natural representation of the argument. Endurantists may, however, prefer to relativize properties and relations to times. In that case a statement such as, for example, “it has been the case that Fa”, should be represented as “a is-at-\(t_1\)-F and \(t_1\) is earlier than now” (or, alternatively, as “a is-F-at-\(t_1\) and \(t_1\) is earlier than now”). We discuss endurantism in Sect. 3.1.
For reasons of space and readability we will not provide the full semantics of first-order modal logic with predicate abstraction. We shall instead explain the meaning of our formulas as we introduce them. The reader can refer to Fitting and Mendelsohn (1998) for a more detailed presentation.
N.B. Neither LL and ND* is valid if we use arbitrary terms t and s, e.g. function-terms, names, constants, etc. instead of variables x, y and z. However since we are currently not talking about objects’ names, but about objects ‘themselves’, we can safely use the unrestricted principles here.
To be precise, the principle of Necessity of Difference in the form (ND) \(x \not = y \rightarrow \Box (x \not = y)\) is not derivable from the standard axioms of first-order modal logic with identity, i.e. the system obtained by adding LL and (I) \(x=x\) to the modal predicate calculus (Hughes and Cresswell 1996, p. 244, p. 312). Indeed, only Necessity of Identity (NI) \(x = y \rightarrow \Box (x = y)\) is derivable, while ND is provable whenever the Brouwer axiom (B) \(p \rightarrow \Box \Diamond p\) is added. This corresponds to the condition that the Kripke frames are symmetric (Hughes and Cresswell 1996, p. 313). A model-theoretic argument shows that ND cannot be proved without it. This is due to the fact that there is a specific class of frames for contingent identity systems that validate I, LL and NI but not ND (Hughes and Cresswell 1996, p. 335).
However, both ND and ND* are provable in the tableau proof system of Fitting and Mendelsohn (1998). There, the Substitutivity Rule\(\sigma _{1} (t=u), \sigma _{2} \phi (t) / \sigma _{2} \phi (u)\) (where \(\sigma _{1},\sigma _{2}\) are prefixes for possible worlds) provides a powerful encoding of (unrestricted) Leibniz’s Law (Fitting and Mendelsohn 1998, p. 151, p. 223) which fully captures varying domain semantics. Here we sketch a tableau proof of ND* (indeed of its universal closure). A derivation of ND is obtained by following the same pattern.
1.
\(\sigma _{1} \lnot \forall x \forall y(\langle \lambda w. \diamond (w=y) \rangle (x) \rightarrow x = y)\)
2.
\(\sigma _{1} \lnot \forall y(\langle \lambda w. \diamond (w=y) \rangle (p_{1}) \rightarrow p_{1} = y)\)
from 1 by Existential Rule
3.
\(\sigma _{1} \lnot (\langle \lambda w. \diamond (w=q_{1}) \rangle (p_{1}) \rightarrow p_{1} = q_{1})\)
from 2 by Existential Rule
4.
\(\sigma _{1} \langle \lambda w. \diamond (w=q_{1}) \rangle (p_{1})\)
from 3 by Conjunctive Rule
5.
\(\sigma _{1} \lnot ( p_{1} = q_{1})\)
from 3 by Conjunctive Rule
6.
\(\sigma _{1} \diamond (p_{1}= q_{1})\)
from 4 by Abstraction Rule
7.
\(\sigma _{1.1} p_{1}= q_{1}\)
from 6 by Possibility Rule
8.
\(\sigma _{1} \lnot (q_{1}= q_{1})\)
from 5 and 7 by Substitutivity Rule
9.
\(\sigma _{1} q_{1}= q_{1}\)
Reflexivity Rule
Step 1 is the negation of the universal closure of ND*. Steps 2 and 3 apply standard Existential Rules (Fitting and Mendelsohn 1998, p. 222) that introduce world-indexed parameters for existential (here negated universal) quantifiers. Step 4 and 5 break down the implication by applying the Conjunctive Rule for \(\rightarrow\) (Fitting and Mendelsohn 1998, p. 48). Step 6 is derived from 4 by the Abstraction Rule (Fitting and Mendelsohn 1998, p. 223). 7 follows from 6 by the Possibility Rule (Fitting and Mendelsohn 1998, p. 49). 8 follows from 5 and 7 by applying the Substitutivity Rule. Finally, 9 is introduced by the Reflexivity Rule (Fitting and Mendelsohn 1998, p. 150). By 8 and 9 the tableau is closed.
Many thanks to an anonymous reviewer for pointing out that this was in need of clarification.
Note that there is no mention of transitivity, nor of Kibble, in our assumptions. Transitivity is indeed superfluous to obtain a reductio since there is a more direct route to a contradiction between the assumptions and the irreflexivity of proper parthood.
We explicitly say ‘is at some point in time identical with’, only thanks to ND* does this entail that the later Clifford is (now) identical with the former Clifford.
There are various ways of explicating endurantism and perdurantism. We gave a measure-theoretic characterisation—“(not) extended in time”—but many prefer a mereological characterisation which says that only perdurantists think that objects have temporal parts (Hawley 2018). Alternatively, one could say that an object endures if it is multiply located on its path, whereas it perdures if it has a single four-dimensional location (Gilmore 2018). We think our arguments go through under each of these characterisations of endurantism and perdurantism.
In the Kripke semantics for quantified modal logic this kind of trans-world identity is reflected by the fact that a valuation v assigns to a given variable v one and the same object at all points (see Fitting and Mendelsohn 1998). This is no surprise, since there are strong reasons for arguing that Kripke semantics for quantified modal logics fit all the desiderata of an endurantist ontology (see Belardinelli 2006).
Those who are familiar with the debate on material constitution might wonder why we don’t discuss the possibility of denying A.1 by holding that Odie is never identical with Clifford but merely constitutes Clifford. The reason is that constitution by itself doesn’t solve the original problem. Constitution theories distinguish real wholes from mere sums and hold that these kinds of object can stand in a one–one relation of constitution. So according to constitution theories we must distinguish Clifford (the real whole) from the sum of Clifford’s parts. The mere sum of Clifford’s parts is then taken by constitution theories to have its parts essentially. So with respect to that object A.2 will be denied—and thus mereological essentialism provides a partial solution, not the theory of constitution. But what about Clifford, the real whole? Clifford is supposed to persist while losing or gaining parts, so denying A.2 is not an option. Moreover, if Clifford can indeed survive the loss of parts, then Clifford can shrink such that all that is left of Clifford at \(t_3\) is Odie, which was merely a proper part of Clifford at \(t_1\). So the original puzzle remains for Clifford, the real whole. (This is in line with Smid (2017) where it is argued that material constitution provides an ad hoc solution to the problem of coincidence.)
For example, with respect to the time travel scenario Eagle (2016, pp. 22–23) denies that Odie is a proper part of Clifford.
The second condition is important because there are mutual parthood theories that analyse coincidence as instances where \(x \ne y\) but \(x <y\) and \(y <x\). The notion of proper parthood being used in those cases is that of ‘non-identical proper part’ (x is a non-identical proper part of y iff x is part of y and x and y are numerically distinct). According to those theorists a statue is a (non-identical) proper part of its bronze, and the bronze is a (non-identical) proper part of the statue. Mutual parthood theorists deny, however, that the two objects stand in a strict proper parthood relation (x is a strict proper part of y iff x is part of y and y is not part of x). See Cotnoir (2010).
An example of this kind of argument can be found in Effingham (2010), p. 335.
Principles like these combine mereology with theories of location such that there is a certain “harmony” between the mereological structure of an object and the mereological structure of its (exact) location. We need not go into any detail here about the interplay, but the interested reader is directed to Parsons (2007), Casati and Varzi (1999, Ch. 7), and Gilmore (2018) for a start. It is important to note, though, is that many of these principles of mereological harmony are logically independent, see Uzquiano (2011), Saucedo (2011), and Leonard (2016).
Indeed this is Kleinschmidt’s response to Effingham (2010, p. 335)’s argument against asymmetry.
References
Barker, S., & Dowe, P. (2003). Paradoxes of multilocation. Analysis, 63, 106–114.
Belardinelli, F. (2006). Quantified modal logic and the ontology of physical objects. Ph.D. thesis.
Braüner, T., & Ghilardi, S. (2007). First-order modal logic. In P. Blackburn, J. Van Benthem, & F. Wolter (Eds.), Handbook of modal logic (pp. 549–620). Amsterdam: Elsevier.
Casati, R., & Varzi, A. C. (1999). Parts and places. Cambridge, MA: MIT Press.
Chisholm, R. (1973). Parts as essential to their wholes. Review of Metaphysics, 26, 581–603.
Cotnoir, A. (2010). Antisymmetry and non-extensional mereology. Philosophical Quarterly, 60(239), 396–405.
Donnelly, M. (2010). Parthood and multi-location. In D. Zimmerman (Ed.), Oxford studies in metaphysics (Vol. 5, pp. 203–243). New York: Oxford University Press.
Eagle, A. (2016). Multiple location defended. Philosophical Studies, 173, 2215–2231.
Effingham, N. (2010). Mereological explanation and time travel. Australasian Journal of Philosophy, 88(2), 333–345.
Effingham, N., & Robson, J. (2007). A mereological challenge to endurantism. Australasian Journal of Philosophy, 85(4), 633–640.
Fitting, M., & Mendelsohn, R. L. (1998). First-order modal logic. Dordrecht: Kluwer Academic Publishers.
Geach, P. (1968). Identity. Review of Metaphysics, 21, 3–12.
Gilmore, C. (2009). Why parthood might be a four-place relation, and how it behaves if it is. In L. Honnefelder, E. Runggaldier, & B. Schick (Eds.), Unity and time in metaphysics (pp. 83–133). Berlin: de Gruyter.
Gilmore, C. (2018). Mereology and location. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/fall2018/entries/location-mereology/.
Hawley, K. (2001). How things persist. Oxford: Oxford University Press.
Hawley, K. (2018). Temporal parts. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/spr2018/entries/temporal-parts/.
Heller, M. (1990). The ontology of physical objects: Four-dimensional hunks of matter. Cambridge: Cambridge University Press.
Hughes, G. E., & Cresswell, M. J. (1996). A new introduction to modal logic. London: Routledge.
Jubien, M. (1993). Ontology, modality and the fallacy of reference. Cambridge: Cambridge University Press.
Kearns, S. (2011). Can a thing be part of itself? American Philosophical Quarterly, 48, 87–93.
Kleinschmidt, S. (2011). Multilocation and mereology. Philosophical Perspectives, 25, 253–276.
Kripke, S. (1971). Identity and necessity. In K. Munitz (Ed.), Identity and individuation (pp. 161–191). New York: New York University Press.
Leonard, M. (2016). What is mereological harmony? Synthese, 193(6), 1949–1965.
Lewis, D. K. (1971). Counterparts of persons and their bodies. Journal of Philosophy, 68, 203–211.
Lewis, D. K. (1976). The paradoxes of time travel. American Philosophical Quarterly, 13(2), 145–152.
Marcus, R. B. [Ruth C. Barcan]. (1947). Identity of individuals in a strict functional calculus of second order. Journal of Symbolic Logic, 12, 12–15.
Parsons, J. (2007). Theories of location. In D. Zimmerman (Ed.), Oxford studies in metaphysics (Vol. 3, pp. 399–418). New York: Oxford University Press.
Quine, W. V. O. (1960). Word and object. New York: MIT Press.
Saucedo, R. (2011). Parthood and location. In K. Bennet & D. Zimmerman (Eds.), Oxford studies in metaphysics (Vol. 6, pp. 225–286). New York: Oxford University Press.
Sider, T. (2001). Four-dimensionalism. An ontology of persistence and time. New York: Oxford University Press.
Smid, J. (2017). Material constitution is ad hoc. Erkenntnis 82(2), 305–325
Uzquiano, G. (2011). Mereological harmony. In K. Bennet & D. Zimmerman (Eds.), Oxford studies in metaphysics (Vol. 6, pp. 199–224). New York: Oxford University Press.
Van Inwagen, P. (1981). The doctrine of arbitrary undetached parts. Pacific Philosophical Quarterly, 62, 123–137.
Varzi, A. C. (2003). Perdurantism, universalism, and quantifiers. Australasian Journal of Philosophy, 81(2), 208–215.
Yanofsky, N. D. (2003). A universal approach to self-referential paradoxes, incompleteness and fixed points. The Bulletin of Symbolic Logic, 9(3), 362–386.
Acknowledgements
Thanks to the audience at the University of Manchester Philosophy PhD seminar where Jeroen presented some of the material of this paper. Jeroen gratefully acknowledges funding received from the Swedish Research Council for his research (Vetenskapsrådet International Postdoc Grant, 2017-06160_3). Carlo gratefully acknowledges funding received from Sveriges Riksbanken (P16-0596:1) and from the European Commission (Marie Skłodowska-Curie Individual Fellowship 2016, 748421) for his research. Finally, special thanks from both authors to anonymous reviewer #2 for this journal whose comments helped to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Proietti, C., Smid, J. Mereology and time travel. Philos Stud 177, 2245–2260 (2020). https://doi.org/10.1007/s11098-019-01308-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-019-01308-x