Abstract
Given reductionism about people, personal persistence must fundamentally consist in some kind of impersonal continuity relation. Typically, these continuity relations can hold from one to many. And, if they can, the analysis of personal persistence must include a non-branching clause to avoid non-transitive identities or multiple occupancy. It is far from obvious, however, what form this clause should take. This paper argues that previous accounts are inadequate and develops a new proposal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Reductionism about people is the view that people exist but they’re not a fundamental part of the world. The view is perhaps best explained through David Hume’s analogy with reductionism about nations.Footnote 1 Most of us are reductionists about nations: We believe that nations exist but also that their existing consists in more basic facts, such as the existence of citizens who organize themselves in certain ways on certain territories. So we could, in principle, provide a complete description of the world (and these more basic facts) without asserting that nations exist. In this manner, reductionism about people says that the world could, in principle, be completely described without asserting that people exist.Footnote 2
Given reductionism about people, personal persistence must fundamentally consist in an impersonal continuity relation holding over time. Some standard candidates for this impersonal continuity are different kinds of psychological, physical, and phenomenal continuity. Typically, these continuity relations can (at least in principle) branch by holding from one person at one time to two or more people at other times. And, if these relations can branch, the analysis of personal persistence must include a non-branching clause in order to avoid either of two problems, namely, the problem of non-transitive identities and the problem of multiple occupancy.Footnote 3 In this paper, I shall explore what form this non-branching clause should take.Footnote 4 I shall argue that previous accounts are implausible. But, with the help of some ideas from these accounts, I shall develop a new proposal.
Assuming a perdurance framework, we analyse personal persistence in terms of person-stages at different times being I-related, that is, being stages of the same continuant person.Footnote 5 A person, on this framework, is a maximal aggregate of I-related person-stages, that is, an aggregate of person-stages such that (i) each stage in the aggregate is I-related to all stages in the aggregate and (ii) no person-stage that isn’t in the aggregate is I-related to all stages in the aggregate.Footnote 6
Person-stages can (but need not) be extended in time, that is, they can be present not only at a single instant but also at each point in an interval of time.Footnote 7 This opens up for some ambiguities about temporal order, which we should try to avoid. Let us say that a person-stage x is simultaneous with a person-stage y if and only if there is a time at which x and y are both present. Let us say that a person-stage x is present before a person-stage y if and only if there is a time at which x is present which is earlier than all times at which y is present. And let us say that a person-stage x is present after a person-stage y if and only if there is a time at which x is present which is later than all times at which y is present.Footnote 8
Given reductionism about people, Relation I is analysed in terms of some basic kind of connectedness, such as psychological, physical, or phenomenal connectedness. Psychological accounts take the relevant kind of connectedness between person-stages to be direct psychological connections, such as one stage’s having an experience memory (or quasi-memory) of the experiences of the other.Footnote 9 Physical accounts take the relevant kind of connectedness between person-stages to be their sharing a sufficiently large portion of their brains.Footnote 10 And phenomenal accounts take the relevant kind of connectedness between person-stages to be their sharing the same stream of consciousness.Footnote 11 For the purposes of our discussion, we can, for the most part, leave open which one of these kinds of connectedness is the relevant one. Let Relation C be a temporally ordered version of the relevant kind of connectedness:
-
Temporally Ordered Connectedness
-
Person-stage x is C-related to person-stage y (xCy) \(=_{\mathrm {df}}\)x and y are connected by the right kind of connection and x is either simultaneous with y or present earlier than y.
And let Relation \(C'\) be a temporally unordered version:
-
Temporally Unordered Connectedness
-
Person-stage x is C′-related to person-stage y (\(xC'y\)) \(=_{\mathrm {df}}\)x and y are connected by the right kind of connection.
We shall assume that Relation C is reflexive and that Relation \(C'\) is reflexive and symmetric over person-stages.Footnote 12
Consider, first, a direct analysis of Relation I as Relation \(C'\):
-
(1)
Person-stage x is I-related to person-stage y if and only if \(xC'y\).
One example of an account of this kind is the memory criterion of personal identity.Footnote 13 This simple account is open to Thomas Reid’s well known counter-example, The Brave Officer:
Suppose a brave officer to have been flogged when a boy at school, for robbing an orchard, to have taken a standard from the enemy in his first campaign, and to have been made a general in advanced life: Suppose also, which must be admitted to be possible, that when he took the standard, he was conscious of his having been flogged at school, and that when made a general he was conscious of his taking the standard, but had absolutely lost the consciousness of his flogging.Footnote 14
That is, as an officer, a man remembers being a boy and, as a general, the man remembers being an officer but not being a boy.Footnote 15 Suppose that The Boy, The Officer, and The General are person-stages from the three periods of the man’s life. Then, if the relevant kind of connections are memories, The Officer is connected both to The Boy and to The General but The General isn’t connected to The Boy. The pattern of connections in this case can be represented diagrammatically as follows, where the double-headed arrows represent \(C'\)-relations:
-
The Brave Officer\((C'\)-relations)
-

In The Brave Officer, (1) yields that The Officer is I-related both to The Boy and to The General and that The Boy isn’t I-related to The General. Accordingly, we have an instance of multiple occupancy, that is, one person-stage is a stage of two or more people. Given (1), we have two maximal aggregates of I-related person-stages in this case: one consisting of The Boy and The Officer and one consisting of The Officer and The General. The Officer is a stage of one person who has The Boy as a stage and of one person who has The General as a stage. These people cannot be identical, since The Boy isn’t I-related to The General.
In order to avoid multiple occupancy in The Brave Officer, we shall—instead of a connectedness relation—rely on a continuity relation of overlapping connectedness. Let Relation R be the relevant kind of temporally ordered continuity (we shall consider temporally unordered continuity later):
-
Temporally Ordered Continuity
-
Person-stage x is R-related to person-stage y (xRy) \(=_{\mathrm {df}}\) either xCy or yCx, or there are person-stages \(z_1\), \(z_2\), ..., \(z_n\) such that either
-
(i)
\(xCz_1\), \(z_1Cz_2\), ..., \(z_{n-1}Cz_n\), \(z_nCy\) or
-
(ii)
\(yCz_1\), \(z_1Cz_2\), ..., \(z_{n-1}Cz_n\), \(z_nCx\).
-
(i)
Given the reflexivity of Relation C, Relation R is reflexive and symmetric over person-stages.
John Perry and David Lewis both suggest
-
(2)
Person-stage x is I-related to person-stage y if and only if xRy.Footnote 16
This proposal avoids multiple occupancy in The Brave Officer: In that case, it yields that all person-stages are I-related.
Even so, (2) still allows for multiple occupancy. It will do so in division cases such as Derek Parfit’s case My Division. Parfit presents My Division as follows:
My body is fatally injured, as are the brains of my two brothers. My brain is divided, and each half is successfully transplanted into the body of one of my brothers. Each of the resulting people believes that he is me, seems to remember living my life, has my character, and is in every other way psychologically continuous with me. And he has a body that is very like mine.Footnote 17
The pattern of connections in this case can be represented diagrammatically as follows, where Wholly is the person-stage before the division and Lefty and Righty are the two resulting person-stages afterwards:Footnote 18
-
My Division \((C'\) -relations)
-
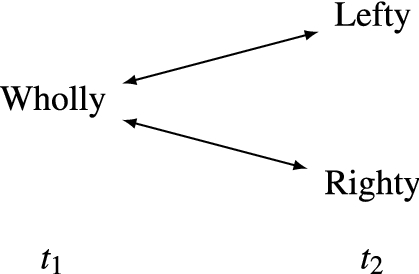
In this case, each of (1) and (2) yields that Wholly is I-related both to Lefty and to Righty while Lefty isn’t I-related to Righty. Wholly is then a person-stage of two persons: one who has Lefty as a stage and one who has Righty as a stage.
To preserve the transitivity of Relation I and to avoid multiple occupancy, reductionist accounts of personal persistence typically include a non-branching clause.Footnote 19 Parfit first suggested that
The criterion might be sketched as follows. “X and Y are the same person if they are psychologically continuous and there is no person who is contemporary with either and psychologically continuous with the other.”Footnote 20
In terms of perdurance, we can state this suggestion as follows:Footnote 21
-
(3)
Person-stage x is I-related to person-stage y if and only if xRy and there is no person-stage z such that either
-
(i)
xRz and y and z are distinct and simultaneous or
-
(ii)
yRz and x and z are distinct and simultaneous.
-
(i)
This proposal yields the desired result in My Division: Wholly, Lefty, and Righty are all I-unrelated to each other.
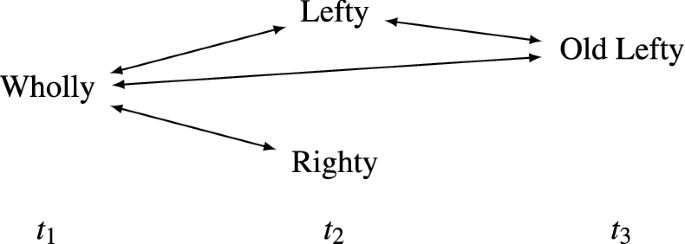
Nevertheless, consider the following unbalanced variant of My Division, which is just like My Division except that the man with the left half of the brain lives on longer than the man with the right half:Footnote 22
-
My Unbalanced Division \((C'\) -relations)
-
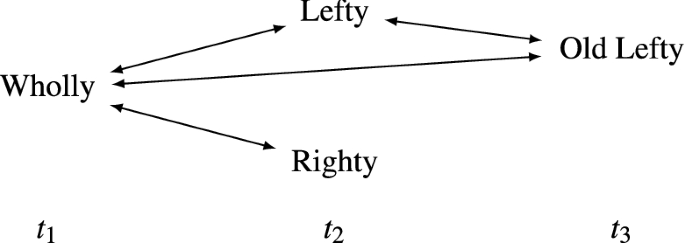
Like Lefty, Old Lefty is a person-stage with the left half of the brain. But Old Lefty is a later stage than Lefty, existing at \(t_3\) after the man with the right half has died. (The \(C'\)-relation between Wholly and Old Lefty won’t be crucial for our discussion, because Wholly would still be R-related to Old Lefty if this connection were removed.)
In My Unbalanced Division, (3) yields that Wholly is I-related to Old Lefty, since they are R-related and neither of them is simultaneous with any other person-stage. Likewise, (3) yields that Old Lefty is I-related to Lefty, since they are R-related and—even though Lefty is simultaneous with Righty—Old Lefty isn’t R-related to Righty. But, according to (3), Wholly isn’t I-related to Lefty, since Wholly is R-related to Righty and Righty is simultaneous with Lefty. So (3) yields that Wholly is I-related to Old Lefty, Old Lefty is I-related to Lefty, and Wholly isn’t I-related to Old Lefty. Hence, given (3), we have a non-transitive Relation I and thus multiple occupancy. Moreover, it’s implausible that Wholly is I-related to Old Lefty, especially given that Wholly isn’t I-related to Lefty.
Consider, furthermore, the following variant of The Brave Officer, where The General is connected to The Boy but not to The Officer:Footnote 23
-
The Senile General \((C'\) -relations)
-

This pattern of connections could occur if the relevant kind of connections are memories and The General has irrevocably lost all memories of the experiences of The Officer but, just like The Officer, The General remembers the experiences of The Boy. This pattern of connections could also be realized on some physical accounts of the relevant kind of connections. Consider a variant of My Division, where the transplant of the right half of the brain is delayed and the man with the left half dies before the transplant of the right half:
-
My Asynchronous Division \((C'\) -relations; The Senile General pattern)
-

The idea here is that, even though the right half of the brain exists at \(t_2\), nothing with the right half qualifies as a person-stage while the man with the left half is alive. Furthermore, if the relevant kind of connections could be preserved through travel by teletransportation, the same pattern of connections could be realized in a teletransportation case. Consider a case where I step into a scanner on Earth at \(t_1\). My body is then scanned and destroyed. My scanned information is beamed both to the Moon and to Mars. My information reaches the Moon first, where a replica is created at \(t_2\). Later on, my information reaches Mars, where another replica is created at \(t_3\). The replica on the Moon, however, has died before \(t_3\). Let Earthy be the person-stage being scanned on earth, let Moony be a person-stage of the man on the Moon, and let Marsy be a person-stage of the man on Mars:
-
My Asynchronous Replication \((C'\) -relations; The Senile General pattern)
-
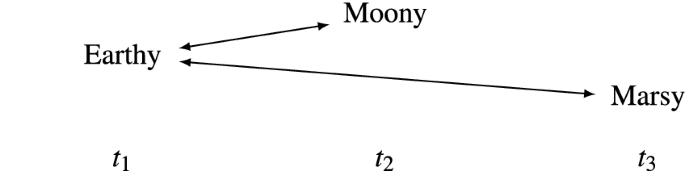
I mention these variants of The Senile General in order to illustrate different ways in which this pattern of connections could arise given different views on the relevant kind of connectedness. For the purposes of our discussion, however, the differences between these cases won’t matter much.
In The Senile General, (3) yields that The Boy is I-related both to The Officer and to The General, since The Boy is R-related to The Officer and to The General while there are no distinct and simultaneous person-stages in that case—so the non-branching clause in (3) doesn’t apply. And, given (3), The Officer isn’t I-related to The General, since these stages are not R-related. So, like before, we have a non-transitive Relation I and hence multiple occupancy. This result is problematic, since the motivation for having a non-branching clause is to retain the transitivity of Relation I and avoid multiple occupancy. If non-transitivity and multiple occupancy weren’t problematic, we could stick with (2), which is simpler than (3), or with (1), which is simpler still.
Parfit later put forward the following suggestion:
The Psychological Criterion: [i] There is psychological continuity if and only if there are overlapping chains of strong connectedness. X today is one and the same person as Y at some past time if and only if [ii] X is psychologically continuous with Y, [iii] this continuity has the right kind of cause, and [iv] there does not exist a different person who is also psychologically continuous with Y.Footnote 24
In terms of perdurance, this suggestion can be interpreted as follows:Footnote 25
-
(4)
Person-stage x is I-related to person-stage y if and only if xRy and there is no person-stage z such that either
-
(i)
xRz and not yIz or
-
(ii)
yRz and not xIz.
-
(i)
This proposal has been charged with circularity since it analyses Relation I partly in terms of itself.Footnote 26 Analysing a relation partly in terms of the same relation needn’t be a problem, however; this is a standard feature of recursive definitions. Rather, the problem with (4) is incompleteness. Consider, for example, The Brave Officer where (4) is both compatible with (a) The Boy, The Officer, and The General all being I-related and compatible with (b) The Boy, The Officer, and The General all being I-unrelated to each other. To see that (4) is compatible with (a), note that, if The Boy, The Officer, and The General are all I-related, then clauses (i) and (ii) in (4) will never hold. To see that (4) is compatible with (b), note that, if The Boy, The Officer, and The General are all I-unrelated to each other, then one of clauses (i) and (ii) in (4) will always hold for some person-stage z. Hence (4) is compatible both with (a) and with (b). So (4) can’t provide a complete account of which person-stages are I-related.
In addition to incompleteness, there’s a further problem with (4). Consider a version of My Division which is extended before the fission, highlighting that the man who divides lived undivided for an extended period of time before the division:
-
My Extended Pre-Division \((C'\) -relations)
-
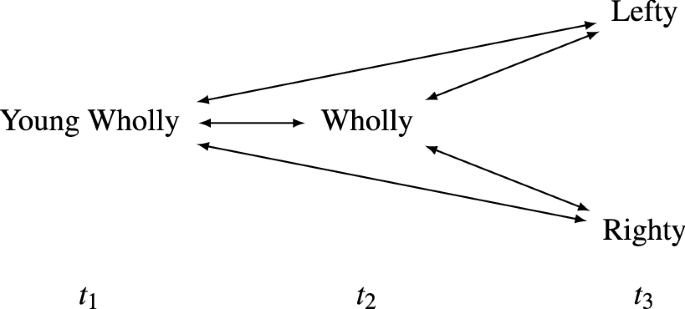
This is, of course, how My Division is usually understood; the difference is merely that we highlight Wholly’s extended past in the model. (The \(C'\)-relations between Young Wholly and Lefty and between Young Wholly and Righty won’t be crucial for our discussion, because Young Wholly would still be R-related both to Lefty and to Righty if these connections were removed.)
In My Extended Pre-Division, it seems that Young Wholly should be I-related to Wholly. But this is ruled out by (4). For proof by contradiction, assume that Young Wholly is I-related to Wholly. Since the non-branching clause in (4) then cannot rule out that Young Wholly is I-related to Wholly, it is not the case that Young Wholly is R-related to Lefty while Wholly isn’t I-related to Lefty. Therefore, since Young Wholly is R-related to Lefty, we have that Wholly is I-related to Lefty. According to (4), Lefty isn’t I-related to Righty, since Lefty isn’t R-related to Righty. Therefore, since Wholly is R-related to Righty while Lefty isn’t I-related to Righty, the non-branching clause in (4) rules out that Wholly is I-related to Lefty. We then have the contradiction that Wholly both is and is notI-related to Lefty.
Parfit’s final suggestion was the following:Footnote 27
-
(5)
Person-stage x is I-related to person-stage y if and only if xRy and there is no person-stage z such that either
-
(i)
xRz and not yRz or
-
(ii)
yRz and not xRz.
-
(i)
This suggestion is better. In fact, it avoids all problems we have discussed so far. And, given (5), Relation I is an equivalence relation—that is, it is reflexive, symmetric, and transitive—over person-stages.
But (5) is still unsatisfactory. Consider a variant of My Division where Lefty and Righty are reunited some time after the division by a second round of transplants in which the two halves are reunited in a single body:
-
My Temporary Division \((C'\) -relations)
-
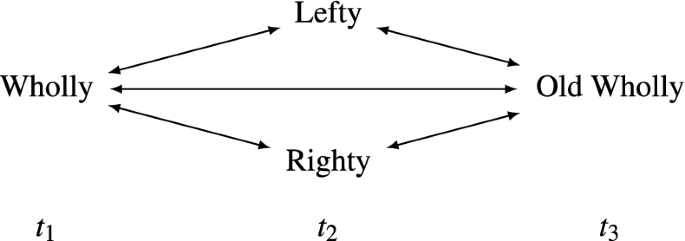
Note that the double-headed arrow between Wholly and Old Wholly just represents a direct connection between these stages and not the existence of a further person-stage at \(t_2\) in addition to Lefty and Righty. This connection won’t matter for our discussion. For our discussion, we may just as well consider a variant without this connection:
-
My Forgetful Temporary Division \((C'\)-relations)
-

In My Temporary Division or My Forgetful Temporary Division, (5) yields that the only I-related person-stages are Wholly and Old Wholly. To see this, note that, for all distinct pairs of person-stages other than the pair of Wholly and Old Wholly, one of Lefty and Righty is R-related to one stage in the pair but not to the other. So, for these pairs, the non-branching clause in (5) rules out that Relation I holds. Wholly and Old Wholly, however, are R-related to the same person-stages. It seems odd that Wholly and Old Wholly would be I-related, because there is branching in the continuity between them (especially in My Forgetful Temporary Division).
We can get around this problem with the following proposal from Sydney Shoemaker:Footnote 28
-
(6)
Person-stage x is I-related to person-stage y if and only if xRy and there is no person-stage z such that
-
(i)
z is not present before each of x and y is present,
-
(ii)
z is not present after each of x and y is present,
-
(iii)
zRx,
-
(iv)
zRy, and
-
(v)
there are two distinct and simultaneous person-stages u and v such that \(zC'u\) and \(zC'v\).
-
(i)
In My Temporary Division and My Forgetful Temporary Division, (6) yields that all person-stages are I-unrelated to each other. According to (6), Lefty and Righty are not I-related, since they’re not R-related. And neither Wholly nor Old Wholly is I-related to any person-stage given (6), since they are both \(C'\)-related to the distinct and simultaneous Lefty and Righty. Note, however, that this entails that Wholly and Old Wholly are not I-related to themselves. So (6) violates the reflexivity of the Relation I. Obviously, each person-stage should be I-related to itself.
In My Extended Pre-Division, (6) yields—just like (4)—the implausible result that Young Wholly isn’t I-related to Wholly. Young Wholly’s being I-related to Wholly is ruled out by the non-branching clause in (6), since Young Wholly is R-related to Wholly while Wholly is R-related to itself and is \(C'\)-related both to Lefty and to Righty.
In The Senile General, the non-branching clause in (6) doesn’t apply, because there are no distinct and simultaneous person-stages in that case. So (6) yields that The Boy is I-related both to The Officer and to The General (since The Boy is R-related to them) and that The Officer isn’t I-related to The General (since they’re not R-related). Hence we get a non-transitive Relation I and thus multiple-occupancy, which defeats the purpose of having a non-branching clause.
Finally, consider a variant of My Extended Pre-Division where Righty isn’t connected to Wholly while Lefty isn’t connected to Young Wholly:
-
My Forgetful Division \((C'\)-relations)
-
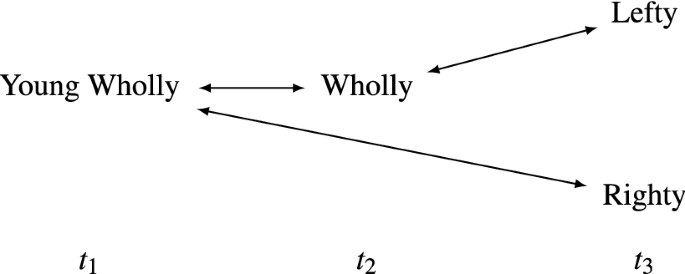
Suppose, for example, that the relevant kind of connections are memories and that the brain transplants cause irrevocable losses of memory: Lefty remembers Wholly but can’t remember Young Wholly; Righty remembers Young Wholly but can’t remember Wholly. And suppose that the transplants happen between \(t_2\) and \(t_3\); so, at \(t_2\), the brain halves are still united in Wholly.
In My Forgetful Division, (6) yields that Young Wholly is I-related both to Lefty and to Righty, even though there is clearly branching here given that Lefty and Righty are distinct and simultaneous person-stages.Footnote 29 Clause (v) in (6) doesn’t hold in this case, because no person-stage is \(C'\)-related to each of two simultaneous person-stages.
Anthony Brueckner maintains that, in The Senile General, The Officer should be I-related to The General. To get this result, Brueckner argues that Relation I needs to be analysed in terms of temporally unordered continuity, rather than the temporally ordered variety. Let Relation \(R'\) be the temporally unordered variant of Relation R:
-
Temporally Unordered Continuity
-
Person-stage x is \(R'\)-related to person-stage y (\(xR'y\)) \(=_{\mathrm {df}}\)\(xC'y\) or there are person-stages \(z_1\), \(z_2\), ..., \(z_n\) such that \(xC'z_1\), \(z_1C'z_2\), ..., \(z_{n-1}C'z_n\), \(z_nC'y\).
Given the reflexivity and symmetry of Relation \(C'\), Relation \(R'\) is reflexive, symmetric, and transitive over person-stages.
Brueckner considers, but does not defend, the following temporally unordered variant of (5):Footnote 30
-
(7)
Person-stage x is I-related to person-stage y if and only if \(xR'y\) and there is no person-stage z such that either
-
(i)
\(xR'z\) and not \(yR'z\) or
-
(ii)
\(yR'z\) and not \(xR'z\).
-
(i)
The main problem with (7) is that, since Relation \(R'\) is already transitive, the non-branching clause in (7) doesn’t rule out anything: (7) is equivalent to an account that identifies Relation I with Relation \(R'\). So, in My Division, (7) yields that all person-stages are I-related. Hence we have that Lefty is I-related to Righty even though they are distinct and simultaneous person-stages, which seems wrong.
Brueckner also considers a temporally unordered variant of (3):Footnote 31
-
(8)
Person-stage x is I-related to person-stage y if and only if \(xR'y\) and there is no person-stage z such that either
-
(i)
\(xR'z\) and y and z are distinct and simultaneous or
-
(ii)
\(yR'z\) and x and z are distinct and simultaneous.
-
(i)
One problem with (8) is that it yields an implausible result in My Unbalanced Division, namely, that Wholly and Old Lefty are the only person-stages that are I-related to each other.Footnote 32 Given (8), Wholly and Old Lefty are I-related, since they are \(R'\)-related and neither of them is simultaneous with another person-stage. The non-branching clause in (8) rules out that Lefty or Righty is I-related to any person-stage, since Lefty and Righty are distinct, simultaneous, and \(R'\)-related to each other. This also entails that Relation I is not reflexive given (8), because it entails that Lefty isn’t I-related to Lefty and that Righty isn’t I-related to Righty.
Harold W. Noonan amends (8) as follows:Footnote 33
-
(9)
Person-stage x is I-related to person-stage y if and only if \(xR'y\) and there are no distinct and simultaneous person-stages u and v such that either
-
(i)
\(uR'x\), \(uR'y\), and \(vR'x\) or
-
(ii)
\(uR'x\), \(uR'y\), and \(vR'y\).
-
(i)
Yet, in My Unbalanced Division, (9) does not yield the desired result that Lefty is I-related to Old Lefty. And, given (9), Relation I still fails to be reflexive, because (9) yields that no person-stage in My Unbalanced Division is I-related to itself.Footnote 34 To see this, note that all person-stages are \(R'\)-related in My Unbalanced Division. Hence the non-branching clause in (9) yields that no person-stages are I-related, since each person-stage is \(R'\)-related to the distinct and simultaneous Lefty and Righty.
Consider once more My Unbalanced Division as diagrammed earlier together with an alternative diagrammatic representation of the case—where, unlike in the earlier diagrams, the double-headed arrows this time represent \(R'\)-relations rather than \(C'\)-relations:
-
My Unbalanced Division \((C'\)-relations)
-
-
My Unbalanced Division \((R'\)-relations)
-
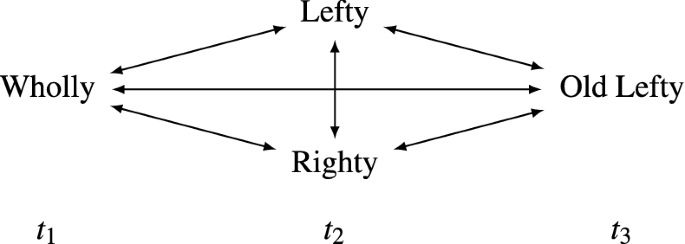
Since there is a temporally unordered chain of \(C'\)-relations linking all person-stages in My Unbalanced Division, we get that all person-stages in My Unbalanced Division are \(R'\)-related. In terms of Relation \(R'\), there is just as much branching between Wholly at \(t_1\) and the person-stages at \(t_2\) as there is between the person-stages at \(t_2\) and Old Lefty at \(t_3\). Rather than a tree-structured pattern of relationships, we have a collection of person-stages all of which are \(R'\)-related to all the others. Plausibly, Lefty and Old Lefty belong to the same branch while Righty and Old Lefty do not. The trouble is that there is no way of accounting for this in terms of any sort of branching of Relation \(R'\), because, in terms of Relation \(R'\), Old Lefty’s relations to Lefty are symmetrical with Old Lefty’s relations to Righty. Hence any approach, like (8) or (9), that tries to analyse non-branching personal identity just in terms of constructions out of Relation \(R'\) will fail.Footnote 35
What Noonan has in mind, however, is probably a variant of (9) with temporally ordered, rather than unordered, continuity:
-
(10)
Person-stage x is I-related to person-stage y if and only if xRy and there are no distinct and simultaneous person-stages u and v such that either
-
(i)
uRx, uRy, and vRx or
-
(ii)
uRx, uRy, and vRy.
-
(i)
This proposal yields that Lefty is I-related to Old Lefty in My Unbalanced Division.
Even so, (10) yields the wrong result in My Extended Pre-Division. The non-branching clause in (10) rules out that Young Wholly is I-related to Wholly. This is because Lefty and Righty are distinct and simultaneous and Lefty is R-related both to Young Wholly and to Wholly while Righty is R-related to Wholly. And (10) yields that Young Wholly and Wholly are not I-related to themselves, because they are R-related to the distinct and simultaneous Lefty and Righty. Hence (10) violates the reflexivity of Relation I.
Moreover, in The Senile General, (10) yields that The Boy is I-related both to The Officer and to The General while The Officer is not I-related to The General. This is because there are no distinct and simultaneous person-stages in that case; so all person-stages are I-related except The Officer and The General. The Officer and The General are not I-related, since they’re not R-related. Hence, as with (3) and (6), we get a non-transitive Relation I and thus multiple occupancy.
We have seen that the previously proposed non-branching clauses don’t work. But there is, I shall argue, a better approach. I propose
-
(11)
Person-stage x is I-related to person-stage y if and only if xRy and there are no person-stages u and v such that
-
(i)
neither u nor v is present before each of x and y is present,
-
(ii)
neither u nor v is present after each of x and y is present,
-
(iii)
uRx,
-
(iv)
vRy, and
-
(v)
there is a person-stage z such that either (a) uRz and not vRz or (b) vRz and not uRz.
-
(i)
Given (11), Relation I is an equivalence relation over person-stages. For a proof of reflexivity, see Appendix A. For a proof of symmetry, see Appendix B. And, for a proof of transitivity, see Appendix C.
The idea behind the non-branching clause in (11) is to characterize the intuitive idea of there being two person-stages u and v in different branches in the continuity between x and y. Clauses (i) and (ii) make sure that the relevant branching doesn’t occur before or after both x and y; so we avoid the problem (4), (6), and (10) had with ruling out that, in My Extended Pre-Division, Young Wholly and Wholly are I-related. Clauses (iii) and (iv) make sure that u and v are part of the relevant continuities to or from x and y respectively. Finally, clause (v) makes sure that u and v belong to different branches in the sense that there is a person-stage that is continuous with one of them but not with the other. Clause (v) is similar to the non-branching clause in (5), but, unlike the non-branching clause in (5), it doesn’t require that u and v are identical with x and y respectively; so it rules out, in My Temporary Division or My Forgetful Temporary Division, that Wholly is I-related to Old Wholly.
Note also that, (11) doesn’t rely on the identity or distinctness of person-stages, which (3), (4), (6), (8), (9), and (10) all rely on. This lets (11) sidestep any worries about the alleged circularity in relying on Relation I, identity, or distinctness between person-stages in an account of Relation I.Footnote 36 And (11)—unlike (1), (2), and (7)—yields the desired result in My Division, namely, that all person-stages are I-unrelated to each other. It also yields acceptable results in the other cases. In these cases, (11) yields the following: In The Brave Officer, all person-stages are I-related. In The Senile General, My Temporary Division, and My Forgetful Temporary Division, all person-stages are I-unrelated to each other. In My Unbalanced Division, the only I-related person-stages are Lefty and Old Lefty. In My Extended Pre-Division, the only I-related person-stages are Young Wholly and Wholly. And, in My Forgetful Division, the only I-related person-stages are Wholly and Lefty.
One might be worried about the result in The Senile General.
First, one might think that The Officer should be I-related to The General.Footnote 37 If so, one might be tempted to rely on Relation \(R'\) rather than Relation R; but, as I argued earlier, relying on temporally unordered continuity doesn’t fit with some plausible ideas about branching in cases like My Unbalanced Division. If there is a possible case structured like The Senile General such that it seems that the stage corresponding to The Officer should be I-related to the stage corresponding to The General, then a more promising approach is to revise the criteria for what counts as the relevant kind of connectedness so that these stages will be connected.Footnote 38
Second, one might think that The Boy should be I-related to The Officer. And one might think that whether The Boy at \(t_1\) is I-related to The Officer at \(t_2\) shouldn’t depend on what person-stages The General at \(t_3\) (after both \(t_1\) and \(t_2\)) is connected to. If The General had a connection to The Officer like in The Brave Officer, then The Boy would be I-related to The Officer. For similar reasons, one might think that, in My Forgetful Division, Young Wholly should be I-related to Wholly.Footnote 39 As long as the connections between person-stages are structured like they are in these cases and we rely on temporally ordered continuity, it is hard to deny that the continuity branches between \(t_1\) and \(t_2\). If this dependence on the future is implausible, there is a more promising way to avoid such dependence than to rely on temporally unordered continuity, namely, to restrict the relevant kinds of connectedness so that it only holds between person-stages without any temporal gaps between them.Footnote 40 Given this restriction, the connection in The Senile General between The Boy and The General would be invalidated, and then (11) would yield that The Boy is I-related to The Officer. Similarly, in My Forgetful Division, this restriction would invalidate the connection between Young Wholly and Righty, and then (11) would yield that Young Wholly is I-related to Wholly.
Notes
Parfit (1984, pp. 210, 212).
A relation over a set is transitive if and only if—for all x, y, and z in the set—if x is related to y and y is related to z, then x is related to z. And a relation over a set is non-transitive if and only if it isn’t transitive.
I won’t, however, defend the use of non-branching clauses from more general objections, for example, that these clauses conflict with the only-x-and-y principle—see Wiggins (1980, p. 96) and Noonan (1989, pp. 233–254)—or that they are ad hoc—see Oderberg (1993, p. 58), Schechtman (1996, p. 43), Olson (1997, p. 49), and Hawley (2005); yet compare Demarest (2016, pp. 577–578).
Lewis (1976b, p. 21). On perdurance, persons persist by having stages present at different times, with no stage being wholly present at more than one time. The assumption of perdurance won’t be crucial for the argument of this paper. An alternative to perdurance is endurance. On endurance, persons persist by being fully present at different times; see Lewis (1986, p. 202) for the endurance/perdurance distinction. While we shall assume a perdurance framework for our discussion, we could translate the proposals from this framework to an endurance framework, replacing person-stages by people and Relation I by personal identity (see Appendix D for an endurance translation of each proposal). This translation would mainly strengthen the arguments for my proposal in so far as they rely on transitivity, because it is more obvious that identity is transitive than that Relation I is transitive. For another advantage, see note 36.
Lewis (1976b, p. 22).
Lewis (1983, p. 76).
To distinguish cases of fission or fusion from cases where someone time travels to a time where a younger or older stage of them is also present, we can rely on some kind of personal time rather than external time; see Lewis (1976a, p. 146). We can then treat the continuities in fission and fusion cases as branching without thereby treating the continuities in time-travel cases as branching (unless they also feature fission or fusion).
A relation over a set is reflexive if and only if, for all x in the set, x is related to x. And a relation over a set is symmetric if and only if, for all x and y in the set, if x is related to y, then y is related to x.
That view is often attributed to John Locke. See, however, Gustafsson (2010) for a rebuttal of that interpretation.
We follow Locke’s (Essay II.xxvii.8–9; 1975, p. 335) distinction between man and person. A man or a woman in Locke’s sense is a human animal rather than a person.
Perry (1972, pp. 471–472) and Lewis (1976b, pp. 18–24). Lewis (1976b, p. 30) allows, however, that Relation R might have some restrictions on the maximal duration between two R-related person-stages, which can come into play in cases of extreme longevity. Lewis is also indecisive regarding whether to emphasize Relation \(C'\) as in (1) or Relation R as in (2). If the sole objection to (1) is that it allows multiple occupancy, (1) should be acceptable to Lewis, since he accepts multiple occupancy.
The ‘Lefty’/‘Righty’ terminology is due to Strawson (1970, p. 186).
The idea of analysing personal identity in terms of a one-many relation in combination with a non-branching clause dates back to Shoemaker (1970, pp. 278–279).
Parfit (1971, p. 13). Against Parfit, Demarest (2016, p. 578) argues that it would be better to just analyse personal persistence in terms of non-branching continuity. The trouble, however, is that it is far from clear when a continuity relation has a non-branching form. Parfit’s proposal is a first attempt to clarify the notion of a non-branching form, on which we shall try to improve.
Brueckner (2005, p. 295) interprets Parfit as relying on a temporally unordered continuity. Parfit (1984, p. 206) doesn’t mention a temporal-order requirement in his main definition of psychological continuity, which is the continuity his (1984, p. 207) psychological criterion relies on. But Parfit (1971, p. 21n, 1984, p. 302; 1993, pp. 23–24) makes clear elsewhere that the chain of psychological connections needs to be temporally ordered. One might object that a difference between our definition of Relation R and Parfit’s definition of psychological continuity is that he (1971, p. 20, 1976, p. 106n23) at times seems to take psychological continuity to be transitive. Parfit (1971, p. 20n29, 1984, p. 302, 1993, pp. 23–24) makes clear, however, that psychological continuity is only supposed to be transitive when considered in one direction in time. Note, however, that, in Parfit’s terminology, ‘Relation R’ isn’t psychological continuity. In his (1984, p. 206) terminology, psychological continuity consists in overlapping chains of strong psychological connectedness, whereas his (1984, p. 215) ‘Relation R’ is ‘psychological connectedness and/or continuity with the right kind of cause.’ As defined by Parfit, ‘Relation R’ differs from psychological continuity, because two person-stages can be psychologically connected without being strongly psychologically connected. Unlike psychological continuity and Relation R as we define it, Parfit’s ‘Relation R’ isn’t transitive when considered in one direction in time. To see this, consider a variant of The Brave Officer with the same pattern of connections except that the connections aren’t strong. Parfit’s relation then holds from The Boy to The Officer and from The Officer to The General but not from The Boy to The General (because The Boy and The General are neither psychologically connected nor related by overlapping chains of strong connectedness).
Parfit (1984, p. 207). In the 1987 reprinting, the fourth clause was changed to “it has not taken a ‘branching’ form.” Nevertheless, in that reprinting, Parfit (1984, p. 267) still claims that, ‘On what I call the Psychological Criterion, a future person will be me if he will be R-related to me as I am now, and no different person will be R-related to me.’ It is hard to make sense of this claim given Parfit’s terminology. In his (1984, p. 215) terminology, ‘Relation R’ isn’t psychological continuity but ‘psychological connectedness and/or continuity with the right kind of cause.’ There can be psychological connectedness without psychological continuity, since psychological continuity requires overlapping chains of strong psychological connectedness and there can be psychological connectedness that isn’t strong; see note 21. Consider a case with two person-stages, \(s_1\) at \(t_1\) and \(s_2\) at \(t_2\), where these stages are psychologically connected but not strongly psychologically connected. Suppose that these stages aren’t psychologically connected to any other person-stages. Then, at \(t_1\), there is only one future person-stage that will be related to \(s_1\) in terms of Parfit’s ‘Relation R’, namely, \(s_2\). But, according to Parfit’s psychological criterion, \(s_1\) and \(s_2\) cannot be I-related, because they’re not psychologically continuous (as they’re not related by overlapping chains of strong connectedness).
Parfit’s criterion only rules out branching in cases of fission and not in cases of fusion. My interpretation, however, treats fission and fusion in the same way. But this difference won’t matter for my objections to (4), because they only rely on cases of fission.
Rather than (4), Brueckner (1993, p. 22n21, 2005, p. 298) actually criticizes a temporally unordered variant of (4), that is, a proposal just like (4) except that Relation R has been replaced by Relation \(R'\) (temporally unordered psychological continuity, defined later). In the same way as (4), this variant is open to the problem with incompleteness in The Brave Officer—presented later. Moreover, in My Extended Pre-Division (presented later), this variant implausibly rules out that Young Wholly is I-related to Wholly unless Lefty is I-related to Righty. For proof by contradiction, assume that Young Wholly is I-related to Wholly and that Lefty isn’t I-related to Righty. Since the non-branching clause in this variant of (4) then cannot rule out that Young Wholly is I-related to Wholly, it’s not the case that Young Wholly is \(R'\)-related to Lefty while Wholly isn’t I-related to Lefty. Therefore, since Young Wholly is \(R'\)-related to Lefty, we have that Wholly is I-related to Lefty. But, given this variant of (4), Wholly isn’t I-related to Lefty, since Wholly is \(R'\)-related to Righty and we assumed that Lefty isn’t I-related to Righty.
Lefty and Righty are distinct and simultaneous not only in external time but also in personal time; see note 8.
Noonan (2006, p. 167n5).
Noonan (2006, p. 167n5).
Yi (2010, p. 195).
Yi (2010, pp. 196–210) explores a series of analyses of xIy as \(xR'y\) in conjunction with a non-branching clause that isn’t expressible in terms of Relation \(R'\). His three preferred proposals all have the following form:
-
Person-stage x is I-related to person-stage y if and only if
-
(i)
\(xR'y\) (‘xRy’ in Yi’s notation),
-
(ii)
xRy (‘\(xC^*y\) or \(yC^*x\)’ in Yi’s notation), and
-
(iii)
there are no distinct and simultaneous person-stages u and v such that ...
-
(i)
First of all, requirement (i) is superfluous given (ii). But the main problem is that proposals of this form do not preserve the transitivity of Relation I. To see this, consider The Senile General. In The Senile General, (iii) cannot fail to hold, since there are no distinct and simultaneous person-stages in that case. Since The Officer is R-related (and thus \(R'\)-related) to The Boy, we have that The Officer is I-related to The Boy. And, since The Boy is R-related (and thus \(R'\)-related) to The General, we have that The Boy is I-related to The General. But, since The Officer is not R-related to The General, (ii) rules out that The Officer is I-related to The General. Hence Relation I is non-transitive given proposals of this form.
-
Brueckner (2005, pp. 298–299) rejects (8) due to this worry about circularity. Others, such as Noonan (2006, pp. 165–166), do not share Bruckner’s worry. See, however, Brueckner and Buford (2008, pp. 383–384) for a reply. This kind of reliance on the identity or distinctness of person-stages is also a problem for Yi’s (2010, pp. 196–210) proposals; see note 35. If we replace our perdurance framework with an endurance framework, these claims about person-stages being distinct become claims about persons being distinct—which raises the worry about circularity when they appear in an account of personal identity. See the endurance translations (3*), (4*), (6*), (8*), (9*), and (10*) in Appendix D.
Brueckner (2005, p. 296).
This is the approach I defend in Gustafsson (2011). I defend the view that the relevant kind of connectedness is phenomenal connectedness and, accordingly, that the relevant kind of continuity is phenomenal continuity, that is, the relation of sharing the same stream of consciousness. In addition, I defend the view that phenomenal connections can hold over temporal gaps such as periods of dreamless sleep. Regarding The Senile General, it seems to me that nothing in the standard memory-loss story for this case rules out that there is temporally ordered phenomenal continuity holding between The Officer and The General. In the rare cases where phenomenal connections really are structured in The Senile General pattern, it seems, I think, that the result of (11) is plausible (that is, the result that The Boy, The Officer, and The General are all I-unrelated to each other), for in that case the stream of consciousness of The Boy would split into two: one stream including the experiences of The Officer but not those of The General and one stream including the experiences of The General but not those of The Officer.
Yi (2010, p. 200, 2013, pp. 176–182). Yi discusses a case similar to My Forgetful Fission with a psychological kind of connectedness (it’s unclear whether Young Wholly is \(C'\)-related to Lefty in his case) where Young Wholly is scanned at \(t_1\) and Righty is a replica created from this scan at \(t_3\). Yi’s complaint is that, if Young Wholly isn’t I-related to Wholly, then a mere scan terminates the person of which Young Wholly is a stage. But it’s not the mere scan that is to blame; it’s the scan combined with the creation of Righty from this scan that rules out Young Wholly being I-related to Wholly.
As mentioned in note 38, this is not the approach I favour.
References
Berkeley, G. (1950). A. A. Luce & T. E. Jessop (Eds.), The works of George Berkeley: Bishop of Cloyne vol. 3. London: Thomas Nelson.
Berkeley, G. (2010). L. Jaffro, G. Brykman & C. Schwartz (Eds.), Berkeley’s Alciphron: English text and essays in interpretation. Hildesheim: Olms.
Brueckner, A. (1993). Parfit on what matters in survival. Philosophical Studies, 70(1), 1–22.
Brueckner, A. (2005). Branching in the psychological approach to personal identity. Analysis, 65(288), 294–301.
Brueckner, A., & Buford, C. T. (2008). The psychological approach to personal identity: Non-branching and the individuation of person stages. Dialogue, 47(2), 377–386.
Dainton, B., & Bayne, T. (2005). Consciousness as a guide to personal persistence. Australasian Journal of Philosophy, 83(4), 549–570.
Demarest, H. (2016). Fission may kill you (but not for the reasons you thought). Philosophy and Phenomenological Research, 93(3), 565–582.
Grice, H. P. (1941). Personal identity. Mind, 50(200), 330–350.
Gustafsson, J. E. (2010). Did Locke defend the memory continuity criterion of personal identity? Locke Studies, 10, 113–129.
Gustafsson, J. E. (2011). Phenomenal continuity and the bridge problem. Philosophia, 39(2), 289–296.
Gustafsson, J. E. (2018). The unimportance of being any future person. Philosophical Studies, 175(3), 745–750.
Hawley, K. (2005). Fission, fusion and intrinsic facts. Philosophy and Phenomenological Research, 71(3), 602–621.
Hume, D. (1978). L. A. Selby-Bigge & P. H. Nidditch (Eds.), A treatise of human nature (2nd edn.). Oxford: Clarendon Press.
Hume, D. (2007). D. F. Norton & M. J. Norton (Eds.), A treatise of human nature. Oxford: Clarendon Press.
Lewis, D. (1976a). The paradoxes of time travel. American Philosophical Quarterly, 13(2), 145–152.
Lewis, D. (1976b) Survival and identity. In A. O. Rorty (Ed.), The identities of persons (pp. 17–40). Berkeley: University of California Press.
Lewis, D. (1983). Postscripts to “Survival and identity”. In Philosophical papers: Volume I (pp. 73–77). New York: Oxford University Press.
Lewis, D. (1986). On the plurality of worlds. Oxford: Blackwell.
Locke, J. (1975). P. H. Nidditch (Ed.), An essay concerning human understanding. Oxford: Clarendon Press.
Noonan, H. W. (1989). Personal identity. London: Routledge.
Noonan, H. W. (2006). Non-branching and circularity: Reply to Brueckner. Analysis, 66(290), 163–167.
Oderberg, D. S. (1993). The metaphysics of identity over time. London: Macmillan.
Olson, E. T. (1997). The human animal: Personal identity without psychology. New York: Oxford University Press.
Parfit, D. (1971). Personal identity. The Philosophical Review, 80(1), 3–27.
Parfit, D. (1976). Lewis, Perry, and what matters. In A. O. Rorty (Ed.), The identities of persons (pp. 91–107). Berkeley: University of California Press.
Parfit, D. (1984). Reasons and persons. Oxford: Clarendon Press.
Parfit, D. (1993). The indeterminacy of identity: A reply to Brueckner. Philosophical Studies, 70(1), 23–33.
Perry, J. (1972). Can the self divide? The Journal of Philosophy, 69(16), 463–488.
Perry, J. (1975). The problem of personal identity. In J. Perry (Ed.), Personal identity (pp. 3–30). Berkeley: University of California Press.
Reid, T. (2002). D. R. Brookes (Ed.), Essays on the intellectual powers of man. Edinburgh: Edinburgh University Press.
Schechtman, M. (1996). The constitution of selves. Ithaca, NY: Cornell University Press.
Shoemaker, S. (1970). Persons and their pasts. American Philosophical Quarterly, 7(4), 269–285.
Shoemaker, S., & Swinburne, R. (1984). Personal identity. Oxford: Blackwell.
Strawson, P. F. (1970). Chisholm on identity through time (a response). In H. E. Kiefer & M. K. Munitz (Eds.), Language, belief, and metaphysics (pp. 183–186). Albany, NY: State University of New York Press.
Unger, P. (1990). Identity, consciousness and value. New York: Oxford University Press.
Wiggins, D. (1967). Identity and spatio-temporal continuity. Oxford: Blackwell.
Wiggins, D. (1980). Sameness and substance. Oxford: Blackwell.
Williams, B. A. O. (1956–1957) Personal identity and individuation. Proceedings of the Aristotelian Society, 57, 229–252.
Yi, H. (2010). Non-branching clause. Metaphysica, 11(2), 191–210.
Yi, H. (2013). Delayed fission and the standard psychological view of personal identity. Organon F, 20(2), 173–191.
Acknowledgements
I wish to thank David Efird, Lisa Forsberg, Tom Stoneham, Robert Trueman, and an anonymous referee for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
1.1 A Reflexivity
To see that Relation I is reflexive over person-stages given (11), assume that a is a person-stage. Note first that, since R is reflexive, we have aRa. Replacing x by a and y by a in (11), any person-stages u and v that are going to make clauses (i)–(iv) true must be simultaneous with a. But then—given uRa, vRa, and that u, v, and a are simultaneous—we have that u and v must be R-related to the same person-stages, because, if a person-stage is related by temporally ordered continuity to one of u and v, this continuity could be extended to the other of u and v without breaking the temporal order. But, if u and v are R-related to the same person-stages, then u and v would not make clause (v) true. Thus, replacing x by a and y by a in (11), no person-stages u and v can make clauses (i)–(v) all true. So we have aRa and that the non-branching clause in (11) doesn’t apply. Hence (11) entails aIa. Since we have derived aIa with the help of (11) without having assumed anything about a other than that a is a person-stage, we have that Relation I is reflexive over person-stages given (11).
1.2 B Symmetry
To see that Relation I is symmetric over person-stages given (11), assume, for proof by contradiction, that a and b are person-stages such that a is I-related to b but b isn’t I-related to a. From aIb, we have, given (11), aRb. Then, since Relation R is symmetric, we have bRa. Since bRa even though b isn’t I-related to a, there must be some person-stages u and v such that, replacing x by b and y by a in (11), clauses (i)–(v) are all true. From clauses (iii) and (iv), we then have uRb and vRa. From uRb and bRa, we have, since Relation R is transitive, uRa. Likewise, from vRa and aRb, we have vRb. Given uRa and vRb, we have that, replacing x by a and y by b in (11), clauses (i)–(v) are all true. To see this, note that, given uRa and vRb, clauses (iii) and (iv) are true and the other clauses are equivalent after the swap of a and b in these clauses. Hence we have that, replacing x by a and y by b in (11), the non-branching clause applies. Hence a isn’t I-related to b, which contradicts our assumption that a is I-related to b. Since we have derived a contradiction from the assumption that a is I-related to b and b isn’t I-related to a, we have that Relation I is symmetric over person-stages given (11).
1.3 C Transitivity
To see that Relation I is transitive over person-stages given (11), note first that, if person-stages x and y are I-related, then, replacing u by x and v by y in (11), we have that clauses (i)–(iv) hold. And then clause (v) cannot hold, because, if it did, the whole non-branching clause would apply and rule out xIy. So, if we have xIy, we also have that there is no person-stage z such that z is R-related to one of x and y but not to the other. Hence we have the first observation that, if two person-stages are I-related, every person-stage that is R-related to one of them is also R-related to the other.
Assume that a, b, and c are person-stages such that aIb and bIc. From aIb and the first observation, we have that a and b are R-related to the same person-stages. And, from bIc and the first observation, we have that b and c are R-related to the same person-stages. Hence we have the second observation that a and c are R-related to the same person-stages.
Let us say that a person-stage is present in thea–cinterval if and only if that stage is neither present before each of a and c nor present after each of a and c. Assume that person-stage d is present in the a–c interval and that d is R-related to at least one of a and c. And assume that person-stage e is R-related to d. Since d is R-related to at least one of a and c, we have, by the second observation, both aRd and cRd. Since we have aRd, cRd, and that d is present in the a–c interval, we have one of two cases: first, that d is simultaneous with at least one of a and c and, second, that d is present after one of a and c, present before the other, and not simultaneous with either. We shall consider these cases in turn.
Consider the first case: that d is simultaneous with at least one of a and c. Let a simultaneousa/cstage be a stage that is simultaneous with d and identical to either a or c. The temporally ordered continuity from e to d can, without breaking the temporal order of this continuity, be extended to any person-stage that is both R-related to d and simultaneous with d. Hence, in this case, we have that e is R-related to a simultaneous a/c stage. Since e is then R-related to at least one of a and c, we have, by the second observation, both eRa and eRc. For any person-stage, if there is temporally ordered continuity from that person-stage to a simultaneous a/c stage, then this continuity can be extended, without breaking the temporal order, to the simultaneous d. Therefore, by the second observation, we also have that d is R-related to all person-stages that a and c are R-related to.
Now, consider the second case: that d is present after one of a and c, present before the other, and not simultaneous with either. If the temporally ordered continuity from one of a and c to d approaches d from one direction in time, then the temporally ordered continuity from the other of a and c to d approaches d from the other direction in time. The temporally ordered continuity from e to d can therefore be extended to at least one of a and c without breaking the temporal order of this continuity. Hence e is R-related to at least one of a and c. Then, by the second observation, we have eRa and eRc. As mentioned, the temporally ordered continuities from a to d and from c to d approach d temporally from different directions. Therefore, by the second observation, we then have that, for any person-stage that is R-related to a or c, there is temporally ordered continuity from at least one of a and c such that this continuity can be extended, without breaking the temporal order, to d. Therefore, by the second observation, we have that d is R-related to all person-stages that a and c are R-related to.
Hence, in either case, e is R-related both to a and to c. And each person-stage that is R-related to one of a and c is R-related to d. Since we haven’t assumed anything about d and e other than that d is present in the a–c interval and R-related to e and to at least one of a and c, we have the third observation that all person-stages present in the a–c interval which are R-related to one of a and c are R-related to the same person-stages.
Since Relation R is reflexive, we have aRa. So, by the second observation, we have aRc. By the third observation, we then have that, replacing x by a and y by c in (11), clauses (i)–(v) cannot all hold. Any person-stages u and v that would make (i)–(iv) true would make (v) false, because u and v would, by the third observation, be R-related to the same person-stages. Therefore, by (11), we then have aIc. Since we have derived aIc from aIb and bIc with the help of (11), Relation I is transitive over person-stages given (11).
1.4 D Endurance translations
This appendix provides translations of the proposals in an endurance framework. According to endurance, persons persist by being fully present at different times. Each starred proposal is an endurance translation of the corresponding unstarred perdurance proposal. These endurance translations show a further advantage of the (11)/(11*) approach: Even if endurance is the correct view of how persons persist, the (11)/(11*) approach clearly avoids problems with circularity, because (11*) doesn’t rely on claims about the identities of persons or their being distinct from each other. Proposals (3*), (4*), (6*), (8*), (9*), and (10*) lack this advantage.
Note that, unlike in the main text, the subscripts and superscripts of times in this appendix do not represent the temporal order of the times. So don’t assume, for example, that \(t_1\) must be earlier than \(t_2\) or that \(t''\) must be later than \(t'\) or t.
-
Temporally Ordered Connectedness (endurance version)
-
Person x at t is \(C_*\)-related to person y at \(t'=_{\mathrm {df}}\)x at t and y at \(t'\) are connected by the right kind of connection and either t is the same time as \(t'\) or t is earlier than \(t'\).
-
Temporally Unordered Connectedness (endurance version)
-
Person x at t is \(C'_*\)-related to person y at \(t'\)\(=_{\mathrm {df}}\)x at t and y at \(t'\) are connected by the right kind of connection.
-
Temporally Ordered Continuity (endurance version)
-
Person x at t is \(R_*\)-related to person y at \(t'\)\(=_{\mathrm {df}}\) either x at t is \(C_*\) related to y at \(t'\) or y at \(t'\) is \(C_*\) related to x at t, or there are persons \(z_1\), \(z_2\), ..., \(z_n\) and times \(t_1\), \(t_2\), ..., \(t_n\) such that either
-
(i)
x at t is \(C_*\)-related to \(z_1\) at \(t_1\), \(z_1\) at \(t_1\) is \(C_*\)-related to \(z_2\) at \(t_2\), ..., \(z_{n-1}\) at \(t_{n-1}\) is \(C_*\)-related to \(z_n\) at \(t_n\), \(z_n\) at \(t_n\) is \(C_*\)-related to y at \(t'\) or
-
(ii)
y at \(t'\) is \(C_*\)-related to \(z_1\) at \(t_1\), \(z_1\) at \(t_1\) is \(C_*\)-related to \(z_2\) at \(t_2\), ..., \(z_{n-1}\) at \(t_{n-1}\) is \(C_*\)-related to \(z_n\) at \(t_n\), \(z_n\) at \(t_n\) is \(C_*\)-related to x at t.
-
(i)
-
Temporally Unordered Continuity (endurance version)
-
Person x at t is \(R'_*\)-related to person y at \(t'\)\(=_{\mathrm {df}}\)x at t is \(C_*'\) related to y at \(t'\) or there are persons \(z_1\), \(z_2\), ..., \(z_n\) and times \(t_1\), \(t_2\), ..., \(t_n\) such that x at t is \(C'_*\)-related to \(z_1\) at \(t_1\), \(z_1\) at \(t_1\) is \(C'_*\)-related to \(z_2\) at \(t_2\), ..., \(z_{n-1}\) at \(t_{n-1}\) is \(C'_*\)-related to \(z_n\) at \(t_n\), \(z_n\) at \(t_n\) is \(C'_*\)-related to y at \(t'\).
-
(1*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(C_*'\)-related to y at \(t'\).
-
(2*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\).
-
(3*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there is no person z such that either
-
(i)
x at t is \(R_*\)-related to z at \(t'\) and y is not identical with z or
-
(ii)
y at \(t'\) is \(R_*\)-related to z at t and x is not identical with z.
-
(i)
-
(4*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there is no person z at a time \(t''\) such that either
-
(i)
x at t is \(R_*\)-related to z at \(t''\) and y is not identical with z or
-
(ii)
y at \(t'\) is \(R_*\)-related to z at \(t''\) and x is not identical with z.
-
(i)
-
(5*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there is no person z at a time \(t''\) such that either
-
(i)
x at t is \(R_*\)-related to z at \(t''\) and y at \(t'\) is not \(R_*\)-related to z at \(t''\) or
-
(ii)
y at \(t'\) is \(R_*\)-related to z at \(t''\) and x at t is not \(R_*\)-related to z at \(t''\).
-
(i)
-
(6*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there is no person z at a time \(t_1\) such that
-
(i)
\(t_1\) is not earlier than each of t and \(t'\),
-
(ii)
\(t_1\) is not later than each of t and \(t'\),
-
(iii)
z at \(t_1\) is \(R_*\)-related to x at t,
-
(iv)
z at \(t_1\) is \(R_*\)-related to y at \(t'\), and
-
(v)
there are two distinct persons u and v at a time \(t_2\) such that z at \(t_1\) is \(C'_*\)-related to u at \(t_2\) and z at \(t_1\) is \(C'_*\)-related to v at \(t_2\).
-
(i)
-
(7*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R'_*\)-related to y at \(t'\) and there is no person z at a time \(t''\) such that either
-
(i)
x at t is \(R'_*\)-related to z at \(t''\) and y at \(t'\) is not \(R'_*\)-related to z at \(t''\) or
-
(ii)
y at \(t'\) is \(R'_*\)-related to z at \(t''\) and x at t is not \(R'_*\)-related to z at \(t''\).
-
(i)
-
(8*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R'_*\)-related to y at \(t'\) and there is no person z such that either
-
(i)
x at t is \(R'_*\)-related to z at \(t'\) and y is not identical with z or
-
(ii)
y at \(t'\) is \(R'_*\)-related to z at t and x is not identical with z.
-
(i)
-
(9*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R'_*\)-related to y at \(t'\) and there are no distinct persons u and v at a time \(t''\) such that
-
(i)
u at \(t''\) is \(R'_*\)-related to x at t, u at \(t''\) is \(R'_*\)-related to y at \(t'\), and v at \(t''\) is \(R'_*\)-related to x at t or
-
(ii)
u at \(t''\) is \(R'_*\)-related to x at t, u at \(t''\) is \(R'_*\)-related to y at \(t'\), and v at \(t''\) is \(R'_*\)-related to y at \(t'\).
-
(i)
-
(10*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there are no distinct persons u and v at a time \(t''\) such that either
-
(i)
u at \(t''\) is \(R_*\)-related to x at t, u at \(t''\) is \(R_*\)-related to y at \(t'\), and v at \(t''\) is \(R_*\)-related to x at t or
-
(ii)
u at \(t''\) is \(R_*\)-related to x at t, u at \(t''\) is \(R_*\)-related to y at \(t'\), and v at \(t''\) is \(R_*\)-related to y at \(t'\).
-
(i)
-
(11*)
Person x at t is identical with person y at \(t'\) if and only if x at t is \(R_*\)-related to y at \(t'\) and there are no persons u and v and times \(t_1\) and \(t_2\) such that
-
(i)
neither \(t_1\) nor \(t_2\) is earlier than each of t and \(t'\),
-
(ii)
neither \(t_1\) nor \(t_2\) is later than each of t and \(t'\),
-
(iii)
u at \(t_1\) is \(R_*\)-related to x at t,
-
(iv)
v at \(t_2\) is \(R_*\)-related to y at \(t'\), and
-
(v)
there is a person z at a time \(t_3\) such that either (a) u at \(t_1\) is \(R_*\)-related to z at \(t_3\) and v at \(t_2\) is not \(R_*\)-related to z at \(t_3\) or (b) v at \(t_2\) is \(R_*\)-related to z at \(t_3\) and u at \(t_1\) is not \(R_*\)-related to z at \(t_3\).
-
(i)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gustafsson, J.E. Non-branching personal persistence. Philos Stud 176, 2307–2329 (2019). https://doi.org/10.1007/s11098-018-1127-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-018-1127-2















