Abstract
In Thinking and Acting John Pollock offers some criticisms of Bayesian epistemology, and he defends an alternative understanding of the role of probability in epistemology. Here, I defend the Bayesian against some of Pollock's criticisms, and I discuss a potential problem for Pollock's alternative account.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
John Pollock did a lot of interesting and important work on the metaphysics and epistemology of probability over several decades. In Thinking About Acting (Pollock 2006), we find many fascinating and thought provoking ideas and arguments (both old and new) about probability. Owing to limitations of space, I will be confining my remarks to a handful of issues addressed in Pollock (2006) pertaining to probability, logic, and epistemology. First, I will discuss some of Pollock’s arguments against Bayesian Epistemology (BE). Here, I’ll try to defend (BE) from what I take to be less than decisive objections. Then, I will make some critical remarks concerning Pollock’s alternative approach to “probabilistic epistemology”, which is based on his (non-Bayesian) theory of “nomic probability” (Pollock 1990). Footnote 1
1 Some remarks on Pollock’s critique of Bayesian epistemology
In Chap. 6, Pollock offers various criticisms of (BE). Before delving into some of Pollock’s criticisms, I would like to begin by pointing out some puzzling things Pollock says about the probability calculus. This will lead, naturally, into a more substantive discussion of Pollock’s critique of (BE). According to Pollock (2006, p. 83), the probability calculus can be axiomatized as follows:
-
(1)
prob \((P \mathbin{\&} \sim P) = 0.\)
-
(2)
prob \((P \vee \sim P) = 1.\)
-
(3)
prob\((P \vee Q) =\)prob(P) + prob(Q) − prob(P & Q).
-
(4)
If P and Q are logically equivalent, then prob(P) = prob(Q)
Pollock claims that the above axiomatization is equivalent to Kolmogorov’s probability calculus (PC) (Kolmogorov 1956).Footnote 2 In fact, Pollock’s intended interpretation of his axiomatization—which I’ll call (PC′), for short—is logically incomparable to (PC). That is, (i) there are some theorems of (PC) that are not theorems of (PC′), and (ii) there are some theorems of (PC′) that are not theorems of (PC). Let’s take (ii) first. The probability calculus defines probability functions prob (·) over sentential languages \({\mathcal{L}}\). As such, if (PC′) is to be equivalent to (PC), then the (schematic) axioms (1)–(4) must be relativized to some such \({\mathcal{L}}\). That is, the metavariables “P” and “Q” in Pollock’s (1)–(4) must be understood as ranging over sentences of some sentential language \({\mathcal{L}}\). If we do not do this, then we may falsely interpret “logically equivalent” in (4) as something stronger than “\({\sl tautologically\,equivalent\,in}\) \({\mathcal{L}}\)” which is all “logically equivalent” means in (PC). [As we’ll see shortly, Pollock’s critique of (BE) makes use of just such a stronger reading of the locution “logically equivalent” in (4).] As a result, (PC′) contains “theorems” that are not theorems of (PC). For instance, Pollock’s (PC′) will entail that prob(P) = prob(Q), for many P and Q that are not even expressible in any sentential language \({\mathcal{L}}\) (e.g., first-order or higher-order equivalences). I’ll return to this, below, in my discussion of Pollock’s critique of (BE). But, first, let me illustrate (i). The following is an axiom of Kolmogorovian (PC) (Fitelson 2008):
-
(5)
For all \(P \in {\mathcal{L}},\) prob(P ≥ 0)
Unfortunately, (5) is not a theorem of (PC′)—even when it is (properly) restricted to sentential languages \({\mathcal{L}}\). To see this, we can construct a simple counterexample to (5) in a properly \({\mathcal{L}}\)-relativized version of (PC′). Let \({\mathcal{L}}\) contain just one atomic sentence A. Hence, only four distinct propositions can be expressed in \({\mathcal{L}}\): A, ∼A, \(A \mathbin{\&} \sim A\), and \(A \vee \sim A\). Now, let prob(·) be defined on \({\mathcal{L}}\), as follows:
-
(6)
prob \((A) = 2\)
-
(7)
prob \((\sim A) = -1\)
-
(8)
prob \((A \vee \sim A) = 1\)
-
(9)
prob \((A \mathbin{\&} \sim A) = 0\)
This 〈\({\mathcal{L}},\) prob〉 pair satisfies all of Pollock’s (PC′) axioms (1)–(4), but it also violates Kolmogorov’s (5), since prob \((\sim A) = -1 < 0\).Footnote 3 Therefore, Pollock’s (PC′) is both too strong [(ii)] and too weak [(i)] to be a proper candidate for an equivalent formulation of (PC). Problem (i) is easily fixed, by adding (5) as an axiom to a properly \({\mathcal{L}}\)-relativized rendition of (PC′). But, problem (ii) is deeper and more intertwined with Pollock’s thinking about Bayesianism. If we fix problem (ii) by limiting the axioms of (PC′) to sentential languages \({\mathcal{L}}\)—and we bear this limitation in mind when we apply (PC′) to (BE)—then some of Pollock’s central criticisms of (BE) will be threatened. Allow me to explain.
One of Pollock’s main lines of criticism of (BE) is that it entails a kind of \({\sl logical\,omniscience}\). As he rightly points out (Pollock 2006, p. 94), some necessary truths seem (intuitively) unjustified for some epistemically rational agents (S). But, Pollock claims, Bayesian epistemology cannot make sense of this, if it is to use prob(p) as a way of gauging the degree to which p is justified (for S). He says:
If Q is a necessary truth, it is logically equivalent to (\(P \vee \sim P\)), so it follows from axioms (2) and (4) that every necessary truth has a prob of 1.
I think this is highly uncharitable to the Bayesian epistemologist. First, this rests on a misunderstanding of (PC), which only entails that tautologies of \({\mathcal{L}}\) must be assigned a prob of 1. Second, it rests on an implausible assumption about “necessary truths”—that they are all logically equivalent to the simple tautology \(P \vee \sim P\). I’m not sure what Pollock has in mind here, but I don’t see why a Bayesian (or anyone else) should be saddled with such a strong commitment. As a result, it’s unclear what reason Bayesians could have for insisting that all necessary truths be assigned the same probability as a tautology. It seems to me that there are better ways to think about (PC) and (BE).
Garber (1983) explains how (PC)—when properly construed and applied—can be used by Bayesian epistemologists to model logically non-omniscient agents. And, he uses his approach to give a novel and compelling resolution of the so-called “old evidence problem” of Bayesian confirmation theory (a branch of Bayesian epistemology). I won’t get into the details of Garber’s approach here. But, I’ll give the basic idea behind it. Pollock’s criticism presupposes a very rich notion of “logical equivalence” in his interpretation of (PC). As I have explained, however, (PC) has an impoverished notion of “logical equivalence”—tautological equivalence in some sentential \({\mathcal{L}}\) (Fitelson 2008). While this impoverishment may seem like a shortcomingFootnote 4—it can be a virtue. It allows Bayesian epistemologists to model agents who may only be omniscient about the tautologies of some sentential language \({\mathcal{L}}\). By exploiting the fact that atomic sentences are not tautologically related to each other, we can then use this “impoverishment” to model ignorance of “higher” logical truths, which are not expressible in \({\mathcal{L}}\). Following Garber, we can do so by extra-systematically interpreting the atomic sentences of \({\mathcal{L}}\). For instance, we could have a language with three atomic sentences A, B, and C, where “C” gets extra-systematically interpreted as “A entails B”, and where this “entailment” is (say) first-order (but not sentential). Then, we could add extra-systematic probabilistic constraints to our probability model, which would selectively capture such “higher” logical knowledge on the part of the agent being modeled. For example, by adding the following extra-systematic constraint, we can model an agent who knows that “modus ponens” for “entails” is extra-systematically valid (in this instance):
-
(10)
prob \((B \mathbin{|} A \mathbin{\&} C) = 1.\)
We could also allow this conditional prob to be less than 1, in which case we’d be modeling an agent who is ignorant of this “extra-systematic modus ponens”. In this way, we can model agents who are justified in believing some extra-systematic (logical, conceptual, or other) necessary truths, but not others. And, that gives a sophisticated Bayesian epistemologist the wherewithal to overcome this criticism of Pollock. Of course, Garber’s framework still presupposes some logical omniscience, and this leaves the Bayesian vulnerable to some objections. Indeed, Pollock (2006, p. 94) rightly points out that sometimes people aren’t even justified in believing some tautologies in simple languages \({\mathcal{L}}\). And, that problem will still plague even a Garberian approach to Bayesian epistemology.Footnote 5 However, as Pollock himself notes (Pollock 2006, p. 95), tautologies are always warranted. So, presumably, Pollock’s logical omniscience objection would not undermine a Garberian application of prob to the modeling of degrees of warrant. In any case, Pollock has another objection to this sort of Bayesian epistemology.
According to Pollock, Bayesian epistemologists who claim that prob is a measure of degree of warrant (or justification) are unable to explain the role of reasoning in epistemology. Pollock seems to think that the following is a desideratum for any adequate (formal) epistemology (Pollock 2006, p. 95):
-
(11)
Any adequate (formal) epistemology must be able to explain why deductive inference from multiple uncertain premises can be expected to preserve justification (and/or warrant).
Pollock argues that (BE) is unable to meet requirement (11). He says (Pollock 2006, p. 97):
If degrees of warrant satisfy the probability calculus, then ... we can only be confident that a deductive argument takes us from warranted premises to a warranted conclusion if all the inferences are probabilistically valid.
where, an inference of the form \(P_1,\ldots,P_n\,\therefore\,Q\) is \({\sl probabilistically\,valid}\) just in case its conclusion Q is at least as probable as its least probable premise—that is, iff for all i: prob(Q) ≥ prob(P i ). As it turns out, no deductively valid form of inference with more than one premise is probabilistically valid in this sense. That explains why Pollock thinks Bayesian epistemology cannot satisfy (11). The reason Pollock thinks violating (11) is undesirable is that he thinks violating (11) prevents probabilism from being able to explain how we can reason “blindly” from multiple warranted (or justified) premises, using a deductively valid inference, and expect that the conclusion will also be warranted (or justified). Since “blind deductive reasoning” seems integral to epistemology, this would be a serious shortcoming of (BE)—or, more generally, of any probabilistic epistemology.
Strictly speaking, it is true that Bayesianism so construed can’t satisfy (11) in this sense. But, I wonder why one would want to both construe Bayesian epistemology in this way, and understand “probabilistic validity” in this way. It seems clear to me that many contemporary Bayesian epistemologists would neither want to equate prob and \({\sl degree\,of\,warrant}\) (or \({\sl degree\,of\,justification}\), for that matter) nor explicate \({\sl probabilistic\,validity}\) in the way Pollock proposes. Let’s take the second point first. There is quite a long tradition of what is known as \({\sl probability\,logic}\) (PL). In recent years, probability-logicians like Adams (1975, 1996) and Hailperin (1996) have done a great deal of work on various notions of “probabilistic validity”. Two important points about (PL) are in order here. First, the notion of “probabilistic validity” that is typically used in (PL) circles is not the one Pollock has in mind. Adams (1975, p. 57) defines a different notion, which I will call prob-validity. I won’t give his definition of prob-validity here, but I will discuss one important consequence of the definition, just to give a sense of how it differs from Pollock’s “probabilistic validity”. Letu(p) = 1 − prob(p) be the \({\sl uncertainty}\) of p. And, consider an inference of the form \(P_1,\ldots,P_n \,\therefore \,Q\). Such an inference will be prob-valid in Adams’s sense only if Footnote 6 the uncertainty of the conclusion is no greater than the sum of the uncertainties of the premises—that is, only if \({\sc{\bf{u}}}(Q) \le \sum_{i = 1}^{n} {\sc{\bf{u}}}(P_i)\). In other words, the uncertainty of the conclusion of a prob-valid inference will never exceed the sum-total of the uncertainties of its premises. Moreover, it is a fundamental theorem of (PL) that all deductively valid arguments are prob-valid. So, in this sense, a Bayesian (probabilist) who adopts Adams’s notion of prob-validity, can explain why (in one precise sense) conclusions of deductively valid inferences will never be more unwarranted (or more unjustified) than the premises already were. Of course, this presupposes a different epistemic explanandum than Pollock has in mind in (11). But, in the interest of giving (PC) and (BE) a fair hearing, it is worth noting that other notions of “probabilistic validity” have been investigated by people who are interested in just the sort of deductive inferences from multiple uncertain premises that Pollock is talking about. Putting these alternative (PL)-investigations of “uncertain deductive inference” to one side, I want to make a second point about (PL)—that it can be illuminating, even with respect to Pollock’s explanandum [(11)].
Consider modus ponens for material implication “\(\supset\)” (“\(\supset\)-MP”, for short). This is a very common and important multi-premise deductive inference that (I take it) is used often in the sort of “blind” deductive reasoning Pollock has in mind. Given Pollock’s definition, \(\supset\)-MP is not “probabilistically valid”. But, (PL) allows us to be more precise in our “diagnosis”. Here is a (PL)-fact about \(\supset\)-MP:
-
(12)
If prob \((P) > 1 - \epsilon\) and prob \((P \supset Q) > 1 - \epsilon\), then prob \((Q) > 1 - 2 \epsilon\).Footnote 7
This is a classical theorem of (PL) (Hailperin 1996, p. 205). While (12) entails that some degree of prob can be “lost” in (material) modus ponens inferences, it also tells us that, when the premises are highly probable, the amount of prob that can be lost in \(\supset\)-MP is rather small. Now, imagine a Bayesian epistemologist who wants to defend the claim that degree of justification \({\bf{\sc{dj}}}\) (or degree of warrant \({\bf{\sc{dw}}}\)) is a prob. I don’t think someone like this is at a complete loss to explain (even on Pollock’s terms) how \(\supset\)-MP can often be “blindly” applied, while preserving justified-ness (or warranted-ness). Let us (naïvely) assume the following prob-reduction of justified-ness (or warranted-ness):
-
(13)
S is justified (warranted) in believing p iff prob\((p) > 1 - 2 \epsilon\), for some suitably “small” \(\epsilon\); and, S is highly justified (warranted) in believing p iff prob\((p) > 1 - \epsilon\).Footnote 8
In light of (12), a Bayesian who endorses (13) can explain how we may “blindly” do \(\supset\)-MP—in cases where the premises are all highly justified, since (12) entails that if the premises of a \(\supset\)-MP-inference are all highly justified, then the conclusion must be justified. Granted, this isn’t as general an explanation of “blind \(\supset\)-MP” as a Bayesian would have if \(\supset\)-MP were “probabilistically valid” in Pollock’s sense. But, I don’t see why this isn’t explanatory at all—even with respect to Pollock’s explanandum (or an explanandum that is very similar to Pollock’s). A similar strategy can be employed for \(\supset\)-transitivity, in light of the following classical theorem of (PL) (Hailperin 1996, p. 205):
-
(14)
If prob \((P \supset Q) > 1 - \epsilon\) and prob \((Q \supset R) > 1 - \epsilon\), then prob \((P \supset R) > 1 - 2 \epsilon\).
Furthermore, if we talk about indicative modus ponens (→-MP), rather than material modus ponens (\(\supset\)-MP), then things get even more interesting.Footnote 9 Many people (Adams 1975; Bennett 2003; Edgington 1995) think that the probability of the indicative conditional P → Q goes according to the conditional probability prob \((Q \mathbin{|} P)\). If that’s right, then we get an even better result of (PL) for the dialectical purposes at hand, namely:
-
(15)
If prob \((P) > 1 - \epsilon\) and prob \((P \rightarrow Q)\) = prob \((Q \mathbin{|} P) > 1 - \epsilon\), then prob(Q) > \((1 - \epsilon)^{2}\).
That is, supposing that →-MP is valid and that the equation prob \((P \rightarrow Q)\) = prob \((Q \mathbin{|} P)\) is correct, this means that even less prob can be “lost” in →-MP inferences than in \(\supset\)-MP inferences. And, so, the analogous Bayesian strategy is even more explanatory (in Pollock’s sense) in that case. There are limits to this strategy, since some multi-premise deductive arguments won’t even be guaranteed to preserve warrant/justification in cases where all the premises are highly warranted/justified. But, there is a fully general theory of “probability logic”, which furnishes such results for many classically deductively valid argument forms (Hailperin 1996). To my mind, this (to some extent) softens the impact of Pollock’s objection to thinking of degree of justification or degree of warrant as a prob.
Finally, I want to return to the question of whether Bayesians should (or do) think of degree of justification (or warrant) as a prob-function. I think many contemporary Bayesians would not want to do this, but for reasons that are independent of the considerations we just discussed in connection with Pollock’s objection. Bayesian epistemologists typically distinguish two types of “evidential support” or “confirmation”—\({\sl firmness}\) and \({\sl increase\,in\,firmness}\) (Carnap 1962, new preface):
-
Confirmation as firmness. E confirms f H, relative to background evidence K if and only if prob\((H \mathbin{|} E \mathbin{\&} K) > t\), for some threshold value t (typically, t > 1/2).
-
Confirmation as increase in firmness. E confirms i H, relative to background evidence K if and only if prob\((H \mathbin{|} E \mathbin{\&} K)\) > prob\((H \mathbin{|} K)\).
The firmness concept is sometimes called “absolute” confirmation, and the increase in firmness concept is sometimes called “incremental” confirmation. The distinction between them is just the distinction between high conditional probability versus probabilistic relevance. While these two concepts are closely related to each other, they can come apart in some rather important ways. Here is an example (to which I’ll return in Sect. 2) that illustrates the confirms f /confirms i distinction.
The example involves a 35-year old American man named Jim, who has received a positive test result for a rare disease X. Only 1 in 10,000 35-year-old males in the U.S. has disease X. But, the test for X is very highly reliable—it has very low false-positive and false-negative rates (each of these error rates is 1/1000). That is, if you have disease X, then there is only a 1/1000 chance of a false negative from an X-test, and if you don’t have X, then there is only a 1/1000 chance of a false positive from an X-test. Let a denote Jim, let Nx assert that x does not have disease X, and let Px assert that x has received a (single) positive test result for disease X. In this case, we (intuitively) have the following probabilistic facts, where K is the background evidence contained in the above story about Jim, the disease, and the test (and prob may be interpreted in various waysFootnote 10):
-
prob\((Na \mathbin{|} Pa \mathbin{\&} K)\) is high (specifically, it’s approximately 9/10).
-
prob\((Na \mathbin{|} Pa \mathbin{\&} K)\) is significantly less thanprob\((Na \mathbin{|} K)\).
In other words, Pa confirms f Na, relative to K; but Pa disconfirms i Na, relative to K. Question: does Pa constitute a reason to believe Na (given background knowledge K)? On the one hand (the firmness hand), Na is highly probable, given Pa (and K). On the other hand (the increase in firmness hand), Pa is strongly negatively relevant to the probability of Na (given K). This conflict between confirms f and disconfirms i seems to pull intuitions about \({\sl whether}\) Pa \({\sl is\,a\,reason\,to\,believe}\) Na in opposite directions. Many advocates of (BE) seem to endorse the following.Footnote 11
-
(16)
A necessary condition for E’s counting as a reason to believe H (or for it being reasonable to believe H on the basis of E), given background evidence/knowledge K, is that E does not disconfirm i H, relative to K.
If (16) is correct, then Pa would not count as a reason to believe Na (and we would not be warranted/justified in believing Na on the basis of Pa), given background knowledge K—despite the fact that prob \((Na \mathbin{|} Pa \mathbin{\&} K)\) is high.Footnote 12 This sort of consideration seems to have led various advocates of (BE) to reject the idea that the degree to which E justifies/warrants H (relative to background knowledge K) is prob \((H \mathbin{|} E \mathbin{\&} K)\). And, this consideration is orthogonal to the considerations raised by Pollock’s objections concerning “blind (uncertain) deductive reasoning”. This example also provides a nice segué into Sect. 2, where I will appeal to similar considerations to pose a challenge to Pollock’s alternative “probabilistic epistemology”.
2 Some worries about Pollock’s alternative “probabilistic epistemology”
Pollock rejects (BE), but he still thinks that probabilities (of some kind) are important in epistemology. Pollock’s alternative is what I will call a theory of \({\sl defeasible\,probabilistic\,reasoning}\) (DPR). Pollock’s (DPR) has three main components, each of which differs in important ways from (BE).
The first component of Pollock’s (DPR) involves indefinite probabilities. The probability calculus (and the example we discussed above) involves only definite probabilities—probabilities over closed sentences (i.e., propositions). Pollock’s (DPR) theory involves \({\sl nomic\,probability}\) (Pollock 1990) functions \({\bf{prob}}\), which (formally) take open sentences as arguments. For instance, \({\bf{prob}}(Nx \mathbin{|} Px)\) is meaningful in Pollock’s theory, and it denotes “the proportion of physically possible P’s that would be N’s”. So, Pollock is talking about a kind of objective, physical probability, which is indefinite. This differs from the prob’s of (BE) in several respects. First, the prob’s of (BE) are (in some sense) epistemic probabilities. And, while there is disagreement among advocates of (BE) as to whether epistemic probabilities are subjective or objective (see footnote 7), it is clear that prob’s are not physical probabilities. Second, Pollock’s \({\bf{prob}}\)’s are indefinite, while (BE)’s prob’s are definite. This is also important, since both Pollock and the advocates of (BE) want to make inferences about particulars. Pollock will do this via defeasible reasoning from his indefinite, nomic \({\bf{prob}}\)’s (plus definite statements about particulars) to (other) definite statements about particulars. Bayesians will do this via direct appeals to definite probabalistic “facts”. Finally, Pollock’s indefinite \({\bf{prob}}\)abilities formally differ from (PC)’s prob’s in various ways. Pollock has developed a sophisticated formal theory of \({\bf{prob}}\), as well as some ingenious computer programs for calculating and proving general claims about \({\bf{prob}}\)’s. Unfortunately, I don’t have the space to discuss any of that formal work here.Footnote 13 Next, I will illustrate how Pollock’s (DPR) approach differs from (BE) on our example above. But, first, I need to mention the other two components of Pollock’s theory of defeasible probabilistic reasoning.
The second component of Pollock’s (DPR) will require some account of how we can come to know the (true) values of (or, at least, ranges of values of or inequalities involving) salient nomic probabilities. Among other things, this will have to give us some grip on how we might come to know something about the “true proportionality function ρ over nomologically possible worlds”. I put this locution in quotation marks, because I am rather skeptical that there are such proportionality functions, and/or that we can come to know what they are. But, because my space is limited here, I won’t be able to get into the (rather extensive) metaphysical and epistemological worries I have about “proportions of nomologically possible worlds”-talk. Pollock does have a lot to say about this second component. And, I refer the interested reader to his 1990 book on nomic probability (Pollock 1990).
The third component (and the most salient one for my purposes here) of Pollock’s (DPR) involves \({\sl principles\,of\,defeasible\,reasoning}\) from facts about particulars + facts about nomic probabilities to further facts about particulars. Pollock discusses various principles of this kind throughout his work on nomic probability. I will focus on just one of these, which is central to his approach—the so-called statistical syllogism (SS). Pollock gives various formulations of (SS) in his work. I will use the following formulation from the book (Pollock 2006, p. 235), which is most convenient for my purposes:
-
(SS)
If F is projectible with respect to G and r > 0.5, then “\(Gc \mathbin{\&} {\bf{prob}}(Fx \mathbin{|} Gx) \ge r\)” is a defeasible reason for believing “Fc”, the strength of the reason depending upon the value of r.
Let’s apply (SS) to our example above, where we will just take the description of Jim, the disease, and the test as part of our background knowledge. Then, I presume, we have a case in which we ought to be able to apply (SS). First, I presume that our background knowledge will (somehow) allow us to know the salient nomic probability \({\bf{prob}}(Nx \mathbin{|} Px)\). Specifically, I presume (and hope) it turns out that we can know that \({\bf{prob}}(Nx \mathbin{|} Px) > 0.5\). Indeed, I presume (and hope) it turns out that we can know this nomic probability is around 0.9 in the example at hand.Footnote 14 Then, it seems to me that (SS) should imply the following, in our example (since I take it we have projectibility here as well):
-
(17)
Pa is a defeasible reason to believe Na (given what we know about the example in question). Moreover, Pa is a strong (defeasible) reason to believe Na (and we can make it as strong a reason as we like, just by turning-up the numbers in our background story about the case).
On its face, (17) suggests that a positive test result from a highly reliable test provides an (arbitrarily) strong reason to believe that the disease is absent. Footnote 15 I find that counter-intuitive. And, I think the story that advocates of (BE) tell about confirms f versus confirms i furnishes a pretty plausible explanation of why (17) sounds counter-intuitive. Moreover, as far as I can tell, Pollock’s (DPR)-theory doesn’t have any obvious way of explaining what’s going on here. It sounds wrong (to my ear) to say that Pa does support Na, but that this support is somehow defeated by something else. On the contrary, it seems to me that Pa (defeasibly) counter-supports Na in this context.
I wish I had more space to discuss other aspects of Pollock’s (DPR) theory, not to mention his theory of “causal probability” and his new approach to decision theory. There is just a ton of really interesting and novel stuff in this book. And, there is also a lot of neat stuff “under the hood” that isn’t (explicitly) discussed in the book (e.g., some very powerful and ingenious computer programs for calculating and proving general claims about the sorts of probabilities Pollock has in mind). Working through Thinking About Acting was challenging and edifying. I highly recommend it to anyone interested in decision theory, probability, epistemology and/or various other related fields. The only bad thing about this book is that it’s the last one John Pollock had the opportunity to write.
Notes
I regret that I will not have a chance here to discuss Pollock’s theory of “causal probability” (and its application to “causal decision theory”), which is one of the newest (and most exciting) ideas in the book. And, I’m sad that I won’t get to talk to John about any of my queries. I’m sure he would have had many illuminating answers. He always did.
Strictly speaking, Kolmogorov gives a set-theoretic, and not a logical axiomatization of (PC). But, one can give an (extensionally) equivalent logical axiomatization. See Fitelson (2008, Sect. 1) for an axiomatization of (PC) that is along these lines.
Pollock is in good company here. Skyrms’s (1999, Chap. 6) axiomatization has exactly the same deficiency. I owe this counterexample to Skyrms’s (and Pollock’s) theory to Mike Titelbaum. As Carnap (1962, p. 341) notes, it is surprisingly easy to give equivalent-looking axioms for (PC), which are non-equivalent. This happens a lot in the literature on (PC).
A bit later in the text, Pollock discusses a related logical impoverishment of (PC), and he complains that it is a shortcoming. On page 108, Pollock rightly points out that (PC) does not say anything (systematically) about probabilities over open first-order sentences. This is true, of course. But, something much stronger is true—namely that (PC) doesn’t say anything (systematically) about \({\bf \sc {prob}}\)abilities over anything other than sentential languages \({\mathcal{L}}.\)
Having conceded this point, it is worth mentioning that this problem is far less pressing than the problem Pollock has in mind—which would saddle proponents of (BE) with the commitment to assign probability 1 to all necessary truths. The main point I want to get across here is that proponents of (BE) have the theoretical tools to distinguish various “levels” of ideal epistemic rationality. As such, their framework is not as hopeless as Pollock makes it sound.
This is only a necessary condition for prob-validity, which is why it is not suitable as a definition (Adams 1975, p. 57).
I haven’t said anything yet about the interpretation of prob. This is intentional. It seems to me that Pollock’s objections are not restricted to (say) subjective (BE). Rather, he’s taking on just about any kind of probabilistic reduction of \({\sc{dj}}\) or \({\bf{\sc{dw}}}\). I presume this would include non-subjective probabilists about evidential support, such as Carnap (1962), Williamson (2000), and Keynes (1921), as well as subjective (BE)—ers, such as Skyrms (1999), Joyce (2009), and others. I’ll return to this issue in Sect. 2. But, in the meantime, I will assume that prob is whatever probability function a particular advocate of (BE) has in mind. This will vary, but in a way that is orthogonal to this line of Pollock’s objections.
Of course, I do not mean to endorse (13), nor do I mean to saddle the proponent of (BE) with it. I am only introducing it here for dialectical purposes—to bring out what I think is an exaggeration in Pollock’s objection to (BE).
Various commentators have recently come to the view that →-MP isn’t even deductively valid (McGee 1985; Kolodny et al. 2009). I will put that controversy to one side here, and I will suppose that modus ponens is deductively valid for the indicative conditional. But, it is worth noting that, if these commentators are right, then “blind deductive →-MP reasoning” would not be kosher. I think that would undermine Pollock’s dialectical position vis-a-vis (BE). But, I can’t go into that here.
As I explained in footnote 7, I am remaining as neutral as possible on the interpretation of prob here. I will return to this issue in Sect. 2. In this example, I think the probabilistic “facts” I cite are robust across various interpretations of prob. And, I think I’m not doing any harm here to Pollock’s usage of prob for definite probabilities.
White (2006, Sect. 5) seems to assume something like (16) in his Bayesian criticism of epistemic dogmatism. Williamson (2000, Chaps. 9 and 10) seems to require some probabilistic relevance in his account of “justification”. And, Shogenji (2009) defends a precise, probabilistic theory of \({\sc {dj}},\) according to which \({\sc {dj}}\) is not a confirms f -function (i.e., not a conditional prob function), but rather a confirms i –function. I’m inclined to think that that a proper Bayesian theory of \({\sc {dj}}\) (if there be such) will have to be sensitive to both firmness and increase in firmness considerations.
Note that we can make prob \((Na \mathbin{|} Pa \mathbin{\&} K)\) as high as we like, just by fiddling with the numbers specified in K.
Pollock has made a lot of progress on the formal/computational side of his theory since the book was written. I have had the pleasure of reading a more recent manuscript (Pollock 2009), which develops the formal side in much more detail and generality. I have also benefited from a very edifying email correspondence with John about his quite extensive and impressive computational work on \({\bf{prob}}\), and its relation to my recent computational work on prob (Fitelson 2008).
Here, I mean only to assume some uncontroversial direct inference principle from what we take to be the salient sorts of objective probabilities in the context at hand. One might object that the kinds of (statistical) probabilities at work in the present example aren’t nomic probabilities (in Pollock’s sense). But, one can strengthen the present (statistical) example by adapting it to a case in which one property is nomologically necessary for another. For instance, we could let Px
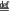
x has stage one syphilis, and Nx
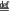
x does not develop paresis (Scriven 1959, p. 480). I presume that the salient nomic probabilities in such an example would have the same sort of structure I have in mind for the simpler (statistical) case I am discussing here [and it would more clearly involve a case of (projectible) nomic probabilities].
Or, in the syphilis/paresis variation of the example (see footnote 14), that the presence of stage one syphilis in a patient is a (arbitrarily strong) reason to believe that the patient will not develop paresis.
References
Adams, E. (1975). The logic of conditionals. Dordrecht: D. Reidel.
Adams, E. (1996). Four probability-preserving properties of inferences. Journal of Philosophical Logic, 25(1), 1–24.
Bennett, J. (2003). A philosophical guide to conditionals. New York: Oxford University Press.
Carnap, R. (1962). Logical foundations of probability (2nd ed.). Chicago: University of Chicago Press.
Edgington, D. (1995). On conditionals. Mind, 104(414), 235–329.
Fitelson, B. (2008). A decision procedure for probability calculus with applications. Review of Symbolic Logic, 1(1), 111–125.
Garber, D. (1983). Old evidence and logical omniscience in Bayesian confirmation theory. In J. Earman (Ed.), Testing scientific theories. Minnesota studies in the philosophy of science (Vol. 10). Minneapolis: University of Minnesota Press.
Hailperin, T. (1996). Sentential probability logic. Bethlehem: Lehigh University Press.
Joyce, J. (2009). Accuracy and coherence: Prospects for an alethic epistemology of partial belief. In F. Huber & C. Schmidt-Petri (Eds.), Degrees of belief. New York: Springer.
Keynes, J. M. (1921). A treatise on probability. London: Macmillan.
Kolmogorov, A. N. (1956). Foundations of probability theory. New York: Chelsea.
Kolodny, N., & MacFarlane, J. (2009). Ifs and oughts. Unpublished manuscript.
McGee, V. (1985). A counterexample to modus ponens. Journal of Philosophy, LXXXII(9), 462–471.
Pollock, J. (1990). Nomic probability and the foundations of induction. New York: Oxford University Press.
Pollock, J. (2006). Thinking about acting. New York: Oxford University Press.
Pollock, J. (2009). Probable probabilities. Unpublished manuscript.
Scriven, M. (1959). Explanation and prediction in evolutionary theory. Science, 130(3374), 477–482.
Shogenji, T. (2009). The degree of epistemic justification and the conjunction fallacy. Synthese (to appear).
Skyrms, B. (1999). Choice and chance: An introduction to inductive logic (4th ed.). Belmont, CA: Wadsworth.
White, R. (2006). Problems for dogmatism. Philosophical Studies, 131(5), 525–557.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Fitelson, B. Pollock on probability in epistemology. Philos Stud 148, 455–465 (2010). https://doi.org/10.1007/s11098-009-9492-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-009-9492-5