Behaviour and the Origin of Organisms

Abstract

It is common in origins of life research to view the first stages of life as the passive result of particular environmental conditions. This paper considers the alternative possibility: that the antecedents of life were already actively regulating their environment to maintain the conditions necessary for their own persistence. In support of this proposal, we describe ‘viability-based behaviour’: a way that simple entities can adaptively regulate their environment in response to their health, and in so doing, increase the likelihood of their survival. Drawing on empirical investigations of simple self-preserving abiological systems, we argue that these viability-based behaviours are simple enough to precede neo-Darwinian evolution. We also explain how their operation can reduce the demanding requirements that mainstream theories place upon the environment(s) in which life emerged.

Introduction

For decades, the primary goal in origins of life research has been to identify environmental conditions under which the molecular precursors of life might have emerged. Particular emphasis has been placed upon understanding how ‘information molecules’ like RNA emerged, and a key underlying assumption has been that once these molecules were in place and replicating, evolution drove an increase in complexity and sophistication, eventually resulting in life as we know it today.

This approach (drawn in schematic in Fig. 1A) sees the first stages of life as the passive result of an evolutionary optimization process rather than as agents capable of action. Interestingly however, a variety of simple abiotic systems demonstrate surprisingly organism-like behaviours (Hanczyc 2014; Kondepudi et al. 2015). As described in detail below, these systems accomplish basic forms of self-preservation, using movement or other mechanisms to change their interaction with their local environment in an adaptive manner that extends their own operation (Lamarck, Spalding and Baldwin also advocated behaviour, especially movement, as a driver of evolutionary change—see e.g., (Burkhardt Jr. 2013)).

We will call these systems ante-organisms (meaning “before organisms”) as they are organism-like in their behaviour and yet simple enough to have existed before genetic evolution. Inspired by these systems, we suggest that behaviour might have already played a role at the very earliest stages of the emergence of life. Even before the operation of gene-based evolution, the antecedents of life could already have been actively choosing or regulating their environment to maintain the conditions necessary for their persistence.

To be clear: it has already been suggested that over long time scales, the earliest forms of life modified their (global or regional) environment. This paper focuses upon a different kind of environmental regulation that we call ‘viability-based behaviour.’ As we explain in detail below, viability-based behaviour (unlike other forms of environmental regulation) (i) is accomplished by an individual rather than a population of individuals, and (ii) is a response to the viability or ‘health’ of an individual.

Fig. 1

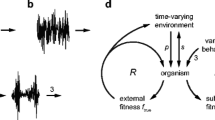
A The conventional perspective on the origin of life starts with an environment that produces an evolving chemical system. Environmental selection pressures eventually result in modern organisms. B The alternative ‘interactional’ perspective explored in this paper recognises the possibility of ‘ante-organisms’ (pre-evolutionary antecedents of life that are capable of selecting and/or modifying their environment and likely some form of basic replication) and that these actions could have facilitated the emergence of more sophisticated forms of life. We distinguish between ante-organisms: life-like systems that are capable of self-preserving behaviour; proto-organisms that are additionally capable of gene-based Darwinian evolution, but possibly lacking some feature found in all modern organisms; and full-fledged organisms

Early Life Could have Regulated its Own Environmental Conditions

Diverse environments have been proposed for cradling the emergence of life—which is itself a difficult thing to define (Cornish-Bowden and Cárdenas 2020, 2022). These include deep sea vents (Barge et al. 2017), hot springs (Damer and Deamer 2020), and extra-terrestrial locations (Kawaguchi 2019). These proposed ‘cradle environments’ are generally seen as existing and operating independently of any life that might develop within them (Fig. 1A). In other words, the environment where life formed just happened to provide all of the conditions necessary for life to emerge.

These required conditions are highly demanding. For life to emerge, conventional theory requires the cradle environments to have:

• (i) supported basic chemical evolution, i.e., to have provided the basic resources and conditions necessary for linear polymerization of informational template molecules, and the heritable replication of those molecules;

• (ii) made possible the emergence of complexity by preventing overly simple evolutionary optima, e.g., due to domination by short, fast-replicating non-contributing ‘parasite’ replicators (Mills et al. 1967; Breaker and Joyce 1994; Fontana and Buss 1994; Ostrowski et al. 2007), or the error catastrophe of an excessive mutation rate (Eigen and Schuster 1977, 2012);

• (iii) provided selection pressures that induced the evolutionary emergence of the functional diversity absent in evolving chemistry but found in organisms (Moreno and Ruiz-Mirazo 2009); here we refer to adaptations in domains other than chemical kinetic rates; e.g., selective boundaries (Piedrafita et al. 2017; Ruiz-Mirazo et al. 2017) or motility (Hanczyc 2011; Froese et al. 2014);

• (iv) provided the materials and energy necessary for operation of any evolved functionality; and

• (v) persisted without interruption, for sufficiently long for complex molecular functions to evolve.

Each of these requirements imposes significant constraints upon what kinds of environment could cradle the emergence of life, but if the earliest forms of life could adaptively regulate aspects of their environment (Fig. 1B), then we need not rely so heavily upon the lucky serendipitous production and maintenance of these conditions. As we shall explain, simple feedback mechanisms can indeed accomplish such regulation and can do so in a manner that responds adaptively to the dynamic needs of the emerging life.

The claim that before evolution, systems could regulate their environment in a self-preserving manner, is not as radical as it might first appear. Non-living phenomena participate in basic forms of negative feedback which regulate their surroundings in such a way that causes them to exist for a longer duration or in a broader set of conditions than would otherwise be possible. A simple example involves glacial ice. Ice has a high albedo compared to land or ocean, reflecting a greater amount of thermal energy back into space. The more ice there is, the cooler its surroundings will be, making more likely the persistence of ice. Ice thus plays a role in maintaining the conditions necessary for its own persistence. We explore below how the first forms of life might have similarly regulated their own environment in ways that increased their chances of survival.

Early Self-Preserving Behaviours May Have Facilitated the Origin of Organisms

Researchers have identified plausible mechanisms for prebiotic synthesis of biologically-relevant molecules (Powner et al. 2009; Ritson and Sutherland 2012; Xu et al. 2018), but it remains unclear how these molecules could have self-organised into integrated organisms (Szostak et al. 2001; Stewart 2019), with some suggesting that this is the central challenge in origins of life research (Piedrafita et al. 2017).

The received theory proposes that evolving chemistry (i.e., RNA-like molecules undergoing mutation and selection) developed into evolving organisms (self-preserving, integrated systems with diverse functionalities such as metabolism, compartmentalization, self-division, motility, etc.). Experiments have shown that evolving chemistry readily adapts to selection pressures, but the evolutionary transformation of autocatalytic chemical reaction networks into integrated organisms is not easily explained. In particular, transitioning from evolving autocatalytic chemistry to organism entails a tremendous increase in complexity. But unfortunately complexity does not easily accrue in evolving chemical systems, where shorter (i.e., simpler) RNA-like template molecules replicate more quickly and thus out-compete longer templates (Mills et al. 1967; Kacian et al. 1972; Breaker and Joyce 1994), impeding complexification. Certain conditions can help to resist the invasion of these ‘parasitic’ short molecules (Szathmáry and Demeter 1987; Hanczyc and Dorit 1998; Ichihashi et al. 2013; Szathmáry and Demeter 1987; Matsumura et al. 2016). Even so, the accrual of diverse and integrated organism-level functionalities, each with its own requirements for operation, is not something that we can simply assume to be the inevitable outcome of evolving template chemistry.

We propose that the viability-based behaviour of ante-organisms might help us understand the emergence of organisms. A key idea within our proposal is that organism-like entities capable of self-preserving behaviours are simple enough to have appeared independently of genetic evolution. To argue this, we start by describing the self-preserving behaviours of four systems that exemplify the properties of ante-organisms (“The Self‑Preserving Behaviours of Ante‑Organisms” section). We do not claim that any particular one of the examples played a role in the origin of life. Instead, we observe that the behaviours of each of these systems is driven by a shared structure or mechanism which we call ‘viability-based behaviour’ and that this mechanism is simple enough to have existed before gene-based evolution. In “Behaviour that Responds to Viability: A Common Structure Underlying the Self‑preserving Behaviours of Ante‑Organisms” section we explain viability-based behaviour in detail before describing the evolutionary and adaptive benefits that it confers (“The Benefits of Viability‑Based Behaviour” section).

The Self-Preserving Behaviours of Ante-Organisms

In this section, we describe four non-biological systems that demonstrate self-preserving behaviours: reaction-diffusion ‘spots,’ motile oil-droplets, ramified charge-transportation networks, and Bénard convection cells (Fig. 2). Each of these systems moves, or reconfigures itself in a manner that changes its environment (e.g., by moving to a different location) or changes the way that it interacts with its environment, and does so in a way that increases the likelihood of its persistence.

In order to talk about self-preservation, we need to consider systems that can stop persisting if they are sufficiently disrupted; that is, systems that exhibit a loose analog of death. Following (Beer and Di Paolo 2023; Di Paolo 2009; Froese 2017; Virgo 2011) we call such systems precarious, and we will see several examples below. A counterexample would be a standing wave, which will reappear no matter how strongly it is perturbed.

Fig. 2

Abiotic self-preserving regulation of environmental conditions. A Motile oil droplets (Hanczyc and Ikegami 2010). B Ramified charge-transportation networks (Kondepudi et al. 2015). C Bénard convection cells. D reaction-diffusion spots (Pearson 1993)

Reaction-diffusion ‘spots’ are dissipative structures that form in the 2D Gray-Scott/Pearson reaction-diffusion model (Gray and Scott 1983, 1984, 1985; Pearson 1993). In this model, an autocatalyst, V, transforms a precursor or ‘food’ molecule, U, into more of itself:

$$\begin{aligned} 2V + U \rightarrow 3V \end{aligned}$$

(1)

Both reactants diffuse through a 2 dimensional space and with appropriate parameter settings, precarious, self-sustaining individual ‘spots’ (regions of high V concentration) emerge and persist indefinitely (see Fig. 2D).

Fig. 3

A common mechanistic structure that accomplished life-like self-preserving behaviour. A Various abiotic dissipative structures, when placed in an environment that contributes asymmetrically to their constituent order-maintaining processes, will move, grow or otherwise reorient to their environment in a way that improves their short term persistence. B A more sophisticated but related form of this ‘metabolism-based’ behaviour is found in modern organisms such as A. brasilense and E. coli

In every parameter range that we have tested, if a spot is placed on a gradient of U it will move in the direction of increasing U. This happens because the production of V will generally be higher on the side of the spot where U is higher. This causes the spot to grow more quickly on that side than the other. The total size of the spot is limited by the rate at which U can diffuse into the interior of the spot and so as the spot grows on one side, it ‘dies off’ (the concentration of V approaches 0) on the side where there is less U. The asymmetric growth and degradation of the spot cause it to effectively move up the U gradient.

A schematic of this motion is provided in the first row of Fig. 3. The initially circular spot (1st column) is situated on a gradient (2nd column) that contributes asymmetrically to the growth of the spot (more at the top than at the bottom). This causes growth at the top, but because the dynamics tend to maintain the circular shape of the spot, this in turn causes shrinkage at the bottom, and over time the spot moves upwards.¹

It is worth emphasising the direct causal relationship between motion and growth. It is not coincidental that the spot moves towards the higher U conditions that are conducive to its self-maintenance. When motion occurs due to the mechanism described above, it is precisely because U contributes positively to the system’s metabolism (self-producing chemical reactions) that the spot moves towards it. The relationship is causal and not coincidental: if U did not contribute positively to the system’s metabolism, the spot would not climb U gradients. We conjecture that this relationship will be general: given some third species W, a spot will tend to move in the direction of increasing W if increasing W accelerates its metabolic self-production, unless there are other interactions that cancel this motion out. As such, we have an autocatalytic reaction that ‘acts to satisfy its own needs’ in the sense that it moves toward environments that are conducive to its persistence. It needs ‘food’ in the form of U and this causes it to move towards local conditions that have higher concentrations of U. Note that this does not imply that the spot always does the best thing for its survival. Figuratively speaking, a region of high-concentration of U might be where some catastrophic event is about to happen—a lightning strike or equivalent. The self-preserving behaviour we are describing is only in response to immediate and local environmental effects.

For some, the causal description above may be concerning as it invokes notions of agency. Different people may have different views on where to draw the line defining fully agential behaviour from lesser versions of agency and there remain fascinating open questions about the legitimacy and utility of both straightforward and metaphorical “agential thinking” in biology (Veit 2021; Okasha 2018). Just as ante-organisms or proto-organisms can be taken as having some, but not all, the properties of full-fledged organisms, they can be taken as having some, but not all, the properties of full-fledged agents. In any case, the discussion here is agnostic on where to draw that line, and whether any such clear line exists (Parke 2023). That said, a recurring theme in this paper is the relationship between different explanations of the same scenario. “Charles entered the shop to buy an ice-cream” can be a complete and accurate description of what happened, without any mention of underlying physics or chemistry; but this level of description is only appropriate in the context of intentional agents. The same events might alternatively be described completely and accurately within the language of physics and chemistry, of movements and molecules—in which case, the concept of intentionality has no place. In most everyday contexts the ‘to buy an ice-cream’ explanation is the practical and useful description for people’s behaviour; just occasionally a physical explanation supervenes (e.g. ‘the wind pushed Charles into the shop’).

The concepts of ‘survival’ or ‘viability’ are not valid terms within physics and chemistry, but are perhaps stepping stones towards a concept of intentionality. The origin of life can be directly related to the potential for a new way of describing events. What we are doing here is outlining how such an intentional level of description can be related to an underlying physical description consistently and without contradictions.

So when we say, e.g., “It is precisely because U contributes positively to the system’s metabolism (self-producing chemical reactions) that the spot moves towards it” the ‘because’ does not refer to (specifically and solely) causation in (1) the underlying physics; likewise it does not refer to (specifically and solely) causation in terms of (2) some behavioural level of description. The ‘because’ here refers to a third, intermediate level of description, one that relates (1) and (2) to each other.

We can consider a hypothetical scenario where U inhibits V’s autocatalysis instead of accelerating it. In this case U is not good for the viability of the spot (a high-level observation as ‘viability’ does not exist at the level of chemistry or physics). It also follows that if that were the case, the droplet would shrink (not grow) at the top, where U is high in concentration. This would stop the causal chain described above in its very first step, and the spot would not move up the U gradient—a set of ‘low level’ physics/chemistry observations. The way that systems like this are organised allows us to relate these different levels of description to each other.

In other models with a similar relationship between movement and autocatalytic growth it has been shown that this kind of behaviour can (i) drive motion back and forth between two spatially-separated resources (Egbert et al. 2009); (ii) drive action-selection-like behaviours where the moving entity effectively prioritizes the diverse effects of its environment upon its self-production (Egbert et al. 2010); and (iii) compete with other dissipative structures (convection cells) for a common essential resource: thermal energy (Bartlett and Bullock 2015).²

These kinds of results are not limited to computational simulations. In the real world, chemistry on the surface of motile oil droplets has shown a similar ability to move itself towards those conditions that allow that active surface chemistry to persist.³ In some cases, the motility of droplets is due to environmental patterning (Chaudhury and Whitesides 1992) or forces due to external gradients (Cejkova et al. 2014). These systems are more akin to a rock rolling down a hill than a precarious individual ‘agent’ that is taking action. However, other droplet systems (Hanczyc et al. 2007; Toyota et al. 2009) carry their own ‘fuel’ in the form of a chemical potential, which they use to move towards conditions that facilitate subsequent movement—allowing the droplet surface chemistry to postpone equilibrium (of surface chemistry and droplet motion). These motile oil droplets work as follows:

• 1. A reaction takes place at the interface between the oil droplet and its aqueous environment that causes a change in surface tension. Random variation or differences in the environment can cause this change to be distributed asymmetrically across the surface of the droplet.

• 2. Marangoni flow causes material to move along the droplet’s interface, to equilibriate the asymmetrical surface tension. When this flow is strong enough, it is sufficient to drive a convective flow that moves the droplet through its aqueous environment due to viscous friction (1st column, 2nd row in Fig. 3).

• 3. Environmental factors contribute to the efficacy of the reaction that produces the Marangoni instability. For instance, the reaction occurs more rapidly in highly alkaline conditions. Accordingly, when the droplet is placed on a pH gradient the convection flow tends to orient toward more alkaline conditions for reasons that are similar to those just described in the reaction-diffusion system: the more alkaline conditions (bigger stars in the third column of the second row of Fig. 3) produce a stronger local difference in surface tension (Marangoni instability) than the more acidic conditions (smaller stars, same figure).

• 4. This creates greater surface tension on one side of the droplet, causing the convection flow to reorient such that the droplet moves toward environments that are more conducive to the operation of the motion-producing reaction.

These droplets move toward high pH conditions not thanks to some coincidence, and not because an evolutionary process has selected for a particular persistence-prolonging relationship between an environmental feature (high pH) and a response to it (taxis). The droplet moves towards particular environments precisely because those conditions better support the metabolism-like reaction that produces and sustains the dissipative structure. This is what we mean when we call the behaviour in these systems ’self-preserving’ — the resulting behavioural mechanism increases the likelihood of that mechanism persisting.

Similar mechanisms underlie the movements of ‘ramified charge-transportation networks.’ These are tree- or wire-like structures that self-organize when high-voltage gradients are applied to a collection of ball bearings that are partially submerged in oil (Kondepudi et al. 2015; Jun and Hübler 2005). The structures that form orient themselves towards voltage gradients in ways that increase the dissipation of energy and strengthen the structures against perturbations. When a voltage gradient is stronger in one area of a petri dish (third column, third row of Fig. 3) the self-organising ‘wire’ reorients to span that gradient (fourth column). A video showing this behaviour is available here: https://youtu.be/ZcMGjhusetM. And preliminary simulations suggest that Bénard convection cells—patterns of convective motion that appear in fluids when there is a sufficient thermal differential between the bottom and top of the fluid (Koschmieder 1974)—also move toward regions with greater thermal differential—see https://youtube.com/shorts/UHjIVBmDtI4.

To reiterate: we are not suggesting that any one of these systems was, in fact, an ante-organism that preceded life as we know it. Rather, they are diverse examples of systems that are not living organisms, but that manifest precisely the sort of self-preserving behaviour we are focusing on here.

It is also worth emphasising that other forms of viability-based abiotic self-preservation are also possible. In fact, subject to very broad conditions, any effect an agent has on a local variable crucial to its viability can only have the effect of increasing (or in the worst case: leaving unchanged) the feasible range of external forcing factors that allow such an agent to remain viable. In this sense of feasibility, any local effect that an agent has can only serve to improve its lot (or leave it unchanged) and never worsens it; a basic form of homeostasis that needs no adaptive or evolutionary explanation. This counterintuitive claim was first developed (Harvey 2018, 2019) in the context of Daisyworld models and Lovelock’s Gaia Hypothesis (Watson and Lovelock 1983) and is explained in detail in the appendices, via (i) a toy example that considers how an icecap, via its influence upon its environment, expands the range of driving forces in which it (the icecap) can persist; (ii) Matlab code for simulating this system; and (iii) a proof generalising the claim to a wide class of dynamical systems.

Consider any system of interacting forces (assumed to be well-behaved in that variables change smoothly and continuously) that has reached a state of stable equilibrium. Then by the definition of ‘stability’ any small temporary perturbation—from wherever it comes—will provoke a resetting internal response that tends towards restoring the original equilibrium. A more permanent perturbation might of course be so big as to pass some tipping point and radically change or ‘destroy’ the system. But if it is small enough to merely shift the system to a nearby new equilibrium point, it must thereby make that resetting change of internal forces more permanent. This truism underlies Le Chatelier’s Principle (Atkins and De Paula 2013; Le Chatelier and Boudouard 1898) and likewise underlies the model presented here.

Each system described above changes its environment. The motile oil-droplet changes its environment from a low pH environment to one that is higher by moving up the pH gradient. The reaction-diffusion spot similarly increases the concentration of U in its environment by moving itself up a U gradient. The ramified charge-transportation network ‘wire’ changes its environment to one where there is a greater voltage gradient by reconfiguring itself to span the shorter gap between electrodes, etc. Each of these environmental changes is not random, but (as described above and elaborated upon below) is a response to the different ways that the local environment affects each system’s ‘metabolic’ process of self-maintenance. For this reason we speak about these processes as ‘regulating the environment’ and not just a ‘change’ or ‘movement.’ Each ante-organism does not just passively take advantage of its environment—the way that a sea anemone might benefit from nutrients being carried past in a current—but instead responds to how local environmental conditions are affecting its self-stabilizing, ‘metabolic’ processes, and moves toward (or in some other way selects) the environmental conditions that are better for these processes.

Behaviour that Responds to Viability: A Common Structure Underlying the Self-Preserving Behaviours of Ante-Organisms

The first four ante-organisms (reaction-diffusion spots, motile oil droplets, ramified charge-transportation networks, and Bénard convection cells) share a basic essential form: each of their behaviours is in response to system viability. To explain, each is a far-from-equilibrium dissipative structure (Nicolis and Prigogine 1989) whose ‘metabolism’ (i.e., energy-dissipating, structure-producing processes of self-construction) is distributed spatially (Fig. 3A). The self-production of each dissipative structure is distributed non-uniformly because certain regions of metabolic activity are better supported by their environment than others. In these regions, the dissipative structure is re-grown or replaced more quickly and so is more robust and more likely to persist relative to the other portions of the structure. Also because the metabolism operates more effectively in these ‘healthier’ or ‘more viable’ regions, each dissipative structure tends to grow or orient itself toward the local environment that better supports its metabolism.

We would like to emphasize that the relationship between each system’s behaviour and its spatially distributed viability is causal: i.e., that the behaviour of each system is asymmetric precisely because the distribution of the viability of the system is asymmetric. To further explain, recall that the motile oil droplet’s motion-producing chemistry operates more efficiently at higher pH. The motile oil droplet moves toward high pH not because it is high pH, but because high pH is more conducive to the motion-producing surface chemistry. If the effects of acidity were inverted such that low pH (instead of high pH) accelerated the reaction, with nothing else changed, the behaviour would change to accommodate the changed ideal operating conditions—the motile oil droplet would start moving toward low pH conditions instead of high ones. The viability-defining processes are causally linked with the behaviour-generating processes (see Barandiaran and Egbert 2013). The situation is similar, but not identical in the icecap system. An icecap is not a dissipative structure, but there nevertheless remains a causal relationship between its viability (icecap size) and its (cooling) influence upon its environment, whereby the larger the icecap is, the greater it cools its environment, expanding its feasible range of survivable external forcing factors.

The Benefits of Viability-Based Behaviour

When we think about behaviour, we tend to think of it as a response to the environment rather than a response to viability. The distinction between responding-directly-to-environment and responding-to-viability has been considered in depth in the study of bacterial chemotaxis. Researchers have investigated whether chemotaxis is ‘metabolism-independent,’ i.e., driven by a response to the presence of particular molecules in the bacterium’s environment, or ‘metabolism-dependent’, i.e., driven by a response to the state or efficacy of the bacterium’s metabolic self-construction (see Fig. 4). The strategy employed depends upon the species of bacteria (Adler 1969; Alexandre et al. 2000) and upon the attractant (Adler 1969; Taylor and Zhulin 1998), with some species employing a mixture of both metabolism-dependent and metabolism-independent strategies.

Fig. 4

An anthropomorphic simplification that contrasts metabolism-independent and metabolism-based behaviours. In the first case, the choice of action is a function of the environment; in the second case, it is a function of the efficacy of the bacterium’s metabolism. Adapted from Fig. 2 in (Egbert et al. 2010)

The ante-organism behaviours presented above fall more naturally into the metabolism-dependent category of behaviour as they are all responses to the internal, self-production dynamics rather than being direct responses to the features of the external environment. We now therefore describe some advantages conferred by this particular type of behaviour, with emphasis on advantages that might be relevant in the earliest stages of life—both before and after the emergence of Darwinian evolution. In doing so, we use the term ‘viability-based behaviour’ to refer broadly to behaviours that are responses to the state or efficacy of internal processes of self-production (Egbert et al. 2010, 2011; Egbert 2013; Egbert and Pérez-Mercader 2016). This includes both the metabolism-dependent behaviours of bacteria, but also the behaviours of the abiotic systems described in the previous section.

Viability-Based Behaviours Can Adapt to Environmental Change Improving System Robustness

Viability-based behaviour can prolong survival. When a motile oil droplet is placed in a petri dish it moves toward the pH conditions that facilitate its motion-driving surface chemistry (Hanczyc 2011). When a toxin inhibits the reaction-diffusion spot’s autocatalytic reaction, the spots move away from that toxin (Froese et al. 2014). In both cases, the movement boosts the dissipative structure’s metabolic⁴ processes, and in so doing makes it more likely to persist.

Accordingly, if the antecedents of life employed viability-based behaviour, they could be less reliant upon serendipitous homeostasis of ‘just-right’ environmental conditions. Instead of the classic cradle environment that just so happens to be maintained in a consistent, just-right, lab-like ‘Goldilocks’ condition (comparable to Fig. 5A), we might instead think about the origins of life as occurring in a place with significant local variation in conditions (Fig. 5C). The environmental variety could be navigated (i.e., selected) via viability-based behaviours, moving toward whichever local environmental conditions are best for metabolic operation. Viability-based behaviour would thus allow the performers of such behaviours to survive a greater range of extrinsic changes and perturbations than would otherwise be possible (compare Fig. 5B and D).

It is worth emphasising that we are not proposing to replace a lucky extrinsic regulation of the environment with a lucky intrinsic regulation. Viability-based behaviour is a closed-loop response to a key element of any ante-organism’s persistence—the efficacy of its self-production. Any extrinsic regulation, on the other hand, is open-loop, i.e., operates independently of the ante-organism’s persistence (recall Fig. 1).

When we recognise this, it becomes apparent that entities performing viability-based behaviour can adapt to changes in multiple concurrent environmental factors—e.g., combinations of pH, redox state, temperature, and the presence of metabolic resources and inhibitors, etc.—without having specific sensors for each factor and without any ‘computational’ or clever signal integrating and manipulating machinery. Viability-based behaviour responds to the combined effects of all of the immediate factors that affect metabolic efficacy and it integrates the effects of diverse environmental features into an appropriate, survival-prolonging response.

This response to the environment has been demonstrated in the computational model presented in (Egbert et al. 2010), and the robustness it confers could have increased the environmental diversity in which the earliest forms of (pre-)life could have persisted, thereby facilitating the conditions that allow for more diverse forms of specialization (Egbert et al. 2011).

Fig. 5

Impact of environmental fluctuations with and without viability-based behaviour. In these images the background colour indicates an environmental property, such as pH, and the face indicates a precarious entity whose ideal operating environment is indicated by the colour of the face—here all the same medium shade of gray. In A, a passive entity is operating in ideal environmental conditions, that are serendipitously maintained by extrinsic environmental factors. B The environment changes, and the entity is no longer capable of persisting. We can compare this situation with C, where an ante-organism uses a viability-based behaviour to move to a local region of its environment that is optimal for its self-production. D The environment fluctuates (just as in B, the background becomes darker everywhere), but in this case, the ante-organism can navigate local environmental variation to find conditions in which it can persist

Viability-Based Behaviour Can Adapt to Internal Changes, Increasing Robustness and Evolvability

Viability-based behaviours adapt to changes in the way that a system’s metabolic self-production operates. In this section we explain what this means and how this kind of adaptation to internal change can improve robustness and evolvability.

The idea of adapting to survive environmental change is familiar, but less familiar is the notion of adapting behaviourally to accommodate internal, metabolic change. In modern organisms, metabolisms are transformed when gene-regulatory networks activate or disactivate metabolic pathways (English et al. 2021). Over longer time-scales, processes such as genetic mutations, recombination, and drift also transform metabolic networks. These include quantitative changes (increases in reaction rates) but also qualitative changes when metabolic pathways are created or destroyed. In the earliest stages of life’s emergence, environmental encounters would have similarly transformed proto-metabolisms (i.e., autocatalytic networks) (Fernando and Rowe 2007; Vasas et al. 2012).

These transitions were an important part of the emergence of life in that the first metabolism was presumably primitive and required significant change to become more efficient, robust, and flexible. Whether these changes took place before full-fledged genetic evolution was in place or not, it is reasonable to expect that as these changes took place, the ideal operating conditions for the metabolism also changed.

Fig. 6

Comparison showing how viability-based behaviour allows systems to adapt to changes in their ideal operating environment. A A passive entity is operating in ideal environmental conditions. B The metabolism changes such that its ideal operating conditions (indicated by change in the colour of the face) are not what they previously were. The passive agent (or an agent whose behaviour is metabolism-independent) does nothing differently and finds itself in a (now) sub-optimal environment. The situation is the same in frames C and D except that in this case, the presence of a viability-based behaviour drives motion to a local region of its environment that is locally optimal for the changed metabolism conditions

In mathematical and computational models (Egbert and Pérez-Mercader 2016; Egbert et al. 2010), we have shown that viability-based behaviours (unlike metabolism-independent behaviour and extrinsic environmental regulation) adapt to these kinds of changes. To explain this idea in a simplified form, Fig. 6 compares two situations where a change in a system’s metabolic operation changes its ideal operating conditions. The first row shows a passive entity, where before the metabolic transformation (A), the passive entity happens to be in an environment that matches its needs (the gray of the face matches its local environment). Certain changes in the metabolism’s operation (e.g., caused by rare environmental interactions as discussed in (Fernando and Rowe 2008)) change the system’s ideal environment, and so the entity’s environment no longer matches its metabolic needs (B). The situation is different when a viability-based motility is included (second row). Here, when the ideal environment has changed, the viability-based mechanism moves to the locally optimal conditions for the (changed) metabolism, adapting to the changed metabolic needs (D). Thanks to the viability-based behaviour, this metabolic transformation is survivable and beneficial instead of deadly. Accordingly, entities with viability-based behaviours (unlike passive entities or entities only capable of metabolism-independent behaviours) can adapt (change their behaviour) to accommodate metabolic transformations. This adaptability improves robustness.

In increasing the diversity of metabolisms that can survive, viability-based behaviour may also have implications for evolvability if and when an evolutionary scenario arises. We do not pursue this idea in this paper as the ideas have already been presented in (Egbert and Pérez-Mercader 2016; Egbert et al. 2010, 2011) which use computational and mathematical models to demonstrate how viability-based behaviour can increase robustness; how it can adapt to take advantage of qualitative changes in metabolism, such as the appearance of a new metabolic pathway (e.g., through rare chance environmental interactions as discussed, for example, in (Fernando and Rowe 2008)) that allows for the consumption of a new metabolic resource; and how these forms of adaptation and robustness could influence evolutionary dynamics when full-fledged evolution is in play.

Fig. 7

Viability-based behaviour adapting to the dynamic metabolic needs of a simulated agent and causing it to oscillate between two environments. A When the ante-organism (black circle) has plenty of resource $R_1$, the factor that limits its maximum metabolic rate is $R_2$ and the ante-organism moves toward that resource. B The situation is reversed once the ante-organism has acquired sufficient $R_2$ and it returns to where it came from. The ante-organism thus oscillates between two environments, and by ‘behaviourally-combining’ the two environments in this way, it becomes capable of surviving. See main text and (Egbert et al. 2009) for details

Viability-Based Behaviour Allows Ante-Organisms to Adaptively Utilize Multiple Diverse Environments

In addition to adapting to long-term (evolutionary scale) changes in metabolism, viability-based behaviour can adaptively accommodate short-term metabolic change, such as the depletion of an intermediate metabolite. In previous work (Egbert et al. 2009), we used a computational model to explore this ability of viability-based behaviours. The model worked as follows: an ante-organism is simulated as a disc situated in a 2D environment that contains diffusing metabolic resources. To persist, the ante-organism must produce metabolite Z and to do so, it requires two intermediary metabolites X and Y. Each of these three metabolites spontaneously degrades and so to persist, resources $R_1$ and $R_2$ must be transformed into new metabolites to replace those that have been lost. Metabolite X catalyzes the transformation of $R_1$ into Y and reflexively, Y catalyzes the transformation of $R_2$ into X. The metabolism of the minimal ante-organism is thus summarised by three reactions:

$$\begin{aligned} X + R_1 \rightarrow X + Y \end{aligned}$$

(2)

$$\begin{aligned} Y + R_2 \rightarrow Y + X \end{aligned}$$

(3)

$$\begin{aligned} X + Y \leftrightarrow 2Z \end{aligned}$$

(4)

The resources are spatially distributed and not collocated (see Fig. 7). The ante-organism moves toward whichever side of the disc is producing Z more rapidly. This is a viability-based behaviour that is similar to the behaviour of the reaction-diffusion spots.

Remarkably, this simple system behaviourally integrates distinct environments to support a metabolism that would be impossible to support without motility. Specifically, with no additional control or behavioural mechanism beyond that described above, the ante-organism moves back and forth between the spatially separate resources, allowing it to accumulate the X and Y resources needed for its persistence (Fig. 7). The viability-based behaviour thus behaviourally combines two distinct environments, oscillating back and forth between them, and doing so in a way that is adapting to its dynamic needs (i. e., conditions that best benefit its self-production). If, on its way to $R_2$ a perturbation radically depleted X (or added Y) such that X was the limiting factor and not Y, the ante-organism would reverse direction and head back to $R_1$ as the system’s metabolic ‘needs’ had changed.

As early life accrued and integrated new functionalities, its needs would change, i.e., what would count as a ‘good’ environment would change. Viability-based behaviour adapts behaviourally to accommodate those changing needs, making it possible for a greater variety of early life forms to persist and thus to develop into more complex, organism-like life. It is also interesting to consider this kind of viability-based motion as an alternative to the serendipitous environmental cycling ideas that have received attention in origins of life research (e.g., wet-dry cycles (Becker et al. 2018)). Laboratory conditions for in vitro evolution require regular cycling of rather specific conditions. Such cycling may have been the result of serendipitous environmental fluctuations, but the model just presented shows that viability-based behaviour can drive a form of environmental cycling that responds to the needs of the system as they change.

Behaviour Provides a Platform of Opportunity for Greater Organismic Functional Diversity

In providing a mechanism of action (i.e., a way that ante-organisms can modulate their interaction with their environment), viability-based behaviour makes relevant an additional functional domain in which natural selection can encourage complexification and functional diversification. To explain, first consider basic evolving chemistry. In a minimal template-replication systems, fitness is reducible to the rate of autocatalytic self-production. A moving ante-organism, on the other hand, would be subject to movement-related selection pressures. Changes to the mechanism of motility that affect how quickly or consistently it approaches beneficial environments would increase fitness. These improvements could be faster or more efficient motility, or improved ability to ‘sense’ (i.e., change actions in response to various environmental phenomena). By starting with entities that do things beyond self-replication we also start with a more diverse array of ways to improve.

Along these lines, it is interesting to investigate how basic forms of viability-based behaviour can become more sophisticated. In this vein, Froese et al. (2014) added the production of a waste product and a secondary autocatalytic reaction to the ‘Gray-Scott / Pearson’ reaction diffusion system presented above. The second autocatalytic reaction feeds on the product of the first, so in addition to the reaction described in Eq. 1, the system includes:

$$\begin{aligned} 2W + V \rightarrow 3W \end{aligned}$$

(5)

This reaction might be classified as ‘parasitic’ upon V in that it consumes the metabolic product (V) and so would be expected to decrease the robustness and adaptability of the V-spot. In fact, when the spatial distribution of these reactants and the motility of RD-spots is considered, we find the opposite can be the case—the ‘parasitic’ reaction actually ends up improving the robustness and rate of growth of the more primitive system in several contexts. Let us explain how: as the secondary ‘parasitic’ reactant, W feeds upon the first (V), the viability-based behaviour of the V-spot causes it to move away from the peak concentration of W (for the same reasons as described above in “The Self-Preserving Behaviours of Ante-Organisms” section). At the same time and by way of the same basic mechanism, the viability-based behaviour of the W-spot causes it to climb its resource gradient, i.e., move toward the V-spot. The result is a perpetual and robust cat-and-mouse behaviour whereby the secondary autocatalytic reaction spot is chasing the first.

Interactions between V and W amplify and maintain spatial asymmetry in their concentrations and thereby produce an intrinsic asymmetry—i.e., one that is not based upon or requiring an environmental gradient—that causes the system to move even when it is situated in a uniform environment. This motion often pushes the $V+W$ system into regions where U has not yet been depleted by transformation into V (Eq. 1), increasing exposure to U. This in turn accelerates the growth and reproduction of the RD-spots and their ability to survive certain perturbations. It also causes the spots to more rapidly colonise spaces where there are not yet any spots (Froese et al. 2014). In certain conditions, the presence of a parasitic autocatalytic cycle is not only beneficial but actually necessary for the persistence of its host (Virgo et al. 2013). Finally, it is worth noting that the parasitic ‘tails’ are inherited when spots fission. Individuals bearing a beneficial parasite would have the advantages described above—ability to survive certain perturbations, to more rapidly colonise spaces, etc.—increasing the likelihood that such systems would be present in the prebiotic world.

To avoid misunderstanding, it is worth pointing out that the viability-based behaviour is not a panacea. In certain environments the detriment of W’s consumption of V outweighs the benefit just described. Also, viability-based behaviour only operates at a relatively short (immediate) time scale, causing its enactors to move toward things that are good now, but in some cases may actually accelerate destruction in the longer term.

Nevertheless, this system exemplifies two important ideas. The first is that when present in systems capable of evolving, the impact of viability-based behaviour upon fitness can be greater than the impact of its underlying ‘chemistry’ properties, such as reaction rates. Phenomena that are “detrimental on the metabolic time scale (i.e., a parasitic reaction) can induce novelty on the behavioural time scale (i.e., self-motility), which then turns out to be adaptive on the evolutionary time scale (i.e., faster replication and wider population distribution)” (Froese et al. 2014, p. 69). The second is that basic forms of viability-based behaviour can be improved upon in a wide variety of ways and therefore provide a new domain of potential functional diversity. For evolution to increase complexity, the systems on which it operates (i.e., the things that are evolving) must be capable of a variety of robust forms; i. e., qualitative diversity in the ways that they exist and operate (Moreno and Ruiz-Mirazo 2009)—and it must be possible to transition between the forms of existence in an incremental manner. No doubt, RNA is capable of a variety of forms with functional variation (e. g., ribozymes), but the presence of a viability-based behaviour opens up additional potential function in that its behaviour (e.g., ways of moving) can be improved in a wide variety of ways (e.g., by sensing or responding to different things or integrating those senses in various ways).

Basic evolving template chemistry may, on its own, be incapable of evolving significant functional diversity. Moreno and Ruiz-Mirazo (2009) write that “a special type of self-maintaining organization, arising from the interplay among a set of different endogenously produced constraints (pre-enzymatic catalysts and primitive compartments included), is required for the appearance of functional diversity in the first place. Starting from that point, [natural selection] can progressively lead to new (and, at times, also more complex) organizations that, in turn, provide wider functional variety to be selected for, enlarging in this way the range of action and consequences of the mechanism of [natural selection], in a kind of mutually enhancing effect.”

Viability-based behaviour facilitates the emergence of functional diversity in at least four distinct ways. First, it increases feasibility or system robustness—the ability of ante-organisms to survive a larger range of environments and environmental perturbations or transformations, allowing for a wider variety of organismic forms to persist in a wider variety of environments. Second, it allows ante-organisms to behaviourally compensate for transformations in their own metabolic operation, allowing them to ‘adapt to their own adaptations’ (Egbert and Pérez-Mercader 2016), thereby further increasing the set of robust forms and facilitating transformations between these forms. Third, viability-based behaviour allows individual (ante-)organisms to integrate or combine diverse environments, increasing the number of ways that they can interact with their world and persist. Finally, a system capable of acting is generally capable of improving upon its way of acting in a wide variety of ways. All else being equal, systems that behave (move around, etc.) have a greater variety of ways that they can improve than systems that are not (yet) capable of behaving. They can move around more slowly or quickly, move in response to different environmental factors etc.

Viability-Based Behaviour is Simply Implemented

The benefits of viability-based behaviour would be irrelevant to the origin of life if they required sophisticated or complex mechanisms to operate. But by way of example and evaluation of the underlying mechanisms of some viability-based behaviours, we have shown that this kind of behaviour is very simply implemented—so simply that it can be found in abiological systems. The essential structure involves a precarious system that responds to how well it is managing to persist. It seems to be a relatively common phenomenon, whenever a dissipative structure is situated in an environment that contributes asymmetrically to its ‘metabolic’ processes.

One reason for its simplicity is that unlike most modern behaviour which requires sophisticated sensors for responding to particular environmental features—transmembrane chemoreceptors, eyes, noses, etc.—viability-based behaviour needs only to respond to the system’s own viability. In some cases, this can be accomplished without any explicit ‘sensor’ at all—their action is simply proportional to the efficacy of their self-maintaining ‘metabolic’ processes. An example of this is found in the reaction-diffusion spots, which have no explicit sensors, but whose asymmetrical growth produces a kind of viability-based movement.

Given the relative simplicity of these systems, it seems plausible that similar systems capable of self-sensitive, self-preserving, viability-based behaviours could have existed in a pre-Darwinian world. We don’t propose that any one of the specific examples provided above played a particular role in the history of life—though it is interesting to note that droplet motion can be fueled by plausible prebiotic chemistry (Hanczyc 2011). We more modestly suggest that similar, self-sensitive, self-preserving behaviours will often be found wherever there exists a dissipative structure that is situated in an environment that contributes asymmetrically to its dissipation of energy, and so the existence of similar systems, capable of viability-based behaviours, likely pre-dated Darwinian evolution. The icecap example shows that similar dynamics can be found even in the absence of a dissipative structure. Perhaps the simplicity of viability-based behaviour and the benefits that it might have conferred to early forms of life suggest that we should consider it (and perhaps other forms of behaviour) as playing a role earlier in the history of life than is typically acknowledged in origins of life research.

Conclusions

For more than a century there has been debate as to whether and to what extent various specific biological traits can best be seen as the consequence of generic physical constraints or of Darwinian evolutionary forces (Thompson 1942; Gould and Lewontin 1979; Maynard Smith et al. 1985; Newman and Comper 1990; Goodwin 1994; Arias et al. 2020). The phenomena presented here are different in that they are not the result of neo-Darwinian evolution within a population, despite appearing to be in some senses ‘adaptive’.

Mainstream theory concerning the origin of life posits a ‘cradle’ environment in which life originated. In this paper, we reviewed some of the stringent requirements that that are demanded of this environment, before explaining how the viability-based behaviours of prebiotic organism-like entities (ante-organisms) could help to reduce some of these requirements. In support of this idea, we presented examples of simple, abiological systems that perform viability-based behaviour. We do not claim that any of the specific example systems presented were present at the origin of life, but we do suggest that the mechanisms underlying their behaviours are simple enough to emerge without (i.e., before) neo-Darwinian evolution. As part of this argument, we explained a shared ‘architecture’ underlying the viability-based behaviours of several of the examples, in that each involves a dissipative structure that is situated in an environment that contributes asymmetrically to its metabolism-like energy-dissipating processes.

In developing this perspective, we have worked to draw attention to a major event in the history of life that we believe needs further explication—the emergence of organism-like entities. Current mainstream approaches to understanding the origins of life focus upon how evolvable chemistry could have emerged in a prebiotic world. This approach often assumes that once evolving chemistry was in place, it would inevitably develop into increasingly organism-like life. We question this assumption and see this transition as in need of further consideration. A complete theory of origins of life must explain not only how evolution (evolving template molecules) came to be, but also how evolving organism-like life emerged. In this vein, we speculate that instead of involving a transition from evolving chemistry to evolving organisms, the origin of life might have involved from the outset abiological entities that perform viability-based behaviours (like the examples presented above), and that these “ante-organisms” became more evolvable over time. But even if this radical idea is not appealing to the reader, viability-based behaviours and their benefits may still have played significant roles in the earliest stages of life’s evolution by allowing the earliest forms of life to adapt to changes in their environment and to changes in their own internal operation.

Appendices

Appendix 1

We analyse here a primeval ‘ur-homeostasis’ (Unevolved and Rudimentary) that naturally emerges from systems whose effect on their environment is conditional on their viability. We model an icecap A as the proportion, in [0, 1], of the area of ‘Greenland’ it covers (Fig. 8a). The icecap A is affected by L, some Local environmental variable (here temperature), and in turn the size of A affects L. Given fixed external conditions, A and L will settle down to some finite equilibrium values. L depends on A and two other factors: E the level of solar output, Externally-set; and Q the ice albedo, that reflects or absorbs the sun. E and Q (each in [0, 1]) change slowly enough for A, L to settle to an equilibrium. We define the ‘Feasibility Region’ FR as the range of solar outputs E that allow an icecap to survive indefinitely. We prove FR is minimal when the ice albedo Q equals underlying rock albedo $Q_{\textrm{null}}=0.5$.

Fig. 8

a The icecap occupies a proportion A of the surface of ‘Greenland’. A affects and is affected by L, the local temperature. b L is also affected by E, the solar output, and Q, albedo of ice; this determines a ‘Feasibility Region’ FR of E-values for which an icecap is viable, $A>0$. c Results show FR is minimal when ice albedo is the same grey as the underlying rock; altering ice albedo can increase the FR (e.g. for white ice) but never decrease it (e.g., see the black ice)

Icecap A grows or shrinks (bounded in [0, 1]), depending on whether L is below or above some freezing point (we arbitrarily use $FP=40$; Fig. 8c).

$$\begin{aligned} \frac{dA}{dt} = (40 - L) \textrm{ for } 0<A<1, \textrm{ and } \end{aligned}$$

(6)

$$\begin{aligned} \frac{dA}{dt} = 0 \textrm{ for } A=0 \textrm{ or } A=1 \end{aligned}$$

(7)

The average albedo $Q^{\star } = A \cdot Q + (1-A) \cdot 0.5$ impacts the effect of solar output E on local temperature L. We model this by:

$$\begin{aligned} \frac{dL}{dt} = 100 (1.5 - Q^{\star }) E \end{aligned}$$

(8)

Changes in icecap cover A will change local temperature L, unless ice albedo Q happens to be the same grey ($Q_{\textrm{null}}=0.5$) as the rock. We define the Viability Region of the icecap as the range of local temperature conditions L that prevent the icecap from disappearing, i.e. $L \le FP$.The Feasibility region FR is crucially different: the range of E-values (solar output) for which at least some minimal ($A > 0$) amount of ice cover can survive in equilibrium. Our concept of ur-homeostasis is based on how changes in Q affect this FR(Q).

The simple equations of our toy icecap model ensure that A and Q settle to an equilibrium. The code producing the plot in Fig. 8c is given in Appendix 2. We initiated the search for equilibrium from a maximum value of A, to ensure that when there were multiple equilibria we found the most viable one. A fuller analysis (Harvey 2018, 2019) expands on such issues.

Unsurprisingly the Feasibility Region for white ice is wider than that for grey ice. Intuitively one might expect that if the ice were black it would decrease the feasibility range - but not so. For ice with albedo darker than grey, Fig. 8c indicates the icecap remains feasible with $A > 0$; though dark ice increases local temperature L, this effect withers away as A withers away. So under a range of possible external forces E, $Q = Q_{\textrm{null}}$ gives the minimal Feasibility Range. Any change to Q from this value can only increase FR, never decrease it. The icecap, though not evolved, nevertheless still has this potential resilience to external forces E via effects on a local buffer L, thus primitive ur-homeostasis.

The viability of an icecap in a given context is increased through ice having high albedo (white) and would have been decreased if ice had happened to be black; in this sense such an effect is a random happenstance. The rule for viability under different random effects (such as high or low albedo) is “You Win Some, You Lose Some”. But for feasibility, under different effects, the result is “You Win Some, You Lose None”. In other words, feasibility as defined here is never negatively affected by effects such as high or low albedo of ice.

The icecap model illustrates this in a specific case. In Appendix 3 we generalise this to “For any Q, $FR(Q) \supseteq FR(Q_{\textrm{null}})$” for a wide variety of dynamics systems. This mathematical result can be further generalised to multiple agent-types (Harvey 2018, 2019; Dyke and Weaver 2013). It explains the Daisyworld phenomenon (Watson and Lovelock 1983); despite a widespread assumption that this needs an adaptive or evolutionary explanation (Lenton et al. 2018) this ur-homeostasis requires neither. It is thus relevant as a primitive form of homeostasis applicable to ante-organisms.

Appendix 2

Appendix 3

Using the same symbols as the icecap example, we generalise by defining a broad family of coupled dynamical systems (DS) of 2 variables A and L, parameterised by 2 parameters: E and Q. The ordinary differential equations (ODE) will constrain A, L to each stay within finite bounds [$A_{min}, A_{max}], [L_{min},L_{max} ]; A_{min} = 0$.

(‘Icecap A (with albedo Q) interacts with local temperature L (heated by solar output E).’)

Parameters E, Q remain fixed long enough for A, L to reach a stable steady state (SSS) at values $A^*, L^*$, with A being either ‘viable’ $(A^*>0)$ or ‘non-viable’ $(A^*=0)$. We then shift timescales and consider how the viability of $A^*$ (at SSS of the DS) is dependent on different values for E, Q. For any given Q, we can define a ‘Feasibility Region’ FR(Q) of E-values that support viable $A^*$. We further define a particular $Q = Q_{null}$, that gives uniquely minimal properties to $FR(Q_{null})$.

Most of the work will be setting up these definitions, after which it will be easy to prove:

Theorem: For any Q, $FR(Q) \supseteq FR(Q_{null})$.

(‘If icecap A can survive some E (sun) when its albedo Q is that of rock, then it can for any Q.’)

We define the family of DSs in variables A, L with parameters E, Q by the ODE

$$\begin{aligned} dA/dt = F_1 (A, L) \end{aligned}$$

(9)

$$\begin{aligned} dL/dt = F_2 (E, L, A \cdot Q_{\textrm{effect}}(Q)) \end{aligned}$$

(10)

where $F_1(), F_2()$ are any continuous single-valued functions of their arguments that do not allow A, L to leave the bounding-box in $A-L$ space defined by $[A_{min} , A_{max}], [L_{min} , L_{max} ]$. I.e., for any L in Eq. 9, there is some attractor $A'$ within or at A’s bounds, such that dA/dt is respectively: positive for $A < A'$; zero for $A = A'$; negative for $A > A'$. Likewise for dL/dt in Eq. 10.

$Q_{\textrm{effect}}(Q)$ is any monotonic continuous function of Q with value zero for some $Q = Q_{null}$. A simple example would be $Q_{\textrm{effect}}(Q) = (Q - Q_{null})$. Since A only enters Eq. 10 within the product $A \cdot Q_{\textrm{effect}}( )$, for any given E and L, dL/dt has the same value when $A=0$ as when $Q = Q_{null}$. (‘If either icecap albedo Q = rock albedo $Q_{null}$ or icecap A is at zero, then Q has no effect on local temperature L.’)

We define a Viability Region VR for A as the support of dA/dt when $A = 0$: the set of values of L for which $dA/dt > 0$ when $A = 0$. Alternatively phrased, VR is the set of L for which A is ‘viable’. This may be a range of L values, e.g. $L_{v-lo}< L < L_{v-hi}$ , but more generally may be any potentially disjoint set of L values. We note that VR is independent of parameters Q and E.

Let $A^*$ be the value of A at any SSS of the DS. We define the set of parameters (E, Q) ‘feasible’ if they support at least one SSS with viable $A^*$ (i.e., $A^* > 0$). For any given Q, the ‘Feasibility Region’ FR(Q) is the set of E-values that support a viable $A^*$.

(‘Solar output E and ice albedo Q are feasible if they can support a non-zero icecap A at SSS.’)

The constraints on Eqs. 9 and 10 as specified above allow us to define a Lyapunov function $((dA/dt)^2 + (dL/dt)^2 )$ that tends continuously to zero as A, L follow the trajectories defined by the DS. Hence the DS must have at least one SSS within (or on boundary of) the bounding-box.

A steady state (whether stable or unstable) entails $dA/dt = 0$ and $dL/dt = 0$. This will be true at any intersection of their respective nullclines, that is the set of points such that;

$$\begin{aligned} F_1 (A, L) = 0 \end{aligned}$$

(11)

and

$$\begin{aligned} F_2 (E, L, A \cdot Q_{\textrm{effect}}(Q, Q_{null} )) = 0. \end{aligned}$$

(12)

The continuity and single-valuedness of these equations means that these can be represented as continuous lines in $A-L$ space across the bounding-box between respectively W-and-E and N-and-S sides of this box, (Appendix 3, Fig. 9).

We wish to prove $\forall Q$, $FR(Q) \supseteq FR(Q_{null})$. We show that the existence of any counter-example (a) some $E= E' \in FR(Q_{null})$ and yet (b) $E' \notin FR(Q')$ for some $Q'$, leads to a contradiction.

To assume (a) $E' \in FR(Q_{null})$ implies $(E', Q_{null})$ is feasible and hence there is a SSS at $(A, L, E, Q) = (A^*, L^*, E', Q_{null})$ for some $A=A^* > 0, L=L^*$. $dA/dt = 0$ at this SSS, and the stability of the SSS means $dA/dt > 0$ if $A < A^*$. Hence at $(A, L, E, Q) = (0, L^*, E', Q_{null}), dA/dt > 0$.

But we note from Eqs. 9 and 10, that Q is irrelevant when $A=0$. And hence we can here without consequence set Q to any arbitrary value $Q'$: at $(A, L, E, Q) = (0, L^*, E', Q'), dA/dt > 0$.

To assume (b) $E' \notin FR(Q')$ for some $Q'$ implies that at $(A, L, E, Q) = (0, L^*, E', Q'), dA/dt= 0$. The assumption of both (a) and (b) thus leads to a contradiction, hence our result is proved.

QED: For any $Q, FR(Q) \supseteq FR(Q_{null})$.

Fig. 9

Lines (solid or dotted) represent nullclines (dL/dt=0, dA/dt=0) across the bounding- box. Necessarily they intersect at least once (left box) at steady states of the DS; possibly more (right box) an odd number of times. Stability analysis shows a single steady state will be stable (SSS); multiple steady states will alternate between stable and unstable