Introduction

Studies of the formation and evolution of planetary systems have entered into a new extremely dynamic phase of the development. One of the main reasons for that is the fact that the Solar System is no longer the only planetary system known in our Galaxy. Many other planetary systems have been discovered till now and they are observed at different stages of their evolution. They provide distinct realizations of the same set of processes which were responsible for the formation of our Solar System.

The discovery of extrasolar planetary systems took place when the dynamical structure of our Solar System was relatively well understood. After the work of Copernicus (1543), Kepler (1609, 1619), Galilei (1632) and Newton (1687), it became clear that the observed motion of the objects in our planetary system is a consequence of the gravitational force. Newton showed that the Kepler laws are natural outcomes of the inverse square law of the universal gravitational force. If the Earth would be the only planet going around our Sun then its orbit would be a closed ellipse around the common center of the mass of the system. However, there are also other planets orbiting the Sun, which perturb the trajectory of the Earth. The interactions between the planets cause that the orbit of our planet precesses in space. Such motion can be followed very accurately with a help of modern computers. A search for regularities in the motion of planets consisted not only in trying to understand the motion of a single planet but also in the determination of the relative distances between planetary orbits. Kepler (1596) suggested a geometrical model which reproduced quite well the observational data available at that time. The next attempt to model the relative distances of planets in the Solar System is known today as the Titius–Bode law. This empirical law in its original form states that the mean distance d from the Sun to each of the six (known to Titius) planets can be approximated by the relation

$$ d=0.4+0.3\times 2^i, $$
(1)

where i = − ∞ , 0, 1, 2, 3, 4, 5 and d is given in astronomical units (AU). Modern observations show however that the structure of our Solar System is much more complex than what can be predicted from these simplified models. An enormous influence on the planetary system dynamical structure is exerted by an apparently small gravitational effect caused by the resonance phenomenon. The resonances can easily form due to the orbital migration and they are a central theme of this article.

Resonances

In most general terms, a resonance occurs when some frequencies ω i of the system are commensurable with each other. This means that there is a linear relation between these frequencies of the kind:

$$ \sum\limits_i k_i\omega_i=0, $$
(2)

where the k i are integers, and the index i spans over a set of consecutive natural numbers. The frequencies ω i can refer to a single object. This is for instance the case of a spin-orbit coupling, where i = 1,2 and ω 1 is the rotational frequency while ω 2 is the orbital frequency. Nevertheless, they can also be related to two or more bodies as in the case of orbit-orbit interactions, where i ≥ 2 and ω i is the orbital frequency of the i-th body. There are also other more complicated relations as for example the secular resonances, which are connected with the orbital precession. Here we will concentrate on the orbit-orbit resonances, in particular, the mean-motion resonances. The name “mean motion” derives from the fact, that the frequency under consideration is the mean motion n i defined through the orbital period P i in the following way \(\omega_i= n_i =\frac{2\pi}{P_i}\).

Let us denote the mean motion of the inner planet as n 2 and that of the outer planet by n 1. The “exact” resonance occurs when

$$ (p+q) n_1 - p n_2 \approx 0, $$
(3)

where p and q are positive integers and q is the order of the resonance. Therefore, if q = 1 then the resonance under consideration is called the first order resonance, if q = 2 then it is the second order, and so on. The nominal resonance location can be found from the relation

$${a_2 \over a_1} = \left({p \over p+q} \right)^{2/3}, $$
(4)

where a 1 and a 2 are the semi-major axes of the outer and inner planets, respectively.

One of the most interesting examples of the commensurabilities in our Solar System is the resonance 4:2:1 between the orbital periods of the Galilean satellites of Jupiter: Io, Europa and Ganymede. Io is in the 2:1 resonance with Europa and Europa is in the 2:1 resonance with Ganymede. This commensurability is called the Laplace resonance. In this case the following relation is satisfied

$$ n_{\rm Io} - 3 n_{\rm Europa} +2n_{\rm Ganimede} = 0, $$
(5)

which prevents the triple conjunction of the satellites. Other examples are provided by the resonances between the Thule and Hilda asteroids and Jupiter and also between Pluto and Neptune. The mean-motion resonances may protect the planets (satellites) from close encounters and enhance the stability of the systems in the long term. The natural questions arising at this point are how such configurations were formed and do they carry some information about the early stages of the evolution of our Solar System?

The same questions become even more intriguing after the discovery of extrasolar planetary systems. It appears that also in those systems the orbital commensurabilities are common. Most mean-motion resonances are observed in systems containing gas giants (Table 1 in Section “Extrasolar Planets Close to Mean-Motion Resonances”), however similar configurations can exist also in systems with low-mass planets. One example is that of the resonance 5:4 in the system Kepler-11 (Lissauer et al. 2011a). The reconstruction of the history of the planetary system formation may be possible thanks to the resonance phenomenon. That is why, it is so important to understand the process of the formation of the mean-motion resonances in the early stages of the planetary system evolution.

Table 1 The planetary systems in which planets are in or close to the mean-motion resonance
Full size table

Early Stages of the Planetary System Evolution

The evolutionary stage of the systems which is relevant for the migration-induced architectures of planetary systems is the following: The planets or planetary cores are already formed, but they are still embedded in the protoplanetary disc from which they originated. The disc is gaseous, its mass is of the order of \(10^{-2} M_{\odot}\), its dust component is a small fraction of the disc mass (around 1%, Moro-Martin 2012).

The time passed from the collapse of the molecular cloud is of the order of 106 years. The protostar has already emerged from the thick envelope of matter and the protoplanetary disc has formed together with the planets in it. Thus, we consider here the processes which take place in the surroundings of the young stellar objects which still did not reach the main sequence. We will concentrate on low-mass stars, called T Tauri stars, which are characterized by masses around one solar mass. The life-time of the protoplanetary disc is short. The gas accreates onto the central star and/or dissipates into the space, some is used to form the bound objects and after 1–10 million years the gas is gone.

In our Solar System, which has been briefly described in the introduction, the central object is a main sequence star, aged 4.5 × 109 years. The interplanetary space in which the planets orbiting the Sun has not much in common with the environment around the T Tauri stars. There is no much gas, the dust which is present has been produced by asteroid collisions and/or comet activity. The upper limit of its total mass in the outer Solar System is \(10^{-5}M_{\oplus}\) (Moro-Martin 2012). So, the dynamics of the system is governed by the gravitational star-planet and planet-planet interactions. In T Tauri stars, instead, the interaction of a planet with the gaseous disc becomes relevant and should be taken into account. The gravitational tidal interaction between the planet and the disc leads to the migration of the planet. The orbital elements of planets are subjected to the continuous changes due to the energy and angular momentum exchange between the planet and the disc. This in turn leads to the phenomenon of resonant capture, providing one of the plausible scenarios in which the observed commensurabilities could form.

Planetary Migration

Gaseous discs around T Tauri stars are likely sites of planet formation (Hartmann et al. 1998). The planetary objects forming or recently formed within such discs interact gravitationally with the gas producing an exchange of energy and angular momentum between the protoplanet and the disc. This exchange results in torques acting on the protoplanets due to waves, generated at Lindblad resonances and corotation torques generated near the orbit of the planet (Goldreich and Tremaine 1979). The disc-planet interactions can influence the protoplanet orbits, changing their semi-major axis (Ward 1997), eccentricity (Goldreich and Sari 2003) and inclination (Thommes and Lissauer 2003). The evolution of the semi-major axis of the protoplanet (called planetary or orbital migration) increases the protoplanet mobility in the disc. The increased mobility facilitates the mass growth of the protoplanet and, for protoplanets in the giant planet mass range it provides a potential explanation of the formation of the so-called “hot Jupiters”. Finally, the convergent migration of planets or protoplanetary cores is one of the most promising processes to explain the formation of resonant configurations. The outcome of the disc-planet interaction depends on the rate and the direction of the migration, which in turn are determined by the planet mass and the disc parameters (see Eqs. 6–8). The migration rates for planets of different mass have been estimated by a number of authors, see for example the review by Papaloizou and Terquem (2006) and, most recently, the paper by Paardekooper et al. (2011). Depending on the planet masses and on the disc properties, three main regimes of orbital migration can be distinguished.

Type I Migration

For low-mass planets (up to several Earth masses for standard Solar nebula parameters) the disc undergoes small linear perturbations that induce density waves propagating away from the planet. The angular momentum transported away by these waves results in a rapid orbital migration called type I migration (Ward 1997). In this type of migration, when the disc is laminar and inviscid, the planet is embedded and the surface density profile of the disc remains approximately unchanged. The rate of migration is proportional to the mass of the planet and the time-scale of inward migration on a circular orbit can be estimated to be given by (Tanaka et al. 2002)

$$ \tau_{I}=(2.7+1.1 \gamma)^{-1} \frac{M}{m_p}\frac{M}{\Sigma {r_p}^2} \left( \frac{c}{r_p \Omega_p}\right)^2 {\Omega_p}^{-1} $$
(6)

Here m p is mass of the planet, r p is the distance from the central star with mass M, Σ is the disc surface density, c and Ω p are respectively the local sound speed and the angular velocity. The coefficient γ depends on the disc surface density profile, which is expressed according to the relation Σ(r) ∝ r  − γ.

However, recent studies showed a strong departure from the linear theory. It has been found that in non-isothermal discs with high opacity (Paardekooper and Mellema 2006) or in the presence of an entropy gradient in the disc (Paarderkooper and Papaloizou 2008) the sign of the total torque can change, reversing in this way the direction of the migration. The migration rate depends on the disc surface density, the temperature profiles and thermodynamics. If co-orbital torques are important, non-linear effects start to play a role (Paardekooper et al. 2011; Yamada et al. 2011). Therefore, a single low-mass planet can migrate with a whole range of speeds, both inwards and outwards, depending on the assumed physical and structural properties of the disc in which it is embedded (see Eqs. 3–7 in Paardekooper et al. 2011).

Type II Migration

For high-mass planets (approximately larger than one Jupiter mass) the disc response is genuinely non linear and a gap forms in the disc around the planet orbit (Lin and Papaloizou 1979, 1986). If the gap is very clean and the disc is stationary, the evolution of the planet is referred to as Type II migration (Ward 1997) and it is determined by the radial velocity drift in the disc (Lin and Papaloizou 1986), namely

$$ v_r=\frac{3\nu}{2r_p}, $$
(7)

where ν is the kinematic viscosity. The migration time of the planet can be estimated as (Lin and Papaloizou 1993)

$$ \tau_{II}=\frac{2 {r_p}^2}{3 \nu}. $$
(8)

However, as it has been showed by Crida and Morbidelli (2007), in a more realistic situation, when the gap opened by the gas giant is not deep and clean, the torque acting on the planet needs to be modified (Crida and Morbidelli 2007) and its expression reads as follows:

$$ \begin{array}{rll} \Gamma & =& 2\pi r^+ \Sigma_{LP}\left(r^+\right)v_r\left(r^+\right)\sqrt{GMr^+} \\ & &\times\left[ 1-f(P)-\frac{10R_H}{\pi r^+}\frac{\Omega_J {r_J}^2}{\sqrt{GMr^+}}\frac{v_r(r_J)}{v_{r}(r^+)}f(P) \frac{d \log\Sigma/B}{d \log r} \right] \end{array} $$

where \(r^+=r_J+2R_H\) is the sum of the radial position of the gas giant and two times the radius of the Hill sphere, Σ LP is a surface density profile taken from Lynden Bell and Pringle (1974), v r and Ω J is the radial and angular velocities, G is the gravitational constant, M is the mass of the central star. Σ is the density inside the gap, B is the second Oort constant. The function

$$ f(P) = \left\{ \begin{array}{l@{\quad}l} (P-0.541)/4 & \mbox{if $P<2.4646$}\\ \\ 1-\exp(-P^{0.75}/3) & \mbox{ if $ P \geq 2.4646$} \\ \end{array} \right . $$

describes the gap depth expressed as the ratio between the gap surface density and the unperturbed density at r  + . The variable P is defined by

$$ P=\frac{3H}{4R_H}+\frac{50}{(m_J/M) R} \lesssim 1 $$

where R is the Reynolds number and m J is the gas giant mass. In this way we are able to take into account the torque exerted on the outer disc by the gas in the gap and the corotation torque. The migration time can be estimated by

$$ \tau_{II} = \frac{(GM)^{1/2}m_Jr_J^{1/2}}{2\Gamma}. $$
(9)

Both types of migration (Types I and II) has been verified by numerical hydrodynamical calculations and good agreement has been found in the respective mass regimes.

Type III Migration

For intermediate-mass planets which open the gap only partially, it has been proposed the type III migration (Masset and Papaloizou 2003). This type of migration occurs if the disc mass is much higher than the mass of the planet. The corotation torques are responsible for this type of migration. This migration can be very fast (Artymowicz 2004) and this is why it is called also “the runaway migration”.

Resonance Capture

It has been recognized that resonant structures may form as a result of the large scale orbital migration in young planetary systems discussed in Section “Planetary Migration”. So resonant structures might be the indicators of the particular migration scenario which took place in the past. The massive objects that we expect to find in forming planetary systems will migrate with different rates depending on their masses. Combining the expected differential migration speeds described in the previous subsection with the strength of the commensurabilities given by Quillen (2006) and Mustill and Wyatt (2011), one can predict if the capture will take place or not. The resonant capture for the first order resonances in the restricted three body problem occurs when

$$ \frac{1}{\frac{1}{\tau_I}-\frac{1}{\tau_{II}}} \geq \frac{3 \pi}{ \dot{\eta}_{\rm crit} \Omega_{J}} $$
(10)

where \(\dot \eta _{\rm crit}\) is the critical mean motion drift rate and Ω J is the angular velocity of the Jupiter-like planet. In the case of an internal 2:1 resonance \(\dot{\eta}_{\rm crit}=22.7~(\mathrm{m_J/M})^{4/3}\), while for a 3:2 commensurability \(\dot{\eta}_{\rm crit}=126.4~(\mathrm{m_J/M})^{4/3}\) (Quillen 2006). From Mustill and Wyatt (2011) it can be easily determined whether capture occurs for planet migrating in Types I or II regimes. For planets migrating through a gaseous disc, a non-zero eccentricity before the capture can cause the large libration amplitudes as it is observed in the HD 128311 system. Thus, when the eccentricities of the Jupiter-like planets are larger than 0.1, we can assume that the resonant capture will result in high libration amplitudes. For lower mass planets the eccentricity is lower. It has been verified (Mustill and Wyatt 2011) that the results obtained by analytical methods and numerical simulations are in a very good agreement with each other.

Now a few examples will be provided in order to illustrate how the studies of mean-motion resonances are able to advance our understanding of planet formation and evolution. The main tools used in order to get information about the possible evolutionary scenarios for resonant configurations are two and three dimensional hydrodynamic simulations, simple analytic modelling and N-body investigations. Constructing simple analytic models we can verify the reliability of our numerical calculations. Combining the hydrodynamic simulations with the results of the N-body technique, we are able to follow the dynamical evolution of the planets for a substantial amount of time comparable with the estimated life time of the gaseous discs.

Giant Planets in Laminar Discs

It has been shown that the convergent migration brings the giant planets closer to each other and they can become locked in low order commensurability (Bryden et al. 2000; Kley 2000; Masset and Snellgrove 2001; Lee and Peale 2002; Nelson and Papaloizou 2002; Papaloizou 2003; Kley et al. 2004; Lee 2004) as it is observed in multiplanet systems (e. g. GJ 876, HD 82943 and 55 Cnc or other examples from Table 1). The best studied system among these is GJ 876 with its two giant planets found in the 2:1 resonance (Marcy et al. 2001). Snellgrove et al. (2001) have explained the resonance trapping in this system via a mechanism of differential migration due to gravitational interactions with the protoplanetary disc. They consider the two protoplanets orbiting in the interior of a tidally maintained disc cavity. When the disc driven migration is sufficiently slow, the more rapidly migrating outer protoplanet approaches the inner one and becomes locked with it in the 2:1 resonance. This commensurability is sustained in the subsequent evolution. However, there is a problem with this scenario. In fact, the eccentricities of the planets trapped in the resonance and migrating together through the disc towards the star, grow to values which exceed the observed ones. Kley et al. (2005) confirmed the previous work and found that in order to get eccentricities that are consistent with the observations, the disk should be depleted on a time scale of the order of the migration time scale. This might occur due to photoevaporation in the late phases of planet formation. Hence, this result limits the radial distance over which the resonant planets can migrate. The solution to this problem has been proposed by Crida et al. (2008). They have found that the torque generated by the inner disc yields an effective damping of the eccentricities which results in moderate final eccentricities even for extended radial migration. Crida et al. (2008) apply the same analysis to three other exoplanetary systems: HD 73526, HD 82943, and HD 128311 and succeeded to recover the observed orbital elements for the resonant planets. The story about the GJ 876 goes on as the extensive observations of this system led to a discovery of a Uranus-mass fourth planetary companion (Rivera et al. 2010). The new planet is in Laplace resonance with the giant planets b and c, and the system marks the first example of a three-body resonance among extrasolar planets. The resonances 2:1 (involving planets e and c) and 4:1 (involving planets e and b) are not so strong as the resonance 2:1 between planets b and c, but they are necessary for a long term stability of the system. This statement is based on the existing observational data. The situation may change when new data will be available.

In the context of the newly suggested Laplace resonance (Rivera et al. 2010), it is worth mentioning a new mechanism for stopping the inward migration of a low-mass planet embedded in a gaseous protoplanetary disc found by Podlewska-Gaca et al. (2012). The mechanism operates when a low-mass planet encounters outgoing density waves excited by another source in the disc. This source could be a gas giant in an orbit interior to that of the low-mass planet. As the low mass planet passes through the wave field, angular momentum is transferred first to the disc matter and then communicated back to the planet through co-orbital dynamics. The consequence of this interchange of angular momentum is that the inward migration of the affected planet can be halted or even reversed. It has been found in this way that a planet with mass in the super-Earth range cannot approach a Jupiter-mass planet close enough in order to form first- order mean-motion resonances with it. In fact, the migration was found to halt when the semi-major axis was ranging between 1.6 and 2.0 times that of the giant. Only when the low-mass planet exceeded 40 m  ⊕  it was able to attain a 2:1 commensurability. For that reason, the formation of the 2:1 commensurability in GJ 876 between planets e and c through planet interaction with the gaseous disc alone would be problematic. This may indicate that the migration induced by planetesimals after the clearance of the gas disc may have been significant in the formation of GJ 876.

Low-Mass Planets in Laminar Discs

Low mass planets can undergo convergent migration too and form in this way a resonant structure (Papaloizou and Szuszkiewicz 2005). The pulsar planets around PSR B1257+12 might be an outcome of such scenario. Papaloizou and Szuszkiewicz (2005) performed an analytic and numerical study of the formation of first order commensurabilities in a system of two planets in the earth mass range migrating in a laminar disc. In Papaloizou and Szuszkiewicz (2010) the authors have extended their study to a larger range of migration rates and commensurabilities and compared the numerical work to the conditions for particular commensurabilities to form derived analytically.

They have also derived the condition for a p+1:p commensurability to be maintained, which means that the planet eccentricities e 1 and e 2 are either almost constant or, more generally, almost constant in a time average sense, while the ratio n 1/n 2 is maintained very close to p/(p + 1). The considered time averages are to be taken over a time long compared to the characteristic orbital period but short enough that the semi-major axes and tidal time scales may be considered constant. The condition found in Papaloizou and Szuszkiewicz (2010) can be written in the form

$$ {p^2 n_2^2 m_2\over(p+1)^2 M} \left({(1-f)m_2C_1^2t_{c1}\over M}+{m_1a_1^2C_2^2t_{c2}\over Ma_2^2}\right) \ge \left({1\over t_{\rm mig1}}-{1\over t_{\rm mig2}}\right){f\over 3}. $$
(11)

where f = m 2 a 1/((p + 1)(m 2 a 1 + m 1 a 2)), m 1, m 2 and M are the masses of planets and star respectively, a 1 and a 2 are the semi-major axes of the planets. The circularization and migration times for planet i are t ci and t migi. C 1 and C 2 are expressed in terms of Laplace coefficients.

For the simple example in which m 1 ≫ m 2 is in a prescribed slowly shrinking circular orbit and controls the migration (t mig2 ≫ t mig1), the relation (11) simplifies to the form

$$ { m_1^2\over M^2} \ge \left({a_2\over 3p a_1 n_1n_2 t_{\rm mig1} t_{c2} C_2^2}\right). $$
(12)

Because it is found that both C 1 and C 2 increase with p, while f decreases with p, the inequality (11) indicates that for given planet masses the maintenance of resonances with larger values of p is favoured. However, the maintenance of resonances with large p may be prevented by resonance overlap and the onset of chaos. Resonance overlap occurs when the difference of the semi-major axes of the two planets is below a limit that, in the case of two equal mass planets, has half-width given by Gladman (1993) as

$${\Delta a\over a} \sim {2\over 3p} \approx 2 \left({m_{\rm planet} \over M_*}\right)^{2/7}, $$
(13)

with a and m planet being the mass and semi-major axis of either planet respectively. Thus for a system consisting a two equal planets of mass 4 m  ⊕  orbiting around a central solar mass, we expect resonance overlap for \(p \gtrsim 8\). Conversely, we might expect isolated resonances in which systems of planets can be locked and migrate together if \(p \lesssim 8\). But note that the existence of eccentricity damping may allow for somewhat larger values of p in some cases. In this context the inequality (11) also suggests that resonances may be more easily maintained for lower circularization rates. However, this may be nullified for large p by the tendency for larger eccentricities to lead to greater instability. Note also that higher order commensurabilities may also be generated in such cases and these are not covered by the theory described above.

Gas Giants and Low-Mass Planets in Laminar Discs

The differences in the migration rates of low and high mass planets may also lead to the convergent migration (Hahn and Ward 1996) The numerical simulations of the resonant captures in a variety of physical conditions for systems with gas giants and low-mass planets have been presented in a series of papers (Podlewska and Szuszkiewicz 2008, 2009; Podlewska-Gaca and Szuszkiewicz 2011; Podlewska-Gaca et al. 2012). These studies reveal the interesting fact that the resonant capture occurs easily if the low-mass planet is on the internal and the gas giant on the external orbit around a solar-type star. This is no longer true if the planet locations will be inverted (Podlewska and Szuszkiewicz 2009; Podlewska-Gaca et al. 2012). If the super-Earth is orbiting its host star outside the gas giant orbit, then the outgoing wave excited by the gas giant prevents the situation in which the super-Earth can approach the gas giant closely enough for the first order commensurability to occur. The explanation of the mechanism can be found in Podlewska-Gaca et al. (2012). The candidate for a planet with mass of about 15 m  ⊕  announced in Maciejewski et al. (2010) and located close to the external 2:1 commensurability with a gas giant, if confirmed, could be an ideal test for this newly found migration scenario.

Disruption of the Resonances

There are several processes which might lead to disruption of the resonance. The absence of the resonance can be indicative of a dynamical history dominated by gravitational planet-planet scattering (Raymond et al. 2008). Let us shortly discuss two of the plausible processes which definitely will play a role in unlocking planets from resonances. These are turbulence and tidal circularization.

Role of Turbulence in Unlocking Planets from Resonances

Turbulence has a significant impact on the capture of two planets in the Earth mass range into the mean-motion resonance and affects the maintenance of the resonant configurations (Adams et al. 2008; Rein and Papaloizou 2009; Ketchum et al. 2011). The torques due to turbulent fluctuations have been studied successfully using magnetohydrodynamical simulations (e.g., Nelson and Papaloizou 2004; Laughlin et al. 2004; Nelson 2005; Oishi et al. 2007). Recently, Pierens et al. (2011) presented the results of their study of the evolution of a system composed of two low-mass planets embedded in a typical turbulent protoplanetary disc. They concluded that in such discs the mean-motion resonances are likely to be disrupted by stochastic density fluctuations.

The Role of Tidal Circularization in Unlocking Planets from Resonances

The tidal circularization of the orbits induced by the tidal interaction with the central star together with later close scatterings and mergers tended to cause the system to move away from earlier established commensurabilities to an extent determined by the effectiveness of these processes.

A high fraction of exoplanetary systems may be near but not actually in resonance (Veras and Ford 2012). Two of such examples have been investigated by Papaloizou and Terquem (2010), namely GJ 581 and HD 40307. The ratio of periods of the planets in GJ 581 (Bonfils et al. 2005; Udry et al. 2007; Mayor et al. 2009a) is 2.41 and 1.70 for GJ 581 b, c and GJ581 c, d respectively. Similarly for HD 40307 (Mayor et al. 2009b) it is 2.23 for HD40307 b, c and 2.13 for HD40307 c, d. Thus the departure from the exact resonance is significant and that is why these configurations, which are only near to the resonance, have not been recognized to be of importance for the dynamical evolution of the systems GJ 581 and HD 40307 (Barnes et al. 2009; Mayor et al. 2009a, b). In fact we did not include these two systems in Table 1. However, the conclusion of Papaloizou and Terquem (2010) is that the system HD 40307 is still resonant, as some of the resonant angles continue to librate. Papaloizou (2011) has undertaken further study of systems of close orbiting planets evolving under the influence of tidal circularization. He has presented simple analytic model describing the evolution away from a general first order resonance. He also has performed numerical simulations of two and four planet system chosen to have parameters related to the GJ 581 and HD 10180.

Observations of Extrasolar Planetary Systems

The Solar System is not the only planetary system in our Galaxy. Until now more than 700 extrasolar planets have been found. In many cases these are not just single objects orbiting around their host star, but two or more (up to seven, as for today) planets moving around the same star. There are already 100 stars with more than one planet, this makes approximately 14% of all stars, which have planets. At the present state of our knowledge these statistics are only indicative and tell us about the progress made in the detection techniques. There is no obvious reason for which systems with a single planet should be more numerous than multi-planet systems. Wright et al. (2009) performed a comparison between the properties of systems with a single object and those having more of them. These authors have noticed that in the case of multi-planet systems the planets have similar eccentricities as in the single-planet systems and their distribution of the orbit distances from the host stars are more uniform than in the case of single-planet systems. A similar analysis has been carried on by Latham et al. (2011) for planetary candidates observed by the Kepler mission. These are definitely valuable attempts to find characteristics of the extrasolar planetary systems, however it is still too early to formulate robust conclusions from such studies. It is most likely that soon new planets will be found in systems which now are apparently with single planets.

The observed planetary systems are very diverse. Planets have been found around brown dwarfs with masses as small as 0.02 M  ⊙  (2M J044144, Todorov et al. 2010), and around very massive stars such as DH 13189 with mass 4.5 M  ⊙  (Hatzes et al. 2005). The extrasolar planet with the smallest mass is PSR 1257+12b. Its mass is as small as 0.019 m  ⊕  (Goździewski et al. 2005). If we limit ourselves to planets orbiting around the main sequence stars then among planets with the very small mass we can mention GJ581 e with a mass of about 1.95 m  ⊕  (Mayor et al. 2009a). The task of identifying the most massive planet is much more difficult, because in this case we encounter the problem of distinguishing planets from brown dwarfs. So let us mentioned just the most massive non-stellar object, which is CD-352722b (31 m J , Wahhaj 2011). Extrasolar planets are observed very close to their host stars, for example in a distance of 0.014 AU (GJ 1214 b, Charbonneau et al. 2009) or 0.006 AU (Kepler 55b, Charpinet et al. 2011), but also far away from the central stars (hundreds of AU). The most distant planet in the system HR 8799 is located at the distance of 68 AU from its host star (Marois et al. 2008). The orbits of Jovian-like planets have eccentricities e, typically in the range from zero till 0.5, while Neptune-like and super-Earths move on orbits with e < 0.2 (Wright 2010). The biggest known eccentricity, e = 0.97, belongs to the planet HD 20782b which has a mass of 1.9 m J (O’Toole et al. 2009). Besides planets orbiting stars there are also planetary objects, which are not bounded gravitationally around any star, we call the latter free floating planets. One example of free floating planets is that of ρ Oph 4450, which has been discovered by direct imaging (Marsh et al. 2010). Such a diversity of objects is a big challenge for the theory of planetary system formation and evolution.

The most common planets detected so far orbiting stars similar to our Sun are gas giants with a mass of the order of that of Jupiter. They move on their orbits very close to their host stars, at a distance of 1 AU or smaller. A typical (as for today) planetary system is then very different from our Solar System. The existence of gas giants so close to the central stars poses severe difficulties in explaining how they were formed if they were really originated where they are located now. These difficulties at least partially have been removed thanks to the theory of the orbital migration developed in details at the end of the seventies of the last century (Goldreich and Tremaine 1979; Lin and Papaloizou 1986). The application of this theory allows the gas giants to form far away from the star, where the conditions are favorable for their formation and then to “walk into” the region where they are observed. The planetary migration should be a common phenomenon occurring in the early stages of the planetary system evolution.

In the study of resonant configurations, there is a particular region of interest around a gas giant, namely a zone extended from 0.6 till 1.7 a J , where a J is the gas giant distance from the host star. The first order commensurabilities are located in this region. One of the questions to ask at this point is the following: Can a low-mass planet, for example, a super-Earth, be located so close to the gas giant? In our solar system the region 0.6–1.7 a J corresponds roughly to the zone between 3 and 9 AU, as Jupiter is located at 5.2 AU. In this zone, there are no other planets, but there are two groups of asteroids from the Main Asteroid Belt, namely Hilde and Thule groups and a few members of these groups are in mean-motion resonances with Jupiter. In the analogous region around the planet Gliese 876 b with mass 2.3 m J there are two planets in mean-motion resonance with it, namely Gliese 876 c with mass 0.7 m J and Gliese 876 e with mass 0.046 m J (15 m  ⊕ ). Gliese 876 e which has a mass similar to Uranus (Rivera et al. 2010), is at the moment the least massive confirmed planet present in the neighborough of a gas giant.

Gliese 876 b has been detected by the radial velocity method (RV) similarly as 51 Peg (Mayor and Queloz 1995) the first discovered extrasolar planet orbiting around a main sequence star. All together there are already about 600 planets (Extrasolar Encyclopedia—www.exoplanet.eu) discovered by RV around stars of different spectral type from A till M. This method uses the fact, that if around the star there is a planet, then the planet and the star move around their common center of mass. The measurements of the changes in the radial velocities using the Doppler shift of the spectral lines allow for the detection of a planet around its star. Until now the best accuracy in the radial velocity measurements has been achieved by using the HARPS (High Accuracy Radial Velocity Planet Searcher) spectrograph located in the La Silla Observatory in Chile. At present HARPS can reach an accuracy better than 0.5 m/s. In the case of not active stars the accuracy can be as high as 0.2 m/s (Mayor and Udry 2008). For comparison, a planet with a mass comparable to that of our Earth orbiting around one solar mass star at a distance of 1 AU from the star will cause a variation of the radial velocity of 0.09 m/s. The application of the radial velocity technique in the case of low mass stars (for example Gliese 876) is more effective because of the more favourable mass ratio.

The RV method not only leads to the discovery of numerous planetary systems but it helps to confirm the detection done by photometric observations, an alternative technique using the change of the luminosity of the star caused by the transit of the planet. The accurate measurement of the intensity of the stellar radiation during this event is the basis for affirming the existence of the transiting planet and determining its size and orbital period. Thanks to the two space missions COROT and Kepler the accuracy of this method has increased to such extent that today it is possible to detect a planet of the terrestrial type as COROT 7b (Leger et al. 2009) or Kepler-20 (Fressin et al. 2012). In February 2011 Borucki et al. (2011) announced that the Kepler satellite has discovered more than 1200 candidates for planets. If confirmed, this claim will put the transit method at the top of the ranking of the most efficient techniques in discovering planets. At least 176 systems identified by the Kepler mission can contain more than one planet. Are there any interesting configurations among those discovered by Kepler?

Kepler-11 is a very interesting planetary system, whose architecture can provide information about the early phases of the evolution of this system and help to reveal the processes responsible for its formation. Knowing the masses and radii of the planets it is possible to evaluate their average density. From the data at our disposal, we can conclude that Kepler-11 d, e and f should have a structure very similar to that of Uranus and Neptune in our Solar System (Lissauer et al. 2011a). Thus, at least these three objects should have been formed before the gaseous protoplanetary disc disappeared. The small eccentricities and inclinations of the orbits of the five internal planets also indicate the presence of gas or planetesimals in the final stage of the formation. The presence of the gas in the system implies that the orbital migration can be working. If it is so, then there should be the favourable conditions for the formation of mean-motion resonances. Planets b and c are close to the 5:4 resonance, but not exactly in this resonance. The lack of exact resonances can be the argument against a slow convergent migration of the planets that has taken place in the early stages of the evolution of this system, unless the dissipation processes in the disc have forced out the planets from the exact resonance. The deviation from the exact position of the resonance does not preclude the existence of the commensurability. Such a scenario has been discussed by Papaloizou and Terquem (2010). The orbital periods of the two other planets (f and g) in this systems are close to the exact commensurability 5:2. However, the mass of Kepler-11 g still has not been determined and its planetary nature has not been confirmed yet. The objects which are not confirmed are indicated in Table 1 by a question mark near the name of the planet.

The observations of transiting planets open also the possibility to detect other planets in the system which do not transit or such that their mass is so low that the effect of the decrease of the star intensity due to its transit in front of the star is not possible to measure. The presence of such planets affects the motion of the transiting one, causing that the time between consecutive transiting planet passages will be different from passage to passage. For example, the difference in the predicted and observed positions of Uranus in our Solar System led to the discovery of Neptune in 1846. Similarly, the perturbation of the motion of the transiting planet can lead to the detection of other planets in any other system. This method is called the Transit Timing Variation (TTV) technique. If the transiting planet is in the mean-motion resonance with an invisible planet, then the effect can be so large that it allows the detection of a planet as small as our Earth (Agol et al. 2005; Holman and Murray 2005). The first candidate to be a planet discovered with the TTV technique has a mass of about 15 m  ⊕  (Maciejewski et al. 2010) and is close to the external 2:1 commensurability with a gas giant Wasp-3b. This observation still waits to be confirmed.

Until now there are at least 48 confirmed planets with masses less than 10 m  ⊕ . Apart from one—the least massive pulsar planet mentioned before—the others are super-Earths. Most of them (43) have been discovered by the RV and transit methods, 2 by microlensing and 3 by pulsar chronometry. Among the candidates for planets detected by Kepler there are about 300 objects with sizes corresponding to super-Earths. The confirmation that these are planets is difficult because we know only their size but not their mass which is necessary to classify them as super-Earths. The preliminary estimates of a quantity of 300 low-mass planets among the 1200 discovered by Kepler seem to be in agreement with the predictions of the percentage of these planets made on the basis of the distribution of mass and orbital periods around 166 stars similar to the Sun (Howard et al. 2010). There should be a lot of low-mass planets in our Galaxy, so it is worth to intensify the studies of systems containing one, two or more of such planets and to predict their most likely relative positions.

Extrasolar Planets Close to Mean-Motion Resonances

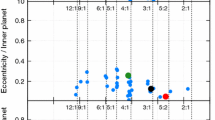
As we have already mentioned, resonance phenomena are important for shaping up the planetary system configurations. We have discussed this using our Solar System as an example. The commensurabilities of the orbital periods in the satellite systems of Jupiter and Saturn can be connected with the early history of these system formation (Goldreich 1965). Similarly, the location of Jupiter and Saturn close to the 5:2 resonance can be helpful in the identification of the processes which took place in the past and brought the Solar System in its present configuration (Morbidelli and Crida 2007). The observations of extrasolar systems have confirmed that the commensurabilities could be the key to solve the problem of planetary system formation, because also in these systems stable resonant configurations have been found in abundance. Wright et al. (2011) show that on average every third well studied multi-planet system indicate the commensurability of the orbital periods. The frequency of the occurrence and the character of the mean-motion resonances could be the tracers of the nature of the planetary migration, which is a common phenomenon during the early phases of the planetary system evolution. Taking into account the fact that resonances play an important role in our understanding of the origin, structure and evolution of a planetary system, we have collected all known systems in which the planets are likely to be in or close to the resonant configuration and described shortly the properties of these systems. The results are presented in Fig. 1 and Table 1. At the moment of writing this paper there are 26 known planetary systems which contain planets in or close to mean-motion resonances or are suspected of having such planets. We do not include here the candidates for planets detected by the Kepler mission, as they still await to be confirmed. The systems are ordered according to the increasing ratio of the orbital periods of the planets in a resonance starting from the system Kepler-11 with two planets close to the 5:4 resonance and closing with HD 208487 with planets in the 7:1 commensurability. In Fig. 1 the planets in a resonance are denoted in red. In Table 1 the planet parameters (their minimal masses m sin(i) and the semi-major axes) are given in boldface. Now, let us have a look at those systems and their properties.

Fig. 1
figure 1

The observed planetary systems in which the mean-motion resonances can be present. The planets reported as being close to the mean-motion commensurability are marked in red, those not involved in any resonance in blue and the super-Earths in green

Full size image

Commensurabilities with the Ratio of Orbital Periods less than Two

Kepler-11   The host star of the system Kepler-11 (KIC 6541920, KOI-157) is a dwarf of spectral type G (Lissauer et al. 2011a). Its effective temperature is of about 5680 ± 100 K, the gravitational acceleration g on the star surface is given by log(g(cm/s2)) = 4.3 ± 0.2, the metallicity is the same as that of our Sun [Fe/H] = 0.0 ± 0.1 dex. (Please note, that from now on we will be using always the same units for the gravitational acceleration and metallicity but they will not be specified explicitly in the text.) The mass and the radius of the host star in the system Kepler-11 are M = 0.95 ± 0.10 M  ⊙  and R = 1.1 ± 0.10 R  ⊙ , respectively. The system is at a distance of about 2000 light years from our Sun (613.5 pc). The age of the star is estimated at about 6 × 109 − 1010 years. On the orbits around this star there are 6 transiting planets. Five of them have their orbital periods in a range from 10 to 47 days (it means they are closer to their host star than Mercury to the Sun). The sixth planet has a longer period that exceeds 100 days. In the previous section (Section “Observations of Extrasolar Planetary Systems”) we have pointed out that with the transit method it is possible to know the size of the planets but not their mass. We have also mentioned the powerful TTV technique, which allows to detect non transiting planets or planets that are too small for their signal to be measured. In the case of Kepler-11, in which all planets are transiting, this technique is able to verify the planetary nature of the observed objects through the evaluation of their masses. In this way the five most internal candidates for planets of this system have been confirmed.

HD 200964   The planets are near the 4:3 mean-motion resonance (Johnson et al. 2011). The host star is a subgiant of spectral type G. Its effective temperature is equal to 5164 ± 44 K, the gravitational acceleration log(g) = 3.6 ± 0.1, the metallicity is [Fe/H] = − 0.15 ± 0.04. The mass of the star is 1.44 ± 0.09 M  ⊙ , and the radius amounts to 4.3 ± 0.09 R  ⊙ . The star distance from the Sun is 68.4 ± 4.8 pc and its age is about 3.0 ± 0.6 × 109 years. Two gas giants orbit around the star with orbital periods respectively given by 613.8 and 825.0 days. The planets in this system most likely arrived at the present locations due to their interactions with the protoplanetary disc and in the process of the convergent migration formed the 4:3 commensurability (Johnson et al. 2011). However, as it has been shown by Kley (2000) and Nelson and Papaloizou (2002), the most probable final state of the convergent migration is the 2:1 resonance and not 4:3. So, how this commensurability could happen? The formation of the 4:3 resonance depends on many circumstances including the initial separation of the planets, their masses, the viscosity in the disc and its mass (Malhotra 1993; Haghighipour 1999; Bryden et al. 2000; Snellgrove et al. 2001). The key property is the migration rate which, if it is sufficiently high, can cause that the planets will pass through the 2:1 commensurability and proceed toward the resonances with smaller ratio of the orbital periods, like for instance the 4:3 resonance.

PSR B1257+12   Here, it is the 3:2 commensurability. PSR B1257+12 is a millisecond pulsar, its distance from the Sun is 0.6 kpc. The standard mass for the pulsars is assumed to be 1.4 M  ⊙ , the age is evaluated at 3 × 109 years. The planets discovered in this system were the first extrasolar planets found (Wolszczan and Frail 1992). The parameters for this system are determined with a very high accuracy (Konacki and Wolszczan 2003), that is why it is one of the best systems for studying the formation of planets and their evolution. Particular attention has been devoted to the configuration of the planets B and C with masses around 4 m  ⊕ , which are close to the 3:2 resonance. Goździewski et al. (2005) have shown that this system with the parameters determined by Konacki and Wolszczan (2003) is stable in the timescale of 109 years.

HD 45364   HD 45364 is the second system described here, in which planets are in the 3:2 resonance. The central star is of spectral type K0V (Hipparcos Catalogue ESA 1997). Its effective temperature is 5434 ± 20 K, its gravitational acceleration is log(g) = − 4.38 ± 0.03, the metallicity amounts to [Fe/H] = − 0.17 ± 0.01 (Sousa et al. 2008). The mass of the star is 0.82 M  ⊙ . The system is located at the distance of 32.6 pc from the Sun. The precise measurements performed by means of the spectrograph HARPS allow for the discovery of two gas giants with masses less than that of Jupiter (Correia et al. 2009). The dynamical analysis has shown that the planets are in the 3:2 resonance and the system is stable in the timescale of about 5 × 109 years. Rein et al. (2010) have studied the formation and evolution of the gas giants in this system and found a model with the migration (type III migration), which leads to the 3:2 commensurability.

Wasp-10   We would like to put some emphasis on the system Wasp-10 and the possibility of the occurrence of a second order resonance. Here we will consider the 5:3 resonance (Maciejewski et al. 2011). The star in this system is a K5 dwarf with the effective temperature of 4675 ± 100 K. Its distance from the Sun is 90 ± 20 pc (Christian et al. 2009). The age of the star is only 270 ± 80 × 106 years (Maciejewski et al. 2011).

Wasp-10b has been discovered by Christian et al. (2009) using the transit method. Maciejewski et al. (2011) have shown that the times of the beginning of the transit are not periodic and postulated that in the system can be present another planetary object with the mass of 0.1 m J and the orbital period 5.23 days. The existence of this planet and then of the resonance still require a confirmation.

Commensurability with the Ratio of Orbital Periods Equals Two

Discussing the possible resonant configurations with increasing ratios of the orbital periods, finally we have arrived to the 2:1 resonance. As it is evident from Table 1, there are already 10 systems in which planets are in or close to the 2:1 commensurability (single 2:1 and double 4:2:1, called Laplace resonance). Most of these resonant configurations contain gas giants. The relatively big number of gas giants locked in the 2:1 resonance in comparison with those involved in the commensurability described before for which the ratio of the orbital periods is less than 2 is in agreement with our expectations based on the numerical simulations done by Lee et al. (2009). They have considered two gas giants formed in the protoplanetary disc with initial ratio of the orbital periods larger than 2 and shown that only 3% of the pair of planets reached the ratio of the orbital periods smaller than 2. None of them got locked in the stable mean-motion resonance with a ratio of the periods smaller than 1.5. The first object in the 2:1 resonance we would like to discuss is HD 90043.

HD 90043   The star HD 90043 (or differently 24 Sextantis) is a subgiant of spectral type G with effective temperature 5098 ± 44 K, gravitational acceleration log(g) = 3.5 ± 0.1 and metallicity [Fe/H] = − 0.03 ± 0.04. The mass and radius of this object are 1.54 ± 0.08 M  ⊙  and 4.9 ± 0.08 R  ⊙  respectively. The age of the star is equal to 2.7 ± 0.4 × 109 years (Johnson et al. 2011). The distance of the star from the Sun is 74.8 ± 4.9 pc. There are two gas giants known to orbit the central star. According to the most accepted model by Pollack et al. (1996) they have been born far away from the place in which they are now. During the early phase of the evolution the orbital migration brought them close to the star and at the same time provided the favourable conditions for a capture and maintenance of the resonance.

HR 8799   The central star has a spectral type A5V, effective temperature 7500 K and it has a low metal abundance [Fe/H] = − 0.47. The mass of the star is 1.5 M  ⊙ , and its age is about 30–160 × 106 or 109 years (Marois et al. 2008). The distance of the star from our Sun is 39.4 pc. This system contains four massive planets and a dusty debris disc. It is likely that the planets d, c and b are in the 4:2:1 resonance. In Table 1 the numbers in parenthesis represent the masses and semi-major axes obtained by Goździewski and Migaszewski (2009) at the time when the most interior planet was not known. This is a very good case to study the processes of gas giant formations at large distances (> 10 AU) from the central star.

HD 73526   Also in the system HD 73526 there are two gas giants close to the 2:1 resonance. The central star around which these planets are orbiting is a dwarf of spectral type G6 (Tinney et al. 2006). Its effective temperature is equal to 5590 K and the metallicity amounts to [Fe/H] = 0.25 ± 0.05 (Fischer and Valenti 2005). Sandor et al. (2007) have proposed different stable fit of the observed radial velocities than that reported in Table 1. Their solution requires that the masses of the planets are 2.415 m J for planet b and 2.55 m J for planet c respectively. Moreover, the semi-major axes of the planetary orbits are 0.659 AU and 1.0445 AU respectively for planets b and c. According to their scenario for the evolution of this system, after a phase of slow convergent migration, which resulted in the 2:1 resonant capture, this system could have undergone a perturbation as for example the loss of matter from the disc or the planet-planet scattering.

HD 82943   It seems that also the two gas giants in the system HD 82943 are in the 2:1 resonance (Goździewski and Konacki 2006). They orbit around a star of spectral type G0V, with effective temperature 5989 K and metallicity [Fe/H] = 0.26. The mass of the star is equal to 1.15 M  ⊙ , the distance from our Sun is 27.46 pc (Sousa et al. 2008). The age of the star is evaluated to be 5 × 109 years (Moro-Martin et al. 2010). In this system apart from the planets also a debris disc is observed (Trilling et al. 2008). The dynamic structure of the system HD 82943 is not very well known. It is enough to remove one observational point from the analysis (one value of the radial velocity measurement) to obtain a completely different solution. There is also the possibility that there is a third planet in this system that is in the Laplace resonance with the other two planets (Wright et al. 2011).

Wasp-3   The resonance 2:1 (Maciejewski et al. 2010) in the system Wasp-3 could be the most interesting for us among all configurations presented here so far, because it may provide a very good test case for the new mechanism of planetary migrations found in Podlewska and Szuszkiewicz (2009) and Podlewska-Gaca et al. (2012). Unfortunately, by now, the existence of the resonance has not been confirmed. New observations have been planned and there is a chance that soon the new data will be able to provide more definitive statements about the existence of the planet Wasp-3c itself and about its orbital parameters (Gracjan Maciejewski private communication). At the moment it is known that a star of spectral type F7V, of mass 1.24  M  ⊙ , radius 1.31  R  ⊙  and effective temperature 6400 K (Pollacco et al. 2009) is the host star of a gas giant with the mass of about 2 m J .

HD 128311   The system HD 128311 is a very good example of a system with the 2:1 resonant configuration. It was formed around a K0 star with the effective temperature equal to 4635 K and metallicity [Fe/H] = − 0.04 (Saffe et al. 2008). Its mass is 0.84 M  ⊙ . The age of the star is about 500 × 106 years (Moro-Martin et al. 2010). In this system, the debris disc has been discovered (Beichman et al. 2005). Rein and Papaloizou (2009) using numerical simulations were able to reproduce the properties of this configuration and suggested the mechanism of its formation. According to their model, the resonance capture occurs due to convergent migration with the participation of the stochastic forces present in the turbulent disc.

GJ 876   The best candidate for a system with a 2:1 resonance was till very recently GJ 876. Its structure, namely that of three planets, two of them forming the 2:1 mean-motion resonance (Marcy et al. 2001), orbiting around a star of spectral type M4V with mass 0.33  M  ⊙ , radius 0.36  R  ⊙ , metallicity [Fe/H] = 0.05 and age 2.5 × 109 years (Correia et al. 2010), was believed to be relatively well known. However, Rivera et al. (2010) have shown that even the most robust mean-motion resonance can appear illusive if new planets are discovered in the system. In GJ 876 the 2:1 resonance still holds, but its evidence is not so strong any more. The newly discovered planet (GJ 876 e) forms with the other two the Laplace resonance.

Kepler-9   The 2:1 resonance is observed also in the system Kepler-9. Kepler-9 is a star similar to our Sun. Its effective temperature is equal to 5777 ± 61 K, its metallicity is [Fe/H] = 0.12 ± 0.04 and its mass is the same as that of the Sun. The radius of the star is estimated to be 1.1 R  ⊙ , and the age 4–6 × 10 9 (Holman et al. 2010). The system contains two planets, Kepler-9 b and c with masses similar to that of Saturn and close to the 2:1 resonance. There is also a third planet, Kepler-9 d, with a structure similar to that of a rocky planet and with mass in the range 4–16 m  ⊕ .

HD 160691   No less interesting is the system HD 160691 known also as μAra. The central star is a G5 dwarf with the effective temperature equal to 5807 K and the mass of 1.08 M  ⊙  (McCarthy et al. 2004). In the system there are at least four planets, the fourth has been discovered by Goździewski et al. (2007) and Pepe et al. (2007) and forms with the planet b a resonant configuration.

HD 37124   The last example of a system containing planets close to the 2:1 commensurability is HD 37124 (HIP 26381). The host star is a dwarf of spectral type G4 with low metallicity [Fe/H] = − 0.44. The mass of the star is 0.85 M  ⊙  (Wright et al. 2011). HD37124 c and d might be in the 2:1 resonance, however the analysis of the radial velocity data performed by Wright et al. (2011) is not conclusive. The stability analysis requires the component d to have an orbit with the eccentricity not larger than 0.3. Wright et al. (2011) have shown also that the planetary orbits should be coplanar and that all the planets have practically the same mass. The differences between masses do not exceed 10%. With this object we are closing the list of known systems which contain planets in or close to the 2:1 mean-motion resonance.

Commensurabilities with the Ratio of Orbital Periods Greater than Two

Now, we discuss the 5:2 resonance in two systems, namely HD 10180 and HD 181433.

HD 10180   The central star is a G1 dwarf, its effective temperature is 5911 ±19 K, log(g) = 4.39 ± 0.03, and the metallicity [Fe/H] = 0.08 ± 0.01. The mass of the star is similar to that of our Sun, 1.06 ± 0.05 M  ⊙ . The age of the star is also very similar to the age of the Sun and is equal to 4.3 ± 0.4 × 109 years (Table 2 in Lovis et al. 2011). There are seven planets around this star (Lovis et al. 2011). Five of them are similar to Neptune in our Solar System with the semi-major axes in the range from 0.06 to 1.4 AU. The most internal planet is not confirmed yet (Olsen and Bohr 2010), but it might be similar to the Earth, its minimal mass is 1.4 m  ⊕ , it orbits very close to the host star, at a distance of 0.022 AU. Planets e and f are close to the 5:2 commensurability, while planets d and e are close to the 3:1 resonance. The system seems to be stable in the long term, in particular, if only the six external planets are taken into account. The present radial velocity measurements exclude the existence of a gas giant planet at a distance of less than 10 AU, so it is unlikely that the gas giant has played a significant role in shaping up the structure of this system.

HD 181433   The second system in which the 5:2 resonance can be present is HD 181433. The central star is a K3 subgiant with the effective temperature T eff = 4962 ± 134 K (Sousa et al. 2008), gravitational acceleration log (g) = 4.37 ± 0.26 and metallicity [Fe/H] = 0.33 ± 0.13. The mass of the star is around 0.78 M  ⊙ , the distance from the Sun 26.15 pc. There are three planets in this system: a super-Earth with the mass of 7.4  m  ⊕  and the orbital period of 9.4 days, a planet with the mass of 0.65 m J and period of 2.6 years and a planet with the mass of 0.53  m J with period of around 6 years. The stability of the system requires the occurrence of the commensurability between the periods of the giant planets.

As mentioned before, in the system HD 10180 there is also the possibility of the existence of the 3:1 resonance. At present we know three more systems in which the 3:1 resonance can occur. These are 55 Cnc, HD 60532 and υ Andromeda.

55 Cnc   55 Cnc (HD 75732) contains a star of late spectral type G or early type K, K0 IV-V (Gray et al. 2003) and five planets. The host star has effective temperature equal to 5196 ± 24 K, log g = 4.45 ± 0.01 (von Braun et al. 2011) and metallicity [Fe/H] = 0.31 ± 0.04 (Fischer and Valenti 2005). The mass and radius of the star are 0.905 ± 0.015 M  ⊙  and 0.943 ± 0.010 R  ⊙  respectively. The age of the star is evaluated to be 10.2 ± 2.5 × 109 years (von Braun et al. 2011). The dominant external planet is a gas giant with a minimal mass equal to 4 m J located at a distance of 5.8 AU from the star. Inside the gas giant orbit there are four less massive planets. The eccentricities of their orbits are very small, comparable to the eccentricities of the planets in the Solar System. The ratio of the orbital periods of planets b and c is 3.027 (Fischer et al. 2008), which might indicate the existence of the 3:1 mean-motion resonance.

HD 60532   HD 60532 has a completely different structure from that of 55 Cnc, as it contains two very massive gas giants close to the 3:1 resonance. The central star of this system is of spectral type F6 IV-V with effective temperature 6095 K, log(g) = − 3.83, and metallicity [Fe/H] = − 0.26. The mass of the star is 1.44 M  ⊙ , while its estimated age is equal to 2.7 ± 0.1 × 109 years. The distance from the Sun is 25.7 pc. Laskar and Correia (2009) have confirmed the existence of the 3:1 commensurability using the global dynamical analysis of the system. They have obtained the best fit for the resonance configuration and for their best fit they have got the stability of the system for at least 5 × 109 years. In Table 1 the parameters of the system are given for the inclination angle i ≈ 20o. Sandor and Kley (2010) have presented one of the possible scenarios for the formation of this system, which is in the very good agreement with the observational data.

υ And   Very recently, it has been suggested that there is the 3:1 resonance in the system υ And. υ And was the first multi-planet extrasolar system discovered with the central star being a main sequence star (Butler et al. 1999). It is a bright star of spectral type F8V with mass 1.3  M  ⊙  and radius 1.56  R  ⊙  (Butler et al. 1999). Its distance from the Sun is 13.47 pc (Perryman et al. 1997). The age of the star is 5 × 109 years (Baliunas et al. 1997). The system contains four planets plus the newly discovered υ And e (Curiel et al. 2011). In this system there is just a 3:1 resonance formed by this recently found planet and planet d (Chavez et al. 2011). The stability analysis performed by Chavez et al. (2011) confirmed the existence of this 3:1 commensurability and indicated the stability of its structure in timescales of the order of 5 × 108 years.

Now it is a turn for the 4:1 resonance, a third order commensurability. Close to this resonance there are planets located in the following systems: GJ 317, HD 108874 and HD 102272.

GJ 317   GJ 317 is a red dwarf of spectral type M3.5 located relatively close to the Sun, namely at a distance of 15.3 pc. The metallicity is equal to [Fe/H] = − 0.36 ± 0.2. The mass of the star is only 0.42 ± 0.05 M  ⊙  (Anglada-Escude et al. 2012). GJ 317 is the third M type star around which a gas giant planet has been detected. The existence of planet c with its orbital period of about 2700 days still requires confirmation.

HD 108874   HD 108874 consists of a G5 dwarf and two giant planets. The central star with metallicity [Fe/H] = 0.14 has the same mass of the Sun and its distance from our star is 68.5 pc (Butler et al. 2003). Goździewski et al. (2006) have confirmed that two gas giants in this system are close to the 4:1 resonance. In addition, similarly to the cases of the systems HR 8799, HD 82943, HD 128311 and HD 202206 (which will be discussed later in this section) in HD 108874 there is also a dusty debris disc (Dodson-Robinson et al. 2011).

HD 102272   In this system the giant planets are close to the 4:1 resonance. HD 102272 a is a giant star of spectral type K0. Its effective temperature is 4908 ± 35 K, log(g) = 3.07 ± 0.12 and the metallicity is [Fe/H] = − 0.26 ± 0.08. The mass of the star is 1.9 ± 0.3 M  ⊙  (Niedzielski et al. 2009) and the radius R = 10.1 ± 4.6 R  ⊙  (Alonso et al. 2000). Only one of the gas giants in this system is fully confirmed, namely the component b. The observational data are still not sufficient in order to demonstrate convincingly the existence of a second planet. The assumption that the two planets are close to the 4:1 resonance would significantly improve the stability of the configuration, which would remain stable during 109 years of evolution.

It is worth looking also at commensurabilities of order higher than three. Two systems might contain planets close to the 5:1 resonance: HD 17156 and HD 202206.

HD 17156   HD 17156 a is a star of spectral type G0 (Fischer et al. 2007), around which there is a planet on a very eccentric orbit, namely e = 0.68 (Fischer et al. 2007; Barbieri et al. 2009). The host star has effective temperature equal to T eff = 6079 ± 80 K and metallicity [Fe/H] = 0.24 ± 0.05 (Fischer et al. 2007). The mass of the star is 1.275 ± 0.018 M  ⊙  and its radius 1.508 ± 0.021 R  ⊙  (Nutzman et al. 2011). The announcement of the discovery of a planet c close to the 5:1 resonance has been reported in a paper which as for today is still unpublished (Short et al. 2008).

HD 202206   HD 202206 a is a star with very high metallicity [Fe/H] = 0.37 ± 0.07. Its spectral type is G6V, the distance from the Sun is 46.3 pc and its effective temperature amounts to T eff = 5765 K. The mass of the star is 1.044  M  ⊙  (Sousa et al. 2008), its age is of about 5.6 ± 1.2 × 109 years (Udry et al. 2002) or 4.2 × 109 years (Saffe et al. 2005). Also in this system a debris disc has been discovered (Moro-Martin et al. 2010). There are two planets: one very massive with minimal mass 16.6 m J and the second with 2.2  m J (Couetdic et al. 2010). In principle, the character of the most massive object is not certain: it can be both a very massive planet or a brown dwarf. The stability of the system is due to the 5:1 resonant configuration. However, despite many indications that such a resonance may exist in this system, one should bare in mind that at the moment it is just a hypothesis.

HD 208487   The highest resonance which has been observed is the sixth order 7:1 commensurability in HD 208487. The observed properties of the central star are the following: The star is a G2 dwarf (Saffe et al. 2005) with effective temperature 5929 ± 20 (Fischer and Valenti 2005), and metallicity [Fe/H] = 0.02 (Fischer and Valenti 2005). The mass of the star is 1.13  M  ⊙  and its age is 6.3–10 × 109 years. The masses of the planet are very similar to each other and their value is 0.4  m J . The presence of planet c is not confirmed yet (Gregory 2007).

Commensurabilities in the Kepler Data

Soon the list of the known resonant configurations will be much longer thanks to the numerous present and future observational programmes. For example using data from the first four months of the Kepler observations published by Borucki et al. (2011), Lissauer et al. (2011b) characterized tenths of multi-planet systems in which orbital periods indicate the presence of planets which are in or close to the mean-motion resonances. We have performed similar analysis in order to estimate how many sysyems observed by Kepler can host planets in the resonant configurations. We have addopted a restrictive assumption that two planets are in a resonance if the ratio of their orbital periods differs from the value corresponding to the exact resonance by less than 2.5%. In Table 2 we present the results showing how many candidates for the resonant configurations we could find concentrating on the strongest commensurabilities of the first and second order. The Kepler-11 and Kepler-9 are not included in the numbers as they have been discussed together with the confirmed objects. Our results are in a good agreement with the overall conclusions made by Lissauer et al. (2011b). Most of the multiple planet candidates are not close to any mean motion resonance, but some planet pairs have orbital periods within 2.5% of exact first order resonance ratios.

Table 2 The numbers of the planetary systems discovered by Kepler, but still not confirmed, containing the planets in the mean-motion resonance of a given type
Full size table

Summary

The interesting observational features of the architecture of the planetary systems are the resonant configurations. They can originate during the early phases of the system evolution, when the very common processes of orbital migration provide the conditions which favour the occurrence of the mean-motion commensurabilities. It is likely that they can carry the information about the conditions in the early state of the evolution of the protoplanetary disc from which planets are formed. This collection of systems containig planets in or close to the mean-motion resonances will be a starting point for a living database of the complete data on systems which possess this interesting property and will be helpful in uncovering the processes responsible for the diversity of the planetary architectures.