1 Introduction

Nonlinear optics research places significant emphasis on the study of optical solitons. Among the intriguing subjects of experimental and theoretical investigation is the behavior of short pulses as they propagate through optical fibers. The fundamental phenomena in this context are elucidated by the nonlinear Schrödinger equation (NLSE). However, the propagation of shorter pulses is influenced by various additional factors. One such detrimental circumstance is the presence of low chromatic dispersion, which occurs in optical pulse transmission. Neglecting the effects of dissipation and dispersion leads to the development of a wave-breaking singularity at a finite fiber length. Subsequently, the formal solution of nonlinear wave equations becomes multivalued and loses its physical significance. Several mathematical approaches have been employed to study various types of nonlinear dissipation, dispersion, self-steepening, and other perturbations, yielding promising results (e.g., Khater et al. 2018; Javid and Raza 2018; Jhangeer et al. 2021; Kopçasız and Yaşar 2023, 2024).

Distinguishable prototypes govern the dynamics of soliton propagation through optical waveguides, including fibers, couplers, metamaterials, and others. One of the prototypes suggested for dissecting these phenomena is the nonlinear Chen–Lee–Liu (CLL) equation, an NLSE commonly investigated in nonlinear optics because the CLL nonlinear equation can define propagation in a single-mode optical fiber (Triki et al. 2017; Biswas 2018; Kudryashov 2019; Arnous et al. 2022).

Technology and science have seen a rise in interest in fractional nonlinear differential equations (FNLDEs). These equations are mathematical prototypes for complex phenomena encountered in real-life scenarios and research areas such as robotics, neuroscience, optical fibers, plasma physics, fluid dynamics, and quantum mechanics. Exploring the wave solutions of these prototypes is paramount to comprehending the underlying phenomena and overwhelming theoretical barriers. Compared to integer-order equations, the analytical solutions of FNLDEs provide a more effective means of investigating complex matters (Khatun and Akbar 2023; Ouahid et al. 2023; Yépez-Martínez et al. 2021).

To comprehend and analyze the nonlinear evolution equations (NLEEs), many researchers have built analytical solutions for years, especially soliton solutions. Today, there are numerous reliable and well-developed methods for obtaining the exact and numerical solutions for NLEEs, including the generalized Riccati equation mapping method (Kumar and Niwas 2023), Kudryashov’s method (Kudryashov 2005), extended modified auxiliary equation mapping (Osman et al. 2022), improved modified Sardar sub-equation method (Khan et al. 2024), \(\exp (-\phi (\Omega ))\)-expansion method (Akram et al. 2023), improved F-expansion method (Akbar and Khatun 2023), Hirota bilinear method (Ur-Rehman and Ahmad 2022), modified rational sine-cosine method (Al-Shara et al. 2024), modified \((G^{\prime }/G)\)-expansion method (Alam et al. 2024), improved modified extended tanh function method (Ahmed et al. 2024), functional variable method (Kopçasız and Yaşar 2023), Jacobi elliptic rational function expansion method (ÇeliK 2024) and others (Wang et al. 2023; Younas et al. 2023; Iqbal et al. 2023; Sadaf et al. 2023; Asghari et al. 2024; Eslami et al. 2024).

In this study, we are dealing with the pCLL equation (Tarla et al. 2022; Khater et al. 2023; Seadawy et al. 2023; Faridi et al. 2022):

$$\begin{aligned} i\Phi _{t}+\beta \Phi _{xx}+i\alpha \left| \Phi \right| ^{2}\Phi _{x}=i\left[ \mu \Phi _{x}+\eta (\left| \Phi \right| ^{2a}\Phi )_{x}+\kappa (\left| \Phi \right| ^{2a})_{x}\Phi \right] , \end{aligned}$$
(1)

in which x and t are the spatial and temporal coordinates, \(\eta\) and \(\kappa\) stand for self-steeping for short pulses and nonlinear dispersion coefficient, respectively, and \(\mu\) represents the inter-model dispersion coefficient. \(\beta\) and \(\alpha\) represent the group velocity dispersion and the nonlinearity coefficient, respectively. The density of the complex wave function is specified by the variable a in the last Eq. (1). The CLL prototype has applications in optical couplers, optoelectronic devices, soliton cooling, and meta-materials and specifies the dynamics of solitary waves in optical fibers. Also, solutions to the equation mentioned above are beneficial in several fields of nonlinear sciences. These include fluid dynamics, optical engineering, oceanographic engineering, condensed matter physics, plasma physics, nonlinear dynamics, and many more areas of engineering, physics, and mathematics (Kumar and Niwas 2023; Baskonus et al. 2021; Yıldırım et al. 2020).

The truncated M-fractional Eq. (1) becomes

$$\begin{aligned}{} & {} i_{0}^{A}\wp _{t}^{\delta }(\Phi )+\beta _{0}^{A}\wp _{xx}^{\delta }(\Phi )+i\alpha \left| \Phi \right| ^{2}{}_{0}^{A}\wp _{x}^{\delta }(\Phi ) \nonumber \\{} & {} \quad =i\left[ \mu _{0}^{A}\wp _{x}^{\delta }(\Phi )+\eta _{0}^{A}\wp _{x}^{\delta }(\left| \Phi \right| ^{2}\Phi )_{x}+\kappa _{0}^{A}\wp _{x}^{\delta }(\left| \Phi \right| ^{2})_{x}\Phi \right] , \end{aligned}$$
(2)

at \(a=1\) (Faridi et al. 2022).

The primary aim of this paper is to use the nGERFM to generate new solutions with different wave structures for Eq. (2). Then, the bifurcation analysis, sensitivity analysis, chaos analysis, and multistability analysis of the related equation will be scrutinized.

The paper is structured as follows: Sect. 1 provides an introduction. Section 2 describes the scheme and application. Section 3 covers the bifurcation analysis, sensitivity analysis, chaos analysis, and multistability analysis of the governing equation. Section 4 offers comparisons, and Sect. 5 presents conclusions.

2 Construction of analytical solutions

A new version of the generalized exponential rational function method (nGERFM) used for the modified M-truncated form of the pCLL equation allows the generation of diverse solitons.

2.1 Description of the nGERFM

This part regards the nGERFM, examined in Ghanbari (2021). Utilizing the strategy is mainly based on the subsequent framework (Ghanbari and Baleanu 2023).

Let us explore the following PDE

$$\begin{aligned} Q_{1}[\Phi ,\Phi _{t},\Phi _{x},\Phi _{tt},\Phi _{xx},...]=0. \end{aligned}$$
(3)

Using \(\Phi =\Phi (x,t)=\Upsilon (\xi )\), and \(\xi =rx-yt\), Eq. (3) is transferred to

$$\begin{aligned} Q_{2}[\Upsilon (\xi ),-y\frac{\partial \Upsilon (\xi )}{\partial \xi },r \frac{\partial \Upsilon (\xi )}{\partial \xi },y^{2}\frac{\partial ^{2}\Upsilon (\xi )}{\partial \xi ^{2}},r^{2}\frac{\partial ^{2}\Upsilon (\xi )}{\partial \xi ^{2}},...]=0. \end{aligned}$$
(4)

This practice contains a symbolic design for the solution, characterized as pursues

$$\begin{aligned} \Upsilon (\xi )=z_{0}+\sum _{n=1}^{n_{0}}z_{n}\left( \frac{\Lambda ^{\prime }(\xi )}{\Lambda (\xi )}\right) ^{n}+\sum _{n=1}^{n_{0}}s_{n}\left( \frac{ \Lambda ^{\prime }(\xi )}{\Lambda (\xi )}\right) ^{-n}, \end{aligned}$$
(5)

in which

$$\begin{aligned} \Lambda (\xi )=\frac{\varsigma _{1}\exp (\jmath _{1}\xi )+\varsigma _{2}\exp (\jmath _{2}\xi )}{\varsigma _{3}\exp (\jmath _{3}\xi )+\varsigma _{4}\exp (\jmath _{4}\xi )}. \end{aligned}$$
(6)

Unknown coefficients \(z_{0},z_{n},s_{n}(1\le n\le n_{0})\) and \(\varsigma _{i},\jmath _{i}\) \((1\le i\le 4)\) are real (or complex) constants to be assessed, such that (5) fulfills the Eq. (4). Additionally, the positive integer \(n_{0}\) is computed by the principles of balancing. Inserting (5) along with (6) into Eq. (4) and gathering all terms, the left-hand side of the resulting equation is altered into a polynomial equation \(\Pi (\Xi _{1},\Xi _{2},\Xi _{3},\Xi _{4})=0\) as to \(\Xi _{r}=\exp (\jmath _{r}\xi )\) for \(r=1,2,3,4.\) We arrive at a set of algebraic equations by taking each coefficient of \(\Pi\) to zero. By using a symbolic computation tool to solve these algebraic equations and then introducing non-trivial solutions into (5), the explicit form of the solutions to Eq. (3) can be obtained.

2.2 Application of the offered method

We employ the fractional traveling wave transformation to identify solutions to Eq. (2)

$$\begin{aligned} \Phi (x,t)=\Upsilon (\xi )\exp (i\phi ),{ \ \ }\xi =\frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta }),{ \ \ }\phi (x,t)=\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta ). \end{aligned}$$
(7)

Equation (2) is subjected to the traveling wave transformation (7), resulting in an ordinary differential equation (ODE)

$$\begin{aligned}{} & {} i\tau \Upsilon ^{\prime }-n\Upsilon +\beta \Upsilon ^{\prime \prime }-2im\beta \Upsilon ^{\prime }-m^{2}\beta \Upsilon +i\alpha \Upsilon ^{\prime }\Upsilon ^{2}+m\alpha \Upsilon ^{3}-i\mu \Upsilon ^{\prime }-m\mu \Upsilon \nonumber \\{} & {} \quad -3i\eta \Upsilon ^{\prime }\Upsilon ^{2}-m\eta \Upsilon ^{3}-2i\kappa \Upsilon ^{\prime }\Upsilon ^{2}=0. \end{aligned}$$
(8)

The real and imaginary components of the above ODE can be obtained as follows

$$\begin{aligned}{} & {} m(\alpha -\eta )\Upsilon ^{3}+\beta \Upsilon ^{\prime \prime }-(n+\beta m^{2}+\mu m)\Upsilon =0, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} (\alpha -3\eta -2\kappa )\Upsilon ^{\prime }\Upsilon ^{2}-(\tau +2\beta m+\mu )\Upsilon ^{\prime }=0. \end{aligned}$$
(10)

We have \(\alpha =3\eta +2\kappa\), \(\tau =-(2\beta m+\mu )\) from Eq. (10 ), and when we insert them into Eq. (9), then Eq. (9) becomes as follows

$$\begin{aligned} \beta \Upsilon ^{\prime \prime }-(n+\beta m^{2}+\mu m)\Upsilon +2m(\kappa +\eta )\Upsilon ^{3}=0. \end{aligned}$$
(11)

Employing some common balancing rules in Eq. (11) between \(\Upsilon ^{3}\) and \(\Upsilon ^{\prime \prime }\) yields \(3n_{0}=n_{0}+2\). Hence, one should take \(n_{0}=1\). As a result (5) can be written as

$$\begin{aligned} \Upsilon (\xi )=z_{0}+z_{1}\left( \frac{\Lambda ^{\prime }(\xi )}{\Lambda (\xi )}\right) +s_{1}\left( \frac{\Lambda ^{\prime }(\xi )}{\Lambda (\xi )} \right) ^{-1}. \end{aligned}$$
(12)

\(\Lambda (\xi )\) is defined by (6).

Class 1

Taking \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[1,1,1,0]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[0,1,-2,0]\) in (6) yields

$$\begin{aligned} \Lambda (\xi )=\frac{1+\exp (\xi )}{\exp (-2\xi )}. \end{aligned}$$
(13)

To obtain parameter values, we use package programs (Maple or Mathematica) to solve algebraic equations. The set of answers that are produced can be provided as

Type 1.1

$$\begin{aligned} m= & {} \mp \frac{\beta +2n}{\mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} \mp \frac{5\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)},\\ z_{1}= & {} \pm \frac{\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{(\kappa +\eta )(\beta +2n)},{ \ \ } s_{1}=0. \end{aligned}$$

By plugging the aforementioned values of \(z_{0}\), \(z_{1}\), \(s_{1}\) into (12), we get

$$\begin{aligned} \Upsilon (\xi )=\frac{\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)}\times \frac{ \exp (\xi )-1}{\exp (\xi )+1}. \end{aligned}$$
(14)

The exponential function may be expressed by combining (14) with (7)

$$\begin{aligned} \Phi _{1,1}(x,t)= & {} \frac{\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{ -2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)} \nonumber \\{} & {} \times \frac{\exp \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) -1}{\exp \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) +1} \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(15)

in which \(m=\mp \frac{\beta +2n}{\mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}}.\)

Type 1.2

$$\begin{aligned} m= & {} \mp \frac{\beta +2n}{\mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} \pm \frac{5\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)},\\ z_{1}= & {} 0,\; s_{1}=\mp \frac{6\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu + \sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{(\kappa +\eta )(\beta +2n)}. \end{aligned}$$

By plugging the aforementioned values of \(z_{0}\), \(z_{1}\), \(s_{1}\) into (12), we get

$$\begin{aligned} \Upsilon (\xi )=\frac{\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)}\times \frac{ (3\exp (\xi )-2)}{(3\exp (\xi )+2)}. \end{aligned}$$
(16)

Using the (16) and (7), the exponential function the solution is found as

$$\begin{aligned} \Phi _{1,2}(x,t)= & {} \frac{\sqrt{(\kappa +\eta )(\beta +2n)\left( \mu +\sqrt{ -2\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(\beta +2n)} \nonumber \\{} & {} \times \frac{\left( 3\exp \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) -2\right) }{\left( 3\exp \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) +2\right) } \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(17)

where \(m=\mp \frac{\beta +2n}{\mu +\sqrt{-2\beta ^{2}-4\beta n+\mu ^{2}}}.\)

Class 2

When we pick \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[1,-1,2i,0]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[i,-i,1,0]\) in (6), we attain

$$\begin{aligned} \Lambda (\xi )=\frac{\sin (\xi )}{\exp (\xi )}. \end{aligned}$$
(18)

Using package programs, we solve algebraic equations to acquire parameter values; the set of answers that arise can be provided as

$$\begin{aligned} m= & {} \mp \frac{2(2\beta -n)}{-\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)},\\ z_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)},{ \ \ } s_{1}=0. \end{aligned}$$

By plugging these values into (12), we yield

$$\begin{aligned} \Upsilon (\xi )=\frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{ 8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)}\times \cot \left( \xi \right) . \end{aligned}$$
(19)

We obtain the singular periodic optical soliton solution by combining (19) with (7)

$$\begin{aligned} \Phi _{2}(x,t)= & {} \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{ 8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)} \nonumber \\{} & {} \times \cot \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \nonumber \\{} & {} \times \exp (i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )), \end{aligned}$$
(20)

in which \(m=\mp \frac{2(2\beta -n)}{-\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2} }}.\)

Class 3

For \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[1,-1,2,0]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[1,-1,-1,0]\) in (6) provides

$$\begin{aligned} \Lambda (\xi )=\frac{\sinh (\xi )}{\exp (-\xi )}. \end{aligned}$$
(21)

Proceeding as the outline of nGERFM, we achieve

$$\begin{aligned} m= & {} \mp \frac{2(2\beta +n)}{\mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta +n)\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta +n)},\\ z_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta +n)\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta +n)},{ \ \ } s_{1}=0. \end{aligned}$$

By plugging these values into (12), we reach

$$\begin{aligned} \Upsilon (\xi )=-\frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta +n)\left( \mu +\sqrt{ -8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta +n)}\times \tanh \left( \xi \right) . \end{aligned}$$
(22)

By using the (22) together with (7), then we obtain the shock wave solution as

$$\begin{aligned} \Phi _{3}(x,t)= & {} -\frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta +n)\left( \mu +\sqrt{ -8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta +n)} \nonumber \\{} & {} \times \tanh \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(23)

where \(m=\mp \frac{2(2\beta +n)}{\mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}}.\)

Class 4

In (6), picking \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[2,0,1,1]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[1,0,i,-i]\) produces

$$\begin{aligned} \Lambda (\xi )=\frac{\exp (\xi )}{\cos (\xi )}. \end{aligned}$$
(24)

We also arrive at

$$\begin{aligned} m= & {} \mp \frac{2(2\beta -n)}{-\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} \mp \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)},\\ z_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)},\; s_{1}=0. \end{aligned}$$

Combining these results with (12) generates

$$\begin{aligned} \Upsilon (\xi )=\frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{ 8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)}\times \tan \left( \xi \right) . \end{aligned}$$
(25)

As an outcome, we uncover that the singular periodic solution may be characterized as

$$\begin{aligned} \Phi _{4}(x,t)= & {} \frac{\sqrt{2}\sqrt{(\kappa +\eta )(2\beta -n)\left( -\mu +\sqrt{ 8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(2\beta -n)} \nonumber \\{} & {} \times \tan \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \nonumber \\{} & {} \times \exp (i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )), \end{aligned}$$
(26)

in which \(m=\mp \frac{2(2\beta -n)}{-\mu +\sqrt{8\beta ^{2}-4\beta n+\mu ^{2} }}.\)

Class 5

In (6), considering \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[2,0,1,1]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[0,0,1,-1]\) create

$$\begin{aligned} \Lambda (\xi )=\frac{1}{\cosh (\xi )}. \end{aligned}$$
(27)

We accomplish

Type 5.1

$$\begin{aligned} m= & {} \mp \frac{2(4\beta -n)}{-\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}},{ \ \ }z_{0}=0,\\ z_{1}= & {} \pm \frac{\sqrt{2}(\kappa +\eta )(4\beta -n)\left( \mu \sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}+2\beta n-\mu ^{2}\right) \beta ^{2}}{\left( (\kappa +\eta )(4\beta -n)\left( -\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta \right) ^{\frac{3}{2}}},\\ s_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(4\beta -n)\left( -\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(4\beta -n)}. \end{aligned}$$

By plugging the values of \(z_{0}\), \(z_{1}\), \(s_{1}\) into (12), we gain

$$\begin{aligned} \Upsilon (\xi )= & {} \frac{\beta \sqrt{2}\left( \mu \sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}+2\beta n-\mu ^{2}\right) }{\sqrt{(\kappa +\eta )(4\beta -n)\left( -\mu + \sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }\left( -\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{1}{\sinh \left( \xi \right) \cosh \left( \xi \right) }. \end{aligned}$$
(28)

Hence, we uncover the combo soliton solutions can be derived as

$$\begin{aligned} \Phi _{5,1}(x,t)= & {} \frac{\beta \sqrt{2}\left( \mu \sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}+2\beta n-\mu ^{2}\right) }{\sqrt{(\kappa +\eta )(4\beta -n)\left( -\mu + \sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }\left( -\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{1}{\sinh \left( \frac{\lambda [\rho +1]}{\delta } (x^{\delta }-\tau t^{\delta })\right) \cosh \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) } \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(29)

where \(\mp \frac{2(4\beta -n)}{-\mu +\sqrt{16\beta ^{2}-4\beta n+\mu ^{2}}}.\)

Type 5.2

We get,

$$\begin{aligned} m= & {} \mp \frac{2(8\beta +n)}{\mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}}, \ \ z_{0}=0,\\ z_{1}= & {} \pm \frac{\sqrt{2}(\kappa +\eta )(8\beta +n)\left( \mu \sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}-16\beta ^{2}-2\beta n+\mu ^{2}\right) \beta ^{2}}{\left( (\kappa +\eta )(8\beta +n)(\mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}})\beta \right) ^{\frac{3}{2}}},\\ s_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(8\beta +n)\left( \mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(8\beta +n)}. \end{aligned}$$

Thus, concerning these solutions and (12), it is likely to reach the subsequent outcome

$$\begin{aligned} \Upsilon (\xi )= & {} -\frac{ \begin{array}{c} \beta \sqrt{2}\left( \mu \sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}} \right. \\ \left. -16\beta ^{2}-2\beta n+\mu ^{2}\right) \end{array} }{\sqrt{(\kappa +\eta )(8\beta +n)\left( \mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2} }\right) \beta }\left( \mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{(2\cosh \left( \xi \right) ^{2}-1)}{(\sinh \left( \xi \right) \cosh \left( \xi \right) )}. \end{aligned}$$
(30)

The mixed form soliton solution may be expressed by combining (30) with (7)

$$\begin{aligned} \Phi _{5,2}(x,t)= & {} -\frac{\beta \sqrt{2}\left( \mu \sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}-16\beta ^{2}-2\beta n+\mu ^{2}\right) }{\sqrt{(\kappa +\eta )(8\beta +n)\left( \mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }\left( \mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{(2\cosh \left( \frac{\lambda [\rho +1]}{\delta } (x^{\delta }-\tau t^{\delta })\right) ^{2}-1)}{(\sinh \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \cosh \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) )} \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(31)

in which \(\mp \frac{2(8\beta +n)}{\mu +\sqrt{-32\beta ^{2}-4\beta n+\mu ^{2}} }.\)

Class 6

As long as, and if it is taken into account in (6), \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[2,0,1,1]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[-2,0,1,-1]\) generates

$$\begin{aligned} \Lambda (\xi )=\frac{\exp (-2\xi )}{\cosh (\xi )}. \end{aligned}$$
(32)

We obtain,

$$\begin{aligned} m= & {} \pm \frac{-\mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}}{2\beta },\\ z_{0}= & {} \mp \sqrt{2}\sqrt{\frac{\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}} \right) \beta }{(\kappa +\eta )(2\beta +n)}},\\ z_{1}= & {} 0,{ \ \ }s_{1}=\frac{3\sqrt{2}}{2}\sqrt{\frac{\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }{(\kappa +\eta )(2\beta +n)}}. \end{aligned}$$

By entering the values of \(z_{0}\), \(z_{1}\), \(s_{1}\) into (12), one obtains

$$\begin{aligned} \Upsilon (\xi )=\frac{\sqrt{2}}{2}\sqrt{\frac{\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }{(\kappa +\eta )(2\beta +n)}}\times \frac{ \left( \cosh (\xi )+2\sinh (\xi )\right) }{2(2\cosh (\xi )+\sinh (\xi ))}. \end{aligned}$$
(33)

The hyperbolic solution in mixed form may be stated as follows by using (33) and (7)

$$\begin{aligned} \Phi _{6}(x,t)= & {} \frac{\sqrt{2}}{2}\sqrt{\frac{\left( \mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }{(\kappa +\eta )(2\beta +n)}} \nonumber \\{} & {} \times \frac{\left( \cosh (\frac{\lambda [\rho +1]}{\delta } (x^{\delta }-\tau t^{\delta }))+2\sinh \left( \frac{\lambda [\rho +1]}{ \delta }(x^{\delta }-\tau t^{\delta })\right) \right) }{2\left( 2\cosh \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) +\sinh \left( \frac{ \lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \right) } \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(34)

where \(m=\pm \frac{-\mu +\sqrt{-8\beta ^{2}-4\beta n+\mu ^{2}}}{2\beta }.\)

Class 7

If we take \([\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4}]=[1,1,2,0]\) and \([\jmath _{1},\jmath _{2},\jmath _{3},\jmath _{4}]=[i,-i,0,0]\) in (6) offers

$$\begin{aligned} \Lambda (\xi )=\cos (\xi ). \end{aligned}$$
(35)

We have,

$$\begin{aligned} m= & {} \mp \frac{2(4\beta +n)}{\mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}},\\ z_{0}= & {} 0, \, \, z_{1}=\pm \frac{\beta ^{2}\sqrt{2}(\kappa +\eta )(4\beta +n)\left( \mu \sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}-2\beta n+\mu ^{2}\right) }{\left( (\kappa +\eta )(4\beta +n)\left( \mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta \right) ^{\frac{3}{2}}}\\ s_{1}= & {} \pm \frac{\sqrt{2}\sqrt{(\kappa +\eta )(4\beta +n)\left( \mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }}{2(\kappa +\eta )(4\beta +n)}. \end{aligned}$$

If these outcomes are taken into account along with (12), the next result is got

$$\begin{aligned} \Upsilon (\xi )= & {} -\frac{\beta \sqrt{2}\left( \mu \sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}-2\beta n+\mu ^{2}\right) }{\sqrt{(\kappa +\eta )(4\beta +n)\left( \mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }\left( \mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{1}{\sin (\xi )\cos (\xi )}. \end{aligned}$$
(36)

Thus, by combining (36) with (7), we have the following periodic solution

$$\begin{aligned} \Phi _{7}(x,t)= & {} -\frac{\beta \sqrt{2}\left( \mu \sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}-8\beta ^{2}-2\beta n+\mu ^{2}\right) }{\sqrt{(\kappa +\eta )(4\beta +n)\left( \mu + \sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) \beta }\left( \mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}\right) } \nonumber \\{} & {} \times \frac{1}{\sin \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) \cos \left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })\right) } \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) , \end{aligned}$$
(37)

in which \(m=\mp \frac{2(4\beta +n)}{\mu +\sqrt{-16\beta ^{2}-4\beta n+\mu ^{2}}}.\)

3 The probe of bifurcation, sensitivity analysis, chaos analysis, and multistability analysis of the governing equation

In this part, an exhaustive investigation of bifurcation analysis, sensitivity analysis, chaos analysis, and multistability analysis is provided for the governing equation. In addition, the dispersive optical solitons and traveling wave solutions are derived via the dynamical theory method.

3.1 Bifurcation analysis

In this subsection, we offer the bifurcation analysis, including phase portraits, of the dynamical system given by Eq. (2).

Equation (11) defined as:

$$\begin{aligned} \beta \Upsilon ^{\prime \prime }-(n+\beta m^{2}+\mu m)\Upsilon +2m(\kappa +\eta )\Upsilon ^{3}=0. \end{aligned}$$

Let’s modify Eq. (11) to make things simpler

$$\begin{aligned} \Upsilon ^{\prime \prime }-\frac{(n+\beta m^{2}+\mu m)}{\beta }\Upsilon + \frac{2m(\kappa +\eta )}{\beta }\Upsilon ^{3}=0. \end{aligned}$$
(38)

Denote \(\Upsilon ^{\prime }=T\) in Eq. (38) to obtain the planar differential dynamical system (PDDS), which is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\Upsilon }{d\xi }=T, \\ \frac{dT}{d\xi }=-\varpi _{1}\Upsilon ^{3}+\varpi _{2}\Upsilon , \end{array}\right. } \end{aligned}$$
(39)

with the following Hamiltonian function:

$$\begin{aligned} H(\Upsilon ,T)=\frac{1}{2}T^{2}+\frac{\varpi _{1}}{4}\Upsilon ^{4}-\frac{ \varpi _{2}}{2}\Upsilon ^{2}=h, \end{aligned}$$
(40)

in which h is the Hamiltonian constant, \(\frac{2\,m(\kappa +\eta )}{\beta } =\varpi _{1}\) and \(\frac{(n+\beta m^{2}+\mu m)}{\beta }=\varpi _{2}.\)

The system’s dynamical behavior and phase portraits (39) are meticulously examined using the bifurcation theory of PDDSs (Li and DAI 2007; Li 2013). Let \(F(\Upsilon )=-\varpi _{1}\Upsilon ^{3}+\varpi _{2}\Upsilon .\)

We may obtain one zero of \(F(\Upsilon )\), which is \(\Upsilon _{3}=0\), if \(\varpi _{1}\varpi _{2}<0\).

If \(\varpi _{1}\varpi _{2}>0\), we may easily get the three zeros of \(F(\Upsilon )\), which are \(\Upsilon _{0}=0,\ \Upsilon _{1}=-\sqrt{\frac{ \varpi _{2}}{\varpi _{1}}}\), \(\Upsilon _{3}=\sqrt{\frac{\varpi _{2}}{\varpi _{1}}}\). Assuming that the equilibrium points of system (39) are \(\chi _{i}(\Upsilon _{i},0)\) \((i=0,1,2)\), the eigenvalue of system (39) at equilibrium may be written as \(\bar{\lambda }_{1,2}=\pm \sqrt{F^{\prime }(\Upsilon )}.\)

For the equilibrium point \(\chi _{i}(\Upsilon _{i},0),\) the bifurcation theory of PDDSs (Aranson and Kramer 2002) states that

(i) when \(F^{\prime }(\Upsilon _{i})>0\), \(\chi _{i}(\Upsilon _{i},0)\) is referred to as the saddle point,

(ii) when \(F^{\prime }(\Upsilon _{i})=0\), the saddle point \(\chi _{i}(\Upsilon _{i},0)\) is said to be degraded,

(iii) center point is defined as \(\chi _{i}(\Upsilon _{i},0)\) when \(F^{\prime }(\Upsilon _{i})<0.\)

Case 1.1 \(\varpi _{1}>0\), \(\varpi _{2}>0\)

It is simple to see that in this situation, the origin \(M_{0}(0,0)\) is the saddle point, and \(\chi _{1}(-\sqrt{\frac{\varpi _{2}}{\varpi _{1}}},0)\) and \(\chi _{2}(\sqrt{\frac{\varpi _{2}}{\varpi _{1}}},0)\) are the center points.

(i) When \(h\in (-\frac{\varpi _{2}^{2}}{4\varpi _{1}},0),\) periodic orbits can be obtained in two groups. Then, (40) is characterized as

$$\begin{aligned} T^{2}= & {} \frac{\varpi _{1}}{2}\left( -\Upsilon ^{4}+\frac{2\varpi _{2}}{ \varpi _{1}}\Upsilon ^{2}+\frac{4h}{\varpi _{1}}\right) \nonumber \\= & {} \frac{\varpi _{1}}{2}\left( \Upsilon ^{2}-\vartheta _{1}^{2}\right) (\vartheta _{2}^{2}-\Upsilon ^{2}), \end{aligned}$$
(41)

in which \(\vartheta _{1}^{2}=\frac{\varpi _{2}}{\varpi _{1}}-\frac{1}{\varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h})\), \(\vartheta _{2}^{2}=\frac{ \varpi _{2}}{\varpi _{1}}+\frac{1}{\varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h})\).

The following two integral equations are obtained by inserting (41) into the first equation of (39) and integrating them along the periodic orbits

$$\begin{aligned} \int _{\Upsilon }^{\vartheta _{2}}\frac{d\Xi }{\sqrt{(\Xi ^{2}-\vartheta _{1}^{2})(\vartheta _{2}^{2}-\Xi ^{2})}}=\pm \sqrt{\frac{\varpi _{1}}{2}} (\xi -\xi _{0}), \end{aligned}$$
(42)

and

$$\begin{aligned} \int _{-\vartheta _{2}}^{\Upsilon }\frac{d\Xi }{\sqrt{(\Xi ^{2}-\vartheta _{1}^{2})(\vartheta _{2}^{2}-\Xi ^{2})}}=\pm \sqrt{\frac{\varpi _{1}}{2}} (\xi -\xi _{0}). \end{aligned}$$
(43)

(42) and (43) allow us to obtain the smooth wave solution in the following form

$$\begin{aligned} \Phi _{1,1}(x,t)= & {} \pm \vartheta _{2}dn\left( \vartheta _{2}\sqrt{\frac{ \varpi _{1}}{2}}\left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })-\xi _{0}\right) ,\frac{\sqrt{\vartheta _{2}^{2}-\vartheta _{1}^{2}}}{ \vartheta _{2}}\right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) . \end{aligned}$$
(44)

Obviously, \(\Phi _{1,1}(x,t)\) stands for the Jacobian elliptic function solution.

(ii) If \(h=0\), we obtain that \(\vartheta _{1}^{2}=0\) ve \(\vartheta _{2}^{2}=\frac{2\varpi _{2}}{\varpi _{1}}\). As a result, we create two families of solutions to Eq. (2) that have bell-shaped solitary waves

$$\begin{aligned} \Phi _{1,2}(x,t)= & {} \pm \sqrt{\frac{2\varpi _{2}}{\varpi _{1}}}\sec h\left( \sqrt{\varpi _{2}}\left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })-\xi _{0}\right) \right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) . \end{aligned}$$
(45)

(iii) If \(0<h<+\infty\), the equation of (39) can be re-written as

$$\begin{aligned} T^{2}= & {} \frac{\varpi _{1}}{2}\left( -\Upsilon ^{4}+\frac{2\varpi _{2}}{ \varpi _{1}}\Upsilon ^{2}+\frac{4h}{\varpi _{1}}\right) \nonumber \\= & {} \frac{\varpi _{1}}{2}\left( \Upsilon ^{2}+\vartheta _{3}^{2}\right) (\vartheta _{4}^{2}-\Upsilon ^{2}), \end{aligned}$$
(46)

in which \(\vartheta _{3}^{2}=-\frac{\varpi _{2}}{\varpi _{1}}+\frac{1}{ \varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h}\), \(\vartheta _{4}^{2}=\frac{ \varpi _{2}}{\varpi _{1}}+\frac{1}{\varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h}\).

By integrating the first equation of system (39) using equation (46), the following integral equation may be found

$$\begin{aligned} \int _{0}^{\Upsilon }\frac{d\Xi }{\sqrt{(\Xi ^{2}+\vartheta _{3}^{2})(\vartheta _{4}^{2}-\Xi ^{2})}}=\pm \sqrt{\frac{\varpi _{1}}{2}} (\xi -\xi _{0}). \end{aligned}$$
(47)

We create two families of periodic wave solutions by (47) in the manner described below

$$\begin{aligned} \Phi _{1,3}(x,t)= & {} \pm \vartheta _{4}cn\left( \sqrt{\frac{\varpi _{1}(\vartheta _{3}^{2}+\vartheta _{4}^{2})}{2}}\left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })-\xi _{0}\right) ,\frac{\vartheta _{4}}{ \sqrt{\vartheta _{3}^{2}+\vartheta _{4}^{2}}}\right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) . \end{aligned}$$
(48)

Case 1.2 \(\varpi _{1}<0\), \(\varpi _{2}<0\)

It is noteworthy in this instance to discover two heteroclinic orbits of the system (39), which link two saddle points, \(\chi _{1}(-\sqrt{\frac{ \varpi _{2}}{\varpi _{1}}},0),\) and \(\chi _{2}(\sqrt{\frac{\varpi _{2}}{ \varpi _{1}}},0)\), and where \(\chi _{0}(0,0)\) is the center.

(i) There is a family of periodic orbits for system (39) when \(0<h<-\frac{\varpi _{2}^{2}}{4\varpi _{1}}\), and they are characterized by the algebraic equation is shown in the following form

$$\begin{aligned} T^{2}= & {} -\frac{\varpi _{1}}{2}\left( \Upsilon ^{4}+\frac{2\varpi _{2}}{ \varpi _{1}}\Upsilon ^{2}-\frac{4h}{\varpi _{1}}\right) \nonumber \\= & {} -\frac{\varpi _{1}}{2}\left( -\Upsilon ^{2}+\vartheta _{1h}^{2}\right) (\vartheta _{2h}^{2}-\Upsilon ^{2}). \end{aligned}$$
(49)

in which \(\vartheta _{1\,h}^{2}=\frac{\varpi _{2}}{\varpi _{1}}-\frac{1}{ \varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h})\), \(\vartheta _{2\,h}^{2}= \frac{\varpi _{2}}{\varpi _{1}}+\frac{1}{\varpi _{1}}\sqrt{\varpi _{2}^{2}+4\varpi _{1}h})\).

Plugging (49) into the first equation of the (39) and integrating them along the periodic orbits, we have

$$\begin{aligned} \int _{0}^{\Upsilon }\frac{d\Xi }{\sqrt{(-\Xi ^{2}+\vartheta _{1h}^{2})(\vartheta _{2h}^{2}-\Xi ^{2})}}=\pm \sqrt{-\frac{\varpi _{1}}{2}} (\xi -\xi _{0}). \end{aligned}$$
(50)

Here \(\xi _{0}\) is an integral constant. We generate the periodic wave solutions of Eq. (2) as follows using the (7) and (50)

$$\begin{aligned} \Phi _{1,4}(x,t)= & {} \pm \vartheta _{1h}sn\left( \vartheta _{2h}\sqrt{-\frac{ \varpi _{1}}{2}}\left( \frac{\lambda [\rho +1]}{\delta }(x^{\delta }-\tau t^{\delta })-\xi _{0}\right) ,\frac{\vartheta _{1h}}{\vartheta _{2h}}\right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) . \end{aligned}$$
(51)

(ii) In the case when \(h=-\frac{\varpi _{2}^{2}}{4\varpi _{1}}\), \(\vartheta _{1\,h}^{2}=\) \(\vartheta _{2\,h}^{2}=\frac{\varpi _{2}}{\varpi _{1}}\) is evident. Namely, we derive two families of kink-shaped solitary wave solutions of solutions Eq. (2) as follows

$$\begin{aligned} \Phi _{1,5}(x,t)= & {} \pm \sqrt{\frac{\varpi _{2}}{\varpi _{1}}}\tan h\left( \sqrt{-\frac{\varpi _{2}}{2}}\left( \frac{\lambda [\rho +1]}{\delta } (x^{\delta }-\tau t^{\delta })-\xi _{0}\right) \right) \nonumber \\{} & {} \times \exp \left( i\frac{\lambda [\rho +1]}{\delta }(-mx^{\delta }+nt^{\delta }+\theta )\right) . \end{aligned}$$
(52)

3.2 Sensitivity analysis

In this section, we operate the Runge–Kutta method to scrutinize the sensitivity of the dynamical system described by (39) (Jhangeer et al. 2022). (39) is chosen for investigation in this subsection utilizing sensitivity inspections. Keeping the parameters as they are in Figs. 1, 2, 3, 4 and 5, respectively, yields five non-identical initial values. It may be shown that (39) exhibits a quasi-periodic pattern under the initial tested circumstances.

Fig. 1
figure 1

Plot of the sensitivity of the dynamical structure (39) for \((\Upsilon (0),T(0))=(0.2,0.0)\) in the red hue, and \((\Upsilon (0),T(0))=(0.1,0.0)\) in the black hue

Full size image
Fig. 2
figure 2

Plot of the sensitivity of the dynamical structure (39) for \((\Upsilon (0),T(0))=(0.29,0.0)\) in the red hue, and \((\Upsilon (0),T(0))=(0.13,0.0)\) in the black hue

Full size image
Fig. 3
figure 3

Plot of the sensitivity of the dynamical structure (39) for \((\Upsilon (0),T(0))=(0.029,0.0)\) in the red hue, and \((\Upsilon (0),T(0))=(0.013,0.0)\) in the black hue

Full size image
Fig. 4
figure 4

Plot of the sensitivity of the dynamical structure (39) for \((\Upsilon (0),T(0))=(0.01,0.0)\) in the red hue, and \((\Upsilon (0),T(0))=(1.01,0.0)\) in the black hue

Full size image
Fig. 5
figure 5

Plot of the sensitivity of the dynamical structure (39) for \((\Upsilon (0),T(0))=(0.001,0.0)\) in the red hue, and \((\Upsilon (0),T(0))=(1.001,0.0)\) in the black hue

Full size image

Remark 1

It is evident from the figures that even minor modifications to the starting conditions result in significant shifts in the system’s behavior.

3.3 Chaotic and quasi-periodic actions

The models’ chaotic and quasi-periodic performances will be examined in this paragraph (Jhangeer et al. 2022). In the ensuing segment, we present a model to implement chaotic and quasi-periodic booming waving for the waves of perturbed dynamical systems. We offer a perturbation term to estimate distributed simulation tasks, including time series analysis, sensitivity analysis, and phase portrait analysis in three dimensions, and to understand the dynamic schemes of nonlinear and super-nonlinear periodic waves. By introducing the perturbation term \(\varsigma ,\) (39) can be expressed in the following system (including \(\varsigma \cos (\gamma \xi )\)) : 

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\Upsilon }{d\xi }=T, \\ \frac{dT}{d\xi }=-\varpi _{1}\Upsilon ^{3}+\varpi _{2}\Upsilon +\varsigma \cos (\gamma \xi ). \end{array}\right. } \end{aligned}$$
(53)

Here, the external perturbation term’s frequency is represented by \(\xi\), and its intensity by \(\varsigma\). Also, (53) is called the nonlinear dynamical system (NLDS). To explore the quasi-periodic and chaotic form, we use time series analytic methods and phase pictures. While the mechanism ( 39) does not exhibit the periodic surface force, NLDS (53) does. We will look at how the frequency term impacts the model in the question in this piece. We examine the reactions of force and frequency on the perturbations while maintaining the physical features of the global assessment.

In Fig. 6, two, and three-dimensional phase portraits, the Poincare section, and the time-series graph are offered for \((\varsigma ,\gamma )=(3.3,3.98).\) The NLDS (53) is found to have chaotic behavior. The time-series picture also demonstrates a waveform, which validates the chaotic behavior at specific physical parameters. We created two, and three-dimensional phase pictures, a time-series graph, and a Poincare section with \(\gamma =0.6\) operating the same settings as in Fig. 7. For \(\gamma =0.6\), NLDS (53) is assumed to have chaotic behavior.

We visualized the three-dimensional phase portraits and time-series graphs operating the same additional settings as Fig. 8, as demonstrated in Fig. 7 for \(\gamma =0.12\). The NLDS (53) that is altered demonstrates quasi-periodic-chaotic characteristics. These particular combinations of factors create a unique pattern that supports the presence of a quasi-periodic-chaotic framework.

Fig. 6
figure 6

The NLDS for \(\varpi _{1}=1.2,\) \(\varpi _{2}=1.56,\) \(\varsigma =3.3,\) and \(\gamma =3.98\) with the initial condition \((\Upsilon (0),T(0))=(0.29,0.13)\) is shown

Full size image
Fig. 7
figure 7

For \(\varpi _{1}=1.2,\) \(\varpi _{2}=-1.56,\) \(\varsigma =3.3,\) and \(\gamma =0.6\) with the same initial conditions are illustrated as the NLDS

Full size image
Fig. 8
figure 8

The NLDS provides graphic representations for \(\gamma =0.12\) with the same parameter and beginning circumstances

Full size image

3.4 Multistability

This subsection handles the multistability of a similar system (53) for the perturbed term. To explore a dynamical system’s tendency toward multistability (53), multistability (Jhangeer et al. 2021; Natiq et al. 2019) is the concurrent combination of numerous, even massive, solutions for a given range of physical variables and variable beginning values (Jhangeer et al. 2022). In Fig. 9, time-series graphs will be studied. For \(\varpi _{1}=0.2,\) \(\varpi _{2}=-0.56,\) \(\varsigma =2.1,\) and \(\gamma =2.923\), two distinct phase portrait types can be created for the beginning conditions \((\Upsilon ,T)=(1.9,1.35)\) and \((\Upsilon ,T)=(0.29,0.13)\), which represent the hues red and black. A quasi-periodic style is detected in the beginning value (1.9, 1.35) by the tested system, although the periodic style indicated a similar number of variables with the initial condition (0.29, 0.13).

Fig. 9
figure 9

Multistability of the NLDS for \((\Upsilon ,T)=(1.9,1.35)\) in red hue, and \((\Upsilon ,T)=(0.29,0.13)\) in a blue hue

Full size image

4 Comparisons

In this part, we discuss some previous work and our newly obtained results. Researchers have so far applied a wide range of productive methods in search of analytical solutions for this prototype. For example, Triki et al. (2017) derived several exact nonlinearly chirped soliton solutions for the CLL equation, which contain three novel kinds of chirped bright soliton solutions accounting for all physical effects. Biswas obtained different types of soliton solutions by using the traveling wave hypothesis and semi-inverse variational principle for the CLL equation in Biswas (2018). Additionally, Kudryashov used the Weierstrass and Jacobi elliptic functions in Kudryashov (2019) to derive singular solutions, dark solitons, and bright solitons for the pCLL equation. However, the authors needed to thoroughly investigate these chirped soliton solutions’ dynamics. In contrast, we obtained various soliton solutions and illustrated their characteristics through numerical simulations, offering 2d, 3d, and contour plots. Also, with Kudryashov’s arbitrary refractive index model, Arnous et al. (2022) retrieved the optical solutions to the pCLL equation. Certain dark and bright soliton solutions were created using successful techniques, particularly Kudryashov’s and the modified extended tanh-function method. Whereas, in this work, using the nGERFM and dynamical system method based on the Hamiltonian system, we examined the considered model and constructed many types of soliton solutions, such as exponential function solutions (15),(17); singular periodic wave solutions (20),(26); shock wave solution 23); combo soliton solution (29); mixed form soliton solution (31); hyperbolic solution in mixed form (34); periodic wave solutions (37), (48), (51); Jacobi elliptic function solution (44); bell-shaped solitary wave (45); kink-shaped solitary wave (52). When the solutions we obtained are compared with the other solutions mentioned above, the extracted solutions’ physical structure differs from previous findings. Also, the solutions derived from our study are more diverse, unique, intriguing, and comprehensive.

5 Conclusions

This study examined the modified M-truncated form of the perturbed Chen–Lee–Liu (pCLL) dynamical equation, representing the propagation of optical pulses in optical fibers and plasma. The pCLL equation allows for the investigation of how perturbations affect the dynamics of the original Chen–Lee–Liu system, providing insights into the behavior of solitons and wave profiles in such systems.

To begin with, we utilized the new version of the generalized exponential rational function technique (nGERFM) to obtain multifarious types of soliton solutions. W presented 3D, contour, density, and 2D plots for some of the soliton solutions we obtained. Also, we observed the change in the graphs for \(\delta =0.5,\) \(\delta =0.75\), \(\delta =0.90\), and \(\delta =1\). Secondly, we created similar two-dimensional planar dynamic systems and identified the equilibrium points of the system using bifurcation theory. Additionally, we examined the periodic, quasi-periodic, and chaotic behaviors of traveling waves when they were influenced by an external periodic perturbation. As the intensity of the periodic perturbation increased, the perturbed system displayed a quasi-periodic path to chaos. We observed quasi-periodic and chaotic motions when an external perturbation was applied, and we used sensitivity analysis to validate the reported results.

The results of this publication indicate that the proposed methods are potential approaches to investigating different soliton solutions of nonlinear equations in optical physics. To our knowledge, all solutions accomplished are distinct and novel from the researchers’ earlier discoveries. Our findings contain a more comprehensive range of functions, including trigonometric, hyperbolic, exponential, etc. Moreover, these accepted solutions can be relevant to studying the other models in nonlinear optics, nuclear physics, fluid mechanics, and other engineering fields. With Maple’s assistance, we double-checked the results by substituting them back into the original formula (Fig. 10, 11, 12, 13 and 14).

Fig. 10
figure 10

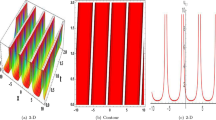
The 3d plots for the real part of the solution \(\left| \Phi _{1,1}(x,t)\right|\) in Eq. (15) by selecting the values \(\delta =0.5,\;\delta =0.75,\;\delta =0.90, \; \delta =1\), respectively, and \(\beta =-2,\;m =1,\;n =-1,\; \tau = 0.03, \;\eta = 0.9,\; \kappa = 0.01, \; \mu =4, \;\lambda = 1,\;\theta =2, \;\rho = 0.2\)

Full size image
Fig. 11
figure 11

The contour plots for the real part of the solution \(\left| \Phi _{1,1}(x,t)\right|\) in Eq. (15) by selecting the values \(\delta =0.5,\;\delta =0.75,\;\delta =0.90, \; \delta =1\), respectively, and \(\beta =-2,\;m =1,\;n =-1,\; \tau = 0.03, \;\eta = 0.9,\; \kappa = 0.01, \;\mu =4, \;\lambda = 1,\;\theta =2, \;\rho = 0.2\)

Full size image
Fig. 12
figure 12

The density plots for the real part of the solution \(\left| \Phi _{1,1}(x,t)\right|\) in Eq. (15) by selecting the values \(\delta =0.5,\;\delta =0.75,\;\delta =0.90, \; \delta =1\), respectively, and \(\beta =-2,\;m =1,\;n =-1,\; \tau = 0.03, \;\eta = 0.9,\; \kappa = 0.01, \;\mu =4, \;\lambda = 1,\;\theta =2, \;\rho = 0.2\)

Full size image
Fig. 13
figure 13

The 2d plots for the real part of the solution \(\left| \Phi _{1,1}(x,t)\right|\) in Eq. (15) by selecting the values \(\delta =0.5,\;\delta =0.75,\;\delta =0.90, \; \delta =1\), respectively, and \(\beta =-2,\;m =1,\;n =-1,\; \tau = 0.03, \;\eta = 0.9,\; \kappa = 0.01, \;\mu =4, \;\lambda = 1,\;\theta =2, \;\rho = 0.2\)

Full size image
Fig. 14
figure 14

The 3d, contour, density and 2d plots for the real part of the solution \(\left| \Phi _{2}(x,t)\right|\) in Eq. (20) by selecting the values \(\delta =0.5,\) \(\beta =1,\;m =-1,\;n =-1,\;\tau = 0.03, \;\eta = 0.9,\; \kappa = 0.01, \; \mu =-2, \;\lambda = 1,\;\theta =2, \;\rho = 0.2\)

Full size image