Internet traffic prediction analog to solitons propagation in optical fibers via the concatenation model and stability analysis

Abstract

Internet traffic (IT) is a measure of data transfer across devices. In this paper, an analogy is made between data transfer and soliton propagation in optical fibers. This is achieved by employing the concatenation model (CM) that describes soliton propagation in optical fibers, which is presented recently in the literature. The CM contains nonlinear space-time dispersion effect, that may lead to bottleneck soliton shape (BNSS). Thus, in view of this model, BNSS effect of soliton propagation may occur, which is analogous to a possible BN in IT. So, the prediction of the characteristics of internet traffic can be depicted via the CM, which is studied here with Caputo-q time derivative. Also, a variety of exact solutions of the CM are derived. These solutions are represented graphically and they show multiple shapes of concatenated solitons. Among them, bottleneck, M-shaped, hybrid M shaped, chirped solitons and vector of dromian patterns. On the other side, the speed of IT and chips heating are estimated. It is found that the speed of IT is constant with time and the effects of distributed time delay (recent memory (RM)) is to slow the traffic speed. This is done via varying the fractional order. Also, it is observed, when accounting for RM, that the chip heating is too small. We think that the results for the speed of IT and chip heat are, qualitatively, realistic. The stability of a steady state solution is analyzed and the controlled parameters for stability is determined.

1 Introduction

The concatenation is a chain model which is a combination of the nonlinear Schrodinger’s equation, Lakshmanan–Porsezian–Daniel model among others. A variety of techniques were used to derive solutions of the CM. Among them, the trial approach, the solutions of the CM were recovered in Wang et al. (2023). In Biswas et al. (2023), the method of undetermined coefficients was used to obtain a full spectrum of 1–soliton solutions of the CM. Quiescent optical solitons that are self-sustaining, localized wave packets that maintain their shape and amplitude over long distances were investigated in Yıldırım et al. (2023). The bifurcation of the concatenation model that arises from nonlinear fiber optics was analyzed in Tang et al. (2023).

Many physical phenomena were reported for the CM. Birefringent fibers were explored for the first time, and optical soliton solutions to the model were presented in Biswas et al. (2023). Painlevé analysis to a CM, that stems from the well-known nonlinear Schrödinger’s equation, Lakshmanan–Porsezian–Daniel model and Sasa–Satsuma equation (SSE), was established in Kudryashov et al. (2023). Optical solitons with the concatenation model having spatio-temporal and chromatic dispersion’s, that can advantageously limit the internet bottleneck effect were derived in Arnous et al. (2023a). The improved modified extended tanh-function method was used to derive new families of solutions that were extracted for the CM in Rabie et al. (2023), Arnous et al. (2023b).

The perturbed nonlinear Schrödinger equation (PNLSE) was currently studied in the literature. A PNLSE admits three optical phenomena; self-phase modulation, self- steepening and Raman scattering, which are described by the presence of the terms ($\mid w\mid _{x}^{2}w)$, ($(\mid w\mid ^{2}w)_{x}$) and ($\mid w\mid ^{2}w_{x}$) respectively (Abdel-Gawad 2022). The effects of the coefficients of group velocity dispersion, self-frequency shift and SS terms on the optical solitons of the (3+1)-dimensional nonlinear Schrödinger equation (NLSE) were investigated in Wu et al. (2022). In Wu et al. (2021), based on the original physics-informed neural networks, an improved physics-informed neural network method by combining the conservation laws was proposed. The extension of the rational sine-cosine method and rational sinh-cosh method to construct the new exact solutions the PNLSE was presented in Ozisik (2022). Dark and singular solitons for the resonance PNLSE with beta derivative were derived in Yusuf et al. (2019).

The analysis of multi-component systems requires a study of the interactions between their multiple wave components. In this context, the coupled NLSEs (CNLSEs) play a pivotal role. In a system of multiple waveguides, governed by CNLSEs, it was found that the modulation instability and rogue waves regimes can be produced (Chan et al. 2016). In Ali et al. (2018), the first and second-order rogue wave solutions, which are localized in space and time, were obtained. The rogue wave dynamics governed by CNLSEs were explored, both theoretically and experimentally (Baronio et al. 2018), The CNLSEs with variable coefficients and gain were investigated in Chakraborty et al. (2015). Exact traveling wave and soliton solutions, including the bright-bright and dark-dark soliton pairs, were found for the system of CNLSEs with harmonic potential and variable coefficients (Zhong and Belić 2010). The dynamics of wave phenomena modeled by (2+1)-dimensional coupled CNLSEs with fractional temporal evolution was studied (Raza and Rafiq 2020).

Various works on the NLSE with nonlinear dispersion were carried out. Rogue waves in a nonlinear fiber with cubic and quintic nonlinearities, linear and nonlinear dispersion effects were inspected (Zhao et al. 2015). The integration of the nonlinear dispersive Schrödinger’s equation by the aid of Lie group analysis was carried out (Biswas and Khalique 2011). The optical soliton solutions of a NLSE involving parabolic law of nonlinearity with the presence of nonlinear dispersion by using the generalized auxiliary equation technique was studied (Akinyemi et al. 2021). Stationary optical solitons with quadratic–cubic law of nonlinear refractive index and nonlinear chromatic dispersion were retrieved (Kudryashov 2022). Sationary optical solitons for the newly established cubic–quartic form of nonlinear refractive index together with nonlinear chromatic dispersion were derived (Sonmezoglu et al. 2021).

The effects of electronic bottle neck and time delay on the internet traffic were considered. To eliminate the electronic bottleneck, new optical switches/routers (hardware) are being built for the next-generation optical internet (Yoo et al. 2001). A novel dynamic clustering algorithm that we apply to update our previous shared bottleneck flow grouping method standardized by the flow of IT, based on delay statistics (Hayes et al. 2020). In Bolot (1993), round trip delays of small probe packets sent at regular time intervals to characterize the end-to-end packet delay and loss behavior, were measured in the internet. A generic-traffic analytical model for the delay-line buffer in an asynchronous network scenario that may be useful for buffer planning and performance evaluation was presented in Almeida et al. (2005).

In the present work, we explore the solitons structures and inspect of BN pattern exists. Further, we estimate the speed of IT and the heating of a chip in devices. Exact solutions of the CM are found by using the unified method (UM) (Abdel-Gawad et al. 2023a, b; Abdel-Gawad 2023). The UM asserts that the solutions of a nonlinear evolution equation is expressed in polynomial and rational solutions in an auxiliary function that satisfies an auxiliary equation.

The organization of the paper is in what follows.

In Sect. 2, the Caputo q-derivative is presented, along with the model equation and the UM. Section 3 is devoted to polynomial solutions, while rational solutions are obtained in Sect. 4. Section 5 is devoted to estimating the speed of IT and the heating of a chip.

2 Mathematical formulation

2.1 Caputo q-derivative

We present the following definitions.

Definition 1

The q-difference operator (q-derivative) is defined in,

$$\begin{aligned} D_{q}h(t)=\frac{h(t)-h(qt)}{(1-q)t},\;0<q<1. \end{aligned}$$

(1)

Definition 2

Let h :  $[0,T]\rightarrow R,h\epsilon H^{1,\alpha }$, $H^{1,\alpha )}=\{h,\intop _{0}^{t}(t-s)^{-\alpha }h(s)ds\epsilon H^{1}([0,T])\}$, H is Holder space. The Caputo fractional derivative is,

$$\begin{aligned} _{0}^{C}D_{t}^{\beta }h(t)=\intop _{0}^{t}(t-s)^{-\beta }\frac{dh(s)}{ds}ds,\;0<\beta <1. \end{aligned}$$

(2)

Definition 3

The Caputo q-derivative is,

$$\begin{aligned} _{0}^{Cq}D_{t}^{\beta }h(t)=\intop _{0}^{t}(t-s)^{-\beta }D_{q}h(s)ds=\intop _{0}^{t}(t-s)^{-\beta }\frac{(h(s)-h(qs))}{(1-q)s}ds,\;0<\beta<1,\;0<q<1. \end{aligned}$$

(3)

Lemma 4

(i) $_{0}^{Cq}D_{t}^{\beta }(h_{1}(t)$+$h_{2}(t)$)=$_{0}^{Cq}D_{t}^{\beta }h_{1}(t)+{}_{0}^{Cq}D_{t}^{\beta }h_{2}(t)$.

(ii) If $_{0}^{Cq}D_{t}^{\beta }h(t)=1\Rightarrow h(t)=\frac{1-q}{1-q^{\beta }}\frac{t^{\beta }}{\Gamma (\beta )}$.

(iii) If $_{0}^{Cq}D_{t}^{\beta }h(t)=h(t)\Rightarrow h(t)=\sum _{n=0}^{\infty }(\frac{1-q}{(1-q^{\beta }})^{n}\frac{t^{n\beta }}{\Gamma (\beta n+1)}$ (Abdel-Gawad et al. 2023a).

It is worth mentioning that a fractional dynamical system intends to take into account of the effect of recent memory (distributed time delay) on the behavior of this system, while the q-derivative stands for memory compression. In this context, we explore the following.

2.2 Memory index

To distinguish between these different memories that arise in dynamical systems, we define a memory index function relative to a dynamical quantity u(f(t)), t is the time variable.

A memory index function is defined as follows (Abdel-Gawad and Eldailami 2010):

$$\begin{aligned} M_{ind}(u(h(t)))=Arg(u(h(t))-t=h(t)-t \end{aligned}$$

(4)

We mention that when $h(t)=t$ then $M_{ind}(u(h(t)))=0$, that is no memory exists. When $h(t)=t\pm 1$, then $M_{ind}(u(h(t)))=\pm 1$.

Definition 5

A system is said to be with memory if $M_{ind}(u(h(t)))<0.$

Example 6

• (i) When $f(t)=t-\tau$, and $M_{ind}(u(f(t)))=-\tau <0$, then the system is with local memory.

• (ii) When $h(t)=\int _{0}^{t}(t-\tau )^{r}f(\tau )d\tau ,$ then the system is with distributed memory (recent memory),

• (iii) When $h(t)=\int _{-\infty }^{t}(t-\tau )^{r}f(\tau )d\tau ,$ then the system is with ancient memory.

• (iv) For q- derivative in (1), we write,

  $$\begin{aligned} \frac{h(t)-h(qt)}{(1-q)t}=h^{\prime }(\theta t),\;q<\theta <1, \end{aligned}$$

  (5)

  and $M_{ind}(u(h^{\prime }(\theta t)))$ $=(\theta -1)t.$ Thus, the q-derivative supports the presence of memory compression, which applies in computer science via (ZIP or RAR). Consequently, in a system with Caputo q-derivative, the behavior of this system is affected by recent and compressed memory.

2.3 The concatenation model

The CM reads (Arnous et al. 2023a),

$$\begin{aligned} \begin{array}{c} iw_{t}+\mu w_{xx}+\sigma w^{*}w^{2}+\alpha _{1}w_{xxxt}+\alpha _{2}w^{*}w_{x}^{2}+\alpha _{3}ww_{x}^{*}w_{x}+\alpha _{4}w^{*}ww_{xx}\\ +\alpha _{5}w^{2}w_{xx}^{*}+\alpha _{6}w^{*2}w^{3}+i\left( \alpha _{7}w_{xxx}+\alpha _{8}w^{*}ww_{x}+\alpha _{9}w^{2}w_{x}^{*}\right) =0, \end{array} \end{aligned}$$

(6)

where $w=w(x,t)$ is the complex field function, $\mu$ is the group dispersion velocity, $\sigma$ is the coefficient of the Kerr nonlinearity, $\alpha _{1}$ is the coefficient of the highest space-time dispersion, $\alpha _{4}$ and $\alpha _{5}$ are the coefficients of the nonlinear dispersion, $\alpha _{6}$ is the quintic nonlinearity coefficient, and $\alpha _{8}$ is the coefficient of the Raman scattering.

The Caputo q-derivative CM is,

$$\begin{aligned} \begin{array}{c} i\;_{0}^{Cq}D_{t}^{\beta }w+\mu w_{xx}+\sigma w^{*}w^{2}+\alpha _{1}\;_{0}^{Cq}D_{t}^{\beta }w_{xxx}+\alpha _{2}w^{*}w_{x}^{2}+\alpha _{3}ww_{x}^{*}w_{x}+\alpha _{4}w^{*}ww_{xx}\\ +\alpha _{5}w^{2}w_{xx}^{*}+\alpha _{6}w^{*2}w^{3}+i\left( \alpha _{7}w_{xxx}+\alpha _{8}w^{*}ww_{x}+\alpha _{9}w^{2}w_{x}^{*}\right) =0. \end{array} \end{aligned}$$

(7)

In (7), we introduce the transformation, and by using (ii) in Lemma 1; $w(x,t)=\bar{w}(x,\tau ),\;$ $\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }$, and (7) reduce to,

$$\begin{aligned} \begin{array}{c} i\bar{w}_{\tau }+\mu \bar{w}_{xx}+\sigma \bar{w}^{*}\bar{w}^{2}+\alpha _{1}\bar{w}_{xxx\tau }+\alpha _{2}\bar{w}^{*}\bar{w}_{x}^{2}+\alpha _{3}\bar{w}\bar{w}_{x}^{*}\bar{w}_{x}+\alpha _{4}\bar{w}^{*}\bar{w}\bar{w}_{xx}\\ +\alpha _{5}\bar{w}^{2}\bar{w}_{xx}^{*}+\alpha _{6}\bar{w}^{*2}\bar{w^{3}}+i\left( \alpha _{7}\bar{w}_{xxx}+\alpha _{8}\bar{w}^{*}\bar{w}\bar{w}_{x}+\alpha _{9}\bar{w}^{2}\bar{w}_{x}^{*}\right) =0. \end{array} \end{aligned}$$

(8)

The solutions of (8) are dealt with, in the literature, by using,

$$\begin{aligned} w(x,\tau )\text {=}R(x,\tau )e^{i(kx-\tau \Omega )}, \end{aligned}$$

(9)

where R is a real function. This imposes constraints on the parameters in (6). So, (7) is considered as a particular solution. Here, we consider R is complex and introduce the transformations,

$$\begin{aligned} \bar{w}(x,\tau )\text {=}(u(x,\tau )+iv(x,\tau ))e^{i(kx-\tau \Omega )},\;w^{*}(x,\tau )\text {=}(u(x,\tau )-iv(x,\tau ))e^{-i(kx-\tau \Omega )}. \end{aligned}$$

(10)

When plugging into (6) together while using the traveling waves transformations $u(x,\tau )\text {=}U(z),\;$ $v(x,\tau )\text {=}V(z)$ and $z=px+r\tau ,$ we get,

$$\begin{aligned}{} & {} \begin{array}{c} U^{3}\left( -\alpha _{2}k^{2}+\alpha _{3}k^{2}-\alpha _{4}k^{2}-\alpha _{5}k^{2}-\alpha _{8}k+\alpha _{9}k+\sigma +2\alpha _{6}V^{2}\right) +\alpha _{6}U^{5}\\ +\left( 3\alpha _{7}k^{2}p+\alpha _{1}k^{2}(kr-3p\Omega )-2k\mu p-2\alpha _{2}kpV^{2}-2\alpha _{4}kpV^{2}-r\right. \\ \left. +2\alpha _{5}kpV^{2}+2\alpha _{2}p^{2}V(z)U'(z)-\alpha _{8}pV^{2}z)^{2}-\alpha _{9}pV^{^{2}}\right) V'(z)+pU^{2}\\ -2\alpha _{2}kV'+2\alpha _{3}kV'-2\alpha _{4}kV'-2\alpha _{5}kV'+\alpha _{4}pU''+\alpha _{5}pU''-\alpha _{8}V'+\alpha _{9}V'\\ +U\left( -\alpha _{1}k^{3}\Omega +\alpha _{7}k^{3}-k^{2}\mu +V^{2}(-\alpha _{2}k^{2}+\alpha _{3}k^{2}-\alpha _{4}k^{2}+\sigma )+\Omega \right. \\ -\alpha _{5}k^{2}V^{2}-2\alpha _{3}kpVU'+4\alpha _{5}kpVU'-\alpha _{8}kV^{2}(+\alpha _{9}kV^{2}+\alpha _{6}V^{4}\\ \left. (\alpha _{2}+\alpha _{3})p^{2}U'^{2}+2\alpha _{5}p^{2}VV''+(-\alpha _{2}+\alpha _{3})p^{2}V'^{2}-2\alpha _{9}pVU'\right) \\ +p(p\left( \alpha _{1}(V^{(3)}(p\Omega -3kr)+prU^{(4)})-\alpha _{7}pV^{(3)}\right) +U''(3\alpha _{1}k(p\Omega -kr)\\ +p(-3\alpha _{7}k+\mu +V^{2}))(\alpha -\alpha _{5})), \end{array} \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \begin{array}{c} V^{3}\left( -\alpha _{2}k^{2}+\alpha _{3}k^{2}-\alpha _{4}k^{2}-\alpha _{5}k^{2}-\alpha _{8}k+\alpha _{9}k+\sigma +2\alpha _{6}U^{2}\right) +\alpha _{6}V^{6}\\ +U'(\alpha _{1}k^{2}(3p\Omega -kr)+2k\mu p+r+2\alpha _{2}p^{2}UV'+U^{2}(\alpha _{8}p+\alpha _{9}p)\\ \left. -3\alpha _{7}k^{2}p+U^{2}(2\alpha _{2}kp+2\alpha _{4}kp-2\alpha _{5}kp)\right) \\ +V\left( \alpha _{1}k^{3}(-\Omega )+\alpha _{7}k^{3}-k^{2}\mu +U^{2}(-\alpha _{2}k^{2}+\alpha _{3}k^{2}-\alpha _{4}k^{2}+\sigma )+\Omega \right. \\ +U^{2}(-\alpha _{5}k^{2}-\alpha _{8}k+\alpha _{9}k)+p^{2}U'^{2}(-\alpha _{2}+\alpha _{3})+\alpha _{6}U^{4}+2\alpha _{3}kpUV'\\ \left. -4\alpha _{5}kpUV'+2\alpha _{5}p^{2}UU''+p^{2}V'^{2}(\alpha _{2}+\alpha _{3})+2\alpha _{9}pUV'\right) \\ +pV^{2}\left( kU'(2\alpha _{2}-2\alpha _{3}+2\alpha _{4}+2\alpha _{5})+pV''(\alpha _{4}+\alpha _{5})+(\alpha _{8}-\alpha _{9})U''\right) \\ +p\left( V''\left( 3\alpha _{1}k(p\Omega -kr)+p\left( -3\alpha _{7}k+\mu +\alpha _{4}U^{2}-\alpha _{5}U^{2}\right) \right) \right. \\ \left. +p\left( \alpha _{1}\left( U^{(3)}(3kr-p\Omega )+prV^{(4)}\right) +\alpha _{7}pU^{(3)}\right) \right) . \end{array} \end{aligned}$$

(12)

2.4 The unified method

2.4.1 Polynomial solutions

With relevance to (9) and (10), the solutions are written,

$$\begin{aligned} U(z)=\sum _{j=0}^{j=n_{1}}a_{j}\phi (z)^{j},\quad V(z)=\sum _{j=0}^{j=n_{2}}b_{j}\phi (z)^{j},{{\;(\phi ^{\prime }(z))^{m}}=}\sum _{j=0}^{j=mH}c_{j}\phi (z)^{j},m=1,2. \end{aligned}$$

(13)

where $\phi (z)$ is the auxiliary function and the last equation in (13) is the auxiliary equation (AE).

The Painleve’ analysis can b used to test the integabilty of (11) and (12) but it is too lengthy. Here, integrability is tested in the sense of existence of (13). A necessary condition for the solutions in (13) to exist, is that there exist integers $n_{1},n_{2},$and k. To this issue, two conditions are examined, the balance condition and the consistency condition We consider the case when $m=1.$The balance condition reads $n_{1}=n_{2}=H-1.$To determine H, we use the consistency condition. We need to calculate the following;

• (i) The number of equations that results when inserting (13) in (11) and (12) (or (10)) and by setting the coefficients of $\phi ^{i}(z),i=0,1,2,...etc.$ equal to zero (which is $(5H-4)).$

• (ii) The number of arbitrary parameters in (11), (which is $(2H+1)$). The CC reads ${{5\,H-4-(2\,H+1)\le s}},$where s is the highest order derivative ($s=4$) Finally, we get $0\le H\le 3.$

2.4.2 Rational solutions

In this case, the solutions of (6) and (7) are written,

$$\begin{aligned} U(z)=\frac{\sum _{j=0}^{j=n}a_{j}\phi (z)^{j}}{\sum _{j=0}^{j=s}s_{j}\phi (z)^{j}},\;V(z)=\frac{\sum _{j=0}^{j=n}b_{j}\phi (z)^{j}}{\sum _{j=0}^{j=s}s_{j}\phi (z)^{j}},{{\;(\phi ^{\prime }(z))^{m}}=}\sum _{j=0}^{j=mH}c_{j}\phi (z)^{j},m=1,2. \end{aligned}$$

(14)

The balance condition is; $n=H-1,H\ge 2$ and $n=1$ when $H=1.$

It was found that a necessary condition for a complex field equation (cf. 9) to be integrable is that the real and imaginary parts are linearly dependent. But this condition is not, in general, sufficient (Abdel-Gawad et al. 2023b).

3 Polynomial solutions of (11) and (12)

3.1 When $H=2,$ $m=1$

In this case, we write,

$$\begin{aligned} U(z)\text {=}a_{1}\phi (z)+a_{0},\,V(z)\text {=}b_{1}\phi (z)+b_{0},\,b_{0}\text {=}\frac{a_{0}b_{1}}{a_{1}}, \end{aligned}$$

(15)

and consider AE,

$$\begin{aligned} \phi '(z)\text {=}c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}. \end{aligned}$$

(16)

By inserting (15) and (16) into (11) and (12) and by setting the coefficients of $\phi ^{i}(z),i=0,1,2,...etc.$ equal to zero, leads to,

$$\begin{aligned} \begin{array}{c} a_{1}\text {=}\frac{2a_{0}c_{2}}{c_{1}},\,\alpha _{7}\text {=}\frac{r\left( \alpha _{1}\left( 2c_{1}^{2}kp^{2}-112k^{3}\right) +\alpha _{1}^{2}\left( 277c_{1}^{2}k^{4}p^{2}-19c_{1}^{4}k^{2}p^{4}-1024k^{6}\right) +2\right) }{c_{1}^{2}p^{3}},\\ c_{0}\text {=}\frac{3k^{2}}{2c_{2}p^{2}},\,\sigma \text {=}-a_{0}^{2}\alpha _{6}+\frac{2a_{0}\alpha _{3}c_{2}k}{b_{1}c_{1}}+\frac{\alpha _{3}b_{1}c_{1}k}{2a_{0}c_{2}}-\alpha _{2}-\frac{\alpha _{6}b_{1}^{2}c_{1}^{2}}{4c_{2}^{2}}-4\alpha _{4}k^{2}-2\alpha _{9}k,\\ \mu \text {=}\frac{2\alpha _{1}r\left( c_{1}^{2}p^{2}-18k^{2}\right) }{p},\,\alpha _{9}\text {=}-\frac{1}{c_{1}^{2}c_{2}^{2}p^{2}\left( 4a_{0}^{2}b_{1}c_{2}^{2}+b_{1}^{3}c_{1}^{2}\right) }\left( -2a_{0}\alpha _{3}b_{1}^{2}c_{1}^{3}c_{2}^{3}p^{2},\right. \\ b_{1}^{3}c_{1}^{2}c_{2}^{2}(8\alpha _{6}a_{0}^{2}k+c_{1}^{2}p^{2}(\alpha _{8}+4\alpha _{4}k))-8a_{0}^{3}\alpha _{3}c_{1}c_{2}^{5}p^{2}+\alpha _{6}b_{1}^{5}c_{1}^{4}k\\ +4b_{1}c_{2}^{4}(c_{1}^{2}p(a_{0}^{2}p(\alpha _{8}+4\alpha _{4}k)-192\alpha _{1}k^{3}r+3r)+4\alpha _{6}a_{0}^{4}k\\ +18\alpha _{1}c_{1}^{4}kp^{3}r)),\,\Omega \text {=}\frac{kr\left( \frac{16k^{2}\left( 1-64\alpha _{1}k^{3}\right) }{c_{1}^{2}}-19\alpha _{1}c_{1}^{2}kp^{4}+p^{2}\left( 277\alpha _{1}k^{3}-3\right) \right) }{p^{3}},\\ r\text {=}-\frac{\left( 4a_{0}^{2}c_{2}^{2}+b_{1}^{2}c_{1}^{2}\right) \left( 4a_{0}^{2}\alpha _{6}c_{2}^{2}+\alpha _{6}b_{1}^{2}c_{1}^{2}+2\alpha _{4}c_{2}^{2}c_{1}^{2}p^{2}+2\alpha _{5}c_{2}^{2}c_{1}^{2}p^{2}\right) }{24\alpha _{1}c_{1}^{4}c_{2}^{4}p^{3}}. \end{array} \end{aligned}$$

(17)

The solutions u(x, t) and v(x, t) are,

$$\begin{aligned} \begin{array}{c} u(x,t)\text {=}\frac{a_{0}\sqrt{c_{1}^{2}p^{2}-6k^{2}}\tanh \left( \frac{(A+z)\sqrt{c_{1}^{2}p^{2}-6k^{2}}}{2p}\right) }{c_{1}p},\;v(x,t)\text {=}\frac{b_{1}c_{1}}{2a_{0}c_{2}}u(x,t),\\ z\text {=}-\frac{\tau \left( \left( 4a_{0}^{2}c_{2}^{2}+b_{1}^{2}c_{1}^{2}\right) \left( 4a_{0}^{2}\alpha _{6}c_{2}^{2}+\alpha _{6}b_{1}^{2}c_{1}^{2}+2\alpha _{4}c_{2}^{2}c_{1}^{2}p^{2}+2\alpha _{5}c_{2}^{2}c_{1}^{2}p^{2}\right) \right) }{24\alpha _{1}c_{1}^{4}c_{2}^{4}p^{3}}+px,\;\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(18)

The results in (18) are used to display Rew(x, t) in Fig. 1i–iv. Here, we fix the values $\alpha _{8}\text {=}0.5,\alpha _{9}\text {=}0.4,\alpha _{1}\text {=}0.7,\alpha _{4}\text {=}0.3,\alpha _{5}\text {=}0.4,\alpha _{6}\text {=}1.2,\alpha _{3}\text {=}1.3,\alpha _{2}\text {=}0.7,q=0.6.$

Fig. 1

(i–v), when $c_{0}\text {=}0.8,c_{1}\text {=}1.3,c_{2}\text {=}0.5,b_{1}\text {=}2.5,a_{1}\text {=}1.5,p\text {=}0.1,A\text {=}0.5,$and for different values of the fractional order $\beta .$ The 3D-plots and contour plots are displayed. (i) and (iii) show M-shaped and undulated M-shaped concatenated solitons (CSs) in space respectively and with tunneling. (ii) and (iv) show disturbed CSs near $x=0$. The effect of time delayed memory (via fractional order) manifest through delaying the propagation. This may have an impact on delaying the internet traffic. In Fig. 1v, the effects of varying the fractional order are shown, where small fractional order acts in delaying the wave behavior and reducing the wave amplitude

3.2 When $H=2$ and $m=2$

3.2.1 Case (a)

We consider (15) and the AE is,

$$\begin{aligned} \phi '(z)\text {=}\phi (z)\sqrt{c_{2}\phi (z)^{2}+c_{0}}. \end{aligned}$$

(19)

From (15) and (19) into (11) and (12) gives rise to,

$$\begin{aligned} \begin{array}{c} \alpha _{9}\text {=}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\,\alpha _{7}\text {=}\frac{\alpha _{1}(p\Omega -3kr)}{p},\,r\text {=}\frac{16\left( \sqrt{19}+1\right) a_{0}^{2}\left( \alpha _{2}+\alpha _{3}\right) kp}{3\left( 2\sqrt{19}+29\right) \left( 4\alpha _{1}k^{3}-1\right) },\\ \alpha _{5}\text {=}\frac{1}{2}\left( \frac{48\alpha _{1}c_{2}k\mu p^{2}}{\left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{1}k^{3}+1\right) }-\frac{\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) }{c_{2}p^{2}}-\alpha _{2}-\alpha _{3}-2\alpha _{4}\right) ,\\ \alpha _{6}\text {=}\frac{c_{2}p^{2}\left( \left( \alpha _{2}+\alpha _{3}\right) \left( a_{1}^{2}+b_{1}^{2}\right) -\frac{96\alpha _{1}c_{2}k\mu p^{2}}{8\alpha _{1}k^{3}+1}\right) }{3\left( a_{1}^{2}+b_{1}^{2}\right) {}^{2}},\,\mu \text {=}\frac{\left( \alpha _{2}+\alpha _{3}\right) b_{1}^{2}\left( 8\alpha _{1}k^{3}+1\right) }{120\alpha _{1}c_{2}kp^{2}},\\ \sigma \text {=}\frac{1}{360\left( 13\sqrt{19}+61\right) \alpha _{1}k}\left( \alpha _{2}\left( 4\left( 4246\sqrt{19}+19447\right) \alpha _{1}k^{3}-76\sqrt{19}-157\right) \right. \\ -\alpha _{3}\left( 28\left( 62\sqrt{19}+359\right) \alpha _{1}k^{3}+76\sqrt{19}+157\right) +720\left( 13\sqrt{19}+61\right) \\ \left. \alpha _{1}k^{2}\left( \alpha _{8}+2\alpha _{4}k\right) \right) ,\,c_{2}\text {=}-\frac{a_{1}^{2}\left( 80\alpha _{1}a_{1}^{2}c_{0}kp^{2}+b_{1}^{2}\left( \alpha _{1}\left( 40c_{0}kp^{2}-12k^{3}\right) +3\right) \right) }{40a_{0}^{2}\alpha _{1}kp^{2}\left( 4a_{1}^{2}-b_{1}^{2}\right) },\\ \Omega \text {=}-\frac{a_{0}^{2}}{1200\left( \sqrt{19}+1\right) \left( \sqrt{19}+2\right) ^{2}\left( 2\sqrt{19}+29\right) \alpha _{1}k\left( 4\alpha _{1}k^{3}-1\right) }\left( 18971\sqrt{19}+50552+\right. \\ 8\alpha _{1}k^{3}\left( 31429\sqrt{19}+194248\right) +16\left( 69371\sqrt{19}+295352\right) \alpha _{1}^{2}k^{6}(\alpha _{2}+\alpha _{3}),\\ a_{1}\text {=}\frac{1}{2}\sqrt{\sqrt{19}+2}b_{1},\,c_{0}\text {=}\frac{\left( 3\sqrt{19}-4\right) \left( 4\alpha _{1}k^{3}-1\right) }{40\left( \sqrt{19}+2\right) \alpha _{1}kp^{2}}. \end{array} \end{aligned}$$

(20)

The solutions in (10) are,

$$\begin{aligned} \begin{array}{c} u(x,t)\text {=}{a_{0}}(\sqrt{\frac{2}{17}\left( 35-3\sqrt{19}\right) }\text {sech}(\frac{1}{2}\sqrt{\frac{1}{30}\left( 13-2\sqrt{19}\right) }(A+z)\sqrt{\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}kp^{2}}})+1,\\ v(x,t)\text {=}\frac{2a_{0}\left( \sqrt{34\left( 71\sqrt{19}+577\right) }\text {sech}(\frac{1}{2}\sqrt{\frac{1}{30}\left( 13-2\sqrt{19}\right) }(A+z)\sqrt{\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}kp^{2}}})+17\left( \sqrt{19}+2\right) \right) }{17\left( \sqrt{19}+2\right) ^{3/2}},\\ z\text {=}px+\frac{16\left( \sqrt{19}+1\right) a_{0}^{2}\left( \alpha _{2}+\alpha _{3}\right) kp\tau }{3\left( 2\sqrt{19}+29\right) \left( 4\alpha _{1}k^{3}-1\right) },\;\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(21)

By using (21), Rew(x, t) is displayed in Fig. 2i–iv.

Fig. 2

(i–iv), when $a_{0}\text {=}1.5,p\text {=}3.6,A\text {=}0.5,k\text {=15. }$ (iii) and (iv) show CSs in time, while (i) and (ii) show undulated CSs in space with high amplitude at $x=0$

3.2.2 Case (b)

We consider the AE,

$$\begin{aligned} \phi '(z)\text {=}\sqrt{c_{4}\phi (z)^{4}+c_{2}\phi (z)^{2}+c_{0}}. \end{aligned}$$

(22)

By inserting (15) and (22) into (11) and (12) yield to,

$$\begin{aligned} \begin{array}{c} \alpha _{9}\text {=}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\;\alpha _{7}\text {=}\frac{\alpha _{1}(p\Omega -3kr)}{p},\;r\text {=}-\frac{2k\mu p}{8\alpha _{1}k^{3}+1},\\ \mu \text {=}\frac{\left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{1}k^{3}+1\right) \left( \alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) +\left( \alpha _{2}+\alpha _{3}+2\left( \alpha _{4}+\alpha _{5}\right) \right) c_{4}p^{2}\right) }{48\alpha _{1}c_{4}^{2}kp^{4}},\\ \alpha _{5}\text {=}-\frac{5\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) +\left( \alpha _{2}+\alpha _{3}+4\alpha _{4}\right) c_{4}p^{2}}{4c_{4}p^{2}},\;\alpha _{3}\text {=}\frac{15\alpha _{6}b_{1}^{2}}{c_{4}p^{2}}-\alpha _{2},\\ \sigma \text {=}-\frac{15}{2}a_{0}^{2}\alpha _{6}-\frac{a_{1}^{2}\alpha _{6}\left( \alpha _{1}\left( 25c_{3}kp^{2}+41k^{3}\right) +1\right) }{4\alpha _{1}c_{4}kp^{2}}+4\alpha _{2}k^{2}+4\alpha _{4}k^{2}+2\alpha _{8}k,\\ c_{2}\text {=}\frac{4\alpha _{1}k^{3}-1}{20\alpha _{1}kp^{2}},\;b_{1}\text {=}\frac{\sqrt{5}a_{1}}{2},\;\Omega \text {=}\frac{9}{6400\alpha _{1}^{2}c_{4}^{2}k^{2}p^{4}}\left( 18000a_{0}^{4}\alpha _{1}^{2}c_{4}^{2}k^{2}p^{4}\right. \\ \left. +900a_{0}^{2}\alpha _{1}a_{1}^{2}c_{4}kp^{2}\left( 4\alpha _{1}k^{3}-1\right) +a_{1}^{4}\left( 144\alpha _{1}^{2}\left( 4k^{6}-175c_{0}c_{4}k^{2}p^{4}\right) +112\alpha _{1}k^{3}+11\right) \right) \alpha _{6}\\ a_{0}\text {=}\frac{1}{4}\sqrt{\frac{a_{1}^{2}\left( 10-40\alpha _{1}k^{3}\right) +\sqrt{2}\sqrt{a_{1}^{4}\left( 16\alpha _{1}^{2}\left( 17k^{6}-900c_{0}c_{4}k^{2}p^{4}\right) -136\alpha _{1}k^{3}+17\right) }}{15\alpha _{1}c_{4}kp^{2}}}. \end{array} \end{aligned}$$

(23)

The solutions u(x, t) and v(x, t) are,

$$\begin{aligned} \begin{array}{c} u(x,t)\text {=}\frac{1}{4}\sqrt{\frac{\sqrt{2}\sqrt{a_{1}^{4}\left( 16\alpha _{1}^{2}\left( 17k^{6}-900c_{0}c_{4}k^{2}p^{4}\right) -136\alpha _{1}k^{3}+17\right) }+a_{1}^{2}\left( 10-40\alpha _{1}k^{3}\right) }{15\alpha _{1}c_{4}kp^{2}}}\\ -\frac{1}{\sqrt{10}M_{+}^{3/2}\sqrt{\alpha _{1}km^{2}p^{2}}}\left( a_{1}\text {sn}\left( 2\sqrt{2}\left( 10A+z\sqrt{5}\right) \sqrt{c_{0}}\sqrt{\frac{km^{2}p^{2}\alpha _{1}}{M_{+}}}|\frac{M_{+}}{M_{-}}\right) \right. \\ \left. 4\alpha _{1}^{2}k^{2}\left( k^{2}p^{2}\sqrt{1600c_{0}m^{2}+\frac{\left( 1-4\alpha _{1}k^{3}\right) {}^{2}}{\alpha _{1}^{2}k^{2}p^{4}}}+200c_{0}m^{2}p^{4}+4k^{4}\right) -M_{+}\right) ,\\ M_{\pm }=\alpha _{1}\left( \pm kp^{2}\sqrt{1600c_{0}m^{2}+\frac{\left( 1-4\alpha _{1}k^{3}\right) {}^{2}}{\alpha _{1}^{2}k^{2}p^{4}}}+4k^{3}\right) -1,\\ v(x,t)\text {=}\frac{b_{1}u(x,t)}{a_{1}},\\ z\text {=}px-\frac{\tau \left( \left( a_{1}^{2}+b_{1}^{2}\right) \left( \alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) +\left( 3\alpha _{2}+\alpha _{3}+4\alpha _{4}\right) c_{4}p^{2}\right) \right) }{24\alpha _{1}c_{4}^{2}p^{3}},\\ \tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(24)

By using (25), $\mid w(x,t)|$ is displayed in Fig. 3i–iv.

Fig. 3

(i–iv), when $b_{1}\text {=}2.5,a_{1}\text {=}1.5,p\text {=}0.5,m\text {=}1.3,c_{0}\text {=}0.6,k\text {=}0.3,A\text {=}0.5.$ Figs. (i) and (iii) show chirped CSs in space and hybrid concatenated waves in time. The effect of memory can be seen when varying $\beta$. For small values of $\beta$, delay occurs in the soliton propagation when compared with the case, when $\beta$ is near 1

3.2.3 Case (c)

We consider the AE,

$$\begin{aligned} \phi '(z)\text {=}\sqrt{c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}}\left( m_{1}\phi (z)+m_{0}\right) . \end{aligned}$$

(25)

From (15) and (26) into (11) and (12) leads to,

$$\begin{aligned} \begin{array}{c} \alpha _{9}\text {=}-\frac{6c_{2}m_{1}^{2}p\left( \alpha _{1}(3kr-p\Omega )+\alpha _{7}p\right) }{a_{1}^{2}+b_{1}^{2}}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\\ a_{0}\text {=}\frac{1}{4}a_{1}\left( \frac{c_{1}}{c_{2}}+\frac{2m_{0}}{m_{1}}\right) ,\,\alpha _{7}\text {=}\frac{\alpha _{1}(p\Omega -3kr)}{p},\,\mu \text {=}-\frac{8\alpha _{1}k^{3}r+r}{2kp}\\ \alpha _{6}\text {=}-\frac{c_{2}m_{1}^{2}p^{2}\left( \left( \alpha _{2}+\alpha _{3}+2\left( \alpha _{4}+\alpha _{5}\right) \right) \left( a_{1}^{2}+b_{1}^{2}\right) +24\alpha _{1}c_{2}m_{1}^{2}pr\right) }{\left( a_{1}^{2}+b_{1}^{2}\right) {}^{2}},\\ \alpha _{5}\text {=}-\alpha _{2}-\alpha _{3}-\alpha _{4},\,\sigma \text {=}\frac{2^{2/3}\alpha _{8}\root 3 \of {\alpha _{1}}+2\alpha _{2}+2\alpha _{4}}{\root 3 \of {2}\alpha _{1}^{2/3}},\,r\text {=}-\frac{\left( \alpha _{2}+\alpha _{3}\right) \left( a_{1}^{2}+b_{1}^{2}\right) }{30\alpha _{1}c_{2}m_{1}^{2}p},\\ c_{0}\text {=}\frac{1}{8}\left( -\frac{4c_{1}m_{0}}{m_{1}}+\frac{4c_{2}m_{0}^{2}}{m_{1}^{2}}+\frac{3c_{1}^{2}}{c_{2}}\right) ,\Omega \text {=}\frac{a_{1}^{2}+b_{1}^{2}}{1280\alpha _{1}^{4/3}c_{2}^{3}m_{1}^{2}p^{2}}\left( -144\alpha _{1}^{4/3}c_{2}^{4}m_{0}^{4}p^{4}\right. \\ -9\alpha _{1}^{4/3}c_{1}^{4}m_{1}^{4}p^{4}+72\alpha _{1}^{4/3}c_{1}^{3}c_{2}m_{0}m_{1}^{3}p^{4}++288\alpha _{1}^{4/3}c_{1}c_{2}^{3}m_{0}^{3}m_{1}p^{4}\\ \left. +8c_{2}^{2}\left( 2\root 3 \of {2}-27\alpha _{1}^{4/3}c_{1}^{2}m_{0}^{2}m_{1}^{2}p^{4}\right) \right) (\alpha _{2}+\alpha _{3}),\,k\text {=}\frac{1}{2^{2/3}\root 3 \of {\alpha _{1}}}. \end{array} \end{aligned}$$

(26)

The solutions are,

$$\begin{aligned} \begin{array}{c} u(x,t)\text {=}-\frac{1}{4c_{2}m_{1}\left( cosh\left( \frac{\sqrt{3}\left( A+\sqrt{2}z\right) \left( 2c_{2}m_{0}-c_{1}m_{1}\right) }{2\sqrt{c_{2}}}\right) -5\right) }\\ 6\sqrt{2}sinh\left( \frac{\sqrt{3}\left( A+\sqrt{2}z\right) \left( 2c_{2}m_{0}-c_{1}m_{1}\right) }{4\sqrt{c_{2}}}\right) +cosh\left( \frac{\sqrt{3}\left( A+\sqrt{2}z\right) \left( 2c_{2}m_{0}-c_{1}m_{1}\right) }{2\sqrt{c_{2}}}\right) +7\\ \\ v(x,t)\text {=}\frac{b_{1}u(x,t)}{a_{1}},\;z\text {=}-\frac{\left( \alpha _{2}+\alpha _{3}\right) \tau \left( a_{1}^{2}+b_{1}^{2}\right) }{30\alpha _{1}c_{2}m_{1}^{2}p}+px,\\ \tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(27)

By using (28), Rew(x, t) is displayed in Fig. 4i–iv.

Fig. 4

(i–iv), when $c_{0}\text {=}0.8,c_{1}\text {=}1.3,c_{2}\text {=}1.5,b_{1}\text {=}0.7,a_{1}\text {=}0.5,p\text {=}0.1,m_{1}\text {=}0.5,k\text {=}0.3$. (i) and (iii) show hybrid M-shaped-rhombus CSs in space

4 Rational solutions of (9) and (10)

4.1 When $H=1$and $m=1$

We write,

$$\begin{aligned} U(z)\text {=}\frac{a_{1}\phi (z)+a_{0}}{s_{1}\phi (z)+s_{0}},\;V(z)\text {=}\frac{b_{1}\phi (z)+b_{0}}{s_{1}\phi (z)+s_{0}},\;b_{0}\text {=}\frac{a_{0}b_{1}}{a_{1}}, \end{aligned}$$

(28)

and the AE is,

$$\begin{aligned} \phi '(z)\text {=}c+d\phi (z). \end{aligned}$$

(29)

From (29) and (30) into (9) and (10) yields,

$$\begin{aligned} \begin{array}{c} \mu \text {=}\frac{1}{k^{2}s_{1}^{4}}\left( a_{1}^{4}\alpha _{6}+\alpha _{6}b_{1}^{4}+s_{1}^{4}\left( \alpha _{1}k^{3}(-\Omega )+\alpha _{7}k^{3}+\Omega \right) +b_{1}^{2}s_{1}^{2}\left( \sigma -\alpha _{2}k^{2}\right. \right. \\ \left. -\alpha _{4}k^{2}-\alpha _{5}k^{2}+\alpha _{3}+k^{2}-\alpha _{8}k+\alpha _{9}k\right) +a_{1}^{2}\left( 2\alpha _{6}b_{1}^{2}+s_{1}^{2}\left( -\alpha _{2}k^{2}\right. \right. \\ +\alpha _{3}k^{2}+\sigma -\alpha _{5}k^{2}-\alpha _{4}k^{2}-\alpha _{8}k+\alpha _{9}k))),\\ \sigma \text {=}k\left( \alpha _{8}-\alpha _{9}+\alpha _{2}k-\alpha _{3}k+\alpha _{4}k+\alpha _{5}k\right) ,\alpha _{9}\text {=}\frac{12rs_{1}^{2}\left( 1-10\alpha _{1}d^{3}p^{3}\right) }{65b_{1}^{2}p}\\ -\alpha _{8}-\frac{104\alpha _{6}b_{1}^{2}}{5dps_{1}^{2}}-\frac{12}{5}\alpha _{2}dp-\frac{2}{5}\alpha _{3}dp-4\alpha _{4}dp,\;\alpha _{7}\text {=}\frac{1}{80d^{3}p^{3}s_{1}^{4}}\left( -16drs_{1}^{4}\right. \\ \left( 5\alpha _{1}^{2}d^{6}p^{6}+19\alpha _{1}d^{3}p^{3}+2\right) -26\left( \alpha _{2}+\alpha _{3}\right) b_{1}^{2}d^{2}p^{2}s_{1}^{2}\left( 3\alpha _{1}d^{3}p^{3}+4\right) \\ \left. +169\alpha _{6}b_{1}^{4}\left( \alpha _{1}d^{3}p^{3}+8\right) \right) ,\,k\text {=}dp;\,c\text {=}\frac{ds_{0}}{4s_{1}},\,a_{1}\text {=}\frac{3b_{1}}{2},\\ \alpha _{5}\text {=}-\alpha _{4}-\frac{\alpha _{2}}{2}-\frac{\alpha _{3}}{2}-\frac{13\alpha _{6}b_{1}^{2}}{2d^{2}p^{2}s_{1}^{2}}-\frac{12\alpha _{1}d^{2}prs_{1}^{2}}{13b_{1}^{2}},\,a_{0}\text {=}-\frac{3b_{1}s_{0}}{4s_{1}},\\ \Omega \text {=}\frac{1}{80}\left( -\frac{78\left( \alpha _{2}+\alpha _{3}\right) b_{1}^{2}d^{2}p^{2}}{s_{1}^{2}}+\frac{169\alpha _{6}b_{1}^{4}}{s_{1}^{4}}-16dr\left( 5\alpha _{1}d^{3}p^{3}+4\right) \right) . \end{array} \end{aligned}$$

(30)

The solutions are,

$$\begin{aligned} u(x,t)\text {=}\frac{3b_{1}\left( 4As_{1}e^{d(px+\frac{(q-1)rt^{\beta }}{\Gamma (\beta )\left( q^{\beta }-1\right) })}-3s_{0}\right) }{2s_{1}\left( 4As_{1}e^{d(px+\frac{(q-1)rt^{\beta }}{\Gamma (\beta )\left( q^{\beta }-1\right) })}+3s_{0}\right) },\;v(x,t)\text {=}\frac{b_{1}u(x,t)}{a_{1}}. \end{aligned}$$

(31)

For (32), Rew(x, t) is displayed in Fig. 5i–iv.

Fig. 5

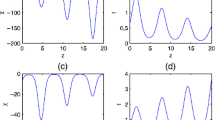
(i)-(iv), when $d\text {=}0.8,s_{1}\text {=}1.3,s_{0}\text {=}1.5,b_{1}\text {=}0.7,a_{1}\text {=}0.5,p\text {=}1.5,A\text {=}0.5,r\text {=}3.$ (i) and (iii) show semi-bottle neck (SBN) solitons shape. (ii) and (iv) consolidate this behavior. The presence of SBN, and also the effects of recent memory act remarkably to delay internet traffic analogous to the delay in solitons propagation

4.2 When $H=2$ and $m=2$

4.2.1 Case (a)

We consider (29) and the AE in (19) into (11) and (12) give rise to,

$$\begin{aligned} \begin{array}{c} \mu \text {=}-\frac{\left( \alpha _{4}+\alpha _{5}\right) {}^{2}\left( 8\alpha _{1}k^{3}+1\right) }{294\alpha _{1}\alpha _{6}k},\,\;\alpha _{9}\text {=}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\\ \alpha _{7}\text {=}\frac{\alpha _{1}(p\Omega -3kr)}{p},\;\Omega \text {=}-\frac{\left( \alpha _{4}+\alpha _{5}\right) {}^{2}\left( 244\alpha _{1}^{2}k^{6}-118\alpha _{1}k^{3}+15\right) }{588\alpha _{1}^{2}\alpha _{6}k^{2}},r\text {=}\frac{\left( \alpha _{4}+\alpha _{5}\right) {}^{2}p}{147\alpha _{1}\alpha _{6}},\\ \sigma \text {=}\frac{2\left( \alpha _{4}+\alpha _{5}\right) }{7\alpha _{1}k}+k\left( 2\alpha _{8}+4\alpha _{2}k+3\alpha _{4}k-\alpha _{5}k\right) ,\;a_{0}\text {=}-\frac{a_{1}s_{0}}{s_{1}},\\ \alpha _{3}\text {=}-\alpha _{2}-\frac{8}{7}\left( \alpha _{4}+\alpha _{5}\right) ,\alpha _{5}\text {=}\frac{\alpha _{4}s_{1}^{2}\left( 1-4\alpha _{1}k^{3}\right) -14\alpha _{1}\alpha _{6}k\left( a_{1}^{2}+b_{1}^{2}\right) }{s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) },\\ c_{2}=-\frac{c_{0}s_{1}^{2}}{2s_{0}^{2}},\;c_{0}\text {=}\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}kp^{2}}. \end{array} \end{aligned}$$

(32)

The solutions are,

$$\begin{aligned} \begin{array}{c} u(x,t)\text {=}\frac{a_{1}\left( \sqrt{2}-cosh\left( (A+z)\sqrt{\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}kp^{2}}}\right) \right) }{s_{1}\left( cosh\left( (A+z)\sqrt{\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}kp^{2}}}\right) +\sqrt{2}\right) },\;v(x,y)\text {=}\frac{b_{1}u(x,t)}{a_{1}},\\ \\ z\text {=}\frac{\tau \left( \left( \alpha _{4}+\alpha _{5}\right) {}^{2}p\right) }{147\alpha _{1}\alpha _{6}}+px,\;\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(33)

Based on (33), Rew(x, t) is displayed in Fig. 6i–iv.

Fig. 6

(i–iv), when $b_{1}\text {=}3,a_{1}\text {=}5,s_{1}\text {=}3,p\text {=}0.7,k\text {=}0.1,A\text {=}0.5$. (i) and (iii) show rhombus (diamond) CSs shape in space

4.2.2 Case (b)

We consider (29) and the AE in (25) into (11) and (12) lead to,

$$\begin{aligned} \begin{array}{c} \mu \text {=}\frac{\left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{1}k^{3}+1\right) \left( 8\alpha _{1}\alpha _{6}k\left( a_{1}^{2}+b_{1}^{2}\right) +\left( \alpha _{4}+\alpha _{5}\right) s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) \right) }{s_{1}^{4}\left( 1-4\alpha _{1}k^{3}\right) {}^{2}},\\ \alpha _{7}\text {=}-\frac{(a_{1}^{2}+b_{1}^{2})\alpha _{1}}{s_{1}^{4}\left( 1-4\alpha _{1}k^{3}\right) {}^{2}}\left( -k^{2}\left( \alpha _{4}+\alpha _{5}\right) s_{1}^{2}\left( 8\alpha _{1}^{2}k^{6}+26\alpha _{1}k^{3}-7\right) \right. \\ \left. +8\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) \left( 14\alpha _{1}^{2}k^{6}-15\alpha _{1}k^{3}+1\right) \right) ,\,c_{0}\text {=}\frac{2c_{2}s_{0}^{2}}{s_{1}^{2}},\\ \alpha _{9}\text {=}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\,\sigma \text {=}-\frac{2\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) \left( 14\alpha _{1}k^{3}-1\right) }{s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) }\\ +k\left( 2\alpha _{8}+4\alpha _{2}k+\alpha _{4}k-3\alpha _{5}k\right) ,\,c_{2}\text {=}\frac{s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) }{4\alpha _{1}km_{1}^{2}p^{2}s_{0}^{2}},\\ r\text {=}-\frac{2kp\left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{1}\alpha _{6}k\left( a_{1}^{2}+b_{1}^{2}\right) +\left( \alpha _{4}+\alpha _{5}\right) s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) \right) }{s_{1}^{4}\left( 1-4\alpha _{1}k^{3}\right) {}^{2}},\\ \Omega \text {=}-\frac{\left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) \left( 14\alpha _{1}^{2}k^{6}-9\alpha _{1}k^{3}+1\right) -\left( \alpha _{4}+\alpha _{5}\right) k^{2}s_{1}^{2}\left( 8\alpha _{1}^{2}k^{6}+2\alpha _{1}k^{3}-1\right) \right) }{s_{1}^{4}\left( 1-4\alpha _{1}k^{3}\right) {}^{2}},\\ \alpha _{3}\text {=}2\left( \frac{10\alpha _{1}\alpha _{6}k\left( a_{1}^{2}+b_{1}^{2}\right) }{s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) }+\alpha _{4}+\alpha _{5}\right) -\alpha _{2}. \end{array} \end{aligned}$$

(34)

The solutions are,

$$\begin{aligned} \begin{array}{c} u(x,t)=\frac{P}{Q},\;P=\left( a_{0}s_{1}\left( m_{0}^{2}s_{1}^{2}-2m_{1}^{2}s_{0}^{2}\sinh ^{2}(\frac{K(A+z)}{2s_{1}})\right) +a_{1}s_{0}\right. \\ \left. \left. \left( 2\sqrt{2}m_{1}^{2}s_{0}^{2}\sinh (\frac{K(A+z)}{2s_{1}})+\right. \sqrt{2}m_{0}^{2}s_{1}^{2}\sinh (\frac{K(A+z)}{2s_{1}})+2m_{0}m_{1}s_{0}s_{1}\cosh ^{2}(\frac{K(A+z)}{2s_{1}})\right) \right) ,\\ Q=s_{0}s_{1}\left( 2m_{1}^{2}s_{0}^{2}\left( \sqrt{2}-\sinh (\frac{K(A+z)}{2s_{1}})\right) \sinh (\frac{K(A+z)}{2s_{1}})\right. \\ \left. m_{0}^{2}s_{1}^{2}\left( \sqrt{2}\sinh (\frac{K(A+z)}{2s_{1}})+1\right) ++2m_{0}m_{1}s_{0}s_{1}\cosh ^{2}(\frac{K(A+z)}{2s_{1}})\right) ,\\ K=\frac{\sqrt{\frac{4\alpha _{1}k^{3}-1}{\alpha _{1}k}}\left( s_{1}\sqrt{2m_{1}^{2}s_{0}^{2}+m_{0}^{2}s_{1}^{2}}\right) }{m_{1}ps_{0}},\,v(x,t)\text {=}\frac{b_{1}u(x,t)}{a_{1}},\,\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) },\\ z\text {=}px-\frac{2kp\tau \left( a_{1}^{2}+b_{1}^{2}\right) \left( 8\alpha _{1}\alpha _{6}k\left( a_{1}^{2}+b_{1}^{2}\right) +\left( \alpha _{4}+\alpha _{5}\right) s_{1}^{2}\left( 4\alpha _{1}k^{3}-1\right) \right) }{s_{1}^{4}\left( 1-4\alpha _{1}k^{3}\right) {}^{2}}. \end{array} \end{aligned}$$

(35)

Rew(x, t) is displayed, by using (35), in Fig. 7i–iv.

Fig. 7

(i–iv), when $s_{1}\text {=}0.03,s_{0}\text {=}2.5,b_{1}\text {=}1.7,a_{1}\text {=}2.5,m_{1}\text {=}2.3,m_{0}\text {=}0.05,a_{0}\text {=}1.6,p\text {=}3.5,A\text {=}0.5,k\text {=}1.3.$ (i) and (iii) show hybrid rhombus-M-shaped CSs in space

4.2.3 Case (c)

We consider (29) and the AE,

$$\begin{aligned} \begin{array}{c} \phi '(z)\text {=}\sqrt{c^{2}\phi (z)^{2}-d^{2}}\end{array}, \end{aligned}$$

(36)

into (11) and (12), and get,

$$\begin{aligned} \begin{array}{c} \alpha _{9}\text {=}-\alpha _{8}-2\alpha _{2}k-2\alpha _{4}k+2\alpha _{5}k,\;\alpha _{7}\text {=}\frac{\alpha _{1}(p\Omega -3kr)}{p}\\ \mu \text {=}\frac{\alpha _{7}\left( 3k^{2}p-c^{2}p^{3}\right) +\alpha _{1}\left( -3c^{2}kp^{2}r+c^{2}p^{3}\Omega +k^{3}r-3k^{2}p\Omega \right) -r}{2kp},\\ \sigma \text {=}-\frac{s_{1}^{2}\left( 2\alpha _{1}k^{4}r+kr+2p\Omega \right) }{2p\left( a_{1}^{2}+b_{1}^{2}\right) }-\frac{\alpha _{6}\left( a_{1}^{2}+b_{1}^{2}\right) }{s_{1}^{2}}+k(2\alpha _{8}+3\alpha _{2}k-\alpha _{3}k\\ +3\alpha _{4}k-\alpha _{5}k),\,\alpha _{6}\text {=}\frac{\left( \alpha _{2}+\alpha _{3}\right) c^{2}p^{2}s_{0}^{2}s_{1}^{2}\left( 1-4\alpha _{1}\left( k^{3}-c^{2}kp^{2}\right) \right) }{8\left( a_{0}^{2}s_{1}^{2}+b_{1}^{2}s_{0}^{2}\right) \left( \alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -1\right) },\\ \\ \Omega \text {=}-\frac{\left( \alpha _{2}+\alpha _{3}\right) \left( a_{0}^{2}s_{1}^{2}+b_{1}^{2}s_{0}^{2}\right) \left( -c^{2}p^{2}+2\alpha _{1}\left( 7c^{4}kp^{4}+2c^{2}k^{3}p^{2}+2k^{5}\right) +2k^{2}\right) }{8s_{0}^{2}s_{1}^{2}\left( \alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -1\right) },\\ \\ r\text {=}\frac{\left( \alpha _{2}+\alpha _{3}\right) kp\left( a_{0}^{2}s_{1}^{2}+b_{1}^{2}s_{0}^{2}\right) }{2s_{0}^{2}s_{1}^{2}\left( \alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -1\right) },\,d\text {=}\frac{s_{0}\sqrt{2\alpha _{1}\left( c^{2}kp^{2}+2k^{3}\right) -1}}{\sqrt{6}\sqrt{\alpha _{1}}\sqrt{k}ps_{1}},\,a_{1}\text {=}-\frac{a_{0}s_{1}}{s_{0}},\\ \\ \alpha _{5}\text {=}\frac{\alpha _{2}\left( 1-4\alpha _{1}\left( 5c^{2}kp^{2}+k^{3}\right) \right) +\alpha _{3}\left( 1-4\alpha _{1}\left( 5c^{2}kp^{2}+k^{3}\right) \right) -4\alpha _{4}\left( \alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -1\right) }{4\alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -4}. \end{array} \end{aligned}$$

(37)

The solutions are,

$$\begin{aligned} \begin{array}{c} u(x,t)=-\frac{P}{Q},\;P=a_{0}\left( 6\sqrt{\alpha _{1}}A^{2}\sqrt{k}ps_{1}e^{2cz}+s_{0}\left( -12\sqrt{\alpha _{1}}Ac\sqrt{k}pe^{cz}\right. \right. \\ \left. \left. +\sqrt{12\alpha _{1}\left( c^{2}kp^{2}+2k^{3}\right) -6}\right) \right) ,\,Q=s_{0}\left( 6\sqrt{\alpha _{1}}A^{2}\sqrt{k}ps_{1}e^{2cz}+s_{0}\left( 12Ace^{cz}\right. \right. \\ \left. \left. \sqrt{12\alpha _{1}\left( c^{2}kp^{2}+2k^{3}\right) -6}+\sqrt{\alpha _{1}}\sqrt{k}p\right) \right) ,\,v(x,t)\text {=}-\frac{\left( b_{1}s_{0}\right) u(x,t)}{a_{0}s_{1}},\\ z\text {=}\frac{\tau \left( \left( \alpha _{2}+\alpha _{3}\right) kp\left( a_{0}^{2}s_{1}^{2}+b_{1}^{2}s_{0}^{2}\right) \right) }{2s_{0}^{2}s_{1}^{2}\left( \alpha _{1}\left( 5c^{2}kp^{2}+4k^{3}\right) -1\right) }+px,\tau \text {=}\frac{(1-q)t^{\beta }}{\Gamma (\beta )\left( 1-q^{\beta }\right) }. \end{array} \end{aligned}$$

(38)

Based on (38), Rew(x, t) is displayed in Fig. 8i–iv.

Fig. 8

(i)-(iv), when $b_{1}\text {=}0.7,c\text {=}-0.7,a_{0}\text {=}0.6,p\text {=}3.5,A\text {=}0.5,k\text {=}3.$ (i) shows retarded lump vector, while (iii) shows lump-vector with periodic waves background CSs

5 Speed of internet traffic and chips heating

A microchip (or a chip) is an integrated circuit. Within each microchip reside billions of silicon transistors. Electrical currents run between these hard-working transistors, and these currents generate heat. There are many types of chips. We consider a typical ship with mass ($m_{0}=5.68$ mg$=5.68\times 10^{-6}$Kg) and with length ($\texttt{l}_{0}=10nm$ $=10^{-8}m$). Here, the chip heat is estimated via Boltzmann equation (BE).

We introduce the speed of IT is the quantity of information downloaded or uploaded per second in an analogy to the speed of traveling wave in optical fibers via the CM by,

$$\begin{aligned} c(t)=\frac{\int _{\mathbb {R}}\mid w_{t}\mid dx}{\int _{\mathbb {R}}\mid w_{x}\mid dx}. \end{aligned}$$

(39)

Here, we use the solutions in (18) to evaluate (39). The results obtained are shown in Fig. 9i and ii to visualize the effects of recent memory and compression memory on the speed of IT.

Fig. 9

(i) and (ii) are displaced for the same figure caption as in Fig. 1i–iv

After Fig. 9i, the speed of IT is constant in time. The speed of IT increases for no recent memory effect (when $\beta =0.99),$while the speed is lowered in the presence of recent memory (when $\beta =0.6).$ These results are realistic. Figure 9ii shows nonuniform speed in the presence of compression memory. As the range of variation is small, then the speed is manly constant.

The chip heat is estimated by using BE, which reads,

$$\begin{aligned} K_{B}\text {T=}\frac{m_{0}l_{0}^{2}}{2}<v^{2}>, \end{aligned}$$

(40)

where T is the temperature, and $K_{B}$ is the Boltzmann constant ($K_{B}=1.38\times 10^{-23}$ $\text {Kg}m^{2}$ $K^{-1}s^{-2})$, and,

$$\begin{aligned} <v^{2}>=\frac{\int _{R^{+}}\int _{\mathbb {R}}(\mid w_{t}\mid )^{2}d\bar{x}dt}{\int _{R^{+}}\int _{\mathbb {R}}(\mid w_{\bar{x}}\mid )^{2}d\bar{x}dt},\;\bar{x}=\frac{x}{l_{0}}. \end{aligned}$$

(41)

By using (40) and (41) to estimate T, and using (18) for the same values of the parameters as in Figs. 1i–iv, we find that when $\beta =0.6,$T=11 K, while when $\beta =0.99$ then $T=26$ K. This may be interpreted by a slow speed of IT gives rise to low chip heat (cf. Fig. 9i) and vise-versa.

6 Stability of a steady state solution (SSS)

The SSSs of (6) are found by setting $w_{t}=0$, which results to an equation governing these solutions. Among them, there exist a constant solution $w^{*}=w=\sqrt{-\frac{\sigma }{\alpha _{6}}}$,$\frac{\sigma }{\alpha _{6}}<0,$ where $\sigma$ and $\alpha _{6}$ are the coefficients of the cubic and quintic nonlinearity respectively. Now, we use the perturbation expansions,

$$\begin{aligned} w(x,t)\text {=}\sqrt{-\frac{\sigma }{\alpha _{6}}}+e^{\lambda t}\left( \epsilon _{1}U(x)+i\epsilon _{2}V(x)\right) ,\;w(x,t)^{*}\text {=}\sqrt{-\frac{\sigma }{\alpha _{6}}}+e^{\lambda t}\left( \epsilon _{1}U(x)-i\epsilon _{2}V(x)\right) . \end{aligned}$$

(42)

From (42) into (6) and by standard calculations lead to,

$$\begin{aligned}{} & {} M\left( \begin{array}{c} \epsilon _{1}\\ \epsilon _{2} \end{array}\right) =0,\; M\left( \begin{array}{cc} a_{11} &{} a_{12}\\ a_{21} &{} a_{22} \end{array}\right) ,\nonumber \\{} & {} a_{11}=-\frac{\sigma }{\alpha _{6}}(-5\frac{\sigma }{\alpha _{6}}\alpha _{6}U(x)+\alpha _{3}U'(x)+3\alpha _{2}U(x)+3\sigma U(x))+\mu U''(x)\nonumber \\{} & {} -\frac{\sigma }{\alpha _{6}}(\alpha _{5}U''(x)+\alpha _{4}+U''(x))+\alpha _{1}\lambda U^{(3)}(x),\nonumber \\{} & {} a_{12}=-\frac{\sigma }{\alpha _{6}}(\alpha _{8}U'(x)+\alpha _{9}U'(x))+\alpha _{7}U^{(3)}(x)+\lambda U(x),\nonumber \\{} & {} a_{21}=-\frac{\sigma }{\alpha _{6}}(-\alpha _{8}V'(x)+\alpha _{7}\alpha _{9}V^{(3)}(x)V'(x))-\lambda V(x),\nonumber \\{} & {} a_{22}\text {=}-{\frac{\sigma }{\alpha _{6}}}(-\sigma V(x)+\alpha _{4}V''(x)+\alpha _{3}V'(x)+\alpha _{2}V(x)+\sigma V(x)\nonumber \\{} & {} \quad -\alpha _{5}V''(x))+\alpha _{1}\lambda V^{(3)}(x)+\mu V''(x). \end{aligned}$$

(43)

The solution of (43) is $det(M)=0,$ which leads to the eigenvalue equation. It is very lengthy to be produced here. It is solved when subjected to the boundary conditions, $U(\pm \infty )=0,$ and $V(\pm \infty )=0.$ To this due, we write,

$$\begin{aligned} \begin{array}{c} U(x)={\left\{ \begin{array}{ll} Ae^{-Kx} &{},K>0.x>0\\ Ae^{Kx} &{} K>0, \end{array}\right. }x<0,\\ V(x)={\left\{ \begin{array}{ll} Be^{-Kx} &{},K>0.x>0\\ Be^{Kx} &{} K>0, \end{array}\right. }x<0. \end{array} \end{aligned}$$

(44)

By inserting (44) into the equation leads to,

$$\begin{aligned} \begin{array}{c} \alpha _{2}\text {=}\frac{K\left( \alpha _{3}\sigma +K\left( \alpha _{6}\mu -\alpha _{4}\sigma +\alpha _{5}\sigma -\alpha _{1}\alpha _{6}\alpha _{7}K^{4}+\alpha _{1}\alpha _{8}K^{2}\sigma +\alpha _{1}\alpha _{9}K^{2}\sigma \right) \right) }{\sigma },\\ \lambda \text {=}\alpha _{7}K^{3}-\frac{\left( \alpha _{8}+\alpha _{9}\right) K\sigma }{\alpha _{6}}. \end{array} \end{aligned}$$

(45)

As $\sigma /\alpha _{6}<0,$the solution is unstable when $\alpha _{i}>0,i=7,8,9$ and it is stable when $\alpha _{i}<0.$

7 Conclusions

The study presented here investigates the characteristics of internet traffic through an analogy to the propagation of traveling waves in optical fibers. This is achieved using a model that incorporates space-time highest order dispersion and the Caputo-q derivative. The model yields exact solutions through the implementation of the unified method. Multiple concatenated solitons are observed. Among them, M-shaped, hybrid M-shaped, hybrid chirped, rhombus shaped, lump vector, and bottle neck shaped. On the other side, the speed of internet traffic is evaluated in a manner similar to the speed of traveling waves in optical fibers. The results indicate that the speed is constant over time. However, the effect of distributed time delay (or recent memory) reduces the internet speed, which aligns with real-world observations. This effect is observed by varying the fractional order. Furthermore, the study estimates the heat generated by a chip in an electronic device. It is noted that a lower (or higher) chip temperature corresponds to a lower (or higher) speed, which is consistent with expectations. This research provides valuable insights into the behavior of internet traffic and could potentially inform the design of more efficient network system.