1 Introduction

Nonlinear evolutionary models have demonstrated their utility in the modern era, addressing challenges spanning across physical–mathematical realms encompassing biology, engineering, chemistry, physics, and practical applications in daily life (Rasool et al. 2023; Rezazadeh et al. 2023; Ullah et al. 2022; Ashraf et al. 2023, 2022; Seadawy et al. 2022; Rizvi et al. 2023). These models encompass a range of challenges within nonlinear sciences, spanning from the Fokas–Lenells model (Ullah et al. 2023) and the BBS model (Ullah et al. 2021) to the Zoomeron model (Irshad and Mohyud-din 2013; Morris and Leach 2014) and the Biswas–Arshed model (Ullah et al. 2022), encompassing phenomena like the KdV model (Arora et al. 2022) and the Schrödingerr system (Xiang and Zuo 2022). Initially introduced by Calogero and Degasperis in 1976, the Zoomeron model describes concealed qualities and solitons observed in nonlinear physics, fluid mechanics, and laser optics (Ullah et al. 2023; Yao et al. 2022). Solitons, as self-reinforcing solitary waves, retain their shape while traveling at a constant speed, arising from the cancellation of nonlinear and dispersive effects in a medium.

The current research is focused on the nonlinear evolutionary Zoomeron equation. In 1976, Calogero and Degasperis reached a breakthrough during the time they investigated the one-dimensional Schrödinger equation and an extension of the well-known KdV equation to depict solitons that travel at different speeds and found a connection between their polarisation effects and velocities. This investigation led to the identification of two distinct soliton types: the Boomeron, traveling from one side in the distant past to the original side in the far future at the same speed, and the Trappon, oscillating around a fixed point while altering direction periodically.

Therefore, discovering precise and analytical solutions to nonlinear evolutionary problems stands as a critical task for mathematical physicists. Several direct methods have been employed to explore the provided incognito evolution equation, some notably being the extended direct algebraic technique (Gao et al. 2020), the extended exp\((-\phi \left( \xi \right) )\)-expansion and exponential rational function techniques (Kumar and Kaplan 2018), as well as the new Jacobi elliptic function expansion method, the exponential rational function method, and the Jacobi elliptic function rational expansion method (Tala-Tebue et al. 2018). Other approaches include the modified Kudryashov method (Hosseini et al. 2021), \(\left( \frac{G^{'}}{G}\right)\)-expansion method (Abazari 2011), sine-cosine function method (Qawasmeh 2013), exp-function method, modified simple equation method (Khan and Akbar 2014), and auxiliary equation method (Topsakal and Taşcan 2020). Additionally, the Zoomeron equation has been demonstrated to satisfy the P-property of integrability by Porsezian (1998), with analyses on symmetry and conservation laws by Motsepa et al. (2017) and stability examinations by Inc et al. (2018).

In this study, our purpose is to get new numerical solutions that are efficient, more accurate, flexible, robustness and stable. Nonlinear evolution equations have attracted extensive research attention, prompting investigations from various perspectives. Chen and Ren proposed an enhanced linear model for researching group competitive sports, delving into stability related to the model’s equilibrium points and Hopf branches (Chen and Ren 2021). Gao et al. utilized the extended sinh Gordon equation expansion technique to study the Hirota-Maccari system, revealing solitary, complex, and single periodic solutions as traveling patterns for the system (Yel et al. 2021). Similarly, Baskonus et al. explored the same technique in analyzing an equation describing nonlinear surface gravity waves over a horizontal seafloor (Sulaiman et al. 2021). Moreover, Bilal et al. utilized the generalized exponential rational function technique to examine the dynamic behavior of a physical model (Bilal et al. 2021), while Zhirong and Alghazzawi employed a fractional differential model to study psychological barriers and methods for overcoming mental challenges in college students (Zhirong and Alghazzawi 2021), with related works incorporating fractional models (Aghili 2021; Yu and Kong 2021). Despite these extensive investigations, numerous physical models remain unexplored, demanding innovative mathematical techniques to comprehend their dynamic processes.

The following is how this work is organized: Sect. 2 provides the Zoomeron model’s ODE conversion. The Mapping method algorithm is presented in Sect. 3, and its essential components exhibit a variety of solutions. The use of the recommended method to solving the Zoomeron problem is demonstrated in Sect. 4 alongside graphical representations of the determined solutions. Finally, we offer some last conclusions in Sect. 5.

2 ODE form of the proposed model

In this section, let’s consider the \((2+1)\)-dimensional nonlinear framework referred to as the Zoomeron model:

$$\begin{aligned} \left( {\frac{Q_{{{ xy}}}}{Q}}\right) _{ tt} - \left( {\frac{Q_{{{ xy}}}}{Q}}\right) _{ xx} +2 \left( Q^2\right) _{ xt} = 0, \end{aligned}$$
(2.1)

The magnitude of the soliton is written as Q(x, y, t), where x, y and t are position and time components, respectively. By taking the linear transformation into account \(Q(x, y, t) = Q(\xi )\), \(\xi = x + ry - vt\), The phenomenon associated to trappons and boomerons is described by the nonlinear Eq. 2.1. It also clarifies the mechanism behind complicated physical problems. Thus, the Zoomeron equation contains specific types of solitons with distinctive properties that arise in a number of physical contexts, such as nonlinear optics, laser physics and fluid dynamics (Duran 2021; Morris and Leach 2014). An ordinary differential form of Eq. 2.1 is as follows:

$$\begin{aligned} r \left( v^2 - 1 \right) \,\, U'' \left( \xi \right) - \,\, 2 \,v { U^3} \left( \xi \right) - k\, { U} \left( \xi \right) =0. \end{aligned}$$
(2.2)

k is the integration constant in this scenario. N is obtained by balancing the nonlinear term \(U^3\) alongside the linear term \(U''\) which gives \(N + 2 = 3N\), and thus, \(N = 1\).

3 The mapping method

Here we use the mapping method (Peng 2003) for finding the solutions of Eq. 2.2. As a consequence, the basic idea is as follows. For a given non-linear partial differential equation, say in three independent variables,

$$\begin{aligned} N(u, u_{t}, u_{x},u_{y},\ldots )=0 \end{aligned}$$
(3.1)

By taking linear transformation in the form

$$\begin{aligned} W=W(\xi )\,\quad , \xi = x+ry-\nu t. \end{aligned}$$
(3.2)

where r is real constant and v is velocity. Substituting Eq. 3.2 into Eq. 3.1 yields an ordinary differential equation of \(U(\xi )\). Then \(U(\xi )\) is expended into a polynomial in \(W(\xi )\).

$$\begin{aligned} U \left( \xi \right) = \sum _{i=0}^{n}a_{{i}}{W}^{i}, \end{aligned}$$
(3.3)

where \(a_{{i}}\) are constants to be determined, and n is fixed by balancing the linear term of the highest order derivative with nonlinear term, while W satisfies the first kind of elliptic equation.

$$\begin{aligned} W'\,^{2} = \,{\frac{1}{2}}\,p_{{1}}{W}^{4}+\,p_{{2}}{W}^{2}+\,p_{{3}} \quad ,\quad W^{''}= p_{2} W + p_{1} W^{3}, \end{aligned}$$
(3.4)

here the primes means the derivatives with respect to \(\xi\). After Eq. 3.3 with Eq. 3.4 is substituted into the ordinary differential equation, the coefficients \(a_{i}\), \(p_{1}\), \(p_{2}\), \(p_{3}\) may be determined. Thus Eq. 3.3 establishes an algebraic mapping relation between the solution for Eq. 3.1 and that of Eq. 3.2.


Where \(p_{1}, p_{2},\) and \(p_{3}\) are actual parameters. We observe that there are various solutions to Eq. 3.4, based on \(p_{1}, p_{2},\) and \(p_{3}\), as shown in the following. Every answer to Eq. 3.4 depend upon for a variation of \(p_{1}, p_{2},\) and \(p_{3}\) values.

Type 1:

If \(p_{1}=2m^{2},\,p_{2}=-(1+m^{2}),\,p_{3}= 1\) then \(W(\xi )= sn(\xi )\),

Type 2:

If \(p_{1}=2, p_{2}=\,2\,{m}^{2}-1,\,p_{3}=- m^{2} \left( 1-{m}^{2} \right)\) then \(W(\xi )= ds(\xi )\),

Type 3:

If \(p_{1}=2, p_{2}=2-m^{2},p_{3}= 1-{m}^{2}\) then \(W(\xi )= cs(\xi )\),

Type 4:

If \(p_{1}=-2\,m^{2}, p_{2}=\,2\,{m}^{2}-1,p_{3}= 1-{m}^{2}\) then \(W(\xi )= cn(\xi )\),

Type 5:

If \(p_{1}=-2, p_{2}=2-{m}^{2},p_{3}= {m}^{2}-1\) then \(W(\xi )= dn(\xi )\),

Type 6:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{1}{4}}\) then \(W(\xi )= {\frac{sn(\xi )}{1\pm dn (\xi )}}\),

Type 7:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{m^{{2}}}{4}}\) then \(W(\xi )= {\frac{sn(\xi )}{1\pm dn (\xi )}}\),

Type 8:

If \(p_{1}={\frac{-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{- \left( 1-{m}^{2} \right) ^{2}}{4}}\) then \(W(\xi )= mcn\left( \xi \right) + dn\left( \xi \right)\),

Type 9:

If \(p_{1}={\frac{{m}^{2}-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{{m}^{2}-1}{4}}\) then \(W(\xi )= {\frac{dn(\xi )}{1\pm sn (\xi )}}\),

Type 10:

If \(p_{1}={\frac{1-{m}^{2}}{2}}, p_{2}={\frac{1-{m}^{2}}{2}},p_{3}= {\frac{1-{m}^{2}}{4}}\) then \(W(\xi )= {\frac{cn(\xi )}{1\pm sn (\xi )}}\),

Type 11:

If \(p_{1}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}}, p_{2}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}},p_{3}= {\frac{1}{4}}\) then \(W(\xi )= {\frac{sn(\xi )}{dn\pm cn (\xi )}}\),

Type 12:

If \(p_{1}=2, p_{2}=0,p_{3}= 0\) then \(W(\xi )={\frac{c}{\xi }}\),

Type 13:

If \(p_{1}=0, p_{2}=1,p_{3}= 0\) then \(W(\xi )= ce^{\xi }\).

Such that \(dn \left( \xi \right) = dn \left( \xi , m\right) , sn \left( \xi \right) = sn \left( \xi , m\right) ,cn \left( \xi \right) = cn \left( \xi , m\right)\) and for \(0<m <1\) seem to be the Jacobi elliptic functions (JEFs) (Ullah et al. 2024). The subsequent hyperbolic functions are generated from JEFs whenever \(m \rightarrow 1\)

$$\begin{aligned} cs \left( \xi \right) \rightarrow csch \left( \xi \right) , sn \left( \xi \right) \rightarrow tanh \left( \xi \right) , cn \left( \xi \right) \rightarrow sech \left( \xi \right) , dn \left( \xi \right) \rightarrow sech \left( \xi \right) , ds \left( \xi \right) \rightarrow csch \left( \xi \right) .\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{aligned}$$

The triangular functions that result from \(m \rightarrow 0\) are just as follows:

$$\begin{aligned}{} & {} sn \left( \xi \right) \rightarrow sin \left( \xi \right) , cn \left( \xi \right) \rightarrow cos \left( \xi \right) , dn \left( \xi \right) \rightarrow 1,\\{} & {} cs \left( \xi \right) \rightarrow cot \left( \xi \right) , ds \left( \xi \right) \rightarrow csc \left( \xi \right) .\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{aligned}$$

4 Application of the mapping method

By applying homogeneous balance number in Eq. 3.3 which is \(N + 2 = 3N\), and thus, \(N = 1\).

$$\begin{aligned} U \left( \xi \right) =a_{{0}}+a_{{1}}W, \end{aligned}$$
(4.1)

where \(a_{0}\), and \(a_{1}\) represent constants that require determination, ensuring that \(a_{1} \ne 0\). By substituting Eqs. 4.1 and 3.4 into Eq. 2.2 and equating the coefficients of all powers of \(W^{i}\), where \(i = 0, 1, 2, 3\), to zero, we obtain the subsequent system of algebraic equations.

$$\begin{aligned} {\left\{ \begin{array}{ll} -ra_{{1}}p_{{1}}-2\,v{a_{{1}}}^{3}+r{v}^{2}a_{{1}}p_{{1}}=0,\\ -6\,va_{{0}}{a_{{1}}}^{2}=0,\\ r{v}^{2}a_{{1}}p_{{2}}-ra_{{1}}p_{{2}}-6\,v{a_{{0}}}^{2}a_{{1}}-ka_{{1 }}=0,\\ -2\,v{a_{{0}}}^{3}-ka_{{0}}=0.\\ \end{array}\right. } \end{aligned}$$
(4.2)

Solving the system of algebraic Eq. 4.2 with the aid of Maple, we have the following set of results:

$$\begin{aligned}{} & {} \begin{aligned} a_{{0}}=0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, a_{{1}}=\pm {\frac{1}{2}}\,{\frac{\sqrt{2}\root 4 \of {r}\sqrt{p_{{1}}}\sqrt{k}}{ \root 4 \of {p_{{2}}}\root 4 \of {rp_{{2}}+k}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v=\pm \sqrt{{\frac{rp_{{2}}+k}{rp_{{2}}}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{aligned} \end{aligned}$$
(4.3)
$$\begin{aligned}{} & {} \begin{aligned} a_{{0}}={\pm \frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, a_{{1}}={\pm \frac{1}{2}}\,{\frac{\sqrt{2}\sqrt{vrp_{{1}} \left( {v}^{2}-1 \right) }}{v}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v=v,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{aligned} \end{aligned}$$
(4.4)

Case 1:

Upon substituting Eqs. 4.3 and 3.4 into Eq. 4.1, we arrive at the subsequent exact solution for Eq. 2.2. Now, Eq. 2.2 has the following many new exact solutions:

If \(m \rightarrow 1\), then we obtain the soliton wave solution

Type 1:

If \(p_{1}=2m^{2},\,p_{2}=-(1+m^{2}),\,p_{3}= 1\) then \(W(\xi )= sn(\xi )\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,1} \left( x,y,t \right) ={\frac{\root 4 \of {r}\sqrt{{m}^{2}}\sqrt{k} \tanh \left( \xi \right) }{\root 4 \of {-1-{m}^{2}}\root 4 \of {r \left( -1 -{m}^{2} \right) +k}}}. \end{aligned}$$
(4.5)

Type 2:

If \(p_{1}=2, p_{2}=\,2\,{m}^{2}-1,\,p_{3}=- m^{2} \left( 1-{m}^{2} \right)\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,2} \left( x,y,t \right) ={\frac{\root 4 \of {r}\sqrt{k}{} { csch} \xi }{\root 4 \of {2\,{m}^{2}-1}\root 4 \of {r \left( 2\,{m}^{2}-1 \right) +k}}}. \end{aligned}$$
(4.6)

Type 3:

If \(p_{1}=2, p_{2}=2-m^{2},p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,3} \left( x,y,t \right) ={\frac{\root 4 \of {r}\sqrt{k}{} { csch} \xi }{\root 4 \of {2-{m}^{2}}\root 4 \of {r \left( 2-{m}^{2} \right) +k}}}. \end{aligned}$$
(4.7)

Type 4:

If \(p_{1}=-2m^{2}, p_{2}=\,2\,{m}^{2}-1,p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,4} \left( x,y,t \right) ={\frac{i\root 4 \of {r}m\sqrt{k}{{\,\textrm{sech}\,}}\xi }{\root 4 \of {2\,{m }^{2}-1}\root 4 \of {2\,r{m}^{2}-r+k} }}. \end{aligned}$$
(4.8)

Type 5:

If \(p_{1}=-2, p_{2}=2-{m}^{2},p_{3}= {m}^{2}-1\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,5} \left( x,y,t \right) ={\frac{i\root 4 \of {r}\sqrt{k}{ sech} \xi }{\root 4 \of {2-{m}^{2}}\root 4 \of {r \left( 2-{m}^{2} \right) +k}}}. \end{aligned}$$
(4.9)

Type 6:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,6}\left( x,y,t \right) =\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}}\sqrt{k }{} { tanh}\xi }{2\root 4 \of { {\frac{1}{2}}\,{m}^{2}-1}\root 4 \of {r \left( {\frac{1}{2}}\,{m}^ {2}-1 \right) +k} \left( 1+{ sech}\xi \right) }}. \end{aligned}$$
(4.10)

Type 7:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{m^{{2}}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,7} \left( x,y,t \right) =\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}}\sqrt{k }{} { tanh}\xi }{2\root 4 \of { {\frac{1}{2}}\,{m}^{2}-1}\root 4 \of {r \left( {\frac{1}{2}}\,{m}^ {2}-1 \right) +k} \left( 1+{ sech}\xi \right) }}. \end{aligned}$$
(4.11)

Type 8:

If \(p_{1}={\frac{-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{- \left( 1-{m}^{2} \right) ^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,8} \left( x,y,t \right) ={\frac{\,i\root 4 \of {r}\sqrt{k} \left( { msech}\xi +{ sech}\xi \right) }{2\root 4 \of {{\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}}}\root 4 \of {r \left( {\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}} \right) +k}}}. \end{aligned}$$
(4.12)

Type 9:

If \(p_{1}={\frac{{m}^{2}-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{{m}^{2}-1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,9}\left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}-1} \sqrt{k}{} { sech}\xi }{\root 4 \of {{\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}}}\root 4 \of {r \left( {\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}} \right) +k} \left( 1+{ tanh}\xi \right) }} \end{aligned}$$
(4.13)

Type 10:

If \(p_{1}={\frac{1-{m}^{2}}{2}}, p_{2}={\frac{1-{m}^{2}}{2}},p_{3}= {\frac{1-{m}^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,10}\left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\root 4 \of {r}\sqrt{1-{m}^{2}} \sqrt{k}{} { sech}\xi }{\root 4 \of {{\frac{1}{2}}-{\frac{1}{2}}\,{m}^{2}}\root 4 \of {r \left( {\frac{1}{2}}-{\frac{1}{2}}\,{m}^{2} \right) +k} \left( 1+{ tanh}\xi \right) }}. \end{aligned}$$
(4.14)

Type 11:

If \(p_{1}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}}, p_{2}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,11} \left( x,y,t \right) ={\frac{1}{4}}\,{\frac{\root 4 \of {r} \left( 1-{m}^{2} \right) \sqrt{k}{} { tanh}\xi }{\root 4 \of {{\frac{1}{2}}\,r \left( 1-{m}^{2} \right) ^{2}+k}{} { sech}\xi }}. \end{aligned}$$
(4.15)

If \(m \rightarrow 0\), then we obtain the soliton wave solution:

Type 1:

If \(p_{1}=2m^{2},\,p_{2}=-(1+m^{2}),\,p_{3}= 1\) then \(W(\xi )= sn(\xi )\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,12} \left( x,y,t \right) = {\frac{\root 4 \of {r}\sqrt{{m}^{2}}\sqrt{k}\sin \xi }{\root 4 \of {-1-{m}^{2}}\root 4 \of {r \left( -1-{m}^{ 2} \right) +k}}}. \end{aligned}$$
(4.16)

Type 2:

If \(p_{1}=2, p_{2}=\,2\,{m}^{2}-1,\,p_{3}=- m^{2} \left( 1-{m}^{2} \right)\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,13}\left( x,y,t \right) = {\frac{\root 4 \of {r}\sqrt{k}\csc \xi }{\root 4 \of {2\,{m}^{2}-1}\root 4 \of {r \left( 2\,{m}^{2}-1 \right) +k}}}. \end{aligned}$$
(4.17)

Type 3:

If \(p_{1}=2, p_{2}=2-m^{2},p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,14} \left( x,y,t \right) = {\frac{\root 4 \of {r}\sqrt{k}\cot \xi }{\root 4 \of {2-{m}^{2}}\root 4 \of {r \left( 2-{m}^{2} \right) +k}}}. \end{aligned}$$
(4.18)

Type 4:

If \(p_{1}=-2m^{2}, p_{2}=\,2\,{m}^{2}-1,p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,15} \left( x,y,t \right) = {\frac{im\root 4 \of {r}\sqrt{k}\cos \xi }{\root 4 \of {2\,{m}^{2}-1}\root 4 \of {r \left( 2\,{m}^{2}-1 \right) +k}}}. \end{aligned}$$
(4.19)

Type 5:

If \(p_{1}=-2, p_{2}=2-{m}^{2},p_{3}= {m}^{2}-1\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,16}\left( x,y,t \right) = {\frac{i\root 4 \of {r}\sqrt{k}}{\root 4 \of {2- {m}^{2}}\root 4 \of {r \left( 2-{m}^{2} \right) +k}}}. \end{aligned}$$
(4.20)

Type 6:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,17}\left( x,y,t \right) = {\frac{1}{4}}\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}} \sqrt{k}\sin \xi }{\root 4 \of {{\frac{1}{2}}\,{m}^{2}-1}\root 4 \of { r \left( {\frac{1}{2}}\,{m}^{2}-1 \right) +k}}}. \end{aligned}$$
(4.21)

Type 7:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{m^{{2}}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,18}\left( x,y,t \right) = {\frac{1}{4}}\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}} \sqrt{k}\sin \xi }{\root 4 \of {{\frac{1}{2}}\,{m}^{2}-1}\root 4 \of { r \left( {\frac{1}{2}}\,{m}^{2}-1 \right) +k}}}. \end{aligned}$$
(4.22)

Type 8:

If \(p_{1}={\frac{-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{- \left( 1-{m}^{2} \right) ^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,19} \left( x,y,t \right) = {\frac{\,i\root 4 \of {r}\sqrt{k} \left( m{ cos} \xi +1 \right) }{2\root 4 \of {{\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}}} \root 4 \of {r \left( {\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}} \right) +k}}}. \end{aligned}$$
(4.23)

Type 9:

If \(p_{1}={\frac{{m}^{2}-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{{m}^{2}-1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,20} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\root 4 \of {r}\sqrt{{m}^{2}-1}\sqrt{k}}{\root 4 \of {{\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}}}\root 4 \of {r \left( {\frac{1}{2}}\,{m}^{2}+{\frac{1}{2}} \right) +k} \left( 1+\sin \xi \right) }}. \end{aligned}$$
(4.24)

Type 10:

If \(p_{1}={\frac{1-{m}^{2}}{2}}, p_{2}={\frac{1-{m}^{2}}{2}},p_{3}= {\frac{1-{m}^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,21}\left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\root 4 \of {r}\sqrt{1-{m}^{2}}\sqrt{k}\cos \xi }{\root 4 \of {{\frac{1}{2}}-{\frac{1}{2}}\,{m}^{2}}\root 4 \of {r \left( {\frac{1}{2}}-{\frac{1}{2}}\,{m}^{2} \right) +k} \left( 1+\sin \xi \right) }}. \end{aligned}$$
(4.25)

Type 11:

If \(p_{1}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}}, p_{2}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{1,22} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\root 4 \of {r} \left( 1-{m}^{2} \right) \sqrt{k}\sin \xi }{\root 4 \of {r \left( {\frac{1}{2}}\, \left( 1-{m}^{2} \right) ^{2} \right) +k} \left( 1+\cos \xi \right) }}. \end{aligned}$$
(4.26)

5 Graphical representation

This section exhibited 3D and contour representations of the Zoomeron equation for case 1.

Fig. 1
figure 1

For the given parameters \(r=1\), \(k=0.1\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,1}(x, y, t)\) is shown on the right

Full size image
Fig. 2
figure 2

For the given parameters \(r=1\), \(k=1\), and \(v=3\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{2,1}(x, y, t)\) is shown on the right

Full size image
Fig. 3
figure 3

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,8}(x, y, t)\) is shown on the right

Full size image
Fig. 4
figure 4

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{2,4}(x, y, t)\) is shown on the right

Full size image
Fig. 5
figure 5

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{2,5}(x, y, t)\) is shown on the right

Full size image
Fig. 6
figure 6

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{2,8}(x, y, t)\) is shown on the right

Full size image
Fig. 7
figure 7

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,12}(x, y, t)\) is shown on the right

Full size image
Fig. 8
figure 8

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,15}(x, y, t)\) is shown on the right

Full size image
Fig. 9
figure 9

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,17}(x, y, t)\) is shown on the right

Full size image
Fig. 10
figure 10

For the given parameters \(r=0.1\), \(k=0.5\), and \(v=0.5\), the 3-D graph is displayed on the left, while the contour graph illustrating the solution \(Q_{1,18}(x, y, t)\) is shown on the right

Full size image

Case 2:

Substituting Eq. 4.4 along with Eq. 3.4 into Eq. 4.1, we get the following exact solution of Eq. 2.2. Now, Eq. 2.2 has the following many new exact solutions:

If \(m \rightarrow 1\), then we obtain the soliton wave solution

Type 1:

If \(p_{1}=2m^{2},\,p_{2}=-(1+m^{2}),\,p_{3}= 1\) then \(W(\xi )= sn(\xi )\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,1} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr{m}^{2} \left( {v}^{2}-1 \right) }\tanh \xi }{v}}. \end{aligned}$$
(5.1)

Type 2:

If \(p_{1}=2, p_{2}=\,2\,{m}^{2}-1,\,p_{3}=- m^{2} \left( 1-{m}^{2} \right)\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,2} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr \left( {v}^{2}-1 \right) }{ csch} \xi }{v}}. \end{aligned}$$
(5.2)

Type 3:

If \(p_{1}=2, p_{2}=2-m^{2},p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,3} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr \left( {v}^{2}-1 \right) }{ csch} \xi }{v}}. \end{aligned}$$
(5.3)

Type 4:

If \(p_{1}=-2m^{2}, p_{2}=\,2\,{m}^{2}-1,p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,4} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ -vr{m}^{2} \left( {v}^{2}-1 \right) }{} { sech} \xi }{v }}. \end{aligned}$$
(5.4)

Type 5:

If \(p_{1}=-2, p_{2}=2-{m}^{2},p_{3}= {m}^{2}-1\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,5} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{i\sqrt{vr \left( {v}^{2}-1 \right) }{ sech} \xi }{v}}. \end{aligned}$$
(5.5)

Type 6:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,6} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr{m}^{2} \left( {v}^{2}-1 \right) }{} { tanh}\xi }{v \left( 1+ { sech}\xi \right) }}. \end{aligned}$$
(5.6)

Type 7:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{m^{{2}}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,7}\left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr{m}^{2} \left( {v}^{2}-1 \right) }{} { tanh}\xi }{v \left( 1+ { sech}\xi \right) }}. \end{aligned}$$
(5.7)

Type 8:

If \(p_{1}={\frac{-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{- \left( 1-{m}^{2} \right) ^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,8} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{i \sqrt{vr \left( {v}^{2}-1 \right) } \left( m{ sech}\xi +{ sech} \xi \right) }{v}}. \end{aligned}$$
(5.8)

Type 9:

If \(p_{1}={\frac{{m}^{2}-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{{m}^{2}-1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,9}\left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr \left( {m}^{2}-1 \right) \left( {v}^{2}-1 \right) }{} { sech}\xi }{v \left( 1+{ tanh}\xi \right) }}. \end{aligned}$$
(5.9)

Type 10:

If \(p_{1}={\frac{1-{m}^{2}}{2}}, p_{2}={\frac{1-{m}^{2}}{2}},p_{3}= {\frac{1-{m}^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,10} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr \left( 1-{m}^{2} \right) \left( {v}^{2}-1 \right) }{} { sech}\xi }{v \left( 1+{ tanh}\xi \right) }}. \end{aligned}$$
(5.10)

Type 11:

If \(p_{1}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}}, p_{2}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,11} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{4}}\,{\frac{ \sqrt{vr \left( {v}^{2}-1 \right) } \left( 1-{m}^{2} \right) { tanh}\xi }{v{ sech}\xi }}. \end{aligned}$$
(5.11)

Type 12:

If \(p_{1}=2, p_{2}=0,p_{3}= 0\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,12}\left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr \left( {v}^{2}-1 \right) }c}{v\xi }}. \end{aligned}$$
(5.12)

Type 13:

If \(p_{1}=2, p_{2}=0,p_{3}= 0\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,13}\left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}. \end{aligned}$$
(5.13)

If \(m \rightarrow 0\), then we obtain the soliton wave solution

Type 1:

If \(p_{1}=2m^{2},\,p_{2}=-(1+m^{2}),\,p_{3}= 1\) then \(W(\xi )= sn(\xi )\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,14} \left( x,y,t \right) ={\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr{m}^{2} \left( {v}^{2}-1 \right) }\sin \xi }{v}}. \end{aligned}$$
(5.14)

Type 2:

If \(p_{1}=2, p_{2}=\,2\,{m}^{2}-1,\,p_{3}=- m^{2} \left( 1-{m}^{2} \right)\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,15} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr \left( {v}^{2}-1 \right) }\csc \xi }{v}}. \end{aligned}$$
(5.15)

Type 3:

If \(p_{1}=2, p_{2}=2-m^{2},p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,16}\left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{ vr \left( {v}^{2}-1 \right) }\cot \xi }{v}}. \end{aligned}$$
(5.16)

Type 4:

If \(p_{1}=-2m^{2}, p_{2}=\,2\,{m}^{2}-1,p_{3}= 1-{m}^{2}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,17}\left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{i\sqrt{vr{m}^{2} \left( {v}^{2}-1 \right) }\cos \xi }{v}}. \end{aligned}$$
(5.17)

Type 5:

If \(p_{1}=-2, p_{2}=2-{m}^{2},p_{3}= {m}^{2}-1\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,18} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{i\sqrt{vr \left( {v}^{2}-1 \right) }}{v}}. \end{aligned}$$
(5.18)

Type 6:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,19} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{4}}\,{\frac{ \sqrt{vr{m}^{2} \left( {v}^{2}-1 \right) }\sin \xi }{v }}. \end{aligned}$$
(5.19)

Type 7:

If \(p_{1}={\frac{m^{{2}}}{2}}, p_{2}={\frac{{m}^{2}-2}{2}},p_{3}= {\frac{m^{{2}}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,20} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{4}}\,{\frac{ \sqrt{vr{m}^{2} \left( {v}^{2}-1 \right) }\sin }{v }}. \end{aligned}$$
(5.20)

Type 8:

If \(p_{1}={\frac{-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{- \left( 1-{m}^{2} \right) ^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,21} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{i \sqrt{vr \left( {v}^{2}-1 \right) } \left( m\cos \xi + 1 \right) }{v}}. \end{aligned}$$
(5.21)

Type 9:

If \(p_{1}={\frac{{m}^{2}-1}{2}}, p_{2}={\frac{{m}^{2}+1}{2}},p_{3}= {\frac{{m}^{2}-1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,22} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr \left( {m}^{2}-1 \right) \left( {v}^{2}-1 \right) }}{v \left( 1+\sin \xi \right) }}. \end{aligned}$$
(5.22)

Type 10:

If \(p_{1}={\frac{1-{m}^{2}}{2}}, p_{2}={\frac{1-{m}^{2}}{2}},p_{3}= {\frac{1-{m}^{2}}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,23} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \sqrt{vr \left( 1-{m}^{2} \right) \left( {v}^{2}-1 \right) }\cos \xi }{v \left( 1+\sin \xi \right) }}. \end{aligned}$$
(5.23)

Type 11:

If \(p_{1}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}}, p_{2}={\frac{ \left( 1-{m}^{2} \right) ^{2}}{2}},p_{3}= {\frac{1}{4}}\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,24} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{1}{2}}\,{\frac{ \left( 1-{m}^{2} \right) \sqrt{vr \left( {v}^{2}-1 \right) }\sin \xi }{v \left( 1+\cos \xi \right) }}. \end{aligned}$$
(5.24)

Type 12:

If \(p_{1}=2, p_{2}=0,p_{3}= 0\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,25} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}+{\frac{\sqrt{vr \left( {v}^{2}- 1 \right) }c}{v\xi }}. \end{aligned}$$
(5.25)

Type 13:

If \(p_{1}=2, p_{2}=0,p_{3}= 0\) and the solution of the Eq. 2.2 are

$$\begin{aligned} Q_{2,26} \left( x,y,t \right) = {\frac{1}{2}}\,{\frac{\sqrt{-2\,vk}}{v}}. \end{aligned}$$
(5.26)

6 The graphical representation

This section exhibited 3D and contour representations of the Zoomeron equation for case 2.

7 Physical interpretation

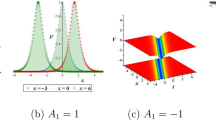
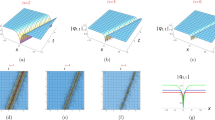
In this section, the contour and 3D plots that are displayed in the graphical representation portion were discussed. These graphs are used to show the form of the wave function and the physical behavior of the found solutions. We discuss how to read these plots and how important they are to comprehending the characteristics of the solutions. The 3D plot and the contour plot of the complex wave function can both be used to see the wave function’s behavior and obtain understanding of the dynamics of the system. Each of the newly found solutions has a unique structure. Dark solitary wave solutions are shown in Figs. 1 and 2. Bright solitary wave solutions are shown in Figs. 3, 4, 5 and 6 and periodic solitary wave solutions are shown in Figs. 7, 8, 9 and 10.

8 Discussion and conclusion

Applying the mapping method, we were able to correctly obtain the analytical solutions to the Zoomeron model. With the use of these methods, the suggested model may be reduced to an algebraic system that can be resolved using any computational tool. Through symbolic computation, we were able to derive the breather waves, kink waves, dark soliton, singular soliton, periodic soliton and bright soliton of this model. A number of previously acquired results are provided in Duran et al. (2023), Butt et al. (2021), Inc et al. (2017), Alshammari et al. (2023), Islam et al. (2024), Uddin et al. (2023), Ullah et al. (2023), Ullah et al. (2023), Rahman et al. (2021), Ullah (2023) and Rahman et al. (2021). Thus, we can draw the conclusion that the provided methods are reliable, credible, and helpful as well as they can be used to tackle a variety of nonlinear structures that occur in nonlinear research. The uniqueness of this study is demonstrated by the fact that the acquired results are unique as they have never been mentioned in the literature (Al-Askar et al. 2022; Ullah et al. 2023). We can predict that these findings will have a significant impact on future studies.A funding declaration is mandatory for publication in this journal. Please confirm that this declaration is accurate, or provide an alternative.