1 Introduction

Solar thermal systems can convert solar energy into heat, which has many practical applications such as water purification, wastewater treatment, distillation, and many other industrial processes. It is also possible, using almost the full solar spectrum, to convert thermal energy into electrical energy for thermal photovoltaic devices (Sakakibara et al. 2019; Shin et al. 2020; Shan et al. 2020; Burger et al. 2020; Verduci et al. 2022; Erixno et al. 2022). These thermal photovoltaic systems, unlike photovoltaic cells alone, achieve greater efficiency in converting solar energy into electricity (Verduci et al. 2022). Solar absorbers are an essential component in many solar thermal system applications. The efficiency of the solar thermal system is significantly affected by these absorbers. The ability of a solar absorber to effectively absorb the spectral band of solar radiation while also reducing mid-infrared emission is essential for improving the overall photo-thermal conversion efficiency (Wu et al. 2018).

Metamaterials with perfect absorption have been developed since 2008 by (Landy et al. 2008). Single-band or multi-band perfect absorption spectra can be achieved depending on the structures of the metamaterials and their constituent materials (Ye et al. 2010; Kim et al. 2017; Bendelala et al. 2018; Durmaz et al. 2023; Abouelez and Abdulaleem 2023; Abou Houran et al. 2023; Zolfaghary et al. 2023).

Most metamaterial absorbers depend, mainly, on noble plasmonic materials, such as silver (Ag) and gold (Au). Light absorption in these materials can be controlled at certain resonance wavelengths by modifying their nanostructure geometries. In photovoltaic systems, the losses in metallic nanostructures, especially ohmic losses, are affected due to the increase in material temperature, which affects the refractive index through the thermo-optic effect (Caldarola et al. 2015). This effect may be reduced utilizing changing the localization of the absorption from metal to the semiconductor layer (Vora et al. 2014) or by using high refractive index nanostructures (Barreda et al. 2021; Caldarola et al. 2015). On the other hand, solar thermo photovoltaic devices usually work in very high-temperature environments, which can damage the noble materials that are used in plasmonic devices. Bulk noble metals such as Ag and Au have high melting temperatures, 961.8 °C and 1064 °C, respectively, but their nanostructures deform and their optical properties can change at temperatures far lower than their melting temperature (Petrova et al. 2006).

Thus, several research groups have studied metamaterial absorbers that are based on materials with high melting points, also called refractory materials, which can be used in solar absorbers. These refractory material-based metamaterial absorbers include chromium (Cr), tungsten (W), nickel (Ni), titanium (Ti), vanadium (V), titanium-nitride (TiN), and molybdenum (Mo) (Wang et al. 2010; Wu et al. 2012; Ding et al. 2016; Kim et al. 2018; Liu et al. 2019, 2021; Karimi Habil et al. 2022; Ehsanikachosang et al. 2022; Yang et al. 2023).

For instance, based on Cr, Kim et al. (2018) created a heat-tolerant ultrathin broadband perfect absorber of visible light. The high melting temperature of Cr metal is 1907 °C. Regardless of the polarization state, the manufactured absorber exhibited an average absorption of over 95% of visible light (wavelengths 500 ≤ λ < 800 nm). Based on W and SiO2, Wu et al. (2018) used a nanoporous hyperbolic metamaterial with multiple W/SiO2 layers to create an effective solar absorber that can achieve an average solar absorption of up to 98.9% in the wavelength range of 260–1580 nm. In the meanwhile, the mid-IR regime can be reached with a low emissivity. This solar absorber is not affected by the angle of incidence or polarization. Specifically, the suggested absorber attains average sunlight absorption of greater than 90% for incoming angles as high as 60°. Due to the high melting points of Ni and Al2O3, Liu et al. (2021) proposed a solar energy absorber comprising a pyramid array of two-dimensional layers of Ni/Al2O3. The suggested absorber is insensitive to the angle of incidence and has strong thermal stability and polarization independence.

The refractory metals such as Ti and TiN also attained great interest from researchers due to their high-temperature resistance. For example, an ultra-wideband absorber based on Ti and TiO2 has been proposed and studied (Ehsanikachosang et al. 2022). The absorber is made up of three Ti/TiO2/Ti square disks that are layered on top of a thin stack of TiO2/Ti layers and enclosed by a Ti square ring resonator. A high average absorption of 96.92% was observed for the suggested structure over the whole wavelength range of 200–3200 nm. For efficient solar energy harvesting, an array of cylinder-shaped metasurface absorber based on TiN and SiO2 was proposed (Yang et al. 2023). At a wavelength range of 300–2500 nm, this proposed absorber has a maximum solar absorption of 94%.

Molybdenum is a high-temperature resistant material with a melting point of 2623 °C and is highly resistant to corrosion. It is found, based on our literature survey, that Mo-based metasurface absorbers are rarely studied (Wang et al. 2010; Yokoyama et al. 2016; Chirumamilla et al. 2021; Quan et al. 2022; Zhang et al. 2023; Yu et al. 2023). For example, in infrared stealth applications, a wideband metamaterial absorber consisting of a multilayer of Mo/Al2O3 is proposed for infrared stealth applications (Quan et al. 2022). For the same applications, a selective thermal emitter based on Mo/Si multilayer films is developed by (Zhang et al. 2023) where the manufactured selective emitter has low emissivity at the atmospheric windows (3–5 μm and 8–14 μm) and high emissivity at the non-atmospheric window (5–8 μm) for radiative cooling. In addition, a planarized Mo/ZnS multilayer film design is created by Yu et al. (2023). The fabricated structure has a low emissivity in the atmospheric window (3–5 μm and 8–14 μm) and exhibits significant emissivity in the non-atmospheric window (5–8 μm). A spectrally selective emitter built on 3D Mo nanopillars is presented in Chirumamilla et al. (2021). The proposed emitter is suitable for the efficient conversion of thermal radiation into electricity using thermophotovoltaic systems because it exhibits high absorptivity/emissivity below the cut-off wavelength of an InGaAsSb photovoltaic cell and a sharp decline in absorptivity/emissivity in the near-infrared regions. In Yokoyama et al. (2016), it was suggested to use Mo-based wavelength-selective mid-infrared thermal emitters. The produced emitters can function steadily at temperatures as high as 1000 °C. Through manipulation of the Mo disk resonators’ size and periodicity, as well as the thickness of the Al2O3 insulator, the thermal emission was flexibly tuned between 3 and 8 μm in wavelength.

In this paper, we propose a novel Mo-based ultra-wideband absorber (UWBA) for solar energy harvesting applications. The unit cell of the proposed absorber is composed mainly of four layers in a metal-dielectric form. The metal (Mo) takes the shape of a square disk in the first layer, a square ring in the second layer, square ring loaded by an inner metal disk in the third and fourth layers. The proposed absorber attains absorption greater than 90% in the band from 300 nm up to 3177 nm (i.e., the absorber covers part of the ultraviolet band and the full bandwidth of visible and near-infrared spectrum with a total bandwidth of 2877 nm) with an average absorption (AA) of 96.46%. Due to the symmetrical property of the proposed design, the absorber exhibits insensitivity to the incident optical wave polarization. In addition, the absorber can support high absorption over a wide angle of incidence of optical waves.

2 Structure design and methods

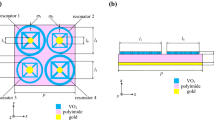
The proposed structure consists of periodic unit cells. Figure 1a–e illustrates the schematic diagrams of a single unit cell. The unit cell is composed of a symmetric multilayer of a dielectric (Al2O3) and a metal (Mo): in the growth direction, layer one (L-1) is composed of a square disc of Mo with a dimension of (\(2Wc1\)×\(2Wc1\)) embedded on the top of Al2O3. Layer two (L-2) is composed of a square ring of Mo with a width of (\(Wc2\)) where the center of \(Wc2\) is aligned with the center of \(Wc1\). Layer three (L-3) consists of a square ring of Mo loaded with a square disc of Mo which is placed on a dielectric layer of Al2O3. The width of the square ring in this layer is \(Wc3\), where the center of \(Wc3\) is aligned with the center of \(Wc1\), and the dimensions of the square disc are (\(Wd1\) × \(Wd1\)). Layer four (L-4) consists of a square ring of Mo loaded with a square disc of Mo which is placed on a dielectric layer of Al2O3. The width of the square ring in this layer is \(Wc4\), where the center radius of \(Wc4\) is aligned with the center of \(Wc1\), and the dimensions of the square disc are (\(Wd2\hspace{0.17em}\times \hspace{0.17em}Wd2\)). The four layers of the structure are built on a continuous thick layer of Mo with a thickness of \(tm\). This layer acts as a back reflector. The length of the unit cell period along the x and y directions equals \(P\).

Fig. 1
figure 1

The model of the proposed UWBA. a–d 3D models of the structure level by level in the growth direction. e Cross-section view. Incidence angle θ for f TM-polarization and g TE-polarization. h Polarization angle

Full size image

The parameters of the proposed structure are optimized to obtain the absorption spectrum shown in Fig. 2. These parameters are as follows (units in nm); \(P\hspace{0.17em}\)= 560, \(tm\hspace{0.17em}\)= 180, \(td1\hspace{0.17em}\)= 50, \(tm1\hspace{0.17em}\)= 25, \(td2\) = 50, \(tm2\) = 20, \(td3\) = 75, \(tm3\) = 20, \(td4\) = 70, \(tm4\) = 40, \(Wc1\) = 230, \(Wc2\) = 115, \(Wc3\) = 85, \(Wc4\) = 45, \(Wd1\) = 105, and \(Wd2\) = 105.

Fig. 2
figure 2

The absorption spectrum of the UWBA calculated by the FD and the TD solvers under normal incidence

Full size image

Based on the experimental work reported in Yokoyama et al. (2016), the integration between Mo and Al2O3 materials is possible. The weak adhesion of Mo metal on the Al2O3 surface may be solved using certain techniques. To the best of our knowledge, there are certain techniques to promote the Mo thin film structure as follows: (a) selection of appropriate and sophisticated deposition technique to enhance the film quality, roughness, and characteristics (Yang and Hao 2016), (b) using of Cr or Ti ultrathin wetting/buffer layer before Mo deposition, (c) using low deposition rate of Mo.

We take the first layer, as shown in Fig. 1a, as an example of the suggested fabrication procedure. The basic substrate is a cleaned polished surface similar to a Si wafer. Ultrathin Cr or Ti interfacial layer could be used before Mo and Al2O3 layers for promoting adhesion. Al2O3 and Mo thin films could be deposited subsequently using the appropriate lithography technique till obtaining the required configuration.

The proposed structure is studied numerically to investigate the electromagnetic behavior inside the structure. For this purpose, we used a CST Microwave Studio frequency-domain (FD) solver that utilizes the finite-element method. In our analysis, the complex refractive index data of Al2O3 is obtained from the data provided in Refractiveindex.info, Boidin et al. (2016), while the complex refractive index data of Mo is obtained from Palik (1998). Only one unit cell of the periodic structure is simulated. In the CST FD solver, the boundary conditions are set as a unit cell for both x and y directions, a perfect electric conductor at the bottom of the unit cell, and open (add space) at the positive z-direction. The adaptive mesh refinement is activated and the local mesh properties are adjusted, specifically for the metals and small dielectric spacer between inner discs and outer rings in layers 3 and 4, to ensure obtaining accurate results. As indicated in Fig. 1, the structure is symmetrical in the x and y directions. The transverse electric (TE) or transverse magnetic (TM) electromagnetic waves are incident on the structure in the x–z plane and propagated in the negative z-direction with an incident angle θ relative to the z-direction as indicated in Fig. 1f and g. The polarization angle, φ, is the angle between the projection of the incident electromagnetic wave on the x–y plane and the x-direction as shown in Fig. 1h.

The spectral absorptivity \(A\left(\lambda \right)\) is calculated by \(A\left(\lambda \right)\hspace{0.17em}=\hspace{0.17em}1-R\left(\lambda \right)-T\left(\lambda \right)\), where the spectral reflection, \(R\left(\lambda \right)\), and spectral transmission, \(T\left(\lambda \right)\), are related to the S parameters (i.e., reflection parameter, \({S}_{11}\), and transmission parameter, \({S}_{21}\)) as \(R\left(\lambda \right)\hspace{0.17em}=\hspace{0.17em}{\left|{S}_{11}\right|}^{2}\) and \(T\left(\lambda \right)\hspace{0.17em}=\hspace{0.17em}{\left|{S}_{21}\right|}^{2}\) (Smith et al. 2005). The thickness of the Mo back reflector is considered much higher than its skin depth in the band under investigation. Thus, the spectral transmission is neglected, i.e., \(T\left(\lambda \right)\hspace{0.17em}\)= 0.

To confirm the results, a simulation of the same proposed model of the UWBA is performed using the time-domain (TD) solver in the CST Microwave Studio which is based on the finite-integration method. The TD solver is used only in the case of normal incidence of the electromagnetic wave with TM polarization.

3 Results and discussion

Figure 2 shows the spectral absorption of the UWBA under investigation for the normal incident of TM polarized wave (the result is the same for TE polarization due to the symmetry). The figure shows the absorption obtained using the FD solver and TD solver. As observed from Fig. 2, there is a very good matching between the obtained result by the TD solver and the FD solver. For the absorption spectrum study, four resonance peaks are considered at \({\lambda }_{1}\) (3.057 µm), \({\lambda }_{2}\) (2.57 µm), \({\lambda }_{3}\) (2.13 µm) and \({\lambda }_{4}\) (1.57 µm), which are indicated in Fig. 2. The absorption is greater than 90% in the band from 0.3 to 3.177 µm with an average absorption (AA) of 96.24%. The AA is calculated with the following equation.

$$AA = \frac{1}{{\lambda_{max} - \lambda_{min} }}\mathop \smallint \limits_{{\lambda_{min} }}^{{\lambda_{max} }} A\left( \lambda \right)d\lambda$$
(1)

Under normal incidence, λmin = 300 nm and λmax = 3177 nm with a bandwidth of 2877 nm.

The total solar spectral absorption relative to a standard AM1.5 (i.e., ASTM G173-03) solar source (Spectra-AM1.5) is given by the following equation.

$$\alpha_{abs} = \frac{{\mathop \smallint \nolimits_{{\lambda_{min} }}^{{\lambda_{max} }} A\left( \lambda \right)I_{{{\text{AM}}1.5}} \left( \lambda \right)d\lambda }}{{\mathop \smallint \nolimits_{{\lambda_{min} }}^{{\lambda_{max} }} I_{{{\text{AM}}1.5}} \left( \lambda \right)d\lambda }}$$
(2)

where \({I}_{{\text{AM}}1.5}\left(\lambda \right)\) is the incident solar spectral irradiation of the Air Mass 1.5 Global spectrum (Spectra-AM1.5). Figure 3 shows the spectral solar absorption of the proposed UWBA at a wavelength band of 300–4000 nm. The calculated total solar spectral absorption calculated by Eq. (2) under normal incidence in the wavelength range (300–3177 nm) is nearly 96.6%.

Fig. 3
figure 3

Absorption of the proposed UWBA under a solar spectrum at AM1.5

Full size image

Since the proposed model has the characteristic of symmetry in shape along the x and y axes, it is expected that it is insensitive to the changes in the polarization angle (φ). Under normal incidence of the electromagnetic wave on the absorber surface, the angle formed by the electric field and the x-axis is known as the polarization angle or φ (see Fig. 1h). The insensitivity of the proposed UWBA against polarization variation is examined. Figure 4 shows the impact of changing the incident wave’s polarization angle from 0° (TM-polarization) to 90° (TE-polarization) on the absorption of the proposed absorber. The obtained results show that the absorption behavior does not change with polarization angle. As a result, the proposed UWBA is not affected by changes in the polarization angle.

Fig. 4
figure 4

Absorption spectrum against polarization angle under normal incidence

Full size image

3.1 Spectral properties of the UWBA

In this subsection, the spectral properties of the proposed UWBA are studied. Firstly, the effect of adding each layer in the absorber unit cell on the spectral properties is analyzed. Figure 5 shows the absorption spectra of the unit cell for each step of the construction growth of the UWBA. For layer 1, it can be noted that the structure with this layer gives two peak resonances around 833 nm and 3025 nm with absorptivity of 0.8 and 0.98, respectively. After adding layer 2, two wide absorption bands are formed with absorption greater than 80%. The first band is in the range (0.3–1.118 µm), while the second band is in the range (2.44–3.21 µm). Also, it can be noted that the second band includes two resonant wavelengths with maximum peaks around 2.6 µm and 3.1 µm. The addition of the third layer causes expansion of both bands emerging from the second layer with absorption greater than 90%. The first band extends from 0.3 to 1.55 µm while the second band extends from 2.21 to 3.17 µm. To fill the gap between the two bands, the fourth layer is added. The addition of the fourth layer introduces a peak absorption around the wavelength 2.13 µm and the final absorption band extends from 0.3 to 3.177 µm with an average absorption of 96.46%. The absorption peaks due to layer 1 in the band below ~ 820 nm are expected to be due to intrinsic losses in the Mo. The absorption of this band increases by adding more Mo layers embedded in layers 2, 3, and 4 (Zhao et al. 2013; Yang et al. 2023).

Fig. 5
figure 5

The absorption spectrum of the UWBA at different levels of the structure design

Full size image

To gain deep insight into the understanding of the behavior of the absorber, the absolute field distributions of electric and magnetic fields are plotted in Figs. 6 and 7 at different wavelengths under normal incidence considering TM-polarization. The chosen wavelengths are 3.057 µm, 2.57 µm (their field distributions are plotted in Fig. 6), 2.13 µm, and 1.57 µm (their field distributions are plotted in Fig. 7).

Fig. 6
figure 6

Field distributions at a, b, c λ1 = 3.057 µm and d, e, f λ2 = 2.57 µm. a, d x component of the electric field, b, e z component of the electric field, and c, f y component of the magnetic field under the vertical incidence of TM polarization

Full size image
Fig. 7
figure 7

Field distributions at a, b, c λ3 = 2.13 µm and d, e, f λ4 = 1.57 µm. a, d x component of the electric field, b, e z component of the electric field, and c, f y component of the magnetic field under the vertical incidence of TM polarization

Full size image

The electromagnetic field distributions of the electric field components \(\left|{E}_{x}\right|\) and \(\left|{E}_{z}\right|\) in the x–z cross-section and the magnetic field component \(\left|{H}_{y}\right|\) in the y–z cross-section are calculated with the CST TD solver. Also, the power loss density monitors are applied at these wavelengths. The obtained x–y plane power loss distributions at considered wavelengths are shown in Fig. 8.

Fig. 8
figure 8

Power loss density distributions inside Mo in each layer for the wavelengths a, b 3.057 µm, c, d 2.57 µm, e, f 2.13 µm, and g, h 1.57 µm

Full size image

At resonance wavelength 3.057 µm, the distributions of electric and magnetic fields shown in Fig. 6a, b and c, indicate that the magnetic polariton (MP) is mainly excited between the Mo disk in layer 1 and the Mo ground plane with the magnetic field \(\left|{H}_{y}\right|\), exited mainly by the incident magnetic field, which is mainly uniform in the y-direction. This magnetic field is accompanied by a current in the Mo layer in the x-direction which decays towards the edges in the x-direction. This current excites positive and negative charges in the x-direction at the edges which are accompanied by \(\left|{E}_{z}\right|\) electric field component (Zhou et al. 2006). The current distribution in the Mo disk in layer 1 causes the power losses in the Mo disk shown in Fig. 8a. The inductance corresponding to the magnetic field and the capacitance between the conducting Mo disk in layer1 and Mo ground plane form, mainly, a resonance circuit which determines the resonance frequency (i.e., 3.057 µm) which decreases, mainly, with the disk length in the x-direction (Zhao et al. 2013; Zhou et al. 2006; Sakurai et al. 2014). At the same wavelength, a moderate magnetic field is excited in the dielectric layer below the Mo square ring at layer 2, as obvious from Fig. 6c. Figure 6a and b reveal that the excited MP is accompanied by localized surface plasmon (LSP) due to the finite Mo ring (Zhang et al. 2011). This description is clear from the power loss distribution in Fig. 8b where localization is evident at the inside corners of the square ring.

At resonance wavelength 2.57 µm, it can be noted from Fig. 6d and e that there is a strong electric field, \({E}_{x}\), concentrated inside the dielectric between the inner Mo square disk and the outer Mo square ring in layer 3 (the arms parallel to the y direction). Also, there is a moderate electric field, \({E}_{z}\), concentrated under the Mo square ring at the MO/Al2O3 interface in layer 2. Additionally, as indicated in Fig. 6f, the magnetic field confined in the dielectric layer beneath the Mo square ring in layer 2 is stronger than the magnetic field confined in the dielectric layer beneath the Mo square ring in layer 3 (along the arms parallel to the x-direction). This situation indicates that the LSP and MP are excited at this wavelength. As explained before, this situation is consistent with power loss distributions in layers 2 and 3 as shown in Fig. 8c and d.

At resonance wavelength 2.13 µm, it can be noted that the Mo square ring loaded by the Mo inner disk in layer 4 plays the main role in the appearance of this resonance. As indicated in Fig. 7a and b, the electric field, \({E}_{x}\), is concentrated inside the dielectric between the inner Mo square disk and the outer Mo square ring in layer 4 (the arms parallel to the y direction). Also, from Fig. 7c, the magnetic field is confined at the top of the Mo square ring (metal/air interface) and the bottom of the Mo square ring (metal/dielectric interface). In addition, the absorption at this wavelength is enhanced by the confinement of the moderate electric field, \({E}_{x}\), in the dielectric spacer between the Mo square ring and Mo inner disk in layer 3 as indicated in Fig. 7a. The field distributions shown in Fig. 7a, b and c indicate an excitation to LSP resonance at resonance wavelength 2.13 µm. This behavior is clearer in the power loss distributions in Fig. 8e and f.

At resonance wavelength 1.57 µm, the absorption at this wavelength is enhanced by the confinement of a strong electric field, \({E}_{x}\), in the dielectric spacer between the outer Mo square ring and Mo inner disk in layer 3 as indicated in Fig. 7d. Also, it can be observed from Fig. 7f that there is a moderate magnetic field in the dielectric layer below the Mo inner disk in layer 3. These field distributions indicate an excitation of LSP resonance at wavelength 1.57 µm. At the wavelength 1.57 µm, the power is dissipated mainly in the inner Mo square disk in layer 3 and the Mo square ring in layer 4 as indicated in Fig. 8g and h.

3.2 Effect of incident angle (TE/TM)

In this subsection, we will examine the absorptivity of the proposed UWBA under the oblique incidence of the optical wave for both TE and TM polarizations. Figure 9a shows the absorption spectrum under TM polarization at different incidence angles which are chosen to be 0°, 15°, 30°, 45°, 50°, 55°, 60°, and 70°. Additionally, the average absorption at each incident angle for both TM (\({AA}_{TM}\)) and TE (\({AA}_{TE}\)) is presented in Table 1. The absorption is greater than 80% in the band from 300 to 3177 nm for incident angles up to 60° with average absorption equal to 92.61% at an incident angle of 60°. Figure 9b displays the absorption spectrum under TE polarization at the same incidence angles. The absorption is greater than 80% in the band from 300 to 3177 nm for incident angles up to 45° with average absorption greater than 90% for incident angles up to 50°.

Fig. 9
figure 9

Absorption spectrum of the proposed UWBA at different incident angles for a TM polarization and b TE polarization

Full size image
Table 1 Average absorption of the proposed UWBA at different incident angles for TM polarization (\({AA}_{TM}\)) and TE polarization (\({AA}_{TM}\))
Full size table

If we consider, for instance, the absorption at the resonance wavelength at 3.057 µm for comparison between the TE and TM polarizations at different incident angles, we note that for the TM case, the absorption at 3.057 µm decreases slightly with the incident angle since the incident magnetic field exciting the MP at that wavelength is constant at the different incident angles. On the other hand, for the TE case, the component of the incident magnetic field \(\left|{H}_{x}\right|\), which excites the MP, decreases steadily with the incident angle, thus, the absorption also decreases rapidly with the incidence angle as shown in Fig. 9b (Ye et al. 2010).

Now, we will compare the proposed UWBA’s performance to the published studies on Mo-based wideband absorbers. The comparison is predicated on the features listed in Table 2: the band of absorption, kind of materials, verification techniques, and wide-incident angle capability.

Table 2 Comparison of the proposed UWBA with various reported Mo-based broadband absorbers
Full size table

4 Conclusions

In this paper, the absorption performance of the proposed UWBA which covers the portion of the ultraviolet, visible, and near-infrared spectral bands is numerically investigated. The absorber’s structure is made up of four layers of Mo and Al2O3 with different shapes. Mo takes the square disk shape in the first layer, a square ring in the second layer, square ring with an inner disk in the third and fourth layers. The absorption of the proposed UWBA at the normal incidence is more than 90% in the wavelength range of 300–3177 nm. Generally, the absorber has the polarization-insensitive property because of the symmetry of the proposed shape. The conducted analyses demonstrate that the generation of LSP and MP resonances at various wavelengths, as well as the inherent losses of Mo, are responsible for ultra-wideband absorption. For both the TE and TM polarizations, the impact of incidence angle variations on the UWBA’s stability is investigated. The simulation findings demonstrate that over a broad range of incident angles, the UWBA performs well for both TE and TM polarizations. It is observed that the absorption is greater than 80% at incident angles up to 50°. This polarization-independent and wide-angle UWBA can be used in solar energy harvesting for thermophotovoltaic devices.