1 Introduction

In recent years, there has been a lot of interest in the properties of laser beams that propagate through turbulent media. This interest is due to the fact that these beams have many interesting applications in various fields such as free-space optical communications, satellite communications, laser radar systems and optical imaging. However, the turbulent media is an inhomogeneous medium where fluctuations in the refractive index occur due to the small temperature and pressure changes. This leads to random fluctuations in light intensity and phase. These fluctuations can limit the performance of the laser beam as propagating (Andrews and Phillips 2005). Therefore, researchers have been working hard to develop a reliable theory to predict the behaviour of laser beams as propagate in turbulent media. Many significant results have been achieved in this area in recent decades. In this regard, the ability of laser beams that carrying orbital angular momentum to reduce the scintillation level then improve the system performance was studied intensively (Secilmis and Elmabruk 2022; Eyyuboğlu 2016; Elmabruk and Eyyuboğlu 2019). Bessel beams are an important type of studied laser beams, where it was demonstrated that the scintillation level of Bessel beams with small beam order is less than the scintillation of Gaussian beams (Eyyuboğlu et al. 2008, 2013). Moreover, the ability of Ince beams with even modes to reduce the scintillation levels in long communication links was studied as well (Elmabruk 2022). On the other hand, the behaviour of laser beams in a different turbulent medium is also considered intensively. In this context, partially coherent flat-topped was studied in oceanic turbulence and it was found that this beam can reduce the scintillation better than the Gaussian beam (Yousefi et al. 2015). Furthermore, the effect of the biological turbulence on the propagating laser beams was examined in many studies (Jin et al. 2016; Xi et al. 2018). Moreover, some researchers have investigated the effect of the anisotropic media on the propagating laser beams (Chen et al. 2022; Vasylyev et al. 2023; Lin et al. 2022).

Gaussian beams are a type of electromagnetic wave that are commonly used in various applications. Recently, these beams were derived directly from Maxwell’s equations when the medium is a cold plasma under a steady external magnetic field (Basdemir and Elmabruk 2023). While the commonly used representation of Gaussian beams is approximate solutions of the wave equation, better beam representations have been obtained that are valid outside the paraxial region (Basdemir and Elmabruk 2023). These improved representations are more accurate and provide a better understanding of the behaviour of Gaussian beams.

In general, in optical communication links, there are two critical factors that incredibility impacts the link performance. The first one is the amount of power captured by the receiver, and the second is scintillation. Both are dependent on the type of beam and its profile. Furthermore, the latest studies revealed that the atmosphere turbulence can be anisotropic due to the rotation of earth (Fu and Zheng 2019; Cui et al. 2015; Galperin et al. 2006). The behaviour of the physical optical parameters is different for optical communication links when compared to the isotropic case. Thus, the investigation of the beam parameters in the anisotropic medium paves the way for more effective communication link systems. The main aim of this study is to analyse the scintillation of Gaussian beams as propagating in both anisotropic and uniaxial media based on the derivative of the beams directly from Maxwell’s equations. In this regard, the point-like and the power scintillation levels are to be investigated as the beam propagates for a 5 Km not only in weak turbulence but also in a strong turbulence regime.

2 Beam and turbulence model

2.1 Gaussian Beam in an anisotropic medium

The electric field components of Gaussian beam produced by a point source in an anisotropic medium are given by

$${E}_{x}=\frac{k}{\omega {\epsilon }_{0}}\left[\frac{j{\epsilon }_{2}}{\left({\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}\right)}\text{sin}\theta {\text{cos}}^{2}\varphi +\frac{{\epsilon }_{1}}{\left({\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}\right)}\text{cos}\theta {\text{cos}}^{2}\varphi \frac{1}{{\epsilon }_{3}}\text{cos}\theta {\text{sin}}^{2}\varphi \right]{H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(1)
$${E}_{y}=\frac{k}{\omega {\epsilon }_{0}}\left[\frac{j{\epsilon }_{2}}{\left({\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}\right)}\text{sin}\theta +\frac{{\epsilon }_{1}}{\left({\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}\right)}\text{cos}\theta -\frac{1}{{\epsilon }_{3}}\text{cos}\theta \right]\text{sin}\varphi \text{cos}\varphi {H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(2)

and

$${E}_{z}=\frac{k}{\omega {\epsilon }_{0}\left({\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}\right)}\left(j{\epsilon }_{2}\text{cos}\theta -{\epsilon }_{1}\text{sin}\theta \right)\text{cos}\varphi {H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(3)

where H0 is the complex amplitude, b is a real number and ρ = [x2 + y2]1/2. When compared to the produced fields of point source in an isotropic medium, the anisotropy is responsible for the extra longitudinal component and the amplitude changes of transverse components. The Gaussian shell model was derived directly from Maxwell’s equations by using complex source point method (CSP) (Basdemir and Elmabruk 2023). Here ε0 is the free space permittivity and ε1, ε2 and ε3 are the tensor elements of the anisotropic medium can be given by

$${\epsilon }_{1}=1-\frac{{\omega }_{p}^{2}}{\omega }{\left[1-\frac{{\omega }_{g}^{2}}{{\omega }^{2}}\right]}^{-1}$$
(4)
$${\epsilon }_{2}=\frac{{\omega }_{p}^{2}{\omega }_{g}}{\omega \left({\omega }^{2}-{\omega }_{g}^{2}\right)}$$
(5)

and

$${\epsilon }_{3}=1-\frac{{\omega }_{p}^{2}}{{\omega }^{2}}$$
(6)

where ωp, ωg are the plasma frequency and gyromagnetic frequency of the electrons separately are given by

$${\omega }_{p}^{2}=\frac{N{e}^{2}}{m{\epsilon }_{0}}$$
(7)

and

$${\omega }_{g}=\frac{e{B}_{0}}{m}$$
(8)

where N is the number of electrons/m3, m is the mass of an electron, e is the charge of an electron and B0 is the magnitude of an external dc magnetic field which causes the anisotropy. The wavenumber k is defined by

$$k={k}_{0}\sqrt{\frac{{\epsilon }_{1}^{2}-{\epsilon }_{2}^{2}}{{\epsilon }_{1}}}$$
(9)

where k0 is the free space wavenumber (Basdemir and Elmabruk 2023).

2.2 Gaussian beam in a uniaxial medium

The uniaxial medium is a special case of the anisotropic medium characterized by the different dielectric tensor. The electric field components of Gaussian beam produced by a point source in the uniaxial medium can then be written as

$${E}_{x}=\frac{k}{\omega {\epsilon }_{0}}\text{cos}\theta \left({\text{cos}}^{2}\varphi +\frac{1}{{\epsilon }_{3}}{\text{sin}}^{2}\varphi \right){H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(10)
$${E}_{y}=\frac{k}{\omega {\epsilon }_{0}}\text{sin}\varphi \text{cos}\varphi \text{cos}\theta \left(1-\frac{1}{{\epsilon }_{3}}\right){H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(11)

and

$${E}_{z}=-\frac{k}{\omega {\epsilon }_{0}}\text{sin}\theta \text{cos}\varphi {H}_{0}\frac{{e}^{-jk\left(z+jb\right)}}{\left(z+jb\right)}exp\left[-\frac{jk}{2}\frac{{\rho }^{2}}{\left(z+jb\right)}\right]$$
(12)

where k is the wavenumber defined by k = k0√ε3.

2.3 Scintillation numerical calculations

The perturbations introduced by the turbulent medium as the laser beam propagates is modelled by the split-step approach. Each component of both Gaussian beam in an anisotropic medium and Gaussian beam in a uniaxial medium is considered as an individual input for the split-step model. Accordingly, the received electric field after the propagation of each component for z Km distance, is given as (Schmidt 2010)

$$\begin{aligned}{E}_{{r}_{ }}\left(\mathbf{r}, z\right)& =\text{exp}\left(jkz\right)\prod _{\mathbf{i}=1}^{{N}_{s}}{\mathbf{F}}^{-1}\left\{\mathbf{F}\left[\frac{j \text{exp}\left(-jk{z}_{i}\right)}{\lambda {z}_{i}} {\iint }_{-\infty }^{\infty }{E}_{s}\left(s, 0\right) \text{e}\text{x}\text{p}\left\{-j\frac{k}{2z}\left[{\left(\mathbf{r}-\mathbf{s}\right)}^{2}\right]\right\}d{s}^{2}\text{e}\text{x}\text{p}\left(\psi \right(r\left)\right)\right]\right.\\&\quad\left.\mathbf{F}\left[\text{e}\text{x}\text{p}\left(-j\frac{k}{2z}\left[{\left(r-s\right)}^{2}\right]\right)\right]\right\} \end{aligned}$$
(13)

where \(\mathbf{r}=({r}_{x},{r}_{y})\) and s\(=({s}_{x},{s}_{y})\) is the receiver and transmitter plane transverse coordinates respectively, \({E}_{s}\) refers to the electric field at the source plane, which is considered as the x, y and z components of both Gaussian beam in an anisotropic medium and Gaussian beam in a uniaxial medium individually, the operators \({\mathbf{F}}^{-1}\) refer to the inverse Fourier transform, \(\mathbf{F}\) is the Fourier transform operator, and \(\psi \left(r\right)\) stands for the induced phase fluctuations by the turbulent medium, which is considered here by the modified von Kármán refractive-index power spectral density, which is (Schmidt 2010),

$${\phi }_{\varnothing }\left(f\right)=\frac{0.0036z{C}_{n}^{2}{k}^{2}{L}_{0}^{11/3}}{\left({\left({L}_{0}^{2}{\left|f\right|}^{2}+1\right)}^{11/6}\right)} exp\left[-1.1265{l}_{0}^{2}{\left|f\right|}^{2}\right]$$
(14)

where \(k\) is the wave number and \({l}_{0}\) and \({L}_{0}\) refer to the inner and outer scales of turbulent medium respectively.

Then, the scintillation index (point-like scintillation) which measures the intensity fluctuations that induced by the turbulent medium is expressed as (Schmidt 2010)

$${b}^{2}\left(\mathbf{r},z\right)= \frac{\frac{1}{{N}_{r}}\sum _{i=1}^{{N}_{r}}{\left[{E}_{r}\left(\mathbf{r},z\right){E}_{r}^{*}\left(\mathbf{r},z\right)\right]}^{2}}{{\left(\frac{1}{{N}_{r}}\sum _{i=1}^{{N}_{r}}{E}_{r}\left(\mathbf{r},z\right){E}_{r}^{*}\left(\mathbf{r},z\right)\right)}^{2}}-1$$
(15)

where \({N}_{r}\) refers to the number of realizations which is applied to be 500 to satisfy the averaging requirement and * stands for the complex conjugate. The limit of the point-like scintillation is the that aperture radius is greater than limit of \({\left(0.5\lambda z/{\uppi }\right)}^{0.5}\), in such a case the scintillation index calculations turns into a power (aperture averaged) scintillation index which is expressed as (Schmidt 2010),

$${m}^{2}=\frac{\underset{0}{\overset{{r}_{x}}{\int }}\underset{0}{\overset{{r}_{y}}{\int }}{dr}_{x}{dr}_{y} \frac{1}{{N}_{r}} \sum _{i=1}^{{N}_{r}}{\left[{E}_{r}\left({r}_{x}, {r}_{y},z\right){E}_{r}^{*}\left({r}_{x}, {r}_{y},z\right)\right]}^{2} }{\underset{0}{\overset{{r}_{x}}{\int }}\underset{0}{\overset{{r}_{y}}{\int }}{dr}_{x}{dr}_{y}{\left[\frac{1}{{N}_{r}} \sum _{i=1}^{{N}_{r}}{E}_{r}\left(\mathbf{r},z\right){E}_{r}^{*}\left(\mathbf{r},z\right)\right]}^{2} }-1$$
(16)

3 Numerical results and discussion

This study considers a 5 Km communication link that operates at 1550 nm. The channel’s turbulence is analysed with two refractive index structure constants of \({C}_{n}^{2}\)\(={10}^{-15}{\text{m}}^{-2/3}\) which stands for weak turbulence and \({{C}_{n}^{2} =10}^{-14}{\text{m}}^{-2/3}\) which refers to strong turbulence regime. The scintillation namely point-like and power scintillation of Gaussian beams as propagate in the anisotropic medium and uniaxial medium are studied and compared with the scintillation levels of fundamental Gaussian beam as propagates in atmospheric turbulence. The general trend of the scintillation level, of Gaussian beam as propagates in the three media, is an increasing behaviour as the propagation distance increases, which is as expected. The simulation parameters were chosen in line with the commonly used in the literature. Accordingly, this gives us a chance to verify our results and compare their trend with the results in the literature.

3.1 Gaussian beam in an anisotropic medium

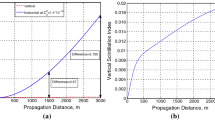
The scintillation of Gaussian beam as propagates in anisotropic medium is investigated in Figs. 1, 2, 3 and 4. Here, Figs. 1 and 2 study the point-like scintillation both in weak and strong turbulence. Figure 1 illustrates the point-like scintillation in strong turbulence regime, where the x-component of the beam as propagate in anisotropic medium has a scintillation level less than the y and z components. However, its scintillation level is as the Gaussian beam that propagates in atmosphere. The same behaviour is in the weak turbulence medium as seen from Fig. 2, the only difference is that the scintillation of x-component is much lower than the other two components.

Fig. 1
figure 1

Point-like scintillation of Gaussian beam in an anisotropic medium under the effect of strong turbulence

Full size image
Fig. 2
figure 2

Point-like scintillation of Gaussian beam in an anisotropic medium under the effect of weak turbulence

Full size image
Fig. 3
figure 3

Power scintillation of Gaussian beam in an anisotropic medium under the effect of strong turbulence

Full size image
Fig. 4
figure 4

Power scintillation of Gaussian beam in an anisotropic medium under the effect of weak turbulence

Full size image

Moreover, the level of power scintillation is examined in Figs. 3 and 4 for both weak and strong turbulence respectively. Both in strong and weak turbulence the x-component of the Gaussian beam as propagate in anisotropic medium has the priority to reduce the turbulence level. However, in case of power scintillation y-component has the highest scintillation level as can be clearly seen from Figs. 3 and 4.

3.2 Gaussian beam in a uniaxial medium

Both the point-like and the power scintillation of Gaussian beam as propagates in uniaxial medium is studies in Figs. 5, 6, 7 and 8. In strong turbulence short links x-component has the advantage of reducing the point-like scintillation level as in Fig. 5. On the other hand, x-component has a much lower point-like scintillation than y and z components of Gaussian beam as propagate in uniaxial medium as can be observed from Fig. 6. In general, x-component of Gaussian beam that propagates in uniaxial medium has a similar scintillation level of Gaussian beam that propagates in atmospheric turbulence.

Fig. 5
figure 5

Point-like scintillation of Gaussian beam in a uniaxial medium under the effect of strong turbulence

Full size image
Fig. 6
figure 6

Point-like scintillation of Gaussian beam in a uniaxial medium under the effect of weak turbulence

Full size image
Fig. 7
figure 7

Power scintillation of Gaussian beam in a uniaxial medium under the effect of strong turbulence

Full size image
Fig. 8
figure 8

Power scintillation of Gaussian beam in a uniaxial medium under the effect of weak turbulence

Full size image

Furthermore, the power scintillation is examined in Figs. 7 and 8, where it is clear that the scintillation level of the three components of Gaussian beam as propagate in uniaxial medium is lower than the fundamental Gaussian beam especially in long communication links.

4 Conclusion

The scintillation of Gaussian beams in anisotropic and uniaxial media is studied numerically. Split step approach is used to model the turbulent media. Both the point-like and the power scintillation of Gaussian beams as propagate in anisotropic and uniaxial media are analysed. The presented results show that x-component of the Gaussian beam as propagate has the lowest scintillation levels in weak and strong turbulent anisotropic medium and uniaxial medium. On the other hand, the three components of the Gaussian beam as propagates in a uniaxial medium have a power scintillation level less than the fundamental Gaussian. Finally, the proposed results are highly promising for free-space optical communication systems and Laser Detection and Ranging (LIDAR) systems. On the other hand, the presented study has a potential avenue for future research in the propagation of laser beams in crystals where the effect of orientation and materials properties can be examined.