1 Introduction

Exact solutions to partial differential equations (PDEs) are foundational in understanding, modeling, and solving a wide range of phenomena. They provide a basis for theoretical analysis, numerical validation, and practical applications in diverse scientific and engineering disciplines (Wazwaz 2010).

Fractional calculus is an extended form of traditional calculus and is related to fractal geometry. Fractals are defined as mathematical structures that form themselves by repeating similar patterns. Fractional calculus is used to better understand and analyze such fractal structures. Fractional calculus is especially used in modeling complex systems, financial markets, and random processes in nature. This can help us understand some features that are difficult or impossible with traditional calculus (Kilbas et al. 2006).

When a classical (integer-order) derivative operator is translated into a fractional derivative operator, the physical dimensions of the system can change. In classical physics, classical derivatives have dimensions of 1/time, reflecting their interpretation as rates of change. However, fractional derivatives have dimensions of time raised to a fractional power, which can lead to different physical interpretations depending on the context.

Fractional derivatives are mathematical operators that extend the concept of differentiation to non-integer orders. There are several types of fractional derivative operators, each defined based on different mathematical approaches. Some common fractional derivative operators include: Riemann–Liouville (RL), Caputo, Grünwald–Letnikov, and M-fractional derivatives (Kilbas et al. 2006; Podlubny 1999, and Sousa and de Oliveira 2017).

RL fractional derivative operator plays crucial role in extending classical calculus to fractional orders, allowing for a more refined understanding of complex systems and phenomena in science and engineering.

In the literature there exist many efficient methods to deduce the exact solutions to PDEs. Some of them can be listed as: Hirota bilinear method, Painleve analysis, Lie symmetry technique, Backlund and Darboux transformations, the invariant subspace method, etc (Hirota 2004; Conte and Musette 2008; Olver 1999; Rogers and Schief 2002, and Galaktionov and Svirshchevskii 2007).

The invariant subspace method (ISM) for PDEs involves decomposing the solution of a PDE into invariant subspaces, which are subspaces of the function space that remain invariant under the evolution of the PDE. This technique is particularly useful for studying the dynamics of complex PDEs by breaking them down into simpler components. In some cases, the ISM can lead to reduced-order models that retain essential dynamics, making numerical simulations more computationally efficient. The method is particularly useful for stability analysis, allowing researchers to determine conditions under which the system’s behavior remains bounded or undergoes specific changes (Galaktionov and Svirshchevskii 2007; Gazizov and Kasatkin 2013, and Sahadevan and Prakash 2016).

Thin film equations (TFEs) describe the behavior of thin layers of material, often encountered in fields like physics and engineering. These equations are typically used to describe the behavior of light when it interacts with thin films, such as coatings on lenses or mirrors. TFEs consider factors like reflection, transmission, and interference of light waves.

On the other hand, optical quantum refers to the study of the quantum nature of light and its interactions with matter. This field involves understanding phenomena like photon absorption, emission, and the quantized nature of light. The connection between TFEs and optical quantum mechanics lies in the microscopic interactions between photons and the electrons in the thin film material. Quantum mechanics provides the underlying principles governing these interactions, influencing the behavior of light in thin films at the fundamental level. Quantum effects, such as energy level transitions and wave-particle duality, play a role in determining the optical properties of thin films.

Common equations include those governing the thickness profile of the film, such as the Young–Laplace equation for liquid films and the equations for interference patterns in optical thin films. In this regard, the Young-Laplace equation relates the pressure difference across the interface of a liquid film to its curvature. For a liquid film with radius of curvature R, the Young–Laplace equation is given by

$$\begin{aligned} \Delta P=\frac{2}{\Lambda }R \end{aligned}$$

where \(\Delta P\) is the pressure difference across the liquid film, \(\Lambda\) is the surface tension of the liquid, R is the radius of curvature of the liquid film. This equation is crucial in understanding phenomena like capillary action and the stability of thin liquid films (Butt et al. 2023).

The fourth-order TFEs

$$\begin{aligned} u_{t}=-(u^{\sigma }u_{xxx})_{x} \end{aligned}$$

with the nonnegative parameter \(\sigma\) was introduced in Cherniha and Myroniuk (2010) and Greenspan (1978). These mathematical formulas, especially the ones that deal with the dynamics of liquid films on solid surfaces, explain how thin films behave. A traditional thin film of Newtonian fluid is described by case \(\sigma =3\), wetting films with a free contact line between the film and substrate are studied by case \(\sigma =2\), and the dynamics of a Hele-Shaw cell are studied by case \(\sigma =1\).

These equations are derived from fundamental principles, including the conservation of mass and the Navier–Stokes equations, and they account for the effects of capillarity, viscosity, and gravity.

A common set of fourth-order TFEs is known as the lubrication approximation. In the context of a thin liquid film on a solid substrate, the fourth-order TFEs can be written as a system of partial differential equations. In Cherniha and Myroniuk (2010), the authors performed a Lie symmetry analysis of the following equation

$$\begin{aligned} \left[ D(u)u_{x}\right] _{x}-\left[ K(u)v_{x}\right] _{x}+F(u)=u_{t},\ v-u_{xx}=0 \end{aligned}$$

allowing for both second-order and fourth-order diffusion terms.

In Prakash et al. (2023), the authors investigate the applicability and efficiency of the invariant subspace method to (2 + 1)- dimensional time-fractional nonlinear PDEs. They demonstrate how to find various types of invariant subspaces and reductions for the (1 + 1) and (2 + 1)-dimensional generalized nonlinear time-fractional TFEs which arise from the motion of liquid film on a solid surface under the influence of surface tension (see also, Prakash et al. 2024 for the case of coupled system of time-fractional convection-reaction-diffusion equations).

In the Galaktionov and Svirshchevskii (2007), the authors discussed a new fourth order TFE

$$\begin{aligned} u_{t}=-\,(uu_{xxx})_{x}-1. \end{aligned}$$
(1)

Equation (1) describes the evolution of a thin film with a non-linear effect represented by the convolution term \((u u_{xxx})_{x}\). This term arises from the nonlinear interaction of the optical wave with the thin film, leading to a diffusion-like process in the intensity profile. Combining these considerations, we can derive the Eq. (1) as a simplified model for the evolution of the intensity profile of an optical wave propagating through a nonlinear medium with a thin film, incorporating both linear and nonlinear effects. In addition, a formal mathematical model that explains important aspects of the extinction processes in Stefan–Florins free boundary issues for TFEs is represented by Eq. (1). In that paper, the authors constructed the exact solution of Eq. (1) using the 3-dimensional invariant subspace method. In this study, we took RL derivative operator into consideration because it is suitable for the model (1) and mathematical expressions that we will present in detail below.

The main motivation of the current study is this. The aim is to consider the Eq. (1) available in the literature as RL time fractional

$$\begin{aligned} ^{RL}D_{t}^{\alpha }u=-\,(uu_{xxx})_{x}-1 \end{aligned}$$
(2)

and construct the exact solution form. In addition, Lie symmetry analysis (LSA) was performed by reducing the model to a two-dimensional ordinary differential equation system (ODEs) and corresponding solution is produced.

The work is organised thusly. In the second part, the necessary preliminaries including fractional calculus, ISM and LSA for two-dimensional dynamical system are presented. In the next section, we apply the ISM and LSA to fourth order TFE. In the last section we demonstrate some graphical illustrations and outputs of the work.

2 Preliminaries

2.1 RL fractional derivative operator

Assume that \(\alpha >0\) and \(a\in \mathbb {R}.\)

$$\begin{aligned} _{a^{+}}^{RL}D_{t}^{\alpha }g(t)=\frac{1}{\Gamma (1-\alpha )}\left( \frac{d}{ dt}\right) \left[ \underset{a}{\overset{t}{\int }}(t-x)^{-\alpha }g(x)dx \right] , \end{aligned}$$

is the definition of RL fractional derivative (see Kilbas et al. 2006). If \(\alpha =0\) then \(_{a^{+}}^{RL}D_{t}^{0}g(t)=g(t).\)

The RL fractional integral, \(_{a^{+}}^{RL}I_{t}^{ \alpha }g,\) of order \(\alpha\) is defined as

$$\begin{aligned} _{a^{+}}^{RL}I_{t}^{\alpha }g(t)=\frac{1}{\Gamma (\alpha )}\overset{t}{ \underset{0}{\int }}\left( t-x\right) ^{\alpha -1}g(x)dx. \end{aligned}$$

Some of the features hold by RL fractional derivative, RL fractional integral, and other outputs fulfilled in examining fractional differential equations (FDEs) are given in Kilbas et al. (2006); Podlubny (1999) as follows:

  1. 1.
    $$\begin{aligned} ^{RL}_{a^{+}}D_{t}^{\alpha }t^{\varsigma }=\frac{\Gamma \left( \varsigma +1\right) }{\Gamma \left( \varsigma -\alpha +1\right) }t^{\varsigma -\alpha } \end{aligned}$$
    (3)

    where \(\alpha \ge 0,\) \(\varsigma >-1,\) \(\varsigma \ne \alpha -1,\) \(t>0.\)

  1. 2.

    \(_{a^{+}}^{RL}D_{t}^{\alpha }z(t)=\vartheta \left[ z(t)\right] ^{2}(t-a)^{\beta },\) \(\left( a<t,~\beta ,\vartheta \in \mathbb {R}, ~\vartheta \ne 0\right)\) for \(1>\vartheta +\beta ,\) possess an exact solution of the structure,

    $$\begin{aligned} z(t)=\frac{\Gamma \left( 1-\alpha -\beta \right) }{\vartheta \Gamma \left( 1-2\alpha -\beta \right) }\left( t-a\right) ^{-\left( \alpha +\beta \right) }. \end{aligned}$$
    (4)
  1. 3.

    Assume that the regular \(\alpha -\)singular point of equation

    $$\begin{aligned} 0=\left( t-t_{0}\right) ^{\alpha }\left( _{a^{+}}^{RL}D_{t}^{\alpha }z\right) (t)+z(t)p(t) \end{aligned}$$
    (5)

    is \(t_{0}\ge a\) and that

    $$\begin{aligned} p(t)=\underset{n=0}{\overset{\infty }{\sum }}p_{n}\left( t-t_{0}\right) ^{n\alpha },\text { for }t\in [a,b]. \end{aligned}$$
    (6)

    Then the solution form

    $$\begin{aligned} z\left( t,\alpha ,s_{1}\right) =\left( t-t_{0}\right) ^{s_{1}}\underset{n=0}{ \overset{\infty }{\sum }}\delta _{n}\left( t-t_{0}\right) ^{n\alpha }, \end{aligned}$$
    (7)

    of Eq. (5) on a certain interim to the right of \(t_{0}\) is available. In this case, \(s_{1}>-1\) represents the actual solution to the equation

    $$\begin{aligned} p_{0}+\frac{\Gamma \left( s+1\right) }{\Gamma \left( s-\alpha +1\right) }=0 \end{aligned}$$
    (8)

    where \(\delta _{0}\) is a non-zero whimsical constant, and the coefficients \(\delta _{n}\) are derived using the ensuing recrudescence formula:

    $$\begin{aligned} \delta _{n}=-\frac{\Gamma \left( n\alpha +s-\alpha +1\right) }{\Gamma \left( n\alpha +s+1\right) }\underset{l=0}{\overset{n-1}{\sum }}\delta _{l}p_{n-l}, ~1\le n. \end{aligned}$$
    (9)
  2. 4.

    For \(\alpha \in (0,1)\)

    $$\begin{aligned} _{a^{+}}^{RL}I_{t}^{\alpha }\left( _{a^{+}}^{RL}D_{t}^{\alpha }g(t)\right) =g(t)-\left[ _{a^{+}}^{RL}D_{t}^{\alpha -1 }g(t)\right] _{t=a}\frac{t^{\alpha -1}}{\Gamma (\alpha )}. \end{aligned}$$
    (10)

2.2 ISM for time-fractional PDEs

In this part, we summarize how the ISM applied in examining PDEs can be adapted to handle FDEs (Galaktionov and Svirshchevskii 2007; Sahadevan and Prakash 2016; Gazizov and Kasatkin 2013). We let a given in the previous part as 0. Denote by \(_{a^{+}}D_{t}^{\alpha }z\) as \(D_{t}^{\alpha }z.\)

We examine a general time-fractional PDE of the shape

$$\begin{aligned} \frac{\partial ^{\alpha }w}{\partial t^{\alpha }}=G\left[ w\right] ,~ t>0, \end{aligned}$$
(11)

where G is a sufficiently smooth \(l\)th-order differential operator,  \(w=w(x,t)\) and G symbolized by

$$\begin{aligned} G\left[ w\right] =G\left[ x,w,w_{x},...,w_{x}^{(l)}\right] \end{aligned}$$
(12)

where

$$\begin{aligned} w_{x}=\frac{\partial w}{\partial x},~w_{xx}=\frac{\partial ^{2}w}{ \partial x^{2}},...,w_{x}^{(l)}=\frac{\partial ^{l}w}{\partial x^{l}}, \end{aligned}$$

and \(\frac{\partial ^{\alpha }w}{\partial t^{\alpha }}\) is the fractional derivative of w of order \(\alpha\) with respect to t.

Assume

$$\begin{aligned} \Omega _{n}=\left\langle m_{1}(x),m_{2}(x),...,m_{n}(x)\right\rangle , \end{aligned}$$

be the linear span of n \(\left( 1\le n\right)\) linearly independent functions \(m_{i}(x)\) where \(i=1,...,n.\) It means that, if \(w\in \Omega _{n},\) then

$$\begin{aligned} w=\underset{i=1}{\overset{n}{\sum }}\tau _{i}m_{i}(x),~i=1,2,...,n,\ \tau _{i}\in \mathbb {C}. \end{aligned}$$
(13)

The \(\Omega _{n}\) is seemingly unchanged under G if, \(G\left[ \Omega _{n} \right] \subseteq \Omega _{n},\) and G is said to accept \(\Omega _{n},\) that is,

$$\begin{aligned} G\left[ \overset{n}{\underset{i=1}{\sum }}\tau _{i}m_{i}(x)\right] =\overset{ n}{\underset{i=1}{\sum }}\xi _{i}\left( \tau _{1},\tau _{2},...,\tau _{n}\right) m_{i}(x), \end{aligned}$$

for any \(\left( \tau _{1},\tau _{2},...,\tau _{n}\right) \in \mathbb {R}^{n}.\)

Here \(\left\{ \xi _{i}\right\}\) are the expansion coefficients of \(G\left[ W \right] \in \Omega _{n}\) on the basis of \(\left\{ m_{i}\right\} .\) If \(\Omega _{n}\) is unchanged under G,  then Eq. (11) possess a solution of the shape

$$\begin{aligned} w(x,t)=\overset{n}{\underset{i=1}{\sum }}m_{i}(x)\tau _{i}(t), \end{aligned}$$

where the quantities \(\left\{ \tau _{i}(t)\right\}\) amuse the system of time-fractional ODEs disposed through

$$\begin{aligned} D_{t}^{\alpha }\tau _{i}(t)=\xi _{i}\left( \tau _{1}(t),\tau _{2}(t),...,\tau _{n}(t)\right) ,~i=1,2,3,...,n. \end{aligned}$$
(14)

Therefore, to examine a considered FDE of the shape (11) by ISM, we detect an invariant subspace accepted through the operator G and handle the matching system of fractional ODEs for the expansion coefficients specified by (14). In Galaktionov and Svirshchevskii (2007), it is obtained that if a subspace \(\Omega _{n}\) is invariant under a differential operator of the form (12) of order \(\chi ,\) accordingly \(n\le 2\chi +1.\)

2.3 Lie symmetry features of FDE coupled systems

In this part we retrieve exact solutions of the Eq. (11) by employing the symmetry properties and two-dimensional invariant subspaces of the corresponding systems

$$\begin{aligned} \left\{ \begin{array}{c} D_{t}^{\alpha }\varpi _{1}(t)=f\left( t,\varpi _{1},\varpi _{2}\right) , \\ D_{t}^{\alpha }\varpi _{2}(t)=g\left( t,\varpi _{1},\varpi _{2}\right) . \end{array} \right. \end{aligned}$$
(15)

Symmetries of systems (15) were studied in the work Kasatkin (2012) (see also Gazizov and Kasatkin 2013).

Recall that the point transformations \(T_{a}\) of the variables \(t,u_{1},u_{2}:\)

$$\begin{aligned} \widetilde{t}= & {} \varphi \left( t,\varpi _{1},\varpi _{2},\epsilon \right) ,\nonumber \\ \widetilde{\varpi }_{1}= & {} \Psi \left( t,\varpi _{1},\varpi _{2},\epsilon \right) ,~\widetilde{\varpi }_{2}=\pi \left( t,\varpi _{1},\varpi _{2},\epsilon \right) \end{aligned}$$
(16)

reckoning on a continuous parameter \(\epsilon\) are said to be symmetry transformations of system (15), if the system possess the unchanged shape in the new variables \(\widetilde{t},\widetilde{\varpi }_{1}, \widetilde{\varpi }_{2}.\)

The set G of all such transformations forms a continuous group, i.e., G contains the identity, inverse to any transformation from G and the composition of any two transformations from G. The symmetry group G is also known as the group admitted by Eq. (15).

According to the Lie theory (see, for example, Ibragimov 1999), construction of the symmetry group G is equivalent to determination of its infinitesimal transformations

$$\begin{aligned} \widetilde{t}= & {} t+\epsilon \varphi \left( t,\varpi _{1},\varpi _{2}\right) +O(\epsilon ), \\ \widetilde{\varpi }_{1}= & {} \varpi _{1}+\epsilon \psi \left( t,\varpi _{1},\varpi _{2}\right) +O(\epsilon ),~\widetilde{\varpi } _{2}=\varpi _{2}+\epsilon \varrho \left( t,\varpi _{1},\varpi _{2}\right) +O(\epsilon ). \end{aligned}$$

It is practical to present the operator

$$\begin{aligned} \Gamma =\varphi \left( t,\varpi _{1},\varpi _{2}\right) \frac{\partial }{ \partial t}+\psi \left( t,\varpi _{1},\varpi _{2}\right) \frac{\partial }{ \partial \varpi _{1}}+\varrho \left( t,\varpi _{1},\varpi _{2}\right) \frac{ \partial }{\partial \varpi _{2}}, \end{aligned}$$
(17)

which is referred to as the generator of the group \(\Gamma\) or infinitesimal operator.

Group transformations (16) corresponding to the known operator (17) are found by solving Lie equations

$$\begin{aligned} \frac{d\widetilde{t}}{d\epsilon }=\varphi \left( t,\varpi _{1},\varpi _{2}\right) ,~\frac{d\widetilde{\varpi }_{1}}{ d\epsilon }=\psi \left( t,\varpi _{1},\varpi _{2}\right) ,~\frac{d \widetilde{\varpi }_{2}}{d\epsilon }=\varrho \left( t,\varpi _{1},\varpi _{2}\right) \end{aligned}$$

with the initial conditions

$$\begin{aligned} \widetilde{t}\left| _{\epsilon =0}\right. =t,~\widetilde{\varpi } _{1}\left| _{\epsilon =0}\right. =\varpi _{1},~\widetilde{\varpi } _{2}\left| _{\epsilon =0}\right. =\varpi _{2}. \end{aligned}$$

The paper (Kasatkin 2012) states that (see also Gazizov and Kasatkin 2013), any symmetry of system (15) has the following form

$$\begin{aligned} \Gamma =C_{1}\Gamma _{1}+C_{2}\Gamma _{2}+C_{3}\Gamma _{3}+C_{4}\Gamma _{4}+C_{5}\Gamma _{5}+C_{6}\Gamma _{6}+\nu _{1}(t)\frac{\partial }{\partial \varpi _{1}}+\nu _{2}(t)\frac{\partial }{\partial \varpi _{2}} \end{aligned}$$

with

$$\begin{aligned} \Gamma _{1} = & {} t\frac{\partial }{\partial t},~\Gamma _{2} = t^{2}\frac{ \partial }{\partial t}+\left( \alpha -1\right) t\varpi _{1}\frac{\partial }{ \partial \varpi _{1}}+\left( \alpha -1\right) t\varpi _{2}\frac{\partial }{ \partial \varpi _{2}}, \nonumber \\ \Gamma _{3}= & {} \varpi _{1}\frac{\partial }{\partial \varpi _{1}},~ \Gamma _{4}=\varpi _{2}\frac{\partial }{\partial \varpi _{1}},\nonumber \\ \Gamma _{5}= & {} \varpi _{1}\frac{\partial }{\partial \varpi _{2}},~ \Gamma _{6}=\varpi _{2}\frac{\partial }{\partial \varpi _{2}}, \end{aligned}$$
(18)

where the constants \(C_{1},\cdots ,C_{6}\) and the functions \(\nu _{1}(t),\, \nu _{2}(t)\) are comprehended to the functions \(f,\,g\) by the ensuing equations:

$$\begin{aligned}{} & {} D_{t}^{\alpha }\nu _{1}(t)-\left[ C_{1}t+C_{2}t^{2}\right] \frac{\partial f}{ \partial t}+\left[ C_{3}-\alpha C_{1}-\left( \alpha +1\right) C_{2}t\right] f+C_{4}g\nonumber \\{} & {} \quad -\left[ \left( \alpha -1\right) C_{2}t\varpi _{1}+C_{3}\varpi _{1}+C_{4}\varpi _{2}+\nu _{1}(t)\right] \frac{ \partial f}{\partial \varpi _{1}}\nonumber \\{} & {} \quad -\left[ \left( \alpha -1\right) C_{2}t\varpi _{2}+C_{5}\varpi _{1}+C_{6}\varpi _{2}+\nu _{2}(t)\right] \frac{ \partial f}{\partial \varpi _{2}}=0, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} D_{t}^{\alpha }\nu _{2}(t)-\left[ C_{1}t+C_{2}t^{2}\right] \frac{\partial g}{ \partial t}+C_{5}f+\left[ C_{6}-\alpha C_{1}-\left( \alpha +1\right) C_{2}t \right] g\nonumber \\{} & {} \quad -\left[ \left( \alpha -1\right) C_{2}t\varpi _{1}+C_{3}\varpi _{1}+C_{4}\varpi _{2}+\rho _{1}(t)\right] \frac{ \partial g}{\partial \varpi _{1}}\nonumber \\{} & {} \quad -\left[ \left( \alpha -1\right) C_{2}t\varpi _{2}+C_{5}\varpi _{1}+C_{6}\varpi _{2}+\nu _{2}(t)\right] \frac{ \partial g}{\partial \varpi _{2}}=0. \end{aligned}$$
(20)

3 Exact solutions of fractional TFE (2) by ISM

This section is devoted to three subsection. In the first subsection, we examine three dimensional invariant subspace and its approximate solution. In the subsequent subsection, two dimensional invariant subspace and its exact solution are deduced, in the last subsection we present initial value problem.

3.1 \(n=3\)

As shown in Galaktionov and Svirshchevskii (2007), Eq. (1) for the integer-order case accepts the 3-dimensional \(\Omega _{3}=\mathfrak {L} \left\{ 1,x^{2},x^{4}\right\}\) space. It means that the exact solution is given by

$$\begin{aligned} u(x,t)=c_{1}(t)+c_{2}(t)x^{2}+c_{3}(t)x^{4} \end{aligned}$$
(21)

through Eq. (13). Substituting the Eq. (21) into the Eq. (2), one gets the following time fractional RL dynamical system

$$\begin{aligned} ^{RL}D_{t}^{\alpha }c_{1}(t)= & {} -\,24c_{1}(t)c_{3}(t)-1, \nonumber \\ ^{RL}D_{t}^{\alpha }c_{2}(t)= & {} -\,72c_{2}(t)c_{3}(t), \nonumber \\ ^{RL}D_{t}^{\alpha }c_{3}(t)= & {} -\,120c_{3}^{2}(t). \end{aligned}$$
(22)

To solve the third equation of the above system (22), we use (4) with \(\beta =0, \vartheta =-120, a=0.\) Then, we obtain

$$\begin{aligned} c_{3}(t)=\frac{-\,\Gamma (1-\alpha )}{120\Gamma (1-2\alpha )}t^{-\alpha }. \end{aligned}$$
(23)

Inserting the Eq. (23) into the the second equation of the system (22), we get the following first order time fractional ODE

$$\begin{aligned} t^{\alpha }~\left( ^{RL}D_{t}^{\alpha }c_{2}(t)\right) -\frac{3}{5} \frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}c_{2}(t)=0. \end{aligned}$$
(24)

We note that, Eq. (24) has the same structure as Eq. (5) mentioned in the second section, where \(t_{0}=0\) and

$$\begin{aligned} \ p(t)=-\frac{3}{5}\frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}. \end{aligned}$$
(25)

Because of the right side of Eq. (25) is a constant, then we have

$$\begin{aligned} p_{0}=-\frac{3}{5}\frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )},~ \end{aligned}$$
(26)

and using the Eq. (8), we get the following condition:

$$\begin{aligned} \frac{\Gamma (s+1)}{\Gamma (s-\alpha +1)}-\frac{3}{5}\frac{\Gamma (1-\alpha ) }{\Gamma (1-2\alpha )}=0. \end{aligned}$$
(27)

If \(s_{1}>-1\) is the value that satisfies the above condition (27) and \(\delta _{0}\ne 0\) then \(c_{2}(t)\) has the following form:

$$\begin{aligned} c_{2}(t)=t^{s_{1}}\delta _{0}. \end{aligned}$$
(28)

If (23) is substituted in the first equation of the system (22), the following time fractional ODE is obtained:

$$\begin{aligned} t^{\alpha }~\left( ^{RL}D_{t}^{\alpha }c_{1}(t)\right) -\frac{1}{5} \frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}c_{1}(t)=-t^{\alpha } \end{aligned}$$
(29)

In this case, let assume that \(c_{1}(t)\) has a structure like

$$\begin{aligned} c_{1}(t)=bt^{\varsigma }. \end{aligned}$$
(30)

If the (30) is substituted into the first equation of the system (22) and the necessary differentiation and simplification operations are performed, then

$$\begin{aligned} b=\frac{1}{-\Gamma (\alpha +1)+\frac{1}{5}\frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}}\text { and }\varsigma =\alpha \end{aligned}$$
(31)

are obtained. Therefore,

$$\begin{aligned} c_{1}(t)=\frac{5\Gamma (1-2\alpha )}{\Gamma (1-\alpha )-5\Gamma (1+\alpha ) \Gamma (1-2\alpha )}t^{\alpha } \end{aligned}$$
(32)

is deduced. If these values are substituted in (21), the solution of the model (2) in the form of

$$\begin{aligned} u(x,t)= & {} \frac{5\Gamma (1-2\alpha )}{\Gamma (1-\alpha )-5\Gamma (1+\alpha ) \Gamma (1-2\alpha )}t^{\alpha } +\left[ t^{s_{1}}\delta _{0}\right] x^{2} \nonumber \\{} & {} -\left[ \frac{\Gamma (1-\alpha )}{120\Gamma (1-2\alpha )}t^{-\alpha } \right] x^{4} \end{aligned}$$
(33)

for \(\alpha \in (0,1]\) is constructed. We note that, due to the structure of \(c_{2}(t)\), the solution (33) obtained is approximate.

3.2 \(n=2\)

In the second part of this section, we will consider the \(\Omega _{2}= \mathfrak {L}\left\{ 1,x^{4}\right\}\) invariant subspace. Because, if one substitutes \(c_{1}+c_{2}x^{4}\) into the right side of Eq. (1), then obtains

$$\begin{aligned} \left( -24c_{1}c_{2}-1\right) -120c_{2}^{2}x^{4}\in \Omega _{2}. \end{aligned}$$

To examine the 2-dimensional dynamic system for the time fractional RL derivative operator, we consider

$$\begin{aligned} ^{RL}D_{t}^{\alpha }c_{1}(t)= & {} -24c_{1}(t)c_{2}(t)-1, \nonumber \\ ^{RL}D_{t}^{\alpha }c_{2}(t)= & {} -120c_{2}^{2}(t). \end{aligned}$$
(34)

If (34) is compared with (15) mentioned in the second section, it is observed that

$$\begin{aligned} f=-24c_{1}(t)c_{2}(t)-1\text { and }g=-120c_{2}^{2}(t). \end{aligned}$$
(35)

If the value (35) is substituted in Eqs. (19–20), the following system is obtained:

$$\begin{aligned}{} & {} ^{RL}D_{t}^{\alpha }\nu _{1}(t)+(d_{3}-\alpha d_{1}-(\alpha +1)d_{2}t)(-24c_{1}c_{2}-1)\nonumber \\{} & {} \quad -120d_{4}c_{2}^{2}+24\left[ (\alpha -1)d_{2}tc_{1}+d_{3}c_{1}+d_{4}c_{2}+\nu _{1}(t)\right] c_{2}\nonumber \\{} & {} \quad +24\left[ (\alpha -1)d_{2}tc_{2}+d_{5}c_{1}+d_{6}c_{2}+\nu _{2}(t)\right] c_{1}=0, \end{aligned}$$
(36)

and

$$\begin{aligned}{} & {} ^{RL}D_{t}^{\alpha }\nu _{2}(t)+d_{5}(-24c_{1}c_{2}-1)-120(d_{6}-\alpha d_{1}-(\alpha +1)d_{2}t)c_{2}^{2}\nonumber \\{} & {} \quad +240\left[ (\alpha -1)d_{2}tc_{2}+d_{5}c_{1}+d_{6}c_{2}+\nu _{2}(t)\right] c_{2}=0. \end{aligned}$$
(37)

Each t,  \(c_{1}\) and \(c_{2}\) should satisfy Eqs. (36) and (37). As a result, for all t, the terms containing \(c_{1},\) \(c_{2},\) \(c_{1}^{2},\) \(c_{2}^{2}\) and \(c_{1}c_{2}\) should equal zero, yielding the system that follows:

$$\begin{aligned} \nu _{1}(t)=0,~\nu _{2}(t)=0,~d_{4}=d_{5}=0,~d_{2}=0, ~d_{3}=-d_{6},~d_{1}\text { is arbitrary.} \end{aligned}$$
(38)

The operator with general admitted form is

$$\begin{aligned} \Gamma =d_{1}\Gamma _{1}+\alpha d_{1}\Gamma _{3}-\alpha d_{1}\Gamma _{6} \end{aligned}$$
(39)

and (34) has a one dimensional Lie algebra of the admitted operator generated by when \(d_{1}=1,\)

$$\begin{aligned} \Gamma =t\frac{\partial }{\partial t}+\alpha c_{1}\frac{\partial }{\partial c_{1}}-\alpha c_{2}\frac{\partial }{\partial c_{2}}. \end{aligned}$$
(40)

With the admitted operators, solutions of (34) can be constructed. To start, let us find with respect to \(\Gamma\). Invariants of \(\Gamma\) are revealed as solutions of \(\Gamma I\left( t,c_{1},c_{2}\right) =0,\) which gives

$$\begin{aligned} c_{1}(t)=k_{1}^{-1}t^{\alpha }, c_{2}(t)=k_{2}^{\alpha }t^{-\alpha }. \end{aligned}$$

These expressions can be substituted into (34), and the well-known differentiation formula (3) can be used to get

$$\begin{aligned} k_{1}=\frac{1}{-\Gamma \left( \alpha +1\right) +\frac{1}{5}\frac{\Gamma \left( 1-\alpha \right) }{\Gamma \left( 1-2\alpha \right) }} \end{aligned}$$

and

$$\begin{aligned} k_{2}=\left( \frac{-1}{120}\frac{\Gamma \left( 1-\alpha \right) }{\Gamma \left( 1-2\alpha \right) }\right) ^{1/\alpha } \end{aligned}$$

where \(\alpha \ne \frac{1}{2}.\) Thus,we obtain the following solution profiles for \(c_{1}(t)\) and \(c_{2}(t)\):

$$\begin{aligned} c_{1}(t)=\frac{5\Gamma (1-2\alpha )}{\Gamma (1-\alpha )-5\Gamma (1+\alpha ) \Gamma (1-2\alpha )}t^{\alpha },~c_{2}(t)=\frac{-1}{120}\frac{\Gamma \left( 1-\alpha \right) }{\Gamma \left( 1-2\alpha \right) }t^{-\alpha }. \end{aligned}$$
(41)

Inserting the Eq. (41) into

$$\begin{aligned} u(x,t)=c_{1}(t)+c_{2}(t)x^{4} \end{aligned}$$
(42)

we yield the following exact solution form of Eq. (2) as follows:

$$\begin{aligned} u(x,t)=\frac{5\Gamma (1-2\alpha )}{\Gamma (1-\alpha )-5\Gamma (1+\alpha ) \Gamma (1-2\alpha )}t^{\alpha }-\frac{1}{120}\frac{\Gamma \left( 1-\alpha \right) }{\Gamma \left( 1-2\alpha \right) }t^{-\alpha }x^{4}. \end{aligned}$$
(43)

3.3 Exact solution for initial value problem of Eq. (2)

Consider the Eq. (2) with the initial condition

$$\begin{aligned} \left[ ^{RL}D_{t}^{\alpha -1}u(x,t)\right] _{t=0}=0. \end{aligned}$$

We use Adomian Method (Wazwaz 2010) to solve the initial value problem as follows:

Applying RL fractional integral to both sides of Eq. (2) gives

$$\begin{aligned} u(x,t)-~\left[ ^{RL}D_{t}^{\alpha -1} u(x,t)\right] _{t=0} \frac{t^{\alpha -1} }{\Gamma \left( \alpha \right) }=^{RL}I_{t}^{\alpha }\left[ -\left( u~ u_{xxx}\right) _{x}\right] -\frac{t^{\alpha }}{\Gamma \left( 1+\alpha \right) }. \end{aligned}$$

Using the initial condition we obtain

$$\begin{aligned} u(x,t)=^{RL}I_{t}^{\alpha }\left[ -\left( uu_{xxx}\right) _{x}\right] -\frac{t^{\alpha }}{\Gamma \left( 1+\alpha \right) }. \end{aligned}$$
(44)

Substituting \(u(x,t)=\overset{\infty }{\underset{n=0}{\sum }}u_{n}(x,t),\) and the nonlinear term by \(-\left( uu_{xxx}\right) _{x}=\overset{ \infty }{\underset{n=0}{\sum }}A_{n}\) into (44) gives

$$\begin{aligned} \overset{\infty }{\underset{n=0}{\sum }}u_{n}(x,t)=^{RL}I_{t}^{\alpha }\left[ \overset{\infty }{\underset{n=0}{\sum }}A_{n}\right] -\frac{t^{\alpha }}{ \Gamma \left( 1+\alpha \right) }. \end{aligned}$$

This gives the recursive relation

$$\begin{aligned} u_{0}(x,t)=\frac{-\,t^{\alpha }}{\Gamma \left( 1+\alpha \right) },~ u_{j+1}(x,t)=0,~A_{j+1}=0\text { for }j\ge 0. \end{aligned}$$

Thus,

$$\begin{aligned} u(x,t)=\frac{-t^{\alpha }}{\Gamma \left( 1+\alpha \right) }. \end{aligned}$$

This solution satisfies Eq. (2) and the initial condition.

4 Conclusion

In this study, we discussed the fourth order fractional order a new TFE. We treated the model in terms of time fractional RL derivative operator. Fractional exact solution forms appearing in (33) and (43) were obtained through the 3- and 2-dimensional invariant subspace method, respectively.

The dynamic system containing the RL derivative operator obtained using a 2-dimensional invariant subspace is examined in terms of Lie symmetries. Leave the dynamical system invariant, the 3-dimensional Lie algebra and the corresponding invariant solution is constructed.

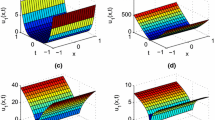
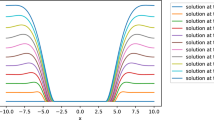
3-dimensional and 2-dimensional graphs were also presented to better understand the exact solution forms obtained. In Fig. 1, we presented 3-dimensional illustration of Eq. (33) when \(\alpha =0.9, s=-0.7750512779\). 2-dimensional illustration of Eq. (33) when \(\alpha =0.9,\) \(s=-\,0.7750512779\) for \(t=1\) and \(t=2\) was given in Fig. 2. Illustration of Eq. (33) with varying alpha (\(\alpha =0.75\) and \(\alpha =0.9\)) was given in Fig. 3. Also, 2-dimensional illustration of Eqs. (33) and (43) when \(\alpha =0.90,\) \(s=-\,0.7750512779,\) and \(t=1\) was presented in Fig. 4. In Prakash et al. (2023), the authors considered the (2+1)- and (1+1)-dimensional TFEs and systematically constructed exact solutions with the corresponding invariant subspaces represented by them. Even if \(f(w)=w,\) \(g(w)=1\) and \(h(w)=l(w)=p(w)=q(w)=0\) or other variants are taken for Eq. (1.8) in that article, Eq. (2) (which we examine in this article) cannot be obtained. The main difference is the constant negative absorption term. In addition, Lie symmetry analysis of the reduced 2-dimensional dynamic system has been examined in this article, and such an analysis has not been performed before for this model. The TFE we examined may have important application areas in quantum mechanics. TFEs find applications in various technologies like optical coatings, where precise control of film thickness is crucial for manipulating light. Quantum mechanics, on the other hand, underpins advancements in semiconductor devices, such as transistors and quantum dots, shaping the foundation of modern electronics and computing. Integrating these fields contributes to innovations in areas like quantum computing and nanotechnology. The physical explanations of the parabolic exact solutions for TFE with time fractional RL derivative can be described as follows: The time fractional RL derivative introduces a fractional order in time, capturing non-local temporal effects. In the case of our 4th-order TFE with RL time fractional derivatives, one might introduce a new length or time scale associated with the fractional order, which could modify the dynamics of the system in a non-trivial way. This means that the physical quantities in our system might behave differently compared to systems described by classical differential equations. In the context of TFEs, this fractional derivative implies that the dynamics of the thin film are influenced by past time instances with varying weights, reflecting the memory effect in the system. The parabolic shape in both 2D and 3D representations signifies the spreading or diffusion of the thin film over time, influenced by the fractional temporal behavior. The parabolic shape commonly associated with diffusion processes suggests that the thin film spreads or diffuses over space and time, driven by the interplay of the TFE components and the unique features introduced by the fractional derivative. The detailed characteristics of the parabolic solutions would depend on the specific parameters and initial/boundary conditions of TFE.

Fig. 1
figure 1

Illustration of Eq. (33) in 3 dimension when \(\alpha =0.9\) and \(s =-\,0.7750512779\)

Full size image
Fig. 2
figure 2

Illustration of Eq. (33) in 2 dimension when \(\alpha =0.9,\) and \(s =-\,0.7750512779\)

Full size image
Fig. 3
figure 3

Illustration of Eq. (33) in 2 dimension when \(\alpha =0.75\) and \(\alpha =0.9\)

Full size image
Fig. 4
figure 4

Illustration of Eqs. (33) and (43) in 2 dimension when \(\alpha =0.9\) and t=1

Full size image