A comparative study on the axial intensity of some laser beams spreading through human and mouse biological tissues

Abstract

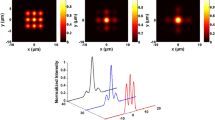
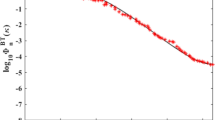
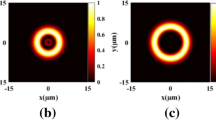
Aiming at the Bessel higher-order cosh-Gaussian beam and the Bessel higher-order sinh-Gaussian beam, we investigate their propagation properties through turbulent biological tissues. In this respect, the analytical expression of the considered beams is obtained and developed, based on the extended Huygens-Fresnel integral. By numerical simulation, the axial intensity of these beams for biological tissue types including the intestinal epithelium and deep dermis of the mouse in addition the human upper dermis versus the propagation distance as a function of the variations of the laser beam parameters. The obtained results indicate that the resistance of our beams against turbulent biological tissues increases as the source parameter increases counting the decentered parameter, the beam-order of the considered beams and the beam waist width. The findings show that the intensity distribution of the propagation of these beams occurs more quickly when they pass through the deep dermis of the mouse. The results presented in this paper are significant due to their potential application in determining the deterioration or disruption of biological tissue, medical imaging and medical diagnosis.

Appendix 1: Derivation of Eq. (11)

The electric field of the BHoChG beam and the BHoShG beam is described by the following equation as (Nossir et al. 2023b; Dalil-Essakali et al. 2023)

$$E\left( {r,\theta ,0} \right) = E_{0} \exp \left( {il\theta } \right)J_{l} \left( {\frac{q\mu }{{\omega_{0} }}r} \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right)f^{ \pm } (r)$$

(19)

with $f^{ + } (r) = ch^{n} \left( {\Omega r^{2} } \right)$ or $f^{ - } (r) = sh^{n} \left( {\Omega r^{2} } \right)$.

Utilizing the identity explicit formulae of cosh (.) and sinh (.) as (Abramowitz and Stegun 1970)

$$\cosh^{n} \left( {\rho^{2} } \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)e^{{a_{sn} \rho^{2} }} }$$

(20)

and

$$\sinh^{n} \left( {\rho^{2} } \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\left( { - 1} \right)^{s} \left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)e^{{ - a_{sn} \rho^{2} }} } ,$$

(21)

with $a_{sn} = 2s - n$ and $\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)$ denotes the binomial coefficient.

By employing an integral of the Huygens-Fresnel principal in calculating the formula for a beam intensity propagating in a medium of tissue (Andrews and Phillips 2005)

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle & = \left\langle {E(\vec{\rho },z,t)E^{ * } (\vec{\rho },z,t)} \right\rangle = \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left\langle {E(\vec{r}_{1} ,0)E^{ * } (\vec{r}_{2} ,0)} \right\rangle } } } } \\ & \quad \times \exp \left[ {\frac{ik}{{2z}}\left( {\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} - \left( {\vec{r}_{2} - \vec{\rho }} \right)^{2} } \right)} \right]\left\langle {\exp \left[ {\psi \left( {\overrightarrow {{r_{1} }} ,\overrightarrow {\rho } } \right) + \psi^{*} \left( {\overrightarrow {{r_{2} }} ,\overrightarrow {\rho } } \right)} \right]\,} \right\rangle d\vec{r}_{1} d\vec{r}_{2} \\ \end{aligned}$$

(22)

The ensemble average term in Eq. (22), can be expressed as (Andrews and Phillips 2005)

$$\left\langle {\exp \left[ {\psi \left( {r_{1} ,\rho } \right) + \psi^{ * } \left( {r_{2} ,\rho } \right)} \right]} \right\rangle = \exp \left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right)} \right]\exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right]$$

(23)

Substituting Eqs. (19) and (23) into Eq. (22) and by putting $\vec{\rho } = \vec{0}$ into Eq. (22), the expression of the axial intensity is written as

$$\begin{aligned} \left\langle {I\left( {0,z} \right)} \right\rangle & = \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} \pi^{2} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( { \pm 1} \right)^{{s_{1} }} \left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( { \pm 1} \right)^{{s_{2} }} \left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \\ & \quad \times \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\exp \left( { - \beta_{1}^{ \pm } r_{1}^{2} } \right)} } } } \exp \left( { - \beta_{2}^{ \pm } r_{2}^{2} } \right)\exp \left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right)} \right] \\ & \quad \times \exp \left[ {il\left( {\theta_{1} - \theta_{2} } \right)} \right]J_{l} \left( {\frac{\mu q}{{\omega_{0} }}r_{1} } \right)\,J_{l} \left( {\frac{\mu q}{{\omega_{0} }}r_{2} } \right)r_{1} dr_{1} d\theta_{1} r_{2} dr_{2} d\theta_{2} , \\ \end{aligned}$$

(24)

where

$$\beta_{1}^{ \pm } = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} \pm a_{{s_{1} n}} \Omega - \frac{ik}{{2z}}$$

(25a)

and

$$\beta_{2}^{ \pm } = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} \pm a_{{s_{2} m}} \Omega + \frac{ik}{{2z}}$$

(25b)

Applying the following integral formula (Gradshteyn and Ryzhik 1994)

$$\int\limits_{0}^{2\pi } {\exp \left[ { - im\theta_{1} + x\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} = 2\pi \exp \left( { - im\theta_{2} } \right)I_{m} \left( x \right),$$

(26)

with $I_{m} \left( z \right) = \left( { - i} \right)^{m} J_{m} \left( {iz} \right)$.

One obtains the expression of the Eq. (24) as follows

$$\begin{aligned} \left\langle {I\left( {0,z} \right)} \right\rangle & = \frac{{\left( { - i} \right)^{l} k^{2} E_{0}^{2} }}{{2^{n + m} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( { \pm 1} \right)^{{s_{1} }} \left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( { \pm 1} \right)^{{s_{2} }} \left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \\ & \quad \times \int\limits_{0}^{\infty } {\exp \left( { - \beta_{2}^{ \pm } r_{2}^{2} } \right)} J_{l} \left( {\frac{\mu q}{{\omega_{0} }}r_{2} } \right)r_{2} dr_{2} \int\limits_{0}^{\infty } {\exp \left( { - \beta_{1}^{ \pm } r_{1}^{2} } \right)} J_{l} \left( {\frac{\mu q}{{\omega_{0} }}r_{1} } \right)J_{l} \left( {i\frac{{2r_{2} }}{{\rho_{0}^{2} }}r_{1} } \right)r_{1} dr_{1} . \\ \end{aligned}$$

(27)

Recalling the integral formula for solving these last integrals

$$\int\limits_{0}^{\infty } {x\exp \left( { - \gamma x^{2} } \right)} J_{n} \left( {\alpha x} \right)J_{n} \left( {\delta x} \right)dx = \frac{1}{2\gamma }\exp \left( { - \frac{{\alpha^{2} + \delta^{2} }}{4\gamma }} \right)I_{n} \left( { - \frac{\alpha \delta }{{2\gamma }}} \right)\;{\text{with}}\;\left[ {{\text{Re}} n > - 1,\left| {\arg \left( \gamma \right)} \right|\langle \frac{\pi }{4},\alpha > 0,\delta > 0} \right]$$

(28)

After tedious forward integral calculations, the expression of Eq. (27) can be arranged as

$$\begin{aligned} \left\langle {I\left( {0,z} \right)} \right\rangle & = i^{l} \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( { \pm 1} \right)^{{s_{1} }} \left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( { \pm 1} \right)^{{s_{2} }} \left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \frac{1}{{\beta^{ \pm } \beta_{1}^{ \pm } }}\exp \left[ { - \frac{{q^{2} \mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{{\beta^{ \pm } }} + \frac{1}{{\beta_{1}^{ \pm } }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{q^{2} \mu^{2} }}{{4\beta^{ \pm } \beta_{1}^{2 \pm } \omega_{0}^{2} \rho_{0}^{4} }}} \right)J_{l} \left( { - \frac{{iq^{2} \mu^{2} }}{{2\beta^{ \pm } \beta_{1}^{ \pm } \omega_{0}^{2} \rho_{0}^{2} }}} \right) \\ \end{aligned}$$

(29)

where

$$\beta^{ \pm } = \beta_{2}^{ \pm } - \frac{1}{{\beta_{1}^{ \pm } \rho_{0}^{4} }}$$

(30)

Equation (29) is Eq. (11) in the text.