1 Introduction

The evolution of systems that display randomness can be described using stochastic partial differential equations (SPDEs), which are mathematical models. These equations have been established for a number of applications in many different domains, including physics, engineering, and finance, among others (Iqbal et al. 2023; Yasin et al. 2021; Baber et al. 2023). The behaviour of the system is significantly influenced by random factors, which are not taken into consideration by deterministic models. The dynamics of the system are thus represented in a more thorough and accurate manner. Due to their widespread use in a number of disciplines, including turbulence, climate modelling, financial engineering, materials science, biology, and neurology, the study of SPDEs has attracted a lot of attention (Yasin et al. 2023, 2022). For instance, the behaviour of turbulent fluids, which is characterised by its chaos and unpredictability, has been modelled using SPDEs. The impact of ambiguous factors, such as solar radiation and greenhouse gas emissions, on the forecast of climatic patterns is taken into consideration in climate modelling by using SPDEs. As with interest rates, which are prone to volatility and unanticipated shocks, financial engineers model stock price and interest rate changes using SPDEs (Ahmed et al. 2023).

One of the primary challenges of SPDEs is crucial to analyze the numerically and analytically. Recently, many researchers have been working on SPDEs to obtain both approximate and exact solutions, such as Iqbal et al. who investigated the nonlinear stochastic Newell-Whitehead-Segel equation numerically (Iqbal et al. 2023), and Yasin et al. who investigated the stochastic Fitzhugh–Nagumo model (Yasin et al. 2022) and the stochastic predator–prey model (Yasin et al. 2023). Raza et al. constructed the reliable numerical analysis for stochastic gonorrhea epidemic model (Raza et al. 2019). On the other hand there are many literatures on exact solitary wave solutions as; Shaikh et al. constructed the soliton solutions for the stochastic Konno-Oono system (Shaikh et al. 2023a), Mohammed et al working on the stochastic Ginzburg-Landau equation (Mohammed et al. 2021), (2+ 1)-dimensional stochastic chiral nonlinear Schrödinger equation (Albosaily et al. 2020), stochastic exact solutions of the Nizhnik–Novikov–Veselov system (Mohammed and El-Morshedy 2021), stochastic Burgers’ equation (Mohammed et al. 2021a), Ahmad et al. created the soliton and lump solutions for M-truncated stochastic Biswas-Arshed model (Ahmad et al. 2023), Solitary wave structures for the stochastic Nizhnik–Novikov–Veselov system (Ahmad et al. 2023), exact soliton solutions to stochastic chiral nonlinear schrödinger equation (Rehman et al. 2023), fractional Boussinesq model (Ali et al. 2023), discussed the dynamic nature of soliton solutions to the fractional coupled nonlinear Schrödinger model (Ali et al. 2023) and explored the soliton solutions to a Konno-Onno model (Chahlaoui et al. 2023). Seadawy et al. worked on the (2+ 1)-dimensional elliptic nonlinear Schrödinger equation (Seadawy et al. 2020a), Shahzad et al. obtained the multi peak solitons and btreather types wave solutions of unstable NLSEs (Shehzad et al. 2023), Arshad et al. studied the (3+ 1)-dimensional extended Zakharov–Kuznetsov dynamical model (Arshad et al. 2023) and fractional order partial differential equations (PDEs) (Arshad et al. 2017). Iqbal et al. also found the different form of soliton solutions for the modified Kortewege-de Vries dynamical equation (Iqbal et al. 2018a, b), (2+ 1)-dimensional nonlinear Nizhnik-Novikov-Vesselov dynamical equation (Iqbal et al. 2020), nonlinear longitudinal wave equation (Iqbal et al. 2019), generalized Kadomtsev–Petviashvili modified equal width dynamical equation (Seadawy et al. 2019), modify unstable nonlinear Schrödinger dynamical equation (Seadawy et al. 2020b, c), nonlinear damped modified Korteweg-de Vries equation (Seadawy et al. 2020d; Seadawy and Iqbal 2021), and nonlinear Zakharov–Kuznetsov modified equal width equation (Iqbal et al. 2023). Tedjani et al. worked on the perturbed Chen–Lee–Liu equation (Tedjani et al. 2023a), nonlinear Schrödinger equations with quadratic nonlinearity with inter-modal and spatio-temporal dispersions (Tedjani et al. 2023b). Ahmed et al. worked on the integrable Schwarz–Korteweg-de vries problem (Ahmed et al. 2023). Rizvi et al, are considered the higher order Boussinesq equation (Rizvi et al. 2023a; Seadawy et al. 2023), and the Kraenkel-Manna-Merle system (Rizvi et al. 2023b, c).

The Davey–Stewartson equation (DSE) was created in 1974 by Davey and Stewartson (1974). The DSE method is used to show how a three-dimensional wave-packet evolves over time on shallow water. It consists of the following linked partial differential equations for the real field (mean flow) and the complex field (wave amplitude). For more detail see Mohammed et al. (2023):

$$\begin{aligned}{} & {} i g_t+\frac{1}{2}\alpha ^2(g_{xx}+\alpha ^2 g_{yy})+\gamma |g|^2g-h_x g+i \nu g \beta _t=0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} h_{xx}-\alpha ^2h_{yy}-2 \gamma (|h|^2)_x=0, \end{aligned}$$
(2)

where \(\alpha ^2=\pm 1\) and \(\beta =\pm 1\). The constants \(\gamma\) measures the cubic nonlinearity. We are considering the multiplicative noise and it is controlled with Borel function \(\nu\). There are two cases if \(\alpha =1\) then it is DS-I equation if \(\alpha =i\) it will be DS-II equation. The DS-I and DS-II, two-dimensional integrable equations, are higher-dimensional variations of the nonlinear Schrödinger equation. The description of shallow water gravity-capillarity surface wave packets is just one example of the many uses for them. Plasma physics, nonlinear optics, hydrodynamics, and other fields have made use of the solutions to the DS –Stewartson Eqs. (1)–(2). For instance, the DS equation’s solutions could explain how well matched microwaves and spatiotemporal optical optics.

Due to its uses, it has become more important to locate the exact solitary wave solutions for the nonlinear dynamical system. The intriguing family of soliton waves is a nonlinear wave solution that keeps its energy and structure while moving across a material. Solitary waves, also known as soliton waves, are frequently used. It is vital to understand how they react to noise because of their unique qualities, which have drawn significant attention in a number of scientific and engineering fields. The study of nonlinear dynamics heavily depends on solitary waves. Gaining knowledge of the interactions between solitary waves and these perturbations is crucial for understanding how the entire system behaves. Nonlinear systems can exhibit a variety of behaviours in response to noise or perturbations. Due to their amazing ability to maintain their shape and energy in the presence of disturbances, solitary wave solutions exhibit significance under the impact of noise. Numerous fields, such as biology, nonlinear dynamics, and communications, have applications for this property. In order to fully utilise solitary waves in a variety of practical applications and to obtain insights into the behaviour of complex systems, it is crucial to understand how they behave in noisy surroundings. There are many techniques are developed to explore the traveling wave solutions for the nonlinear dynamical systems such as; new modified extended direct algebraic method (Rehman et al. 2022; Younis et al. 2021; Islam et al. 2023), \(\phi ^6\)-model expansion method (Shahzad et al. 2023; Younas et al. 2021), Hirota bilinear method (Younas et al. 2022; Ceesay et al. 2023), He’s iteration variation method (Nisar et al. 2022), Fan-subequation method (Jafari et al. 2012), \(G'/G\)-model expansion method (Shang and Zheng 2013), Sardar subequation (Baber et al. 2023), Generalized exponential rational function method (Sharif and Eslami 2023), sine-cosine function method (Mirzazadeh et al. 2015), Kudryashov method (Eslami 2016; Asghari et al. 2023a), fractional transformation method (Asghari et al. 2023b), first integral method (Eslami and Rezazadeh 2016) and etc. The sardar subequation method is a well known technique to obtain the exact solutions for the nonlinear dynamical systems. This technique is provided us the different form of soliton solutions such as dark, bright, combine dark-bright and periodic wave solutions. So, this technique is we effective over other methods that will provided us the better solutions.The limitations of this study is that the sardar subequation is only applicable on the even order ODEs. Moreover, these results are very effective when we study the SDS model at the microlevel that will show us how the dynamical system pretend under the effect of noise. These result are classical soliton solutions when the noise srenght is zero. In this study we consider the stochastic Davey–Stewartson equation to show the effect of noise on it analytically. This is an integrable equations, are higher-dimensional variations of the nonlinear Schrödinger equation. Among their many applications is the description of surface wave packets in shallow water gravity-capillarity systems. The solutions to the DS equations (1)-(2) have been applied in hydrodynamics, plasma physics, and nonlinear optics, among other domains. For instance, the these solutions could explain how well matched microwaves and spatiotemporal optical optics when we see them as the microlevel.

2 Wiener process

Consider a Wiener process \(\beta (t)\) that is non-differentiable and has the following characteristics (Mohammed et al. 2022a):

$$\begin{aligned}{} & {} \lim _{\Delta t\rightarrow 0} \Delta \beta _t=0; \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \lim _{\Delta t\rightarrow 0} \frac{(\Delta \beta _t)^N}{\Delta t}=\left\{ \begin{array}{ll} 1, \quad N=2\\ 0, \quad N=3,4,\cdots \end{array} \right. \end{aligned}$$
(4)

Definition 1

Stochastic process \((\beta _{t})_{t\le 0}\) is if the following criteria are met, a motion is said to be Brownian;

  • \(\beta _t\) is continues function if \(t\le 0\).

  • \(\beta _0\)=0.

  • For \(t_1<t_2\), \(\beta _{t_2}-\beta _{t_1}\) is independent.

  • \(\beta _{t_2}-\beta _{t_1}\) has a normal distribution \(\kappa (0, t_2-t_1)\).

Where the time derivative of the Wiener process \(\beta (t)\) is expressed as \(\beta _t=\frac{d\beta }{dt}\).

3 Wave transformation

In order to obtain the wave equation for the SFDSEs, the subsequent wave transformation is taking as Albosaily et al. (2020); Mohammed et al. (2021); Shaikh et al. (2023b, 2023c);

$$\begin{aligned} g(x, y, t)=G(\varpi )e^{i \kappa - \nu \beta (t)-\nu ^2 t}, \qquad h(x, y, t)=H(\varpi )e^{-2 \nu \beta (t)-2 \nu ^2 t}, \end{aligned}$$
(5)

where

$$\begin{aligned} \varpi =\varpi _1 x+\varpi _2y-\varpi _3 t, \qquad \kappa =\kappa _1 x+\kappa _2 y +\kappa _3 t, \end{aligned}$$
(6)

where \(\varpi _i, \kappa _i (i=1,2,3)\) are constants while G and H are deterministic functions.

So, we taking derivatives of above transformations such as

$$\begin{aligned} g_t= & {} (-\varpi _3 G^{'}+i\kappa _3 G-\nu G \beta (t)+\frac{\nu ^2}{2}-\nu ^2G)e^{i \kappa - \nu \beta (t)-\nu ^2 t},\\= & {} (-\varpi _3 G^{'}+i\kappa _3 G-\nu G \beta (t)-\frac{\nu ^2}{2})e^{i \kappa - \nu \beta (t)-\nu ^2 t},\\= & {} (-\varpi _3 G^{'}+i\kappa _3 G-\nu G \beta (t))e^{i \kappa - \nu \beta (t)-\nu ^2 t}, \\ g_{xx}= & {} (\varpi _1^2G^{''}+2 i \kappa _1\varpi _1 G^{'}-\kappa _1^2G) e^{i \kappa - \nu \beta (t)-\nu ^2 t},\\ g_{yy}= & {} (\varpi _2^2G^{''}+2 i \kappa _2\varpi _2 G^{'}-\kappa _2^2G) e^{i \kappa - \nu \beta (t)-\nu ^2 t},\\ (|g|^2)_x= & {} \varpi _1(G^2)^{'}e^{- \nu \beta (t)-\nu ^2 t},\\ h_x= & {} \varpi _1 H^{'}e^{- \nu \beta (t)-\nu ^2 t},\\ h_{xx}= & {} \varpi _1^2 H^{''}e^{- \nu \beta (t)-\nu ^2 t},\\ h_{yy}= & {} \varpi _2^2 H^{''}e^{- \nu \beta (t)-\nu ^2 t}.\\ \end{aligned}$$

Substituting these derivatives along with Eq. (5) into Eqs. (1) & (2) and compare the real and imaginary part such as

$$\begin{aligned}{} & {} (\frac{1}{2}\varpi _1^2\alpha ^2 +\frac{1}{2}\varpi _2^2\alpha ^4 )G^{''}-(\kappa _3+\frac{1}{2}\varpi _1^2\kappa _1^2+\frac{1}{4}\kappa _2^2\alpha ^4 )G +(\gamma G^3-\varpi _1 G H^{'})e^{- \nu \beta (t)-\nu ^2 t}=0, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} (\varpi _1^2-\alpha ^2\varpi _2^2)H^{''}-2 \varpi _1 \gamma (G^2)^{'}=0, \end{aligned}$$
(8)

imaginary part is

$$\begin{aligned} (-\varpi _3+2\varpi _2 \kappa _1+2 \varpi _2\kappa _2)G^{'}=0. \end{aligned}$$
(9)

Now from the Eq. (9) we obtain the constraint condition such as

$$\begin{aligned} \varpi _3=2\varpi _2 \kappa _1+2 \varpi _2\kappa _2. \end{aligned}$$
(10)

Now, Eq. (8) integrated once and take integrating constants zero and we get

$$\begin{aligned} H^{'}=\frac{2\varpi _2 \gamma }{(\varpi _1^2-\alpha ^2\varpi _2^2)}G^2, \end{aligned}$$
(11)

substituting Eq. (11) into Eq. (7) and get

$$\begin{aligned} G^{''}-c_2G +c_1 G^3e^{- \nu \beta (t)-\nu ^2 t}=0, \end{aligned}$$
(12)

here we let \(c_1=\frac{2\gamma }{\alpha ^2(\varpi _1^2-\alpha ^2\varpi _2^2)}\) and \(c_2=\frac{2\kappa _3+\alpha ^2\kappa _1^2+\alpha ^4\kappa _2^2}{\alpha ^2(\varpi _1^2+\alpha ^2\varpi _2^2)}\). Now we are taking expectation \({\mathbb {E}}\) on Eq. (12) and get (Mohammed et al. 2021b, 2022b);

$$\begin{aligned} G^{''}-c_2G +c_1 G^3e^{-\nu ^2 t}{\mathbb {E}}(e^{- \nu \beta (t)})=0, \end{aligned}$$
(13)

where \(\beta (t)\) is standard Wiener process, so \({\mathbb {E}}(e^{- \nu \beta (t)})=e^{\nu ^2 t}\). Thus Eq. (13) becomes

$$\begin{aligned} G^{''}-c_2G +c_1 G^3=0. \end{aligned}$$
(14)

4 Exact soliton solutions via Sardar subequation method

The Sardar subequation approach is used to gain the exact soliton solution for Davey Stewartson model and suppose that the general solution in the form of polynomial for the Eq. (14) such as Hussain et al. (2022); Rehman et al. (2022),

$$\begin{aligned} G(X)= \sum _{i=0}^N \chi _i \Upsilon ^i(\varpi ), \end{aligned}$$
(15)

where \(\chi _i\) is a constant that can be calculated later, for \(i=0, 1, 2 \cdots N\). The homogeneous balancing principle is used to find the positive integer N by applying it to the terms \(G^{''}\) and \(G^3\), which results is \(N=1\). So, \(\Upsilon (\varpi )\) is satisfy the ODE as follows

$$\begin{aligned} \Upsilon ^{'}(\varpi )=\sqrt{M+N \Upsilon (\varpi )+ \Upsilon ^2(\varpi )}, \end{aligned}$$
(16)

where M, and N are constants. Substituting the \(N=1\) in the Eq. (15) and we get

$$\begin{aligned} G(\varpi )= \chi _0+\chi _1\Upsilon (\varpi ). \end{aligned}$$
(17)

By inserting the Eq. (17) into Eq. (14) with the aid of Eq. (16), we were able to generate the infinite series in \(\Upsilon (\varpi )\). A system of equations results from setting all identical powers of \(\Upsilon (\varpi )\) to zero. Using Mathematica, we can gather the following unknowns in order to determine the values of constants:

$$\begin{aligned} \left\{ \begin{array}{ll} \chi _0=0, \chi _1=\frac{i \sqrt{2}}{\sqrt{c_1}}, N=c_2. \end{array} \right. \end{aligned}$$

Using wave transformation, we were able to find the various forms of Soliton, trigonometric, and rational solutions of Eqs. (1–2) by substituting these values in Eq. (17):

Family-1: For \(N>0\) and \(M= 0\), we explored soliton solutions for Eqs. (1–2) such as

$$\begin{aligned} G_{1}(\varpi )= \frac{i \sqrt{2} \sqrt{-c_2} \text {sech}_{AB}\left( \sqrt{c_2} \varpi \right) }{\sqrt{c_1}}, \end{aligned}$$
(18)

using the transformation Eq. (5), the bright soliton solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{1}(x, y, t)= \left[ \frac{i \sqrt{2} \sqrt{- A B c_2}}{\sqrt{c_1}} \text {sech}_{AB}\left( \sqrt{c_2} \left( \varpi _1x+ \varpi _2 y- \varpi _3 t\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(19)

Now putting Eq. (18) into the Eq. (11) and integrate once we obtained the dark soliton solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{1}(x, y, t)= \left[ \frac{4 \beta \sqrt{c_2} \omega _2}{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) } \tanh _{AB} \left( \sqrt{AB c_2} \left( \varpi _1x+ \varpi _2 y- \varpi _3 t\right) \right) \right] e^{-\nu \beta (t)-\nu ^2 t}. \end{aligned}$$
(20)

And

$$\begin{aligned} G_{2}(\varpi )= \frac{i \sqrt{2} \sqrt{c_2} \text {csch}_{AB}\left( \sqrt{c_2} \varpi \right) }{\sqrt{c_1}}, \end{aligned}$$
(21)

using the transformation Eq. (5), the singular soliton solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{2}(x, y, t)= \left[ \frac{i \sqrt{2} \sqrt{c_2}}{\sqrt{c_1}} \text {csch}_{AB}\left( \sqrt{AB c_2} \left( \varpi _1x+ \varpi _2 y- \varpi _3 t\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(22)

Now putting Eq. (21) into the Eq. (11) and integrate once we obtained the singular soliton solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{2}(x, y, t)= \left[ -\frac{4 \beta \sqrt{c_2} \omega _2}{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) } \coth _{AB} \left( \sqrt{AB c_2} \left( \varpi _1 x+ \varpi _2 y- \varpi _3 t\right) \right) \right] e^{-\nu \beta (t)-\nu ^2 t}. \end{aligned}$$
(23)

Where \(\text {sech}_{AB}=\frac{2}{A e^{\varpi }+B e^{-\varpi }}\) and \(\text {csch}_{AB}=\frac{2}{A e^{\varpi }- B e^{-\varpi }}\).

Family-2: For \(N<0\) and \(M= 0\), we explored exact solitary wave solutions for Eqs. (1–2) such as

$$\begin{aligned} G_{3}(\varpi )=\frac{i \sqrt{2} \sqrt{-c_2} \sec _{AB} \left( \sqrt{-c_2} \varpi \right) }{\sqrt{c_1}}, \end{aligned}$$
(24)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{3}(x, y, t)= \left[ \frac{i \sqrt{2} \sqrt{-c_2}}{\sqrt{c_1}} \sec _{AB} \left( \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(25)

Now putting Eq. (24) into the Eq. (11) and integrate once we obtained the periodic wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{3}(x, y, t)= \left[ \frac{4 \beta c_2 \omega _2 \tan _{AB} \left( \sqrt{-c_2}(-t \omega _3+x \omega _1+y \omega _2) \right) }{c_1 \sqrt{-c_2} \left( \omega _1^2-\alpha ^2 \omega _2^2\right) } \right] e^{-\nu \beta (t)-\nu ^2 t}. \end{aligned}$$
(26)

And

$$\begin{aligned} G_{4}(\varpi )= \frac{i \sqrt{2} \sqrt{-c_2} \csc _{AB} \left( \sqrt{-c_2} \varpi \right) }{\sqrt{c_1}}, \end{aligned}$$
(27)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{4}(x, y, t)= \left[ \frac{i \sqrt{2} \sqrt{-c_2}}{\sqrt{c_1}} \csc _{AB} \left( \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(28)

Now putting Eq. (27) into the Eq. (11) and integrate once we obtained the periodic wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{4}(x, y, t)= \left[ -\frac{4 \beta c_2 \omega _2}{c_1 \sqrt{-c_2} \left( \omega _1^2-\alpha ^2 \omega _2^2\right) } \cot _{AB} \left( \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}. \end{aligned}$$
(29)

Where \(\sec _{AB}=\frac{2}{A e^{i \varpi }+B e^{-i \varpi }}\) and \(\csc _{AB}=\frac{2}{A e^{i \varpi }-B e^{-i \varpi }}\).

Family-3: For \(N<0\) and \(M= \frac{N^2}{4}\), we explored different types of solitons for Eqs. (1–2) such as

$$\begin{aligned} G_{5}(\varpi )=\frac{i \sqrt{-c_2} \tanh _{AB} \left( \frac{\sqrt{-c_2} \varpi }{\sqrt{2}}\right) }{\sqrt{c_1}}, \end{aligned}$$
(30)

using the transformation Eq. (5), the Dark soliton is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{5}(x, y, t)= \left[ \frac{i \sqrt{-c_2}}{\sqrt{c_1}} \tanh _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(31)

Now putting Eq. (30) into the Eq. (11) and integrate once we obtained the Dark soliton for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{5}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2 }{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) }\left( -\frac{\sqrt{2} \tanh _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{-c_2}}(-t \omega _3+x \omega _1+y \omega _2)\right) \right] \nonumber \\ e^{-\nu \beta (t)-\nu ^2 t}.~~~ \end{aligned}$$
(32)

And

$$\begin{aligned} G_{6}(\varpi )= \frac{i \sqrt{-c_2} \coth _{AB} \left( \frac{\sqrt{-c_2} \varpi }{\sqrt{2}}\right) }{\sqrt{c_1}}, \end{aligned}$$
(33)

using the transformation Eq. (5), the singular soliton is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{6}(x, y, t)= \left[ \frac{i \sqrt{-c_2} }{\sqrt{c_1}}\coth _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(34)

Now putting Eq. (33) into the Eq. (11) and integrate once we obtained the singular soliton for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{6}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2}{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) } \left( -\frac{\sqrt{2} \coth _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{-c_2}}(-t \omega _3+x \omega _1+y \omega _2)\right) \right] \nonumber \\ e^{-\nu \beta (t)-\nu ^2 t}.~~~ \end{aligned}$$
(35)

And

$$\begin{aligned} G_{7}(\varpi )= \frac{i \sqrt{-c_2} \left( \tanh \left( \sqrt{2} \sqrt{-c_2} \eta \right) +i \text {sech}\left( \sqrt{2} \sqrt{-c_2} \eta \right) \right) }{\sqrt{c_1}}, \end{aligned}$$
(36)

using the transformation Eq. (5), the complex combined dark-bright solitons is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{7}(x, y, t)= \left[ \frac{i \sqrt{-c_2} }{\sqrt{c_1}}\left( \tanh \left( \sqrt{2} \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) +\hspace{2cm}\nonumber \right. \right. \\\left. \left. i \text {sech}\left( \sqrt{2} \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(37)

Now putting Eq. (36) into the Eq. (11) and integrate once we obtained the singular soliton for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{7}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2}{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) } \left( -\frac{2 \sqrt{2} \sinh \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{-c_2} \left( \cosh \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) +i \sinh \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right) }\right. \right. \nonumber \\ \left. \left. +(-t \omega _3+x \omega _1+y \omega _2)\right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}. \end{aligned}$$
(38)

And

$$\begin{aligned} G_{8}(\varpi )=\frac{i \sqrt{-c_2} \left( \coth _{AB} \left( \sqrt{2} \sqrt{-c_2} \eta \right) +\text {csch}_{AB}\left( \sqrt{2} \sqrt{-c_2} \eta \right) \right) }{\sqrt{c_1}}, \end{aligned}$$
(39)

using the transformation Eq. (5), the combined singular soliton is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{8}(x, y, t)= \left[ \frac{i \sqrt{-c_2}}{\sqrt{c_1}} \left( \coth _{AB} \left( \sqrt{2} \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \hspace{2cm}\right. \right. \nonumber \\ \left. \left. +\text {csch}_{AB}\left( \sqrt{2} \sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(40)

Now putting Eq. (39) into the Eq. (11) and integrate once we obtained the mixed singular soliton for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{8}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2 }{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) }\left( -\frac{\sqrt{2} \coth _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{-c_2}}-t \omega _3+x \omega _1+y \omega _2\right) \right] \nonumber \\ e^{-\nu \beta (t)+\nu ^2 (-t)}.~~~~~ \end{aligned}$$
(41)

And

$$\begin{aligned} G_{9}(\varpi )=\frac{i \sqrt{-c_2} \left( \tanh _{AB} \left( \frac{\sqrt{-c_2} \varpi }{2 \sqrt{2}}\right) +\coth _{AB} \left( \frac{\sqrt{-c_2} \varpi }{2 \sqrt{2}}\right) \right) }{2 \sqrt{c_1}}, \end{aligned}$$
(42)

using the transformation Eq. (5), the combo soliton is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{9}(x, y, t)= \left[ \frac{i \sqrt{-c_2}}{2 \sqrt{c_1}} \left( \tanh _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{2 \sqrt{2}}\right) \hspace{2cm}\nonumber \right. \right. \\\left. \left. +\coth _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{2 \sqrt{2}}\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(43)

Now putting Eq. (42) into the Eq. (11) and integrate once we obtained the combo soliton for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{9}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2 }{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) }\left( -\frac{\sqrt{2} \coth _{AB} \left( \frac{\sqrt{-c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{-c_2}}(-t \omega _3+x \omega _1+y \omega _2)\right) \right] \nonumber \\e^{-\nu \beta (t)+\nu ^2 (-t)}.~~~ \end{aligned}$$
(44)

Where \(\text {tanh}_{AB}=\frac{A e^{\varpi }-B e^{-\varpi }}{A e^{\varpi }+B e^{-\varpi }}\) and \(\text {coth}_{AB}=\frac{A e^{\varpi }+ B e^{-\varpi }}{A e^{\varpi }- B e^{-\varpi }}\).

Family-4: For \(N>0\) and \(M= \frac{N^2}{4}\), we explored different types of solitary wave solutions for Eqs. (1–2) such as

$$\begin{aligned} G_{10}(\varpi )=\frac{i \sqrt{c_2} \tan _{AB} \left( \frac{\sqrt{c_2} \varpi }{\sqrt{2}}\right) }{\sqrt{c_1}}, \end{aligned}$$
(45)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{10}(x, y, t)= \left[ \frac{i \sqrt{c_2} }{\sqrt{c_1}}\tan _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(46)

Now putting Eq. (45) into the Eq. (11) and integrate once we obtained the periodic wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{10}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2}{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) } \left( \frac{\sqrt{2}}{\sqrt{c_2}} \tan _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) +(t \omega _3-x \omega _1-y \omega _2)\right) \right] \nonumber \\e^{-\nu \beta (t)-\nu ^2 t}.~~~~ \end{aligned}$$
(47)

And

$$\begin{aligned} G_{11}(\varpi )= \frac{i \sqrt{c_2} \cot _{AB} \left( \frac{\sqrt{c_2} \varpi }{\sqrt{2}}\right) }{\sqrt{c_1}}, \end{aligned}$$
(48)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{11}(x, y, t)= \left[ \frac{i \sqrt{c_2}}{\sqrt{c_1}} \cot _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(49)

Now putting Eq. (48) into the Eq. (11) and integrate once we obtained the solitary wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{11}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2}{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) } \left( -\frac{\sqrt{2} }{\sqrt{c_2}}\cot _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right. \right. \nonumber \\ \left. \left. +(t \omega _3-x \omega _1-y \omega _2)\right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}.~~~~ \end{aligned}$$
(50)

And

$$\begin{aligned} G_{12}(\varpi )= \frac{i \sqrt{-c_2} \left( \tanh _{AB} \left( \sqrt{2} \sqrt{-c_2} \varpi \right) +i \text {sech}_{AB}\left( \sqrt{2} \sqrt{-c_2} \varpi \right) \right) }{\sqrt{c_1}}, \end{aligned}$$
(51)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{12}(x, y, t)= \left[ \frac{i \sqrt{c_2}}{\sqrt{c_1}} \left( \tan _{AB} \left( \sqrt{2} \sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \hspace{2cm}\right. \right. \nonumber \\ \left. \left. +\sec _{AB} \left( \sqrt{2} \sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(52)

Now putting Eq. (51) into the Eq. (11) and integrate once we obtained the solitary wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{12}(x, y, t)= \left[ -\frac{2 \beta c_2 \omega _2}{c_1 \left( \omega _1^2-\alpha ^2 \omega _2^2\right) } \left( \frac{2 \sqrt{2} \sin _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{c_2} \left( \cos _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) -\sin _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right) }\right. \right. \nonumber \\ \left. \left. +(t \omega _3-x \omega _1-y \omega _2)\right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}. \end{aligned}$$
(53)

And

$$\begin{aligned} G_{13}(\varpi )=\frac{i \sqrt{c_2} \left( \cot _{AB} \left( \sqrt{2} \sqrt{c_2} \varpi \right) +\csc _{AB} \left( \sqrt{2} \sqrt{c_2} \varpi \right) \right) }{\sqrt{c_1}}, \end{aligned}$$
(54)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{13}(x, y, t)= \left[ \frac{i \sqrt{c_2}}{\sqrt{c_1}} \left( \cot _{AB} \left( \sqrt{2} \sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \hspace{2cm}\right. \right. \nonumber \\ \left. \left. +\csc _{AB} \left( \sqrt{2} \sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) \right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(55)

Now putting Eq. (39) into the Eq. (11) and integrate once we obtained the solitary wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{13}(x, y, t)= \left[ \frac{2 \beta c_2 \omega _2 }{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) }\left( -\frac{\sqrt{2} \cot _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) }{\sqrt{c_2}}\right. \right. \nonumber \\ \left. \left. +(t \omega _3-x \omega _1-y \omega _2)\right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}. \end{aligned}$$
(56)

And

$$\begin{aligned} G_{14}(\varpi )=\frac{i \sqrt{c_2} \left( \tan _{AB} \left( \frac{\sqrt{c_2} \varpi }{2 \sqrt{2}}\right) +\cot _{AB} \left( \frac{\sqrt{c_2} \varpi }{2 \sqrt{2}}\right) \right) }{2 \sqrt{c_1}}, \end{aligned}$$
(57)

using the transformation Eq. (5), the solitary wave solution is obtained for the SDS Eq. (1) such as

$$\begin{aligned} g^{\pm }_{14}(x, y, t)= \left[ \frac{i \sqrt{c_2}}{2 \sqrt{c_1}} \left( \tan _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{2 \sqrt{2}}\right) \hspace{2cm}\right. \right. \nonumber \\ \left. \left. +\cot _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{2 \sqrt{2}}\right) \right) \right] e^ {-\nu \beta (t)-\nu ^2 t+i \left( \kappa _3 t+\kappa _1 x+\kappa _2 y\right) }. \end{aligned}$$
(58)

Now putting Eq. (57) into the Eq. (11) and integrate once we obtained the solitary wave solution for the SDS Eq. (2) such as

$$\begin{aligned} h^{\pm }_{14}(x, y, t)= \left[ -\frac{2 \sqrt{2} \beta \sqrt{c_2} \omega _2}{c_1 \left( \alpha ^2 \omega _2^2-\omega _1^2\right) } \cot _{AB} \left( \frac{\sqrt{c_2} \left( -t \omega _3+x \omega _1+y \omega _2\right) }{\sqrt{2}}\right) \right] e^{-\nu \beta (t)+\nu ^2 (-t)}. \end{aligned}$$
(59)

Where \(\text {tan}_{AB}=-i\frac{A e^{i \varpi }-B e^{-i \varpi }}{A e^{i\varpi }+B e^{-i \varpi }}\) and \(\text {cot}_{AB}=i\frac{A e^{i \varpi }+ B e^{-i \varpi }}{A e^{i \varpi }- B e^{-i \varpi }}\).

5 Physical effects of noise

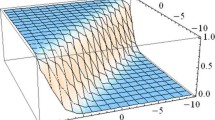
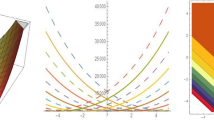
In this section, the effects of noise is describes physically. The different types of solitons are constructed for the SDS model by using the Sardar subequation technique. This technique is efficient and easy to calculate mathematical derivation that will provided us the exact solitary waves and Soliton solutions. The different types of Dark, Bright, combo and periodic wave solitons are successfully obtained. Some solutions are plots in 3-dim, line and their corresponding contour representation by using the different values of parameters. The Figure (1) is drawn for the solution \(g_1^{+}(x,t)\) which gives us the bright soliton. Further we show the different behaviors for the different values of noise strength the subfigure (1a,1d) drawn for \(\nu =0\), subfigures (1b,1f) drawn for \(\nu =0.5\), and subfigure (1c,1f) drawn for \(\nu =0.8\). The Figure (2) is drawn for the solution \(h_1^{+}(x,t)\) which gives us the dark soliton and the different values of noise strength are used to show the randomness. Also, Figures (3,4) are plotted for the solutions \(g_3^{+}(x,t)\) and \(g_{12}^{+}(x,t)\) solutions respectively. Solitons for the Davey–Stewartson equation are possible. Localized wave solutions known as soliton preserve their form and speed as they travel. In optical systems when unpredictability or stochastic effects are present, solitons are referred to as stochastic optical solitons. Plotting the Davey–Stewartson equation solutions allows you to see stochastic optical solitons. These are usually complicated solutions with real and imaginary components that can be illustrated with color maps or plotted in three dimensions, two dimensions and corresponding contours. An effective method for visualizing the amplitude or intensity of soliton solutions is to utilize contour plots. These plots display lines with constant values, which frequently depict the solution’s phase or magnitude. Contour plots can show the spatial and temporal evolution of stochastic photonic solitons. For contour plots, consider plotting the intensity or magnitude of the solutions over space and time to observe the behavior and evolution of the solitons.

Fig. 1
figure 1

The subfigures (1a,1b,1c) shows the 3D, subfigures (1d,1e,1f) shows the 2D, and subfigures (1g,1h,1i) shows the contours for the solution \(g_1^{+}(x,t)\) under the different noise strengths

Full size image
Fig. 2
figure 2

The subfigures (2a,2b,2c) shows the 3D, subfigures (2d,2e,2f) shows the 2D, and subfigures (2g,2h,2i) shows the contours for the solution \(h_1^{+}(x,t)\) under the different noise strengths

Full size image
Fig. 3
figure 3

The subfigures (3a,3b,3c) shows the 3D, subfigures (3d,3e,3f) shows the 2D, and subfigures (3g,3h,3i) shows the contours for the solution \(g_3^{+}(x,t)\) under the different noise strengths

Full size image
Fig. 4
figure 4

The subfigures (4a,4b,4c) shows the 3D, subfigures (4d,4e,4f) shows the 2D, and subfigures (4g,4h,4i) shows the contours for the solution \(g_{12}^{+}(x,t)\) under the different noise strengths

Full size image

6 Results and Discussion

In this section, we discuss result and compare them with the existing literature. The classical Davey–Stewartson (DS) equation is developed by Davey and Stewartson in 1974. Recently, Yan et al. worked on the DS model and explored the high-order lump solutions (Yan et al. 2023), while Behera et al. found the soliton solutions by using the \(G'/G\)-model expansion method (Behera and Virdi 2023). Ding et al. obtained the dark and anti-dark solitons (Ding et al. 2023) and Coppini et al. obtained the N breather anomalous wave solution (Coppini et al. 2023). Guo et al. analyzed the lie point symmetries, similarity reductions, conservation laws (Guo et al. 2023). Liu et al. considered the DS equation under the effect of multiplicative time noise (Liu and Li 2023). But in this study we consider the SDS and obtained the different types of optical soliton solutions via sardar subequation method. This technique is provided us the different types of abundant families of solutions which are including the dark, bright, singular, combined and periodic wave solutions. Also the different physical effects of noise are discussed for these solutions. Using the Mathematica we draw these solutions and their plot for the various values of noise. If we select the noise equal to zero these result are the classical optical soliton solutions for the DS equations. Hence our results are very fruitful for the further study of the dynamical system under the noisy internments.

7 Conclusions

In this work, we examined the stochastic Davey–Stewartson equation under the randem environment. This is two-dimensional integrable equations, are higher dimensional variations of the nonlinear Schrodinger equation. This equation have many applications in the plasma physics, nonlinear optics, hydrodynamics, and other fields. We acquired the exact optical soliton solutions for the SDS model by using the Sardar subequation technique. These solutions can explain a broad variety of exciting and complex physical phenomena due to the application of the SDS eqaution in describing nonlinear pulse propagation in plasma physics and optical fibres. To explain the effects of Brownian motion on the many obtained solutions, we illustrated the dynamic behaviours of the solutions using 3D and 2D curves for different values of noise strength. For the future work, this study is provided us the idea to deals the different physical problems under the effect of noise.