1 Introduction

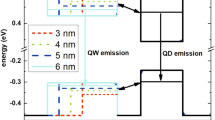
Quantum dots (QDs) are promising candidates as an alternative to quantum wells (QWs) in laser sources for photonic integrated circuits (PICs) (Smowton and Blood 2010). This is due to lower threshold current densities (Dikshit and Pikal 2004), lower temperature sensitivity (Arakawa and Sakaki 1982), and greater tolerance to threading dislocation defects incurred during epitaxy on silicon substrates (Zhang et al. 2018). Additionally, III-V compound semiconductors offer high electron mobility and direct bandgaps at telecom wavelengths (Zhao et al. 2021), with InAs/InGaAs QDs demonstrating high performance in lasers at 1.3 μm (Qiu et al. 2001). These properties make III-V QDs attractive for use in silicon photonics, creating opportunities for mass producing low-cost PICs, provided remaining challenges can be overcome (Norman et al. 2019).

III-V alloys suffer from large differences between electron and hole effective masses, leading to imbalanced carrier occupation in the conduction and valence bands. This leads to asymmetric movement of the quasi-Fermi levels resulting in poor ground state operation in lasers (Smowton et al. 2007). In QWs, this is corrected by inclusion of strained-layers, however, in self-assembled QDs the strain profile is integral to the Stranski–Krastanov growth mode (Smowton et al. 2007) and not available as a design parameter. One solution is modulation doping: incorporating a narrow layer of p-type dopant within the barrier region of the waveguide core. This provides a reservoir of holes, populating the highest valence band states (Kim and Chuang 2006) and correcting the asymmetry.

P-modulation doped InAs/InGaAs QD lasers have been examined theoretically and experimentally, demonstrating temperature insensitive threshold current densities, increased modal and differential gain, and improved ground state operation (Kim and Chuang 2006; Otsubo et al. 2004; Sandall et al. 2006). Conversely, saturation in these enhancements occurs above certain levels of p-doping with the dominant mechanisms behind this still disputed. Saturation has been attributed to increased carrier scattering rates and nonradiative recombination mechanisms (Zhang et al. 2018), with (Kim and Chuang 2006) highlighting the increases in the Auger scattering rate. Increased free carrier absorption was suggested by (Korenev et al. 2017b), and inhibited electron injection reducing the density in the conduction band due to electrostatic effects in potential barriers by (Saldutti et al. 2020). Optimisation of the doping density (Inoue et al. 2010) and position is challenging because of the difficulty in decoupling the effects of p-doping from variations in growth—such as size distributions (Rihani et al. 2009), interdiffusion between dot and barrier (Shchekin et al. 2001), and carrier induced index changes (Norman et al. 2019).

The quantum confined Stark effect (QCSE) responsible for electroabsorption modulator (EAM) operation has been characterised in undoped InAs/InGaAs QDs, demonstrating maximum Stark shifts and data rates of 20 meV and 2.5 Gbps respectively (Chu et al. 2007). A 3 dB bandwidth of 3.3 GHz with a voltage swing of 6 V, was demonstrated by (Lin et al. 2011). (Malins et al. 2007) investigated electroabsorption as well as electrorefraction, observing a Stark shift of 15 meV, with insertion losses (ILs) up to 21 dB, and a 0.001 refractive index change below the bandgap suggesting applicability to electro-optic modulators. Extinction ratios (ERs) of 10 dB for a voltage swing between 0 and 10 V were measured by (Ngo et al. 2009), with ER and IL of 13 dB and 14.8 dB subsequently measured (Ngo et al. 2010) for 10-layer structures. Finally (Le Boulbar et al. 2019) characterised a near constant ER of 4.1dBmm−1 between 25 °C and 125 °C, suggesting temperature insensitivity across a wide range. To our best knowledge, only (Mahoney et al. 2021) has directly compared measurements of the QCSE in p-doped structures. A maximum ER of 12dBmm−1 was measured for a voltage swing between 1 and 10 V in the undoped structure, yet the p-doped structure presented up to three times the FoM: figure of merit (ER/IL) across a temperature range from 21 °C to 100 °C. This was attributed to a reduced IL from carrier blocking in the conduction band. Knowledge of the QCSE in p-doped QDs will be essential for monolithic integration of externally modulated optimised laser sources (Ngo et al. 2009).

In this study, a semi-empirical model is presented to predict absorption, gain, and QCSE characteristics in undoped and p-doped InAs/InGaAs QDs. Fitted absorption spectra provide sample dependent model parameters, while differentiating some of the effects of p-doping from growth dependent variations. Agreement between calculated and measured modal absorption corroborates our methodology. Subsequent forward and reverse bias calculations utilise a simple drift–diffusion model to predict laser and EAM performance for undoped and p-doped structures respectively, through the analysis of the position, movement, and separation of the global quasi-Fermi levels across full device band structures.

2 Materials & methods

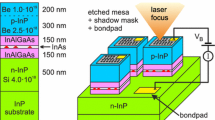
Nominally identical InAs/InGaAs QD structures were considered, except for the inclusion of p-doping, shown in Fig. 1. Active regions consisted of seven dots-in-a-well (DWELL) layers of InAs QDs within In0.16Ga0.84As QWs. GaAs spacers separated each DWELL, with a narrow layer of Beryllium doped GaAs grown within the spacer in the p-doped sample. Core and cladding layers were composed of GaAs/Al0.4Ga0.6As. A dot areal density of 5 × 1010 cm−2 and mean height of 5 nm was determined by atomic force microscopy (AFM) of an uncapped sample, with nominal modulation doping corresponding to 10 holes per dot (hpd). Samples were fabricated into segmented contact devices with modal absorption measured using the segmented contact method (Blood et al. 2003).

Fig. 1
figure 1

Epistructure of measured and modelled QD structures with seven InAs/InGaAs DWELL layers and GaAs spacers in the active region, with cladding composed of GaAs/AlGaAs

Full size image

Full device band structure calculations were conducted via a self-consistent Schrödinger-Poisson-current continuity equation solver from Nextnano (Birner et al. 2007). A single band effective mass approximation (EMA) was used to compute bound states and wavefunctions in the DWELL layers, with resulting band diagrams shown in figs. 2 and 3. Quasi-Fermi levels were calculated by solving the current continuity equations for electrons and holes with a simple drift–diffusion transport model. The band alignment was calculated with average valence band energies with considerations of homogeneous strain through deformation potentials defined by (Chris G. Van de Walle 1986; Van De Walle 1987; C. G. Van de Walle 1989). Material parameters in the Nextnano database were generally from (Vurgaftman et al. 2001) and evaluated at k = 0, the extrema of the Γ-valley with isotropic, parabolic effective masses assumed in the EMA. A finite difference method was employed along a user defined grid and solved iteratively until a self-convergence criterion was met.

Fig. 2
figure 2

Full device band diagram calculated in Nextnano for undoped structure including corrections, with active region shown in inlay. Conduction band Ec, valence band, Ev, and overlapping electron and hole quasi-Fermi levels, Efe and Efh respectively

Full size image
Fig. 3
figure 3

Full device band diagram calculated in Nextnano for p- doped structure including corrections, with active region shown in inlay

Full size image

The current continuity equations, balancing generation and recombination processes (radiative, Shockley–Read–Hall, and Auger), were solved using a simple drift–diffusion transport approach, neglecting the peculiarities of quantum transport as in (Saldutti et al. 2020) and differing from the traditional rate equation models in previous work (Gioannini 2012; Tong et al. 2006). Hence, it was possible to model the entire structure within a fully self-consistent Schrödinger-Poisson-current continuity equation solver, recalculating the band structure and quasi-Fermi levels for each step under reverse or forward bias. This method allowed for the assessment of the position, movement, and separation of the global quasi-Fermi levels, describing population and depletion of carriers in calculated states, for temperatures between 200 and 300 K where thermal carrier distributions have been experimentally observed in InAs QDs (Hutchings et al. 2014). Though, as subsequently described, further approximations were necessary to maintain realistic outputs.

A one-dimensional geometry was employed, modelling the band structure as a function of the growth direction (along the z-axis), hence only the layer thickness and average dot height were required as structural inputs. This removed quadratic or even cubic dependencies associated with two- and three-dimensional computation times. QD regions were initially predicted with QW-like properties, with only one dimension of confinement available. Further approximations were input via the QD layer material parameters to correct the effective density of states, effective mass, and band gap energy to reflect experimental measurements. The effective density of states, used to calculate band edge densities and hence critical to the magnitudes of the generation/recombination processes involved in the current continuity equations, was initially predicted as a QW, following Eq. 1.

$$N_{eff} \left( {z,T} \right) = \frac{{m_{DOS}^{*} \left( z \right)}}{{\pi \hbar^{2} }}k_{b} T$$
(1)

The temperature dependent effective density of states, \({N}_{eff}\), was given as a function of growth direction \(z\) and temperature, \(T\). \({m}_{DOS}^{*}\) was the density of states effective mass, calculated using Eq. 2, with \(\hslash\) and \({k}_{b}\) the reduced Planck constant and Boltzmann constant respectively.

$$m_{DOS}^{*} \left( x \right) = \left( {m_{x}^{*} \left( x \right) \cdot m_{y}^{*} \left( x \right) \cdot m_{z}^{*} \left( x \right)} \right)^{1/3}$$
(2)

\({m}_{DOS}^{*}\) described the average of the effective mass tensor relating the effective mass \({m}^{*}\) along each axis, in each band. In the EMA, bands are considered parabolic and isotropic near the band edge, with \({m}_{x}^{*}={m}_{y}^{*}={m}_{z}^{*}\). Although only the z-dimension was evaluated by the Schrödinger-Poisson equations, the current continuity equations required an average of all dimensions via \({m}_{DOS}^{*}\). The in-plane effective masses \({m}_{x}^{*}, {m}_{y}^{*}\) were reduced to alter the effective density of states while not impacting calculations of band alignment and quantization. Therefore, an effective mass tensor ellipsoid was employed, shown in Fig. 4, equating the effective density of states in the QD regions to twice that of the dot density observed during epitaxy, accounting for spin degeneracy. This reduction corrected the recombination/generation magnitudes in the QD regions and provided realistic calculation of the movement of the global quasi-Fermi levels across the full structure.

Fig. 4
figure 4

Diagram of (a) an isotropic effective mass tensor and b an effective mass tensor ellipsoid

Full size image

To replicate the three experimentally observed QD absorption peaks and the corresponding nearly equally spaced transition energies, a parabolic potential was created by varying the composition of In(x)Ga(1−x)As between x = 0.16 at the well and x = 1.0 at the center of the QD region. This was suggested by Blood as a method of representing the confining potential in the plane of self-assembled QDs in 3D calculations and in one dimension is a suitable approximation to predict near equally spaced transition energies, corresponding to the experimentally observed absorption peak separation (Blood 2015). A further correction, this time to the effective mass in the growth direction \({m}_{z}^{*}\) was used to match the energy separation between the absorption peaks.

Nextnano calculated homogeneous strain and was unable to capture the intricacies of a non-uniform strain distribution in a region with only one dimensional confinement (Nabetani et al. 2005), therefore an additional correction was made to the band gap energy to match the experimentally observed ground state transition energy ≈ 0.98 eV, similarly to (Kim and Chuang 2006). Three electron and twelve hole states were calculated in each dot layer.

The resulting one-dimensional confining potentials were shallow, and while predicting the transition energies well, the wavefunction overlap integral was not suitable for prediction of the QCSE. Capturing a realistic approximation for the overlap with only a single dimension available for confinement required a separate analysis, to consider the wavefunctions in a deeper potential, matching the barrier energy in (Kim and Chuang 2006). The confinement potential was inversely related to the size (Bohr radius) of the dot in (Chukwuocha et al. 2012) hence a deeper potential was required to approximate the increased confinement associated with a three dimensional quantum dot. This yielded overlap integrals of 95% and 94% under zero bias, decreasing at the same rate to 90% and 89% under a 5 V reverse bias, for undoped and p-doped structures respectively. Under forward bias, the bands flattened and overlap was ≈ 100% in both structures. The high overlap was attributed to the narrow confining potential in the z-direction, which is consistent with measurements of narrow quantum wells in (Mendez et al. 1982).

Undoped and p-doped structures were simulated under reverse, zero, and forward bias to predict the QCSE, modal absorption, and peak gain respectively, with the central dot layer shown in figs. 5 and 6.

Fig. 5
figure 5

Calculated confined electron (E1) and hole (H1) ground state energy levels and wavefunctions for the undoped structure in the conduction and valence band under (a) reverse bias, (b) zero bias, and (c) forward bias conditions

Full size image
Fig. 6
figure 6

Calculated confined ground state energy levels and wavefunctions for the p-doped structure in the conduction and valence band under (a) reverse bias, b zero bias, and c forward bias conditions

Full size image

Optical confinement factor weightings at each layer of dots were determined using an eigenmode expansion solver from Lumerical, with the mode profile and weightings as percentages shown in Fig. 7. This permitted calculation of modal absorption and gain, which was directly comparable to experimental measurements. A layer thickness of 3MLs was used for the QD layers, equal to the quantity of InAs deposited during epitaxy. Note, this differed from the 5 nm thickness used in the full device band structure calculations, which referred to the mean height of the QDs observed during AFM. InAs dot layers, shown in the table of Fig. 7, were labelled as deposited, 1 through to 7.

Fig. 7
figure 7

Optical confinement weighting at each layer of dots, where layer 1 is adjacent to the n-side, calculated in Lumerical’s MODE waveguide simulator suite device width scaled here to clearly distinguish active region layer structure

Full size image

Measured absorption spectra were fitted with Gaussian functions representing the inhomogeneously broadened ground and first excited state transitions, as shown in Figs. 8 and 9. Internal optical losses of < 1 cm−1 were extracted for each sample and combined homogeneous and inhomogeneous broadening was approximated from the extracted standard deviations. InAs QDs have been shown to exhibit two distinct size distributions under higher growth temperatures, becoming multimodal at lower temperatures (Kissel et al. 2000). Here a bimodal dot size distribution was verified from modal absorption spectra and observed to provide the best fit with absorption data, similarly to (O’Driscoll et al. 2010). Measurements using AFM, photoluminescence, and transmission electron microscopy methods have found similar conclusions for InAs QDs (Maximov et al. 2000). Bimodality was assumed based on higher growth temperatures and modal absorption spectra to determine a ratio of the large dot (LD) to small dot (SD) densities from the area under the fitted Gaussians (O’Driscoll et al. 2009), which were used in subsequent calculations of absorption and gain.

Fig. 8
figure 8

Fitted experimental data for modal absorption coefficient against photon energy for undoped structure. LD ground and excited state, and SD ground state fitting functions represented by solid and dashed lines respectively

Full size image
Fig. 9
figure 9

Fitted experimental data for modal absorption coefficient against photon energy for p-modulation doped structure. LD ground and excited state, and SD ground state fitting functions represented by solid and dashed lines respectively

Full size image

Additionally, the separation between LD and SD ground state energy was identified and used to approximate the size difference in terms of the height of the dot. This was used to calculate the difference in energy shift experienced by the SD under forward and reverse bias following the same procedure in Nextnano described previously. The bimodal ratios calculated from fitted data were ≈41:59 and ≈63:37, between large to small dot distributions for undoped and p-doped structures respectively. This difference may have resulted from variation in growth temperatures between undoped and p-doped wafers during epitaxy (Kissel et al. 2000). The energy separation between ground state absorption peaks for LD and SD was fitted as 30 meV and 32 meV for undoped and p-doped structures respectively.

Preceding data from Nextnano, Lumerical, combined with parameters extracted from fitted absorption data were used with an in-house program for calculating absorption and gain, similarly to (Dikshit and Pikal 2004), using Eq. 3. Reverse and forward bias conditions employed in the band structure calculations were used to predict the QCSE and gain spectra respectively.

$$\alpha \left( {\hbar \omega } \right) = \mathop \sum \limits_{l} \mathop \sum \limits_{D} \mathop \sum \limits_{nm} \frac{{\Gamma_{l} \pi e^{2} \hbar M_{b}^{2} \left| {I_{ov} } \right|^{2} N_{L, S} s_{i} }}{{cm_{0} \varepsilon_{0} n_{r} L_{z} E_{nm} }}S\left( {E_{nm} } \right)G\left( {E_{nm} } \right)\left( {f_{v} - f_{c} } \right)$$
(3)

Modal absorption as a function of photon energy was first calculated by summing for all transitions in the QD region, with \(n\) and \(m\) the energy levels in the conduction and valence band respectively. These were summed for \(D\) dot size contributions LD and SD, and at each layer of the structure, \(l\). Here, elementary charge was \(e\), speed of light in a vacuum \(c\), and electron rest mass \({m}_{0}\). The areal dot densities for LDs and SDs were \({N}_{L,S}\). \({s}_{i}\) was the degeneracy of the transition (2 and 4 for ground and first excited state respectively). The real refractive index was \({n}_{r}\), dot height \({L}_{z}\), and \({M}_{b}^{2}\) was the bulk matrix element relating to the Kane energy parameter (\({M}_{b}^{2}=\frac{{m}_{0}}{6}{E}_{p}\)). \({\Gamma }_{l}\) was the optical confinement layer weighting. \({f}_{v}-{f}_{c}\) was the difference in valence and conduction band electron occupation probabilities, calculated using Fermi–Dirac statistics with corresponding quasi-Fermi level energies, resulting in modal gain once population inversion was achieved. The wavefunction overlap integral was \({\left|{I}_{ov}\right|}^{2}\). Homogeneous \(S\left({E}_{nm}\right)\), and inhomogeneous \(G({E}_{nm})\), broadening distributions were modelled as hyperbolic secant as in (Blood 2015; Dikshit and Pikal 2004), and Gaussian distributions respectively as functions of the transition energy \({E}_{nm}\), as shown in Eqs. 5 and 6.

$$S\left( {E_{cv} } \right) = {\text{sech}} \left( {\frac{{E_{cv} \tau }}{\hbar }} \right)$$
(4)

Here, \(\tau\) was the time between dephasing events. Inhomogeneous broadening, was modelled as a Gaussian function, where \(\sigma\) is the standard deviation in transition energies due to dot size variation during growth. \(\sigma\) was assumed constant at ≈ 22 meV in the fitting procedure, from photoluminescence spectra after growth, resulting in a calculated decrease of ≈ 35 fs in \(\tau\) in p-doped structures.

$$G\left( {E_{cv} } \right) = \frac{1}{{\sqrt {2\pi } \sigma }}e^{{ - \frac{{\left( {E_{cv} - \hbar \omega } \right)^{2} }}{{2\sigma^{2} }}}}$$
(5)

The ER and IL were evaluated from 0 to 5 V reverse biased structures in terms of dBmm−1 in Eqs. 6 and 7, with the FoM taken as the ratio between ER and IL.

$$ER = - \frac{{4.34\alpha_{ON} }}{10} + \frac{{4.34\alpha_{OFF} }}{10}$$
(6)
$$IL = - \frac{{4.34\alpha_{OFF} }}{10}$$
(7)

3 Results

The calculated modal absorption under zero bias was compared to experimental data to verify the modelling procedure prior to simulating structures under applied reverse and forward bias to predict the QCSE and gain. The inhomogeneous broadening and dot density was assumed to be constant in these calculations. Appropriate replication of the band edge absorption, though with some departure at the first excited state was observed in figs. 8 and 9.

Additionally, modal absorption was calculated a second time, this time with the degree of inversion fixed to fv –fc = 1. The difference between the two calculations indicated the magnitude of the effects of state-filling and resulting carrier blocking of the absorption process, which has been thought to be important for p-doped structures (Mahoney et al. 2021), and was evident in the calculated band structures (shown in Fig. 2 and 3). A negligible change was observed for the undoped structure, signifying that electrons and holes in the conduction and valence bands respectively were almost completely depleted under zero bias. In the p-doped structure there was a difference with an increase in the maximum modal absorption by ≈ 11 cm−1 when fv –fc = 1.

However, this difference was only a fraction of the total difference between p-doped and undoped absorption spectra and we therefore attributed the larger part of the effect to greater homogeneous broadening caused by increased carrier scattering rates. A 41% increase in the carrier scattering rate, calculated from the values of τ, used in the homogeneous broadening term was necessary to describe the remaining difference between p and undoped structures (Figs. 10 and 11).

Fig. 10
figure 10

Modelled and experimentally measured modal absorption coefficient against photon energy for undoped structure. Model run a second time with fv−fc = 1 to evaluate the role of carrier blocking overlaps original spectrum

Full size image
Fig. 11
figure 11

Modelled and experimentally measured modal absorption coefficient against photon energy for p-doped structure. Model run a second time with fv−fc = 1 to evaluate the role of carrier blocking

Full size image

When reverse bias was applied, we calculated further depletion of the QD layers in the p-doped structure. This led to an increase in the effective absorption with applied reverse bias, an uncommon but beneficial phenomenon for modulating devices. The band diagrams, shown in figs. 12 and 13, demonstrated increased deformation in the active region of the p-doped structure, signifying the non-uniformity of carrier depletion across the QD layers.

Fig. 12
figure 12

Full device band diagram calculated for undoped structure under reverse bias, with active region shown in inlay

Full size image
Fig. 13
figure 13

Full device band diagram calculated for p-doped structure under reverse bias, with active region shown in inlay

Full size image

Qualitatively, under a reverse bias of 5 V, the relevant quasi-Fermi levels in the undoped structure were always distant from the dot potential signifying minimum carrier-blocking. Whereas, the hole quasi-Fermi level in the p-doped structure remained very close to two dot layers under a 5 V reverse bias. This signifies appreciable population of holes in valence states, with continued blocking of absorption compared to the undoped structure.

The calculated absorption spectra for undoped and p-doped structures are shown in Fig. 14 under a zero and 5 V reverse bias respectively. Stark shifts of 7.5 nm and 5.4 nm are observed in undoped and p-doped structures respectively, suggesting enhanced ER in the undoped structure. The reduced broadening and higher magnitude in absorption coefficient in the undoped structure shown in Fig. 14 gives a sharper absorption edge and is indicative of potentially higher peak ERs. The p-doped data derived from an absorption spectrum that is significantly broader than the undoped spectrum and increases in magnitude under bias, resulting from growing depletion in the conduction band, reducing carrier blocking, may have benefits for modulating devices, with a low IL and improved temperature stability as suggested by (Mahoney et al. 2021).

Fig. 14
figure 14

Calculated absorption spectra shown as solid and dashed lines under 0 V and 5 V reverse bias respectively for (a) undoped, and b p-doped structures

Full size image

To assess the relative potential of the undoped and p-doped material for electro-absorption modulation the ER and the IL, calculated in Eqs. 6 and 7, are plotted in figs. 15 and 16. The FoM defined in the literature as the ratio between ER and IL, was used to compare potential modulator performance (Nojima and Wakita 1988; Chin 1992) (equivalent to \(\frac{\Delta \alpha }{{\alpha }_{0}}\)) and is plotted in Fig. 17.

Fig. 15
figure 15

Predicted ER for undoped and p-doped structures respectively

Full size image
Fig. 16
figure 16

Predicted IL for undoped and p-doped structures respectively

Full size image
Fig. 17
figure 17

Predicted FoM for undoped and p-doped structures

Full size image

Considering the ER, the undoped structure exhibited the highest peak ER of over 8dBmm−1, though an increase in the ER for the p-doped structure was predicted at wavelengths higher than 1300 nm. The ER predicted in the p-doped structure is at its maximum at 1300 nm with ER of 6 dBmm−1. Nevertheless, due to the additional homogeneous broadening associated with the p-doped structure, the FoM is limited by the IL between wavelengths 1300-1311 nm. This finding is contrary to (Mahoney et al. 2021) who found reduced IL beneficial to the FoM, though this may indicate the importance of a better understanding of the broadening mechanisms and careful selection of the doping concentration to yield full benefits.

Although there is a reduction in the peak of the IL, this is not necessarily an improvement to the modulator performance, as the increased broadening caused protrusion of the absorption edge at higher wavelengths where the QCSE is most pronounced.

Figure 17 shows the amplitude and breadth of the FoM in the p-doped structure are enhanced, although a lower peak extinction ratio was observed in the p-doped structure as with (Mahoney et al. 2021), with a greater FoM achieved for wavelengths > 1310 nm. For operation at the peak FoM wavelength of 1336 nm a very low modulation of an incident beam would be achieved for the current structure and for practical use a greater interaction length or additional dot layers would be required for this epistructure. However, as shown in figs. 15 and 16, the p-doped structure has ERs > 4dBmm−1 with ILs < 4dBmm−1 at 1310 nm. Though these structures have not been optimised for electroabsorption, this result suggests potential benefits which may become significant at appropriate levels and positioning of the p-modulation doping layer. The breadth in the p-doped FoM in Fig. 17 is also suggestive of enhanced temperature stability. Furthermore, for enhanced operation at 1310 nm, smaller dot sizes may yield better results for this level of p-doping.

The laser performance of the structures was predicted under forward bias to calculate modal gain and peak modal gain with the resulting band diagrams shown in figs. 18 and 19, and calculated modal gain spectra in figs. 20 and 21. A linearly increasing carrier scattering rate was included to account for the predicted increase with carrier injection, following (Zhang et al. 2018). Initial values were derived from the fitted absorption spectra increasing to a value around three times that in the undoped structure for the given p-dopant concentration.

Fig. 18
figure 18

Full device band diagram calculated for undoped structure under forward bias, with active region shown in inlay

Full size image
Fig. 19
figure 19

Full device band diagram calculated for undoped structure under forward bias, with active region shown in inlay

Full size image
Fig. 20
figure 20

Modal gain spectra for undoped structure. Modal absorption shown by dashed line, and gain spectra shown with increasing current density

Full size image
Fig. 21
figure 21

Modal gain spectra for p-doped structure. Modal absorption shown by dashed line, and gain spectra shown with increasing current density

Full size image

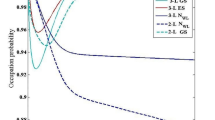
The detrimental effect of the increased carrier scattering rate is apparent in figs. 20 and 21 from the broadened spectra of the p-doped structure. Though, we also attributed this in part to a reduced contribution of the excited state, enhancing ground state operation, the p-doped structure also has an increased contribution from the LD distribution which produces lower confinement energy and occupies longer wavelengths. We note that the operational wavelength of these structures is not optimal for simple integration with the EAM derived above with reverse bias. To combine the functionality on a single chip would require a further processing step perhaps via ion-implantation. The peak gain can be described by \({G}_{pk}={g}_{max}({f}_{c}-{f}_{v})\), where \({g}_{max}\) is the maximum potential modal gain achieved in Eq. 3 neglecting the degree of inversion, \(({f}_{c}-{f}_{v})\). Therefore, the occupation probabilities, calculated from the global quasi-Fermi levels, indicate the impact of p-modulation doping on the population of the valence and conduction bands. The calculated occupation probabilities in the conduction band \({f}_{c}\) and valence band \({f}_{v}\) using Fermi–Dirac statistics are shown in figs. 22 and 23, and the degree of inversion in Fig. 24.

Fig. 22
figure 22

Conduction band occupation for the first bound state in each dot layer for undoped and p-doped structures. Solid and translucent lines represent the mean, and the minimum to maximum between the seven layers respectively

Full size image
Fig. 23
figure 23

Valence band occupation for the first bound state in each dot layer for undoped and p-doped structures. Solid and translucent lines represent the mean, and the minimum to maximum between the seven layers respectively

Full size image
Fig. 24
figure 24

Degree of inversion for the first bound state in each dot layer for undoped and p-doped structures. Solid and translucent lines represent the mean, and the minimum to maximum between the seven layers respectively

Full size image

Figure 22 demonstrates reduced electron injection into the conduction band ground state across all layers of the p-doped structure, though there is less variance between the minimum and maximum contributions across those layers. At a calculated current density of 680A/cm−2 the mean occupation probability in the conduction band of the p-doped structure is equal to the undoped structure and surpasses it at higher current densities, suggesting only a minimal reduction in potential gain due to inhibited electron injection. Thus at this doping level, we do not attribute saturation in the ground state gain to inhibited electron injection, though the impact of these electrostatic effects may drastically increase with surplus doping, which would significantly increase the potential barriers between dot layers compared to that shown in Fig. 19, as suggested by (Saldutti et al. 2020). At 10 hpd we do not attribute inhibited electron injection to saturation in the ground state gain.

Figure 23 exhibits the effect of state filling for holes in the ground state of the valence band as a result of p-doping. The significance of this reduction can clearly be linked to potential decreases in the threshold current density of p-doped laser diodes. Figure 24 further supports these claims, with a significantly reduced transparency current density shown by the degree of inversion in the p-doped structure, with a reduced variance across all dot layers. This is contrary to several examples (Deng et al. 2022; Korenev et al. 2017a; Dong et al. 2020) of experimental measurements observing increased threshold current densities with p-doping. This discrepancy is attributed to an optimal range of p-doping concentration which is difficult to measure and to appropriately incorporate in real devices. This is corroborated by (Zhang et al. 2018) with calculations of threshold current density versus increasing p-doping concentration and experimentally verified reductions in transparency at appropriate p-doping levels. P-type modulation doping has been found to improve gain but also increase internal optical loss (Shchekin and Deppe 2002) and non-radiative recombination (Jang et al. 2008) with reduced threshold current typically observed under high gain operation.

Additionally, the gradient by which the degree of inversion increases past transparency and threshold, is suggestive of greater differential gain associated with p-doped QD laser diodes, as shown by (Kim and Chuang 2006). The increase in differential gain paired with improved linewidth enhancement factor is desirable for high-speed modulated laser diodes. Beneficial effects of the state-filling effect are evident in Fig. 24 through the degree of inversion, and translate directly to the peak modal gain shown in Fig. 25. Increased gain amplitude and differential gain at lower current densities are advantageous although gain saturation is more evident at high current densities for the p-doped case, associated with increased carrier scattering causing more significant broadening of the gain spectrum. These characteristics are beneficial where the threshold gain requirement is relatively low as for long cavity laser diodes. Combining such lasers with the predicted EAMs would provide an efficient externally modulated laser diode, though additional analysis to optimally tune the doping is required in addition to considerations of ion-implantation induced intermixing to match peak operational wavelengths.

Fig. 25
figure 25

Peak modal gain versus current density for undoped and p-doped structures

Full size image

4 Summary

We report a semi-empirical model combining full device band structure calculations with a Maxwell equation solver to calculate modal absorption and gain in p-modulation doped InAs/InGaAs QDs. Under reverse and forward bias, the QCSE and peak modal gain was evaluated. Reduced amplitude, broadened absorption spectra were shown to provide increased FoM in p-doped structures, indicating the potential of this material for use in modulators. We found this to be predominantly caused by increased homogeneous broadening associated with greater carrier scattering rates, though there was partial reduction from state filling induced carrier-blocking in p-doped structures, which provided particular benefits through increasing the absorption magnitude under reverse bias in p-doped structures. A 72% increase in the maximum modulator FoM was observed from a bias change of 0–5 V with peak operating wavelengths of 1310 nm and 1336 nm for undoped and p-doped structures respectively. Though additional dot layers or increased cavity lengths may be required for operation at this wavelength where the ER is lower than the undoped structure, an ER > 4 dB is still present for the p-doped structure at 1311 nm. Structures incorporating p-doping outperformed undoped structures at 1311 nm, with an increasing benefit at longer wavelengths. Further depletion of holes in p-doped structures with increasing reverse bias led to an increasing absorption amplitude, enhancing the ER. Under forward bias, state-filling resulted in reduced predicted threshold current density and increased differential and modal gain at ground state operation. The increased carrier scattering rate in p-doped structures created a severe gain saturation effect at higher current density. P-doping was shown to offer benefit when carefully used with selection of operating wavelength and operating conditions to mitigate the effects of increased carrier scattering for use in modulators and lasers in single material system. Reduced threshold current density in p-doped structures under forward bias contrasts with many experimental findings, which we attribute to idealisation in our model dopant concentration, highlighting the importance of optimal incorporation and accurate quantification of p-doping concentration during epitaxy.