1 Introduction

Infected water had been found to contain several harmful bacteria, including giardia, vibrio Cholera (V. Cholera), Salmonella, E.Coli (Escherichia Coli), Shigella Flxaneri, Legionella and others (Craun et al. 2006; Liu and Lay 2007). When contaminants enter our bodies throughout food and drink, they have an impact on human health and can lead to a variety of illnesses, including hepatitis A, abdominal pain, vomiting and diarrheal, which can sometimes result in fatal dehydration (Clark et al. 2003). According to the world health organization (WHO), elderly people and young children under the age of five are regarded to be the groups most susceptible to it (World Health Organization. Rolling revisions of the guidelines for drinking-water quality: aspects of protection and control and of microbiological quality: report on a WHO meeting, Medmenham, United Kingdom 1998). Due to the recent rise in death rates caused due to water pollution, researchers and other experts from all over the world are concerned. Various methods and procedures for identifying and reducing it (Centers for Disease Control and Prevention (CDC. "Surveillance for waterborne disease outbreaks associated with drinking water and other nonrecreational water-United States 2013) especially in densely populated areas, Wherein, The most vital and essential component of life on earth is water. Among these methods and techniques there is the ELISA (enzyme-linked immunosobentassay method) and PCR (Polymerase chain reaction) (Environmental Protection and Agency. "Method 1604: total coliforms and Escherichia coli in water by membrane filtration using a simultaneous detection technique (MI medium).", 1604; Jasson et al. 2010 Sep; Hasan et al. 2005). However, these methods take a long time to obtain reports and complete the tests. As a result, there was a need for other methods that are more advanced, more efficient and more sensitive to detect waterborne bacteria in a short and inexpensive time. Therefore, it was indispensable to develop and design sensitive sensors free of labels for early detection of waterborne bacteria so photonic technology is considered a suitable for realization as a biosensor among the various technologies. Recently, sensor technology based on PhCs biosensor is becoming versatile and show an excellent accuracy rather than its electronic counterparts. Therefore, many researchers used optical biosensor in many applications such as blood sensor (El-Khozondar et al. 2019), motoring environment, medical diagnostics (Aly et al. 2020a), urea concentration sensor (Wan et al. 2021a; Yadav et al. 2023a, 2023b; Kumar et al. 2023), blood glucose sensor and detection of harmful pathogens (Yoo and Lee 2016). This is because they used refractive index as a parameter to develop optical biosensors devices using PhCs. Wherein, optical biosensors are characterized by rapid response time and high sensitive to the small change in the refractive index of the sample (analyte) (Aly et al. 2009; Almawgani et al. 2022). Sometimes, the periodicity of PhCs is broken by introducing a layer in the structure called a defect layer. As a result a defect mode is appeared through the band gap. In the three last decades, propagation of electromagnetic wave and PhCs have been widely discussed in term of designs and manufactures. PhCs are consisting of dielectric material arranged periodically with a difference in refractive index (Wang and Liu 2007; Shadrivov et al. 2005). Wherein, they are classified to three categories, one, two and three dimension structure. The simplest one of these structures is one dimensional (1D) for easy manufacturing and low cost (Aly and Mohamed 2015; Yao et al. 2014; Malek et al. 2022, 2021; Aly et al. 1533; Aly and Sabra 2016; Mohamed et al. 2020, 2021). The most important features of PCs are the presence of the band gap (PBG). This gab is a frequency region which it is not allowed for light to propagate through it. PBG is as high as sensitive for the external parameters including salinity, pressure, temperature, magnetic field and electric field (Aly et al. 2020b, 2017; Abd El-Aziz et al. 2019; Wan et al. 2021b; Arafa and Aly., Zaky, A., Zaky. 2019; Qutb et al. 2021; Sabra et al. 2023; Malek et al. 2023; Sabra 2021; Elsayed et al. 2021; Aly et al. 2020, 2023). Refractive index values of different types of waterborne bacteria are significantly differ from the values of pure water. This property can enable attractive candidates for sensing applications. Wherein, the refractive indices of Salmonella, Shigella Flxaneri, E.Coli, V. Cholera and pure water are 1.430, 1.422, 1388,1.365, and 1.333, respectively (Kumar et al. 2022; Liu et al. 2014).

In 2023, Numayer A Zaman et al. (Zaman et al. 2023) proposed a1D-PhCs for detection of waterborne bacteria with sensitivity \(2486.57{\kern 1pt} nm/RIU\). In 2021, Panda et al. (Panda and Pukhrambam 2021) designed a defective 1D PhCs for investigation of real time detection of waterborne with optimum sensitivity of \(387.5nm/RIU\). In 2022,(Karki et al. 2022) Bhishma Kark et al. proposed a biosensor for detection of hemoglobin concentration based on surface Plasmon resonance with sensitivity \(161{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \deg /RIU\). In 2023, Singh, T.I., Singh, P et al. (Singh et al. 2023) presented the detection of chikungunya virus utilizing the surface plasmon resonance with high sensitivity of \(287.3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \deg /RIU\). In 2023, Karki, B., Salah, N.H., Srivastava, G. et al. (Karki et al. 2023a, 2023b) proposed a hetrostructure sensor of surface plasmon resonance for detecting dengue viruses with sensitivity of \(203.22{\kern 1pt} {\kern 1pt} \deg /RIU\). In 2020, (Goyal and Pal 2020) a Bloch surface waves (BSW) based sensor is proposed to estimate the hemoglobin concentration in human blood with average sensitivity of 0.0133 /(g/L). In 2020, Goyal et al. (Goyal et al. 2023, 2022; Goyal and Saini 2020) presented Bloch surface wave (BSW)-based sensor using transition metal dichalcogenides (TMDC) is proposed for refractive index sensing analysis.

In the present work, we are investigating the reflectance spectrum of a 1D-PhC biosensor design by using defect layers from different types of bacteria samples such as (vibrio Cholera (V. Cholera), Salmonella, E.C (Escherichia Coli) and Shigella Flxaneri). The suggested design is consisting of two layers with high and low refractive indices. In the proposed design, the first layer is Molybdenum disulphide \(\left( {MoS_{2} } \right)\) while the second layer is Titanium nitride \(\left( {TiN} \right)\). The novelty in this design can be described by existing these two layers together to consist such biosensor structure. The reflectance spectrum of the proposed structure is investigated based on transfer matrix method (TMM). Various parameters such as the effect of the incident angle and the effect of the central wavelength are discussed for enhancing the performance of the proposed biosensor design.

2 Theoretical analysis

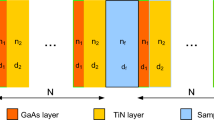
The suggested structure of the optical biosensing being discussed consists of two alternate dielectric materials \((MoS_{2} /TiN)^{N} D(MoS_{2} /TiN)^{N} /glass\) as shown in Fig. 1. The first layer is \(MoS_{2}\) (Molybdenum disulphide) with refractive index \(n_{1}\) and thickness \(d_{1}\) and the second layer is \(TiN\) (Titanium nitride) with index of refraction \(n_{2}\) and thickness \(d_{2}\). The analyte sample represented by \(D\) with \(n_{c}\) and thickness \(d_{c}\). This structure is repeated for \(N\) periods with normal of the incident angle \(\theta = 0^{o}\). In the proposed design, we will investigate the reflectance spectrum of 1D-PhCs by using defect layers from different types of bacteria samples such as (vibrio Cholera (V. Cholera), Salmonella, E.C (Escherichia Coli) and Shigella Flxaneri). The optical properties of our design can be simulated with various techniques like as finite element method (FEM) and transfer matrix method (TMM). For 1D-PhCs the transfer matrix method is used to analysis and simulates our structure at boundary condition. wherein, the tangential component of the electric field at one side of the electric boundary is equal to the tangential component at the other side and the normal component of the electric flux density at one side of the dielectric boundary is equal to the normal component to the other side (electric flux density is continuous across the boundary). The incident light interaction with our proposed structure can be described by the following total matrix (Thompson 1990).

$$U = \left( {\begin{array}{*{20}c} {U_{11} } & {U_{12} } \\ {U_{21} } & {U_{22} } \\ \end{array} } \right) = \left( {u_{1} u_{2} } \right)^{N} \left( {u_{c} } \right)\left( {u_{1} u_{2} } \right)^{N}$$
(1)
Fig.1
figure 1

A schematic diagram of the proposed 1-D PhC design for detection the waterborne bacteria (V. Cholera, Salmonella, E.Coli and Shigella Flxaneri)

Full size image

Here \(U_{11}\), \(U_{12}\), \(U_{21}\) and \(U_{22}\) are the elements of the total matrix, \(N\) is the number of periodicity, The characteristic transfer matrices of our design are represent by \(u_{1}\), \(u_{2}\) and \(u_{c}\) which are given by:

$$u_{1} = \left( {\begin{array}{*{20}c} {\cos \beta_{1} } & {\frac{{ - i\sin \beta_{1} }}{{p_{1} }}} \\ { - ip_{1} \sin \beta_{1} } & {\cos \beta_{1} } \\ \end{array} } \right)$$
(2)
$$u_{2} = \left( {\begin{array}{*{20}c} {\cos \beta_{2} } & {\frac{{ - i\sin \beta_{2} }}{{p_{2} }}} \\ { - ip_{2} \sin \beta_{2} } & {\cos \beta_{2} } \\ \end{array} } \right)$$
(3)
$$u_{c} = \left( {\begin{array}{*{20}c} {\cos \beta_{c} } & {\frac{{ - i\sin \beta_{c} }}{{p_{c} }}} \\ { - ip_{c} \sin \beta_{c} } & {\cos \beta_{c} } \\ \end{array} } \right)$$
(4)

The phase difference of each layer is given by:

$$\beta_{1} = \frac{{2\pi n_{1} d_{1} \cos \theta_{1} }}{\lambda },\;\beta_{2} = \frac{{2\pi n_{2} d_{2} \cos \theta_{2} }}{\lambda }\;{\text{and}}\;\beta_{c} = \frac{{2\pi n_{c} d_{c} \cos \theta_{c} }}{\lambda }$$
(5)

The value of \(p\) according to transverse electric field (TE) is given as follows.

$$p_{1} = n_{1} \cos \theta_{1} ,\;p_{2} = n_{2} \cos \theta_{2} \;{\text{and}}\;p_{c} = n_{c} \cos \theta_{c}$$
(6)

Then, the incident angles \(\theta_{1}\), \(\theta_{2}\) and \(\theta_{c}\) on the \(MoS_{2}\), \(TiN\), and analyte layers are satisfied to the Snell's law as follows.

$$n_{o} \sin \theta_{o} = n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2} = n_{c} \sin \theta_{c}$$
(7)

Then \(n_{o}\), \(n_{1}\), \(n_{2}\) and \(n_{c}\) are the refractive indices of air, \(MoS_{2}\) material, \(TiN\) and analyte sample, respectively.

For N period of our periodic design, the matrix \(\left( {u_{1} u_{2} } \right)^{N}\) is calculated based on the second type of Chebyshev polynomial (White and Fan 2008).

The reflection coefficient is given by the following equation:

$$r = \frac{{(U_{11} + U_{12} p_{s} )p_{o} - (U_{21} + U_{22} p_{s} )}}{{\left( {U_{11} + U_{12} p_{s} } \right)p_{o} + \left( {U_{21} + U_{22} p_{s} } \right)}}$$
(8)

Here \(p_{o} = n_{o} \sin \theta_{o}\) for air and \(p_{s} = n_{s} \sin \theta_{s}\) for substrate.

The reflectivity of the proposed biosensing is given by:

$$R = \left| {r^{2} } \right|$$
(9)

The performance of the optical detector can be investigated by several parameters. These parameters determine the efficiency and accuracy of the optical biosensor. Sensitivity is considering the main parameter that indicates the efficiency of the proposed design. In which, it is defined as the change in the wavelength to the change in the refractive index. Also, we calculated the detection limit (DL) which characterized the smallest change in the refractive index of the sample. In addition to that, we calculated the quality factor (QF) which shows the performance of the proposed biosensor and the figure of merit (FOM) based on the full width at a half maximum (FWHM) that define as the difference between the left and right edges of the defect mode at half maximum. All of these parameters are determined mathematically as follow (Al-Dossari, et al. 2022):

$$S = {\raise0.7ex\hbox{${\Delta \lambda_{R} }$} \!\mathord{\left/ {\vphantom {{\Delta \lambda_{R} } {\Delta n}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\Delta n}$}} = \frac{{\lambda_{bacteria} - \lambda_{water} }}{{n_{bacteria} - n_{water} }}$$
(10)

where in, \(\Delta \lambda = \lambda_{bacteria} - \lambda_{o}\), \(\Delta n = n_{bacteria} - n_{o}\), \(\lambda_{o}\) and \(n_{o}\) are the wavelength and refractive index of pure water, \(\lambda_{R}\) is the resonant wavelength.

$$QF = {\raise0.7ex\hbox{${\lambda_{R} }$} \!\mathord{\left/ {\vphantom {{\lambda_{R} } {_{FWHM} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${_{FWHM} }$}}$$
(11)
$$DL = \frac{{\lambda_{R} }}{20\,S\,QF}$$
(12)
$$\zeta = \frac{1}{2 \times QF}$$
(13)

All of these parameters are determining the performance of the biosensor.

3 Results and discussion

The reflectance spectrum of the suggested 1D-PhCs is investigated based on TMM (transfer matrix method) and using of the MATLAB software. The materials which used in our proposed design are non-magnetic (relative permeability equal unity). The incident light beam of our structure is considered to be normal on the plane of incidence (TE mode) with an incident angle \(\theta = 0^{0}\). The refractive indices of materials used in our structure are \(TiN\) (Daher et al. 2022a), with \(n_{2} = 1.288\) and \(MoS_{2}\) (Ma et al. 2018), with refractive index is \(n_{1} = 3.26\). The thicknesses of TiN and MoS2 are \(d_{1} = 678.978\,nm\) and \(d_{2} = 268.{\kern 1pt} {\kern 1pt} 404\,\,nm\), respectively. The thickness of these layers are considered based on condition of Bragg–quarter wavelength \(d_{i} = \frac{{\lambda_{c} }}{{4\,n_{i} }}\) (West and Helmy 2006), where \(\lambda_{c}\) is the central wavelength. The defect layer thickness is taken to be \(d_{c} = d_{1} + d_{2}\). Figure 2 illustrates the reflectance spectrum of the proposed 1D-PhC structure which has the configuration of \(air/(MoS_{2} /TiN)^{N} (MoS_{2} /TiN)^{N} /glass\). Figure 2a gives the reflectance spectrum for the structure without any defect layer where the number of periods and the central wavelength are taken as \(N = 5\) \(\lambda_{c} = 3500\,nm\), respectively. Figure 2b illustrates the proposed structure with bacteria samples which has the configuration of \(air/(MoS_{2} /TiN)^{N} \,D\,(MoS_{2} /TiN)^{N} /glass\). From this figure, we noticed a resonance peak appeared at a wavelength position of 3958.0729 nm for water sample which is taken as a reference for other bacteria samples.

Fig. 2
figure 2

The reflectance spectrum of the proposed design. a The design has the configuration of \(air/(MoS_{2} /TiN)^{N} (MoS_{2} /TiN)^{N} /glass\). b The design has the configuration of \(air/(MoS_{2} /TiN)^{N} \,D\,(MoS_{2} /TiN)^{N} /glass\)

Full size image

Then, we present the variation of defect layer thickness of 1D-PhCs depending on the condition of the Bragg–quarter wavelength \(\left( {d_{i} = \frac{{\lambda_{c} }}{{4\,n_{i} }}} \right)\) where \(\lambda_{c}\) is the central wavelength and \(n_{i}\) is the refractive index of the layers \(i = 1\,,2\). We found that the variation in the central wavelength leads to change in the layer thickness of our structure, which in turn leads to change in the sensitivity and performance of the proposed biosensor. So, the thickness of the layers is considering an effective parameters for the optical biosensor. The central wavelength is changing from 3000 to 4000 nm as shown in Fig. 3. For studying a different types of bacteria such as (V. Cholera, E. Coli, Salmonella and Shigella Flxaneri), we calculated the position of the defect mode, FWHM (full width at half maximum), quality factor, sensitivity and damping ratio for each type of bacteria as a described in tables from 1 to 4 by using Eqs. (10–13). We observed that by increasing the central wavelength, the position of the defect mode is shifted to a higher region of the wavelength values when the types of bacteria are replaced instead of pure water in the defect layer with the incident angle of zero value as shown in Fig. 3.

Fig. 3
figure 3

Reflectance spectrum of the proposed design at different values of \(\lambda_{c}\) (central wavelength) at constant angle \(\theta = 0^{0}\)

Full size image

This shift is due to the dependence of the refractive index on the type of the defect sample. Also, from the Tables 1, 2, 3, 4, we can see that the FWHM for water sample, V. Cholera, E. Coli, Salmonella, and Shigella Flxaneri increases with increasing in \(\lambda_{c}\) (central wavelength) where the position of the defect layer is shifted to a higher region of wavelength values. Also, the dependence of the reflectance peak position on the central wavelength is linear for each type of bacteria sample as shown in Fig. 4. Besides, each type of bacteria sample has a high reflectance peak position compared with pure water.

Table 1 The defect mode position, FWHM and PhCs sensitivity of V. Cholera variance with the \(\lambda_{c}\) (central wavelength)
Full size table
Table 2 The defect mode position, FWHM and PhCs sensitivity of E. Coli variance with the \(\lambda_{c}\) (central wavelength)
Full size table
Table 3 The defect mode position, FWHM and PhCs sensitivity of Shigella variance with the \(\lambda_{c}\) (central wavelength)
Full size table
Table 4 The defect mode position, FWHM and PhCs sensitivity of Salmonella variance with the \(\lambda_{c}\) (central wavelength)
Full size table
Fig. 4
figure 4

The defect mode position of V. Cholera, E. Coli, Salmonella, and Shigella Flxaneri with the central wavelength \(\left( {\lambda_{c} } \right)\)

Full size image

Figure 5 illustrates the sensitivity of the proposed design variation with the central wavelength. From this figure, we observed that the sensitivity is linearly dependent on the \(\lambda_{c}\) (central wavelength). For (V. Cholera), the sensitivity is improved from (1007.86 nm/RIU) to (1326.628 nm/RIU) by an increase in \(\lambda_{c}\) (central wavelength) from 3000 to 4000 nm. The sensitivity of E. Coli is enhanced form (1006.414 nm/RIU) to (1341.885 nm/RIU) when the central wavelength is increased from (3000–4000 nm). Also, the sensitivity for Shigella and Salmonella is increased from (1085.447 nm/RIU, 992.832 nm/RIU) to (1336.58 nm/RIU, 1334.602 nm/RIU) with increasing in the central wavelength from 3000 to 4000 nm, respectively.

Fig. 5
figure 5

The sensitivity of V. Cholera, E. Coli, Salmonella and Shigella Flxaneri variance with the central wavelength \(\left( {\lambda_{c} } \right)\)

Full size image

The relation between the FWHM and the central wavelength for each type of bacteria samples is shown in Fig. 6. It is worth mentioning that the FWHM is defined as the difference between right and left edge of the reflection peak inside the cavity region at half maximum. From Fig. 6, the increase in the central wavelength with increasing the FWHM is not linear like the case of the sensitivity in Fig. 5.

Fig. 6
figure 6

The FWHM for different types of bacteria samples with the central wavelength

Full size image

Besides the FWHM, the detection accuracy is another parameter from the parameters which can describe the design performance. This parameter is related to the full width at half maximum which is defined as the reciprocal of FWHM

$$DA = \frac{1}{FWHM}$$
(14)

Where in, the less value of FWHM lead to a high value of the detection accuracy that leads to a good performance of the proposed sensor. In other words, the good sensor has low FWHM and high value of the detection accuracy.

In the following part, we discussed the impact of the central wavelength on the sensor performance parameters of V. Cholera, E. Coli, Salmonella and Shigella Flxaneri as shown in Tables 1, 2, 3, 4. According to V. Cholera and other types of bacteria samples, there are some variations in the quality factor value corresponding to the change in the central wavelength which be small oscillations as indicated in Tables 1, 2, 3, 4. The smallest change in refractive index can be detected is called detection limit, which slightly increases with increasing in the central wavelength for each type of bacteria samples. From Tables 1, 2, 3, 4, the detection limit is enhanced with enhanced in the central wavelength. Wherein, the small value of the detection limit is considered a good sign for the performance of the proposed biosensor. Another parameter which is affected by the value of central wavelength is the FWHM (full width at half maximum). Consequently, for every each type of bacteria sample, there is a change in the central wavelength which results in an enhancement in the FWHM. Thus, the good performances of biosensor design have a small of full width at half maximum. Also, the detection accuracy is another parameter which is defined as the reciprocal of FWHM is change from 1.6 at central wavelength 3000 nm to 0.8 at central wavelength 4000 nm. As the biosensor's full width at half maximum is small and its detection accuracy is high so this gives a good performance for the suggested design. Finally, we calculate the damping ratio which describes haw the oscillation in the system decays after distributions. It’s a dimensionless parameter. It’s clear that for the Tables 1, 2, 3, 4, all parameters such as sensitivity, quality factor, detection limit and damping ratio enhanced with increasing in the central wavelength.

In this part, the reflectance spectra of the proposed structure of types of bacteria will be discussed at constant \(\lambda_{c}\) (central wavelength) of 3500 nm with changing the incident angle form \(0^{o}\) to \(70^{o}\). The full width at half maximum (FWHM), sensitivity, quality factor, detection limit, and damping ratio are calculated as indicated in Tables 5, 6, 7, 8. From theses tables, we found that by increasing in the incident angle, the FWHM of V. Cholera, E. Coli, Salmonella, and Shigella Flxaneri are greater than pure water sample. Also, the defect mode positions for the bacteria samples are shifted to the lower wavelength values with the variation in the incident angle according to Bragg- Snell’s law which can be described as follows (Mayonado et al. 2015).

$$m\lambda = 2\,D\sqrt {n_{eff} - \sin^{2} \theta }$$
(15)
Table 5 The defect mode position, FWHM and PhCs sensitivity of V. Cholera variance with the incident angle
Full size table
Table 6 The defect mode position, FWHM and PhCs sensitivity of E.Coli variance with the incident angle
Full size table
Table 7 The defect mode position, FWHM and PhCs sensitivity of Shigella variance with the incident angle
Full size table
Table 8 The defect mode position, FWHM and PhCs sensitivity of Salmonella variance with the incident angle
Full size table

From this equation, m is the diffracted order, \(\lambda\) is the wavelength of light, \(D\) is the interplanar space, \(n_{eff}\) is the effective refractive index, and \(\theta\) is the incident angle. In this equation, we noticed that the incident wavelength is related to the incident angle where the increase in the incident angle leads to a lower shift in the wavelength as shown in Fig. 7. In this study, the incident angle changes from \(0^{o}\) to \(70^{o}\). From Fig. 8, the sensitivity is increased from 1175.84 to 1683.678 nm/RIU for V. Cholera. Also, for E. Coli, the sensitivity is increased from 1165.969 to 1700.161 nm/RIU. For Shigella Flxaneri, the sensitivity is increased from 1162.979 to 1717.830 nm/RIU. Also, for Salmonella sensitivity is increased from1167.584 to 1457.347 nm/RIU as shown in Fig. 8.

Fig. 7
figure 7

The defect mode position of different types of bacteria samples with increasing the incident angle at constant value of the central wavelength \(\lambda_{c} = 3500nm\)

Full size image
Fig. 8
figure 8

The sensitivity variation for different species of bacteria samples with increasing the incident angle at constant value of the central wavelength \(\lambda_{c} = 3500nm\)

Full size image

The detection limit and the damping ratio are slightly decreased with increasing the incident angle. So, all parameters which discussed in the Tables 5, 6, 7, 8 are considered as effective parameters that describe the performance of the proposed design.

Here, we study the reflectance spectra of the suggested biosensor for the case of the incident angle \(\theta = 65^{0}\) and the defect layer thickness is \(d_{c} = 6d\,{\kern 1pt} \,nm\) as shown in Fig. 9. As noticed in this figure, the higher sensitivity value for the proposed design can be obtained at the condition of the incident angle \(\theta = 65^{0}\) and the defect layer thickness is \(d_{c} = 6d\,{\kern 1pt} \,nm\). At this condition, the sensitivity of the proposed structure has the value of 4203.33437 nm/RIU for V. Cholera. According to this condition, we obtained a high sensitivity, high quality factor, and small of detection limit which gives a good performance of the suggested biosensor design as shown in Table 9.

Fig. 9
figure 9

The reflectance spectra of 1D-PhCs of different types of bacteria samples at defect layer thickness \(d_{c} = 6d\,nm\) and incident angle \(\theta = 65^{0}\)

Full size image
Table 9 The defect mode position, FWHM and PhCs sensitivity of V. Cholera, E. coli, Shigella and Salmonella at defect layer thickness \(d_{c} = 6d\,{\kern 1pt} \,nm\) and incident angle \(\theta = 65^{0}\)
Full size table

Here, we present a comparative performance study between this work and some recent reports in the literature as presented in Table 10. As demonstrated in this table, our suggested design gives high values of the average sensitivity, quality factor and detection limit compared to the other works in the literature. In other words, by using the proposed design, the performance is improved compared to the mentioned works in the literature. It’s noteworthy that the proposed of water borne bacteria sensor is simple and easy to fabricate, also can be used for any application of biosensor. It can be used for detect bioalochol in waste water, concentration of haemoglobin in blood, glucose concentration and ethanol concentration. This is because of the sensor proposing based on the variations of refractive index between reference sample and the investigation sample.

Table 10 A comparative study between the proposed work and some recent reports in the literature
Full size table

4 Conclusion

In this paper, we have demonstrated the theoretical studies of the 1D-photonic crystal biosensor to detect water borne-bacteria. The transfer matrix method and MATLAB software are used for investigating and analysing the reflectance spectrum of the proposed design. The different types of water-borne bacteria such as vibrio Cholera, Salmonella, E. Coli and Shigella Flxaneri with different values of the refractive indices are investigated to demonstrate the sensing process by the proposed design. The variations in the refractive indices lead to shifting in the defect mode position of the corresponding bacteria samples. The impact of the central wavelength and incident angle on the sensitivity and other parameters such as full width at half maximum, detection limit, quality factor and damping ratio are calculated. We found that the increasing in the central wavelength and the incident angle lead to an enhancement in the sensitivity and the other parameters of the proposed biosensor design. Wherein, the incident angle and the central wavelength are considering significant parameters that have an effect on the performance of the proposed biosensor. The suggested design exhibits an average sensitivity value of 4073 nm/RIU at an optimum condition of the defect layer thickness and the incident angle. Also, the proposed biosensor design exhibits a high quality factor value of 10996.2165 and a low detection limit value of \(0.44607 \times \,10^{ - 5}\) RIU.