1 Introduction

Magnetic trajectories play a notable role in many applications in differential and physical geometry. These trajectories are obtained thanks to the magnetic fields on Riemann manifold. Thus, magnetic trajectories are determined depending on the specific form of manifold. For instance, in Comtet (1987), Druta-Romaniuc and Munteanu (2011), Druta-Romaniuc and Munteanu (2013), Efimov (2005), Munteanu and Nistor (2012), Novikov (1982), Yeneroğlu (2016), authors have shown that trajectories of magnetic areas characterized on manifold with constant Gaussian curvature can be determined. Also, it is quite important that the dynamics of charged particles correspond to trajectories of a certain type of curve in electromagnetic areas. The motion charged particles in homogeneous electromagnetic fields have been studied by researchers (Honig et al. 1974).

Many researchers presented the work of curves in ordinary space. Also, some authors analyzed the definitions and features of helices in Minkowski space and gave differential equations with respect to Frenet-Serret vectors definitive helices (Ilarslan 2002). Moreover, differential equations which define the Frenet fibers in Minkowski space and ordinary space are acquired (Kocayigit 2004).

Bishop model, which is named parallel or alternative frame of curves, has been introduced by means of parallel vector areas. Newly, many works with respect to this approach have been studied in ordinary space. For instance, in Yilmaz (2009), researchers defined a new form for Bishop model and application for spherical indicators. Also, some researchers considered the Minkowski space (Yılmaz and Turgut 2010). The Bishop model has many implementations in computer graphics, geometrical physics, and biology. For instance, it may be feasible to calculate data about the form of a series of DNA utilizing a fiber defined with Bishop model. Bishop’s model ensures a new method to examine simulated cameras in PC animations (Büyükkütük and Öztürk 2015). Moreover, after defining this alternative frame, parallel transport frame has been characterized for non-null curves in Minkowski space (Özdemir and Ergin 2008). Also, in Kazan and Karadağ (2018), authors have defined magnetic non-null curves according to parallel transport frames in Minkowski space.

Fractional calculation has attracted the attention of many researchers in the last centuries and today (Samko et al. 1993; Podlubny et al. 2002; Kilbas et al. 2006). The effect of this calculation on applied subjects of science and engineering started to improve essentially during the last years. Many studies have started to be interested in the separate models of fractional calculus utilizing the theory of time system (Gray and Zhang 1988; Miller and Ross 1988; Atici and Eloe 2009; Abdeljawad and Atici 2012; Abdeljawad 2013).

Fermi–Walker carried systems are enormously substantial in various basic functions. Many experts improved areas such as quantum structures alternated to experts move through optional spherical particles on space-time. Completely, they altered these systems inside F–W transported constructions. Consequently, a simple instruction for the F–W transported frame out of an alternative class of areas has been demonstrated by many researchers (Maluf and Faria 2008).

In this work, magnetic timelike curves are examined using a Bishop model in Minkowski space. First, the conformable derivatives of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) Lorentz force have been calculated for these curves. Then, we compute normalizing and recursion operators of magnetic vector fields according to Bishop model. Finally, we have determined F–W conformable derivatives of normalizing and recursional operators.

2 Preliminaries

In this part, some fundamental definitions in Minkowski space are given.

Definition 1

Let \({\textbf{G}}\) be the magnetic field and \(\vartheta :I\rightarrow {{\mathbb {E}}}_{1}^{3}\) be a regular parametrized particle. Therefore, following equations is expressed

$$ \begin{gathered} D_{{\vartheta ^{\prime } }} {\mathbf{t}} = k_{1} {\mathbf{m}}_{1} + k_{2} {\mathbf{m}}_{2} , \hfill \\ D_{{\vartheta ^{\prime } }} {\mathbf{m}}_{1} = k_{1} {\mathbf{t}}, \hfill \\ D_{{\vartheta ^{\prime } }} {\mathbf{m}}_{2} = k_{2} {\mathbf{t}}, \hfill \\ \end{gathered} $$
(1)

where \(\left\{ {\textbf{t}},\text { }{\textbf{m}}_{1},\text { }\mathbf { m_{2}}\right\} \) is Bishop model for \(\vartheta \) timelike curve.

Definition 2

For magnetic timelike curve, the conformable derivatives are written as

$$\begin{aligned} D_{\vartheta {^{\prime }}}{\textbf{t}}= & {} k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{1}+\varsigma ^{1-\theta }k_{2}{\textbf{m}}_{2}, \nonumber \\ D_{\vartheta {^{\prime }}}{\textbf{m}}_{1}= & {} k_{1}\varsigma ^{1-\theta }{\textbf{t}}, \\ D_{\vartheta {^{\prime }}}{\textbf{m}}_{2}= & {} k_{2}\varsigma ^{1-\theta }{\textbf{t}}. \nonumber \end{aligned}$$
(2)

Definition 3

The vector field \({\textbf{t}}\) of Bishop model providing Lorentz force equation

$$\nabla_{{\vartheta ^{\prime } }} {\mathbf{t}} = {\mathbf{G}} \times {\mathbf{t}} = \Gamma \left( {\mathbf{t}} \right),$$

is called timelike \(T{\textbf{t}}\)-magnetic curve.

Thus, the conformable derivatives are defined by \(T\mathbf {t-}\)magnetic curve

$$\begin{aligned} \begin{aligned} \Gamma ({\textbf{t}})&=k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{1}+k_{2}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ \Gamma ({\textbf{m}}_{1})&=k_{1}\varsigma ^{1-\theta }{\textbf{t}}+\rho {\textbf{m}}_{2}, \\ \Gamma ({\textbf{n}}_{2})&=k_{2}\varsigma ^{1-\theta }\mathbf {t-}\rho {\textbf{m}} _{1}, \end{aligned} \end{aligned}$$
(3)

where \(\rho =g(\Gamma \left( {\textbf{m}}_{1}\right) \), \({\textbf{m}} _{2})\) is certain potential.

Definition 4

The vector field \({\textbf{m}}_{1}\) of Bishop model providing the Lorentz force equation

$$ \nabla _{{\vartheta ^{\prime } }} {\mathbf{m}}_{1} = \Gamma \left( {{\mathbf{m}}_{1} } \right) = {\mathbf{G}} \times {\mathbf{m}}_{1} , $$

is named timelike \(T{\textbf{m}}_{1}\)-magnetic curve.

Then, the conformable derivatives are defined by \(T{\textbf{m}}_{1}\mathbf {-}\)magnetic curve

$$\begin{aligned} \Gamma \left( {\textbf{t}}\right)= & {} k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{1} + \mu {\textbf{m}}_{2}, \\ \Gamma \left( {\textbf{m}}_{1}\right)= & {} k_{1}\varsigma ^{1-\theta }\textbf{t,}\\ \Gamma \left( {\textbf{m}}_{2}\right)= & {} \mu \textbf{t,} \end{aligned}$$

where \(\mu =g(\Gamma \left( {\textbf{t}}\right) \), \({\textbf{m}}_{2})\) is certain potential.

Definition 5

The vector field \({\textbf{m}}_{2}\) of Bishop model providing the Lorentz force equation

$$\nabla _{\vartheta {^{\prime }}}{\textbf{m}}_{2}=\Gamma \left( {\textbf{m}} _{2}\right) ={\textbf{G}}\times {\textbf{m}}_{2},$$

is named timelike \(T{\textbf{m}}_{2}\)-magnetic curve.

Thus, the conformable derivatives are defined by \(T{\textbf{m}}_{2}\mathbf {-}\)magnetic curve according to Bishop model

$$\begin{aligned} \Gamma \left( {\textbf{t}}\right)= & {} \gamma {\textbf{m}}_{1} + \varsigma ^{1-\theta }k_{2}{\textbf{m}}_{2}, \\ \Gamma \left( {\textbf{m}}_{1}\right)= & {} \gamma \textbf{t,} \\ \Gamma \left( {\textbf{m}}_{2}\right)= & {} \varsigma ^{1-\theta }k_{2}\textbf{t,} \end{aligned}$$

where \(\gamma =g(\Gamma \left( {\textbf{t}}\right) ,{\textbf{m}}_{1})\) is certain potential.

Then, inner and vector cross of vector fields are given as

$$\begin{aligned} \begin{aligned} -{\textbf{t}}={\textbf{m}}_{1}\times \mathbf {m_{2}},\quad {\textbf{m}}_{1}={\textbf{m}} _{2}\times \textbf{t},\quad {\textbf{m}}_{2}=\textbf{t}\times \mathbf {m_{1}}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \langle {\textbf{m}}_{2},\textbf{m}_{2}\rangle =1, \quad \langle \textbf{t,t}\rangle =-1, \quad \langle \mathbf {m_{1},m_{1}}\rangle =1. \end{aligned}$$

Also, normalizing operators of \(\vartheta \) timelike curve is

$$\begin{aligned} \mathbb{N}\mathbb{F}=-{\textbf{I}}_{\theta }^{x}(h_{1}\varsigma ^{1-\theta }k_{1}+h_{2}\varsigma ^{1-\theta }k_{2}){\textbf{t}}+h_{1}{\textbf{n}}_{1}+h_{2} {\textbf{n}}_{2}. \end{aligned}$$

Here magnetic field is \({{\mathbb {F}}}=h_{0}{\textbf{t}}+h_{1}{\textbf{n}}_{1}+h_{2} {\textbf{n}}_{2}\). Recursion functions \({\varvec{R}}{{\mathbb {F}}}\)

$$\begin{aligned} -{{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }{{\mathbb {F}}}\right) =\varvec{ R}{{\mathbb {F}}}, \end{aligned}$$

and \({\varvec{R}}^{2}{{\mathbb {F}}}\) are

$$\begin{aligned} -{{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }{{\mathcal {R}}}{{\mathbb {F}}}\right) = {\varvec{R}}^{2}{{\mathbb {F}}}. \end{aligned}$$

3 Conformable derivative characterizations of magnetic timelike curves

In this section, definitions conformable fractional derivative and conformable integration of curves are presented. Then, we have given conformable derivatives of normalizing function and \(\Gamma \left( {\textbf{t}} \right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}} _{2}\right) \) Lorentz physical energies for magnetic timelike curves.

Definition 6

The definition of conformable derivatives is defined by

$$\begin{aligned} (_{t_{0}}T_{\theta }f)(t) \ =\underset{\varepsilon \rightarrow 0}{lim }\dfrac{f((t-t_{0})^{1-\theta }\varepsilon +t)-f(t)}{\varepsilon }, \end{aligned}$$

where \(f:[t_{0},\infty )\rightarrow R\) of order \(\theta \in (0,1]\) and \(t>0\).

Definition 7

Corresponding conformable integration is characterized as

$$\begin{aligned} _{t_{0}}{\textbf{I}}^{\theta }(f)(t)={\textbf{I}}_{t}^{x}(t^{1-\theta }f)=\int _{t_{0}}^{t}\dfrac{f(t)}{(t-t_{0})^{1-\theta }}dt, \end{aligned}$$

\(\theta \in (0,1)\) and \(x\ge 0\).

Thus, the following conformable derivative equations for \(\left\{ {\textbf{t}}, {\textbf{m}}_{1}, \mathbf {m_{2}}\right\} \) Bishop model are given

$$\begin{aligned} \ D_{\theta }{\textbf{t}}= & {} k_{1}\varsigma ^{1-\theta } {\textbf{m}}_{1}+k_{2}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \nonumber \\ D_{\theta }{\textbf{m}}_{1}= & {} k_{1}\varsigma ^{1-\theta }{\textbf{t}}, \\ D_{\theta }{\textbf{m}}_{2}= & {} k_{2}\varsigma ^{1-\theta }{\textbf{t}}. \nonumber \end{aligned}$$
(4)

  • Conformable derivatives of normalizing function for \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}} _{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) of timelike \(T{\textbf{t}}\)-magnetic curves are obtained as follows

    $$\begin{aligned} D_{\theta }\Gamma \left( {\textbf{t}}\right)= & {} \left( (k_{1}\varsigma ^{1-\theta })^{2}+(k_{2}\varsigma ^{1-\theta })^{2}\right) \textbf{t}+\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta } +\varsigma ^{1-2\theta }(1-\theta )k_{1}\right) {\textbf{m}}_{1} \\{} & {} +\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }+(-\theta +1)\varsigma ^{1-2\theta }k_{2}\right) {\textbf{m}}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right)= & {} \left( k_{1}(-\theta +1)\varsigma ^{1-2\theta }+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }\rho k_{2}\right) {\textbf{t}} \\{} & {} + (k_{1}\varsigma ^{1-\theta })^{2}{\textbf{m}}_{1}+\left( \dfrac{d\rho }{ d\varsigma }\varsigma ^{1-\theta }+k_{1}\varsigma ^{2-2\theta }k_{2}\right) \textbf{ m}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right)= & {} \left( (1-\theta )\varsigma ^{1-2\theta }k_{2}+\varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }-\rho \varsigma ^{1-\theta }k_{1}\right) {\textbf{t}} \\{} & {} + \left( \varsigma ^{2-2\theta }k_{1}k_{2}-\varsigma ^{1-\theta }\dfrac{ d\rho }{d\varsigma }\right) {\textbf{m}}_{1}+(\varsigma ^{1-\theta }k_{2})^{2}\textbf{ m}_{2}. \end{aligned}$$

    Then, normalizing functions of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) are

    $$\begin{aligned} {{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} -{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2}+(k_{2}\varsigma ^{1-\theta })^{2}){\textbf{t}} \\{} & {} +\varsigma ^{1-\theta }k_{1}{\textbf{m}}_{1}+\varsigma ^{1-\theta }k_{2}{\textbf{m}}_{2}, \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{\textbf{I}}_{\theta }^{x}(\rho k_{2}\varsigma ^{1-\theta }){\textbf{t}}+\rho {\textbf{m}}_{2}\textbf{,} \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} {\textbf{I}}_{\theta }^{x}(\rho k_{1}\varsigma ^{1-\theta })\mathbf {t-}\rho {\textbf{m}}_{1}, \end{aligned}$$

    and

    $$\begin{aligned} {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right)= & {} -{\textbf{I}}_{\theta }^{x}\left( -k_{1}\varsigma ^{1-\theta }\left( (1-\theta )k_{2}\varsigma ^{1-2\theta }+\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) \right. \\{} & {} \left. +k_{2}\varsigma ^{1-\theta }\left( \varsigma ^{1-2\theta }k_{1}(1-\theta ) +\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }\right) \right) {\textbf{t}}\\{} & {} -\left( (1-\theta )k_{2}\varsigma ^{1-2\theta }+\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) {\textbf{m}}_{1}\\{} & {} +\left( \varsigma ^{1-2\theta }k_{1}(1-\theta )+\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }\right) {\textbf{m}}_{2}, \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{1}\right) \right)= & {} {\textbf{I}}_{\theta }^{x}\left( \dfrac{d\rho }{d\varsigma } \varsigma ^{2-2\theta }k_{1}\right) {\textbf{t}}-\left( k_{1}\varsigma ^{2-2\theta }k_{2}+\varsigma ^{1-\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{m}} _{1}+(\varsigma ^{1-\theta }k_{1})^{2}{\textbf{m}}_{2}, \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{2}\right) \right)= & {} {\textbf{I}}_{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta } \dfrac{d\rho }{d\varsigma }\right) {\textbf{t}}-(\varsigma ^{1-\theta }k_{2})^{2} {\textbf{m}}_{1}+\left( k_{1}k_{2}\varsigma ^{2-2\theta }-\dfrac{d\rho }{d\varsigma } \varsigma ^{1-\theta }\right) {\textbf{m}}_{2}. \end{aligned}$$

    Moreover, we get recursions of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) vector fields

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {\textbf{I}} _{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( (1-\theta )k_{2}\varsigma ^{-2\theta +1}+\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) \right. \\{} & {} \left. +\varsigma ^{-\theta +1}k_{2}\left( k_{1}\varsigma ^{-2\theta +1}(1-\theta )+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) \right) {\textbf{t}}\\{} & {} +\left( k_{2}(1-\theta )\varsigma ^{1-2\theta }+\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) {\textbf{m}}_{1}-\left( k_{1}(1-\theta )\varsigma ^{1-2\theta }+\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }\right) {\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) =-{\textbf{I}} _{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{t}} \\{} & {} +\left( k_{1}k_{2}\varsigma ^{2-2\theta }+\dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }\right) {\textbf{m}}_{1}-(\varsigma ^{1-\theta }k_{1})^{2}{\textbf{m}}_{2},\\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) =-{\textbf{I}} _{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{t}} \\{} & {} +(\varsigma ^{1-\theta }k_{2})^{2}{\textbf{m}}_{1}-\left( k_{1}k_{2}\varsigma ^{2-2\theta }-\dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }\right) {\textbf{m}} _{2}. \end{aligned}$$

  • Conformable derivatives of normalizing function for \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}} _{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) of timelike \(T{\textbf{m}}_{1}\)-magnetic curves are obtained

    $$\begin{aligned} {{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} -{\textbf{I}}_{\theta }^{x}(\varsigma ^{2-2\theta }k_{1}{}^{2}+\varsigma ^{1-\theta }\mu k_{2}) {\textbf{t}} \\{} & {} +\varsigma ^{1-\theta }k_{1}{\textbf{m}}_{1} + \mu {\textbf{m}}_{2}, \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} d_{0}\textbf{t,} \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} d_{1}{\textbf{t}}, \end{aligned}$$

    where \(d_{0}\) and \(d_{1}\) are recursion constants and moreover, derivatives of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) , \) \(\Gamma \left( {\textbf{m}}_{2}\right) \) are

    $$\begin{aligned} D_{\theta }\Gamma \left( {\textbf{t}}\right)= & {} ((k_{1}\varsigma ^{1-\theta })^{2}+\varsigma ^{1-\theta }\mu k_{2})\textbf{t}+\left( \varsigma ^{2-2\theta } \dfrac{dk_{1}}{d\varsigma } +(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) {\textbf{m}}_{1}+\varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma }{\textbf{m}}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right)= & {} \left( (1-\theta )\varsigma ^{1-2\theta }k_{1}+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) {\textbf{t}} + k_{1}^{2}\varsigma ^{2-2\theta }{\textbf{m}}_{1}+k_{1}k_{2}\varsigma ^{2-2\theta }{\textbf{m}}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right)= & {} \varsigma ^{1-\theta }\dfrac{ d\mu }{d\varsigma }\textbf{t}+\mu \varsigma ^{1-\theta }k_{1}{\textbf{m}} _{1}+k_{2}\varsigma ^{1-\theta }\mu {\textbf{m}}_{2}. \end{aligned}$$

    We have that

    $$\begin{aligned} {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right)= & {} -{{\textbf{I}}}_{\theta }^{x}\left( -\varsigma ^{2-2\theta }\dfrac{ d\mu }{d\varsigma }+\varsigma ^{1-\theta }k_{2}(\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma } +(1-\theta )\varsigma ^{1-2\theta }k_{1})\right) {{\textbf{t}}}\\{} & {} -\varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma }{\textbf{m}}_{1}+\left( \varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) {\textbf{m}}_{2}, \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{1}\right) \right)= & {} -d_{2}{{\textbf{t}}}-k_{1}\varsigma ^{-2\theta +2}k_{2}{\textbf{m}}_{1}+(k_{1}\varsigma ^{1-\theta })^{2}{\textbf{m}}_{2}, \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{2}\right) \right)= & {} -d_{3}{{\textbf{t}}}-\mu \varsigma ^{1-\theta }k_{2}{\textbf{m}}_{1}+\mu k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}. \end{aligned}$$

    Thus, we get

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {{\textbf{I}} }_{\theta }^{x}\left( -\dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }k_{2}\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta } +(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) {{\textbf{t}}}\\{} & {} +\varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma }{\textbf{m}}_{1}-\left( \varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) {\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) =d_{2} {{\textbf{t}}}+\varsigma ^{2-2\theta }k_{1}k_{2}{\textbf{m}} _{1}-(\varsigma ^{1-\theta }k_{1})^{2}{\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) =d_{3} {{\textbf{t}}}+\mu \varsigma ^{1-\theta }k_{2}{\textbf{m}}_{1}-\mu k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \end{aligned}$$

    where \(d_{2}\) and \(d_{3}\) are recursion constants.

  • Conformable derivatives of normalizing function for timelike \(T{\textbf{m}}_{2}\)-magnetic curves are obtained

    $$\begin{aligned} D_{\theta }\Gamma \left( {\textbf{t}}\right)= & {} \left( (\varsigma ^{1-\theta }k_{2})^{2}+\gamma \varsigma ^{1-\theta }k_{1}\right) \textbf{t}+\varsigma ^{1-\theta }\dfrac{d\gamma }{d\varsigma }{\textbf{m}}_{1} \\{} & {} +\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) {\textbf{m}}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right)= & {} \varsigma ^{1-\theta }\dfrac{ d\gamma }{d\varsigma }\textbf{t}+\gamma k_{1}\varsigma ^{1-\theta }{\textbf{m}} _{1}+\gamma k_{2}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right)= & {} \left( (1-\theta )\varsigma ^{1-2\theta }k_{2}+\varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }\right) {\textbf{t}} \\{} & {} + \varsigma ^{2-2\theta }k_{1}k_{2}{\textbf{m}}_{1}+(\varsigma ^{1-\theta }k_{2})^{2}{\textbf{m}}_{2}. \end{aligned}$$

    Then, normalizing functions of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) are

    $$\begin{aligned} {{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} -{\textbf{I}}_{\theta }^{x}(\varsigma ^{2-2\theta }k_{2}^{2}+k_{1}\varsigma ^{1-\theta }\gamma ){\textbf{t}} \\{} & {} +\gamma {\textbf{m}}_{1} + \varsigma ^{-\theta +1}k_{2}{\textbf{m}}_{2}, \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} d_{4}\textbf{t,} \\ {{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} d_{5}{\textbf{t}}, \end{aligned}$$

    where \(d_{4}\) and \(d_{5}\) are recursion constants and moreover, we give that

    $$\begin{aligned} {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right)= & {} -{\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1} \left( \dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }+(-\theta +1)\varsigma ^{1-2\theta }k_{2}\right) +k_{2}\varsigma ^{2-2\theta }\dfrac{d\gamma }{d\varsigma }\right) \textbf{t}\\{} & {} -\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) {{\textbf{m}}_{1}+}\varsigma ^{1-\theta }\dfrac{ d\gamma }{d\varsigma }{{\textbf{m}}_{2},} \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{1}\right) \right)= & {} -d_{6}\mathbf {t-}\gamma k_{2}\varsigma ^{1-\theta } {\textbf{m}}_{1}-\gamma k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ {{\mathbb {N}}}\left( {\textbf{t}}\times D_{\theta }\Gamma \left( {\textbf{m}} _{2}\right) \right)= & {} -d_{7}\mathbf {t-}(\varsigma ^{1-\theta }k_{2})^{2} {{\textbf{m}}_{1}\mathbf {-}}\varsigma ^{2-2\theta }k_{1}k_{2}\mathbf { {\textbf{m}}_{2}.} \end{aligned}$$

    Recursions for \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}} _{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) are

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {\textbf{I}} _{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}(\dfrac{dk_{2}}{ d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-2\theta }(1-\theta )k_{2}) +k_{2}\varsigma ^{2-2\theta }\dfrac{d\gamma }{d\varsigma }\right) \textbf{t}\\{} & {} +\left( \dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) {{\textbf{m}}_{1}-}\dfrac{d\gamma }{d\varsigma } \varsigma ^{1-\theta }{{\textbf{m}}_{2},} \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) =d_{6} \mathbf {t+}\gamma k_{2}\varsigma ^{1-\theta }{\textbf{m}}_{1}+\gamma k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) =d_{7} \mathbf {t+}(\varsigma ^{1-\theta }k_{2})^{2}{{\textbf{m}}_{1}+} \varsigma ^{2-2\theta }k_{1}k_{2}{{\textbf{m}}_{2},} \end{aligned}$$

    where \(d_{6}\) and \(d_{7}\) are recursion constants.

4 Fermi–Walker conformable derivative

In this part, we have computed F–W conformable fractional derivative for some characterization of magnetic timelike curves correlated to a given magnetic field in Minkowski space.

Let \(\rho \) be a unit speed magnetic curve lying on space. Thus, the F–W conformable relation to \(\rho \), \({\widetilde{D}}_{\theta }\) is stated by

$$\begin{aligned} {\widetilde{D}}_{\theta }X=\langle D_{\theta }\rho ,X\rangle D_{\theta } \mathbf {t+}D_{\theta }X\mathbf {-}\langle D_{\theta }{\textbf{t}},X\rangle D_{\theta }\rho , \end{aligned}$$
(5)

where X is a vector field along \(\rho \).

4.1 F–W conformable derivative for normalizing function

  • Conformable derivative of normalizing functions of timelike \(T{\textbf{t}}\)-magnetic curves are given as follows

    $$\begin{aligned} D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} \left( \dfrac{dk_{1}}{ d\varsigma }\varsigma ^{-2\theta +2}+k_{1}\varsigma ^{1-\theta }{\textbf{I}} _{\theta }^{x}((\varsigma ^{1-\theta }k_{1})^{2}+(\varsigma ^{1-\theta }k_{2})^{2})\right) {\textbf{m}}_{1} \\{} & {} +\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }+k_{2}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}((\varsigma ^{1-\theta }k_{1}) ^{2}+(\varsigma ^{1-\theta }k_{2})^{2}){\textbf{m}}_{2}, \right. \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -\varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}(\rho \varsigma ^{1-\theta }k_{2}) {\textbf{m}}_{1}+\left( \dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }-\varsigma ^{1-\theta }k_{2}{\textbf{I}}_{\theta }^{x}(k_{2}\rho \varsigma ^{1-\theta })\right) {\textbf{m}}_{2}, \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} \left( \varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}(k_{1}\rho \varsigma ^{1-\theta })-\varsigma ^{1-\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{m}} _{1}+\varsigma ^{1-\theta }k_{2}{\textbf{I}}_{\theta }^{x}(k_{1}\rho \varsigma ^{1-\theta }){\textbf{m}}_{2}. \end{aligned}$$

    Moreover, F–W conformable derivative for \({{\mathbb {N}}}\Gamma \left( {\textbf{t}} \right) \), \({{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right) \), \({{\mathbb {N}}} \Gamma \left( {\textbf{m}}_{2}\right) \) normalizing functions are obtained

    $$\begin{aligned} {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} -(\varsigma ^{3-3\theta }k_{1}^{2}+\varsigma ^{3-3\theta }k_{2}^{2})\textbf{t}+\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta } \right. \\{} & {} +\varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}((\varsigma ^{1-\theta }k_{1})^{2}+(\varsigma ^{1-\theta }k_{2})^{2})+\varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}((\varsigma ^{1-\theta }k_{1} )^{2} \\{} & {} +(k_{2}\varsigma ^{1-\theta })^{2})){\textbf{m}}_{1}+\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }+k_{2}\varsigma ^{1-\theta }\textbf{I }_{\theta }^{x}((\varsigma ^{1-\theta }k_{1})^{2} \right. \\{} & {} +(k_{2}\varsigma ^{1-\theta })^{2})-\varsigma ^{2-2\theta }k_{2} {\textbf{I}}_{\theta }^{x}((\varsigma ^{1-\theta }k_{1}) ^{2}+(\varsigma ^{1-\theta }k_{2})^{2})){\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -k_{2}\rho \varsigma ^{2-2\theta }{\textbf{t}}+(-\varsigma ^{1-\theta }k_{1} {\textbf{I}}_{\theta }^{x}(k_{2}\rho \varsigma ^{1-\theta }) \\{} & {} +k_{1}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}(k_{2}\rho \varsigma ^{1-\theta })){\textbf{m}}_{1}+\left( \dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta } \right. \\{} & {} \left. \left. -k_{2}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}(\rho k_{2}\varsigma ^{1-\theta })+k_{2}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}(\rho k_{2}\varsigma ^{1-\theta }\right) \right) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} k_{1}\rho \varsigma ^{2-2\theta }\textbf{t}-(k_{1}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}(\rho k_{1}\varsigma ^{1-\theta }) \\{} & {} \left. \left. +\dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }+\varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}(\rho k_{1}\varsigma ^{1-\theta }\right) \right) {\textbf{m}} _{1} \\{} & {} +(\varsigma ^{2-2\theta }k_{2}{\textbf{I}}_{\theta }^{x}(k_{1}\rho \varsigma ^{1-\theta })+\varsigma ^{1-\theta }k_{2}{\textbf{I}}_{\theta }^{x}(k_{1}\rho \varsigma ^{1-\theta })){\textbf{m}}_{2}. \end{aligned}$$

  • Conformable derivative of normalizing functions of timelike \(T{\textbf{m}}_{1}\)-magnetic curves are given

    $$\begin{aligned} D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} (\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }-k_{1}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2} \\{} & {} +\mu k_{2}\varsigma ^{1-\theta })+\varsigma ^{1-2\theta }(1-\theta )k_{1}){\textbf{m}}_{1} \\{} & {} +(-k_{2}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2}+\mu k_{2}\varsigma ^{1-\theta })+\dfrac{d\mu }{ d\varsigma }\varsigma ^{1-\theta }){\textbf{m}}_{2}, \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} k_{1}d_{0}\varsigma ^{1-\theta }{\textbf{m}}_{1}+k_{2}d_{0}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} k_{1}d_{1}\varsigma ^{1-\theta }{\textbf{m}}_{1}+k_{2}d_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}. \end{aligned}$$

    F–W conformable derivative for \({{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right) \), \({{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right) \), \({{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right) \) normalizing functions are obtained

    $$\begin{aligned} {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} (-\varsigma ^{3-3\theta }k_{1}^{2}-k_{2}\mu \varsigma ^{2-2\theta })\textbf{t} \\{} & {} +\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta }) ^{2}+k_{2}\mu \varsigma ^{1-\theta })+\varsigma ^{1-2\theta }(1-\theta )k_{1}\right. \\{} & {} +\varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2}+k_{2}\mu \varsigma ^{1-\theta })){\textbf{m}} _{1}+(\varsigma ^{1-\theta }k_{2}{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2} \\{} & {} +\mu k_{2}\varsigma ^{1-\theta })+\dfrac{d\mu }{d\varsigma }\varsigma ^{1-\theta }+k_{2}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}((k_{1}\varsigma ^{1-\theta })^{2}+\mu k_{2}\varsigma ^{1-\theta })){\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} (k_{1}d_{0}\varsigma ^{1-\theta }-k_{1}d_{0}\varsigma ^{2-2\theta })\textbf{ m}_{1}+(k_{2}d_{0}\varsigma ^{1-\theta }-k_{1}d_{0}\varsigma ^{2-2\theta }) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} (k_{1}d_{1}\varsigma ^{1-\theta }-k_{1}d_{1}\varsigma ^{2-2\theta })\textbf{ m}_{1}+(k_{2}d_{1}\varsigma ^{1-\theta }-k_{1}d_{1}\varsigma ^{2-2\theta }) {\textbf{m}}_{2}. \end{aligned}$$

  • Conformable derivative of normalizing functions of timelike \(T{\textbf{m}}_{2}\)-magnetic curves are obtained

    $$\begin{aligned} D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} \left( \dfrac{d\gamma }{ d\varsigma }\varsigma ^{1-\theta }-k_{1}\varsigma ^{1-\theta }{\textbf{I}} _{\theta }^{x}(\gamma k_{1}\varsigma ^{1-\theta } \right. \\{} & {} \left. +(k_{2}\varsigma ^{1-\theta })^{2})\right) {\textbf{m}}_{1}+\left( -k_{2}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}(\gamma k_{1}\varsigma ^{1-\theta }\right. \\{} & {} \left. +(k_{2}\varsigma ^{1-\theta })^{2})+\varsigma ^{1-2\theta }(1-\theta )k_{2}+\varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma }\right) {\textbf{m}}_{2}, \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} k_{1}d_{4}\varsigma ^{1-\theta }{\textbf{m}}_{1}+k_{2}d_{4}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ D_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} k_{1}d_{5}\varsigma ^{1-\theta }{\textbf{m}}_{1}+k_{2}d_{5}\varsigma ^{1-\theta }{\textbf{m}}_{2}. \end{aligned}$$

    F–W conformable derivative for \({{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right) \), \({{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right) \), \({{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right) \) normalizing functions are obtained

    $$\begin{aligned} {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{t}}\right)= & {} (k_{2}^{2}\varsigma ^{3-3\theta }+k_{1}\gamma \varsigma ^{2-2\theta }) {\textbf{t}}+\left( \dfrac{d\gamma }{d\varsigma }\varsigma ^{1-\theta }+k_{1}\varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}(\gamma k_{1}\varsigma ^{1-\theta }+(k_{2}\varsigma ^{1-\theta })^{2}\right) \\{} & {} +k_{1}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}(k_{1}\gamma \varsigma ^{1-\theta }+(\varsigma ^{1-\theta }k_{2})^{2}){\textbf{m}}_{1}+(-k_{2} \varsigma ^{1-\theta }{\textbf{I}}_{\theta }^{x}(\gamma k_{1}\varsigma ^{1-\theta }+(k_{2}\varsigma ^{1-\theta })^{2}) \\{} & {} +\varsigma ^{1-2\theta }(1-\theta )k_{2}+\varsigma ^{2-2\theta }\dfrac{dk_{2} }{d\varsigma }+k_{2}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}(\varsigma ^{2-2\theta }k_{2}^{2}+k_{1}\gamma \varsigma ^{1-\theta })) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} (k_{1}d_{4}\varsigma ^{1-\theta }-k_{1}d_{4}\varsigma ^{2-2\theta })\textbf{ m}_{1}+(k_{2}d_{4}\varsigma ^{1-\theta }-k_{1}d_{4}\varsigma ^{2-2\theta }) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{{\mathbb {N}}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} (k_{1}d_{5}\varsigma ^{1-\theta }-k_{1}d_{5}\varsigma ^{2-2\theta })\textbf{ m}_{1}+(k_{2}d_{5}\varsigma ^{1-\theta }-k_{1}d_{5}\varsigma ^{2-2\theta }) {\textbf{m}}_{2}. \end{aligned}$$

4.2 F–W conformable derivative for recursion function

  • Recursion functions of \(\Gamma \left( {\textbf{t}}\right) ,\Gamma \left( {\textbf{m}}_{1}\right) ,\Gamma \left( {\textbf{m}}_{2}\right) \) of timelike \(T{\textbf{t}}\)-magnetic curves are given

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {\textbf{I}} _{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( (1-\theta )k_{2}\varsigma ^{-2\theta +1}+\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) +\varsigma ^{-\theta +1}k_{2}\left( k_{1}\varsigma ^{-2\theta +1}\right. \right. \\{} & {} \left. \left. (1-\theta )+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) \right) {\textbf{t}} +\left( k_{2}(1-\theta )\varsigma ^{1-2\theta }+\dfrac{dk_{2}}{d\varsigma } \varsigma ^{2-2\theta }\right) {\textbf{m}}_{1}\\{} & {} -\left( k_{1}(1-\theta )\varsigma ^{1-2\theta }+\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }\right) {\textbf{m}} _{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) \\= & {} -{\textbf{I}} _{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{t}}+\left( k_{1}k_{2}\varsigma ^{2-2\theta }+\dfrac{d\rho }{d\varsigma } \varsigma ^{1-\theta }\right) {\textbf{m}}_{1}-(\varsigma ^{1-\theta }k_{1})^{2} {\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) \\= & {} -{\textbf{I}} _{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) {\textbf{t}}+(\varsigma ^{1-\theta }k_{2})^{2}{\textbf{m}}_{1}-\left( k_{1}k_{2} \varsigma ^{2-2\theta }-\dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }\right) {\textbf{m}}_{2}. \end{aligned}$$

    F–W conformable derivative for \({\varvec{R}}\Gamma \left( {\textbf{t}} \right) \), \({\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right) \), \( {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right) \) recursion functions are obtained

    $$\begin{aligned} {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} \left( -\varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( (1-\theta )k_{2}\varsigma ^{-2\theta +1}+\dfrac{dk_{2}}{ d\varsigma }\varsigma ^{2-2\theta }\right) \right. \right. \\{} & {} +\varsigma ^{-\theta +1}k_{2}\left( k_{1}\varsigma ^{-2\theta +1}(1-\theta )+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) +\varsigma ^{-\theta +1}\dfrac{d}{d\varsigma }(k_{2}(1-\theta )\varsigma ^{1-2\theta }\\{} & {} \left. \left. +\dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) \right) {{\textbf{m}}_{1}} +\left( -\varsigma ^{2-2\theta }k_{2}{\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( (1-\theta )k_{2}\varsigma ^{-2\theta +1}+\dfrac{dk_{2}}{ d\varsigma }\varsigma ^{2-2\theta }\right) \right. \right. \\{} & {} +\varsigma ^{-\theta +1}k_{2}\left( k_{1}\varsigma ^{-2\theta +1}(1-\theta )+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) -\varsigma ^{-\theta +1}\dfrac{d}{d\varsigma }(k_{1}(1-\theta )\varsigma ^{1-2\theta } \\{} & {} +\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma })){{\textbf{m}}_{2}} +\left( -\varsigma ^{2-2\theta }k_{1}\left( \dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) +\varsigma ^{2-2\theta }k_{2}\left( \varsigma ^{2-2\theta } \dfrac{dk_{1}}{d\varsigma }\right) \right. \\{} & {} -\varsigma ^{1-\theta }k_{1}\left( (1-\theta )k_{2}\varsigma ^{-2\theta +1}+\dfrac{ dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) +\varsigma ^{-\theta +1}k_{2} \left( k_{1}\varsigma ^{-2\theta +1}(1 \right. \\{} & {} \left. -\theta )+\dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }\right) + \varsigma ^{-\theta +1}k_{1}\left( k_{2}(1-\theta )\varsigma ^{1-2\theta }+\dfrac{ dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }\right) \\{} & {} \left. -\varsigma ^{-\theta +1}k_{2}\left( k_{1}(1-\theta )\varsigma ^{1-2\theta }+\varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }\right) \right) \textbf{t}, \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} \varsigma ^{-\theta +1}k_{2}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{ d\varsigma }\right) \textbf{t}+\left( \varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) \right. \\{} & {} \left. +\varsigma ^{-\theta +1}\dfrac{d}{d\varsigma }\left( k_{1}k_{2}\varsigma ^{2-2\theta }+\dfrac{d\rho }{d\varsigma }\varsigma ^{1-\theta }\right) -\varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{ d\rho }{d\varsigma }\right) \right) {{\textbf{m}}_{1}} \\{} & {} +\left( \varsigma ^{2-2\theta }k_{2}{\textbf{I}}_{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) -\varsigma ^{-\theta +1}\dfrac{d}{ d\varsigma }(\varsigma ^{1-\theta }k_{1})^{2}-\varsigma ^{1-\theta }k_{2} {\textbf{I}}_{\theta }^{x}\left( k_{1}\varsigma ^{2-2\theta }\dfrac{d\rho }{ d\varsigma }\right) \right) {{\textbf{m}}_{2},} \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -k_{2}\varsigma ^{2-2\theta }\left( \varsigma ^{1-\theta }\dfrac{d\rho }{ d\varsigma }\right) \textbf{t}+\left( k_{1}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) \right. \\{} & {} \left. -\varsigma ^{-\theta +1}k_{1}{\textbf{I}}_{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) +\varsigma ^{-\theta +1}\dfrac{d}{ d\varsigma }(\varsigma ^{1-\theta }k_{2})^{2}\right) {{\textbf{m}}_{1}} +\left( k_{2}\varsigma ^{2-2\theta }{\textbf{I}}_{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) \right. \\{} & {} \left. -\varsigma ^{-\theta +1}k_{2}{\textbf{I}}_{\theta }^{x}\left( k_{2}\varsigma ^{2-2\theta }\dfrac{d\rho }{d\varsigma }\right) -\varsigma ^{-\theta +1}\dfrac{d}{ d\varsigma }\left( k_{1}k_{2}\varsigma ^{2-2\theta }-\dfrac{d\rho }{d\varsigma } \varsigma ^{1-\theta }\right) \right) {{\textbf{m}}_{2}.} \end{aligned}$$

  • Recursion functions of \(\Gamma \left( {\textbf{t}}\right) ,\Gamma \left( {\textbf{m}}_{1}\right) ,\Gamma \left( {\textbf{m}}_{2}\right) \) of timelike \(T{\textbf{m}} _{1}\)-magnetic curves are presented

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {{\textbf{I}} }_{\theta }^{x}\left( -\dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta }+k_{2}\varsigma ^{1-\theta }\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta } \right. \right. \\{} & {} \left. \left. +(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) {{\textbf{t}}}+\varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma }{\textbf{m}}_{1}-\left( \dfrac{dk_{1} }{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-2\theta }(1-\theta )k_{1}\right) {\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) =d_{2} {{\textbf{t}}}+\varsigma ^{2-2\theta }k_{1}k_{2}{\textbf{m}} _{1}-(\varsigma ^{1-\theta }k_{1})^{2}{\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) =d_{3} {{\textbf{t}}}+\mu \varsigma ^{1-\theta }k_{2}{\textbf{m}}_{1}-\mu k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}. \end{aligned}$$

    F–W conformable derivative for \({\varvec{R}}\Gamma \left( {\textbf{t}} \right) \), \({\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right) \), \( {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right) \) recursion functions are obtained

    $$\begin{aligned} {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} \left( \left( - \dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }k_{2} \left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right. \right. \\{} & {} +\varsigma ^{2-2\theta }\dfrac{d\mu }{d\varsigma }k_{1}-\varsigma ^{1-\theta }k_{2}\left( \varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) -\varsigma ^{2-2\theta }k_{1}\varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma } \\{} & {} \left. +\varsigma ^{2-2\theta }k_{2}\left( \varsigma ^{2-2\theta }\dfrac{dk_{1}}{ d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) {{\textbf{t}}} +\left( \varsigma ^{1-\theta }k_{1}{{\textbf{I}}}_{\theta }^{x}\left( -\dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta } \right. \right. \\{} & {} \left. +\varsigma ^{1-\theta }k_{2}\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) +\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }\left( \varsigma ^{1-\theta }\dfrac{d\mu }{d\varsigma }\right) \\{} & {} \left. -\varsigma ^{2-2\theta }k_{1}{{\textbf{I}}}_{\theta }^{x}\left( -\dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }k_{2}\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) \right) {\textbf{m}}_{1} \\{} & {} +\left( \varsigma ^{1-\theta }k_{2}{{\textbf{I}}}_{\theta }^{x}\left( -\dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-\theta }k_{2}\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) \right. \\{} & {} -\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }\left( \varsigma ^{2-2\theta }\dfrac{dk_{1}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) -\varsigma ^{2-2\theta }k_{2}{{\textbf{I}}}_{\theta }^{x}\left( - \dfrac{d\mu }{d\varsigma }\varsigma ^{2-2\theta } \right. \\{} & {} \left. \left. +\varsigma ^{1-\theta }k_{2}\left( \dfrac{dk_{1}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{1}\right) \right) \right) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} \left( k_{1}d_{2}\varsigma ^{1-\theta }+\varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\varsigma ^{2-2\theta }k_{1}k_{2})-\varsigma ^{2-2\theta }d_{2}k_{1}\right) {\textbf{m}}_{1} \\{} & {} +\left( -\varsigma ^{2-2\theta }d_{2}k_{2}+k_{2}d_{2}\varsigma ^{1-\theta }-\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }(\varsigma ^{1-\theta }k_{1})^{2}\right) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} \left( k_{1}d_{3}\varsigma ^{1-\theta }+\varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\mu \varsigma ^{1-\theta }k_{2})-\varsigma ^{2-2\theta }d_{3}k_{1}\right) {\textbf{m}}_{1} \\{} & {} \left( k_{2}d_{3}\varsigma ^{1-\theta }-\varsigma ^{2-2\theta }d_{3}k_{2}-\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }(\mu k_{1}\varsigma ^{1-\theta })\right) {\textbf{m}}_{2}. \end{aligned}$$

  • Recursion functions of \(\Gamma \left( {\textbf{t}}\right) ,\Gamma \left( {\textbf{m}}_{1}\right) ,\Gamma \left( {\textbf{m}}_{2}\right) \) of timelike \(T{\textbf{m}} _{2}\)-magnetic curves are presented

    $$\begin{aligned} {\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} -{{\mathbb {N}}}\left( {\textbf{t}} \times D_{\theta }\Gamma \left( {\textbf{t}}\right) \right) \\= & {} {\textbf{I}} _{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( \dfrac{dk_{2}}{ d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-2\theta }(1-\theta )k_{2}\right) \right. \\{} & {} \left. +k_{2}\varsigma ^{2-2\theta }\dfrac{d\gamma }{d\varsigma }\right) \textbf{t}+ \left( \dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) {{\textbf{m}}_{1}-}\dfrac{d\gamma }{d\varsigma } \varsigma ^{1-\theta }{{\textbf{m}}_{2},} \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{1}\right) \right) =d_{6} \textbf{t}+\gamma k_{2}\varsigma ^{1-\theta }{\textbf{m}}_{1}+\gamma k_{1}\varsigma ^{1-\theta }{\textbf{m}}_{2}, \\ {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} -{{\mathbb {N}}}\left( \textbf{ t}\times D_{\theta }\Gamma \left( {\textbf{m}}_{2}\right) \right) =d_{7} \textbf{t}+(\varsigma ^{1-\theta }k_{2})^{2}{{\textbf{m}}_{1}+} \varsigma ^{2-2\theta }k_{1}k_{2}{{\textbf{m}}_{2}.} \end{aligned}$$

    F–W conformable derivative for \({\varvec{R}}\Gamma \left( {\textbf{t}} \right) \), \({\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right) \), \( {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right) \) recursion functions are given

    $$\begin{aligned} {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{t}}\right)= & {} \left( \left( -\varsigma ^{1-\theta }k_{1}(\varsigma ^{2-2\theta } \dfrac{dk_{2}}{d\varsigma }+(-\theta +1)\varsigma ^{1-2\theta }k_{2})+k_{2}\varsigma ^{2-2\theta }\dfrac{d\gamma }{d\varsigma }\right) \right. \\{} & {} +k_{1}\varsigma ^{1-\theta }\left( \dfrac{dk_{2}}{d\varsigma } \varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) -k_{2}\varsigma ^{2-2\theta }\dfrac{d\gamma }{d\varsigma } \\{} & {} -\varsigma ^{2-2\theta }k_{1}\left( \varsigma ^{2-2\theta } \dfrac{dk_{2}}{d\varsigma }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) +\varsigma ^{3-3\theta }k_{2}\dfrac{d\gamma }{d\varsigma }){\textbf{t}}\\{} & {} +\left( \varsigma ^{1-\theta }k_{1}{\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma } +(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) +k_{2}\varsigma ^{2-2\theta }\dfrac{ d\gamma }{d\varsigma }\right) \right. \\{} & {} +\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }\left( \dfrac{dk_{2} }{d\varsigma }\varsigma ^{2-2\theta }+(1-\theta )\varsigma ^{1-2\theta }k_{2}\right) -\varsigma ^{2-2\theta }k_{1}{\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{ d\varsigma } \right. \right. \\{} & {} \left. \left. \left. +\varsigma ^{1-2\theta }(1-\theta )k_{2}\right) +k_{2}\varsigma ^{2-2\theta }\dfrac{ d\gamma }{d\varsigma }\right) \right) {{\textbf{m}}_{1}}+\left( \varsigma ^{1-\theta }k_{2} {\textbf{I}}_{\theta }^{x}\left( -\varsigma ^{1-\theta }k_{1}\left( \varsigma ^{2-2\theta }\dfrac{dk_{2}}{d\varsigma } \right. \right. \right. \\{} & {} \left. \left. +\varsigma ^{1-2\theta }(1-\theta )k_{2}\right) +k_{2}\varsigma ^{2-2\theta }\dfrac{ d\gamma }{d\varsigma }\right) -\varsigma ^{1-\theta }\dfrac{d}{d\varsigma }\left( \dfrac{ d\gamma }{d\varsigma }\varsigma ^{1-\theta }\right) \\{} & {} \left. \left. -\varsigma ^{2-2\theta }k_{2}{\textbf{I}}_{\theta }^{x}(-\varsigma ^{1-\theta }k_{1}\left( \dfrac{dk_{2}}{d\varsigma }\varsigma ^{2-2\theta }+\varsigma ^{1-2\theta }(1-\theta )k_{2}\right) +\varsigma ^{2-2\theta }\dfrac{ d\gamma }{d\varsigma }k_{2}\right) \right) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right)= & {} \left( k_{1}d_{6}\varsigma ^{1-\theta } + \varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\gamma k_{2}\varsigma ^{1-\theta })\mathbf {-}\varsigma ^{2-2\theta }k_{1}d_{6}\right) {\textbf{m}}_{1} \\{} & {} +\left( k_{2}d_{6}\varsigma ^{1-\theta }+\varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\gamma k_{1}\varsigma ^{1-\theta })-k_{2}d_{6}\varsigma ^{2-2\theta }\right) {\textbf{m}}_{2}, \\ {\widetilde{D}}_{\theta }{\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right)= & {} \left( k_{1}d_{7}\varsigma ^{1-\theta } + \varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\varsigma ^{1-\theta }k_{2})^{2}\mathbf {-}\varsigma ^{2-2\theta }d_{7}k_{1}\right) {\textbf{m}}_{1} \\{} & {} +\left( k_{2}d_{7}\varsigma ^{1-\theta } + \varsigma ^{1-\theta }\dfrac{d}{ d\varsigma }(\varsigma ^{2-2\theta }k_{1}k_{2})-d_{7}k_{2}\varsigma ^{2-2\theta }\right) {\textbf{m}}_{2}. \end{aligned}$$

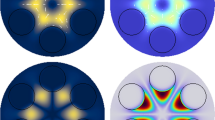
Numerically the effects of conformable axial heat conduction manipulation of fluids at the conformable microscale, typically in channels or chambers with dimensions on the order of solid micrometers with simultaneously modeling laminar flow for \({\varvec{R}}\Gamma \left( {\textbf{t}}\right) \), \({\varvec{R}}\Gamma \left( {\textbf{m}}_{1}\right) \), \( {\varvec{R}}\Gamma \left( {\textbf{m}}_{2}\right) \) Figs. 1, 2 and 3.

Fig. 1
figure 1

Electromagnetic \({\varvec{R}}\Gamma \left( \textbf{t }\right) \) model with conformable axial heat density

Full size image
Fig. 2
figure 2

Electromagnetic \({\varvec{R}}\Gamma \left( \textbf{m }_{1}\right) \) model with conformable axial heat density

Full size image
Fig. 3
figure 3

Electromagnetic \({\varvec{R}}\Gamma \left( \textbf{m }_{2}\right) \) model with conformable axial heat density

Full size image

5 Conclusions

In this section, magnetic timelike curves are examined using Bishop model in Minkowski space. First, the conformable derivatives of \(\Gamma \left( {\textbf{t}}\right) \), \(\Gamma \left( {\textbf{m}}_{1}\right) \), \(\Gamma \left( {\textbf{m}}_{2}\right) \) Lorentz force are calculated for these curves. Furthermore, we have computed normalizing and recursion operators of magnetic vector fields according to Bishop model. Finally, we have determined F–W conformable derivatives of normalizing and recursion operators.