1 Introduction

Many physical phenomena that arising in various fields of science can be described by nonlinear evolution equations (NLEEs) for instance optics, plasma, solid state physics, chemical physics, and mathematical physics. To understand these nonlinear phenomena, many physicist and mathematicians have made efforts to get various exact solutions of them. The investigation of the exact solutions is an important to provide better information about the mechanism and the applications of NLEEs. Abundant methods are extensively studied to obtain exact solutions, for example the B\(\ddot{a}\)cklund transform (Rogers and Shadwick 1982; El-Sabbagh et al. 2015), the extended tanh-function method (Abdelsalam 2017), the F-expansion method (Zhou et al. 2003), sine-cosine method (Wazwaz 2004), the Jacobi elliptic function (JEF) method (Liu et al. 2001), the Kudryashov method (Kudryashov 2012; Malik et al. 2023), the extended Kudryashov method (Hassan et al. 2014, 2022a), the Bernoulli sub-equation function method (Baskonus et al. 2015), the lie point symmetry method (Naz 2012; Hassan et al. 2022b; Yong et al. 2012) and other methods (Hassan 2004; Khater et al. 2010; Shehata 2010; Shehata and Abu-Amra 2018).

In this study, we apply the Bernoulli sub-equation function method to construct exact solutions of two nonlinear models. Also, we obtain the conservation laws by the Lie symmetry method and multiplier approach. The first model is (2+1)-dimensional hyperbolic nonlinear Schrödinger (HNLS) equation (Apeanti et al. 2019; Tebue et al. 2020; Seadawy et al. 2018; Guo and Lin 2012), which given as

$$\begin{aligned} \begin{array}{l} i\,\Theta _{y}-\frac{1}{2}\,(\Theta _{xx}-\Theta _{tt})+|\Theta |^{2}\,\Theta =0, \end{array} \end{aligned}$$
(1.1)

and the second model (2+1)-dimensional Heisenberg ferromagnetic spin chain (HFSC) equation (Bashar et al. 2021; Han et al. 2022; Hosseini et al. 2021; Sahoo and Tripathy 2022), in the form

$$\begin{aligned} \begin{array}{l} i\,\Theta _{t}+\alpha _{1}\,\Theta _{xx}+\alpha _{2}\,\Theta _{yy}+\alpha _{3}\,\Theta _{xy}-\alpha _{4}\,|\Theta |^{2}\,\Theta =0, \end{array} \end{aligned}$$
(1.2)

where \(\Theta (x,y,t)\) is a complex envelope of the electric field, \(x,\,y\) and t denote the scaled spatial and time coordinates, respectively and the coefficients \(\alpha _{i},\,(i=1,2,3,4)\) are real constants given by

$$\begin{aligned} \alpha _{1}=\delta ^{4}\,(\chi +\chi _{2}),\,\,\,\alpha _{2}=\delta ^{4}\,(\chi _{1}+\chi _{2}),\,\,\,\alpha _{3}=2\,\delta ^{4}\,\chi _{2},\,\,\,\alpha _{4}=2\,\delta ^{4}\,\Omega , \end{aligned}$$

where the parameters \(\chi ,\,\chi _{1}\) represent the coefficients of bilinear exchange interactions in the xy-plane, \(\chi _{2}\) denotes the neighboring interaction along the diagonal, \(\Omega\) is the uniaxial crystal field anisotropy parameter, and \(\delta\) is a lattice parameter. Equation (1.1) expresses of the elevation of water wave surface for slowly modulated wave trains in deep water in hydrodynamics, and also governs the propagation of electromagnetic fields in self-focusing and normally dispersive planar wave guides in optics. Moreover, this equation is used to describe the dynamics of optical soliton promulgation in optical fibers. The (2+1)-dimensional HFSC equation show a significant role in modern theory of magnets which defines nonlinear dynamics of magnets. Heisenberg-type models for spin-spin interactions have been proposed to explain the magnetic ordering in ferromagnetic materials. Also, Eq. (1.2) can be used to depict the propagation of long waves, which has many applications in the percolation of water.

Different methods have been used to extract solutions for Eq. (1.1). Apeanti et al. (2019) using generalized elliptic equation rational expansion method to construct several types of complex solutions. The exact solutions of (1.1) was considered by Tebue et al. (2020) in terms of JEFs. Also, Seadawy et al. (2018) derived new many solutions such as dark, bright, combined dark-bright, singular and combined singular solitons by using the extended sinh-Gordon equation expansion method. Moreover, Guo and Lin (2012) applied the classical Lie group symmetry method to obtain the Lie-point symmetries and also derive exact solutions. Several types of solutions of Eq. (1.2) are obtained by many researchers with different techniques (Bashar et al. 2021; Han et al. 2022; Sahoo and Tripathy 2022). This includes the \(\exp (-\varphi (\xi ))\)-expansion and the extended tanh-function methods in Bashar et al. (2021), the complete discrimination system method (Han et al. 2022) and modified version of the Jacobi elliptic expansion method (Hosseini et al. 2021). Although, many authors studied (2+1)-dimensional HNLS and (2+1)-dimensional HFSC equations, we study these models by the Bernoulli sub-equation function method to obtain other solutions. Furthermore, conservation laws for these models are derived by using multiplier approach (Naz 2012).

In the 19th century, Lie group classification method is initialed by Sophus Lie Fritzsche (1999) and studied by many authors (Naz 2012; Hassan et al. 2022b; Yong et al. 2012; Hassan et al. 2022; Singh et al. 2022; Devi et al. 2021). Lie symmetry analysis is one of the important approaches to investigate the exact solutions of nonlinear partial differential equations  ( NLPDEs ). Lie point symmetry and extended F-expansion methods are applied to obtain exact solutions and conservation laws of ion sound and Langmuir waves (ISLWs) model (Hassan et al. 2022). In Singh et al. (2022), the lie group theoretic approach was employed to find the similarity reductions and analytic solutions of the (2+1)-dimensional modified dispersive water-wave system. A number of methods for finding exact solutions of NLPDEs have been applied by the authors in Malik et al. (2023); Akbulut et al. (2023) and Mirzazadeh et al. (2023). The goal of this paper is to obtain exact solutions and conservation laws for the models (1.1) and (1.2).

This paper is formed as follows: Firstly, we summarized the analytical method that we will use to construct novel exact solutions for Eqs. (1.1) and (1.2) in Sect. 2. In Sect. 3, we get the solutions of the studied models. The geometrical shape of some solutions in the form of two-dimensional and three-dimensional have been plotted. Furthermore, the Lie point symmetry, group transformations, new solutions corresponding to the symmetry groups and the conservation laws for (1.1) and (1.2) are obtained in Sects. 4 and 5, respectively. Finally, conclusions of the paper are presented.

2 Description of the Bernoulli sub-equation function method

In this section, we summarize the Bernoulli sub-equation function method (Baskonus et al. 2015) as follows:

Consider a NLPDE with independent variables \(x,\,y\) and t

$$\begin{aligned} G(p,p_{x},p_{y},p_{t},p_{xx},p_{yy},p_{tt},...)=0. \end{aligned}$$
(2.1)

Step 1 Suppose that \(\,p(x,y,t)=P(\alpha ),\,\, \alpha =x+\rho \,y-\sigma \,t+\alpha _{0}.\) where \(\rho\) and \(\sigma\) are constants to be evaluated later and \(\alpha _{0}\) is an arbitrary constant. Then (2.1) is transformed to an ordinary differential equation (ODE)

$$\begin{aligned} H(P,\, P^{\prime },\, P^{\prime \prime },...)=0, \end{aligned}$$
(2.2)

Step 2 We propose the solutions of (2.2) as the following:

$$\begin{aligned} p(x,y,t)=P(\alpha )= \sum _{i=0}^{K}\, d_{i} W^{i}(\alpha ), \end{aligned}$$
(2.3)

where

$$\begin{aligned} W^{\prime }(\alpha )= a\,W(\alpha )+b\,W^{S}(\alpha ),\,a\ne 0,\,b\ne 0,\,\,\,S \in R-\{{0,1\}}. \end{aligned}$$
(2.4)

By balancing principle, we can calculate a relationship for K and S. The balancing number K is a positive integer and we will take the corresponding S in (2.4) by various positive integer values to derive many solitary wave solutions of Eq. (2.2). Also, the solution of Bernoulli differential Eq. (2.4) given as

$$\begin{array}{*{20}l} {W(\alpha ) = \left[ {\frac{{ - b}}{a} + \frac{c}{{e^{{a{\kern 1pt} (S - 1){\kern 1pt} \alpha }} }}} \right]^{{\frac{1}{{1 - S}}}} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a \ne b,} \hfill \\ {W(\alpha ) = \left[ {\frac{{(c - 1) + (c + 1){\mkern 1mu} {\text{tanh}}\left( {\frac{{a{\mkern 1mu} (1 - S){\mkern 1mu} \alpha }}{2}} \right)}}{{1 - {\text{tanh}}\left( {\frac{{a{\mkern 1mu} (1 - S){\mkern 1mu} \alpha }}{2}} \right)}}} \right]^{{\frac{1}{{1 - S}}}} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a = b,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} c \in R.} \hfill \\ \end{array}$$
(2.5)

Step 3 Putting (2.3) with (2.4) in (2.2), we can obtain a polynomial in \(W^{i}(\alpha )\). Setting each coefficients of it to zero, we get a system of algebraic equations for \(d_{i}, (i=0,1,\, 2,\ldots , \, K)\) and a. Solving the system by using Mathematica or Maple and substituting the coefficients into (2.3), then the general formula solutions of the NLPDE (2.1) can be constructed.

Step 4 Substituting the solutions of \(W(\alpha )\) that given in (2.5) into the general formal solutions that we obtained, we get exact solutions of Eq. (2.1).

3 The exact solutions

In this section, we apply the Bernoulli sub-equation function method to obtain the exact solutions of the studied models (1.1) and (1.2).

3.1 The exact solution of (2+1)-dimensional HNLS equation

To get the solutions of (1.1), we look for the solution as

$$\begin{aligned} \Theta (x,y,t)=P(\alpha )\,e^{i\,\beta },\,\,\,\,\alpha =x+\rho \,y-\sigma \,t+\alpha _{0},\,\,\,\,\beta =l\,x+r\,y+\omega \,t,\end{aligned}$$
(3.1)

where \(\rho ,\,\sigma ,\,l,\,r\) and \(\omega\) are constants to be calculated. Putting (3.1) into (1.1) and splitting the real and the imaginary parts, we get

$$\begin{aligned} (\rho -l-\sigma \,\omega )\,P^{\prime }=0\,\,\,\,\,\Rightarrow \rho =(l+\sigma \,\omega ), \end{aligned}$$
(3.2)
$$\begin{aligned} (\sigma ^{2}-1)\,P^{\prime \prime }+(l^{2}-\omega ^{2}-2\,r)\,P+2\,P^{3}=0. \end{aligned}$$
(3.3)

By applying the Bernoulli sub-equation function method and after balancing procedure, we get \(S=K+1\). Now, we may choose the following three values of the parameter K to construct new exact solitary wave solutions of Eq. (1.1):

Case 1 If we put \(K=1\), then \(S=2\). Thus (2.3) and (2.4) take the form

$$\begin{aligned} P(\alpha )=d_{0}+d_{1}\,W(\alpha ), \end{aligned}$$
(3.4)
$$\begin{aligned} W^{\prime }(\alpha )= a\,W(\alpha )+b\,W^{2}(\alpha ), \end{aligned}$$
(3.5)

where \(\,d_{0}, \,d_{1}, \,d_{2},\,a\) and b are undetermined constants. Putting (3.4) into (3.3) and using (3.5), we get a polynomial in \(W(\alpha )\). Setting all coefficients of it equal to zero and with the help of Maple, we have

$$\begin{aligned} a=\pm {\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{{1-\sigma }^{2}}}} },\,\,d_{{0}}=\pm \frac{1}{2}\,\sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}},\,\,d_{{1}}=\pm \sqrt{1-{\sigma }^{2}}\,\,b. \end{aligned}$$
(3.6)

Substituting (3.6) into (3.4) with (2.5) and (3.1) we obtain the solution of model (1.1) as,

$$\Theta (x,y,t) = \left\{ {\begin{array}{*{20}l} {\left[ { \pm \frac{1}{2}{\mkern 1mu} \sqrt {2{\mkern 1mu} \omega ^{2} + 4{\mkern 1mu} r - 2{\mkern 1mu} l^{2} } \pm \frac{{{\mkern 1mu} b{\mkern 1mu} \sqrt {1 - \sigma ^{2} } {\mkern 1mu} }}{{ \pm b{\mkern 1mu} \sqrt {\frac{{1 - \sigma ^{2} }}{{2{\mkern 1mu} \omega ^{2} + 4{\mkern 1mu} r - 2{\mkern 1mu} l^{2} }}} + \frac{c}{{{\text{e}}^{{ \pm \sqrt {\frac{{2{\kern 1pt} \omega ^{2} + 4{\kern 1pt} r - 2{\kern 1pt} l^{2} }}{{1 - \sigma ^{2} }}} {\kern 1pt} {\kern 1pt} \alpha }} }}}}} \right]e^{{i{\kern 1pt} \beta }} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a \ne b,} \hfill \\ {} \hfill \\ {\sqrt {2{\mkern 1mu} \omega ^{2} + 4{\mkern 1mu} r - 2{\mkern 1mu} l^{2} } \left[ { \pm \frac{1}{2} \pm \frac{{1 - {\text{tanh}}\left( { \pm \frac{1}{2}{\mkern 1mu} \sqrt {\frac{{2{\mkern 1mu} \omega ^{2} + 4{\mkern 1mu} r - 2{\mkern 1mu} l^{2} }}{{1 - \sigma ^{2} }}} {\mkern 1mu} {\mkern 1mu} \alpha } \right)}}{{(c - 1) + (c + 1){\mkern 1mu} {\text{tanh}}\left( { \pm \frac{1}{2}{\mkern 1mu} \sqrt {\frac{{2{\mkern 1mu} \omega ^{2} + 4{\mkern 1mu} r - 2{\mkern 1mu} l^{2} }}{{1 - \sigma ^{2} }}} {\mkern 1mu} {\mkern 1mu} \alpha } \right)}}} \right]e^{{i{\kern 1pt} \beta }} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a = b,} \hfill \\ \end{array} } \right.$$
(3.7)

where \(\alpha =x+\rho \,y-\sigma \,t+\alpha _{0}\) and \(\beta =l\,x+r\,y+\omega \,t\).

Case 2 If we take \(K=2\), then \(S=3\). Therefor (2.3) and (2.4) take the form

$$\begin{aligned}{} & {} P(\alpha )=d_{0}+d_{1}\,W(\alpha )+d_{2}\,W^2(\alpha ), \end{aligned}$$
(3.8)
$$\begin{aligned}{} & {} W^{\prime }(\alpha )= a\,W(\alpha )+b\,W^{3}(\alpha ). \end{aligned}$$
(3.9)
Fig. 1
figure 1

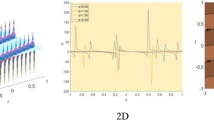
a–f 3D and 2D the solitary wave solution (3.7) when \(a=b\) are plotted with the parameters \(l=\sigma = r = 0.5, \,\omega = 1,\,c=0.8,\,\alpha _{0}= 1\) and \(y=1\) for 3D plots, \(y=1\) and \(t = 1\) for 2D plots

Full size image

Setting (3.8) into (3.3) and using (3.9), we get a polynomial in \(W(\alpha )\). Setting all coefficients of it equal to zero and with the aid of Maple, we obtain

$$\begin{aligned} a=\pm \frac{1}{2}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} },\,\,d_{{0}}=\pm \frac{1}{2}\,\sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}},\,\,d_{{1}}=0,\,\,d_{{2}}=\pm 2\,\sqrt{1-{\sigma }^{2}}\,\,b. \end{aligned}$$
(3.10)

Putting (3.10) into (3.8) with (2.5) and (3.1) we obtain the solution of model (1.1) as,

$$\begin{aligned} \Theta (x,y,t)=\left\{ \begin{array}{l}\left [\pm \frac{1}{2}\,\sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}\pm \frac{2\,b\,\sqrt{1-{\sigma }^{2}}}{ \pm 2\,b\,{\sqrt{\frac{1-{\sigma }^{2}}{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}}}+\frac{c}{{\textrm{e}^{{\pm \sqrt{\frac{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}{1-{\sigma }^{2}}}\,\,\alpha }}}}} \right ]\,e^{i\,\beta },\,\,\,\,\,\,\,\,\,\,\,\,\,\,a\ne b, \\ \\ \sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}\,\left [\pm \frac{1}{2}\pm \frac{1-\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} }\,\,\alpha )}{(c-1)+(c+1)\,\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} }\,\,\alpha )}\right ]\,\,e^{i\,\beta },\,\,\,\,\,\,\,\,\,a= b. \end{array}\right. \end{aligned}$$
(3.11)
Fig. 2
figure 2

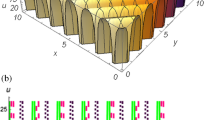
a–f 3D and 2D the solution (3.11) when \(a\ne b\) are plotted with the parameters \(l=\sigma = r = 0.5, \,\omega = 1,\,b=0.6,\,c=0.8,\,\alpha _{0}= 1\) and \(y=1\) for 3D plots, \(y=1\) and \(t = 1\) for 2D plots

Full size image

Case 3 If we let \(K=3\), then \(S=4\). So (2.3) and (2.4) take the form

$$\begin{aligned}{} & {} P(\alpha )=d_{0}+d_{1}\,W(\alpha )+d_{2}\,W^2(\alpha )+d_{3}\,W^3(\alpha ), \end{aligned}$$
(3.12)
$$\begin{aligned}{} & {} W^{\prime }(\alpha )= a\,W(\alpha )+b\,W^{4}(\alpha ). \end{aligned}$$
(3.13)

Substituting (3.12) into (3.3) and using (3.13), we get a polynomial in \(W(\alpha )\). Setting all coefficients of it equal to zero and with the Maple software, we get

$$\begin{aligned} a=\pm \frac{1}{3}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} },\,\,d_{{0}}=\pm \frac{1}{2}\,\sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}},\,\,d_{{1}}=d_{{2}}=0,\,\,d_{{3}}=\pm \,3\,\sqrt{1-{\sigma }^{2}}\,\,b. \end{aligned}$$
(3.14)

Putting (3.14) into (3.12) with (2.5) and (3.1) we have the solution of model (1.1) as,

$$\begin{aligned} \Theta (x,y,t)=\left\{ \begin{array}{l}\left [\pm \frac{1}{2}\,\sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}\pm \frac{3\,b\,\sqrt{1-{\sigma }^{2}}}{ \pm 3\,b\,{\sqrt{\frac{1-{\sigma }^{2}}{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}}}+\frac{c}{{\textrm{e}^{{\pm \sqrt{\frac{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}{1-{\sigma }^{2}}}\,\,\alpha }}}}} \right ]\,e^{i\,\beta },\,\,\,\,\,\,\,\,\,\,\,\,\,\,a\ne b,\\ \\ \sqrt{2\,{\omega }^{2}+4\,r-2\,{l}^{2}}\,\left [\pm \frac{1}{2}\pm \frac{1-\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} }\,\,\alpha )}{(c-1)+(c+1)\,\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{\frac{ {2\,{\omega }^{2}+4\,r-2\,{l}^{2}}}{{1-{\sigma }^{2}}}} }\,\,\alpha )}\right ]\,\,e^{i\,\beta },\,\,\,\,\,\,\,\,\,a= b. \end{array}\right. \end{aligned}$$
(3.15)

From the previous cases when \(a\ne b\), the solutions that we obtained are similar to each others, but with a simple difference in the second term of these solutions. In the other hand at \(a= b\) the solutions are the same.

3.2 The exact solution of (2+1)-dimensional HFSC equation

To construct the solutions of (1.2). Putting (3.1) in (1.2) and splitting the real and the imaginary parts, we have

$$\begin{aligned}{} & {} [l\,(2\,\alpha _{1}+\rho \,\alpha _{3})+r\,(2\,\rho \,\alpha _{2}+\alpha _{3})-\sigma ]\,P^{\prime }=0\,\,\,\,\,\Rightarrow \sigma =l\,(2\,\alpha _{1}+\rho \,\alpha _{3})+r\,(2\,\rho \,\alpha _{2}+\alpha _{3}), \end{aligned}$$
(3.16)
$$\begin{aligned}{} & {} (\alpha _{1}+\alpha _{2}\,\rho ^{2}+\alpha _{3}\,\rho )\,P^{\prime \prime }-(\omega +\alpha _{1}\, l^{2}+\alpha _{2}\,r^2+\alpha _{3}\,r\,l)\,P-\alpha _{4}\,P^{3}=0. \end{aligned}$$
(3.17)

By using the Bernoulli sub-equation function method and after balancing procedure, we get \(S=K+1\). Now, we may choose the following three values of the parameter K to construct new exact solitary wave solutions of Eq. (1.2):

Case 1 If we put \(K=1\), then \(S=2\). Thus (2.3) and (2.4) are take the same form that given in (3.4) and (3.5), respectively. Putting (3.4) into (3.17) and using (3.5), we get a polynomial in \(W(\alpha )\). Setting all coefficients of it equal to zero and with the help of Maple, we have

$$\begin{aligned} a=\pm \sqrt{-{\frac{2\,({l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2}\alpha _{{2 }}+\omega )}{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{ {1}}}}},\,\,\,\,d_{{0}}=\pm \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2} \alpha _{{2}}+\omega }{\alpha _{{4}}}}},\, \end{aligned}$$
$$\begin{aligned} d_{{1}}=\pm \sqrt{{\frac{2\,({\rho }^{2}\alpha _{{2}}+\alpha _{{1}} +\rho \,\alpha _{{3}})}{\alpha _{{4}}}}}\,b. \end{aligned}$$
(3.18)

Substituting (3.18) into (3.4) with (2.5) and (3.1) we obtain the solution of model (1.2) as,

$$\Theta (x,y,t) = \left\{ \begin{gathered} \left[ { \pm \sqrt { - \frac{{l^{2} \alpha _{1} + lr\alpha _{3} + r^{2} \alpha _{2} + \omega }}{{\alpha _{4} }}} \pm \frac{{b{\mkern 1mu} \sqrt {\frac{{2{\mkern 1mu} (\rho ^{2} \alpha _{2} + \rho {\mkern 1mu} \alpha _{3} + \alpha _{1} )}}{{\alpha _{4} }}} }}{{ \pm b\sqrt { - \frac{{\rho ^{2} \alpha _{2} + \rho {\mkern 1mu} \alpha _{3} + \alpha _{1} }}{{2{\mkern 1mu} l^{2} \alpha _{1} + 2{\mkern 1mu} lr\alpha _{3} + 2{\mkern 1mu} r^{2} \alpha _{2} + 2{\mkern 1mu} \omega }}} + \frac{c}{{{\text{e}}^{{ \pm \sqrt { - \frac{{2{\kern 1pt} l^{2} \alpha _{1} + 2{\kern 1pt} lr\alpha _{3} + 2{\kern 1pt} r^{2} \alpha _{2} + 2{\kern 1pt} \omega }}{{\rho ^{2} \alpha _{2} + \rho {\kern 1pt} \alpha _{3} + \alpha _{1} }}} {\kern 1pt} {\kern 1pt} \alpha }} }}}}} \right]{\mkern 1mu} e^{{i{\kern 1pt} \beta }} ,{\mkern 1mu} {\mkern 1mu} a \ne b, \hfill \\ \sqrt { - \frac{{l^{2} \alpha _{1} + lr\alpha _{3} + r^{2} \alpha _{2} + \omega }}{{\alpha _{4} }}} \left[ { \pm 1 \pm \frac{{1 - {\text{tanh}}\left( { \pm \frac{1}{2}{\mkern 1mu} \sqrt { - \frac{{2{\mkern 1mu} l^{2} \alpha _{1} + 2{\mkern 1mu} lr\alpha _{3} + 2{\mkern 1mu} r^{2} \alpha _{2} + 2{\mkern 1mu} \omega }}{{\rho ^{2} \alpha _{2} + \rho {\mkern 1mu} \alpha _{3} + \alpha _{1} }}} {\mkern 1mu} {\mkern 1mu} \alpha } \right)}}{{(c - 1) + (c + 1){\mkern 1mu} {\text{tanh}}\left( { \pm \frac{1}{2}{\mkern 1mu} \sqrt { - \frac{{2{\mkern 1mu} l^{2} \alpha _{1} + 2{\mkern 1mu} lr\alpha _{3} + 2{\mkern 1mu} r^{2} \alpha _{2} + 2{\mkern 1mu} \omega }}{{\rho ^{2} \alpha _{2} + \rho {\mkern 1mu} \alpha _{3} + \alpha _{1} }}} {\mkern 1mu} {\mkern 1mu} \alpha } \right)}}} \right]{\mkern 1mu} e^{{i{\kern 1pt} \beta }} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} a = b, \hfill \\ \end{gathered} \right.$$
(3.19)

where \(\alpha =x+\rho \,y-\sigma \,t+\alpha _{0}\) and \(\beta =l\,x+r\,y+\omega \,t\).

Case 2 If we take \(K=2\), then \(S=3\). Thus (2.3) and (2.4) take the same form that we obtained in (3.8) and (3.9), respectively. Setting (3.8) into (3.17) and using (3.9), we get a polynomial in \(W(\alpha )\). Putting all coefficients of it equal to zero and with the aid of Maple, we get

$$\begin{aligned} a=\pm \frac{1}{2}\sqrt{-{\frac{2\,({l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2}\alpha _{{2 }}+\omega )}{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{ {1}}}}},\,d_{{0}}=\pm \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2} \alpha _{{2}}+\omega }{\alpha _{{4}}}}},\,d_{{1}}=0, \end{aligned}$$
$$\begin{aligned} \,d_{{2}}=\pm 2\,\sqrt{{\frac{2\,({\rho }^{2}\alpha _{{2}}+\alpha _{{1}} +\rho \,\alpha _{{3}})}{\alpha _{{4}}}}}\,b. \end{aligned}$$
(3.20)

Putting (3.20) into (3.8) with (2.5) and (3.1) we obtain the solution of model (1.2) as,

$$\begin{aligned} \Theta (x,y,t)=\left\{ \begin{array}{l}\left [\pm \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _ {{3}}+{r}^{2}\alpha _{{2}}+\omega }{\alpha _{{4}}}}}\pm \frac{2\,b\,\sqrt{{ \frac{2\,({\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}})}{\alpha _ {{4}}}}}}{ \pm 2\,b\sqrt{-{\frac{{\rho }^{2}\alpha _{{2}}+\rho \, \alpha _{{3}}+\alpha _{{1}}}{2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2 \,{r}^{2}\alpha _{{2}}+2\,\omega }}}+\frac{c}{ {\textrm{e}^{\pm \sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha }} } } \right ]\,e^{i\,\beta },\,a\ne b, \\ \\ \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _ {{3}}+{r}^{2}\alpha _{{2}}+\omega }{\alpha _{{4}}}}}\,\left [\pm 1\pm \frac{1-\hbox {tanh}(\pm \frac{1}{2}\,{{\sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha } })}{(c-1)+(c+1)\,\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha })}\right ]\,\,e^{i\,\beta },\,\,\,\,\,a= b. \end{array}\right. \end{aligned}$$
(3.21)
Fig. 3
figure 3

a-f 3D and 2D the solitary wave solution (3.21) at \(a\ne b\) are plotted with the parameters \(l=1.5,\, r = 0.5, \,\omega = 1,\,\rho =0.7,\,b=0.6,\,c=0.8,\,\alpha _{0}= 1\) and \(y=1\) for 3D plots, \(y=1\) and \(t = 1\) for 2D plots

Full size image

Case 3 If we let \(K=3\), then \(S=4\). So (2.3) and (2.4) become the same equations (3.12) and (3.13). Substituting (3.12) into (3.17) and using (3.13), we get a polynomial in \(W(\alpha )\). Setting all coefficients of it equal to zero and with the Maple software, we have

$$\begin{aligned} a=\pm \frac{1}{3}\sqrt{-{\frac{2\,({l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2}\alpha _{{2 }}+\omega )}{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{ {1}}}}},\,d_{{0}}=\pm \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _{{3}}+{r}^{2} \alpha _{{2}}+\omega }{\alpha _{{4}}}}},\,d_{{1}}=d_{{2}}=0, \end{aligned}$$
$$\begin{aligned} \,d_{{3}}=\pm 3\,\sqrt{{\frac{2\,({\rho }^{2}\alpha _{{2}}+\alpha _{{1}} +\rho \,\alpha _{{3}})}{\alpha _{{4}}}}}\,b. \end{aligned}$$
(3.22)

Putting (3.22) into (3.12) with (2.5) and (3.1) we have the solution of model (1.2) as,

$$\begin{aligned} \Theta (x,y,t)=\left\{ \begin{array}{l}\left [\pm \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _ {{3}}+{r}^{2}\alpha _{{2}}+\omega }{\alpha _{{4}}}}}\pm \frac{3\,b\,\sqrt{{ \frac{2\,({\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}})}{\alpha _ {{4}}}}}}{ \pm 3\,b\sqrt{-{\frac{{\rho }^{2}\alpha _{{2}}+\rho \, \alpha _{{3}}+\alpha _{{1}}}{2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2 \,{r}^{2}\alpha _{{2}}+2\,\omega }}}+\frac{c}{ {\textrm{e}^{\pm \sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha }} } } \right ]e^{i\,\beta },a\ne b, \\ \\ \sqrt{-{\frac{{l}^{2}\alpha _{{1}}+lr\alpha _ {{3}}+{r}^{2}\alpha _{{2}}+\omega }{\alpha _{{4}}}}}\,\left [\pm 1\pm \frac{1-\hbox {tanh}(\pm \frac{1}{2}\,{{\sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha } })}{(c-1)+(c+1)\,\hbox {tanh}(\pm \frac{1}{2}\,{\sqrt{-{\frac{ 2\,{l}^{2}\alpha _{{1}}+2\,lr\alpha _{{3}}+2\,{r}^{2}\alpha _{{2}}+2\, \omega }{{\rho }^{2}\alpha _{{2}}+\rho \,\alpha _{{3}}+\alpha _{{1}}}}} \,\,\alpha})}\right ]\,\,e^{i\,\beta },\,\,\,\,\,\,\,a= b. \end{array}\right. \end{aligned}$$
(3.23)
Fig. 4
figure 4

a–f 3D and 2D the solution (3.23) at \(a=b\) are plotted with the parameters \(l=1.5,\, r = 0.5, \,\omega = 1,\,\rho =0.7,\,c=0.8,\,\alpha _{0}= 1\) and \(y=1\) for 3D plots, \(y=1\) and \(t = 1\) for 2D plots

Full size image

The solutions that we get in Case 1, Case 2 and Case 3 are similar to each others, but with a simple difference in the second term of these solutions at \(a\ne b\). But when \(a= b\) the solutions are the same in all cases.

Here, we discuss the physical interpretations of figures of plotted solutions. Kink types of solitary wave solutions are an important to describe phenomena in many fields of science such as optical fibers, material physics and plasma physics. Some of the obtained solutions of the HNLS and HFSC equations are shown graphically by 3D surface plots with appropriate parametric selections. In Figs. 1, 2, 3 and 4, we plot 3D and 2D graphics of absolute, real and imaginary parts of solutions (3.7), (3.11),(3.21) and (3.23), respectively, which denote the dynamics behavior of solutions. We plot 3D graphics of Figs. 1, 2, 3 and 4 when \(-10<x<10,\, -10<t<10\). The exact solutions and figures obtained in this paper give us the physical interpretation for the two models (1.1) and (1.2).

Figure 1 depicts the physical behavior of solitary wave solution of (3.7) and shows its corresponding 3D and intensity plots, respectively.

Figure 2 shows kink type solitary wave solution of (3.11).

Figure 3 illustrates the solitary wave solution for (3.21).

Figure 4 demonstrates the traveling wave solution of (3.23).

4 Symmetry analysis and group transformation

A Lie symmetry of differential equations is a transformations, that maps one solution to other solution. In this section, we derive the Lie point symmetry, symmetry group and new solutions

corresponding to the symmetry group for two models that given in (1.1) and (1.2).

4.1 Symmetry groups and new solutions of (2+1)-dimensional HNLS equation

First, we consider the transformation

$$\begin{aligned} \Theta (x,y,t)=n(x,y,t)+i\,m(x,y,t). \end{aligned}$$
(4.1)

Substituting (4.1) into (1.1) and splitting the result into real and imaginary parts, we get the following system:

$$\begin{aligned} \begin{array}{l} m_{y}+\frac{1}{2}\,(n_{xx}-n_{tt})-(n^{3}+n\,m^2)=0, \\ n_{y}-\frac{1}{2}\,(m_{xx}-m_{tt})+(m^{3}+m\,n^2)=0. \end{array} \end{aligned}$$
(4.2)

The Lie point symmetries for (4.2) is generated by a vector field in the form

$$\begin{aligned} X=\tau ^{1}(x,y,t,n,m)\partial _{ x}+\tau ^{2}(x,y,t,n,m)\partial _{ y}+\tau ^{3}(x,y,t,n,m)\partial _{ t}+\nu ^{1}(x,y,t,n,m)\partial _{n}+\nu ^{2}(x,y,t,n,m)\partial _{m}. \end{aligned}$$
(4.3)

Appling the prolongation Pr\(^{(2)} X\) to (4.2), we obtain a determined system of linear PDEs. Solving it by Maple, we get the infinitesimals as follows:

$$\begin{gathered} \tau ^{1} = \frac{1}{2}{\mkern 1mu} c_{1} {\mkern 1mu} x + c_{3} {\mkern 1mu} t + c_{5} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \tau ^{2} = c_{1} {\mkern 1mu} y + c_{2} , \hfill \\ \tau ^{3} = \frac{1}{2}{\mkern 1mu} c_{1} {\mkern 1mu} t + c_{3} {\mkern 1mu} x + c_{4} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \nu ^{1} = - \frac{1}{2}c_{1} {\mkern 1mu} m,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \nu ^{2} = - \frac{1}{2}{\mkern 1mu} c_{1} {\mkern 1mu} n, \hfill \\ \end{gathered}$$
(4.4)

where \(c_{1},\,c_{2},\,c_{3},\,c_{4}\) and \(c_{5}\) are constants. Substituting (4.4) into (4.3) we admit the algebra of Lie point symmetries generators of Eq. (4.2) as

$$\begin{aligned} \begin{array}{l} X_{1}=\frac{1}{2}\,(x\,\partial _{x} +2\,y\,\partial _ {y}+t\,\partial _{t}-m\,\partial _ {n}-n\,\partial _ {m}), \,X_{2}=\partial _{y}, \,X_{3}=t\,\partial _{x}+x\,\partial _{t},\,X_{4}=\partial _{t},\,X_{5}=\partial _{x}. \end{array} \end{aligned}$$
(4.5)

Group transformations

To get the group transformation \(G_{i}: (x,y,t,n,m)\rightarrow\) \(({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}})\) that is generated by the generator \(X_{i}\) for \(i=1,2,3,4,5\). We want to solve the initial problems of ODEs that given as

$$\begin{gathered} \frac{{d(\hat{x},\hat{y},\hat{t},\hat{n},\hat{m})}}{{d\epsilon }} = (\tau ^{1} ,\tau ^{2} ,\tau ^{3} ,\nu ^{1} ,\nu ^{2} ), \hfill \\ (\hat{x},\hat{y},\hat{t},\hat{n},\hat{m})_{{\epsilon = 0}} = (x,y,t,n,m), \hfill \\ \end{gathered}$$

where \(\tau ^{1}=\tau ^{1}({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}}),\, \tau ^{2}=\tau ^{2}({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}}),\, \tau ^{3}=\tau ^{3}({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}}),\, \nu ^{1}=\nu ^{1}({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}}),\,\nu ^{2} =\nu ^{2}({\hat{x}},{\hat{y}},{\hat{t}},{\hat{n}},{\hat{m}})\) and \(\epsilon\) is a group parameter. Then the one-parameter symmetry groups \(G_{i}\) corresponding to the generators \(X_{i}\) that given in (4.5) can be obtained as

\(G_{1}: (x,y,t,n,m)\rightarrow\) \((x\,e^{\frac{1}{2}\,\epsilon },y\,e^{\epsilon },t\,e^{\frac{1}{2}\,\epsilon },n-\frac{\epsilon }{2}\,m,m-\frac{\epsilon }{2}\,n),\)

\(G_{2}: (x,y,t,n,m)\rightarrow\) \((x,y+\epsilon ,t,n,m),\)

\(G_{3}: (x,y,t,n,m)\rightarrow\) \((x+\epsilon \,t,y,t+\epsilon \,x,n,m),\)

\(G_{4}: (x,y,t,n,m)\rightarrow\) \((x,y,t+\epsilon ,n,m).\)

\(G_{5}: (x,y,t,n,m)\rightarrow\) \((x+\epsilon ,y,t,n,m).\)

New solutions via group transformations

Consider \(n=\lambda (x,y,t)\) and \(m=\mu (x,y,t)\) is a solution of the system in (4.2), by using the one-parameter symmetry groups \(G_{i} (i=1,2,3,4,5)\) that obtained above, we have the following:

$$\begin{gathered} n^{{(1)}} = \lambda \left( {x{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} ,y{\mkern 1mu} e^{{ - \epsilon }} ,t{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} } \right) - \frac{\epsilon }{2}{\mkern 1mu} \mu \left( {x{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} ,y{\mkern 1mu} e^{{ - \epsilon }} ,t{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} } \right), \hfill \\ m^{{(1)}} = \mu \left( {x{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} ,y{\mkern 1mu} e^{{ - \epsilon }} ,t{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} } \right) - \frac{\epsilon }{2}{\mkern 1mu} \lambda \left( {x{\mkern 1mu} e^{{ - \frac{1}{2}\epsilon }} ,y{\mkern 1mu} e^{{ - \epsilon }} ,t{\mkern 1mu} e^{{ - \frac{1}{2}{\kern 1pt} \epsilon }} } \right). \hfill \\ n^{{(2)}} = \lambda (x,y - \epsilon ,t), \hfill \\ m^{{(2)}} = \mu (x,y - \epsilon ,t). \hfill \\ n^{{(3)}} = \lambda (x - \epsilon {\mkern 1mu} t,y,t - \epsilon {\mkern 1mu} x),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} m^{{(3)}} = \mu (x - \epsilon {\mkern 1mu} t,y,t - \epsilon {\mkern 1mu} x). \hfill \\ n^{{(4)}} = \lambda (x,y,t - \epsilon ),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} m^{{(4)}} = \mu (x,y,t - \epsilon ). \hfill \\ n^{{(5)}} = \lambda (x - \epsilon ,y,t),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} m^{{(5)}} = \mu (x - \epsilon ,y,t). \hfill \\ \end{gathered}$$

Substituting the above values for n and m into equation (4.1), we get new solutions of the model (1.1).

Exact solutions by reduction

To illustrate the exact solutions by similarity reduction of model (1.1), we give the following example:

Using the generator \(X_{2}=\partial _{y}\) that given in (4.5) and applying the characteristic equation which is equivalent to solve the invariant surface condition, we get the similarity solutions and the similarity variable as

$$\begin{aligned} n=f(\delta _{1},\delta _{2}),\,\,\,\,m=g(\delta _{1},\delta _{2}),\,\,\,\,\,\delta _{1}=x,\,\,\,\,\delta _{2}=t. \end{aligned}$$

Substituting these solutions into Eq. (4.2), we have the reduced equations as,

$$\begin{aligned} f_{\delta _{1}\delta _{1}}-f_{\delta _{2}\delta _{2}}-2\,f\,(f^{2}+g^2)=0,\,\,\,\,\,\,\, -g_{\delta _{1}\delta _{1}}+g_{\delta _{2}\delta _{2}}+2\,g\,(f^2+g^{2})=0. \end{aligned}$$

The solutions of this system can be studied by using one of the methods given in Zhou et al. (2003); Kudryashov (2012); Malik et al. (2023); Shehata (2010). Therefore, we can construct the exact solutions of model (1.1).

4.2 Symmetry groups and new solutions of (2+1)-dimensional HFSC equation

Substituting (4.1) into (1.2) and splitting the result into real and imaginary parts, we get the following system

$$\begin{aligned} \begin{array}{l} m_{t}-\alpha _{1}\,n_{xx}-\alpha _{2}\,n_{yy}-\alpha _{3}\,n_{xy}+\alpha _{4}\,(n^{3}+n\,m^2)=0, \\ n_{t}+\alpha _{1}\,m_{xx}+\alpha _{2}\,m_{yy}+\alpha _{3}\,m_{xy}-\alpha _{4}\,(m^{3}+m\,n^2)=0. \end{array} \end{aligned}$$
(4.6)

Appling the prolongation Pr\(^{(2)} X\) to (4.6), we obtain a determined system of linear PDEs. Solving it by Maple, we get the infinitesmals as follows:

$$\begin{aligned} \begin{array}{l} \tau ^{1}=(c_{1}-c_{3})\,x+\frac{\alpha _{1}}{\alpha _{3}}\,(-c_{1}+2\,c_{3})\,y+c_{5},\,\,\,\tau ^{2}=c_{3}\,y+\frac{\alpha _{2}}{\alpha _{3}}\,(c_{1}-2\,c_{3})\,x+c_{4},\,\,\,\tau ^{3}=c_{1}\,t+c_{2},\,\,\, \\ \nu ^{1}=-\frac{1}{2}c_{1}\,m,\,\,\,\nu ^{2}=-\frac{1}{2}\,c_{1}\,n. \end{array} \end{aligned}$$
(4.7)

Setting (4.7) into (4.3) Eq. (4.6) admits the algebra of Lie point symmetries generators as

$$\begin{aligned} \begin{array}{l} X_{1}=(x-\frac{\alpha _{1}}{\alpha _{3}}\,y)\,\partial _{x} +\frac{\alpha _{2}}{\alpha _{3}}\,x\,\partial _ {y}+t\,\partial _{t}-\frac{1}{2}\,m\,\partial _ {n}-\frac{1}{2}\,n\,\partial _ {m}), \,\,\,X_{2}=\partial _{t}, \\ \,X_{3}=(-x+\frac{2\,\alpha _{1}}{\alpha _{3}}\,y)\,\partial _{x}+(y-\frac{2\,\alpha _{2}}{\alpha _{3}}\,x)\,\partial _{y},\,\,\,X_{4}=\partial _{y},\,\,\,X_{5}=\partial _{x}. \end{array} \end{aligned}$$
(4.8)

Group transformations

The one-parameter symmetry groups \(G_{i}\) corresponding to the generators \(X_{i}\) that given in (4.8) can be obtained as follows: \(G_{1}: (x,y,t,n,m)\rightarrow\) \(\big (\frac{(\alpha _{3}^{2}-\alpha _{1}\,\alpha _{2}\,\epsilon )}{\alpha _{3}^{2}}\,[\,x\,(1+\epsilon )-\frac{\alpha _{1}\,\epsilon y}{\alpha _{3}}],\frac{(\alpha _{3}^{2}-\alpha _{1}\,\alpha _{2}\,\epsilon )}{\alpha _{3}^{2}}\,[\,\frac{\alpha _{2}\,\epsilon }{\alpha _{3}} (1+\epsilon )(x-\frac{\alpha _{1} }{\alpha _{3}}\,y)-y],te^{\epsilon },n-\frac{m\epsilon }{2},m-\frac{n\epsilon }{2}\big ),\)

\(G_{2}: (x,y,t,n,m)\rightarrow\) \((x,y,t+\epsilon ,n,m),\)

\(G_{3}: (x,y,t,n,m)\rightarrow\) \(\big (x\,(1+\epsilon )+\frac{4\alpha _{1}\alpha _{3}\epsilon }{\alpha _{3}^{2}-4\alpha _{1}\alpha _{2}}\,y,y\,(1+\epsilon )+\frac{8\alpha _{1}\alpha _{2}\epsilon }{\alpha _{3}^{2}-4\alpha _{1}\alpha _{2}}\,y,t,n,m\big ),\)

\(G_{4}: (x,y,t,n,m)\rightarrow\) \((x,y+\epsilon ,t,n,m),\)

\(G_{5}: (x,y,t,n,m)\rightarrow\) \((x+\epsilon ,y,t,n,m).\)

New solutions via group transformations

Consider \(n=\lambda (x,y,t)\) and \(m=\mu (x,y,t)\) is a solution of the system in (4.6), by using the one-parameter symmetry groups \(G_{i} (i=1,2,3,4,5)\), we obtain

$$\begin{aligned}{} & {} n^{(1)}=\lambda \big (\frac{\alpha _{3}^2[\alpha _{1}\epsilon y+(\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )\,x)]}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},\frac{\alpha _{3}^3(\alpha _{3}y-\alpha _{2}x)}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},t\,e^{-\epsilon }\big )\\{} & {} -\frac{\epsilon }{2}\,\mu \big (\frac{\alpha _{3}^2[\alpha _{1}\epsilon y+(\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )\,x)]}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},\frac{\alpha _{3}^3(\alpha _{3}y-\alpha _{2}x)}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},t\,e^{-\epsilon }\big ), \\{} & {} m^{(1)}=\mu \big (\frac{\alpha _{3}^2[\alpha _{1}\epsilon y+(\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )\,x)]}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},\frac{\alpha _{3}^3(\alpha _{3}y-\alpha _{2}x)}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},t\,e^{-\epsilon }\big )\\{} & {} -\frac{\epsilon }{2}\,\lambda \big (\frac{\alpha _{3}^2[\alpha _{1}\epsilon y+(\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )\,x)]}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},\frac{\alpha _{3}^3(\alpha _{3}y-\alpha _{2}x)}{(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )[\alpha _{1}{\alpha _{2}}-(\alpha _{3}^2-\alpha _{1}\alpha _{2}\epsilon )]},t\,e^{-\epsilon }\big ).\\{} & {} n^{(2)}=\lambda (x,y,t-\epsilon ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, m^{(2)}=\mu (x,y,t-\epsilon ). \\{} & {} n^{(3)}=\lambda \big (\frac{x}{1+\epsilon }-\frac{4\alpha _{1}\alpha _{3}\epsilon y}{\alpha _{3}^2(1+\epsilon )^2-4\alpha _{1}\alpha _{2}},\frac{\alpha _{3}^2-4\alpha _{1}\alpha _{2} }{\alpha _{3}^2(1+\epsilon )-2\alpha _{1}\alpha _{2}(2-\epsilon )}\,y,t\big ), \\{} & {} m^{(3)}=\mu \big (\frac{x}{1+\epsilon }-\frac{4\alpha _{1}\alpha _{3}\epsilon y}{\alpha _{3}^2(1+\epsilon )^2-4\alpha _{1}\alpha _{2}},\frac{\alpha _{3}^2-4\alpha _{1}\alpha _{2} }{\alpha _{3}^2(1+\epsilon )-2\alpha _{1}\alpha _{2}(2-\epsilon )}\,y,t\big ).\\{} & {} n^{(4)}=\lambda (x,y-\epsilon ,t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m^{(4)}=\mu (x,y-\epsilon ,t).\\{} & {} n^{(5)}=\lambda (x-\epsilon ,y,t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m^{(5)}=\mu (x-\epsilon ,y,t). \end{aligned}$$

Putting the above values for n and m into Eq. (4.1), we get novel solutions of the model (1.2).

5 Conservation laws via multiplier approach

In this section, we will mention the multiplier method (Naz 2012) and then we using it to obtain the conservation laws for models (1.1) and (1.2). Firstly, suppose that a Nth-order system of PDEs of \(\gamma\) dependent variables \(u=(u^{1},u^{2},\ldots ,u^{\gamma })\) and \(\nu\) independent variables \(x=(x^{1},x^{2},\ldots ,x^{\nu })\), define as

$$\begin{aligned} \Gamma _{\eta }(x,u,u_{(1)},\ldots ,u_{(N)})=0, \,\,\eta =1,2,\ldots ,\gamma , \end{aligned}$$
(5.1)

where, \(u_{(1)},u_{(2)},\ldots ,u_{(N)}\) denote the collections of all first, second,...,Nth-order partial derivatives. Also, consider a vector \(C = (C^{1}, C^{2},\ldots ,C^{\nu })\), is said to be a conserved vector of system (5.1) if \(D_{i}(C^{i}) = 0\) for every solution of system (5.1). Now, we will summary the multiplier method in the following steps:

Step 1 Consider the multiplier of the form \(M^{\eta } = M^{\eta }(x,u,u_{(1)},\ldots ,u_{(\nu )})\) \(=0, \nu \le N\) for obtaining the conserved vectors of system (5.1). These vectors satisfy the condition

$$\begin{aligned} D_{i}\,C^{i}=M^{\eta }\,\Gamma _{\eta }. \end{aligned}$$
(5.2)

where

$$\begin{aligned} D_{i}=\frac{\partial }{\partial x^{i}}+u_{i}^{\eta }\,\frac{\partial }{\partial u^{\eta }}+u_{ij}^{\eta }\,\frac{\partial }{\partial u_{j}^{\eta }}+..., \,\,\,i=1,2,\ldots ,\nu , \end{aligned}$$
(5.3)

is the total derivative operator with respect to \(x^{i}\).

Step 2 Using variational derivative of (5.2) that given as

$$\begin{aligned} \frac{\delta }{\delta u^{\eta }}(M^{\eta }\,\Gamma _{\eta })=0. \end{aligned}$$
(5.4)

to obtain the determining system of equations and \(\frac{\delta }{\delta u^{\eta }}\) is the Euler operator that define as follows:

$$\begin{aligned} \frac{\delta }{\delta u^{\eta }}=\frac{\partial }{\partial u^{\eta }}-D_{i}\,\frac{\partial }{\partial u_{i}^{\eta }}+D_{i}\,D_{j}\,\frac{\partial }{\partial u_{ij}^{\eta }}-..., \end{aligned}$$
(5.5)

Step 3 Solving the determining system of equations that we obtain from (5.4) by Maple, we yields the required multipliers.

Step 4 Substituting the multipliers that we obtained in (5.2), we construct the conservation laws for the system (5.1).

5.1 Conservation laws of (2+1)-dimensional HNLS equation

To calculate the conservation laws for (1.1), we consider multipliers for (4.2) in the form \(M^{1}(t,x,y,n,m,n_{t},m_{t},n_{x},m_{x},n_{y},m_{y}), M^{2}(t,x,y,n,m,n_{t},m_{t},n_{x},m_{x},n_{y},m_{y})\) and applying (5.4), we have

$$\begin{aligned} \begin{array}{l} \frac{\delta }{\delta n}\,[M^{1}\,\Gamma _{1}+M^{2}\,\Gamma _{2}]=0, \\ \frac{\delta }{\delta m}\,[M^{1}\,\Gamma _{1}+M^{2}\,\Gamma _{2}]=0, \end{array} \end{aligned}$$
(5.6)

where, \(\frac{\delta }{\delta n}\) and \(\frac{\delta }{\delta m}\) are the standard Euler operators which we can obtain from (5.3) with (5.5). Expanding (5.6) and separating the different combinations of derivatives of n and m, we have system of equations for \(M^{1}\) and \(M^{2}\). Solving it by Maple software, we get

$$\begin{aligned} \begin{array}{l} M^{1}= -\left[ \left( t\,{ n_{t}}+x\,{ n_x}+n \right) y+{y}^{2}\,{ n_y}-\frac{1}{2} \, \left( {x}^{2}-{t}^{2} \right) m \right] { c_{1}} -\left( t\, { n_t}+x\,{ n_x}+2\,y\,{ n_y}+n \right) { c_{2}} \\ +\left( xm-y\,{ n_x}\right) { c_{3}}+\left( y\,{ n_t} +tm \right) { c_{4}}+m{ c_{5}}- \left( x{ n_t}+t{ n_x} \right) { c_{6}}-{ n_x}\,{ c_{7}}-{ n_t}\,{ c_{8}}-{ n_y}\,{ c_{9}},\\ M^{2}=\left[ \left( t\,{ m_t}+x\,{ m_x}+m \right) y+{y}^{2}{ m_y}-\frac{1}{2} \, \left( {t}^{2}-{x}^{2} \right) n \right] { c_{1}} + \left( t\,{ m_t}+x\,{ m_x}+2\,y\,{ m_y}+m \right) { c_{2}} \\ +\left( y\,{ m_x}+xn \right) { c_{3}}+ \left( tn -y\,{ m_t} \right) { c_{4}}+n{ c_{5}}+ \left( x{ m_t}+t{ m_x} \right) { c_{6}}+{ m_x}\,{ c_{7}}+{ m_t}\,{ c_{8}}+{ m_y}\,{ c_{9}}. \end{array} \end{aligned}$$
(5.7)

From (5.2) and (5.7), we get the following conserved vectors:

Case 1 When \(M^{1}=-\left( t\,{ n_{t}}+x\,{ n_x}+n \right) y-{y}^{2}\,{ n_y}+\frac{1}{2} \, \left( {x}^{2}-{t}^{2} \right) m\) and \(M^{2}=\left( t\,{ m_t}+x\,{ m_x}+m \right) y+{y}^{2}{} { m_y}-\frac{1}{2} \, \left( {t}^{2}-{x}^{2} \right) n\), then we get

$$\begin{aligned} \begin{array}{l} C^{x}=[ -\frac{1}{4}\,{m_{{t}}}^{2}x-3\,{n}^{3}n_{{t}}t x-\frac{1}{2}\,n_{{x}}n_{{t}}t-\frac{1}{2}\,n_{{x}}n-\frac{1}{4}\,{n_{{x}}}^{2}x-\frac{1}{4}\,{n_{{t}} }^{2}x+\frac{1}{4}\,x{m}^{4}-\frac{1}{2}\,m_{{x}}m-\frac{1}{4}\,{m_{{x}}}^{2}x \\ +n_{{y}}xm+\frac{1}{2}\, x{n}^{2}{m}^{2}-\frac{1}{2}\,m_{{x}}m_{{t}}t] y+ \left( -\frac{1}{2}\,m_{{y}}m_{{x}}-\frac{1}{2}\,n_{{x}}n_{{y}}+n_{{y}}x{n}^{3} \right) {y}^{2}-\frac{1}{4}\,m_{{x}}n{x}^{2}+\frac{1}{6}\,n_{{y}}n{x}^{3} \\ -\frac{1}{2}\,n_{{y}}xn{t}^{2}-\frac{1}{4}\,n_{{x}}m{t}^{2}+\frac{1}{2}\,mnx +\frac{1}{4}\,n_{{x}}m{x}^{2}+\frac{1}{4}\,m_{{x}}n{t}^{2}, \\ C^{y}=\left( \frac{1}{4}\,{m_{{x}}}^{2}+\frac{1}{4}\,{m}^{4}-\frac{1}{4}\,{m_{{t}}}^{2}-{n}^{3}n_{ {x}}x-\frac{1}{4}\,{n_{{t}}}^{2}+\frac{1}{2}\,{n}^{2}{m}^{2}+\frac{1}{4}\,{n_{{x}}}^{2} \right) {y}^{2}- \left( mtn_{{t}}+mxn_{{x}}+mn \right) y \\ -\frac{1}{4}\,{t}^{2 }{m}^{2}+\frac{1}{4}\,{x}^{2}{m}^{2}+\frac{1}{2}\,nn_{{x}}{t}^{2}x-\frac{1}{6}\,n_{{x}}n{x}^{3 }, \\ C^{t}=\left( \frac{1}{2}\,n_{{y}}n_{{t}}+\frac{1}{2}\,m_{{y}}m_{{t}} \right) {y}^{2}+[ 3\,{n}^{3}n_{{x}}tx+{n}^{4}t+\frac{1}{2}\,n_{{t}}n+\frac{1}{4}\,{m}^{4}t+\frac{1}{4}\, {m_{{t}}}^{2}t+\frac{1}{4}\,m_{{x}}t+\frac{1}{4}\,{n_{{x}}}^{2}t+\frac{1}{2}\,m_{{t}}m \\ +\frac{1}{4}\,{n _{{t}}}^{2}t+n_{{y}}mt+\frac{1}{2}\,m_{{x}}m_{{t}}x+\frac{1}{2}\,{m}^{2}{n}^{2}t+\frac{1}{2}\, n_{{t}}n_{{x}}x ] y +\frac{1}{2}\,mnt+\frac{1}{4}\,n_{{t}}m{t}^{2}-\frac{1}{4}\,n_{{t}}m{ x}^{2}+\frac{1}{4}\,m_{{t}}n{x}^{2}-\frac{1}{4}\,m_{{t}}n{t}^{2}. \end{array} \end{aligned}$$
(5.8)

Case 2 When \(M^{1}=-\left( t\, { n_t}+x\,{ n_x}+2\,y\,{ n_y}+n \right)\) and \(M^{2}=\left( t\,{ m_t}+x\,{ m_x}+2\,y\,{ m_y}+m \right)\), thus we have

$$\begin{aligned} \begin{array}{l} C^{x}= \frac{1}{4} \,\left( {m}^{4}-{{ m_t}}^{2}-12\,{n}^{3}{ n_t}\,t-{ { m_x}}^{2}-{{ n_t}}^{2}+4\,{ n_y}\,m+2\,{m}^{2}{n}^{2}+8\,{ n_y}\,y{n}^{3}-{{ n_x}}^{2} \right) x- \left( { m_y}\,{ m_x}+{ n_x}\,{ n_y} \right) y- \\ \frac{1}{2}\,({ n_x}\,n+{ n_x}\,{ n_t}\,t+\,{ m_x}\,{ m_t}\,t+{ m_x}\,m), \\ C^{y}=\left( -2\,{n}^{3}{} { n_x}\,y-m{ n_x} \right) x+ \frac{1}{2} \,\left( -{{ n_t}}^{2} +{{ m_x}}^{2}-{{ m_t}}^{2}+{m}^{4}+ \,{{ n_x}}^{2}+2\,{m}^{2}{n}^{2} \right) y-tm{ n_t}-nm, \\ C^{t}= \frac{1}{4}\,({m}^{4}t+{{ m_t}}^{2}t+2\,{ m_t}\,m+2\,{m} ^{2}{n}^{2}t+2\,{ n_t}\,n+{{ m_x}}^{2}t+{{ n_x}}^{2} t+{{ n_t}}^{2}t)+{n}^{4}t+{ n_y}\,mt \\ +\frac{1}{2}\,\left( 6\,{n}^{3}{ n_x}\,t +{ n_t}\,{ n_x}+{ m_x}\,{ m_t} \right) x+ \left( { m_y}\,{ m_t}+{ n_y}\,{ n_t} \right) y. \end{array} \end{aligned}$$
(5.9)

Case 3 If \(M^{1}=mx-{ n_x}\,y\) and \(M^{2}={ m_x}\,y+nx\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}= \frac{1}{4}\left( - {{ m_x}}^{2}-{{ n_t}}^{2}-{{ m_t}}^{2}+2\,{n}^{2}{m}^{2}-4\,{n}^{3}{} { n_t}\,t-{{ n_x}}^{2 }+4\,{ n_y}\,m+{m}^{4} \right) y \\ + \frac{1}{2}\,({ n_y}\,n{x}^{2}+nm)- \frac{1}{2} \left( { m_x}\,n-m{ n_x} \right) x, \\ C^{y}= \frac{1}{2}\,(x{m}^{2}-{ n_x}\,n{x}^{2})-m{ n_x}\,y, \\ C^{t}=\frac{1}{2}\,\bigg [ \left( -{ n_t}\,m+{ m_t}\,n \right) x+ \left( { n_x}\,{ n_t}+{ m_x}\,{ m_t}+2\,{n}^{3}{ n_x}\,t \right) y\bigg ]. \end{array} \end{aligned}$$
(5.10)

Case 4 When \(M^{1}={ n_t}\,y+mt\) and \(M^{2}=-{ m_t}\,y+nt\), we obtain

$$\begin{aligned} \begin{array}{l} C^{x}= \frac{1}{2}\,\bigg [\left( 2\,{ n_y}\,xn+{ n_x}\,m+{ m_x}\,n \right) t+ \left( { n_x}\,{ n_t}+{ m_x}\,{ m_t} \right) y \bigg ],\,\,\,\, C^{y}=-n{ n_x}\,tx+m{ n_t}\,y+ \frac{1}{2}\,t{m}^{2}, \\ C^{t}= \frac{1}{2}\,(\left( m{ n_t}+{ m_t}\,n \right) t-n\,m)- \frac{1}{4}\,\left( 2\,{m}^{2}{n}^{2}+4\,{ n_y}\,m+{m}^{4}+{n}^{4}+{{ m_x}}^{2}+{{ n_t}}^{2}+{{ m_t}}^{2}+{{ n_x}}^{2} \right) y.\end{array} \end{aligned}$$
(5.11)

Case 5 When \(M^{1}=m\) and \(M^{2}=n\), thus we have

$$\begin{aligned} \begin{array}{l} C^{x}= \frac{1}{2}\,(-{ m_x}\,n+{ n_x}\,m+2\,{ n_y}\,xn), \\ C^{y}= \frac{1}{2}\,{m}^{2}-n{ n_x}\,x, \\ C^{t}= \frac{1}{2}\,({ m_t}\,n-{ n_t}\,m). \end{array} \end{aligned}$$
(5.12)

Case 6 If \(M^{1}=-{ n_t}\,x-{ n_x}\,t\) and \(M^{2}={ m_t}\,x+{ m_x}\,t\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}= -\frac{1}{2}\,{ n_t}\,{n}^{3}{t}^{2}+ \frac{1}{4} \left( 4\,{ n_y}\,m+2\,{m}^{2}{n}^{2} -{{ n_x}}^{2}-{{ n_t}}^{2}-{{ m_t}}^{2}-{{ m_x}}^{2}+{m}^{4} \right) t- \frac{1}{2}\,\left( { n_t}\,{ n_x}+{ m_x}\,{ m_t} \right) x, \\ C^{y}= -m{ n_t}\,x-m{ n_x}\,t, \\ C^{t}= \frac{1}{2}\,{ n_x}\,{n}^{3}{t}^{2}+\frac{1}{2} \left( { m_x}\,{ m_t}+{ n_t}\,{ n_x} \right) t+\frac{1}{4}\, \left( 2\,{m}^{2}{n}^{2}+{n}^{4}+{{ n_t}}^{2}+{{ m_t}}^{2}+{{ m_x}}^{2}+{m}^{4 }+{{ n_x}}^{2}+4\,{ n_y}\,m \right) x. \end{array} \end{aligned}$$
(5.13)

Case 7 If \(M^{1}=-{ n_x}\) and \(M^{2}={ m_x}\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}=m{ n_y} -{n}^{3}{} { n_t}\,t+\frac{1}{4}\,({m}^{4}-{{ m_x}}^{2}-{{ n_x}}^{2}-{{ m_t}}^{2}-{{ n_t}}^{2}+2\,{m}^{2}{n}^{ 2}), \\ C^{y}= -{ n_x}\,m,\,\,\,\,\,\, C^{t}=\frac{1}{2}\,({ m_t}\,{ m_x}+{ n_t}\,{ n_x})+{n}^{3}{} { n_x}\,t.\end{array} \end{aligned}$$
(5.14)

Case 8 At \(M^{1}=-{ n_t}\) and \(M^{2}={ m_t}\), we get

$$\begin{aligned} \begin{array}{l} C^{x}= -\frac{1}{2}\,({ m_t}\,{ m_x}+{ n_t}\,{ n_x}),\,\,\,\,\,\,\, C^{y}= -{ n_t}\,m, \\ C^{t}=m{ n_y}+\frac{1}{4}\,({n}^{4}+{m}^{4}+{{ m_x}}^{2}+{{ n_x} }^{2}+{{ m_t}}^{2}+{{ n_t}}^{2}+2\,{m}^{2}{n}^{2}). \end{array} \end{aligned}$$
(5.15)

Case 9 If \(M^{1}=-{ n_y}\) and \(M^{2}={ m_y}\), then we obtain

$$\begin{aligned} \begin{array}{l} C^{x}=-\frac{1}{2}\,({ n_y}\,{ n_x}+{ m_y}\,{ m_x})+{ n_y}\,x{n}^{3}, \\ C^{y}= \frac{1}{4}\,({m}^{4}+{{ m_x}}^{2}+{{ n_x}}^{2}-{{ m_t}}^{ 2}-{{ n_t}}^{2}-4\,{n}^{3}{ n_x}\,x+2\,{m}^{2}{n}^{2}), \\ C^{t}=\frac{1}{2}\,({ m_t}\,{ m_y}+{ n_t}\,{ n_y}). \end{array} \end{aligned}$$
(5.16)

5.2 Conservation laws of (2+1)-dimensional HFSC equation

To calculate the conservation laws for (1.2), we consider multipliers for (4.6) in the same form for (4.2) and by the same steps, we get

$$\begin{aligned} \begin{array}{l} M^{1}= \left[ \left( t\, { n_t}+x\,{ n_x}+y\,{ n_y}+n \right) \,t +\frac{\left( \alpha _{1}\, {y}^{2}+\alpha _{2}\, {x}^{2}- \alpha _{3}\,x\,y\right) \, m}{(4\,\alpha _{1}\,\alpha _{2}-\alpha _{3}^{2})} \right] { c_{1}}+ \left( 2\,t\, { n_t}+x\,{ n_x}+2\,y\,{ n_y}+n \right) { c_{2}} \\ - \left( 2\,\alpha _{1}\,t\, { n_x}+\alpha _{3}\,t\, { n_y}+m\,x \right) { c_{3}}- \left( 2\,\alpha _{2}\,t\, { n_y}+\alpha _{3}\,t\, { n_x}+m\,y \right) { c_{4}}-m{ c_{5}}+ \\ \left( 2\,\alpha _{1}\,y\, { n_x}-2\,\alpha _{2}\,x\, { n_y}-\alpha _{3}\,(x\, { n_x}-y\, { n_y}) \right) { c_{6}}+{ n_x}\,{ c_{7}}+{ n_t}\,{ c_{8}}+{ n_y}\,{ c_{9}},\\ \\ M^{2}= \left[ \left( t\, { m_t}+x\,{ m_x}+y\,{ m_y}+m \right) \,t -\frac{\left( \alpha _{1}\, {y}^{2}+\alpha _{2}\, {x}^{2}- \alpha _{3}\,x\,y\right) \, n}{(4\,\alpha _{1}\,\alpha _{2}-\alpha _{3}^{2})} \right] { c_{1}} + \left( 2\,t\,{ m_t}+x\,{ m_x}+y\,{ m_y}+m \right) { c_{2}} \\ -\left( 2\,\alpha _{1}\,t\, { m_x}+\alpha _{3}\,t\, { m_y}-n\,x \right) { c_{3}}- \left( 2\,\alpha _{2}\,t\, { m_y}+\alpha _{3}\,t\, { m_x}-n\,y \right) { c_{4}}+n{ c_{5}}+ \\ \left( 2\,\alpha _{1}\,y\, { m_x}-2\,\alpha _{2}\,x\, { m_y}-\alpha _{3}\,(x\, { m_x}-y\, { m_y}) \right) { c_{6}}+{ m_x}\,{ c_{7}}+{ m_t}\,{ c_{8}}+{ m_y}\,{ c_{9}}. \end{array} \end{aligned}$$
(5.17)

From (5.2) and (5.17), we construct the conserved vectors of Eq. (1.2) as

Case 1 When \(M^{1}= \left( t\, { n_t}+x\,{ n_x}+y\,{ n_y}+n \right) \,t +\frac{\left( \alpha _{1}\, {y}^{2}+\alpha _{2}\, {x}^{2}- \alpha _{3}\,x\,y\right) \, m}{(4\,\alpha _{1}\,\alpha _{2}-\alpha _{3}^{2})}\) and

\(M^{2}= \left( t\, { m_t}+x\,{ m_x}+y\,{ m_y}+m \right) \,t -\frac{\left( \alpha _{1}\, {y}^{2}+\alpha _{2}\, {x}^{2}- \alpha _{3}\,x\,y\right) \, n}{(4\,\alpha _{1}\,\alpha _{2}-\alpha _{3}^{2})}\), then we get

$$\begin{aligned} \begin{array}{l} C^{x}=\frac{1}{4}\,\bigg [( 4\,{ m_t}\,{ m_x}\,{t}^{2}+2\,{{ m_x}}^{2}tx+4\, { m_x}\,{ m_y}\,ty+4\,{ n_t}\,{ n_x}\,{t}^{2}+2\,{{ n_x}}^{2 }tx+4\,{ n_x}\,{ n_y}\,ty+4\,m{ m_x}\,t+4\,n{ n_x}\,t ) \alpha _{{1}}+ \\ \left( -2\,{{ m_y}}^{2}tx-2\,{{ n_y}}^{2}tx \right) \alpha _{{2}}+ \left( 2\,{ m_t}\,{ m_y}\,{t}^{2}+2\,{{ m_y}}^{2}t y+2\,{ n_t}\,{ n_y}\,{t}^{2}+2\,{{ n_y}}^{2}ty+4\,m{ m_y}\,t+4 \,n{ n_y}\,t \right) \alpha _{{3}}+ \\ \left( 4\,{n}^{3}{} { n_t}\,{t}^{2 }x-4\,{n}^{3}{ n_y}\,txy-{m}^{4}tx-2\,{m}^{2}{n}^{2}tx \right) \alpha _{{4}}+4\,m{ n_t}\,tx+\frac{1}{4\,\alpha _{{1}}\alpha _{{2}}-{\alpha _{{3}}}^{2}}\,\bigg ( \left( 4\,m{ n_x}\,{y}^{2}-4\,{ m_x }\,n{y}^{2} \right) {\alpha _{{1}}}^{2}+ \\ \left( \left( 4\,m{ n_x}\,{ x}^{2}-4\,{ m_x}\,n{x}^{2}+8\,mnx \right) \alpha _{{2}}+ \left( -4\,m { n_x}\,xy+4\,{ m_x}\,nxy-4\,{ m_y}\,n{y}^{2}-4\,mny \right) \alpha _{{3}} \right) \alpha _{{1}} \\ -4\,\alpha _{{2}}\alpha _{{3}}{} { m_y} \,n{x}^{2}+4\,{\alpha _{{3}}}^{2}{} { m_y}\,nxy\bigg )\bigg ], \\ \\ C^{y}=\frac{-1}{4}[\left( 2\,{{ m_x}}^{2}ty+2\,{{ n_x}}^{2}ty \right) \alpha _{{1}}+ ( -4\,{ m_t}\,{ m_y}\,{t}^{2}-4\,{ m_x}\,{ m_y}\, tx-2\,{{ m_y}}^{2}ty-4\,{ n_t}\,{ n_y}\,{t}^{2}-4\,{ n_x}\,{ n_y}\,tx \\ -2\,{{ n_y}}^{2}ty -4\,m{ m_y}\,t-4\,n{ n_y}\,t ) \alpha _{{2}}+ \left( -2\,{ m_t}\,{ m_x}\,{t}^{2}-2\,{{ m_x}}^{2}tx-2\,{ n_t}\,{ n_x}\,{t}^{2}-2\,{{ n_x}}^{2}tx \right) \alpha _{{3}}+ ( -4\,{n}^{3}{} { n_x}\,txy \\ +4\,{m}^{4}ty +2 \,{m}^{2}{n}^{2}ty) \alpha _{{4}}-4\,m{ n_t}\,ty]+\frac{1}{4\,\alpha _{{1}}\alpha _{{2}}-{\alpha _{{3}}}^{2}}\, ( \alpha _{{1}}\alpha _{{2}} \left( m{ n_y}\,{y}^{2}-{ m_y}\,n{y}^{2}+ 2\,mny \right) +\alpha _{{1}}\alpha _{{3}}m{ n_x}\,{y}^{2}+ \\ {\alpha _{{2 }}}^{2} ( x \left( m{ n_y}-4\,{ m_y}\,n \right) ) ^{2} +\alpha _{{2}}\alpha _{{3}}( m{ n_x}\,{x}^{2}-m{ n_y}\,xy+{ m_y}\,nxy+mnx ) -{\alpha _{{3}}}^{2}my ( { n_x}\,x+n ) ), \\ \\ C^{t}=\frac{-1}{4}[\left( 2\,{{ m_x}}^{2}{t}^{2}+2\,{{ n_x}}^{2}{t}^{2} \right) \alpha _{{1}}+ \left( 2\,{{ m_y}}^{2}{t}^{2}+2\,{{ n_y}}^{ 2}{t}^{2} \right) \alpha _{{2}}+ \left( 2\,{ m_x}\,{ m_y}\,{t}^{2}+ 2\,{ n_x}\,{ n_y}\,{t}^{2} \right) \alpha _{{3}}+ \\ \left( 4\,{n}^{3} { n_x}\,{t}^{2}x+4\,{m}^{4}{t}^{2}+2\,{m}^{2}{n}^{2}{t}^{2}+2\,{n}^{ 4}{t}^{2} \right) \alpha _{{4}}+4\,m{ n_x}\,tx+4\,m{ n_y}\,ty+4\,mn t]-{\frac{ \left( {m}^{2}+{n}^{2} \right) \left( {x}^{2}\alpha _{{2}}- xy\alpha _{{3}}+{y}^{2}\alpha _{{1}} \right) }{2\,(4\,\alpha _{{1}}\alpha _{{2 }}-{\alpha _{{3}}}^{2})}}. \end{array} \end{aligned}$$
(5.18)

Case 2 If \(M^{1}= \left( 2\,t\, { n_t}+x\,{ n_x}+2\,y\,{ n_y}+n \right)\) and \(M^{2}=\left( 2\,t\,{ m_t}+x\,{ m_x}+y\,{ m_y}+m \right)\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}= \left( 2\,{ m_t}\,{ m_x}\,t+\frac{1}{2}\,{{ n_x}}^{2}x+{ n_x}\,{ n_y}\,y+m{ m_x}+n{ n_x}+\frac{1}{2}\,{{ m_x}}^{2}x+{ m_x} \,{ m_y}\,y+2\,{ n_t}\,{ n_x}\,t \right) \alpha _{{1}}+ \\ \left( \frac{-1}{2}\,{{ m_y}}^{2}x-\frac{1}{2}\,{{ n_y}}^{2}x \right) \alpha _{{2}}+ \left( { m_t}\,{ m_y}\,t+m{ m_y}+n{ n_y}+\frac{1}{2}\,{{ m_y}}^{2}y+{ n_t }\,{ n_y}\,t+\frac{1}{2}\,{{ n_y}}^{2}y \right) \alpha _{{3}}+ \\ \left( -{n}^ {3}{ n_y}\,xy-\frac{1}{4}\,{m}^{4}x-\frac{1}{2}\,{m}^{2}{n}^{2}x+2\,{n}^{3}{ n_t} \,tx \right) \alpha _{{4}}+m{ n_t}\,x, \\ C^{y}=\frac{1}{2}\,y\,\left( {{ m_x}}^{2}+{{ n_x}}^{2} \right) \alpha _{{1}}+ ( n{ n_y}+2\,{ m_t}\,{ m_y}\,t+{ m_x}\,{ m_y}\,x+\frac{1}{2}\,{{ m_y}}^{2}y+2\,{ n_t}\,{ n_y}\,t+{ n_x }\,{ n_y}\,x+\frac{1}{2}\,{{ n_y}}^{2}y \\ +m{ m_y} ) \alpha _{{2}}+ \left( { m_t}\,{ m_x}\,t+{ n_t}\,{ n_x}\,t+\frac{1}{2}\,{{ n_x}}^{2 }x+\frac{1}{2}\,{{ m_x}}^{2}x \right) \alpha _{{3}}+ \left( {n}^{3}{} { n_x}\, xy-\frac{1}{4}\,{m}^{4}y-\frac{1}{2}\,{m}^{2}{n}^{2}y \right) \alpha _{{4}}+m{ n_t}\, y, \\ C^{t}= \left( -{{ m_x}}^{2}t-{{ n_x}}^{2}t \right) \alpha _ {{1}}+ \left( -{{ m_y}}^{2}t-{{ n_y}}^{2}t \right) \alpha _{{2}}+ \left( -{ m_x}\,{ m_y}\,t-{ n_x}\,{ n_y}\,t \right) \alpha _{{ 3}} \\ + \left( -{n}^{4}t-2\,{n}^{3}{ n_x}\,tx-\frac{1}{2}\,{m}^{4}t-{m}^{2}{n}^ {2}t \right) \alpha _{{4}}-m{ n_x}\,x-m{ n_y}\,y-mn. \end{array} \end{aligned}$$
(5.19)

Case 3 When \(M^{1}=- \left( 2\,\alpha _{1}\,t\, { n_x}+\alpha _{3}\,t\, { n_y}+m\,x \right)\) and \(M^{2}=-\left( 2\,\alpha _{1}\,t\, { m_x}+\alpha _{3}\,t\, { m_y}-n\,x \right)\), we obtain

$$\begin{aligned} \begin{array}{l} C^{x}=( -{{ m_x}}^{2}t-{{ n_x}}^{2}t ) {\alpha _{{1}}}^{2}+ [( {{ m_y}}^{2}t+{{ n_y}}^{2}t ) \,\alpha _{{2}}+ ( -{ m_x}\,{ m_y}\,t-{ n_x}\,{ n_y}\,t ) \alpha _{{3}}+ ( {m}^{2}{n}^{2}t-{n}^{3}{} { n_t}\,{t}^{2} +\frac{1}{2}\,{m}^{4}t ) \alpha _{{4}} \\ -2\,m{ n_t}\,t-m{ n_x}\,x+{ m_x}\,nx-mn \alpha _{{1}}]+ ( -\frac{1}{2}\,{{ n_y}}^{2}t-\frac{1}{2}\,{{ m_y}}^{2}t ) {\alpha _{{3}}}^{2}+ ( \alpha _{{4}}{n}^{3}{ n_y}\,tx+{ m_y}\,nx ) \alpha _{{3}},\\ C^{y}= \left( \left( -2\,{ m_x}\,{ m_y}\,t-2\,{ n_x}\,{ n_y}\,t \right) \alpha _{{2}}+ \left( -\frac{1}{2}\,{{ n_x}}^{2}t-\frac{1}{2}\,{{ m_x}}^{2}t \right) \alpha _{{3}} \right) \alpha _{{1}}+ ( ( -\frac{1}{2}\,{{ n_y}}^{2}t-\frac{1}{2}\,{{ m_y}}^{2}t ) \alpha _{{3} } \\ -m{ n_y}\,x+{ m_y}\,nx ) \alpha _{{2}} + ( \left( \frac{1}{2}\, {m}^{2}{n}^{2}t-{n}^{3}{} { n_x}\,tx+\frac{1}{4}\,{m}^{4}t \right) \alpha _{{4}} -m{ n_t}\,t-m{ n_x}\,x-mn ) \alpha _{{3}},\\ C^{t}=\left( \alpha _{{4}}{n}^{3}{} { n_x}\,{t}^{2}+2\,m{ n_x }\,t \right) \alpha _{{1}}+\frac{1}{2}\,x{n}^{2}+\alpha _{{3}}m{ n_y}\,t+\frac{1}{2}\, {m}^{2}x. \end{array} \end{aligned}$$
(5.20)

Case 4 If \(M^{1}=- \left( 2\,\alpha _{2}\,t\, { n_y}+\alpha _{3}\,t\, { n_x}+m\,y \right)\) and \(M^{2}=- \left( 2\,\alpha _{2}\,t\, { m_y}+\alpha _{3}\,t\, { m_x}-n\,y \right)\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}=2\,\alpha _{{2}}\alpha _{{4}}{n}^{3}{} { n_y}\,tx-t \left( \frac{1}{2}\,{n}^{3}{ n_t}\,t-\frac{1}{4}\,{m}^{4}-\frac{1}{2}\,{m}^{2}{n}^{2} \right) \alpha _{{3}}\alpha _{{4}}-2\,t \left( { m_x}\,{ m_y}+{ n_x}\,{ n_y} \right) \alpha _{{1}}\alpha _{{2}} \\ -\frac{1}{2}\,t \left( {{ m_x}}^{2}+ \frac{1}{2}\,{{ n_x}}^{2} \right) \alpha _{{1}}\alpha _{{3}}-\frac{1}{2}\,t \left( {{ m_y}}^{2}+{{ n_y}}^{2} \right) \alpha _{{2}}\alpha _{{3}}-y \left( m{ n_x}-{ m_x}\,n \right) \alpha _{{1}}- \left( m{ n_t}\,t-{ m_y}\,ny \right) \alpha _{{3}}, \\ C^{y}= \left( {{ m_x}}^{2}t+{{ n_x}}^{2}t \right) \alpha _{ {2}}\alpha _{{1}}+ \left( -{{ m_y}}^{2}t-{{ n_y}}^{2}t \right) { \alpha _{{2}}}^{2}+ \left( -\frac{1}{2}\,{{ m_x}}^{ 2}t-\frac{1}{2}\,{{ n_x}}^{2}t \right) {\alpha _{{3}}}^{2}-\alpha _{{3}}m{ n_x}\,y \\ + [ \left( -{ m_x}\,{ m_y}\,t-{ n_x}\,{ n_y}\,t \right) \alpha _{{3}}+ \left( {m}^{2}{n}^{2}t-2\,{n}^{3}{ n_x}\,tx+\frac{1}{2}\,{m}^{4}t \right) \alpha _{{4}} -2\,m{ n_t}\,t-m{ n_y}\,y+{ m_y}\,ny-mn ] \alpha _{{2}}, \\ C^{t}=2\,\alpha _{{2}}m{ n_y}\,t+ \left( \frac{1}{2}\,\alpha _{{4}}{n} ^{3}{} { n_x}\,{t}^{2}+m{ n_x}\,t \right) \alpha _{{3}}+\frac{1}{2}\,y{m}^{2}+ \frac{1}{2}\,{n}^{2}y. \end{array} \end{aligned}$$
(5.21)

Case 5 If \(M^{1}=-m\) and \(M^{2}=n\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}= \alpha _{{1}} \left( -m{ n_x}+{ m_x}\,n \right) + \alpha _{{3}}{} { m_y}\,n, \\ C^{y}= \alpha _{{2}} \left( -m{ n_y}+{ m_y}\,n \right) - \alpha _{{3}}m{ n_x}, \\ C^{t}= \frac{1}{2}\,({m}^{2}+{n}^{2}). \end{array} \end{aligned}$$
(5.22)

Case 6 If \(M^{1}=\left( 2\,\alpha _{1}\,y\, { n_x}-2\,\alpha _{2}\,x\, { n_y}-\alpha _{3}\,(x\, { n_x}-y\, { n_y}) \right)\) and

\(M^{2}=\left( 2\,\alpha _{1}\,y\, { m_x}-2\,\alpha _{2}\,x\, { m_y}-\alpha _{3}\,(x\, { m_x}-y\, { m_y}) \right)\), then we have

$$\begin{aligned}{} & {} C^{x}= \left( {{ m_x}}^{2}y+{{ n_x}}^{2}y \right) {\alpha _ {{1}}}^{2}+ \left( \left( -\frac{1}{2}\,{{ m_y}}^{2}x-\frac{1}{2}\,{{ n_y}}^{2}x \right) \alpha _{{3}}+\alpha _{{4}}{n}^{3}{} { n_y}\,{x}^{2 } \right) \alpha _{{2}}+ \left( \frac{1}{2}\,{{ n_y}}^{2}y+\frac{1}{2}\,{{ m_y}}^{2 }y \right) {\alpha _{{3}}}^{2} \nonumber \\{} & {} \left[ \left( -2\,{ m_x}\,{ m_y}\,x-{{ m_y}}^{2}y-2 \,{ n_x}\,{ n_y}\,x-{{ n_y}}^{2}y \right) \alpha _{{2}}+ \left( - \frac{1}{2}\,{{ m_x}}^{2}x+{ m_x}\,{ m_y}\,y-\frac{1}{2}\,{{ n_x}}^{2}x+{ n_x}\,{ n_y}\,y \right) \alpha _{{3}}\right. \nonumber \\{} & {} \left. + \left( 2\,{n}^{3}{ n_t}\,ty-\frac{1}{2}\,{m}^{4}y-{m}^{2}{n}^{2}y \right) \alpha _{{4}}+2\,m{ n_t}\,y \right] \alpha _{{1}}+ \left( \left( \frac{1}{4}\,{m}^{4}x+\frac{1}{2}\,{m}^{ 2}{n}^{2}x-{n}^{3}{ n_y}\,xy \right) \alpha _{{4}}-m{ n_t}\,x \right) \alpha _{{3}}, \nonumber \\{} & {} C^{y}=\left[ \left( {{ m_x}}^{2}x+2\,{ m_x}\,{ m_y}\,y +{{ n_x}}^{2}x+2\,{ n_x}\,{ n_y}\,y \right) \alpha _{{2}}+ \left( \frac{1}{2}\,{{ n_x}}^{2}y+\frac{1}{2}\,{{ m_x}}^{2}y \right) \alpha _{{3}} \right] \alpha _{{1}}+ \left( -{{ m_y}}^{2}x-{{ n_y}}^{2}x \right) {\alpha _{{2}}}^{2} \nonumber \\{} & {} + \left[ \left( \frac{1}{2}\,{{ n_y}}^{2}y+\frac{1}{2}\, {{ m_y}}^{2}y-{ m_x}\,{ m_y}\,x-{ n_x}\,{ n_y}\,x \right) \alpha _{{3}}+ \left( {m}^{2}{n}^{2}x-{n}^{3}{ n_x}\,{x}^{2}+\frac{1}{2}\,{m} ^{4}x \right) \alpha _{{4}}-2\,m{ n_t}\,x \right] \alpha _{{2}} \nonumber \\{} & {} + \left( -\frac{1}{2}\,{{ n_x}}^{2}x-\frac{1}{2}\,{{ m_x}}^{2}x \right) {\alpha _{{3 }}}^{2}+ \left[ \left( -\frac{1}{4}\,{m}^{4}y+{n}^{3}{} { n_x}\,xy-\frac{1}{2}\,{m}^{2 }{n}^{2}y \right) \alpha _{{4}}+m{ n_t}\,y \right] \alpha _{{3}}, \nonumber \\{} & {} C^{t}=\left( -2\,{n}^{3}{} { n_x}\,ty\alpha _{{4}}-2\,m{ n_x} \,y \right) \alpha _{{1}}+2\,\alpha _{{2}}m{ n_y}\,x+ \left( m{ n_x} \,x-m{ n_y}\,y \right) \alpha _{{3}}. \end{aligned}$$
(5.23)

Case 7 If \(M^{1}={ n_x}\) and \(M^{2}={ m_x}\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}=\frac{1}{2}\,\left( {{ m_x}}^{2}+ {{ n_x}}^{2} \right) \alpha _{{1}}- \frac{1}{2}\, \left( {{ m_y}}^{2}+ {{ n_y}}^{2} \right) \alpha _{{2}}+ \left( { n_t}\,{n}^{3}t- \frac{1}{4}\,{m}^{4}- \frac{1}{2}\,{m}^{2}{n}^{ 2} \right) \alpha _{{4}}+m{ n_t}, \\ C^{y}= \left( { m_x}\,{ m_y}+{ n_x}\,{ n_y} \right) \alpha _{{2}}+ \frac{1}{2}\,\left( {{ m_x}}^{2}+ {{ n_x}}^{2} \right) \alpha _{{3}}, \\ C^{t}=-{n}^{3}t{ n_x}\,\alpha _{{4}}-m{ n_x}. \end{array} \end{aligned}$$
(5.24)

Case 8 If \(M^{1}={ n_t}\) and \(M^{2}={ m_t}\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}= \left( { m_t}\,{ m_x}+{ n_t}\,{ n_x} \right) \alpha _{{1}}+ \frac{1}{2}\,\left( { m_t}\,{ m_y}+{ n_t}\,{ n_y} \right) \alpha _{{3}}, \\ C^{y}=\left( { m_t}\,{ m_y}+{ n_t}\,{ n_y} \right) \alpha _{{2}}+ \frac{1}{2}\,\left( { m_t}\,{ m_x}+{ n_t}\,{ n_x} \right) \alpha _{{3}}, \\ C^{t}=\frac{-1}{4}\,[\left( 2\,{{ m_x}}^{2}+{{ n_x}}^{2} \right) \alpha _{{1}}+ 2\,\left( {{ m_y}}^{2}+{{ n_y}}^{2} \right) \alpha _{{2}}+2\, \left( { m_x}\,{ m_y}+{ n_x}\, { n_y} \right) \alpha _{{3}}+ \left( {m}^{4}+2\,{m}^{2}{n}^{2 }+{n}^{4} \right) \alpha _{{4}}]. \end{array} \end{aligned}$$
(5.25)

Case 9 If \(M^{1}={ n_y}\) and \(M^{2}={ m_y}\), then we have

$$\begin{aligned} \begin{array}{l} C^{x}=\left( { m_x}\,{ m_y}+{ n_x}\,{ n_y} \right) \alpha _{{1}}+ \frac{1}{2}\,\left( {{ m_y}}^{2}+{{ n_y}}^{2} \right) \alpha _{{3}}-\alpha _{{4}}{n}^{3}{} { n_y}\,x, \\ C^{y}= \frac{-1}{4}\,[2\,\left( {{ n_x}}^{2}+{{ m_x}}^{2} \right) \alpha _{{1}}- 2\,\left( {{ m_y}}^{2}+{{ n_y}}^{2} \right) \alpha _{{2}}+ \left( {m}^{4}+2\,{m}^{ 2}{n}^{2} -4\,x{n}^{3}{} { n_x}\right) \alpha _{{4}}+m{ n_t}], \\ C^{t}=-m{ n_y}. \end{array} \end{aligned}$$
(5.26)

6 Conclusion

In this paper, we introduced the application of the Bernoulli sub-equation function method to derive novel exact travelling wave solutions for two significant physical models: the (2+1)-dimensional HNLS equation and the (2+1)-dimensional HFSC equation. By this method, we discuss the obtained solutions at different values of K and S in Eqs. (2.3) and (2.4), respectively by using the relation \(S=K+1\) that we get from the balancing procedure. We observe that when \(a\ne b\), the solutions that we obtained are similar to the other and at \(a= b\) the solutions are the same. Thus, we notice that some exact solutions when \(S=3\) or \(S=4\) may be reduced to the solutions derived when \(S=2\). The computer systems like as Maple is used to solve the complicated algebraic equations to get these solutions. Also, by Maple software we have checked the obtained solutions. To the best of our knowledge, some of the obtained solutions for these models are new. Many authors obtained exact solutions of these models using various methods (Apeanti et al. 2019)- (Sahoo and Tripathy 2022). We compered our results for (1.1) and (1.2), with the solutions studied by using other methods (Apeanti et al. 2019; Tebue et al. 2020; Bashar et al. 2021; Han et al. 2022; Sahoo and Tripathy 2022), our results are novel. The geometrical shape for some of the obtained results are plotted in the form of two-dimensional and three-dimensional for various choices of the parameters that appear in the results. The absolute, real and imaginary parts of the solutions are plotted to discuss the physical behavior of the HNLS and HFSC equations. The obtained solutions can be classified as dark, singular and rational which may help researchers to known some physical meaning of these models. The behavior of solutions (3.7), (3.11),(3.21) and (3.23) are presented graphically through 3D and 2D in Figs. 1, 2, 3 and 4, respectively. Furthermore, by applying the Lie symmetry method, we construct the infinitesimal generators and using them to construct the symmetry group. Also, we investigate novel solutions of the studied models by the group transformations. In addition, the conservation laws for the models are obtained by multiplier approach. We hope that the obtained solutions are useful in the study of optics and other important equations of mathematical physics. The methods used here could be applied to other NLPDEs.