1 Introduction

Leaky modes have been a subject of interest for many years (Sun et al. 2017; Pick and Moiseyev 2018). Although leaky modes appear in lossless waveguides, they are characterized by their complex propagation constant. This fact has been a source of conceptual confusion about such solutions. In a Hermitian system, solutions should strictly have real propagation constant. Thus, leaky modes are not part of the system’s orthogonal complete basis set with real propagation constants (Marcuvitz 1956). For the simplest type of leaky waveguides, W-type waveguides, the complete set contains only a continuum of radiation modes and no discrete guided modes. It has been shown that leaky modes are a superposition of radiation modes that dominate propagation (Hu and Menyuk 2009). The attenuation results from the wave spreading ’leaking’ into the transverse plane of the waveguide away from the propagation direction with an oscillating pattern. Such modes commonly appear in the analysis of bent waveguides (Wu and Xiao 2021), antiresonant reflecting optical waveguides (ARROWs) (Testa et al. 2016; Wang et al. 2020), and devices on high refractive index substrates (Pruszyńska-Karbownik et al. 2022).

Numerically, there are many numerical methods to study leaky optical waveguides. The finite differences method (FDM) (Hu and Menyuk 2009) and the finite elements method (FEM) are the most common (Uranus and Rahman 2018). Spectral methods can also be used, where the solution is expanded in terms of spectral functions (Abdrabou et al. 2016.) Additionally, one can use propagation methods such as beam propagation method (BPM) with imaginary distance (ID-BPM) to analyze leaky modes by the appropriate selection of propagation step size (Obayya et al. 2002). However, the finite element method (FEM) is the most prominent numerical method for modeling photonic devices (Agrawal and Rahman 2013; Koshiba 1993). The customizable meshing capabilities give it a clear advantage over other methods. Therefore, the FEM is utilized in many mode-solving commercial packages. Unlike the analytical solution, leaky modes are a part of the complete mode decomposition of the system. As with most open boundary conditions treatments, it transforms the system into non-hermitian, where the propagation constant can generally be complex.

To model open boundaries using the FEM, a special treatment needs to be carried out to truncate the finite element mesh. Basic boundary conditions such as Neumann and Dirichlet boundary conditions can only model lossless guided modes. For leaky modes, on the other hand, one can add a matching absorbing layer, i.e., perfectly matched layer (PML), to eliminate spurious reflection at the domain boundaries (Rogier and Zutter 2002). However, the PML parameters such as absorption strength, layer thickness, and distance to the structure are vauge in literature and require careful “design” to achieve the optimum performance. Another class of boundary conditions is called transparent boundary conditions (TBCs) (Arai et al. 1993; Hernandez-Figueroa et al. 1995). TBCs entirely revolves around eliminating an analytical approximation of the reflected wave. For instance, this approximation is a plane wave in Sommerfeld boundary condition (Hernandez-Figueroa et al. 1995), and a spherical wave in the case of Bayliss-Turkel condition (Uranus et al. 2004). The accuracy order of the Sommerfeld boundary condition is \(O(r^{-3/2})\) with r denoting the radius of the computational domain. Bayliss-Turkel condition, however, offers an accuracy one order higher of \(O(r^{-5/2})\). Therefore, TBCs are placed as far as possible to maintain a valid approximation of the reflected wave, which in return enlarges the required computational resources. One of the most natural solutions to deal with open domains in the FEM is using infinite elements (IEs) (Koshiba 1993). IE exploits the irregular meshing capability of the FEM to extend the boundary element towards infinity in one end. The seminal work of Bettess firstly introduced IE for fluid flow problems (Bettess 1977), and it has been refined since then (Gerdes 2000). The accuracy of an infinite element depends mainly on the choice of the shape function and its parameters. Decay-type infinite elements have been long used to model lossless optical waveguides (Hayata et al. 1988; Rahman and Davies 1984). However, it cannot calculate the effective index imaginary part of leaky modes.

In this regard, we introduce a computationally efficient mesh truncation treatment for complex optical modes. Our treatment adopts a more physical representation of the shape functions describing the outgoing field in the semi-infinite subdomains. A complex infinite element (CIE) that can efficiently and accurately calculate the complex effective index of refraction of leaky and lossy optical waveguides. The proposed treatment is easier to be implemented compared to the conventional PML. Moreover, there is no need to extend the computational domain using the suggested CIE. Thus, the CIE requires less computational resources, less memory and time with a relative error of two orders of magnitude less than the PML in some cases. To verify our approach, we examine an ARROW structure and SPP modes nanostructures.

2 Mathematical formulation

Fig. 1
figure 1

Node representation of the domain with complex infinite elements

Full size image

We start with the Helmholtz scalar wave equation for both TE/TM modes propagating in 1D optical waveguides:

$$\begin{aligned} \frac{d}{d y}\left( p \frac{d \phi }{d y}\right) +\left( q k_{o}^{2}-p \beta ^{2}\right) \phi =0 \end{aligned}$$
(1)

where \(k_o\) is the vacuum wave number. Propagation in z-direction takes the form \(e^{-j \beta z}\), where \(\beta\) is the propagation constant. The field \(\phi\) and the constants p and q are written as shown,

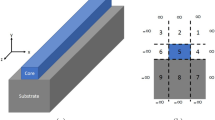
$$\begin{aligned} \begin{aligned} \begin{array}{ll|ll} \text{ TE } \text{ mode: } &{} \phi =E_{x} &{} \text{ TM } \text{ mode: } &{} \phi =H_{x} \\ &{} p=1 &{} &{} p=1 / n^{2} \\ &{} q=n^{2} &{} &{} q=1 \end{array} \end{aligned} \end{aligned}$$
(2)

Figure 1 shows a schematic representation of a leaky planer waveguide with two semi-infinite subdomains. We now have two types of elements to deal with, finite elements for the interior domain and complex infinite elements for the elements on the edge of the computational domain. The analytical solution for this equation in the semi-infinite subdomains is on the form of,

$$\begin{aligned} \phi (y)=\textrm{A} e^{-j \beta _{y} y}+\textrm{B} e^{+j \beta _{y} y} \end{aligned}$$
(3)

where \(\beta _{y}=\sqrt{k_{o}^{2} n^{2}-\beta ^{2}}\). The shape function must realistically represent the outgoing field. Thus, we will assume the interpolation function to be in the form,

$$\begin{aligned} \textrm{N}=e^{\mp \textrm{j} \beta _{y}\left( y \mp y_{o}\right) } \end{aligned}$$
(4)

where \(y_o\) is the end of the computational domain. Adopting Galerkin’s approach on Eq. (1), the infinite element equation could be written as,

$$\begin{aligned} \begin{aligned}&-p \int _{y_{o}}^{\infty }\left\{ \textrm{N}_{y}\right\} \left\{ \textrm{N}_{y}\right\} ^{T} d y+q k_{o}^{2} \int _{y_{o}}^{\infty }\{N\}\{N\}^{T} d y \\&\quad =p \beta ^{2} \int _{y_{o}}^{\infty }\{N\}\{N\}^{T}d y \end{aligned} \end{aligned}$$
(5)

The corresponding global matrix eigenvalue equation is given as follows,

$$\begin{aligned} {[}\widetilde{\varvec{K}}]\{\phi \}-\beta ^{2}[\widetilde{\varvec{M}}]\{\phi \}=0 \end{aligned}$$
(6)

where,

$$\begin{aligned} {[}\widetilde{\varvec{K}}]=[\varvec{K}]+\left[ \begin{array}{cccc} -\frac{j \beta _{y} p_{1}}{2}+\frac{k_{o}^{2} q_{1}}{2 j \beta _{y}} &{} 0 &{} \ldots &{} 0 \\ 0 &{} 0 &{} &{} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} -\frac{j \beta _{y} p_{N}}{2}+\frac{k_{o}^{2} q_{N}}{2 j \beta _{y}} \end{array}\right] \end{aligned}$$
(7)

and

$$\begin{aligned} {[}\tilde{\varvec{M}}]=[\varvec{M}]+\left[ \begin{array}{cccc} \frac{ p_{1}}{2j \beta _{y}} &{} 0 &{} \ldots &{} 0 \\ 0 &{} 0 &{} &{} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \frac{ p_{N}}{2j \beta _{y}} \end{array}\right] \end{aligned}$$
(8)

where \(\{\phi \}\) is the field vector and the subscript in \((p_i,q_i)\) indicates the element number. The \(\left[ \varvec{K}\right]\) and \(\left[ \varvec{M}\right]\) matrices are the characteristic global finite element matrices attained by discretizing the waveguide transverse axis into \(1^{st}\) order line elements.

The CIE approach can be further extended to solve two dimensional problems and calculate the complex effective index of leaky optical waveguides and bent waveguides. To demonstrate this, we will consider the scalar wave equation,

$$\begin{aligned} p \frac{\partial ^{2} \phi }{\partial x^{2}}+p \frac{\partial ^{2} \phi }{\partial y^{2}}-p \beta ^{2} \phi +q k_{0}^{2} \phi =0 \end{aligned}$$
(9)

Similarly, Eq. (9) is reduced to matrix equation as in Eq. (6) where the matrices \(\left[ \varvec{K}\right]\) and \(\left[ \varvec{M}\right]\) are defined as,

$$\begin{aligned} \begin{aligned} {[\varvec{K}]=}&\sum _{e} \iint _{e}\left[ q k_{0}^{2}\{N\}\{N\}^{\textrm{T}}-p\left\{ N_{x}\right\} \left\{ N_{x}\right\} ^{\textrm{T}}\right. \left. -p\left\{ N_{y}\right\} \left\{ N_{y}\right\} ^{\textrm{T}}\right] d x d y \\ {[\varvec{M}]=}&\sum _{e} \iint _{e} p\{N\}\{N\}^{\textrm{T}} d x d y \end{aligned} \end{aligned}$$
(10)

The CIEs are then added at the edges of the computational domain boundaries. For rectangular domains, there are two possible types of complex infinite elements as shown in Fig. 2. The horizontal CIE has the following shape functions for linear elements,

$$\begin{aligned} N_{1}^H=\frac{x_{2}-x}{x_{2}-x_{1}} e^{\mp \textrm{j} \beta _{e}\left( y \mp y_{0}\right) }; \; \; N_{2}^H=\frac{x-x_{1}}{x_{2}-x_{1}}e^{\mp \textrm{j} \beta _{e}\left( y \mp y_{0}\right) } \end{aligned}$$
(11)

Similarly, the CIEs for vertical boundaries shape functions are,

$$\begin{aligned} N_{1}^V=\frac{y_{2}-y}{y_{2}-y_{1}} e^{\mp \textrm{j} \beta _{e}\left( x \mp x_{0}\right) }; \; \; N_{2}^V=\frac{y-y_{1}}{y_{2}-y_{1}}e^{\mp \textrm{j} \beta _{e}\left( x \mp x_{0}\right) } \end{aligned}$$
(12)

where

$$\begin{aligned} \beta _{e}=\sqrt{k_{o}^{2} n_e^{2}-\beta ^{2}} \end{aligned}$$
(13)

and \(n_e\) is the material refractive index at the edge of the element e. The initial \(\beta\) value required in Eq. (4) and Eq. (13) could be chosen close to the real part of the required mode. Then, by feeding the resulting complex \(\beta\) eigenvalue to the infinite element and iterating the process, the complex \(\beta\) converges. The convergence usually does not exceed 2 subsequent iterations. The \(\beta\) value should be complex to have a convergent integral value, additionally, a complex \(\beta\) could be interpreted as a product of two field profiles. An exponentially decaying field representing a tangential field component at the boundary interface, and a sinusoidal propagating field normal to the boundary interface, which can fully describe a wave at the boundary. The elegance of our suggested CIE is that it properly and physically describes the mode in the semi-infinite region, unlike placing an artificial layer such as PML.

Fig. 2
figure 2

a Horizontal boundaries CIE and b Vertical boundaries CIE

Full size image

3 Numerical results

To validate the accuracy and efficiency of our approach, we consider an ARROW structure (Anemogiannis et al. 1999; Abdrabou et al. 2016). Figure 3b shows the index profile of the waveguide where the refractive indices are \(n_a=1\) for air, \(n_c=1.46\), \(n_1=2.3\), and \(n_s=3.85\) for substrate. The operating wavelength equals \(0.6328 \mu m\). Their thicknesses are \(d_1=0.142\lambda\), \(d_2=3.15\lambda\), and the core layer \((d_c)\) equals \(6.3\lambda\). The normalized electric field for the \(TE_1\), \(TE_3\), \(TE_6\) and \(TE_{18}\) are plotted in Fig. 3a. Table 1 shows the effective indices of the ARROW modes in comparison with the results obtained by the argument principle method (APM) and rational Chebyshev multi-domain pseudo-spectral method (RC- MDPSM) in (Anemogiannis et al. 1999; Abdrabou et al. 2016). As shown in Table 1, the CIE can accurately calculate the complex effective index of refraction of different modes.

Fig. 3
figure 3

a Anti-resonant reflecting optical waveguide index profile, and b Normalized \(TE_1\), \(TE_3\), \(TE_6\) and \(TE_{18}\) electric fields at \(\lambda =0.6328 \mu m\)

Full size image
Table 1 Effective index for the TE modes of the ARROW
Full size table
Fig. 4
figure 4

a Cross-sectional view of a leaky optical waveguide. b Meshing of finite elements with CIE on the bottom edge

Full size image

Next, we will analyze a 2D leaky waveguide studied in (Berry et al. 1993; Obayya et al. 2002). A schematic diagram of the waveguide cross-section is given in Fig. 4a. The operating wavelength is \(\lambda =1.064\mu m\) and The refractive indexes are 3.59 for GaAs, 3.555 for 5% AlGaAs, and 3.452 for 20% AlGaAs. Despite that the refractive indices are real (no gain nor loss), there’s a power leakage of the guided modes into the high index substrate due to the high GaAs substrate index. This leakage requires a robust boundary condition to evaluate.

Table 2 The effective indices of the three guided modes of the leaky optical waveguide
Full size table
Fig. 5
figure 5

Field plots of the first three guided modes, \(H^y_{11}\), \(H^y_{12}\) and \(H^y_{13}\)

Full size image

In this structure, the leakage is expected to be at the bottom boundary. Therefore, for simplicity we will apply the CIE boundaries at the bottom edge only. Moreover, the structure has a mirror symmetry, which can be exploited to reduce the computational domain and increase the accuracy of our solution. To force the even modes, the left edge is left unchanged (zero flux Neumann BCs) as shown in Fig. 4b. Table 2 shows the complex effective index of three guided modes in comparison with the results obtained form spectral index method (SIM) (Berry et al. 1993) and imaginary distance vectorial finite element beam propagation method (ID-VFEBPM) (Obayya et al. 2002). As shown in the table, the CIE results agree with the ones reported on literature. The field profiles of the three guided modes are shown in Fig. 5.

Optical waveguide bending is a common scenario while routing between different optical components. Ideally, this problem is modeled using a propagation solver as the structure is longitudinally varying in the propagation direction. However, one way to model this, is to apply an index transformation that mimics this curvature. This approach is known as the conformal transformation approach (Heiblum and Harris 1975),

$$\begin{aligned} {\tilde{n}}=n\left( 1+\frac{x}{R_{c}}\right) \end{aligned}$$
(14)
Fig. 6
figure 6

A schematic diagram of a the index transformation, and b the curved rib waveguide cross section showing the CIE placement

Full size image

where n is the original refractive index of the structure, \({\tilde{n}}\) is the transformed index of refraction, x is the horizontal distance measured from the waveguide centre and \(R_c\) is the radius of curvature. This transformation models a bending to the left as shown in Fig. 6a. On the other hand, right bends is preformed by simply changing the positive sign to negative. Herein, we study a typical rib waveguide with a cross-section given in Fig. 6b (Xiao and Sun 2012). The refractive indexes of the substrate, the core, the upper cladding are \(n_s =3.17\) (InP), \(n_f = 3.27\) (InGaAsP), and \(n_c = 1.0\) (air) at the operating wavelength of 1.55 \(\mu m\). The width of the rib is 3 \(\mu m\), with a thickness of 1.2 \(\mu m\), the upper cladding thickness is 0.5 \(\mu m\) and the thickness of the rib bottom layer is 0.1 \(\mu m\). Again, for simplicity, we will apply the CIE on the bottom and right boundaries, leaving the upper and left boundaries unchanged (zero flux). Figure 7a shows the real part of the effective refractive index of the bent waveguide with a bending range from \(R=50\) \(\mu m\) to \(R=160\) \(\mu m\) in comparison with the results obtained using a modified finite-difference method in a local cylindrical coordinate system given in (Xiao and Sun 2012). More importantly, the leakage losses in logarithmic scale is shown in Fig. 7b. Moreover, to show this leakage, the major field component squared for the TE and TM modes at \(R=50\) \(\mu m\) are shown in logarithmic scale in Fig. 8. As can be drawn from the figure, the new boundary condition can capture the salient features of bent leakage fields.

Fig. 7
figure 7

Effective indexes of the fundamental modes for a typical bending rib waveguide as a function of the bending radius: real (a) and imaginary (b) parts

Full size image
Fig. 8
figure 8

At R=50 \(\mu m\), a the \(E_y^2\) of the TE mode and b the \(H_x^2\) of the TM mode

Full size image

4 Conclusion

In summary, we have introduced complex infinite elements for characterizing unbounded complex modes in optical waveguides. We have shown the accuracy of this treatment by solving an ARROW structure, high index substrate waveguide and curved waveguides. The CIEs are computationally efficient as it does not require extending the computational domain. Thus, making this approach less memory consuming compared to other conventional mesh truncation methods. Additionally, this approach could be extended to solve full vectorial wave equation formulations and explore different complex shape functions by introducing the CIE in different coordinate system.