1 Introduction

In the recent years, special features of photonic crystal fibers (PCFs) have made them an efficient candidate in many applications in different fields. These features include single mode behavior along wide band of frequency range (Knight et al. 1996), large birefringence (Schreiber et al. 2014; Mohammadd et al. 2022), high nonlinearity (Broeng and Tünnermann 2005; Su et al. 2014), and large effective mode area (Knight et al. 1998). Further, the chromatic dispersion in PCFs could be easily controlled along wide range of wavelengths (Hameed et al. 2017). Consequently, the PCFs may be exploited in many potential applications, such as supercontinuum generation devices (Lanh et al. 2019), dispersion compensating fibers (Islam et al. 2017; Ranathive et al. 2022), ultra-flattened-dispersion (Le et al. 2018), and polarization maintaining fibers (Yin and Xiong 2014), lasers (Cui et al. 2019). The PCF properties can be also adjusted by changing the shape, size, pitch, number of air-holes rings around the core, and the positions of cladding air-holes. Also, filling PCFs with other materials increases the degree of freedom (Eggleton et al. 2001; Xuan et al. 2017; Yiou et al. 2015; Sun et al. 2016). Therefore, new applications have been reported using PCFs such as plasmonic sensors (Chen et al. 2023a, b), cancer cell detector (Habib et al. 2021; Mohammed et al. 2023) and photonic analog-to-digital converters (Mohammadi et al. 2022).

To improve data capacity in optical communication through PCFs, the dispersion should be controlled. Initially, Saitoh et al. (2003) have shown that the PCFs can be controlled to obtain nearly zero flattened dispersion over studied wavelength range. Further, several optimization algorithms have been exploited to control the dispersion of PCFs such as metaheuristic algorithms (Hameed et al. 2016), genetic algorithms (Kerrinckx et al. 2004; Poletti et al. 2005; Abdelaziz et al. 2013), radial basis function artificial neural network (RBF-ANN) (El-Mosalmy et al. 2014; Hameed et al. 2008) and trust region (TR) techniques (Hameed et al. 2017). In (Hameed et al. 2016), a central force optimization algorithm (CFO) is used to optimize 6 design parameters to reach an ultra-flat zero dispersion between + 0.1 and − 0.609 Ps/km nm over a range of wavelengths from 1.25 to 1.6 μm. Also, a particle swarm optimization (PSO) algorithm could obtain a dispersion between + 0.1974 and − 0.7404 Ps/km nm over the same range of wavelengths. The previous results are obtained by a specified range for each design parameter. Further, Kerrinckx et al. (2004) have used genetic algorithm (GA) to optimize only two design parameters to achieve a dispersion between + 7.75 and + 1.41 Ps/km nm over a wavelength range from 1.25 to 1.6 μm. Furthermore, a dispersion between + 0.1 and − 0.1 Ps/km nm is obtained by Poletti et al. (2005) using another GA over a limited range of wavelengths from 1.5 to 1.6 μm. Moreover, a GA is used by Abdelaziz et al. (2013) to obtain a dispersion between \(\pm\) 0.1 Ps/km nm over a wide wavelength range from 1.335 to 1.584 μm. Besides, RBF-ANN (El-Mosalmy et al. 2014) is used to obtain a dispersion between + 0.28 and − 0.59 Ps/km nm over a range of wavelengths from 1.25 to 1.6 μm. In addition, a trust region algorithm (Hameed et al. 2017) could achieve a nearly flat zero dispersion using several designs over wavelength range from 1.45 to 1.6 μm. Also, the trust region algorithm (Hameed et al. 2017) has obtained a highly negative flat dispersion with an average value – 155 Ps/km nm through wavelength from 1.4 to 1.6 μm for the quasi TM mod.

The metaheuristic algorithms and genetic algorithms (Hameed et al. 2016; Kerrinckx et al. 2004; Poletti et al. 2005) have several drawbacks as they may stuck in local optimal point and reaching to the global optimum is not guaranteed. Further, they can be sensitive for the initial conditions and have a slow rate of convergence in the optimization process. Additionally, they are not based on any mathematical basis compared to the classical optimization techniques (Viana et al. 2005). Also, trust region algorithms suffer from the absence of a general rule to choose the trust region radius and their dependence on the solved problem (Kamandi et al. 2015). In addition, the newly ANN algorithms (Chen et al. 2023a, b; Yang et al. 2023) suffer from several disadvantages (Zhang et al. 2023; Lin et al. 2023; Abdolrasol et al. 2021) such as the unexplained way of selecting the outputs of the network. Further, the ANN structure is determined by the experience without any deterministic laws. Furthermore, the newly ANNs may have a gradual corruption during the optimization process which increases the simulation time where large amount of memory is needed. Moreover, the network training is complex and may be trapped in local optimum.

In this paper, mixed integer nonlinear programming (MINLP) optimization technique called branch and bound optimization (Dakin 1965) is exploited to optimize the dispersion characteristics of PCFs. In this class of optimization technique, some of the design parameters take real values while the others are integers. This feature will be very helpful to control the filling material in each hole of the PCFs during the optimization process. However, in the previous studies, only the geometrical parameters are optimized assuming fixed infiltration. The branch and bound technique is considered one of the most efficient optimization methods for MINLP problems which have some or all of its design parameters are restricted to take discrete values only and the performance of the objective function is affected by nonlinear dynamics. In addition, due to the computational cost of the objective function, computationally efficient surrogate-based models could be constructed to replace the objective function. Further, the suggested technique branches the original problem into sequence of subproblems. Then, some of the subproblems are solved to obtain upper and lower bounds for the objective function value. These bounds enable us to discard some other subproblems to save computational time. Therefore, the suggested technique covers all the design space with less complexity and time than the ANN algorithms.

In this study, the proposed algorithm relies on kriging surrogate models (Lophaven et al. 2002). Further, a MINLP branch and bound optimization algorithm with kriging surrogate model is used along with full vectorial finite difference method (FVFDM) (Fallahkhair et al. 2008) to achieve an ultra-flat dispersion with zero value over a wide band of wavelengths from 1.25 to 1.6 μm. Moreover, the introduced technique is employed to reach a highly negative flat dispersion of − 163 ± 0.9 and − 170 ± 1.2 ps/Km. nm over the same wavelength range for the quasi TM and the quasi TE modes, respectively. These results are compared with other algorithms (Hameed et al. 2008; Hameed et al. 2016; Hameed et al. 2017; Kerrinckx et al. 2004; Poletti et al. 2005; El-Mosalmy et al. 2014) to show the strength of the proposed algorithm.

It should be noticed that, in the proposed algorithm all design parameters can be changed at the same time which enable us to benefit from the entire design space and to obtain a global optimal solution. However, most of the preceding designs are obtained using the parametric sweep methodology where only one parameter can be changed at a time while the other parameters are kept constant leading to reduced design space.

2 MINLP branch and bound optimization algorithm

MINLP problems are optimization problems which involve discrete design parameters and nonlinear dynamics. The general form of the MINLP problem is

$$\min ~\left\{ {f\left( {{\varvec{x}}_1 ,~{\varvec{x}}_2 } \right)|h_i \left( {{\varvec{x}}_1 ,~{\varvec{x}}_2 } \right) \le 0~,\;i = 1,2, \ldots ,c~,\;{\varvec{x}}_1 \in \mathbb{R}^{n_1 } ,\;{\varvec{x}}_2 \in \mathbb{z}^{n_2 } } \right\}$$
(1)

where \(\varvec{c}, \varvec{n}_1\) and \({\varvec{n}}_2\) denote the number of constraints, the number of continuous design parameters and the number of discrete design parameters respectively. The function \({\varvec{f}}\left( {{\varvec{x}}_1 , {\varvec{x}}_2 } \right)\) represents the objective function, the function \({\varvec{h}}_i \left( {{\varvec{x}}_1 ,{\varvec{x}}_2 } \right)\) used to represent ith constraint. \({\varvec{x}}_1 , {\varvec{x}}_2\) denote the continuous and discrete design parameters respectively. The reported algorithm belongs to the mixed integer nonlinear programming optimization class where the computationally expensive objective function is approximated by a computationally cheaper kriging surrogate model \({\varvec{\hat{y}}}\left( {\varvec{x}} \right)\) (Lophaven et al. 2002):

$$\hat{y}\left( {\varvec{x}} \right){ } = \mathop \sum \limits_{j = 1}^m \alpha_j g_j \left( {\varvec{x}} \right) + e\left( {\varvec{x}} \right)$$
(2)

The first part is a quadratic regression polynomial with \(m = \left( {n + 1} \right){ }\left( {n + 2} \right)/2\) where \(n\) is the total number of continuous and discrete design parameters, unknown regression coefficients \({\varvec{\alpha}} = [\alpha_1 , \alpha_2 , \ldots , \alpha_m ] \in {\mathbb{R}}^m\) and \(g_j ({\varvec{x}})\) are the basis functions of the regression model where \(g_1 \left( {\varvec{x}} \right) = 1\), \(g_2 ({\varvec{x}}) = {\varvec{x}}_1\), …, \(g_{n + 1} ({\varvec{x}}) = {\varvec{x}}_n\), \(g_{n + 2} ({\varvec{x}}) = {\varvec{x}}_1^2\),…, \(g_{2n + 1} ({\varvec{x}}) = {\varvec{x}}_1 {\varvec{x}}_n\), …, \(g_{2n + 2} ({\varvec{x}}) = {\varvec{x}}_2^2\),…, \(g_{3n + 1} ({\varvec{x}}) = {\varvec{x}}_2 {\varvec{x}}_n\),…, \(g_m ({\varvec{x}}) = {\varvec{x}}_n^2\).

The second part, \(e({\varvec{x}})\), is a Gaussian random error function with zero mean and variance \(\sigma^2\). The covariance matrix \({\varvec{\varSigma}} \in {{\mathbb{R}}}^{s \times s}\) of \(e({\varvec{x}})\) is calculated as follows:

$$\sum {\left[ {e\left( {\varvec{x}^{(i)} } \right),~e\left( {\varvec{x}^{(j)} } \right)} \right] = \sigma ^2 \rho \left( {\varvec{x}^{(i)} ,\varvec{x}^{(j)} } \right),} ~\quad i,j = 1,2, \ldots ,~s$$
(3)

where \(s\) is the number of sample data; \({\varvec{\rho}}\) \(\in {{\mathbb{R}}}^{s \times s}\) is a symmetric positive semidefinite matrix with diagonal elements of all ones that represents the Gaussian spatial correlation function. The entries of \({\varvec{\rho}}\) is computed by the kernel function

$$\rho \left( {\varvec{x}^{(i)} ,\varvec{x}^{(j)} } \right) = \exp \left[ { - \mathop \sum \limits_{k = 1}^n \varphi _k \left| {\varvec{x}_k ^{(i)} - \varvec{x}_k ^{(j)} } \right|^2 } \right]$$
(4)

where \(\varphi_k \ge 0\) and \(\varvec{\varphi } = \left[ {\begin{array}{*{20}c} {\varphi _1 } & \ldots & {\varphi _n } \\ \end{array} } \right]\) represents distance weights. Let \({\varvec{x}}^{\left( 1 \right)}\), \({\varvec{x}}^{\left( 2 \right)}\), …, \({\varvec{x}}^{\left( s \right)} \in {{\mathbb{R}}}^n\) be a set of \(s\) inputs to the high-fidelity model and the resulting outputs are \({\varvec{Y}} = [y({\varvec{x}}^{\left( 1 \right)} )\), \(y({\varvec{x}}^{\left( 2 \right)} )\), …, y(\({\varvec{x}}^{\left( s \right)} )] \in {{\mathbb{R}}}^s\). The kriging model \(\hat{y}\left( {\varvec{x}} \right)\) linearly predict \(y\left( {\varvec{x}} \right)\) at an unknown point \({\varvec{x}} \in {{\mathbb{R}}}^n\) as follows

$$\hat{y}\left( {\varvec{x}} \right) = {\varvec{\mu}}^T \left( {\varvec{x}} \right){\varvec{Y}}$$
(5)

The optimal of \({\varvec{\mu}}\left( {\varvec{x}} \right)\) is then obtained through reducing the mean square error of the prediction and this leads to the following predictor equation

$$\hat{y}\left( {\varvec{x}} \right) = {\varvec{g}}^T \left( {\varvec{x}} \right){\varvec{\alpha}} + {\varvec{r}}^T \left({\varvec{x}} \right){\varvec{\rho}}^{ - 1} \left( {\varvec{Y}} - {\varvec{G\alpha}} \right)$$
(6)

where \({\varvec{g}}\left( {\varvec{x}} \right)\) is \(m \times 1\) vector contains the basis functions of the quadratic regression model, \(\varvec{G} = \left[ {\begin{array}{lll} {\varvec{g}({\varvec{x}}^{(1)} )} & \ldots & {\varvec{g}(\varvec{x}^{(s)} )} \\ \end{array} } \right]^T \in \mathbb{R}^{s \times m}\) is the regression matrix and \({\varvec{r}}\left( {\varvec{x}} \right) = \left[ {{\varvec{\rho}}\left( {{\varvec{x}}, {\varvec{x}}^{\left( 1 \right)} } \right){ } \ldots {\varvec{\rho}}\left( {{\varvec{x}},{\varvec{x}}^{\left( s \right)} } \right)} \right]^{\varvec{T}} \in {{\mathbb{R}}}^s\). The value of \({\varvec{\alpha}}\) is given by:

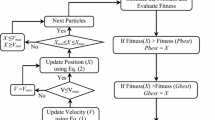
$${\varvec{\alpha}} = \left( {{\varvec{G}}^{\varvec{T}} {\varvec{\rho}}^{ - 1} {\varvec{G}}} \right)^{ - 1} {\varvec{G}}^{\varvec{T}} {\varvec{\rho}}^{ - 1} {\varvec{Y}}$$
(7)

The MINLP branch and bound algorithm starts by solving a relaxed version of MINLP in (1) obtained by relaxing the integrality condition. If the solution to the relaxed problem satisfies the integrality conditions on the discrete design parameters, then it also solves the original MINLP. Otherwise, the algorithm branches on any discrete design parameter with fractional value and creates two MINLP subproblems with additional constraint on the value of the selected discrete design parameter. In the first subproblem, the selected discrete design parameter takes at least the ceil of the fractional value. In the second subproblem, it takes at most the floor of it. Then the algorithm solves the new subproblems after relaxing the integrality condition. This process continues till the algorithm solves all the created subproblems. The optimal solution is the solution with the minimum value for the objective function. A flowchart for the steps of the proposed algorithm is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of the main steps of the suggested algorithm

Full size image

3 Numerical results

3.1 Optimization of PCF with ultra-flat zero dispersion

Figure 2 shows cross section of the suggested PCF to achieve an ultra-flat zero dispersion over a wide range of wavelengths. The reported PCF has four rings of air holes with different diameters \(d_1 ,{ }d_2 ,{ }d_3\text{ and }d_4 .\) Further, the first two rings are selectively infiltrated with ethanol material. In this study, the material dispersion of the silica background (Hlubina 2001) is taken into consideration where the wavelength dependent refractive index of the silica is taken as

$$n_{{\text{Silica}}} = \sqrt {{1 + \frac{\alpha_0 \lambda^2 }{{\lambda^2 - \alpha_1^2 }} + \frac{\beta_0 \lambda^2 }{{\lambda^2 - \beta_1^2 }} + \frac{\gamma_0 \lambda^2 }{{\lambda^2 - \gamma_1^2 }}}}$$
(8)

where \(n_{{\text{Silica}}}\) is the refractive index of the \({\text{silica}}\) material \(\alpha_0 = 0.6961663, \alpha_1 = 0.0684043\, {\upmu}{\text{m}}^2\), \(\beta_0 = 0.407942\), \({ }\beta_1 = 0.1162414\,{\upmu}{\text{m}}^2\), \(\gamma_0 = 0.8974794\) and \(\gamma_1 = 9.8961610\,{\upmu}{\text{m}}^2\) (Hlubina 2001). Additionally, the Sellmeier equation of the Ethanol material is given by Thuy et al. (2020)

$$n_{{\text{Ethanol}}} = \sqrt {{1 + \frac{\alpha_1 \lambda^2 }{{\lambda^2 - \alpha_2 }} + \frac{\alpha_3 \lambda^2 }{{\lambda^2 - \alpha_4 }}}}$$
(9)

where \(n_{{\text{Ethanol}}}\) is the refractive index of the \({\text{Ethanol}}\) material \(\alpha_1 = 0.83189,{ }\alpha_2 = 0.93 \times 10^{ - 2} \,{\upmu}{\text{m}}^2\), \(\alpha_3 = - { }0.15582\), \(\alpha_4 = - { }49.4520\,{\upmu}{\text{m}}^2\) (Thuy et al. 2020).

Fig. 2
figure 2

The initial structure of the PCF

Full size image

The aim of the optimization process is to achieve an ultra-flat zero dispersion over the wavelength range from 1.25 to 1.6 μm. The full vectorial finite difference method (FVFDM) (Fallahkhair et al. 2008) is used to calculate the modal properties of the suggested PCF with perfect matched boundary conditions (Chew et al. 1997). A computational domain of size \(15 \times 15\,{\upmu}{\text{m}}\) is used. Fine meshes of \(\Delta x = \Delta y = 0.03\) are used to obtain accurate results. The dispersion of the PCF at certain wavelength λ is given by:

$$D = - \frac{\lambda }{C}\left( {\frac{{d^2 \left[ {{\text{Re}}(n_{{\text{eff}}} )} \right]}}{d\lambda^2 }} \right)$$
(10)

where \(n_{{\text{eff}}}\) is the effective index of the investigated mode and C is the speed of light through the vacuum.

To achieve our aim, the following function will be optimized.

$$f\left( x \right) = \mathop \sum \limits_{\lambda = 1.25}^{\lambda = 1.6} \left| {D\left( \lambda \right)} \right|$$
(11)

The cladding hole diameters \({ }d_1\), \(d_2\), \(d_3\), \(d_4\), the hole pitch \(\Lambda\), and two integer variables responsible for selective infiltration of the ethanol material in the first two rings are the designable parameters. The first ring contains six holes and due to the symmetry of the structure, we control the infiltration of four holes only through the first integer variable whose value is integer from 0 to 15. The second ring contains twelve holes and due to the symmetry of the structure, we control the infiltration of seven holes only through the second integer variable whose value is integer from 0 to 127. After assigning a value to the integer variables, they converted to a 4-bit and 7-bit binary numbers, each bit may be zero or one. If the value is zero, the corresponding bit is filled with air otherwise it filled with ethanol.

The number of calculated function values (N) is always considered as a measure of the performance of the optimization techniques. The values of the objective function of the MINLP algorithm after different numbers of function evaluations is shown in Fig. 3a. It should be noted that about 360 function evaluations are needed by the introduced technique to converge to the optimal value of the objective function. Further, it is revealed from Fig. 3a that the objective function value is kept almost the same while increasing the number of function evaluations to 400 which verify the convergence to the optimal solution. In addition, the dispersion results and the mean square error (MSE) with the required dispersion; zero in our study; are shown in Table 1. In this investigation, the MSE is calculated as follows:

$${\text{MSE}} = \frac{1}{{\text{number of sampling points}}}\mathop \sum \limits_{\lambda = 1.25}^{\lambda = 1.6} \left( {D\left( \lambda \right)} \right)^2$$
(12)
Fig. 3
figure 3

a Variation of the objective function versus the number of the evaluated functions and b the wavelength dependent dispersion of the quasi TE mode

Full size image
Table 1 The initial and optimized geometrical parameters of the studied PCF selectively infiltrated with Ethanol material. The initial and final dispersion and MSE of the quasi TE mode are also included
Full size table

The dispersion of the quasi TE mode obtained by the proposed algorithm is shown in Fig. 3b. The inset figures show the main component \({\varvec{H}}_y\)of the quasi TE mode at the wavelengths \(\lambda = 1.3\;{\upmu }\)m and \(1.55\;{\upmu }\)m.

The inset of Fig. 3a shows the final structure of the PCF with the optimal selective filling in the first two rings. The obtained results show the effectiveness of the suggested algorithm in the design of the selectively infiltrated PCFs. Further, the reported technique took about 18 h to reach the optimal design. The trust region algorithm (Hameed et al. 2017) took about 132 h with five air hole rings to obtain comparable results on a PC with the same specifications. The central force optimization (CFO) (Hameed et al. 2016) took about 155 h with five air hole rings. The genetic algorithm (Poletti et al. 2005) took about 20 h to reach ultra-flat dispersion with zero value over only a wavelength range from 1.5 to 1.6 μm with 5 sampling points. Also, the trust region algorithm (Hameed et al. 2017) achieves ultra-flat dispersion with zero value on only a wavelength range from 1.45 to 1.6 μm. However, the proposed technique achieves an ultra-flat dispersion with zero value over a wavelength range from 1.25 to 1.6 μm with 14 sampling points. In addition, the genetic algorithm (Kerrinckx et al. 2004) is used to optimize only two design parameters, the hole pitch \(\Lambda\) and the hole diameters d, to achieve ultra-flattened zero dispersion \(3 \pm { }4{\text{ Ps/km}}\;{\text{nm}}\) on a wavelength range from 1.2 to 1.7 μm. However, the proposed technique is used to optimize seven design parameters to achieve ultra-flattened zero dispersion \(0.237 \pm { }0.24{\text{ Ps/km}}\;{\text{nm}}\) on a wavelength range from 1.25 to 1.6 μm. Further, the trained RBF-ANN (El-Mosalmy et al. 2014; Hameed et al. 2008) is used to optimize only the diameters of three air hole rings while the other parameters are kept fixed. Furthermore, the accuracy for predicting the dispersion of such algorithm is highly dependent on the range of the trained data. The dispersion results of the proposed algorithm compared with the other techniques (Hameed et al. 2017, 2016; Kerrinckx et al. 2004; Poletti et al. 2005; El-Mosalmy et al. 2014) is listed in Table 2.

Table 2 A comparison between the proposed MINLP algorithm, trust region algorithm (Hameed et al. 2017), CFO (Hameed et al. 2016), GA (Kerrinckx et al. 2004), GA (Poletti et al. 2005) and RBF-ANN (El-Mosalmy et al. 2014)
Full size table

3.2 Dispersion compensation of selectively infiltrated NLC-PCF

To overcome the dispersion problem during the transmission, dispersion compensation-based PCF may be used. For this reason, a highly negative flat dispersion over a broad band range of wavelengths can be obtained by employing the proposed algorithm. Figure 4 shows the optimized PCF with a soft glass of type SF57 as a background material. Further, four rings of air holes are used with diameters \({ }d_1\), \(d_2\), \(d_3\) and \(d_4\). The air holes are arranged in a triangular lattice with a hole pitch \(\Lambda .\) Additionally, nematic liquid crystal (NLC) of type E7 (Li et al. 2005) is used to selectively fill the holes in the first two rings. The E7 material is characterized by two indices: an ordinary index \(n_{0{ }}\)and extraordinary index \(n_{e{ }}\)with the following Cauchy model (Li et al. 2005).

Fig. 4
figure 4

Initial Structure of a soft glass PCF selectively infiltrated with E7 material

Full size image
$$n_e = A_e + \frac{B_e }{{\lambda^2 }} + \frac{C_e }{{\lambda^4 }}$$
(13)
$$n_0 = A_0 + \frac{B_0 }{{\lambda^2 }} + \frac{C_0 }{{\lambda^4 }}$$
(14)

where \(A_e\), \({ }B_e\), \(C_e\), \({ }A_0\), \({ }B_0\) , and \(C_0\) are the coefficients of the Cauchy model. The variation of the Cauchy model coefficients at different temperatures T from \(15\) to \(50\,{\circ} {\text{C}}\) is introduced in Li et al. (2005). In this investigation, the temperature was fixed at \(25\;{\circ} {\text{C}}\). Further, the average orientation of the E7 material molecules is described by the unit vector n with a rotation angle \(\phi\) which can be controlled using external voltages Vx and Vy (Zografopoulos et al. 2006) as shown in Fig. 4. For instance, by applying a high voltage (in order of 250 V) to Vx while keeping Vy = 0, zero rotation angle will be achieved. However, applying the high voltage to Vy while Vx = 0 will result in \(\phi =\) 90° (Zografopoulos et al. 2006).

The coefficients of absorption for ordinary and extraordinary waves are 0.5001 cm and 1.5573 cm at 1 THz. Moreover, the study in (Yang et al. 2010) shows that there is no sharp absorption in the range of frequency from 0.2 to 1.4 THz. So the absorption loss caused by liquid crystal will be ineffective. Most of LC devices operates with AC voltages but with very low frequency compared to the propagating wave optical frequency, so it appears as a DC. When a DC bias voltage is applied to the NLC, the molecules will be reoriented along the direction of the external electric field. According to the study in (Hou et al. 2014), when the applied voltage increases from 1 to 2.3 kV, the rotation angle increases rapidly. If the value of the voltage is more than 3 kV, the rotation angle will be approximately flat where the molecules are oriented along the E-field direction.

The relative permittivity tensor \({\upvarepsilon }_{\text{r}}\) of the NLC material is taken as (Ren et al. 2008).

$$\varepsilon_r = \left( {\begin{array}{*{20}l} {n_0^2 \sin^2 \phi + n_e^2 \cos^2 \phi } \hfill & {\left( {n_e^2 - n_0^2 } \right)\cos \phi \sin \phi } \hfill & 0 \hfill \\ {\left( {n_e^2 - n_0^2 } \right)\cos \phi \sin \phi } \hfill & {n_0^2 \cos^2 \phi + n_e^2 \sin^2 \phi } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {n_0^2 } \hfill \\ \end{array} } \right)$$
(15)

The material dispersion of the soft glass background is also taken into consideration according to the following Sellmeier equation (Leong 2007):

$$n_{SF57} = \sqrt {{\alpha_0 + \alpha_1 \lambda^2 + \frac{\alpha_2 }{{\lambda^2 }} + \frac{\alpha_3 }{{\lambda^4 }} + \frac{\alpha_4 }{{\lambda^6 }} + \frac{\alpha_5 }{{\lambda^8 }}}}$$
(16)

where \(n_{SF57}\) is the refractive index of the SF57 material, \(\alpha_0 = 3.24748\), \(\alpha_1 = - 0.954782 \times 10^{ - 2} \,{\upmu}{\text{m}}^{ - 2}\), \(\alpha_2 = 0.0493626\,{\upmu}{\text{m}}^2\), \(\alpha_3 = 0.294294 \times 10^{ - 2} \,{\upmu}{\text{m}}^4\),\({ }\alpha_4 = - 1.48144 \times 10^{ - 4} \,{\upmu}{\text{m}}^6\), and \(\alpha_5 = 2.78427 \times 10^{ - 5} \,{ \upmu }{\text{m}}^8\)(Leong 2007).

The studied PCF has an indexing guiding where the refractive index of core material is higher than the refractive indices of the NLC material (Leong 2007). At \(\lambda = 1.55\;{\upmu }\)m, \(n_e = 1.697\) and \(n_o = 1.5024\) at temperatures = 25 °C and \(n_{SF57} = 1.802\). In this study, the cladding hole diameters\({ }d_1\), \(d_2\), \(d_3\), \(d_4\), the hole pitch \(\Lambda\), are used for the optimization process. Further, two integer variables are used for the selective infiltration of the NLC material in the first two rings which form the design vector \({\varvec{x}}\). However, the rotation angle is kept constant at either \(0{\circ}\) for the quasi TE mode or \(90{\circ}\) for the quasi TM mode. To obtain the optimal dispersion compensation PCFs, the proposed MINLP algorithm is employed to solve the following optimization problem.

$$\begin{aligned} & {\mathop {\min }\limits_x} \left( {{\mathop {\max }\limits_\lambda } \left| {D\left( \lambda \right)} \right| - {\mathop {\min }\limits_\lambda } \left| {D\left( \lambda \right)} \right|} \right) \\ & \quad {\text{such}}\;{\text{that}}\;\left| {D\left( \lambda \right)} \right| \ge 150{ }\forall { }\lambda = 1.25\;{\text{to}}\;1.6 \\ & \quad D\left( \lambda \right) \le 0{ }\;\forall { }\lambda = 1.25{\text{ to}}\;1.6 \\ \end{aligned}$$
(17)

The values of the objective function obtained by the MINLP algorithm after different numbers of function evaluations (N) for the quasi TM mode and quasi TE mode are shown in Fig. 5. For the quasi TM mode at \({\upvarphi } = 90{\circ}\), the proposed algorithm could achieve a highly negative flat dispersion of \({ } - 163 \pm { }0.9{\text{ Ps/km}}\;{\text{nm }}\) as shown in Fig. 6. Further, Fig. 6 shows that the proposed algorithm could achieve a highly negative flat dispersion of \({ } - 170 \pm { }1.2{\text{ Ps/km}}\;{\text{nm}}\), for the quasi TE mode at \({\upvarphi } = 0{\circ}\). These results could be achieved over a broad band of wavelengths from \(1.25\) to \(1.6\,{ \upmu}{\text{m}}\). However, the trust region algorithm (Hameed et al. 2017) achieved a dispersion compensation with an average value \({ } - 155{\text{ Ps/km}}\;{\text{nm}}\) over only a wavelength from \(1.4{ }\) to \(1.6\,{\upmu}{\text{m}}\) for the quasi-TM mode. The results of the dispersion compensation at initial and optimized parameters compared with the trust region algorithm (Hameed et al. 2017) are listed in Table 3. Further, the inset figures in Fig. 6 show the optimal designs for both modes. The results show that the reported MINLP algorithm is efficient and strong in optimizing selectively infiltrated PCFs. It is also worth noting that, the proposed algorithm depends only on the objective function regardless of the design platform or geometry. For example, it can be used to maximize the sensitivity for PCF sensors based on SPR (Li et al. 2019; Chen et al. 2023a, b; Islam et al. 2023) or to maximize the absorption of a solar cell (Wang et al. 2022) or a metamaterial absorber (Saadeldin et al. 2023). Further, it can be used to improve the other propagation characteristics of PCFs such as birefringence (Mohammadd et al. 2022) and nonlinearity.

Fig. 5
figure 5

The calculated objective function values versus the number of the evaluated functions of the quasi TM mode (\(\phi =\) 90°) and the quasi TE mode (\(\phi =\) 0°)

Full size image
Fig. 6
figure 6

Wavelength dependent dispersion of the two optimized PCFs at \(\phi =\) 0° and 90° with the optimized structures

Full size image
Table 3 Results of the dispersion compensation of the quasi TM mode and quasi TE mode using the selectively infiltrated NLC-PCF compared with the trust region algorithm (Hameed et al. 2017)
Full size table

The selective infiltration of the optimized PCFs can be achieved using several techniques (Nielsen et al. 2005; Vieweg et al. 2010; Woliñski et al. 2005; Huang et al. 2004). In (Nielsen et al. 2005), arc fusion method is employed to selectively fill the holes of the PCF with the liquid crystal material. Further, two-photon direct laser method for selective infiltration with large degree of freedom have been suggested (Vieweg et al. 2010). Furthermore, filling selective holes with a NLC is successfully performed in (Woliñski et al. 2005) for hole diameters with diameter of less than 1.0 µm. In addition, the relation between the filling time and the cladding hole size is discussed in (Huang et al. 2004). Accordingly, the fabrication of the optimized selectively infiltrated PCFs can be accomplished experimentally.

4 Conclusion

In this paper, MINLP with kriging model algorithm is employed in the design and optimization of dispersion characteristics of PCFs. The reported technique is very reliable and gives an accurate prediction for the objective function values compared with other surrogate models like polynomials, radial basis functions…etc. The effectiveness of the proposed algorithm is illustrated by designing a nearly zero flat dispersion over a broad wavelength range from 1.25 to 1.6 \({\upmu }\) m using silica PCF selectively filled with Ethanol material. Further, the proposed algorithm is used for optimizing two soft glass NLC-PCFs for dispersion compensation through the same wavelength range for the quasi TM and quasi TE modes. The suggested MINLP technique with kriging model could achieve a highly negative flat dispersion up to − 163 Ps/Km nm and up to − 170 Ps/Km nm for the quasi TM mode and the quasi TE mode, respectively over the wavelength range from 1.25 to 1.6 μm. Therefore, the MINLP algorithms could prove strength and effectiveness for the dispersion control of selectively filling photonic devices. Further, the proposed MINLP algorithm can be integrated with other surrogate models other than kriging models such as neural networks models and space mapping techniques to effectively replace the computationally expensive objective function.