Two forms of transfer matrix for one-dimensional optical structures

Abstract

Two forms of the transfer matrix applied for treatment of light propagation through one-dimensional optical structures are discussed. A detailed comparison between those forms is presented. A case of structures with absorption (gain) is included. The relation between the transfer matrix method and the Floquet-Bloch theory is highlighted for the case of a periodic structure.

1 Introduction

The subject of this paper is review and generalization of the transfer matrix method, see Refs. Born and Wolf (1999), Heavens (1960), Yeh et al. (1977), Sprung et al. (1993), Lekner (1994), Bendickson et al. (1996), Griffiths and Steinke (2001), Markos and Soukoulis (2008), Morozov and Placido (2011), Morozov et al. (2011), Mackay and Lakhtakia (2020), for light propagation through an inhomogeneous isotropic slab with a complex-valued refractive index (i.e. absorption or gain could be present), which varies along one particular direction. We choose this direction as the z-axis and assume that the slab occupies the region $z_{i}<z<z_{e}$, surrounded by a homogeneous transparent media with real-valued refractive index $n_i$ from the left and by a homogeneous (could be absorptive) medium with complex-valued refractive index ${\tilde{n}}_e$ from the right. Then, the overall refractive index is given by

$$\begin{aligned} {\tilde{n}}(z)= {\left\{ \begin{array}{ll} n_{i}, &{}\quad z<z_{i}, \\ {\tilde{n}}_{s}(z), &{}\quad z_{i}<z<z_{e}, \\ {\tilde{n}}_{e}, &{}\quad z>z_{e}, \end{array}\right. } \end{aligned}$$

(1)

where the complex-valued slab refractive index ${\tilde{n}}_s(z)$ can be represented as

$$\begin{aligned} {\tilde{n}}_s(z)=n_s(z)+i\kappa _s(z). \end{aligned}$$

(2)

In the case of light absorption the imaginary part, $\kappa _s$, is the extinction coefficient and $\kappa _s>0$, while in the case of light amplification it is the gain coefficient and $\kappa _s<0$. We should note that the use of the refractive index with a negative imaginary part in the case of slabs with gain regions is well-founded, provided no lasing occurs in those regions, see Ref. Dorofeenko et al. (2012). Further in the paper, we will use the notation ${\tilde{n}}$ when the refractive index could take complex values (extinction or gain could be present), and use the notation n when the refractive index is restricted to real values (transparent media).

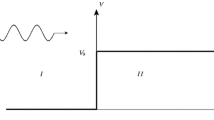
We assume that electromagnetic fields inside the slab are generated by linearly polarized monochromatic waves of frequency $\omega$ and vacuum wave number $k=\omega / c$, entering the slab at normal incidence from the left (incident medium, $z<z_{i}$). Without loss of generality, we choose the y-axis along the direction of wave polarization, i.e. along the direction of electric field $\textbf{E}$, see Fig. 1.

Fig. 1

Schematic of a linearly polarized plane optical wave, normally incident on an inhomogeneous slab of complex-valued refractive index ${\tilde{n}}_s(z)$, surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

In accordance with Maxwell’s equations, the overall electric and magnetic fields are given by

$$\begin{aligned} {\textbf{E}}({\textbf{r}}, t) = E(z) \exp (-i\omega t) \hat{{\textbf{y}}}, \quad {\textbf{B}}({\textbf{r}},t) = \frac{i}{\omega} \frac{d E(z)}{d z} \exp (-i\omega t)\hat{{\textbf{x}}}, \end{aligned}$$

(3)

with the function E(z) obeying the equation

$$\begin{aligned} \frac{d^{2} E(z)}{d z^{2}}+k^{2} {\tilde{n}}^{2}(z) E(z)=0. \end{aligned}$$

(4)

The basic idea of the transfer matrix method is to divide the slab into segments, each described by its complex-valued refractive index ${\tilde{n}}_{j}(z)=$ $n_{j}(z)+i \kappa _{j}(z)$. Within each segment a fundamental system of solutions of Eq. (4) is assumed to be known, so adjoining segments can be linked by appropriate boundary conditions at their interfaces. For the above case of normal propagation, these conditions are that the function E(z) and its derivative $E'(z)$ must be continuous. The former provides continuity of the electric field, while the latter provides continuity of the magnetic field. Besides the cases of segments with constant refractive index (homogeneous layers), there are other situations where a fundamental system of solutions of Eq. (4) is available in analytical form. This includes the practically important case of segments with a linearly graded refractive index, see Refs. Rauh et al. (2010), Wu et al. (2011), Morozov et al. (2013b), Fernandez-Guasti and Diamant (2015).

In the main body of this paper we discuss the transfer matrix method applied to normal light propagation. While many aspects of the method have been extensively covered in the literature, see Refs. Born and Wolf (1999), Heavens (1960), Yeh et al. (1977), Sprung et al. (1993), Lekner (1994), Bendickson et al. (1996), Griffiths and Steinke (2001), Markos and Soukoulis (2008), Morozov and Placido (2011), Morozov et al. (2011), Mackay and Lakhtakia (2020), there are still some lesser-known facets which will be discussed in the context of this paper. In particular, the relations between the two forms of the transfer matrix, the $\textbf{W}$-matrix and the $\textbf{M}$-matrix, will be clarified. Also, more details will be revealed about the connection between the transfer matrix method for slabs with periodic refractive indices and the Floquet-Bloch theory.

The extension of the transfer matrix method to oblique incidence of TE polarized light is straightforward and will be discussed in the "Appendix A". However, the peculiarities of the method applied to the case of oblique incidence of TM polarized light deserve separate consideration. The main difference with the TE case as well as with the case of normal incidence will be the inclusion of a term containing $E'(z)$ in the governing equation, analogous to Eq. (4).

2 W-matrix

The first form of the transfer matrix is the so-called $\textbf{W}$-matrix, see Refs. Sprung et al. (1993), Lekner (1994), Morozov and Placido (2011), Morozov et al. (2011). In the context of optics, for the case of normal light propagation, it links the overall field E(z) and its derivative $E^{\prime }(z)$ at two arbitrary points $z_{1}$ and $z_{2}$ along the z-axis

$$\begin{aligned} \left[ \begin{array}{c} E\left( z_{2}\right) \\ E^{\prime }\left( z_{2}\right) \end{array}\right] ={\textbf{W}}\left( z_{2}, z_{1}\right) \left[ \begin{array}{c} E\left( z_{1}\right) \\ E^{\prime }\left( z_{1}\right) \end{array}\right] . \end{aligned}$$

(5)

The $\textbf{W}$-matrix is constructed in terms of two arbitrary linearly independent solutions of Eq. (4), $E_{1}(z)$ and $E_{2}(z)$, as follows. Since the overall field E(z) is given by the superposition $E(z)=C_{1} E_{1}(z)+C_{2} E_{2}(z)$, we have

$$\begin{aligned} \left[ \begin{array}{c} E\left( z_{2}\right) \\ E^{\prime }\left( z_{2}\right) \end{array}\right] ={\textbf{P}}\left( z_{2}\right) \left[ \begin{array}{l} C_{1} \\ C_{2} \end{array}\right] , \quad \left[ \begin{array}{l} C_{1} \\ C_{2} \end{array}\right] ={\textbf{P}}^{-1}\left( z_{1}\right) \left[ \begin{array}{l} E\left( z_{1}\right) \\ E^{\prime }\left( z_{1}\right) \end{array}\right] , \end{aligned}$$

(6)

where the “point” matrix $\textbf{P}\left( z_{2}\right)$ and the “inverse point” matrix $\textbf{P}^{-1}\left( z_{1}\right)$ are given by the expressions

$$\begin{aligned} {\textbf{P}}\left( z_{2}\right) =\left[ \begin{array}{ll} E_{1}\left( z_{2}\right) &{}\quad E_{2}\left( z_{2}\right) \\ E_{1}^{\prime }\left( z_{2}\right) &{}\quad E_{2}^{\prime }\left( z_{2}\right) \end{array}\right] ,\quad {\textbf{P}}^{-1}\left( z_{1}\right) =\frac{1}{w\left( z_{1}\right) }\left[ \begin{array}{cc} E_{2}^{\prime }\left( z_{1}\right) &{}\quad -\,E_{2}\left( z_{1}\right) \\ -E_{1}^{\prime }\left( z_{1}\right) &{}\quad E_{1}\left( z_{1}\right) \end{array}\right] , \end{aligned}$$

(7)

with $w\left( z_{1}\right)$ being the Wronskian of $E_{1}(z)$ and $E_{2}(z)$ at the point $z=z_{1}$. The Wronskian is the same at all points z since there is no first derivative term in Eq. (4). Now one can see that the ${\textbf{W}}$-matrix is simply the product of the above two “point” matrices, i.e.

$$\begin{aligned} {\textbf{W}}\left( z_{2}, z_{1}\right) ={\textbf{P}}\left( z_{2}\right) {\textbf{P}}^{-1}\left( z_{1}\right) , \end{aligned}$$

(8)

and

$$\begin{aligned} {\text {det}} {\textbf{W}}\left( z_{2}, z_{1}\right) = 1. \end{aligned}$$

(9)

We should note here that particular solutions $E_1(z)$ and $E_2(z)$ must be continuously differentiable functions in the segment $z_1 \le z \le z_2$, i.e. $E_{1,2}(z)$ is a fundamental system of Eq. (4) in this segment. Inverting the matrix ${\textbf{W}}\left( z_{2}, z_{1}\right)$, we obtain

$$\begin{aligned} {\textbf{W}}^{-1}\left( z_{2}, z_{1}\right) ={\textbf{P}}\left( z_{1}\right) {\textbf{P}}^{-1}\left( z_{2}\right) \equiv {\textbf{W}}\left( z_{1}, z_{2}\right) , \end{aligned}$$

(10)

where

$$\begin{aligned} \left[ \begin{array}{c} E\left( z_{1}\right) \\ E^{\prime }\left( z_{1}\right) \end{array}\right] ={\textbf{W}}\left( z_{1}, z_{2}\right) \left[ \begin{array}{c} E\left( z_{2}\right) \\ E^{\prime }\left( z_{2}\right) \end{array}\right] . \end{aligned}$$

(11)

We should emphasize that the unit determinant is the only relation between the elements of the ${\textbf{W}}$-matrix, which is valid for a segment with an arbitrarily varying complex-valued refractive index ${\tilde{n}}(z)$. There are further restrictions on these elements if the refractive index is real (no absorption/gain), see Refs. Sprung et al. (1993), Lekner (1994), summarized as

$$\begin{aligned} \Im (W_{11}) = \Im (W_{22}) = \Im (W_{12}) = \Im (W_{21}) = 0, \end{aligned}$$

(12)

i.e. the ${\textbf{W}}$-matrix is real in this case and due to Eq. (9) can be characterized by only three independent parameters. In addition, if a real refractive index of the segment is reduced in a properly arranged coordinate system to an even function, $n(-z)=n(z)$, the diagonal matrix elements are the same,

$$\begin{aligned} W_{22} = W_{11}, \end{aligned}$$

(13)

and the number of required independent parameters is only two. For a PT-symmetric segment, i.e. for a segment with a complex refractive index ${\tilde{n}}(z)$, satisfying in a particular coordinate system the conditions $n(-z) = n(z)$ and $\kappa (-z) = -\kappa (z)$, the restrictions on the elements of the ${\textbf{W}}$-matrix are

$$\begin{aligned} W_{22} = W^{*}_{11}, \quad \Im (W_{12}) = \Im (W_{21}) = 0, \end{aligned}$$

(14)

see Ref. Morozov et al. (2017). As a result, the number of independent parameters needed to describe the ${\textbf{W}}$-matrix is four.

A further crucial property of the ${\textbf{W}}$-matrix for a segment with an arbitrarily varying complex-valued refractive index ${\tilde{n}}(z)$ is as follows. It does not matter which two linearly-independent solutions of Eq. (4) in this segment are used; one always ends up with the same ${\textbf{W}}$-matrix. To justify this property, one should recognize that Eqs. (5, 11) show a one-to-one correspondence between two single-valued physical functions (the electric field and its derivative).

The matrix ${\textbf{W}}(z,0)$, linking the overall field E(z) and its derivative $E'(z)$ at the point $z=0$ and at an arbitrary point z, takes a particularly simple form if the so-called normalized solutions u(z) and v(z) of Eq. (4), i.e. those which satisfy

$$\begin{aligned} u(0)=1, \quad u^{\prime }(0)=0, \quad v(0)=0, \quad v^{\prime }(0)=1, \end{aligned}$$

(15)

are used. Equations (7, 8) with $z_2=z$ and $z_1=0$ then lead to

$$\begin{aligned} \left[ \begin{array}{c} E(z) \\ E^{\prime }(z) \end{array}\right] ={\textbf{W}}(z, 0)\left[ \begin{array}{c} E(0) \\ E^{\prime }(0) \end{array}\right] ,\quad {\textbf{W}}(z, 0)=\left[ \begin{array}{cc} u(z) &{} v(z) \\ u^{\prime }(z) &{} v^{\prime }(z) \end{array}\right] . \end{aligned}$$

(16)

2.1 Homogeneous layers

As an illustration, let us consider the ${\textbf{W}}$-matrix, ${\textbf{W}}\left( z_{2}, z_{1}\right) ={\textbf{W}}_{1}$, for a homogeneous layer of thickness $d_1=z_{2}-z_{1}$ and refractive index ${\tilde{n}}_{1}$, where $z_i< z_1< z_2 < z_e$. Taking two linearly-independent solutions of Eq. (4) within the layer in the form

$$\begin{aligned} E_{1}(z)=e^{i k_{1} z}, \quad E_{2}(z)=e^{-i k_{1} z}, \end{aligned}$$

where $k_{1}=k{\tilde{n}}_{1}$, we obtain

$$\begin{aligned} {\textbf{W}}_{1}=\left[ \begin{array}{ll} e^{i k_{1} z_{2}} &{}\quad e^{-i k_{1} z_{2}} \\ i k_{1} e^{i k_{1} z_{2}} &{}\quad -\,i k_{1} e^{-i k_{1} z_{2}} \end{array}\right] \frac{1}{(-2 i k_{1})}\left[ \begin{array}{ll} -\,i k_{1} e^{-i k_{1} z_{1}} &{}\quad -\,e^{-i k_{1} z_{1}} \\ -\,i k_{1} e^{i k_{1} z_{1}} &{}\quad e^{i k_{1} z_{1}} \end{array}\right] , \end{aligned}$$

or, choosing intstead

$$\begin{aligned} E_{1}(z)=\cos \left( k_{1} z\right) , \quad E_{2}(z)=\sin \left( k_{1} z\right) / k_{1}, \end{aligned}$$

we have

$$\begin{aligned} {\textbf{W}}_{1}=\left[ \begin{array}{ll} \cos \left( k_{1} z_{2}\right) &{}\quad \sin \left( k_{1} z_{2}\right) / k_{1} \\ -k_{1} \sin \left( k_{1} z_{2}\right) &{}\quad \cos \left( k_{1} z_{2}\right) \end{array}\right] \left[ \begin{array}{ll} \cos \left( k_{1} z_{1}\right) &{}\quad -\,\sin \left( k_{1} z_{1}\right) / k_{1} \\ k_{1} \sin \left( k_{1} z_{1}\right) &{}\quad \cos \left( k_{1} z_{1}\right) \end{array}\right] . \end{aligned}$$

The result after the matrix multiplication is the same and is given by

$$\begin{aligned} {\textbf{W}}_{1}=\left[ \begin{array}{ll} \cos \left( k_{1} d_1\right) &{}\quad \sin \left( k_{1} d_1\right) / k_{1} \\ -k_{1} \sin \left( k_{1} 1\right) &{}\quad \cos \left( k_{1} d_1\right) \end{array}\right] . \end{aligned}$$

(17)

This illustrates the aforementioned important property of the ${\textbf{W}}$-matrix being invariant with respect to the choice of a fundamental system of solutions.

If we know the ${\textbf{W}}$-matrices for each of two adjacent segments along the z-axis, the overall ${\textbf{W}}$-matrix for the two segments is given by the product of individual segment matrices. For example, for the matrix ${\textbf{W}}\left( z_{3}, z_{1}\right)$, where $z_{3}>z_{2}>z_{1}$, we have

$$\begin{aligned} {\textbf{W}}\left( z_{3}, z_{1}\right) ={\textbf{W}}\left( z_{3}, z_{2}\right) {\textbf{W}}\left( z_{2}, z_{1}\right) . \end{aligned}$$

(18)

In the case of two adjacent homogeneous layers of thicknesses $d_1=z_{2}-z_{1}$ and $d_2=z_{3}-z_{2}$, and refractive indices ${\tilde{n}}_{a}$ and ${\tilde{n}}_{b}$, see Fig. 2, we have

$$\begin{aligned} \left[ \begin{array}{c} E\left( z_{3}\right) \\ E^{\prime }\left( z_{3}\right) \end{array}\right] ={\textbf{W}}\left( z_{3}, z_{1}\right) \left[ \begin{array}{c} E\left( z_{1}\right) \\ E^{\prime }\left( z_{1}\right) \end{array}\right] , \quad {\textbf{W}}\left( z_{3}, z_{1}\right) ={\textbf{W}}_2 {\textbf{W}}_1, \end{aligned}$$

(19)

and the elements of the matrix ${\textbf{W}}\left( z_{3}, z_{1}\right)$ are

$$\begin{aligned} \begin{aligned} W_{11}&= \cos \left( k_{2} d_2\right) \cos \left( k_{1} d_1\right) -\frac{k_{1}}{k_{2}} \sin \left( k_{2} d_2\right) \sin \left( k_{1} d_1\right) , \\ W_{21}&= -k_{2} \sin \left( k_{2} d_2\right) \cos \left( k_{1} d_1\right) -k_{1} \cos \left( k_{2} d_2\right) \sin \left( k_{1} d_1\right) , \\ W_{12}&= \frac{1}{k_{2}} \sin \left( k_{2} d_2\right) \cos \left( k_{1} d_1\right) +\frac{1}{k_{1}} \cos \left( k_{2} d_2\right) \sin \left( k_{1} d_1\right) , \\ W_{22}&= \cos \left( k_{2} d_2\right) \cos \left( k_{1} d_1\right) -\frac{k_{2}}{k_{1}} \sin \left( k_{2} d_2\right) \sin \left( k_{1} d_1\right) . \end{aligned} \end{aligned}$$

(20)

Fig. 2

Schematic of an inhomogeneous slab, containing two adjacent homogeneous layers of thicknesses $d_1 = z_2 - z_1$ and $d_2 = z_3 - z_2$, and constant refractive indices ${\tilde{n}}_1$ and ${\tilde{n}}_2$. The slab is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

2.2 Periodic slabs

The representation of the ${\textbf{W}}$-matrix in terms of the normalized solutions, see Eq. (16), particularly facilitates the description of light propagation through a segment with periodic refractive index ${{{\tilde{n}}}}_p(z) = {{{\tilde{n}}}}_p(z+d)$. Without loss of generality, we assume that the slab occupies the region $z_1 = 0 \le z \le Nd = z_2$. The matrix ${\textbf{W}}(z_2, z_1) = {\textbf{W}}(Nd, 0)$ for such a slab is given by the product

$$\begin{aligned} {\textbf{W}}(Nd, 0) = {\textbf{W}}(Nd, Nd-d) \, \cdots \, {\textbf{W}}(2d, d) \, {\textbf{W}}(d, 0) = \left[ {\textbf{W}}_d\right] ^N, \end{aligned}$$

(21)

where ${\textbf{W}}_d$ is the ${\textbf{W}}$-matrix for any single period of the slab. In terms of the normalized solutions, the elements of the above ${\textbf{W}}$-matrices are

$$\begin{aligned} {\textbf{W}}(Nd, 0)=\left[ \begin{array}{ll} u(N d) &{}\quad v(N d) \\ u^{\prime }(N d) &{}\quad v^{\prime }(N d) \end{array}\right] , \quad {\textbf{W}}_d = \left[ \begin{array}{ll} u(d) &{} v(d) \\ u^{\prime }(d) &{}\quad v^{\prime }(d) \end{array}\right] . \end{aligned}$$

(22)

The eigenvalues $\rho$ of the matrix ${\textbf{W}}_d$ are defined by the equation

$$\begin{aligned} {\text {det}}\left[ \begin{array}{ll} u(d)-\rho &{}\quad v(d) \\ u^{\prime }(d) &{}\quad v^{\prime }(d)-\rho \end{array}\right] = 0. \end{aligned}$$

(23)

We therefore arrive at the point of connection between the Floquet-Bloch theory, see Refs. Magnus and Winkler (2004), Yakubovich and Starzhinskii (1975), Eastham (1975), and the ${\textbf{W}}$-matrix for periodic structures. Equation (23) is the same as the characteristic equation for the Floquet multipliers, see Refs. Morozov and Sprung (2011, 2015), Morozov et al. (2013a), i.e. the eigenvalues of the ${\textbf{W}}_d$ matrix are exactly the Floquet multipliers. Further, using the expression for the N-th power of a unimodular matrix ${\textbf{W}}_d$, it is possible to show, see Refs. Sprung et al. (1993), Bendickson et al. (1996), that

$$\begin{aligned} \left[ {\textbf{W}}_d\right] ^N = {\textbf{W}}_d \frac{\sin N\phi }{\sin \phi }-\hat{{\textbf{1}}} \frac{\sin (N-1) \phi }{\sin \phi }, \end{aligned}$$

(24)

where $\hat{{\textbf{1}}}$ is the unit matrix, and the Bloch phase $\phi$ of the periodic structure is determined by

$$\begin{aligned} 2 \cos \phi = {\text {Tr}}\, {\textbf{W}}_d = u(d) + v^{\prime }(d). \end{aligned}$$

(25)

3 M-matrix

Let us consider again a region between the points $z_1$ and $z_2$ along the z-axis. We now assume that the refractive index in some adjacent segment to the left of the point $z_1$ is constant and equal to ${{{\tilde{n}}}}_a$, while the refractive index in some adjacent segment to the right of the point $z_2$ is constant and equal to ${\tilde{n}}_b$, see Fig. 3 The thicknesses a and b of these segments can be arbitrarily small. The solution of Eq. (4) in each of the segments with refractive indices ${\tilde{n}}_a$ and ${\tilde{n}}_b$ respectively, can be separated into the component $E^+(z)$ moving in the positive direction (from left to right), and the component $E^-(z)$ moving in the negative direction (from right to left), i.e.

$$\begin{aligned} E(z) = E^+(z) + E^-(z). \end{aligned}$$

(26)

Fig. 3

Schematic of an inhomogeneous slab with two internal non-adjacent homogeneous layers of thicknesses a and b and constant refractive indices ${\tilde{n}}_a$ and ${\tilde{n}}_b$. The slab is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

The second form of the transfer matrix, the so-called ${\textbf{M}}$-matrix, is defined as the matrix which relates the above components at the points $z_1$ and $z_2$ as

$$\begin{aligned} \left[ {\begin{array}{l} E^+_a(z_1)\\ E^-_a(z_1) \\ \end{array}} \right] = \textbf{M}(z_1,z_2) \left[ {\begin{array}{l} E^+_b(z_2) \\ E^-_b(z_2) \\ \end{array}} \right] . \end{aligned}$$

(27)

We should note that $E^{\pm }_a(z)$ is a fundamental system of Eq. (4) in the segment with refractive index ${\tilde{n}}_a$, while $E^{\pm }_b(z)$ is a fundamental system of Eq. (4) in the segment with refractive index ${\tilde{n}}_b$. Using the following forms for $E^{\pm }_{a,b}(z)$,

$$\begin{aligned} \begin{aligned} E^+_a(z)&= A e^{ik_a \left( {z - z_1} \right) }, \quad E^-_a(z) = B e^{-ik_a \left( {z - z_1} \right) },\\ E^+_b(z)&= C e^{ik_b \left( {z - z_2} \right) }, \quad E^-_b(z) = D e^{-ik_b \left( {z - z_2} \right) }. \end{aligned} \end{aligned}$$

(28)

where $k_{a,b} = k{{{\tilde{n}}}}_{a,b}$, we see that the ${\textbf{M}}$-matrix simply links the coefficients C and D with A and B, see Refs. Yeh et al. (1977), Sprung et al. (1993), Bendickson et al. (1996), Griffiths and Steinke (2001), i.e. Equation (27) takes the form

$$\begin{aligned} \left[ {\begin{array}{l} A \\ B \\ \end{array}} \right] = \textbf{M}(z_1,z_2) \left[ {\begin{array}{l} C \\ D \\ \end{array}} \right] . \end{aligned}$$

(29)

In summary, while the ${\textbf{W}}$-matrix relates the overall field E(z) and its derivative at the points $z_1$ and $z_2$, the M-matrix relates two counter-propagating components $E^{\pm }(z)$ of the overall field at the same points. Therefore, the ${\textbf{M}}$-matrix can only be utilized if it is possible to divide the overall field into such components. There are no restrictions for the use of the ${\textbf{W}}$-matrix though. We also choose to go from the right point $z_2$ to the left point $z_1$ in the case of the ${\textbf{M}}$-matrix, so the original matrix is ${\textbf{M}}(z_1,z_2)$, see Eq. (27). However, we go from the left point $z_1$ to the right point $z_2$ in the case of the ${\textbf{W}}$-matrix, so the original matrix is ${\textbf{W}}(z_2, z_1)$, see Eq. (5).

The relation between the two transfer matrices is given by

$$\begin{aligned} \textbf{M}(z_1,z_2) = \textbf{L}^{-1}(z_1^-)\textbf{W}(z_1,z_2)\,\textbf{L}(z_2^+), \end{aligned}$$

(30)

where

$$\begin{aligned} \textbf{L}^{-1}(z_1^-) = -\frac{1}{2ik_a}\left[ \begin{array}{ll} -\,ik_a &{}\quad -\,1 \\ -\,ik_a &{}\quad 1 \\ \end{array}\right] , \quad \textbf{L}(z_2^+) = \left[ \begin{array}{ll} 1 &{}\quad 1\\ ik_b &{}\quad -\,ik_b\\ \end{array}\right] . \end{aligned}$$

(31)

The determinant of the ${\textbf{M}}$-matrix is then

$$\begin{aligned} \det \textbf{M}(z_1,z_2) = \frac{k_b}{k_a}. \end{aligned}$$

(32)

As it was for the ${\textbf{W}}$-matrix, the expression for the determinant is the only relation between the elements of the ${\textbf{M}}$-matrix which is valid for an arbitrarily varying complex-valued refractive index between the points $z_1$ and $z_2$. The inverse of the ${\textbf{M}}$-matrix is

$$\begin{aligned} \textbf{M}^{-1}(z_1,z_2)=\textbf{L}^{-1}(z_2^+)\textbf{W}(z_2,z_1)\,\textbf{L}(z_1^-) \equiv \textbf{M}(z_2,z_1), \end{aligned}$$

(33)

where

$$\begin{aligned} \left[ \begin{array}{l} C \\ D \end{array}\right] = {\textbf{M}}\left( z_2,z_1\right) \left[ \begin{array}{l} A \\ B \end{array}\right] . \end{aligned}$$

(34)

Very often, we are interested in the cases when a segment between the points $z_1$ and $z_2$ is surrounded by a matched transparent medium, i.e. ${\tilde{n}}_b = n_b ={\tilde{n}}_a = n_a$. Then, $\det {M} = 1$, and if the refractive index of the segment is also real-valued, further restrictions on the elements of the ${\textbf{M}}$-matrix include

$$\begin{aligned} M_{22} = M^{*}_{11}, \quad M_{12} = M^{*}_{21}. \end{aligned}$$

(35)

In addition, if the refractive index is an even function (in a properly arranged coordinate system), one has

$$\begin{aligned} M_{12} = -M_{21}. \end{aligned}$$

(36)

The number of required independent parameters for the ${\textbf{M}}$-matrix for the above cases is two and three respectively. One particularly useful choice of such parameters is given in Ref Sprung et al. (2004). For a PT-symmetric segment the restrictions include, see Refs. Morozov et al. (2017), Phang et al. (2017),

$$\begin{aligned} M_{22} = M^{*}_{11}, \quad \Re (M_{12}) = \Re (M_{21}) = 0, \end{aligned}$$

(37)

and the number of required independent parameters is four.

The ${\textbf{M}}$-matrix connects the amplitudes of plane waves propagating in the homogeneous layer on the right of the segment $z_1<z< z_2$ with the amplitudes of waves propagating in the homogeneous layer on the left, see Eq. (29), or vice versa, see Eq. (34). A closely related ${\textbf{S}}$-matrix connects the amplitudes of plane waves incident on the segment $z_1<z< z_2$ (A and D) with the amplitudes of plane waves propagating away from it (B and C).

In general, the ${\textbf{M}}$-matrices (or ${\textbf{W}}$-matrices) are well suited for analytical description of light propagation through a one-dimensional slab of complex-valued refractive index. The rule of their multiplication, which allows one to find the transfer matrix of a slab from the transfer matrices of individual segments, coincides with the ordinary matrix multiplication. However, in numerical calculations the use of ${\textbf{M}}$-matrices is more problematic, since it leads to exponential accumulation of errors, when calculating the propagation through segments with absorption or gain. In contrast, calculations based on the use of the ${\textbf{S}}$-matrices are numerically stable, see Ref. Cotter et al. (1995), but this advantage comes at the cost of the complexity of their multiplication. However, one should expect the ${\textbf{W}}$-matrix formalism to be numerically more stable than the ${\textbf{M}}$-matrix formalism, as a fundamental system of Eq. (4) in a segment with absorption/gain can be chosen arbitrarily, not necessarily in terms of counter-propagating components.

3.1 Homogeneous layers

Suppose the points $z_1$ and $z_2$ are within a homogeneous layer of refractive index ${\tilde{n}}_1$ and $z_2-z_1=d_1$, see Fig. 4.

Fig. 4

Schematic of an inhomogeneous slab containing a homogeneous layer of complex-valued refractive index ${\tilde{n}}_1$. The slab is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

Substituting $k_a = k_b = k_1 = k{\tilde{n}}_1$ in Eq. (28), we obtain

$$\begin{aligned} {\textbf{M}}\left( z_1,z_2\right) = \textbf{M}_1= \left[ \begin{array}{ll} e^{-ik_1d_1} &{}\quad 0 \\ 0 &{}\quad e^{ik_1d_1}\\ \end{array}\right] . \end{aligned}$$

(38)

The matrix ${\textbf{M}}_1$ can also be obtained from the relation given by Eq. (30) where $\textbf{W}(z_1,z_2)=\textbf{W}^{-1}_1$,

$$\begin{aligned} \textbf{M}_1 = -\frac{1}{2ik_1}\left[ \begin{array}{ll} -\,ik_1 &{}\quad -\,1 \\ -\,ik_1 &{}\quad 1 \\ \end{array}\right] \left[ \begin{array}{ll} \cos \left( k_{1} d_1\right) &{}\quad -\,\sin \left( k_{1} d_1\right) / k_{1} \\ k_{1} \sin \left( k_{1} d_1\right) &{}\quad \cos \left( k_{1} d_1\right) \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_1 &{}\quad -\,ik_1\\ \end{array}\right] , \end{aligned}$$

which immediately leads to Eq. (38).

For a step-like refractive index profile, i.e. for the case

$$\begin{aligned} n(z) = \left\{ \begin{array}{ll} {\tilde{n}}_a, &{}\quad z_1 - a< z< z_1,\\ {\tilde{n}}_b, &{}\quad z_1< z < z_1 + b,\\ \end{array}\right. \end{aligned}$$

(39)

see Fig. 5, we substitute $z_2=z_1$ in Eq. (28) and obtain

$$\begin{aligned} {\textbf{M}}\left( z_1^-,z_1^+\right) = \textbf{M}_{n_{ab}} = \left[ \begin{array}{ll} \frac{k_a+k_b}{2k_a} &{}\quad \frac{k_a-k_b}{2k_a}\\ \frac{k_a-k_b}{2k_a} &{}\quad \frac{k_a+k_b}{2k_a} \\ \end{array}\right] . \end{aligned}$$

(40)

Fig. 5

Schematic of an inhomogeneous slab containing a step-like refractive index segment. The slab is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

We can also obtain the matrix $\textbf{M}_{n_{ab}}$ from the relation given by Eq. (30), adapted for the case as

$$\begin{aligned} \textbf{M}(z_1^-,z_1^+) = \textbf{M}_{n_{ab}} = \textbf{L}^{-1}(z_1^-)\textbf{W}(z_1^-,z_1^+)\textbf{L}(z_1^+), \quad \textbf{W}(z_1^-,z_1^+) = \textbf{1}, \end{aligned}$$

i.e.

$$\begin{aligned} \textbf{M}_{n_{ab}} = -\frac{1}{2ik_a}\left[ \begin{array}{ll} -\,ik_a &{}\quad -\,1 \\ -\,ik_a &{}\quad 1 \\ \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad 0 \\ 0 &{}\quad 1 \\ \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_b &{}\quad -\,ik_b\\ \end{array}\right] , \end{aligned}$$

which immediately leads to Eq. (40).

The overall ${\textbf{M}}$-matrix for any adjacent parts of the refractive index profile ${{{\tilde{n}}}}(z)$ can be expressed as the product of the individual ${\textbf{M}}$-matrices of these parts. For example, in the case of a homogeneous layer of thickness $d_1=z_2-z_1$ and refractive index ${\tilde{n}}_1$, surrounded from both sides by segments with refractive index ${\tilde{n}}_a$ i.e.

$$\begin{aligned} n(z) = \left\{ \begin{array}{ll} {\tilde{n}}_a, &{}\quad z_1 - a< z<z_1,\\ {\tilde{n}}_1, &{}\quad z_1< z< z_2,\\ {\tilde{n}}_a, &{}\quad z_2< z < z_2 + b, \end{array}\right. \end{aligned}$$

(41)

see Fig. 6, we have $\textbf{M}(z_1,z_2) = \textbf{M}_{n_{a1}}\textbf{M}_1\textbf{M}_{n_{1a}}$, which gives us

$$\begin{aligned} \textbf{M}(z_1,z_2) = \left[ \begin{array}{ll} \frac{k_a+k_1}{2k_a} &{}\quad \frac{k_a-k_1}{2k_a}\\ \frac{k_a-k_1}{2k_a} &{}\quad \frac{k_a+k_1}{2k_a} \\ \end{array}\right] \left[ \begin{array}{ll} e^{-ik_1 d_1} &{}\quad 0\\ 0 &{}\quad e^{ik_1 d_1} \\ \end{array}\right] \left[ \begin{array}{ll} \frac{k_1+k_a}{2k_1} &{}\quad \frac{k_1-k_a}{2k_1} \\ \frac{k_1-k_a}{2k_1} &{}\quad \frac{k_1+k_a}{2k_1} \\ \end{array}\right] . \end{aligned}$$

We can also use Eq. (30) instead,

$$\begin{aligned} \textbf{M}(z_1,z_2) =-\frac{1}{2ik_a}\left[ \begin{array}{ll} -\,ik_a &{}\quad -\,1 \\ -\,ik_a &{}\quad 1 \\ \end{array}\right] \left[ \begin{array}{ll} \cos (k_1d_1) &{}\quad -\,\sin (k_1d_1)/k_1\\ k_1\sin (k_1d_1) &{}\quad \cos (k_1d_1) \\ \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_a &{}\quad -\,ik_a\\ \end{array}\right] . \end{aligned}$$

Both of the above products lead to the final result in the form of

$$\begin{aligned} \textbf{M}(z_1^-,z_2^+) = \left[ \begin{array}{ll} \cos k_1d_1-i\frac{k_a^2+k_1^2}{2k_ak_1}\sin k_1d_1 &{}\quad i\frac{k_a^2-k_1^2}{2k_ak_1}\sin k_1d_1 \\ -i\frac{k_a^2-k_1^2}{2k_ak_1}\sin k_1d_1 &{}\quad \cos k_1d_1 + i\frac{k_a^2+k_1^2}{2k_1k_a}\sin k_1d_1 \end{array}\right] . \end{aligned}$$

(42)

In the case of $n_1$ and $n_a$ being real-valued, the factors before $\sin (k_1d_1)$ become also real-valued, and the above ${\textbf{M}}$-matrix satisfies all relations given by Eqs. (35, 36) as expected.

Fig. 6

Schematic of an inhomogeneous slab containing a homogeneous layer of refractive index ${\tilde{n}}_1$ and thickness $d_1$, surrounded by matched segments of refractive index ${\tilde{n}}_a$. The slab itself is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

Let us now consider two adjacent homogeneous layers of thicknesses $d_1=z_2-z_1$ and $d_2=z_3-z_2$ and refractive indices ${\tilde{n}}_1$ and ${\tilde{n}}_2$ (such a system is called a bi-layer), surrounded by a segment with refractive index ${\tilde{n}}_a$ to the left of the point $z_1$ and by a segment with refractive index ${\tilde{n}}_b$ to the right of the point $z_3$, i.e.

$$\begin{aligned} n(z) = \left\{ \begin{array}{ll} {\tilde{n}}_a, &{}\quad z_1 - a< z< z_1,\\ {\tilde{n}}_1, &{}\quad z_1< z< z_2,\\ {\tilde{n}}_2, &{}\quad z_2< z< z_3,\\ {\tilde{n}}_b, &{}\quad z_3< z < z_3 + b, \end{array}\right. \end{aligned}$$

(43)

see Fig. 7.

Fig. 7

Schematic of an inhomogeneous slab containing a bi-layer of refractive indices ${\tilde{n}}_{1,2}$ and thicknesses $d_{1,2}$, surrounded by a segment of refractive index ${\tilde{n}}_a$ from the left and by a segment of refractive index ${\tilde{n}}_b$ from the right. The slab itself is surrounded by a homogeneous medium of real-valued refractive index $n_i$ to the left and by a homogeneous medium of complex-valued refractive index ${\tilde{n}}_e$ to the right

The corresponding $\textbf{M}$-matrix can be found either from the product

$$\begin{aligned} \textbf{M}(z_1,z_3) = \textbf{M}_{n_{a1}}{} \textbf{M}_1\textbf{M}_{n_{12}}{} \textbf{M}_2\textbf{M}_{n_{2b}}, \end{aligned}$$

i.e

$$\begin{aligned} \left[ \begin{array}{ll} \frac{k_a+k_1}{2k_a} &{}\quad \frac{k_a-k_1}{2k_a}\\ \frac{k_a-k_1}{2k_a} &{}\quad \frac{k_a+k_1}{2k_a} \end{array}\right] \left[ \begin{array}{ll} e^{-ik_1 d_1} &{}\quad 0 \\ 0 &{}\quad e^{ik_1 d_1} \end{array}\right] \left[ \begin{array}{ll} \frac{k_1+k_2}{2k_1} &{}\quad \frac{k_1-k_2}{2k_1}\\ \frac{k_1-k_2}{2k_1} &{} \quad \frac{k_1+k_2}{2k_1} \end{array}\right] \left[ \begin{array}{ll} e^{-ik_2 d_2} &{}\quad 0 \\ 0 &{}\quad e^{ik_2 d_2} \end{array}\right] \left[ \begin{array}{ll} \frac{k_2+k_b}{2k_2} &{}\quad \frac{k_2-k_b}{2k_2} \\ \frac{k_2-k_b}{2k_2} &{}\quad \frac{k_2+k_b}{2k_2} \end{array}\right] , \end{aligned}$$

or from the product

$$\begin{aligned} \textbf{M}(z_1,z_3) = \textbf{L}^{-1}(z_1^-)\textbf{W}_1^{-1}{} \textbf{W}_2^{-1}{} \textbf{L}(z_3^+), \end{aligned}$$

i.e

$$\begin{aligned} \left[ \begin{array}{ll} \frac{1}{2} &{}\quad \frac{1}{2ik_a} \\ \frac{1}{2} &{}\quad -\,\frac{1}{2ik_a} \end{array}\right] \left[ \begin{array}{ll} \cos (k_1d_1) &{}\quad -\,\frac{\sin (k_1d_1)}{k_1}\\ k_1\sin (k_1d_1) &{}\quad \cos (k_1d_1) \end{array}\right] \left[ \begin{array}{ll} \cos (k_2d_2) &{}\quad -\,\frac{\sin (k_2d_2)}{k_2}\\ k_b\sin (k_2d_2) &{}\quad \cos (k_2d_2)\\ \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_b &{}\quad -\,ik_b\\ \end{array}\right] . \end{aligned}$$

For a matched bi-layer, i.e for the case ${\tilde{n}}_a = {\tilde{n}}_b = {\tilde{n}}_1$, the elements of the matrix ${\textbf{M}}(z_1,z_3)$ are

$$\begin{aligned} \begin{aligned} M_{11}(z_1,z_3)&= \left\{ \cos (k_2d_2)-\frac{i}{2}\left[ \frac{k_1}{k_2}+\frac{k_2}{k_1}\right] \sin (k_2d_2)\right\} \,e^{-ik_1d_1},\\ M_{21}(z_1,z_3)&= -\frac{1}{2}i\left[ \frac{k_1}{k_2}-\frac{k_2}{k_1}\right] \sin (k_2d_2)\,e^{ik_1d_1},\\ M_{12}(z_1,z_3)&= \frac{1}{2}i\left[ \frac{k_1}{k_2}-\frac{k_2}{k_1}\right] \sin (k_2d_2)\,e^{-ik_1d_1},\\ M_{22}(z_1,z_3)&= \left\{ \cos (k_2d_2)+\frac{i}{2}\left[ \frac{k_1}{k_2}+\frac{k_2}{k_1}\right] \sin (k_2d_2)\right\} \,e^{ik_1d_1}. \end{aligned} \end{aligned}$$

(44)

3.2 Periodic slabs

Let us consider the ${\textbf{M}}$-matrix for a finite periodic segment of N periods, each of thickness d, occupying, as before, the region $z_1 = 0 \le z \le Nd = z_2$ with refractive index being ${\tilde{n}}_p(z+d)={\tilde{n}}_p(z)$. The value of refractive index on the boundaries between periods is ${\tilde{n}}_{0}$, i.e ${\tilde{n}}_{0} \equiv {\tilde{n}}(0^+) = {\tilde{n}}(d) = {\tilde{n}}(2d) =\cdots = {\tilde{n}}(Nd^-)$. The periodic segment is surrounded by homogeneous segments with refractive indices ${\tilde{n}}_a$ and ${\tilde{n}}_b$.

For a matched periodic segment, i.e. for the case ${\tilde{n}}_a = {\tilde{n}}_b ={\tilde{n}}_{0}$, we have

$$\begin{aligned} \textbf{M}_{\textrm{match}}(0, Nd) = \textbf{M}(0^+,d)\,\textbf{M}(d,2d) \cdots \textbf{M}(Nd-d,Nd^-) = \left[ \textbf{M}_d\right] ^N, \end{aligned}$$

(45)

where $\textbf{M}_d$ is the $\textbf{M}$-matrix for any single period. With the aid of Eq. (30), it can be expressed as

$$\begin{aligned} \textbf{M}_d = -\displaystyle \frac{1}{2ik_0}\left[ \begin{array}{ll} -\,ik_0 &{}\quad -\,1 \\ -\,ik_0 &{}\quad 1 \\ \end{array}\right] \textbf{W}_d^{-1} \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_0 &{}\quad -\,ik_0 \\ \end{array}\right] , \end{aligned}$$

(46)

where $k_{0} = k{\tilde{n}}_{0}$ and $\textbf{W}_d^{-1}$ is given in terms of the normalized solutions as

$$\begin{aligned} \textbf{W}_d^{-1} = \left[ \begin{array}{ll} v'(d) &{}\quad -\,v(d) \\ -\,u'(d) &{}\quad u(d) \end{array}\right] . \end{aligned}$$

The two essential properties of the matrix $\textbf{M}_d$ are then the same as those of the matrix $\textbf{W}_d$,

$$\begin{aligned} \textrm{Tr}\,\,\textbf{M}_d = \textrm{Tr}\,\,\textbf{W}_d = 2\cos \phi , \quad \det \textbf{M}_d = \det \textbf{W}_d = 1, \end{aligned}$$

(47)

where $\cos \phi$ is the Bloch phase of the periodic structure, and, as a result,

$$\begin{aligned} \textbf{M}_{\textrm{match}}(0, Nd) =\left[ \textbf{M}_d\right] ^N = \textbf{M}_d\,\frac{\sin (N\phi )}{\sin \phi }-\mathbf{{\hat{1}}}\,\frac{\sin (N-1)\phi }{\sin \phi }. \end{aligned}$$

(48)

If we apply Eq. (30) to all matched periodic segment, we obtain

$$\begin{aligned} \textbf{M}_{\textrm{match}}(0, Nd) = -\frac{1}{2ik_0}\left[ \begin{array}{ll} -\,ik_0 &{}\quad -\,1 \\ -\,ik_0 &{}\quad 1 \\ \end{array}\right] \textbf{W}(0, Nd) \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_0 &{}\quad -\,ik_0\\ \end{array}\right] , \end{aligned}$$

(49)

where

$$\begin{aligned} \textbf{W}(0, Nd) = \textbf{W}^{-1}(Nd,0) = \left[ \textbf{W}_d^{-1}\right] ^N = \left[ \begin{array}{ll} v'(d) &{}\quad -\,v(d) \\ -\,u'(d) &{}\quad u(d)\\ \end{array}\right] ^N, \end{aligned}$$

which is in agreement with Eqs. (45, 46).

For a general case (non-matched periodic segment) one has

$$\begin{aligned} \textbf{M}(0,Nd) = \left[ \begin{array}{ll} \frac{k_a+k_0}{2k_a} &{}\quad \frac{k_a-k_0}{2k_a} \\ \frac{k_a-k_0}{2k_a} &{}\quad \frac{k_a+k_0}{2k_a} \\ \end{array}\right] \textbf{M}_{\textrm{match}}(0, Nd) \left[ \begin{array}{ll} \frac{k_0+k_b}{2k_0} &{}\quad \frac{k_0-k_b}{2k_0} \\ \frac{k_0-k_b}{2k_0} &{}\quad \frac{k_0+k_b}{2k_0}\\ \end{array}\right] , \end{aligned}$$

(50)

or

$$\begin{aligned} \textbf{M}(0,Nd) = -\frac{1}{2ik_a}\left[ \begin{array}{ll} -ik_a &{}\quad -1 \\ -ik_a &{}\quad 1 \\ \end{array}\right] \textbf{W}(0, Nd) \left[ \begin{array}{ll} 1 &{}\quad 1 \\ ik_b &{}\quad -\,ik_b\\ \end{array}\right] . \end{aligned}$$

(51)

4 M-matrix and scattering coefficients

Let us now consider a scattering problem for the region $z_1< z < z_2$, assuming again that the refractive index to the left from the point $z_1$ is constant and equal to ${\tilde{n}}_a$, and the refractive index to the right from the point $z_2$ is constant and equal to ${\tilde{n}}_b$. For a scattering problem, the solutions of Eq. (4) in the regions $z<z_1$ and $z>z_2$ should be consistent with the following radiation conditions,

$$\begin{aligned} \begin{aligned} E_l(z) =&\left\{ \begin{aligned}&e^{ik_a \left( {z - z_1} \right) } + r_l e^{ - ik_a \left( {z - z_1} \right) },&z_1 - a< z< z_1, \\&t_l e^{ik_b \left( {z - z_2} \right) },&z_2< z< z_2+b, \end{aligned} \right. \\ E_r(z) =&\left\{ \begin{aligned}&t_r e^{ - ik_a \left( {z - z_1} \right) },&z_1 - a< z< z_1, \\&e^{-ik_b \left( {z - z_2} \right) } + r_r e^{ik_b \left( {z - z_b} \right) },&z_2< z < z_2+b, \end{aligned} \right. \end{aligned} \end{aligned}$$

(52)

where $r_l$, $t_l$ and $r_r$, $t_r$ are the amplitude reflection and transmission coefficients for waves impinging on the region $z_1<z<z_2$ from the left and from the right. If we compare the above expressions with the ones given by Eq. (28), we can see that for the wave impinging from the left $A=1$, $B=r_l$, $C=t_l$, and $D=0$, while for the wave impinging from the right $A=0$, $B=t_r$, $C=r_r$, and $D=1$. Substituting these coefficients in Eq. (29), we obtain the matrix $\textbf{M}(z_1,z_2)$ in the form

$$\begin{aligned} \textbf{M}(z_1,z_2) = \left[ \begin{array}{ll} \displaystyle \frac{1}{t_l} &{}\quad -\,\displaystyle \frac{r_r}{t_l} \\ \displaystyle \frac{r_l}{t_l} &{} \quad t_r-\displaystyle \frac{r_l\,r_r}{t_l}\\ \end{array}\right] , \end{aligned}$$

(53)

with its determinant expressed as

$$\begin{aligned} \det \textbf{M}(z_1,z_2) = \frac{t_r}{t_l}. \end{aligned}$$

(54)

To illustrate the representation of the $\textbf{M}$-matrix in terms of the amplitude reflection and transmission coefficients, let us go back to the previously considered cases of a homogeneous layer of refractive index ${\tilde{n}}_1$ and thickness $d_1$ and a step-like refractive index profile given by Eq. (39). For the former case we have in Eq. (52)

$$\begin{aligned} \begin{aligned} r_l = 0,&\quad e^{ik_1(z - z_1)} = t_l e^{ik_1(z - z_1 - d_1)}, \\ r_r = 0,&\quad t_r e^{-ik_1(z - z_1)} = e^{-ik_1(z - z_1 - d_1)}, \end{aligned} \end{aligned}$$

from which $t_l = t_r = e^{ik_1d_1} \equiv t_1$, and, as a result,

$$\begin{aligned} \textbf{M}_1 = \left[ \begin{array}{ll} 1/t_1 &{}\quad 0 \\ 0 &{} \quad t_1 \end{array}\right] = \left[ \begin{array}{ll} e^{-ik_1d_1} &{}\quad 0 \\ 0 &{}\quad e^{ik_1d_1}\\ \end{array}\right] , \end{aligned}$$

(55)

confirming Eq. (38). For the latter case we substitute $z_2 = z_1$ in Eq. (52) and using the continuity conditions for $E_{l,r}(z)$ at the point $z=z_1$, obtain

$$\begin{aligned} \begin{aligned} r_l = \frac{k_a-k_b}{k_a+k_b} \equiv r_{ab},&\quad t_l = \frac{2k_a}{k_a+k_b} \equiv t_{ab}, \\ r_r = \frac{k_b-k_a}{k_b+k_a} \equiv r_{ba},&\quad t_r = \frac{2k_b}{k_b+k_a} \equiv t_{ba}, \end{aligned} \end{aligned}$$

where $r_{ab}$ and $t_{ab}$ are the Fresnel reflection and transmission coefficients for the light going from medium ${\tilde{n}}_a$ to medium ${\tilde{n}}_b$, while $r_{ba}$ and $t_{ba}$ are the Fresnel reflection and transmission coefficients for the light going from medium ${\tilde{n}}_b$ to medium ${\tilde{n}}_a$. Then, the matrix $\textbf{M}_{n_{ab}}$ is given by

$$\begin{aligned} \textbf{M}_{n_{ab}} = \left[ \begin{array}{ll} \frac{1}{t_{ab}} &{}\quad \frac{r_{ab}}{t_{ab}}\\ \frac{r_{ab}}{t_{ab}} &{}\quad \frac{1}{t_{ab}}\\ \end{array}\right] = \left[ \begin{array}{ll} \frac{k_a+k_b}{2k_a} &{}\quad \frac{k_a-k_b}{2k_a} \\ \frac{k_a-k_b}{2k_a} &{}\quad \frac{k_a+k_b}{2k_a} \\ \end{array}\right] , \end{aligned}$$

(56)

confirming Eq. (40).

5 Conclusion

The transfer matrix connects the electromagnetic (optical) fields through a slab with refractive index ${\tilde{n}}_s(z)$. We discussed two forms of the transfer matrix, the $\textbf{W}$-matrix and the $\textbf{M}$-matrix, in the case of normal (along the z-axis) light propagation, with a particular emphasis on the relations between them. It was noticed that the ${\textbf{M}}$-matrix is introduced if it is possible to divide the overall field into two counter-propagating components. The utilization of ${\textbf{W}}$-matrix does not require any preliminary assumptions. An advantage of the ${\textbf{M}}$-matrix formalism, however, is that the elements of $\textbf{M}$-matrix can be easily expressed in terms of the reflection and transmission amplitudes. We were trying to avoid (where possible) any additional assumptions about the involved refractive index. As a result, the majority of the obtained results are applicable to a slab with an arbitrarily varying complex-valued (absorption/gain might occur) refractive index. For a slab consisting of a finite number of identical cells N, the relations between the transfer matrix method and the Floquet-Bloch theory were also discussed.

Appendix A TE-polarized light

The relative geometry of the incident wave and the slab in case of oblique incidence is shown in Fig. 8. It implies complete homogeneity in the (x, y) plane, which is normal to the z-axis. Then, the dependence of solutions of Maxwell’s equations on x and y must be the same in all space. A second preferred direction is provided by the incident plane wave. Together with the z-axis they define a plane of incidence. Without loss of generality, we now choose the x-axis in the plane of incidence, so the solutions will depend on x and z only. As was mentioned in the Introduction, the fields inside the slab are generated by linearly polarized monochromatic waves of frequency $\omega$ and vacuum wave number $k=\omega /c$, but now we assume that the waves enter the slab at the incident angle $\theta _i$.

Fig. 8

Schematic of TE polarized plane optical wave incident on an inhomogeneous slab of a complex-valued refractive index ${\tilde{n}}_s$, from a transparent medium of refractive index $n_i$. The angle of incidence is $\theta _i$. The complex-valued refractive index of the exit medium is ${\tilde{n}}_e$

At this point we should mention that the restriction on the incident medium being transparent becomes crucial for an oblique (non-normal) incidence. If the refractive index of the incident medium has an imaginary part (i.e the medium is either dissipative or active), the normals to the planes of constant phase and constant amplitude in the incident wave do not coincide, and the above 2D problem transforms into the 3D one, see Refs. Dupertuis et al. (1994), Chang et al. (2005). This will invalidate our considerations below

The x dependence of the fields in all space takes the form $\exp\,(i \beta x)$, where

$$\begin{aligned} \beta =k n_{i} \sin \theta _{i}. \end{aligned}$$

(A1)

In the case of TE polarization, the electric field ${\textbf{E}}({\textbf{r}},t)$ is perpendicular to the (x, z) plane (plane of incidence) and it is given by the expression

$$\begin{aligned} {\textbf{E}}({\textbf{r}},t) = E(z) e^{i(\beta x-\omega t)} \hat{{\textbf{y}}}, \end{aligned}$$

(A2)

where the function E(z) obeys the equation

$$\begin{aligned} \frac{d^{2} E(z)}{d z^{2}}+\left[ k^{2} {\tilde{n}}^{2}(z)-\beta ^{2}\right] E(z)=0. \end{aligned}$$

(A3)

The magnetic field is recovered from the equation $\textrm{curl}\,\textbf{E} = i\omega\,\textbf{B}$, which leads to

$$\begin{aligned} {\textbf{B}}({\textbf{r}},t)=\frac{i}{\omega} \frac{d E(z)}{d z} e^{i(\beta x-\omega t)} \hat{{\textbf{x}}}+\frac{\beta }{\omega} E(z) e^{i(\beta x-\omega t)} \hat{{\textbf{z}}}. \end{aligned}$$

(A4)

Since the parameter $\beta$ is a real constant, one can see that all fields inside the slab decay/rise in the z-direction only (perpendicular to the interface). As was the case for normal propagation, the function E(z) must be continuous and have a continuous derivative. The former provides continuity of the electric field, see Eq. (A2), as well as continuity of the normal component (the z-component) of the magnetic field, see Eq. (A4). The latter provides continuity of the tangential component (the x-component) of the magnetic field, see Eq. (A4) again. For propagation along the z-axis (light incident normally on the slab), the parameter $\beta =0$, and Eqs. (A2–A4) reduce to Eqs. (3, 4). At this point it becomes clear that all results obtained for normal propagation are applicable to TE polarized light, provided all the magnitudes of the wave vectors are replaced by their z-components, i.e.

$$\begin{aligned} \begin{aligned} k_i&\rightarrow k_{iz} = \sqrt{k^2n_i^2-\beta ^2} = kn_i\cos \theta _i, \\ k_1&\rightarrow k_{1z} = \sqrt{k^2{\tilde{n}}_1^2-\beta ^2} = k\sqrt{{\tilde{n}}_1^2-n_i^2\sin \theta _i^2}, \\ k_a&\rightarrow k_{az} = \sqrt{k^2{\tilde{n}}_a^2-\beta ^2} = k\sqrt{{\tilde{n}}_a^2-n_i^2\sin \theta _i^2}, \end{aligned} \end{aligned}$$

(A5)

etc. However, some caution should be exercised when choosing the sign for the above square roots in the case of media with gain, see Refs. Macleod (2011, 2012).