Experimentally verified analytical models for the dynamic response of perovskite solar cells using measured I–V and C–V characteristics

Abstract

Perovskite solar cells (PSC) have gained significant attention recently due to their high efficiency and potential for low-cost fabrication. Understanding the dynamic behavior of these cells is crucial for optimizing their performance and stability. In this paper, we propose experimentally verified analytical models for the dynamic response of perovskite solar cells. The models are developed based on the measured current–voltage ($I-V$) and capacitance–voltage ($C-V$) characteristics obtained from experiments. The study introduces the first fully analytical model for the dynamic response of perovskite solar cells, considering single, double, and triple diode models with three polynomials $C-V$ fitting functions. The analytical models are fed by experimental measured data and coefficients and pot-processed by an equilibrium optimizer. The proposed methodology was investigated using five batches of cesium lead chloride perovskite solar cells, with a power conversion efficiency of around 16.35% ±   0.32%. The suggested analytical model with an equilibrium optimizer showed a significant capability to predict the cell circuit parameters with a root-mean-square error below 0.00103, as the minimum error recorded so far in PSCs.

1 Introduction model

Perovskite solar cells (PSCs) typically consist of several layers of materials that combine to convert sunlight into electrical energy (Shao et al. 2023; Lye et al. 2023; Ji et al. 2023; Bati et al. 2023). The basic structure for a perovskite solar cell can be represented as follows: a light-absorbing layer of perovskite material (typically ABX₃) that absorbs photons of sunlight and generates electron–hole pairs (Aminzare et al. 2023). This layer acts as the primary source of energy for the cell. Additionally, a hole transport layer (HTL) collects the holes generated by the perovskite layer and facilitates their movement toward the top electrode (Mahajan et al. 2022; Ke et al. 2022). An electron transport layer (ETL) collects the electrons generated by the perovskite layer and facilitates their movement toward the bottom electrode (Zhang et al. 2022). Finally, the top and bottom electrodes serve as contacts for the generated electrons and holes to flow out from the cell and into an external circuit (Xu et al. 2022; Lyu et al. 2022; Chen et al. 2022).

Solar cells, in general, can be equivalented by circuit elements in the form of a solar cell circuit model (Rawa et al. 2022a, 2022b). The circuit model can be further refined to consider various losses and gains within the cell, such as recombination losses, resistive losses, and power losses due to the non-ideal behavior of the materials or interfaces. These factors can be quantified and optimized through careful design (Jošt et al. 2020). Generally, the I-V performance in solar cells can be described analytically, which is reflected in the circuit model in a non-capacitive form. However, perovskite solar cells exhibit a capacitive effect due to the perovskite layer and the interfaces between the different layers in the device (Taukeer Khan et al. 2022; Hernández-Balaguera et al. 2020; Alvarez et al. 2020). This capacitive effect arises from the accumulation of charges at the interfaces, which creates an electric field within the device. The capacitive effect in perovskite solar cells can benefit device performance as it can improve charge separation and transport within the device. However, it can also lead to charge recombination and loss, reducing the solar cell’s overall efficiency (Hernández-Balaguera et al. 2020). Researchers are working to understand and optimize the capacitive effect in perovskite solar cells to improve their performance and stability (Taukeer Khan et al. 2022; Hernández-Balaguera et al. 2020; Alvarez et al. 2020).

Hypothetically, the solar cell’s circuit model can demonstrate the $I-V$ characteristic of the solar cells. However, when compared with experimental results, mismatching is usually observed. One approach to minimize the mismatching between the solar cell’s models and the experimentally measured data is to use parameter extraction optimizers, such as equilibrium optimizers, capable of simulating a PSC’s behavior under different operating conditions (Wang et al. 2021; Abdel-Basset et al. 2020). In perovskites, the optimizer considers the effects of hysteresis and charge accumulation by incorporating these phenomena into the model’s equations (Abdelrazek et al. 2022). The model accounts for the layers and components of a PSC. This includes the absorber layer, transport layers, electrodes, and other relevant materials. Each layer is described by a set of equations that describe its electrical behavior. The model also accounts for the effects of external factors such as temperature, humidity, and light intensity (Abdelrazek et al. 2022). These factors can significantly impact a PSC’s performance, and accurately modeling them is crucial for predicting the device’s behavior in real-world conditions. Once the model is constructed, the equilibrium optimizer simulates the system’s behavior and optimizes its parameters for maximum efficiency. The optimizer uses various techniques to explore the parameter space and identify the optimal settings for each component of the PSC. Utilizing such optimizers for investigating the PSC performance is still restricted to initial seeded values that can reduce the number of iterations needed for optimization and, consequently, the time and the computational cost. Due to the nature of the PSC, as demonstrated earlier, a capacitive-based $I-V$ model should be used to model the cell performance, or in other words, dynamic model (Abdelrazek et al. 2022).

Dynamic circuit models are essential for perovskite solar cells with parasitic capacitance due to several reasons. Initially, perovskite solar cells exhibit dynamic behavior, which means their electrical characteristics change over time and under different operating conditions. Dynamic circuit models allow for a more accurate representation of this behavior, capturing the transient response and time-dependent effects of the cell. In addition, parasitic capacitance (Routray and Hur 2022; Kang and Park 2019; Eid et al. 2020) is an inherent characteristic of perovskite solar cells and can significantly impact their performance. Dynamic circuit models incorporate parasitic capacitance into the model, allowing for a more comprehensive analysis of the cell’s behavior (Hernández-Balaguera et al. 2022; Filipoiu et al. 2022; Munoz-Diaz et al. 2022; Aleksandrova 2023). This includes accounting for the charging and discharging of the parasitic capacitance, which can affect the overall efficiency and response time of the cell (Filipoiu et al. 2022; Munoz-Diaz et al. 2022). Dynamic circuit models enable the prediction and analysis of dynamic effects in perovskite solar cells, such as voltage and current fluctuations, transient response, and frequency-dependent behavior (Kang and Park 2019). These dynamic effects can arise from the interplay between the cell’s intrinsic properties and the parasitic capacitance. By incorporating these effects into the model, researchers can better understand and optimize the performance of perovskite solar cells. Concerning fabrication, dynamic circuit models provide a platform for designing and optimizing control strategies for perovskite solar cells (Routray and Hur 2022). By simulating the dynamic behavior of the cell with parasitic capacitance (Eid et al. 2020), researchers can evaluate the effectiveness of different control techniques, such as feedback control or modulation schemes, in mitigating the impact of parasitic capacitance and improving the overall performance of the solar cell. By screening literature, an analytical model has yet to be found to determine the main circuit parameters for PSC under parasitic capacitance impact. Accordingly, we consider such an analytical model a research gap for optimizing the circuit model parameters.

Herein, we provide an entire attempt to combine experientially measured $I-V$ and $C-V$ characteristics to seed a newly driven dynamic analytical model for PSCs. The output parameters determined from the analytical model are optimized with an equilibrium optimizer against the experimentally measured I-V characteristics, seeking minimum root-mean-square (RMS) error. Nine analytical models were driven, considering the single, double, and triple diode models (see Fig. 1a–c) and three polynomial fitting for the $C-V$ characteristics, as in Fig. 1d. The entire process is illustrated in the flowchart illustrated in Fig. 2. It is worth highlighting that the current study was tested on our fabricated cesium lead chloride (CsPbCl₃) PSC, cf., Fig. 3a and b, and other types of PSCs captured from the literature.

Fig. 1

The circuit model for a PSC using a single-diode model, b double-diode model, and c triple diode model. d The C-V characteristics with the proposed fitting curves. Herein, three analytical polynomial functions were proposed, linear, second-order, and third order functions, with root-mean square deviation of 27%, 24%, and 8% against the experimental data

Fig. 2

A flow-chart showing the entire process of fabricating, characterizing, modeling, and optimizing PSC for obtaining the optimized circuit model parameters

Fig. 3

Cesium lead chloride PSC a segmented layer, b complete cell, and c device under test (DUT) $\mathrm{I}-\mathrm{V}$, and $\mathrm{C}-\mathrm{V}$ characterization setup

2 Experimental work and measurement setups

The CsPbCl₃ perovskite solar cell fabrication process, see Fig. 3a and b, started by cleaning the FTO transparent conducting substrate (80 nm FTO coated glass commercially purchased from Sigma Aldrich) for 20 min of sonication in acetone, deionized water, and isopropanol. The FTO substrate was preserved with UV-ozone for 15 min, then annealing the substrate at 75 °C before using them. The Triton-X-based TiO₂ paste for mesoporous was prepared. First, add 3 ml Triton-X polymer with 2.5 g of TiO₂ powder. Afterward, the mixture was pestled until it got homogenous. Next, add 0.75 ml of isopropanol to the mixture using a micro pipet and then pestle the mixture again (Hatem et al. 2021a, 2021b; Hassan et al. 2021; Abdellatif et al. 2020, 2022). The mesoporous TiO₂ layer was deposited on the substrate by spreading the paste using a glass rod, see Fig. 4. The spreading speed, controlled by the driver motor voltage, can tune the mesoporous TiO2 layer thickness from 1 μm to 15 μm ± 50 nm. Afterward, the substrate was sintered in the muffle furnace at 225 °C for 2 h until drying out completely.

Fig. 4

depositing mesoporous TiO₂ using automatically controlled glass rod a past spreading on FTO coated BK7 glass, and b glass rod deposition process

The CsPbCl₃ layer was prepared using a two-step sequential deposition method (Chen et al. 2021). Firstly, 367 mg of PbCl₃ in 0.5 ml DMF and 0.5 ml DMSO was stirred on a hot plate at 75 °C for 10 min in a wrapped container. Afterward, 30 mg of CsCl was dissolved in 2 ml of methanol and then heated for 10 min in the wrapped container. Subsequently, a 0.22 μm pore size PTFE filter was used to filter the substrate, and then it would be ready to be used. The PbCl2 layer was spin-coated at 500 rpm for 20 s, followed by 2000 rpm for 30 s. Resulting a thin film of 250 nm ± 10 nm. Then it was dried on the hot plate at 180 °C for 30 min. After drying, the substrate was dipped for 5–15 min in a heated 15 mg/ml CsCl solution. Finally, it was annealed at 180 °C for 30 min on the hot plate directly. For the hole transport layer, the prepared NiO layer was spin-coated on the substrate at 500 rpm for 20 s, followed by 2000 rpm for 30 s, reaching a thickness of 800 nm ± 10 nm. (Qin et al. 2019). Consequently, it dried at 275 °C for 45 min. Once the sample is completely stained, the cell is closed using the counter electrode, leaving a space for the probes to connect. Paper clips hold the two sides together to hold the solar cell. Another critical consideration in PSCs is the defects control. Semiconductor crystals have always had defects that play a crucial role in determining their optical and electronic properties. Despite the increasing popularity of CsPbX₃ (X = Cl, Br, I) in various applications due to their tolerance to defects, the characteristics, stability, and practical usability of these materials are still heavily influenced by these defects. Consequently, passivation strategies were utilized as in Seth et al. (2019) to address defects.

Based on the flow chart shown in Fig. 2, two main characteristic curves are targeted, the $I-V$ and the $C-V$ characteristics; see the proposed measuring setups in Fig. 3c. Herein, we utilize our LED solar simulator for optical injection, with optimized spectra agonist, our previous work in Hassan et al. (2020); Abdellatif and Ghali 2021). The LED’s array is designed using while, an ultra-violet, violable and infrared high-power LED with an AM1.5G filter (model no. 81094, Newport Corporation). The spectral mismatch showed nearly 8.2%, within the 200 nm to 1100 nm range, as measured by our UV–Vis-NIR OceanOptics spectrometer (Fig. 5a). The device under test (DUT) is attached to an x-y-z controller. The z-variation is mainly utilized to control level intensity up to one sun condition, while the x–y scanning is mainly for light uniformity calibration. The spatial uniformity recorded for 56 mm × 56 mm showed around 95% uniformity; see Fig. 5b with 0.1 mm resolution. Concerning temporal stability, the designed system achieved an extremely high response, with minimum ripples, shown in Fig. 5c. For the sake of $I-V$ measurements, Keithley 2410 source meter unit (SMU) is used with a varying D.C. voltage generated across the two terminals of the cell, while current is acquired Semitonically. A calibration stage is done using a calibrated reference solar cell (model no. 91150-KG5, Newport Corporation). The $I-V$ characterization curve for the calibrated solar cell, made of monocrystalline silicon, makes it possible to calibrate the SMU and the optical injection LED source, showing less than 0.78% RMS error.

Fig. 5

a spectral mismatching, b spatial uniformity, and c temporal stability in the customized high power LED array acting as a solar simulator

Alternatively, we adopted the experimental technique used in Kim et al. (2016) to characterize the $C-V$ curve for our fabricated PSC. As demonstrated in Fig. 3c, a simple technique based on a sinusoidal function generator and digital oscilloscope was conducted through a 50 Ω probe. This experiment uses a digital storage oscilloscope MDO-2102AG, where the artificial function generator (AFG) is functionalized. The experiment was designed to enable $C-V$ measurements in the pF to fF range, as previously introduced in Kim et al. (2016).

3 Analytical model

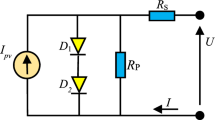
As described above, the $I-V$ optimizer should be seeded with initial values that reflect the experimentally measured data. In this regard, an analytical model is derived to express each targeted parameter. Due to the nature of perovskite solar cells, a capacitance-dependent model is a must. Accordingly, the standard D.C. analytical model, such as the model in Abdulrazzaq et al. (2022), cannot be utilized. Consequently, a transient analytical model is suggested. The general form for the I-V equation, while applying the single diode model, can be written as (Abdelrazek et al. 2022):

$$I={I}_{ph}-{I}_{01}\left(\mathrm{exp}\left(\frac{q(V+{R}_{s}I)}{{n}_{1}kT}\right)-1\right)-\frac{(V+I{R}_{s})}{{R}_{sh}}-{C}_{eq}\frac{d(V+I{R}_{s})}{dt}$$

(1.a)

$$I={I}_{ph}-{I}_{01}\left(\mathrm{exp}\left(\frac{q\left(V+{R}_{s}I\right)}{{n}_{1}kT}\right)-1\right)-{I}_{02}\left(\mathrm{exp}\left(\frac{q\left(V+{R}_{s}I\right)}{{n}_{2}kT}\right)-\frac{(V+I{R}_{s})}{{R}_{sh}}-{C}_{eq}\frac{d(V+I{R}_{s})}{dt}\right)$$

(1.b)

$$I={I}_{ph}-{I}_{01}\left(\mathrm{exp}\left(\frac{q(V+{R}_{s}I)}{{n}_{1}kT}\right)-1\right)-{I}_{02}(\mathrm{exp}\left(\frac{q\left(V+{R}_{s}I\right)}{{n}_{2}kT}\right)-{I}_{03}\left(\mathrm{exp}\left(\frac{q(V+{R}_{s}I)}{{n}_{3}kT}\right)-\frac{(V+I{R}_{s})}{{R}_{sh}}-{C}_{eq}\frac{d(V+I{R}_{s})}{dt}\right)$$

(1.c)

where ${I}_{ph}$ is the photo-generated current in (A), ${I}_{\mathrm{01,2},3}$ are the first, second, and third diode reverse saturation current in (A), respectively, ${n}_{\mathrm{1,2},3}$ are the first, second, and third diode ideality factor, respectively, ${R}_{s}$ is the series resistance in (Ω), ${R}_{sh}$ is the shunt resistance in (Ω), $I$, and $V$ are the output PSC’s current and voltage, respectively, $k$ is the Boltzmann’s constant (1.38065 × 10⁻²³ J/K), $T$ is the cell temperature in (K), ${C}_{eq}$ is the equivalent capacitance in (F), $q$ is the unit charge ($1.6 \times 10^{ - 19}$C), and the differential operator − DDT indicates the rate of change for the independent variable $t$, representing time in (sec.).

It can be observed that the three above equations represent the possible three dynamic electronic models for PSCs, considering single diode model (SDM), double diode model (DDM), and triple diode model (TDM), respectively. As discussed earlier, the PSC equivalent capacitance is a voltage-dependent parameter. Accordingly, the $C-V$ characteristic can be a linear, quadratic, or third-order polynomial (see Fig. 1d). as given by Abdelrazek et al. (2022):

$${C}_{eq}=a+b\left(V+{R}_{s}I\right)$$

(2.a)

$${C}_{eq}=a+b\left(V+{R}_{s}I\right)+c{\left(V+{R}_{s}I\right)}^{2}$$

(2.b)

$${C}_{eq}=a+b\left(V+{R}_{s}I\right)+c{\left(V+{R}_{s}I\right)}^{2}+ d{\left(V+{R}_{s}I\right)}^{3}$$

(2.c)

where $a$, $b$, $c$, and $d$ are positive fitting parameters extracted from the experimental C-V characteristic fitting processes. Solving Eqs. (1) and (2) can result in nine different analytical models based on the selected diode model and the C-V fitting. The following sub-sections demonstrated the complete analytical solutions, seeking a final symbolic time-dependent closed form for each electronic model’s parameters.

3.1 Single-diode PV model with linear C-V fitting

In this solution, Eqs. (1.a) and (2.a) are used. The analytical solution procedure is initiated by substituting the boundary conditions values, including short-circuit, open-circuit, and maximum points. At open circuit conditions, $I=0$ and $V= {V}_{oc}.$ At such a condition, substituting Eq. (2.a) into Eq. (1.a), we get:

$${I}_{ph}={I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{oc}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right) \times \frac{d}{dt}({V}_{oc})\right)$$

(3)

where, ${V}_{oc}$ is the open circuit voltage. Substitute Eq. (3) into (1.a), we get:

$$I=\left({I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\right)-{I}_{01}\left(\mathrm{exp}\left(\frac{q(V+{R}_{s}I)}{{n}_{1}kT}\right)-1\right)-\frac{(V+I{R}_{s})}{{R}_{sh}}-(a+b\left(V+{R}_{s}I)\right)\frac{d(V+I{R}_{s})}{dt}$$

(4.a)

Applying short circuit condition, $I = {I}_{sc}$ and $V= 0$, one can obtain:

$${I}_{sc}=\left({I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\right)-{I}_{01}\left(\mathrm{exp}\left(\frac{q({I}_{sc}{R}_{s})}{{n}_{1}kT}\right)-1\right)-\frac{({I}_{sc}{R}_{s})}{{R}_{sh}}-\left(a+b\left({R}_{s}{I}_{sc}\right)\frac{d({I}_{sc}{R}_{s})}{dt}\right)$$

(4.b)

$${I}_{sc}={I}_{01}\left[\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\mathrm{exp}\left(\frac{q{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)\right]+\frac{{V}_{oc}-{I}_{sc}{R}_{s}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)- (a+b\left({R}_{s}{I}_{sc}\right)\frac{d({I}_{sc}{R}_{s})}{dt}$$

(4.c)

where ${I}_{sc}$ is the short circuit current. At maximum power point, $I = {I}_{mp}$ and $V= {V}_{mp}$, solving Eq. (4.a) at maximum point results:

$${I}_{mp}={I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d({V}_{oc})}{dt}\right)-{I}_{01}(\mathrm{exp}\left(\frac{q\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}{{n}_{1}kT}\right)-1)-\frac{{V}_{mp}+{I}_{mp}{R}_{s}}{{R}_{sh}}-(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right))\frac{d({V}_{mp}+{I}_{mp}{R}_{s})}{dt}$$

(5.a)

$${I}_{mp}\left(1+\frac{{R}_{s}}{{R}_{sh}}\right)={I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{\mathit{oc}}}{{n}_{1}\mathit{kT}}\right)-\mathrm{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s}}{{n}_{1}kT}\right)\right)+\frac{{V}_{oc}- {V}_{mp}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d({V}_{oc})}{dt}\right)-\left((a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right))\frac{d({V}_{mp}+ {I}_{mp}{R}_{s})}{dt}\right)$$

(5.b)

where ${I}_{mp}$ is the maximum power point current, ${V}_{mp}$ is the maximum power point voltage. The output power of PV module at each point on the $I-V$ curve is calculated as

$$P=V \times I$$

(6.a)

and its derivative with respect to voltage is given by:

$$\frac{dP}{dV}=I+V\frac{dI}{dV}$$

(6.b)

Knowing that the maximum power point is a turning point with zero slope, the power derivative can be written as:

$${\left.\frac{dP}{dV}\right|}_{P={p}_{{m}_{P}}}=0$$

(6.c)

Accordingly, Eq. (6.b) can be reformatted as:

$${\left.\frac{dI}{dV}\right|}_{P={P}_{{m}_{P}}}=-\frac{{I}_{mp}}{{V}_{mp}}$$

(6.d)

The term $\frac{dI}{dV}$ is obtained by differentiating the Eq. (1.a) with respect to voltage, while considering voltage independent photo-generated current as resulted in Eq. (3), the $\frac{dI}{dV}$ can be formulated as:

$$\frac{dI}{dV}=\frac{-q {I}_{01}}{{n}_{1}kT}\left(1+{R}_{s}\frac{dI}{dV}\right)\mathrm{exp}\left(\frac{q(V+I{R}_{s})}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}\left(1+{R}_{s}\frac{dI}{dV}\right)-(a+b\left(V+{R}_{s}I)\right)\frac{d}{dt}\left[1+{R}_{s}\frac{dI}{dV}\right]-\left(\frac{d}{dt}\left(V+I{R}_{s}\right)\right) \left(b\left(1+{R}_{s}\frac{dI}{dV}\right)\right)$$

(7)

Solving Eq. (7) at the maximum point, and substituting in (6.d) we get:

$$\frac{{I}_{mp}}{{V}_{mp}}=\frac{q {I}_{01}}{{n}_{1}kT}\left(1-{R}_{s} \frac{{I}_{mp}}{{V}_{mp}}\right)\mathit{exp}\left(\frac{q({V}_{mp}+{I}_{mp}{R}_{s})}{{n}_{1}kT}\right)+\frac{1}{{R}_{sh}}\left(1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right)+\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)\right)\frac{d}{dt}\left[1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right]+\left(\frac{d}{dt}\left({V}_{mp}+{I}_{mp}{R}_{s}\right)\right)\left(b\left(1+{R}_{s}\frac{dI}{dV}\right)\right)$$

(8)

Alternatively, Eq. (7) can be reformulated as:

$$\frac{dI}{dV}\left(1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left(V+I{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left(V+I{R}_{s}\right)}{dt}\right)=\left(\frac{-q{I}_{01}}{{n}_{1}kT}exp\frac{q\left(V+I{R}_{s}\right)}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-(a+b\left(V+{R}_{s}I)\right)\frac{d}{dt}\left({R}_{s}\frac{dI}{dV}\right)-b\frac{d\left(V+I{R}_{s}\right)}{dt}$$

(9.a)

$$\frac{dI}{dV}=\frac{\left(\frac{-q{I}_{01}}{{n}_{1}kT}\mathrm{e}xp\frac{q\left(V+I{R}_{s}\right)}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-(a+b\left(V+{R}_{s}I\right))\frac{d}{dt}\left({R}_{s}\frac{dI}{dV}\right)-b\frac{d\left(V+I{R}_{s}\right)}{dt}}{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left(V+I{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left(V+I{R}_{s}\right)}{dt}}$$

(9.b)

Considering that the shunt resistance is inversely proportional to the $\frac{dI}{dV}$ close to the short-circuit point, then, solving Eq. (9.b) at short0circuit condition results:

$${\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}= \frac{\frac{-q{I}_{o1}}{{n}_{1}kT}exp\left(\frac{q\left({I}_{sc}{R}_{s}\right)}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-\left(a+b\left({R}_{s}{I}_{sc}\right))\frac{d}{dt}({R}_{s}{\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}\right)-b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt} }{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left({I}_{sc}{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}$$

(10)

The term ${I}_{01}\mathrm{exp}\left(\frac{q{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)$ represents the diode current and this is too small compared to the short-circuit current and thus it can be neglected. In addition, since ${R}_{s}$< < ${R}_{sh}$, the term ${R}_{s}$/${R}_{sh}$ may also be neglected. Therefore, the derivative can be approximated as

$${\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}=\frac{ -\frac{1}{{R}_{sho}}-\left(a+b\left({R}_{s}{I}_{sc}\right)\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}\right)-b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}\right) }{1+{R}_{s}b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}$$

(11)

Substituting Eq. (11) into Eq. (7), applying short-circuit condition, one can obtain:

$$\begin{gathered} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}} \hfill \\ = \frac{{ - q I_{01} }}{{n_{1} kT}}\left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} } \right)}}{{n_{1} kT}}} \right) \hfill \\ - \frac{1}{{R_{sho} }}\left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left[ {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right] \hfill \\ - \frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\left( {b\left( {1 + R_{s} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ \end{gathered}$$

(12.a)

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) + b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}} \hfill \\ = \left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\frac{{q I_{01} }}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} } \right)}}{{n_{1} kT}}} \right) + \frac{1}{{R_{sho} }} + b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}} \right) + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right) \hfill \\ \frac{d}{dt}\left[ {1 + R_{s} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(12.b)

Here the term ${R}_{sho}$ indicates the initial guess for the ${R}_{sh}$ at the short-circuit point. The same approach can be applied to estimate the series resistance by solving Eq. (9.b) under the open-circuit condition, to reach:

$${\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}} =\frac{\frac{-q{I}_{01}}{{n}_{1}kT}exp\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-\left(a+b\left({V}_{oc}\right)\right)\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}\right)- b\frac{d\left({V}_{oc}\right)}{dt}}{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left({V}_{oc}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left({V}_{oc}\right)}{dt}}$$

(13)

This gives a simple expression to find the initial value of the series resistance (${R}_{so}$) defined by the negative slope of the $I-V$ curve near the open circuit region, while considering the same approximations concerning the diode current and the series-shunt resistance ratio, here we reach:

$${\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}=\frac{ -\left(a+b\left({V}_{oc}\right)\right)\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}\right)- b\frac{d\left({V}_{oc}\right)}{dt} }{1+{R}_{s}b\frac{d\left({V}_{oc}\right)}{dt}}$$

(14)

Substitute (14) in (7), and applying open-circuit condition, one can obtain:

$$\begin{gathered} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right) = \frac{{ - q I_{01} }}{{n_{1} kT}}\left( {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{n_{1} kT}}} \right) \hfill \\ - \frac{1}{{R_{sh} }}\left( {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right) - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left[ {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right] \hfill \\ - \frac{{d\left( {V_{oc} } \right)}}{dt}\;b\left( {1 + R_{s} \left( { \frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right) \hfill \\ \end{gathered}$$

(15.a)

$$\begin{gathered} \left( {\frac{{ \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) + b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right) = \left( {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\frac{{q I_{01} }}{{n_{1} kT}}\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{n_{1} kT}}} \right) + \frac{1}{{R_{sh} }} + b\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) + \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left[ {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right] \hfill \\ \end{gathered}$$

(15.b)

In addition to the two parasitic resistances, the diode saturation current can be extracted by Eqs. (3) and (4.c), we can reach:

$${I}_{o1}=\frac{{I}_{sc}({R}_{sh}+{R}_{s})-{V}_{oc}-{R}_{sh}\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)+ {R}_{sh}(a+b\left({R}_{s}{I}_{sc})\right)\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}{{R}_{sh}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\mathrm{exp}\left(\frac{\left(q{R}_{s}{I}_{sc}\right)}{{n}_{1}kT}\right)\right)}$$

(16)

The open-circuit voltage can be obtained from the experimental data. However, the ideality factor is still an unknown, that needs to be determined.

Since, ${R}_{sh}\gg {R}_{s}$, accordingly, $1+\frac{{R}_{s}}{{R}_{sh}}\approx 1,$ and ${I}_{sc}\gg \frac{{V}_{oc}}{{R}_{sh}}$. Furthermore, $\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)\gg \mathrm{exp}\left(\frac{{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)$ is a valid assumption. Therefore, Eq. (16) can be approximated to:

$${I}_{o1}={I}_{sc}\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)-\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)+ \left(\left(a+b\left({R}_{s}{I}_{sc}\right)\right)\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)$$

(17)

Substituting Eqs. (17) into (3), while considering $\frac{{V}_{0c}}{{R}_{sh}}$ tends to zero:

$${I}_{ph}={I}_{sc}\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)-\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)+ (a+b\left({R}_{s}{I}_{sc})\right)\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}+\frac{{V}_{oc}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)*\frac{d}{dt}({V}_{oc})\right)$$

(18)

Equation (5.b) can be written as by substituting Eq. (17) in it:

$$\begin{gathered} I_{mp} \left( {1 + \frac{{R_{s} }}{{R_{sh} }}} \right) = \left( {I_{sc} \exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right) \hfill \\ \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) + \frac{{V_{oc} - V_{mp} }}{{R_{sh} }} + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{d\left( {V_{mp} + I_{mp} R_{s} } \right)}}{dt}} \right) \hfill \\ \end{gathered}$$

(19)

Assume: $\frac{{V}_{oc}-{V}_{mp}}{{R}_{sh}} \approx 0$ and $1+\frac{{R}_{s}}{{R}_{sh}}\approx 1$

$$\begin{aligned} I_{mp} & = I_{sc} \left( {1 - \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \\ + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} - \left( {\left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\left( {\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right)} \right)\left( {\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) \\ + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{d\left( {V_{mp} + I_{mp} R_{s} } \right)}}{dt}} \right) \\ \end{aligned}$$

(20)

Considering $\frac{1}{{R}_{sh}}\left(1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right)\approx 0$, Eq. (8) can be written as,

$$\begin{aligned} I_{{m_{P} }} & = V_{{m_{P} }} = \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right)\exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{n_{1} kT}}} \right)\left( {I_{sc} \exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right) \\ - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) + \left( {\left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right) \\ + \left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{d}{dt}\left[ {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right] + \left( {\frac{d}{dt}\left( {V_{mp} + I_{mp} R_{s} } \right)} \right)\left( {b\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right)} \right) \\ \end{aligned}$$

(21)

It can be observed that both Eqs. (20), and (21) are function in $R_{s}$, and ${n}_{1}$. However, the series resistance is associated with the differentiation operator. Consequently, we equalize both equations seeking for a first order differential equation (DE) in terms of $R_{s}$. Towards simplification, and as mentioned earlier, the boundary conditions points, at short circuit, open-circuit, and maximum power point, are treated as time independent constants, extracted from experimental measurements. Following that, the first order DE can be written as:

$$\begin{gathered} I_{sc} \left( {1 - \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) + \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)\frac{{dR_{s} }}{dt} - \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)\frac{{dR_{s} }}{dt} \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \hfill \\ - aI_{mp} \frac{{dR_{s} }}{dt} - b\left( {V_{mp} + R_{s} I_{mp} } \right)I_{mp} \frac{{dR_{s} }}{dt} - I_{sc} V_{{m_{P} }} \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \hfill \\ - \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)V_{{m_{P} }} \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)\frac{{dR_{s} }}{dt} \hfill \\ - \frac{{I_{mp} }}{{V_{mp} }}\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{dR_{s} }}{dt} - bI_{mp} \left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \frac{{dR_{s} }}{dt} = 0. \hfill \\ \end{gathered}$$

(22)

Equation (22) can be treated as:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(23.a)

where:

$$\begin{aligned} f^{1} \left( {R_{s} } \right) = & \left( {aI_{{{\text{sc}}}} + bR_{s} I_{{{\text{sc}}}}^{2} } \right) - \left( {aI_{{{\text{sc}}}} + bR_{s} I_{{{\text{sc}}}}^{2} } \right)\exp \left( {\frac{{q(V_{{{\text{mp}}}} - V_{{{\text{oc}}}} + I_{{{\text{mp}}}} R_{s} )}}{{n_{1} kT}}} \right) \\ & - aI_{{{\text{mp}}}} - b\left( {V_{{{\text{mp}}}} + R_{s} I_{{{\text{mp}}}} } \right)I_{{{\text{mp}}}} - \left( {aI_{{{\text{sc}}}} + bR_{s} I_{{{\text{sc}}}}^{2} } \right)V_{{m_{P} }} \\ & \;\;\;\frac{q}{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{{{\text{mp}}}} }}{{V_{{{\text{mp}}}} }}} \right)\exp \left( {\frac{{q(V_{{{\text{mp}}}} - V_{{{\text{oc}}}} + I_{{{\text{mp}}}} R_{s} )}}{{n_{1} kT}}} \right) \\ & - \frac{{I_{{{\text{mp}}}} }}{{V_{{{\text{mp}}}} }}\left( {a + b\left( {V_{{{\text{mp}}}} + R_{s} I_{{{\text{mp}}}} } \right)} \right) - {\text{ b}}I_{{{\text{mp}}}} \left( {1 - R_{s} \frac{{I_{{{\text{mp}}}} }}{{V_{{{\text{mp}}}} }}} \right) \\ \end{aligned}$$

(23.b)

$$f^{2} \left( {R_{s} } \right) = I_{sc} \left( {1 - { }\exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) - I_{sc} V_{{m_{P} }} { }\frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)$$

(23.c)

Equation (23) can’t be solved analytically, however, an iterative numerical solution for both Eqs. (20) and (23) can converge with both ${R}_{s} (t)$, and ${n}_{1}(t)$. Referring to Eq. (12.b), with replacing the diode saturation current as given in (16), the shunt resistance can be calculated as:

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}} = \hfill \\ \left( {1 + R_{s} \left( t \right) \left( {\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)} \right)\left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} + R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}} \right) \hfill \\ + \left( {a + b\left( {R_{s} \left( t \right)I_{sc} } \right)} \right)\frac{d}{dt}\left[ {R_{s} \left( t \right)\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(24)

Substituting (23.a) in (24) we get:

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}} = \left( {1 + R_{s} \left( t \right)\left( {\frac{{ - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \hfill \\ \left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} - R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ + \left( {a + bR_{s} \left( t \right)I_{sc} } \right) \hfill \\ \left( \begin{gathered} \left[ {R_{s} \left( t \right)\frac{{\left( { - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} } \right)\left( { - R_{s} bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right) - \left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( { - \frac{1}{{R_{sho}^{2} }} \frac{{d\left( {R_{sho} } \right)}}{dt} + bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right] \hfill \\ + \left( {\frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered}$$

(25)

Again, Eq. (25) can’t be solved analytically, however, an iterative numerical solution can be extracted for ${R}_{sho} (t)$. Equation (25) can be treated as:

$${g}^{1}\left({R}_{sho}\right)\frac{d{R}_{sho}}{dt}+ {g}^{2}\left({R}_{sho}\right)=0$$

(26.a)

where:

$${g}^{1}\left({R}_{sho}\right)=(a+b{R}_{s}\left(t\right){I}_{sc})\left(\left[{R}_{s}\left(t\right)\frac{ \left(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}\right)\left(-\frac{1}{{R}_{sho}^{2}} \right)}{(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}{)}^{2}}\right]\right)$$

(26.b)

$$\begin{gathered} g^{2} \left( {R_{sho} } \right) = \left( {1 + R_{s} \left( t \right)\left( {\frac{{{ } - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \hfill \\ \left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} - R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ - \frac{{{ }\frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}} + \left( {a + bR_{s} \left( t \right)I_{sc} } \right) \hfill \\ \left( {\left[ {R_{s} \left( t \right)\frac{{\left( { - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right)\left( { - R_{s} bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right) - \left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( {bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right] + \left( {\frac{{{ }\frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}{ }}}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ \end{gathered}$$

(26.c)

Solving the first order DE in (26) results with the estimated shunt resistance at the short-circuit point. Substituting back in (16) with the extracted functions from (20), (23), and (26) results:

$${I}_{o1 }(t)=\frac{{I}_{sc}({R}_{sho}(t))-{V}_{oc}+ {R}_{sh0}(t)(a-b\left({R}_{s}(t){I}_{sc}^{2}\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}}{{R}_{sho}(t)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}(t)kT}\right)-\mathrm{exp}\left(\frac{\left(q{R}_{s}(t){I}_{sc}\right)}{{n}_{1}(t)kT}\right)\right)}$$

(27)

Finally, the photo-generated current can be driven from Eq. (3) as:

$${I}_{ph}(t)={I}_{01}(t)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}\left(t\right)kT}\right)-1\right)+\frac{{V}_{oc}}{{R}_{sho}(t)}$$

(28)

3.2 Single-diode PV model with second and third-order C-V fitting.

Herein, we proceeded in the same derivation sequence as in Sect. 3.1, utilizing Eqs. (2.c) and (2.d) for the second and third-order capacitive voltage fitting. Considering the second-order model, a differential equation concerning ${R}_{s}$ can be extracted, typically as Eq. (22) in the first-order linear model. Towards simplification, and as implemented earlier, the boundary conditions points, at short circuit, open-circuit, and maximum power point, are treated as time-independent constants extracted from experimental measurements. Following that, the first-order D.E. can be written as:

$$I_{ph} = I_{01} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} kT}}} \right) - 1} \right) + \frac{{V_{oc} }}{{R_{sh} }} + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)x\frac{d}{dt}\left( {V_{oc} } \right)} \right)$$

(29)

where, ${V}_{oc}$ is the open circuit voltage. Substitute Eq. (3) into (1.a), we get:

$$I=(\left({I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\right)-{I}_{01}\left(\mathrm{exp}\left(\frac{q(V+{R}_{s}I)}{{n}_{1}kT}\right)-1\right)-\frac{(V+I{R}_{s})}{{R}_{sh}}-(a+b\left(V+{R}_{s}I)\right)\frac{d(V+I{R}_{s})}{dt}$$

(30.a)

Applying short circuit condition, $I = {I}_{sc}$ and $V= 0$, one can obtain:

$${I}_{sc}=\left({I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\right)-{I}_{01}\left(\mathrm{exp}\left(\frac{q({I}_{sc}{R}_{s})}{{n}_{1}kT}\right)-1\right)-\frac{({I}_{sc}{R}_{s})}{{R}_{sh}}-\left(a+b\left({R}_{s}{I}_{sc}\right)\frac{d({I}_{sc}{R}_{s})}{dt}\right)$$

(30.b)

$${I}_{sc}={I}_{01}\left[\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\mathrm{exp}\left(\frac{q{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)\right]+\frac{{V}_{oc}-{I}_{sc}{R}_{s}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)- (a+b\left({R}_{s}{I}_{sc}\right)\frac{d({I}_{sc}{R}_{s})}{dt}$$

(30.c)

where ${I}_{sc}$ is the short circuit current. At maximum power point, $I = {I}_{mp}$ and $V= {V}_{mp}$, solving Eq. (4.a) at maximum point results:

$${I}_{mp}={I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+\frac{{V}_{0c}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d({V}_{oc})}{dt}\right)-{I}_{01}\left(\mathrm{exp}\left(\frac{q\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}{{n}_{1}kT}\right)-1\right)-\frac{{V}_{mp}+{I}_{mp}{R}_{s}}{{R}_{sh}}-(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right))\frac{d({V}_{mp}+{I}_{mp}{R}_{s})}{dt}$$

(31.a)

$${I}_{mp}\left(1+\frac{{R}_{s}}{{R}_{sh}}\right)={I}_{01}\left(\mathrm{exp}\left(\frac{q{V}_{\mathit{oc}}}{{n}_{1}\mathit{kT}}\right)-\mathrm{exp}\left(\frac{q\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}{{n}_{1}kT}\right)\right)+\frac{{V}_{oc}- {V}_{mp}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)\frac{d({V}_{oc})}{dt}\right)-\left((a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right))\frac{d({V}_{mp}+ {I}_{mp}{R}_{s})}{dt}\right)$$

(31.b)

where ${I}_{mp}$ is the maximum power point current, ${V}_{mp}$ is the maximum power point voltage. The output power of PV module at each point on the $I-V$ curve is calculated as

$$P=V \times I$$

(32.a)

and its derivative with respect to voltage is given by:

$$\frac{dP}{dV}=I+V\frac{dI}{dV}$$

(32.b)

Knowing that the maximum power point is a turning point with zero slope, the power derivative can be written as:

$${\left.\frac{dP}{dV}\right|}_{P={p}_{{m}_{P}}}=0$$

(32.c)

Accordingly, Eq. (6.b) can be reformatted as:

$${\left.\frac{dI}{dV}\right|}_{P={P}_{{m}_{P}}}=-\frac{{I}_{mp}}{{V}_{mp}}$$

(32.d)

The term $\frac{dI}{dV}$ is obtained by differentiating the Eq. (1.a) with respect to voltage, while considering voltage independent photo-generated current as resulted in Eq. (29), the $\frac{dI}{dV}$ can be formulated as:

$$\frac{dI}{dV}=\frac{-q {I}_{01}}{{n}_{1}kT}\left(1+{R}_{s}\frac{dI}{dV}\right)\mathrm{exp}\left(\frac{q(V+I{R}_{s})}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}\left(1+{R}_{s}\frac{dI}{dV}\right)-(a+b\left(V+{R}_{s}I)\right)\frac{d}{dt}\left[1+{R}_{s}\frac{dI}{dV}\right]-\left(\frac{d}{dt}\left(V+I{R}_{s}\right)\right)\left(b\left(1+{R}_{s}\frac{dI}{dV}\right)\right)$$

(33)

Solving Eq. (7) at the maximum point, and substituting in (32.d) we get:

$$\frac{{I}_{mp}}{{V}_{mp}}=\frac{q {I}_{01}}{{n}_{1}kT}\left(1-{R}_{s} \frac{{I}_{mp}}{{V}_{mp}}\right)\mathrm{exp}\left(\frac{q({V}_{mp}+{I}_{mp}{R}_{s})}{{n}_{1}kT}\right)+\frac{1}{{R}_{sh}}\left(1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right)+(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right))\frac{d}{dt}\left[1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right]+\left(\frac{d}{dt}\left({V}_{mp}+{I}_{mp}{R}_{s}\right)\right)\left(b\left(1+{R}_{s}\frac{dI}{dV}\right)\right)$$

(34)

Alternatively, Eq. (33) can be reformulated as:

$$\frac{dI}{dV}\left(1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left(V+I{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left(V+I{R}_{s}\right)}{dt}\right) =\frac{-q{I}_{01}}{{n}_{1}kT}exp\frac{q\left(V+I{R}_{s}\right)}{{n}_{1}kT})-\frac{1}{{R}_{sh}}-(a+b\left(V+{R}_{s}I)\right)\frac{d}{dt}\left({R}_{s}\frac{dI}{dV}\right)-b\frac{d\left(V+I{R}_{s}\right)}{dt}$$

(35.a)

$$\frac{dI}{dV}=\frac{\left(\frac{-q{I}_{01}}{{n}_{1}kT}\mathrm{exp}\frac{q\left(V+I{R}_{s}\right)}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-(a+b\left(V+{R}_{s}I\right))\frac{d}{dt}\left({R}_{s}\frac{dI}{dV}\right)-b\frac{d\left(V+I{R}_{s}\right)}{dt}}{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}\mathrm{exp}\frac{q\left(V+I{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left(V+I{R}_{s}\right)}{dt}}$$

(35.b)

Considering that the shunt resistance is inversely proportional to the $\frac{dI}{dV}$ close to the short-circuit point, then, solving Eq. (9.b) at short0circuit condition results:

$${\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}= \frac{\frac{-q{I}_{o1}}{{n}_{1}kT}exp\left(\frac{q\left({I}_{sc}{R}_{s}\right)}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-(a+b\left({R}_{s}{I}_{sc}\right))\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}\right)-b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt} }{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}exp\frac{q\left({I}_{sc}{R}_{s}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}$$

(36)

The term ${I}_{01}\mathrm{exp}\left(\frac{q{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)$ represents the diode current and this is too small compared to the short-circuit current and thus it can be neglected. In addition, since ${R}_{s}$< < ${R}_{sh}$, the term ${R}_{s}$/${R}_{sh}$ may also be neglected. Therefore, the derivative can be approximated as

$${\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}=\frac{ -\frac{1}{{R}_{sho}}-(a+b\left({R}_{s}{I}_{sc}\right)\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I={I}_{sc},V=0}\right)-b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt} }{1+{R}_{s}b\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}$$

(37)

Substituting Eq. (37) into Eq. (33), applying short-circuit condition, one can obtain:

$$\begin{gathered} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}} = \frac{{ - q I_{01} }}{{n_{1} kT}} \hfill \\ \left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ \exp \left( {\frac{{q\left( {I_{sc} R_{s} } \right)}}{{n_{1} kT}}} \right) - \frac{1}{{R_{sho} }}\left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left[ {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right] \hfill \\ - \frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\left( {b\left( {1 + R_{s} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ \end{gathered}$$

(38.a)

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) + b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}} = \left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\frac{{q I_{01} }}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} } \right)}}{{n_{1} kT}}} \right) + \frac{1}{{R_{sho} }} + b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}} \right) + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt} \hfill \\ \left[ {1 + R_{s} \frac{{ - \frac{1}{{R_{sho} }} - \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = I_{sc} ,V = 0}} } \right) - b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(38.b)

Here the term ${R}_{sho}$ indicates the initial guess for the ${R}_{sh}$ at the short-circuit point. The same approach can be applied to estimate the series resistance by solving Eq. (9.b) under the open-circuit condition, to reach:

$${\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}} =\frac{\frac{-q{I}_{01}}{{n}_{1}kT}\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\frac{1}{{R}_{sh}}-(a+b\left({V}_{oc}\right))\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}\right)- b\frac{d\left({V}_{oc}\right)}{dt}}{1+\frac{{R}_{s}}{{R}_{sh}}+\frac{q{I}_{01}{R}_{s}}{{n}_{1}kT}\mathrm{exp}\frac{q\left({V}_{oc}\right) }{{n}_{1}kT}+{R}_{s}b\frac{d\left({V}_{oc}\right)}{dt}}$$

(39)

This gives a simple expression to find the initial value of the series resistance (${R}_{so}$) defined by the negative slope of the $I-V$ curve near the open circuit region, while considering the same approximations concerning the diode current and the series-shunt resistance ratio, here we reach:

$${\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}=\frac{ -(a+b\left({V}_{oc}\right))\frac{d}{dt}\left({R}_{s}{\left.\frac{dI}{dV}\right|}_{I=0,V={V}_{oc}}\right)- b\frac{d\left({V}_{oc}\right)}{dt} }{1+{R}_{s}b\frac{d\left({V}_{oc}\right)}{dt}}$$

(40)

Substitute (40) in (33), and applying open-circuit condition, one can obtain:

$$\begin{gathered} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right) = \frac{{ - q I_{01} }}{{n_{1} kT}}\left( {1 + R_{s} \left( { \frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{n_{1} kT}}} \right) - \frac{1}{{R_{sh} }} \hfill \\ \left( {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right) - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt} \hfill \\ \left[ {1 + R_{s} \left( { \frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right] - \frac{{d\left( {V_{oc} } \right)}}{dt}\left( {b\left( {1 + R_{s} \left( { \frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right)} \right) \hfill \\ \end{gathered}$$

(41.a)

$$\begin{gathered} \left( {\frac{{ \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) + b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right) = \left( {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\frac{{q I_{01} }}{{n_{1} kT}}\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{n_{1} kT}}} \right) + \frac{1}{{R_{sh} }} + b\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) + \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt} \hfill \\ \left[ {1 + R_{s} \left( {\frac{{ - \left( {a + b\left( {V_{oc} } \right)} \right)\frac{d}{dt}\left( {R_{s} \left. {\frac{dI}{{dV}}} \right|_{{I = 0,V = V_{oc} }} } \right) - b\frac{{d\left( {V_{oc} } \right)}}{dt} }}{{1 + R_{s} b\frac{{d\left( {V_{oc} } \right)}}{dt}}}} \right)} \right] \hfill \\ \end{gathered}$$

(41.b)

In addition to the two parasitic resistances, the diode saturation current can be extracted by Eqs. (3) and (4.c), we can reach:

$${I}_{o1}=\frac{{I}_{sc}({R}_{sh}+{R}_{s})-{V}_{oc}-{R}_{sh}\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)+ {R}_{sh}(a+b\left({R}_{s}{I}_{sc})\right)\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}}{{R}_{sh}\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-\mathrm{exp}\left(\frac{\left(q{R}_{s}{I}_{sc}\right)}{{n}_{1}kT}\right)\right)}$$

(42)

The open-circuit voltage can be obtained from the experimental data. However, the ideality factor is still an unknown, that needs to be determined.

Since, ${R}_{sh}\gg {R}_{s}$, accordingly, $1+\frac{{R}_{s}}{{R}_{sh}}\approx 1,$ and ${I}_{sc}\gg \frac{{V}_{oc}}{{R}_{sh}}$. Furthermore, $\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)\gg \mathrm{exp}\left(\frac{{I}_{sc}{R}_{s}}{{n}_{1}kT}\right)$ is a valid assumption. Therefore, Eq. (42) can be approximated to:

$${I}_{o1}={I}_{sc}\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)-\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)+ (a+b\left({R}_{s}{I}_{sc})\right)\left(\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)$$

(43)

Substituting Eqs. (43) into (29), while considering $\frac{{V}_{0c}}{{R}_{sh}}$ tends to zero:

$${I}_{ph}={I}_{sc}\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)-\left((a+b\left({V}_{oc})\right)\frac{d\left({V}_{oc}\right)}{dt}\right)\mathrm{exp}\left(\frac{-q{V}_{oc}}{{n}_{1}kT}\right)+ (a+b\left({R}_{s}{I}_{sc})\right)\frac{d\left({I}_{sc}{R}_{s}\right)}{dt}+\frac{{V}_{oc}}{{R}_{sh}}+\left((a+b\left({V}_{oc})\right)*\frac{d}{dt}({V}_{oc})\right)$$

(44)

Equation (31.b) can be written as by substituting Eq. (43) in it:

$$\begin{aligned} I_{mp} \left( {1 + \frac{{R_{s} }}{{R_{sh} }}} \right) & = (I_{sc} \exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{{{\text{d}}t}}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) \\ \left( {\left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) \\ + \frac{{V_{oc} - V_{mp} }}{{R_{sh} }} + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{d\left( {V_{mp} + I_{mp} R_{s} } \right)}}{dt}} \right) \\ \end{aligned}$$

(45)

Assume: $\frac{{V}_{oc}-{V}_{mp}}{{R}_{sh}} \approx 0$ and $1+\frac{{R}_{s}}{{R}_{sh}}\approx 1$

$$\begin{aligned} I_{mp} & = I_{sc} \left( {1 - \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) \\ + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \\ + \left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt} - \left( {\left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\left( {\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right)} \right) \left( {\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) \\ + \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{d\left( {V_{mp} + I_{mp} R_{s} } \right)}}{dt}} \right) \\ \end{aligned}$$

(46)

Considering $\frac{1}{{R}_{sh}}\left(1-{R}_{s}\frac{{I}_{mp}}{{V}_{mp}}\right)\approx 0$, Eq. (8) can be written as,

$$\begin{aligned} I_{{m_{P} }} & = V_{{m_{P} }} \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right)\exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{n_{1} kT}}} \right)\left( {I_{sc} \exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right)} \right) \\ - \left( {\left( {a + b\left( {V_{oc} } \right)} \right)\frac{{d\left( {V_{oc} } \right)}}{dt}} \right)\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) + \left( {\left( {a + b\left( {R_{s} I_{sc} } \right)} \right)\frac{{d\left( {I_{sc} R_{s} } \right)}}{dt}\exp \left( {\frac{{ - qV_{oc} }}{{n_{1} kT}}} \right) } \right) \\ + \left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{d}{dt}\left[ {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right] + \left( {\frac{d}{dt}\left( {V_{mp} + I_{mp} R_{s} } \right)} \right)\left( {b\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right)} \right) \\ \end{aligned}$$

(47)

It can be observed that both Eqs. (46), and (47) are function in ${R}_{s}$, and ${n}_{1}$. However, the series resistance is associated with the differentiation operator. Consequently, we equalize both equations seeking for a first order differential equation (DE) in terms of ${R}_{s}$. Towards simplification, and as mentioned earlier, the boundary conditions points, at short circuit, open-circuit, and maximum power point, are treated as time independent constants, extracted from experimental measurements. Following that, the first order DE can be written as:

$$\begin{gathered} I_{sc} \left( {1 - \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)} \right) + \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)\frac{{dR_{s} }}{dt} - \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)\frac{{dR_{s} }}{dt} \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \hfill \\ - aI_{mp} \frac{{dR_{s} }}{dt} - b\left( {V_{mp} + R_{s} I_{mp} } \right)I_{mp} \frac{{dR_{s} }}{dt} - I_{sc} V_{{m_{P} }} \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \hfill \\ - \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)V_{{m_{P} }} \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right)\frac{{dR_{s} }}{dt} \hfill \\ - \frac{{I_{mp} }}{{V_{mp} }}\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{dR_{s} }}{dt} - bI_{mp} \left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \frac{{dR_{s} }}{dt} = 0. \hfill \\ \end{gathered}$$

(48)

Equation (48) can be treated as:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(49.a)

where:

$$\begin{gathered} f^{1} \left( {R_{s} } \right) = { }\left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right) - \left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right){ }\exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) \hfill \\ - aI_{mp} - b\left( {V_{mp} + R_{s} I_{mp} } \right)I_{mp} - { }\left( {aI_{sc} + b R_{s} I_{sc}^{2} } \right)V_{{m_{P} }} \hfill \\ \frac{q }{{n_{1} kT}}\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \exp \left( {\frac{{q(V_{mp} - V_{oc} + I_{mp} R_{s} )}}{{n_{1} kT}}} \right) - \frac{{I_{mp} }}{{V_{mp} }}\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right) - {\text{ b}}I_{mp} { }\left( {1 - R_{s} \frac{{I_{mp} }}{{V_{mp} }}} \right) \hfill \\ \end{gathered}$$

(49.b)

$${f}^{2}\left({R}_{s}\right)= {I}_{sc} \left(1-\mathrm{ exp}\left(\frac{q{(V}_{mp}-{V}_{oc}+ {I}_{mp}{R}_{s})}{{n}_{1}kT}\right)\right)-{I}_{sc} {V}_{{m}_{P}}\frac{q }{{n}_{1}kT}\left(1-{R}_{s} \frac{{I}_{mp}}{{V}_{mp}}\right)\mathrm{ exp}\left(\frac{q{(V}_{mp}-{V}_{oc}+ {I}_{mp}{R}_{s})}{{n}_{1}kT}\right)$$

(49.c)

Equation (49) can’t be solved analytically, however, an iterative numerical solution for both Eqs. (20) and (23) can converge with both ${R}_{s} (t)$, and ${n}_{1}(t)$. Referring to Eq. (48.b), with replacing the diode saturation current as given in (16), the shunt resistance can be calculated as:

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}} = \hfill \\ \left( {1 + R_{s} \left( t \right) \left( {\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)} \right)\left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} + R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}} \right)}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}} \right) \hfill \\ + \left( {a + b\left( {R_{s} \left( t \right)I_{sc} } \right)} \right)\frac{d}{dt}\left[ {R_{s} \left( t \right)\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(50)

Substituting (49.a) in (50) we get:

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}} \hfill \\ = \left( {1 + R_{s} \left( t \right)\left( {\frac{{ - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \hfill \\ \left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} - R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ + \left( {a + bR_{s} \left( t \right)I_{sc} } \right) \hfill \\ \left( {\left[ {R_{s} \left( t \right)\frac{{ \left( { - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} } \right)\left( { - R_{s} bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right) - \left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( { - \frac{1}{{R_{sho}^{2} }} \frac{{d\left( {R_{sho} } \right)}}{dt} + bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right]} \right. \hfill \\ \left. { + \left( {\frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ \end{gathered}$$

(51)

Again, Eq. (51) can’t be solved analytically, however, an iterative numerical solution can be extracted for ${R}_{sho} (t)$. Equation (51) can be treated as:

$${g}^{1}\left({R}_{sho}\right)\frac{d{R}_{sho}}{dt}+ {g}^{2}\left({R}_{sho}\right)=0$$

(52.a)

where:

$${g}^{1}\left({R}_{sho}\right)=(a+b{R}_{s}\left(t\right){I}_{sc})\left(\left[{R}_{s}\left(t\right)\frac{ \left(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}\right)\left(-\frac{1}{{R}_{sho}^{2}} \right)}{(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}{)}^{2}}\right]\right)$$

(52.b)

$$\begin{gathered} g^{2} \left( {R_{sho} } \right) = \left( {1 + R_{s} \left( t \right)\left( {\frac{{{ } - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \hfill \\ \left( {\frac{q }{{n_{1} \left( t \right)kT}}\left( {\frac{{I_{sc} \left( {R_{sho} + R_{s} \left( t \right)} \right) - V_{oc} - R_{sho} \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)}}{{R_{sho} \left( {\exp \left( {\frac{{qV_{oc} }}{{n_{1} \left( t \right)kT}}} \right) - \exp \left( {\frac{{\left( {qIsc Rs\left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right)} \right)}}} \right)\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} \left( t \right)kT}}} \right) + \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ - \frac{{{ }\frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}} + \left( {a + bR_{s} \left( t \right)I_{sc} } \right) \hfill \\ \left( {\left[ {R_{s} \left( t \right)\frac{{\left( { - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right)\left( { - R_{s} bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right) - \left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( {bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right]} \right. \hfill \\ \left. { + \left( {\frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ \end{gathered}$$

(52.c)

Solving the first order DE in (26) results with the estimated shunt resistance at the short-circuit point. Substituting back in (16) with the extracted functions from (20), (23), and (26) results:

$${I}_{o1 }(t)=\frac{{I}_{sc}({R}_{sho}(t))-{V}_{oc}+ {R}_{sh0}(t)(a-b\left({R}_{s}(t){I}_{sc}^{2}\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}}{{R}_{sho}(t)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}(t)kT}\right)-\mathrm{exp}\left(\frac{\left(q{R}_{s}(t){I}_{sc}\right)}{{n}_{1}(t)kT}\right)\right)}$$

(53)

Finally, the photo-generated current can be driven from Eq. (3) as:

$${I}_{ph}(t)={I}_{01}(t)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}\left(t\right)kT}\right)-1\right)+\frac{{V}_{oc}}{{R}_{sho}(t)}$$

(54)

3.3 Double-diode PV model with first, second, and third-order C-V fitting.

Scaling up the circuit model to a double-diode model, cf. Figure 1b directly impacted the analytical model procedure, adding two new unknowns, ${I}_{02}$, and ${n}_{2}$. Consequently, two new equations are introduced. Simple the summation of the diode ideality factors can be expressed as:

$$\sum_{i=1}^{n}{n}_{i}=n+1$$

(55)

where $n$ represents the diode model order, for example, $n=2$ for the double diode model. Additionally, the exact derivation procedure for the linear $C-V$ model in Sect. 3.1 can be applied up to Eq. (15.b) by applying the general $I-V$ equation in (1. b) instead of (1. a). Applying the same assumptions as in (16), we can reach the following:

$$I_{{sc}} = I_{{o1}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{n_{1} kT}}} \right)} \right) + I_{{o2}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{n_{2} kT}}} \right)} \right) + \left( {\left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right) - ~\left( {a + b\left( {R_{s} I_{{sc}} } \right)} \right)\frac{{d\left( {I_{{sc}} R_{s} } \right)}}{{dt}}$$

(56)

$$\begin{gathered} I_{{mp}} =\, I_{{o1}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{n_{1} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} } \right)}}{{n_{1} kT}}} \right)} \right) + I_{{02}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{n_{2} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} } \right)}}{{n_{2} kT}}} \right)} \right) \hfill \\ + \left( {\left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right) - \left( {\left( {a + b\left( {V_{{mp}} + R_{s} I_{{mp}} } \right)} \right)\frac{{d\left( {V_{{mp}} + ~I_{{mp}} Rs} \right)}}{{dt}}} \right) \hfill \\ \end{gathered}$$

(57)

Therefore, using above two equations, ${I}_{o1}$ can be obtained from Eq. (56) and ${I}_{o2}$ can be obtained from Eq. (57) as the following:

$$I_{{o1}} = I_{{sc}} \left( {\exp \left( { - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right)} \right) - I_{{o2}} \left( {\exp \left( {\frac{{ - qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right)} \right) - \frac{{\left( {a + b\left( {V_{{oc}} } \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right)~ - ~\left( {a + b\left( {R_{s} I_{{sc}} } \right)} \right)\frac{{d\left( {I_{{sc}} R_{s} } \right)}}{{dt}}~~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right)} \right)}}$$

(58)

$$I_{{o2}} = \;\frac{\begin{gathered} I_{{mp}} - ~I_{{o1}} \left( {\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{{mp}} + I_{{mp}} R_{s} )}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)} \right)\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} } \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right) \hfill \\ - \left( {\left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right) + \left( {\left( {a + b\left( {V_{{mp}} + R_{s} I_{{mp}} } \right)} \right)\frac{{d\left( {V_{{mp}} + ~I_{{mp}} Rs} \right)}}{{dt}}} \right)~ \hfill \\ \end{gathered} }{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{{mp}} + I_{{mp}} R_{s} )}}{{{\mathbf{n}}_{2} kT}}} \right)} \right)}}$$

(59)

Utilizing Eqs. (58), and (59), one can reach a general equation for the series resistance, given by:

$$\begin{gathered} \left( {\frac{{~b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}~}}{{1 + R_{s} b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}} + \left( {a + b\left( {\left( {V_{{oc}} } \right)} \right)} \right)\frac{d}{{dt}}\left( {R_{s} } \right)}}} \right) = \left( {1 + R_{s} ~\left( {\frac{{~ - ~b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}~}}{{1 + R_{s} b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}} + \left( {a + b\left( {\left( {V_{{oc}} } \right)} \right)} \right)\frac{d}{{dt}}\left( {R_{s} } \right)}}} \right)} \right) \hfill \\ \left( {\frac{{q~\left( {I_{{sc}} \left( {\exp \left( { - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right)} \right)} \right) - I_{{o2}} \left( {\exp \left( {\frac{{ - qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right) - \frac{{\left( {\left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right)~ - ~\left( {a + b\left( {R_{s} I_{{sc}} } \right)} \right)\frac{{d\left( {I_{{sc}} R_{s} } \right)}}{{dt}}~~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right)} \right)}}} \right)~}}{{n_{1} kT}}} \right. \hfill \\ \frac{{\exp \left( {\frac{{q\left( {V_{{oc}} } \right)}}{{n_{1} kT}}} \right) + q~\left( {\frac{{I_{{mp}} - ~I_{{o1}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} } \right)}}{{{\mathbf{n}}_{{\mathbf{1}}} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right) + \left( {\left( {a + b\left( {V_{{mp}} + R_{s} I_{{mp}} } \right)} \right)\frac{{d\left( {V_{{mp}} + ~I_{{mp}} Rs} \right)}}{{dt}}} \right)~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} } \right)}}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right)} \right)}}} \right)}}{{{\mathbf{n}}_{{\mathbf{2}}} kT}} \hfill \\ \left. {\exp \left( {\frac{{q\left( {V_{{oc}} } \right)}}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right) + b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}} \right) \hfill \\ + \left( {a + b\left( {V_{{oc}} } \right)} \right)\frac{d}{{dt}}\left[ {1 + R_{s} \left( {~\frac{{~ - ~b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}}~}}{{1 + R_{s} b\frac{{d\left( {V_{{oc}} } \right)}}{{dt}} + \left( {a + b\left( {\left( {V_{{oc}} } \right)} \right)} \right)\frac{d}{{dt}}\left( {R_{s} } \right)}}} \right)} \right] \hfill \\ \end{gathered}$$

(60)

It can be observed that Eq. (60) is a function in ${R}_{s}$, ${n}_{1}$, and ${n}_{2}$, but ${n}_{1}$ and ${n}_{2}$ can be estimated based on Eq. (55). However, the series resistance is associated with the differentiation operator. Consequently, we seek a first-order differential equation (D.E.) regarding ${R}_{s}$. Towards simplification, and as mentioned earlier, the boundary conditions points, at short circuit, open-circuit, and maximum power point, are treated as time-independent constants extracted from experimental measurements. Following that, the first-order D.E. can be written as:

$$\begin{gathered} \left( {\frac{q }{{n_{1} kT}}\left( {I_{sc} } \right) - I_{o2} \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)\left( {\frac{{q\left( {V_{oc} } \right)}}{{n_{1} kT}}} \right)} \right) - \left( {a + b\left( {R_{s} I_{sc}^{2} } \right)} \right)\frac{{d\left( {R_{s} } \right)}}{dt}} \right) \hfill \\ + \frac{q }{{n_{2} kT}}\left( {\frac{{I_{mp} \exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right) - I_{o1} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{1} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right) + \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)I_{mp} \exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)\frac{{d\left( {R_{s} } \right)}}{dt}} \right) }}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{2} kT}}} \right)} \right)}}} \right) = 0 \hfill \\ \end{gathered}$$

(61)

Equation (61) can be treated as:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(62.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{\left(\mathrm{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right)\right)}\right)$$

(62.b)

$${f}^{2}\left({R}_{s}\right)=\frac{q }{{n}_{1}kT}(\left({I}_{sc}\right)-{I}_{o2}\left(\mathrm{exp}\left(\frac{-q{V}_{oc}}{{{\varvec{n}}}_{2}kT}\right)\mathrm{exp}\left(\frac{q\left({V}_{oc}\right)}{{n}_{1}kT}\right)\right)+\frac{q }{{n}_{2}kT}\left(\frac{{I}_{mp}\mathrm{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)- {I}_{o1}\left((\mathrm{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{1}\mathit{kT}}\right)-\mathrm{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{1}kT}\right)\right)\mathrm{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right) }{(\left(\mathrm{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathrm{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right)\right)}\right)$$

(62.c)

Extracting the series resistance numerically, and solving (44) and (45) simultaneously results:

$$I_{{o1}} \left( t \right) = \frac{\begin{gathered} ~I_{{mp}} \left( {\exp \left( { - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{{mp}} + R_{s} \left( t \right)I_{{mp}} } \right)} \right)I_{{mp}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}~} \right) - \left( {\left( {\exp \left( {\frac{{qV_{{oc}} }}{{\user2{n}_{2} kT}}} \right)} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} \left( t \right)} \right)}}{{\user2{n}_{2} kT}}} \right)} \right) \hfill \\ \left( {\left( {I_{{sc}} \left( {\exp \left( { - \frac{{qV_{{oc}} }}{{\user2{n}_{1} kT}}} \right)} \right)} \right) + ~\frac{{~\left( {a + b\left( {R_{s} \left( t \right)I_{{sc}}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}~~~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{\user2{n}_{1} kT}}} \right)} \right)}}} \right) \hfill \\ \end{gathered} }{{\left( {\exp \left( {\frac{{ - qV_{{oc}} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{{oc}} }}{{\user2{n}_{1} kT}}} \right)} \right) - \exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} \left( t \right)} \right)}}{{\user2{n}_{1} kT}}} \right)} \right){\text{~}} + {\text{~}}\left( {\exp \left( {\frac{{q\left( {V_{{mp}} + I_{{mp}} R_{s} \left( t \right)} \right) - V_{{oc}} }}{{\user2{n}_{2} kT}}} \right)} \right)}}$$

(63.a)

$$I_{o2} \left( t \right) = \frac{{ - \left( {\left( {a + b\left( {V_{mp} + R_{s} \left( t \right)I_{mp} } \right)} \right)I_{mp} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right) + I_{mp } - I_{sc} + I_{sc} {\text{e}}\left( {{\text{xp}}\left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right))}}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} } \right)}}{{{\mathbf{n}}_{1} kT}}} \right)}}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right)} \right) + \left( {\left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right){\text{exp}}\left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right))}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}}$$

(63.b)

Again, following the same procedure as in Sect.  3.1, a DE for the shunt resistance can be determined by:

$${g}^{1}\left({R}_{sho}\right)\frac{d{R}_{sho}}{dt}+ {g}^{2}\left({R}_{sho}\right)=0$$

(64.a)

where:

$${g}^{1}\left({R}_{sho}\right)=(a+b{R}_{s}\left(t\right){I}_{sc})\left(\left[{R}_{s}\left(t\right)\frac{ \left(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}-(a+b\left(\left({I}_{sc}{R}_{s}(t)\right)\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}\right)\left(-\frac{1}{{R}_{sho}^{2}} \right)}{(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}{-(a+b\left(\left({I}_{sc}{R}_{s}(t)\right)\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)})}^{2}}\right]\right)$$

(64.b)

$$\begin{aligned} g^{2} \left( {R_{sho} } \right) & = \left( {1 + R_{s} \left( t \right)\left( {\frac{{{ } - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - (a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \\ \left( {\frac{{q I_{o1} \left( t \right)}}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} kT}}} \right) + + \frac{{q I_{o2} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{2} kT}}} \right) + \frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \\ - \frac{{{ }\frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}} + \left( {a + bR_{s} \left( t \right)I_{sc} } \right) \\ \left( {\left[ {\begin{array}{*{20}c} {R_{s} \left( t \right)\frac{{\left( { - \frac{1}{{R_{sho} }} + bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right)\left( { - R_{s} bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right) \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{sc} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \\ { - R_{s} \left( t \right)\frac{{{ }\left( {1 - R_{s} \left( t \right)bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( {bI_{sc} \frac{d}{dt}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right)}}{{\left( {1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}})^{2} }}} \\ { + \left( {\frac{{{ }\frac{1}{{R_{sho} }} - bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }}}{{1 - R_{s} bI_{sc} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \\ \end{array} } \right]} \right) \\ \end{aligned}$$

(64.c)

Finally, the photo-generated current can be driven as:

$${I}_{ph}\left(t\right)={I}_{01}\left(t\right)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+{I}_{02}\left(t\right)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{2}kT}\right)-1\right)+\frac{{V}_{oc}}{{R}_{sho}(t)}$$

(65)

Following the same procedure as from Eq. (56) to (65), a similar analytical solution for the double-diode second order C-V fitting can be obtained. The DE representing the series resistance, as in (48), can be driven as:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(66.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)+c({I}_{sc}^{3}{R}_{s}^{2})\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)+c{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{2}\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right))}\right)$$

(66.b)

$${f}^{2}\left({R}_{s}\right)=\frac{q }{{n}_{1}kT}(\left({I}_{sc}\right)-{I}_{o2}(\mathit{exp}\left(\frac{-q{V}_{oc}}{{{\varvec{n}}}_{2}kT}\right)\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{n}_{1}kT}\right)))+\frac{q }{{n}_{2}kT}\left(\frac{{I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)- {I}_{o1}((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{1}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{1}kT}\right))\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right) }{((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right))}\right)$$

(66.c)

Accordingly, the dark saturation current can be extracted as:

$$I_{o1} \left( t \right) = \frac{\begin{gathered} \frac{{ I_{mp} \left( {\exp \left( { - \frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} \left( t \right)I_{mp} } \right) + c\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)^{2} } \right)I_{mp} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} } \right){ } }}{{\left( {\left( {{ }\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right))}}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right){ } + { }\left( {\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right)}} - \hfill \\ \left( {\left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right)} \right)\left( {\left( {I_{sc} \left( {\exp \left( { - \frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right) + \frac{{ \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right) + c\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right)} \right)}}} \right)} \right){ } \hfill \\ \end{gathered} }{{\left( {{ }\left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right) + { }\left( {\exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right)}}$$

(67.a)

$$I_{o2} \left( t \right) = \frac{{\frac{{\left( {\left( {a + b\left( {V_{mp} + R_{s} \left( t \right)I_{mp} } \right) + c\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)^{2} } \right)I_{mp} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right) + I_{mp } - I_{sc} + I_{sc} \left( {{\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{2} kT}}} \right) - \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right){\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}} + }}{{\frac{{\left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right) + c\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} + c\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} } \right)}}{{{\mathbf{n}}_{1} kT}}} \right)}}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right){\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}}}}$$

(67.b)

The DE in terms of ${R}_{sho} (t)$ is obtained as:

$${g}^{1}\left({R}_{sho}\right)\frac{d{R}_{sho}}{dt}+ {g}^{2}\left({R}_{sho}\right)=0$$

(68.a)

where:

$${g}^{1}\left({R}_{sho}\right)=(a+b{R}_{s}\left(t\right){I}_{sc}+c{\left({I}_{sc}{R}_{s}(t)\right)}^{2})\left(\left[{R}_{s}\left(t\right)\frac{ \left(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}-2\mathrm{c}{R}_{s}{I}_{sc}^{2}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}-(a+b\left(\left({I}_{sc}{R}_{s}(t)\right)+c{\left({I}_{sc}{R}_{s}(t)\right)}^{2}\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}\right)\left(-\frac{1}{{R}_{sho}^{2}} \right)}{(1-{R}_{s}b{I}_{sc}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}-2{R}_{s}^{2}(t)c{I}_{sc}^{2}\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)}{-(a+b\left(\left({I}_{sc}{R}_{s}(t)\right)+c{\left({I}_{sc}{R}_{s}(t)\right)}^{2}\right)\frac{{f}^{2}\left({R}_{s}\left(t\right)\right)}{{f}^{1}\left({R}_{s}\left(t\right)\right)})}^{2}}\right]\right)$$

(68.b)

$$\begin{gathered} g^{2} \left( {R_{{sho}} } \right) = ~\left( {1 + R_{s} \left( t \right)\left( {\frac{{ - ~\frac{1}{{R_{{sho}} }} + bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} + 2cR_{s} I_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}{{1 - R_{s} \left( t \right)bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {I_{{sc}} R_{s} } \right) + c\left( {R_{s} I_{{sc}} } \right)^{2} } \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)} \right) \hfill \\ \left( {\left( {\frac{{q~I_{{o1}} \left( t \right)}}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{{sc}} R_{s} \left( t \right)} \right)}}{{n_{1} kT}}} \right) + + \frac{{q~I_{{o2}} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}\exp \left( {\frac{{q\left( {I_{{sc}} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{2} kT}}} \right) + \frac{1}{{R_{{sho}} }} - bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) - 2cR_{s} I_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ - \frac{{{\text{~}}\frac{1}{{R_{{sho}} }} - bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2cR_{s} I_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{\text{~}}}}{{1 - R_{s} \left( t \right)bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{{sc}} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}~ \hfill \\ + \left( {a + bR_{s} \left( t \right)I_{{sc}} + c\left( {I_{{sc}} R_{s} \left( t \right)} \right)^{2} } \right) \hfill \\ \left( {\left[ {R_{s} \left( t \right)\frac{{{\text{~}}\left( { - \frac{1}{{R_{{sho}} }} + bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} + 2cR_{s} I_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}~} \right)\left( { - R_{s} bI_{{sc}} ~\frac{d}{{dt}}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - bI_{{sc}} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} ~\frac{d}{{dt}}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - 4R_{s} cI_{{sc}}^{2} \left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} - \left( {a + b\left( {\left( {I_{{sc}} R_{s} \left( t \right)} \right) + c\left( {I_{{sc}} R_{s} \left( t \right)} \right)^{2} } \right)} \right)~\frac{d}{{dt}}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right] - \left( {bI_{{sc}} - 2cR_{s} I_{{sc}}^{2} } \right)\left( {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} } \right)}}{{\left( {1 - R_{s} bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{{sc}} R_{s} \left( t \right)} \right)} \right) + c\left( {I_{{sc}} R_{s} \left( t \right)} \right)^{2} } \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right.} \right. \hfill \\ \left. { - R_{s} \left( t \right)\frac{{\left( {\left( {1 - R_{s} bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {I_{{sc}} R_{s} } \right) + c\left( {R_{s} I_{{sc}} } \right)^{2} } \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)\left( {bI_{{sc}} \frac{d}{{dt}}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} + 2cR_{s} I_{{sc}}^{2} \frac{d}{{dt}}\left[ {\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right]} \right]} \right)}}{{\left( {1 - R_{s} bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{{sc}} R_{s} \left( t \right)} \right)} \right) + c\left( {I_{{sc}} R_{s} \left( t \right)} \right)^{2} } \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right)^{2} }}} \right] \hfill \\ \left. {\left( {\frac{{{\text{~}}\frac{1}{{R_{{sho}} }} - bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2cR_{s} I_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{\text{~}}}}{{1 - R_{s} bI_{{sc}} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - 2R_{s}^{2} \left( t \right)cI_{{sc}}^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {\left( {I_{{sc}} R_{s} \left( t \right)} \right)} \right)} \right) + c\left( {I_{{sc}} R_{s} \left( t \right)} \right)^{2} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}}}} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}} \right) \hfill \\ \end{gathered}$$

(68.c)

Finally, the photo-generated current can be driven with the same general form as in Eq. (65). Finally, a typical model is found to the double diode model with third order C-V fitting, as follows:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(69.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)+c\left({I}_{sc}^{3}{R}_{s}^{2}\right)+d({I}_{sc}^{4}{R}_{s}^{3}\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)+c{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{2}+d{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{3}\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right))}\right)$$

(69.b)

$$f^{2} \left( {R_{s} } \right) = \frac{{q~}}{{\user2{n}_{1} kT}}(\left( {I_{{sc}} } \right) - I_{{o2}} (\exp \left( {\frac{{ - qV_{{oc}} }}{{\user2{n}_{2} kT}}} \right)\exp \left( {\frac{{q\left( {V_{{oc}} } \right)}}{{n_{1} kT}}} \right))) + \frac{{q~}}{{n_{2} kT}}\left( {\frac{{I_{{mp}} \exp \left( {\frac{{q\left( {V_{{oc}} } \right)}}{{n_{2} kT}}} \right) - ~I_{{o1}} ((\exp \left( {\frac{{qV_{{oc}} }}{{n_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{{mp}} + I_{{mp}} R_{s} )}}{{n_{1} kT}}} \right))\exp \left( {\frac{{q\left( {V_{{oc}} } \right)}}{{\user2{n}_{2} kT}}} \right)~}}{{((\exp \left( {\frac{{qV_{{oc}} }}{{\user2{n}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{{mp}} + I_{{mp}} R_{s} )}}{{n_{2} kT}}} \right))}}} \right)$$

(69.c)

$$\begin{gathered} I_{o1} \left( t \right) \hfill \\ = \frac{{I_{mp} \left( {\exp \left( { - \frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\left( {a + b\left( {V_{mp} + R_{s} \left( t \right)I_{mp} } \right) + c\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)^{2} + d\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)^{3} } \right)I_{mp} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} } \right)}}{{\left( {\left( {{ }\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right))\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right))}}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right){ } + { }(\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right)}} \hfill \\ - \frac{{\left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right)\left( {\left( {I_{sc} \left( {\exp \left( { - \frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right) + \frac{{ \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right) + c(I_{sc}^{3} R_{s}^{2} \left( t \right) + d(I_{sc}^{4} R_{s}^{3} \left( t \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} }}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right)} \right)}}} \right)} \right)}}{{\left( {\left( {\left( {{ }\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right){ } + { }\left( {\exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right)} \right)}} \hfill \\ \end{gathered}$$

(70.a)

$$\begin{gathered} I_{o2} \left( t \right) = \frac{{ - \left( {\left( {a + b\left( {V_{mp} + R_{s} \left( t \right)I_{mp} } \right) + c\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)^{2} + d\left( {V_{mp} + I_{mp} R_{s} } \right)^{3} } \right)I_{mp} \frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{ }} \right) + I_{mp } - I_{sc} + I_{sc} \left( {{\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right){\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}} \hfill \\ + \frac{{\left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} } \right) + c\left( {I_{sc}^{3} R_{s}^{2} \left( t \right) + d\left( {I_{sc}^{4} R_{s}^{3} \left( t \right)} \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}} - \left( {a + b\left( {R_{s} \left( t \right)I_{sc}^{2} + c\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)} \right) + d\left( {I_{sc}^{4} R_{s}^{3} \left( t \right)} \right)} \right)\frac{{f^{2} \left( {R_{s} \left( t \right)} \right)}}{{f^{1} \left( {R_{s} \left( t \right)} \right)}}{\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right) - V_{oc} } \right)}}{{{\mathbf{n}}_{1} kT}}} \right)}}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) - \left( {\exp \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {\frac{{ - qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right){\text{exp}}\left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)}}. \hfill \\ \end{gathered}$$

(70.b)

The shunt resistance can be calculated as

$$\begin{gathered} \frac{{ \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 2cR_{s} \left( t \right)I_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 3d\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} }}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 2R_{s}^{2} \left( t \right)cI_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 3R_{s}^{3} \left( t \right)dI_{sc}^{3} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {I_{sc} R_{s} } \right) + c\left( {R_{s} I_{sc} } \right)^{2} + d\left( {I_{sc} R_{s} } \right)^{3} } \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}} \hfill \\ = \left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} - 2cR_{s} \left( t \right)I_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} - 3d\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 2R_{s}^{2} \left( t \right)cI_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 3R_{s}^{3} \left( t \right)dI_{sc}^{3} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {I_{sc} R_{s} } \right) + c\left( {R_{s} I_{sc} } \right)^{2} + d\left( {I_{sc} R_{s} } \right)^{3} } \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\frac{{q I_{01} }}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} (t} \right)}}{{n_{1} kT}}} \right) + \frac{{q I_{o2} }}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} (t} \right)}}{{{\mathbf{n}}_{{\mathbf{2}}} kT}}} \right) + \frac{1}{{R_{sho} }} + b\frac{{d\left( {I_{sc} R_{s} (t} \right)}}{dt} + 2c\left( {(I_{sc} R_{s} } \right)\frac{{d\left( {I_{sc} R_{s} (t} \right)}}{dt} + 3d\left( {I_{sc} R_{s} } \right)^{2} \frac{{d\left( {I_{sc} R_{s} (t} \right)}}{dt}} \right) \hfill \\ + \left( {a + b\left( {R_{s} I_{sc} ) + c\left( {I_{sc} R_{s} } \right)^{2} + d\left( {I_{sc} R_{s} } \right)^{3} } \right)} \right)\frac{d}{dt}\left[ {1 + R_{s} \frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} - 2cR_{s} \left( t \right)I_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} - 3d\left( {I_{sc}^{3} R_{s}^{2} \left( t \right)} \right)^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 2R_{s}^{2} \left( t \right)cI_{sc}^{2} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + 3R_{s}^{3} \left( t \right)dI_{sc}^{3} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {I_{sc} R_{s} } \right) + c\left( {R_{s} I_{sc} } \right)^{2} + d\left( {I_{sc} R_{s} } \right)^{3} } \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(71)

3.4 Triple-diode PV model with first, second, and third-order C-V fitting.

Finally, the triple-diode model, cf. Figure 1c and Eq. (1.c) are presented in this section. The updated analytical model is performed by adding two new unknowns, ${I}_{03}$, and ${n}_{3}$. The ideality factor summation in Eq. (41) can still be valid, where the ideality factors are assumed accordingly. The linear C-V fitting showed:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(72.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{\left(\mathit{exp}\left(\frac{q{V}_{oc}}{{{\varvec{n}}}_{2}kT}\right)-exp\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right)\right)}\right)$$

(72.b)

$$\begin{gathered} f^{2} \left( {R_{s} } \right) = \frac{q }{{n_{1} kT}}(\left( {I_{sc} } \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right) - I_{o3} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right)} \right) + \frac{q }{{n_{2} kT}} \hfill \\ \left( {\frac{{I_{mp} \exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right) - I_{o1} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{1} kT}}} \right)} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right) - I_{o3} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{{\mathbf{n}}_{3} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) }}{{\left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right)} \right)}}} \right) \hfill \\ + \frac{q }{{n_{3} kT}}\left( {I_{ph} - I_{o1} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)} \right) \hfill \\ \end{gathered}$$

(72.c)

$$I_{{o1}} = I_{{sc}} \left( {\exp - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right) - I_{{o2}} \left( {~\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)\left( {\exp \left( { - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right)~ - I_{{o3}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{3} kT}}} \right)} \right)\left( {\exp \left( { - \frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) + \left( {\frac{{~~\left( {a + b\left( {R_{s} I_{{sc}} } \right)} \right)\frac{{d\left( {I_{{sc}} R_{s} } \right)}}{{dt}}~~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{kT}}} \right)} \right)}}} \right)$$

(73.a)

$$I_{o2} = \;\frac{{I_{mp} - I_{o1} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{{\mathbf{n}}_{1} kT}}} \right)} \right)} \right) - I_{o3} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{{\mathbf{n}}_{3} kT}}} \right)} \right)} \right) + \left( {\left( {a + b\left( {V_{mp} + R_{s} I_{mp} } \right)} \right)\frac{{d\left( {V_{mp} + I_{mp} Rs} \right)}}{{{\text{d}}t}}} \right){ }}}{{\left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\mathbf{n}}_{2} kT}}} \right)} \right)} \right)}}$$

(73.b)

$$I_{{o3}} = \frac{{I_{{ph}} - I_{{o1}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) - I_{{o2}} \left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)~~}}{{\left( {\exp \left( {\frac{{qV_{{oc}} }}{{{\mathbf{n}}_{3} kT}}} \right)} \right)}}$$

(73.c)

$$\begin{gathered} \frac{{{ }\frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}{ }}}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}} \hfill \\ = \left( {1 + R_{s} \left( {\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}{ }}}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right)} \right) \hfill \\ \left( {\left( {\frac{{q I_{o1} \left( t \right)}}{{n_{1} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{n_{1} kT}}} \right) + \frac{{q I_{o2} \left( t \right)}}{{{\mathbf{n}}_{2} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{2} kT}}} \right) + \frac{{q I_{o3} \left( t \right)}}{{{\mathbf{n}}_{3} kT}}\exp \left( {\frac{{q\left( {I_{sc} R_{s} \left( t \right)} \right)}}{{{\mathbf{n}}_{3} kT}}} \right)} \right) + \frac{1}{{R_{sho} }} + bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}} \right) \hfill \\ + \left( {a + b\left( {R_{s} \left( t \right)I_{sc} } \right)} \right)\frac{d}{dt}\left[ {R_{s} \left( t \right)\frac{{ - \frac{1}{{R_{sho} }} - bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}{ }}}{{1 + R_{s} \left( t \right)bI_{sc} \frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt} + \left( {a + b\left( {\left( {I_{sc} R_{s} \left( t \right)} \right)} \right)} \right)\frac{{d\left( {R_{s} \left( t \right)} \right)}}{dt}}}} \right] \hfill \\ \end{gathered}$$

(74)

then, the photo-generated current can be driven as:

$${I}_{ph}\left(t\right)={I}_{01}\left(t\right)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{1}kT}\right)-1\right)+{I}_{02}\left(t\right)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{2}kT}\right)-1\right)+{I}_{03}\left(t\right)\left(\mathrm{exp}\left(\frac{q{V}_{oc}}{{n}_{3}kT}\right)-1\right)+\frac{{V}_{oc}}{{R}_{sho}(t)}$$

(75)

Similar outputs were reached for the triple-diode second, and third order C-V fitting, respectively, summarized as:

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(76.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)+c({I}_{sc}^{3}{R}_{s}^{2})\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)+c{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{2}\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{\left((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right)\right)}\right)$$

(76.b)

$$\begin{gathered} f^{2} \left( {R_{s} } \right) = \frac{q }{{n_{1} kT}}\left( {\left( {I_{sc} } \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right) - I_{o3} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right)} \right)} \right) + \frac{q }{{n_{2} kT}} \hfill \\ \left( { \frac{{I_{mp} \exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right) - I_{o1} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{1} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right) - I_{o3} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\mathbf{n}}_{3} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) }}{{\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q\left( {V_{mp} + I_{mp} R_{s} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right)}}} \right) \hfill \\ + \frac{q }{{n_{3} kT}}\left( {I_{ph} - I_{o1} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)} \right) \hfill \\ \end{gathered}$$

(76.c)

$${f}^{1}\left({R}_{s}\right)\frac{d{R}_{s}}{dt}+ {f}^{2}\left({R}_{s}\right)=0$$

(77.a)

where:

$${f}^{1}\left({R}_{s}\right)=-\frac{q }{{n}_{1}kT}\left(a+b\left({R}_{s}{I}_{sc}^{2}\right)+c\left({I}_{sc}^{3}{R}_{s}^{2}\right)+d({I}_{sc}^{4}{R}_{s}^{3}\right)+\frac{q }{{n}_{2}kT}\left(\frac{\left(a+b\left({V}_{mp}+{R}_{s}{I}_{mp}\right)+c{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{2}+d{\left({V}_{mp}+{I}_{mp}{R}_{s}\right)}^{3}\right){I}_{mp}\mathit{exp}\left(\frac{q\left({V}_{oc}\right)}{{{\varvec{n}}}_{2}kT}\right)\frac{d\left({R}_{s}\right)}{dt} }{((\mathit{exp}\left(\frac{q{V}_{\mathit{oc}}}{{{\varvec{n}}}_{2}\mathit{kT}}\right)-\mathit{exp}\left(\frac{q{(V}_{mp}+{I}_{mp}{R}_{s})}{{{\varvec{n}}}_{2}kT}\right))}\right)$$

(77.b)

$$\begin{gathered} f^{2} \left( {R_{s} } \right) = \frac{q }{{n_{1} kT}}\left( {I_{sc} } \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right)} \right) - I_{o3} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right)} \right) + \frac{q }{{n_{2} kT}} \hfill \\ \left( {\frac{{I_{mp} \exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right) - I_{o1} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{1} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{1} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\varvec{n}}_{2} kT}}} \right)} \right) - I_{o3} \left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{3} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\mathbf{n}}_{3} kT}}} \right)} \right)\exp \left( {\frac{{q\left( {V_{oc} } \right)}}{{{\mathbf{n}}_{2} kT}}} \right)} \right) }}{{\left( {\left( {\exp \left( {\frac{{qV_{oc} }}{{{\varvec{n}}_{2} kT}}} \right) - \exp \left( {\frac{{q(V_{mp} + I_{mp} R_{s} )}}{{{\varvec{n}}_{2} kT}}} \right)} \right)} \right)}}} \right) \hfill \\ \frac{q }{{n_{3} kT}}\left( {I_{ph} - I_{o1} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{1} kT}}} \right)} \right) - I_{o2} \left( {\exp \left( {\frac{{qV_{oc} }}{{{\mathbf{n}}_{2} kT}}} \right)} \right)} \right) \hfill \\ \end{gathered}$$

(77.c)

Substituting Eq. (76) or (77) in Eq. (70) to (74) results in the final closed forms for the second and third-order $C-V$ fitting in the triple-diode model. The nine analytical solutions are attached to this paper in supplementary material S1. The nine derived analytical models seed the equilibrium optimizer (E.O.) and the measured $I-V$ data, seeking optimum parameters extraction with minimum RMS error. The E.O. algorithm along with all previously mentioned numerically solved differential equations are scripted using MATLAB. This is demonstrated in the next section.

4 Results and discussion

The first phase in extracting the results is characterizing the fabricated CsPbCl₃ PSC using both $I-V$ and $C-V$ characteristics, cf. Figure 6. Herein, we intended to fabricate five different batches of the PSCs with slight variations in the mesoporous TiO₂ layer thickness. The variable electron transport layer thickness is implemented to show variation in the resistive path seen by the carriers, which impacted the overall $I-V$ characteristics, as observed in Fig. 6a. Such variation in the $I-V$ m characteristics facilitates the capability to validate the robustness of the proposed methodology to extract solar cell circuit parameters. Alternatively, and with the aid of the setup presented in Fig. 3c, the $C-V$ characteristic curves for the five batches are demonstrated in Fig. 6b. The primary purpose of measuring the $C-V$ characteristic curves is to obtain the fitting coefficients, as described in Eqs. (2.a) to (2.c) and shown in Fig. 1d. As the output from this stage, the main experimental parameters are extracted from the $I-V$ characteristic curves and the fitting coefficients from the $C-V$ characteristic curves, as listed in Table 1. The hysteresis index was calculated as defined in Chen et al. (2020).The recorded power conversion efficiency ($PCE$) for the five batches showed, on average, 16.35% ± 0.32%, which nearly matched the best CsPbCl₃ PSC reported in the literature (Wang et al. 2017).

Fig. 6

a $\mathrm{I}-\mathrm{V}$, and b $\mathrm{C}-\mathrm{V}$ characteristic curve for five different CsPbCl₃ PSC. The characterization variation is due to variable electron transport layer thicknesses as follows: Sample #1 with 1 μm ± 50 nm, Sample #2 with 11 μm ± 50 nm, Sample #3 with 15 μm ± 50 nm, Sample #4 with 5 μm ± 50 nm, and Sample #5 with 7 μm ± 50 nm

Table 1 extracted experimental parameters for five different CsPbCl₃ PSC

Applying the procedure in the flowchart in Fig. 2, the extracted experimental parameters listed in Table 1 are inputted in the nine analytical models in Sect. 3. The main target of this stage is to reach an analytical value for the circuit parameters shown in the diode models in Fig. 1a–c. These analytical values are listed in Table 2 for single, double, and triple diode models while applying linear, second-order, and third-order fitting for the $C-V$ characteristic curves. The values presented in Table 2 correspond to sample #1, where similar data for the other four samples are attached in Supplementary Material S2. Although the data listed in Table 2 are the outcome of analytical models for the dynamic characteristic of a PSC, these parameters still need to be optimized for minimum RMS error against the measured $I-V$ data. The reason beyond the limited capabilities of the analytical models to catch exact, or in other words optimized, circuit’s parameter values is attributed to the nature of the analytical procedure. In the analytical models, boundary conditions at the short-circuit and open-circuit points are utilized to express an analytical form for the shunt and series resistance, respectively. Using single-point conditions can be analytically recommended for reaching a closed form for parasitic resistances. However, this can deviate from agonist experimental data. For example, the data reported in this study reflect five different batches of samples with nearly the same open-circuit voltage and short-circuit current but with variation in the parasitic resistance, as observed in Fig. 6a. This can be observed in Fig. 7, where the analytical outputs are sketched agapist the experimental data for sample #1. Results for the four other samples are attached in Supplementary Material S2. Generally, across the five samples, a relatively high RMS error is found while referring to the experimental measurements, see Fig. 8. The RMSE indicates the $I-V$ model efficiency to accurately predict and match the experimental measurements of the cell. Alternatively, utilizing more complex models, i.e., a triple-diode model with third-order $C-V$ fitting, reached minimum RMS error. This glows up the expected trade-off between complexity and accuracy in parameter extraction, as highlighted in the following paragraphs.

Table 2 extracted parameters from the analytical models for CsPbCl₃ PSC sample #1

Fig. 7

$\mathrm{I}-\mathrm{V}$ characteristic curve for CsPbCl₃ PSC sample #1 experimentally, against analytical results for a Single-diode model (SDM), b Double-diode model (DDM), and c Triple-diode model (TDM)

Fig. 8

Root-mean square error (RMSE) calculated against the experimental $\mathrm{I}-\mathrm{V}$ characteristic curve for CsPbCl₃ PSC, for the five sample #1 for the different nine models using both analytical and optimized parameters in each

As stated above, the analytical results cannot be treated as optimized for the solar cell’s parameter extraction procedure. However, it can still be used as a seed input to the equilibrium optimizer, seeking minimum RMS error concerning experimental data. The optimized parameters for sample #1 are listed in Table 3, showing the RMS error per model. The optimized $I-V$ curves are shown in Fig. 9, again for sample #1, while the remaining four samples are listed in Supplementary Material S3. Observing Fig. 8 can validate the effectiveness of the equilibrium optimizer to narrow down the RMS error, targeting optimum parameters extraction. Generally, the optimized parameters showed enhanced behavior to analytical results in predicting the experimental results. Another observation is related to the triple-diode model’s capability to describe best the experimental data concerning the single and the double-diode models. In this context, it is watchable to investigate the trade-off between parameter extraction model accuracy and complexity. The complexity is represented here as the number of iterations the equilibrium optimizer needs to converge to the optimum values, cf. Fig. 10.

Table 3 optimized parameters from the analytical models for CsPbCl₃ PSC sample #1

Fig. 9

$\mathrm{I}-\mathrm{V}$ characteristic curve for CsPbCl₃ PSC sample #1 experimentally, against optimized results for a Single-diode model (SDM), b Double-diode model (DDM), and c Triple-diode model (TDM)

Fig. 10

Number of iterations needed to optimize the circuit parameter using equilibrium optimizer, against the experimental $\mathrm{I}-\mathrm{V}$ characteristic curve for CsPbCl₃ PSC, for sample #1, for the different nine models using both analytical and randomly selected initial parameters in each

The interesting trade-off demonstrated in Figs. 8 and 10 can be utilized to find a compensation point per batch to benefit the maximum possible accuracy with the minimum possible iterations. Another impotent perspective here is the volubility of the driven analytical models. On the one hand, this is considering the first analytical approach for the dynamic response for the PSC, which can be applied to any PSC. On the other hand, integrating the analytical models in estimating the seeded values to the equilibrium optimizer contributed to the system’s simplicity. In Fig. 10, we evaluate the same optimizer under a different set of initial values, using the analytically driven values and another randomly selected initial guess. The results in Fig. 10 illustrate the impact of the analytical model in initializing the values needed for optimization. An overall reduction of around 30% is recorded in the number of iterations the optimizer needs to converge while utilizing the analytical values as initial values.

5 Conclusion

In conclusion, this study presents experimentally verified analytical models for the dynamic response of perovskite solar cells, utilizing measured $I-V$ and $C-V$ characteristics. These models provide valuable insights into the performance and stability of perovskite solar cells, aiding in designing and optimizing future photovoltaic devices. To validate the accuracy of the proposed models, extensive experimental measurements are conducted on a fabricated CsPbCl3 perovskite solar cell. The dynamic response of the cell is compared with the predictions of the analytical models. Equilibrium optimizers optimize circuit elements in the single, double, and triple-diode models for minimum mismatching. The results demonstrate a high degree of agreement, confirming the effectiveness of the proposed models in capturing the dynamic behavior of perovskite solar cells, with the minimum recorded RMSE in PSC of 0.00103. Various experimental parameters affecting the PSC, including but not limited; the morphological, mechanical, or physiochemical properties of the segmented layers used in fabrication the solar cell can influence the dynamic behavior of the cell. We consider the impact of these parameter on the parasitic capacitance and the dynamic circuit model as a part of the future work.