1 Introduction

Water is the most crucial commodity for life. Therefore, the consumption of water by humans should be safe, easily accessible, adequate, and free from any kind of contamination (Madhav et al. 2020). Pollutants in water bodies pose a severe threat to human health as well as aquatic ecosystem. Thus, the development of simple and accurate devices for the detection of water pollutants is necessary to have a healthy society. Optical sensors, via which the polluted water samples can be distinguished from the normal water samples, have their uniqueness in water quality assessment due to their compact size, high sensitivity, and immunity to stray fields. One of the major optical sensing mechanisms is surface plasmon resonance (SPR). Such technique relies on the coupling between surface plasmon modes (SPMs) constructed at the metal/dielectric interfaces and the guided core modes (Younis et al. 2017, 2018). At resonance, the effective indices of the SPM and core guided mode are equal. In this situation, phase matching occurs where maximum power transfer takes place from the guided core mode to the SPM. A shift in the resonance wavelength is detected when the analyte refractive index is changed, and thus the sensitivity can be measured. Many forms of optical devices including optical absorbers (Wang et al. 2020b), sensors (Hameed et al. 2017; Abdelghaffar et al. 2022), filters (Gamal et al. 2021a), polarization rotators (Hameed et al. 2010, 2013b; Hameed and Obayya 2011a, b), polarization converters (Hameed et al. 2011a, 2013a), and optical instruments (Hameed et al. 2009a, b, 2011b) have been also designed based on the SPR mechanism. The general idea of an optical sensor is to track the sensitivity of electromagnetic coupling phenomenon to the change in the refractive index of the analyte.

In recent times, plasmonic photonic crystal fibers (PCFs) based sensors have gathered a considerable attention due to its exceptional characteristics (Abdelghaffar et al. 2023). PCFs have many advantages including large degrees of design freedom due to the flexibility of air holes arrangement and diversity of filling materials (Poli et al. 2007). Moreover, PCFs have many outstanding properties in comparison to the standard optical fibers, such as high birefringence, endless single-mode propagation over a wide wavelength range, low-loss guidance, high nonlinearity, transfer of high power and low bending loss (De et al. 2019). Therefore, PCFs have been widely employed in refractive index sensing applications. In this context, Dash and Jha (2016) have reported a simple Indium Tin Oxide (ITO) based D-shaped PCF sensor. Their sensor showed a relatively low wavelength sensitivity of 5200 nm/RIU and a resolution of 1.92 × \({10}^{-5}\) RIU in the wavelength range from 1600 to 2100 nm (Dash and Jha 2016). Another D-shaped PCF sensor with gold as a plasmonic material has been numerically investigated in Wu et al. (2018). A maximum sensitivity of 31,000 nm/RIU has been obtained in the near-infrared band (Wu et al. 2018). Moreover, Chen et al. (2018) have demonstrated a different structure of D-shaped PCF–SPR sensor for low RI detection where a maximum spectral sensitivity of 11,055 nm/RIU and RI resolution of 9.05 × \({10}^{-6}\) RIU have been achieved in the wavelength range from 2.35 to 2.65 µm. Additionally, Gao et al. (2014) have presented an optical fiber based SPR sensor with bi-layered plasmonic films of gold and TiO2. The RI resolution has been estimated to be 2.7 × \({10}^{-5}\) RIU and the resonance wavelength has been extended to the near-infrared region. Further, an extra-broad PCF RI sensor has been investigated based on a triangular lattice PCF and four large-size channels (An et al. 2017b). The detection range of RI was 1.30–1.79 and the resonance wavelength has been increased from 1680 to 1870 nm. Turduev et al. (2017) have presented a Mid IR T-shaped photonic crystal waveguide for RI sensing with sensitivities of 1040 nm/RIU, 500 nm/RIU, 530 nm/RIU and 390 nm/RIU within the analyte RI ranges of 1.05–1.10, 1.10–1.30, 1.10–1.25 and 1.00–1.30, respectively. Additionally, An et al. (2017a) have introduced a Mid IR RI sensor based on D-shaped PCF to achieve a sensitivity of 10,493 nm/RIU with a very high resolution of 9.53 × \({10}^{-6}\) RIU. Wang et al. (2020a) have presented a near IR dual core SPR-PCF sensor based on dual gold nanowires with sensitivity of 17,500 nm/RIU. Further, Gayraud et al. (2007) have demonstrated a methane gas sensor based on hollow core PCF. Such sensor has been utilized to measure the transmission spectra through the methane absorption region of 3.15–3.35 µm (Gayraud et al. 2007). Another methane sensor based on Fourier transform infrared spectroscopy has been developed by Gayraud et al. (2008). This sensor (Gayraud et al. 2008) is fabricated to measure qualitative methane concentrations to 1000 ppm (parts in \({10}^{6}\)). Furthermore, Liu et al. (2017) have reported a low RI sensor with two open-ring channels based on SPR-PCF. The sensor achieves sensitivity of 5500 nm/RIU with maximum resolution of 7.69 × \({10}^{-6}\) RIU in the Mid IR region between 2550 and 2900 nm. Recently, Gamal et al. (2022b) have introduced a multifunctional RI and temperature sensor with sensitivities of 34,600 nm/RIU and 21.05 nm/°C, respectively, in the near IR region. Moreover, Gamal et al. (2022a) have reported an environmental and low RI sensor in near IR with sensitivity of 19,100 nm/RIU.

Herein, a highly sensitive plasmonic PCF based water pollutant sensor is introduced. The suggested PCF structure consists of two successive rings of air holes. The first ring of air holes is composed of four ellipses arranged in a square lattice and infiltrated with the targeted water samples. The outer ring consists of twenty circular air holes organized in a circular lattice to create the cladding region in a silica (SiO2) background. In addition, two gold nanorods are attached to the inner surfaces of the two horizontal ellipses to allow the SP coupling with the core modes. COMSOL Multiphysics software package (COMSOL 5.1 2020) based on finite element method (FEM) (Obayya et al. 2002) is employed to perform the modal analysis of the reported sensor. The suggested optical sensor is designed and optimized to efficiently detect the dissolved pollutants in water such as nitric acid (HNO3) with concentrations of 14, 23 and 35% and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) with concentrations of 7, 15 and 30%. In this regard, a very high RI sensitivity of 36,000 nm/RIU is obtained which is much higher than those reported by similar devices in the literature (De et al. 2019; Dash and Jha 2016; Wu et al. 2018; Chen et al. 2018; Gao et al. 2014; An et al. 2017b). Moreover, the structure is shown to be robust against fabrication tolerances.

The rest of the manuscript is organized into 4 subsections. Section 2 presents the design considerations, the utilized materials, and structural parameters of the proposed device. In Sect. 3, the simulation results are shown and discussed. In addition, the optimization of the geometrical parameters to sustain sensitivity at maximum value is also proposed. Further, Sect. 3 also includes the study of different pollutants with different concentrations in water with the obtained sensitivities. The conclusions and summary of the proposed results are drawn in Sect. 4.

2 Design considerations

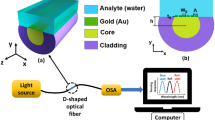
The two-dimensional cross-section of the suggested PCF water pollutants sensor is depicted in Fig. 1a. The proposed PCF has 4 elliptical holes; two large elliptical holes with radii of \({\mathrm{a}}_{\mathrm{x}}\) = 3 µm and \({\mathrm{a}}_{\mathrm{y}}\) = 5 µm, and two smaller ones with radii of \({\mathrm{b}}_{\mathrm{x}}\) = 2.1 µm and \({\mathrm{b}}_{\mathrm{y}}\) = 3 µm as may be seen in Fig. 1a. In addition, an outer ring of air holes arranged in a circular lattice with a hole diameter (d) = 1.1 μm and a hole pitch (Λ) = 2.2 μm is added to construct the cladding region. Moreover, two gold nano-rods are attached to the inner surfaces of the two large elliptical holes with diameter (dg) of 300 nm as depicted in Fig. 1a. It is worth noting that the four large elliptical holes are infiltrated with the studied water sample. In the same context, the outer layer of air holes is used to reduce the cladding average refractive index. Thus, the index contrast between the solid core region and the cladding increases which ensures a good confinement of the core mode in the core region. Therefore, the light matter interaction with the analyte sample and hence sensor sensitivity will be increased.

Fig. 1
figure 1

a 2D cross section view of the proposed water sensor, and b The schematic diagram of the proposed sensing system

Full size image

The permittivity of gold is given by Eq. (1) (Johnson and Christy 1972):

$$\upvarepsilon _{Au} \left(\upomega \right) =\upvarepsilon _{\infty } - \frac{{\upomega _{D}^{2} }}{{\upomega \left( {\upomega - {\text{i}}\upomega _{\uptau } } \right)}} - \frac{{\Delta\upvarepsilon \times \upomega _{p}^{2} }}{{\left( {\upomega ^{2} -\upomega _{p}^{2} } \right) - i\upomega _{{\text{l}}}\upomega }}$$
(1)

where \({\upvarepsilon }_{\infty }\), \({\upomega }_{\mathrm{D}}\), \({\upomega }_{\uptau }, {\upomega }_{\mathrm{p}}, {\upomega }_{\mathrm{l}}\) and \(\Delta\upvarepsilon\) denote the frequency dependent dielectric constant, plasma frequency, the damping frequency, and the weighted coefficient which are taken to 5.9673, \(2{\uppi } \times 2113.6\;{\text{THz}}\), \(2{\uppi } \times 15.92\;{\text{THz}},\;2{\uppi } \times 650.07{ }\;{\text{THz}},\;2{\uppi } \times 104.86\;{\text{THz}}\;{\text{and}}\;1.09\), respectively while ω is the angular frequency. Additionally, the wavelength-dependent Sellmeier equation defines the refractive index of the silica (Tan 1998) as follows:

$$\mathrm{n}\left(\uplambda \right)=\sqrt{1+\frac{{\mathrm{A}}_{1}{\uplambda }^{2}}{{\uplambda }^{2}-{\mathrm{B}}_{1}}+\frac{{\mathrm{A}}_{2}{\uplambda }^{2}}{{\uplambda }^{2}-{\mathrm{B}}_{2}}+\frac{{\mathrm{A}}_{3}{\uplambda }^{2}}{{\uplambda }^{2}-{\mathrm{B}}_{3}}}$$
(2)

where λ is the wavelength in µm and the Sellmeier coefficients \({\text{A}}_{1} ,{\text{ A}}_{2} ,{\text{ A}}_{3} ,{\text{ B}}_{1} ,{\text{ B}}_{2} ,\;{\text{and}}\;{\text{B}}_{3}\) are equal to \(0.696166300\), \(0.407942600\), \(0.897479400\), \(4.67914826 \times 10^{ - 3} \;\upmu {\text{m}}^{2}\), \(1.35120631{ } \times { }10^{ - 2} \;\upmu {\text{m}}^{2}\), and \(97.9340025\;\upmu {\text{m}}^{2}\), respectively. According to Tan (1998), silica has been employed as a background material in the proposed structure due to its wide transparency wavelength range that extend from 500 to 6700 nm.

The sensing system can be built by coupling the laser source with the PCF sensor via single mode fiber (SMF) (Leon-Saval et al. 2005) as depicted in Fig. 1b. A standard mid infrared single mode fiber (SMF) (Thorlabs) with core RI of 1.49229, cladding RI of 1.47, core diameter of 9 μm, and cladding diameter of 125 μm can be used for the excitation of the proposed PCF. To ensure the coupling between the fundamental modes of the SMF and the suggested PCF, the overlap integral and power coupling coefficient between them are investigated. The numerical results show that the overlap integral is close to unity (~ 0.99). So, it can be concluded that the coupling losses and reflections at the junctions between the SMF and the PCF have relatively little effect on the efficiency of the proposed structure. The transmitted light will be coupled again to the spectrometric system via SMF to measure the transmission and hence the losses through the proposed design. Due to the plasmonic effect, maximum loss occurs at a resonance wavelength depending on the RI of the water sample. The shift in the resonance wavelength can be used to detect the RI variation.

In this work, the suggested PCF is analyzed using the full vectorial finite element method (FVFEM) (Koshiba and Tsuji 2000) via COMSOL Multiphysics software package (COMSOL 5.1 2020) with computational domain of 328.6 µm2 where the number of degrees of freedom solved for is 64,269 with a maximum element size of 0.5 µm2. The cross section of the proposed structure is discretized into very small triangular elements with nonuniform meshing capabilities. In the simulation model, the outer coating (polymer or plastic) of the proposed optical fiber is replaced by a perfectly matched layer (PML) (Koshiba and Tsuji 2000) is applied to the transverse directions to truncate the simulation domain. Initially, extensive convergence tests are performed to ensure the numerical accuracy and stability of the results for the proposed sensor. The numerical results show that convergence occurs when the PML thickness is ≥ 0.3 µm and the maximum element size is ≤ 3.0 µm is used. Therefore, a PML with thickness of 2.0 µm is applied to ensure a maximum element size of 0.5 µm. However, an element size of 1 nm is utilized in the thin layers, i.e., Au and silica layers.

Different modes supported by the suggested structure are characterized by two main parameters: mode effective index (\({\mathrm{n}}_{\mathrm{eff}}\)) and confinement loss (L). In this study, L is calculated from the imaginary part of the mode effective index according to Eq. (3) (Crutchfield et al. 2004):

$$\mathrm{L}(\mathrm{dB}/\mathrm{cm})= \frac{20}{\mathrm{ln}(10)}\times \frac{2\uppi }{\uplambda }\times \mathrm{imaginary}({\mathrm{n}}_{\mathrm{eff}})$$
(3)

The sensitivity of the proposed SPR sensor can be calculated for the RI range 1.35–1.355 using the wavelength interrogation method depicted in Eq. (4) (Rifat et al. 2015):

$${\mathrm{S}}_{\uplambda }(\uplambda )=\frac{\Delta {\uplambda }_{\mathrm{r}}}{\Delta \mathrm{n}} (\mathrm{nm}/\mathrm{RIU})$$
(4)

where \(\Delta {\uplambda }_{\mathrm{r}}\) is the shift occurs to the resonance wavelength due to the polluted water sample and \(\Delta \mathrm{n}\) is the analyte RI change that is equal to 0.001. The resolution is another critical parameter for sensing process as it represents the smallest change that can be detected in the RI and is determined through the following equation (Gamal et al. 2021b):

$$\mathrm{R}=\Delta \mathrm{n }\frac{\Delta {\uplambda }_{\mathrm{min}}}{\Delta {\uplambda }_{\mathrm{r}}} (\mathrm{RIU})$$
(5)

where the wavelength resolution is represented by \(\Delta {\uplambda }_{\mathrm{min}}\). In this work, it is assumed that \(\Delta {\uplambda }_{\mathrm{min}}\) is 0.1 nm as suggested in Wang et al. (2020a). Moreover, the figure of merit (FOM) parameter is also studied for the proposed sensor to show the accuracy and high degree of selectivity. In this investigation, FOM is defined as the ratio of the sensitivity to the full width half maximum as depicted in Eq. (6) (Gamal et al. 2022b):

$$\mathrm{FOM}=\frac{\mathrm{senstivity}}{\mathrm{FWHM}} ({\mathrm{RIU}}^{-1})$$
(6)

where FWHM is the full width at half-maximum of the corresponding resonance peak.

Figure 2 depicts the wavelength dependent refractive index (n) and the extinction coefficient (k) of HNO3 and H2O2 with different concentrations in water. It is revealed from Fig. 2 that there are slight changes in both n and k of the two materials in water by changing the concentration. This may reflect on the behavior of the proposed sensor. However, comparing each case with pure water is the most important thing in calculating the sensitivity of the proposed sensor. In addition, this small difference in refractive indices may be compensated by the structure of the sensor in order to keep the sensitivity as high as possible. In the proposed structure, the wavelength sensitive coupling process between the fundamental mode and SPM is significantly affected by very small changes in the analyte RI. Thus, the shift in λr would be large and the sensitivity becomes sufficient.

Fig. 2
figure 2

a, b Wavelength dependent refractive index and extinction coefficient of \({\mathrm{HNO}}_{3}\), respectively, c, d wavelength dependent refractive index and extinction coefficient of \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\), respectively with different concentrations in water (Hale and Querry 1973)

Full size image

3 Simulation results

The calculated effective indices of the studied x- and y-polarized core modes supported by the PCF core are 1.3676 + 7.0269 × \({10}^{-4}\) i (Fig. 3a, x-polarized core mode), 1.3671 + 7.0293 ×  \({10}^{-4}\) i (Fig. 3b, x-polarized SP mode), and 1.3664 + 1.23899 ×  \({10}^{-7}\) i (Fig. 3c, y-polarized core mode) at \(\uplambda\) = 3116 nm and analyte RI of 1.355. It is worth noting that the imaginary part of the effective index of the x-polarized core mode is large due to the strong coupling with the x-polarized SP mode shown in Fig. 3b where both modes have approximately the same field distribution and effective indices. However, the y-polarized mode (Fig. 3c) is well confined in the core region and is not coupled to the SP modes around the plasmonic materials. This is evident by the very small imaginary part of the effective index of the y-polarized core mode (Fig. 3c).

Fig. 3
figure 3

The supported modes by the reported PCF structure at \(\uplambda\) = 3116 nm and analyte RI of 1.355

Full size image

The dispersion characteristics and the loss behavior of the x-polarized and y-polarized core modes and SPM for na = 1.355 are depicted in Fig. 4. The real parts of the \({\mathrm{n}}_{\mathrm{eff}}\) of the x-polarized core mode and the corresponding SPM are shown as red and blue lines, respectively. It may be seen that throughout the whole studied wavelength range, \({\mathrm{R}}_{\mathrm{e}}({\mathrm{n}}_{\mathrm{eff}})\) of both x-polarized mode and SPM decreases with the increase of the wavelength. The confinement loss of the x-polarized and y-polarized core modes are represented by the black and green lines, respectively. The confinement loss of the x-polarized core mode has a peak at λ = 3.116 μm, while the confinement loss of the y-polarized core mode (represented by the green line) is very small throughout the whole wavelength range with no loss peaks as shown in Fig. 4. The insets (a), (b) and (c) in Fig. 4 show the electric field norm of the SPM, at the phase matching point and the x-polarized core mode, respectively. At the resonance wavelength (3.116 μm), there is a strong coupling between the SPM and the x-polarized core mode where these two modes have approximately the same electric field distribution with nearly identical effective indices. This results in a very strong coupling and accordingly a peak in the loss spectrum x-polarized mode at λ = 3.116 μm as may be seen in Fig. 4.

Fig. 4
figure 4

Wavelength dependent \({{\varvec{n}}}_{{\varvec{e}}{\varvec{f}}{\varvec{f}}}\) of the x-polarized mode core (red) X-polarized SPM (blue), y-polarized core mode (green), and the confinement losses (black) at \({\mathrm{n}}_{\mathrm{a}}\) = 1.355. (Color figure online)

Full size image

According to the world health organization (WHO) statistics (WHO 2022), the accepted limits of the pollutants in water are in the range of milligram per 1 l of water. Therefore, these small, dissolved amounts will not have a large effect on the RI change of the water and the RI of the pure and polluted water are very close to each other. Accordingly, our analysis of water sample RI depends on a very small RI variation of 0.001 RIU throughout the rest of the work. This small variation will be taken above the MIR average water RI value (n = 1.35) according to Hale and Querry (1973).

Initially, the geometrical parameters of the proposed PCF structure are taken as \({\mathrm{a}}_{\mathrm{x}}\) = 3 µm, \({\mathrm{a}}_{\mathrm{y}}\) = 5 µm, \({\mathrm{b}}_{\mathrm{x}}\) = 2.1 µm, \({\mathrm{b}}_{\mathrm{y}}\) = 3 µm, \({\mathrm{d}}_{\mathrm{g}}\) = 300 nm, and \(\mathrm{d}\) = 1.1 µm at which the calculated sensitivity is equal to 11,100 nm/RIU. Figure 5 shows the effective indices of the coupled x-polarized core and SP modes and the loss spectra of the x-polarized mode at the two analyte RIs of 1.35 and 1.355. It may be seen that by increasing the analyte refractive index, the index contrast between the core and the analyte region decreases. Thus, strong leakage from the core region to the analyte occurs leading to a strong interaction between the core mode and the SPM (that has larger neff in this case). Due to the increase in neff of the SPM, the coupling will occur at a shorter wavelength. Thus the variation in the analyte RI induces a shift in the resonance wavelength of 55.5 nm. It can also be observed that, for the two analyte samples, there is a strong coupling between the core and SP modes with the same effective indices and the phase matching occurs at the same wavelength of the confinement loss’s peak.

Fig. 5
figure 5

Corresponding effective mode index and loss spectra of the x-polarized core mode at analyte refractive indices of 1.35 and 1.355

Full size image

The geometrical parameters of the proposed sensor are the studied to maximize the sensor sensitivity at \({\mathrm{n}}_{\mathrm{a}}\) = 1.35. It is expected that, the radius of gold nano-rods, \(({\mathrm{d}}_{\mathrm{g}})\) would be a very important parameter in controlling the sensitivity of the SPR proposed sensor. To prove this concept, a separate study on the effect of \({\mathrm{d}}_{\mathrm{g}}\) on the sensing performance is performed and the results are depicted in Fig. 6. Figure 6a shows the loss spectra of the x-polarized core mode at different values of \({\mathrm{d}}_{\mathrm{g}}\). In this study, the parameters, \({\mathrm{a}}_{\mathrm{x}}\), ay, bx, by, Ʌ, and \(\mathrm{d}\) are fixed to 3 µm, 5 µm, 2.1 µm, 3 µm, 2.2 µm and 1.1 µm, respectively. As may be noted from Fig. 6a, the loss peak has a blue shift from λ = 2807 nm to λ = 3150 nm by increasing \({\mathrm{d}}_{\mathrm{g}}\) from 300 to 340 nm. The radius of the metallic nano-rods influences the decay rate of the evanescent wave out from the core region and accordingly affects the shape of the SPM. As may be seen from Fig. 6a, thicker gold nano-rod is responsible for increasing the sensitivity, decreasing the loss value, and increasing the FWHM. With continuous increase in the gold nano-rod diameter, the energy of evanescent field decreases, and the confinement loss decreases dramatically. The RI sensitivity as a function of \({\mathrm{d}}_{\mathrm{g}}\) is also studied when the analyte RI is changed to \({\mathrm{n}}_{\mathrm{a}}=1.355\) as shown in Fig. 6b. It is evident from this figure that the RI sensitivity reaches its maximum of 33,200 nm/RIU at \({\mathrm{d}}_{\mathrm{g}}\) = 330 nm which will be used in the subsequent simulations.

Fig. 6
figure 6

a The loss spectra of the x-polarization core mode at different radii of gold rod \({\mathrm{d}}_{\mathrm{g}}\) where \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}\), bx, by and \(\mathrm{d}\) are fixed to 3 µm, 5 µm, 2.1 µm, 3 µm, and 1.1 µm, respectively, and b the RI sensitivity for different values of \({\mathrm{d}}_{\mathrm{g}}\)

Full size image

As the guiding core is a small region that is surrounded by four nonidentical elliptical holes, it is expected that the geometrical parameters of the elliptical holes i.e., \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{ a}}_{\mathrm{y}} {,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}}\) would influence the guided modes and consequently the sensitivity of the proposed water pollutant sensor. The variation of \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}\), bx, and \({\mathrm{b}}_{\mathrm{y}}\) is classified into four cases as depicted in Table 1. The effect of these dimensions on the attenuation loss of the x-polarized core mode is studied and the obtained results are depicted in Fig. 7. In this investigation, d and \({\mathrm{d}}_{\mathrm{g}}\) are fixed to 1.1 µm and 330 nm, respectively, where the analyte RI is equal to 1.355. It may be seen from Fig. 7a that enlarging the two elliptical holes (i.e., increasing \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}{,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}})\) by 0.1 µm (Case 2), \({\uplambda }_{\mathrm{r}}\) increases from 2864 to 3234 nm. It is worth mentioning that as the size of the two elliptical holes increases, the index contrast between the core and cladding regions increases. Thus, the core mode will be more confined in the core region with higher \({\mathrm{n}}_{\mathrm{eff}}\) value. Further, increasing the operating wavelength decreases the \({\mathrm{n}}_{\mathrm{eff}}\) of the core mode to approach the \({\mathrm{n}}_{\mathrm{eff}}\) of the SPM. Thus, the phase matching between the two modes i.e., core mode and SPM can be obtained at longer wavelengths. The RI sensitivity as a function of \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}{,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}}\) is also calculated and depicted in Fig. 7b. It may be seen from this figure that the sensitivity has a peak value at \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}{,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}}\) equals 2.9 µm, 4.9 µm, 1.7 µm and 2.9 µm, respectively (Case 3). Therefore, the diameters of the two elliptical air holes (\({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}{,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}}\)) are set to 2.9 µm, 4.9 µm, 1.7 µm and 2.9 µm, respectively, to keep the RI sensitivity at its highest value of 36,000 nm/RIU.

Table 1 Elliptical air holes diameters of the PCF structure depicted in Fig. 1a
Full size table
Fig. 7
figure 7

a Attenuation loss spectra as a function of ellipse dimensions for the four cases depicted in Table 1, where \({\mathrm{d}}_{\mathrm{g}}\) is taken as 330 nm, and b the RI sensitivity of the studied four cases

Full size image

Since the outer ring of air holes is positioned relatively far away from the core and analyte regions, the variation in its dimensions has a negligible effect on the optical characteristics of the core and SP modes. Thus, d is kept at its original value of 1.1 µm throughout the subsequent simulations.

The variations in the analyte RI have potential applications such as water pollutant detection therefore the RI sensitivity of the proposed structure is also studied. In this investigation, the RI sensitivity of the suggested sensor is analyzed at the optimized geometrical parameters; \({\mathrm{a}}_{\mathrm{x}}\) = 2.8 µm, \({\mathrm{a}}_{\mathrm{y}}\) = 4.9 µm, \({\mathrm{ b}}_{\mathrm{x}}\) = 1.7 µm, \({\mathrm{b}}_{\mathrm{y}}\) = 2.9 µm, \({\mathrm{d}}_{\mathrm{g}}\) = 330 nm, and \(\mathrm{d}\) = 1.1 µm as in Table 2.

Table 2 The optimized geometrical parameters of the proposed structure
Full size table

Figure 8a presents the wavelength-dependent loss spectra at various analyte RIs of 1.350, 1.351, 1.352, 1.353, 1.354 and 1.355 with very small RI variation of 0.001 RIU. Therefore, the proposed sensor can detect dissolved pollutants in water like nitric acid (\({\mathrm{HNO}}_{3}\)) with percentages of 14, 23 and 35% in water and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) with percentages of 7, 15 and 30% in water and corresponding RIs that overlap with the studied refractive index range (1.350–1.355) (Myers et al. 2018). It is evident from Fig. 8a that generally the resonance wavelength decreases by increasing the analyte RI. Figure 8b shows the resonance wavelength as function of the analyte RI and the fitted line represents the linear fitting over the studied RI range from n = 1.350 to 1.355. The fitted line has a correlation coefficient (r) and coefficient of determination of 0.9999 and 0.9998, respectively, while the sensitivity slope is equal to 36,000 nm/RIU with 36 nm wavelength difference for analyte RI change of 0.001. Therefore, the suggested sensor has a linear-like behavior with high sensitivity through the RI range from 1.35 to 1.355 and is suitable for water pollutant screening.

Fig. 8
figure 8

a Confinement loss spectra of the multi-functional sensor for analyte RI of 1.35, 1.351, 1.352, 1.353, 1.354 and 1.355, and b the effect of the analyte refractive index on the resonance wavelength

Full size image

Figure 9 depicts the FOM of the proposed sensor calculated in the RI range from 1.35 to 1.355. Best FOM value of 250 \({\mathrm{RIU}}^{-1}\) is obtained at RI of 1.355\(.\) It can be noticed from Fig. 9 that the FOM increases with increasing the RI. Additionally, the obtained FOM in this work is higher than those reported in Dash and Jha (2016), Wu et al. (2018), Chen et al. (2018), Gao et al. (2014), An et al. (2017a, b), Turduev et al. (2017), Wang et al. (2020a), Gayraud et al. (2007). Moreover, the achieved FOM is higher than those introduced in Lu et al. (2015) Huang et al. (2012) Ameling et al. (2010) where the achieved FOM are 25, 3.1 and 7.1, respectively. The resolution (R) is another important parameter in the sensing process and is determined via Eq. (5) when \(\Delta {\uplambda }_{\mathrm{r}}\) is 180 nm and the analyte RI is changed from 1.35 to 1.355. Assuming \(\Delta {\uplambda }_{\mathrm{min}}\) is 0.05 nm (Wang et al. 2020a), R will be \(2.78 \times 10^{ - 6} \;{\text{RIU}}\). The achieved R is larger than those reported in Dash and Jha (2016), Wu et al. (2018), Chen et al. (2018), Gao et al. (2014), An et al. (2017a, b), Turduev et al. (2017), Wang et al. (2020a), Gayraud et al. (2007, 2008), Liu et al. (2017), Gamal et al. (2022a, b).

Fig. 9
figure 9

The FOM of the suggested water pollutant sensor as a function analyte RI

Full size image

In order to test the performance of the suggested sensor in detecting different types of pollutants dissolved in water, a study is performed to investigate the effect of adding different concentrations of \({\mathrm{HNO}}_{3}\) and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (Hale and Querry 1973) in water. In this study, the geometrical parameters are fixed to their optimal values based on the previous parametric analysis. Figure 10a, b show the wavelength dependent confinement loss of the core mode for pure water with different concentrations of \({\mathrm{HNO}}_{3}\) and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) in water, respectively. It can be noticed from Fig. 10a that there is a large resonance shift between the case of pure water and that of \({\mathrm{HNO}}_{3}\) (14%), \({\mathrm{HNO}}_{3}\) (23%) and \({\mathrm{HNO}}_{3}\) (35%) in water. In addition, Fig. 10b shows that there is also a resonance shift exists between the case of pure water and that of \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (7%), \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\)(15%) and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (30%) in water. Table 3 summarizes the resonance wavelengths and the difference in \(\Delta {\uplambda }_{\mathrm{r}}\) for each concentration. From this table, it is revealed that the proposed sensor can be used to detect different pollutants in water with relatively high sensitivity.

Fig. 10
figure 10

Confinement loss spectra of the proposed sensor for a pure water, \({\mathrm{HNO}}_{3}\) (14%), \({\mathrm{HNO}}_{3}\) (23%) and \({\mathrm{HNO}}_{3}\) (35%) and b pure water, \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (7%), \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (15%) and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) (30%)

Full size image
Table 3 The resonance wavelengths and difference shift for different tested pollutants
Full size table

Table 4 summarizes a comparison between the proposed sensor with similar devices that have been reported in literature. It is evident that the resolution and RI sensitivity of the proposed water pollutants sensor are better than those introduced with similar devices reported in Dash and Jha (2016), Wu et al. (2018), Chen et al. (2018), Gao et al. (2014), An et al. (2017a, b), Turduev et al. (2017), Wang et al. (2020a), Gayraud et al. (2007, 2008), Liu et al. (2017), Gamal et al. (2022a, b).

Table 4 Comparison between previously reported SPR-PCF sensors and the proposed water pollutant sensor
Full size table

The suggested device can be fabricated using the well-known stack and draw method (Russell 2003; Pysz et al. 2014), while the elliptical air holes can be fabricated in different ways. Issa et al. successfully fabricated a consistently oriented elliptical-hole fiber (Issa et al. 2004). Guiyao et al. fabricated an SF6 glass made of PCF using the die casting and suggested that this method can also be used for making various PCF structures, including elliptical holes (Guiyao et al. 2006). Zhang et al. reported the fabrication of a methyl methacrylate-based elliptical-hole PCF using the in-situ chemical polymerization method (Zhang et al. 2006). Zhang et al. reported the fabrication of a PCF with elliptical holes using extrusion, canning, and drawing fabrication methods (Zhang et al. 2011). Further, 3D printing technology can be also an effective method for fabricating elliptical-hole PCFs (Ebendorff-Heidepriem et al. 2014). Then, two gold nanorods can be grown and self-aligned to the central air hole’s inner surface using stepwise seeded growth method as reported in Feng et al. (2019). In addition, silicone glue can be utilized to cover the cladding circular air holes in order to selectively fill the four elliptical air holes with the analyte (Huang et al. 2004). The suggested PCF is then immersed in the analyte solution, and the fluid will fill the uncovered four elliptical air holes due to the capillary forces that keep the analyte inside them and avoid its drop out. To push out the analyte form the infiltrated holes, a pressure is applied on the syringe pump (Huang et al. 2004). Furthermore, the PCF is spliced to a standard mid infrared SMF (Thorlabs 2023) to ensure strong coupling to the proposed design. Thus, a laser source (Leon-Saval et al. 2005) is used to launch light to the SMF directly. The suggested design has a loss peak of 14,379 dB/cm at the resonance wavelength of 2.795 μm. The specified device length can also be adjusted to meet the requirement of acceptable total leakage loss. For example, a device length of 1 µm can be used to have a total loss of less than 1.5 dB. Therefore, it is believed that the reported device can be experimentally fulfilled.

3.1 Fabrication tolerance study

The fabrication tolerance of the proposed water pollutant sensor is also investigated. As of current fabrication technology of silica-based optical fibers, the fabrication tolerance of ± 5% is considered for the proposed designed parameters (Chang et al. 2019). It is found that the diameter of small circular air holes (d) has no effect on the loss spectra of the guided x-polarized mode. However, \({\mathrm{d}}_{\mathrm{g}}\), \({\mathrm{a}}_{\mathrm{x}}\), \({\mathrm{a}}_{\mathrm{y}}{,\mathrm{ b}}_{\mathrm{x}}\), and \({\mathrm{b}}_{\mathrm{y}}\) are considered in this study and the corresponding sensitivities are summarized in Table 5. It may be seen that the sensitivity is better than 32,000 nm/RIU with a variation of ± 5% in the considered geometrical parameters that may occur during the fabrication process. Thus, the tolerance study shows that with the available technology (Chang et al. 2019), the proposed sensor can still be resistant to fabrication inconsistencies.

Table 5 Fabrication tolerance study of the different geometrical parameters of the proposed sensor: diameter of gold nanorods \({\mathrm{d}}_{\mathrm{G}}\) and ellipses dimensions \({\mathrm{a}}_{\mathrm{X}}\), \({\mathrm{a}}_{\mathrm{Y}}\), bX and \({\mathrm{b}}_{\mathrm{Y}}\)
Full size table

4 Conclusion

A highly sensitive RI water pollutant sensor over the range of (1.35:1.355) based on PCF with SPR mechanism is reported and analyzed. The suggested device can detect pollutants like nitric acid (\({\mathrm{HNO}}_{3}\)) with percentages of 14, 23 and 35% in water and \({\mathrm{H}}_{2}{\mathrm{O}}_{2}\) with percentages of 7, 15 and 30% in water which have RIs within the sensing range (1.35–1.355). The proposed sensor has four elliptical holes infiltrated with the analyte with two gold nanorods attached to the inner surface of the two horizontal elliptical holes. An ultra-high RI sensitivity of 36,000 nm/RIU over the range of (1.35:1.355) is achieved. Therefore, the sensitivity of the suggested sensor surpasses all the recent designs operating in the same ranges. In addition, the reported sensor has advantages in terms of linear sensitivity, simplicity of fabrication, and high robustness to fabrication errors.