Suppression of chaos in the periodically perturbed generalized complex Ginzburg–Landau equation by means of parametric excitation

Abstract

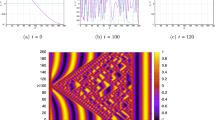
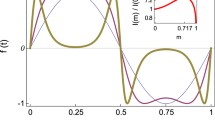
The generalized complex Ginzburg–Landau equation is considered. An analytical condition for the existence of horseshoe chaos is obtained for the traveling wave reduction of the investigated equation by using the Melnikov method. A way to control chaos in the dynamical system is proposed. An analytical prediction is tested numerically by plotting attraction basins of attraction of the Poincare section of the studied system.

Appendices

Appendix 1: Homoclinic orbits (12) and (13).

Here we provide details about finding homoclinic orbits (12) and (13). For the first orbit (12), substituting $A=(1-n)/n, \ n\in \mathbb {Z} \$ in (10) yields

$$\begin{aligned} H(u,v) = \frac{v^{2}}{2}+\frac{B \,u^{2}}{2 n}+\frac{D u^{2 n +2}}{2 n \left( n +1\right) }, \quad n\in \mathbb {Z}. \end{aligned}$$

(30)

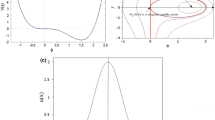
In the considered case of $B<0$ and $D>0$, the homoclinic orbit $({u_{hom}}_1,{v_{hom}}_1)$ is a level curve of (30), which passes through the saddle point $O=(0,0)$ and satisfies $u_z=v$. This gives

$$\begin{aligned} \frac{du}{dz} = \frac{u\sqrt{-Bn-Du^{2n}-B}}{\sqrt{n(n+1)}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(31)

Separating the variables in Eq. (31) and integrating both sides of the resulting expression yields

$$\begin{aligned} -\frac{ \,\textrm{arctanh}\! \;\left( \frac{\sqrt{B n +D u^{2 n}+B}}{\sqrt{n +1}\, \sqrt{B}}\right) }{\sqrt{n}\, \sqrt{|B|}} = z, \quad n\in \mathbb {Z}. \end{aligned}$$

(32)

Solving (32) for u, we get

$$\begin{aligned} {u^\pm _{hom}}_1(z) = \pm \; \left( \frac{\left( n +1\right) {| B |} \left( 1-\left( \tanh ^{2}\left( \sqrt{n {| B |}}\, z \right) \right) \right) }{D}\right) ^{\frac{1}{2 n}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(33)

The expression for ${v^\pm _{hom}}_1(z)$ is obtained by differentiating (33). For the second orbit (13), letting $A=n/(n+1)$in (10) leads to

$$\begin{aligned} H(u,v) = \frac{v^{2}}{2}+\frac{B \left( 2 n +1\right) u^{2}}{2 n +2}+\frac{D \left( 2 n +1\right) ^{2} u^{\frac{6 n +4}{2 n +1}}}{6 n^{2}+10 n +4}, \quad n\in \mathbb {Z}. \end{aligned}$$

(34)

Similarly, we get that the homoclinic orbit $({u_{hom}}_2,{v_{hom}}_2)$ at $B<0$ and $D>0$ solves the following equation

$$\begin{aligned} \frac{du}{dz} = \frac{ \sqrt{2 n +1}\, \sqrt{-D \left( 2 n +1\right) u^{\frac{6 n +4}{2 n +1}}- \left( 3n +{2}\right) u^{2} B}}{\sqrt{3 n^{2}+5 n +2}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(35)

Integrating Eq. (35), after the separation of variables, results in

$$\begin{aligned} \frac{ \sqrt{3 n^{2}+5 n +2}\, \sqrt{2 n +1}\, \textrm{arctanh}\!\; \left( \frac{\sqrt{\left( 2 D n +D\right) u^{\frac{2 n +2}{2 n +1}}+3 B n +2 B}}{\sqrt{3 n +2}\, \sqrt{B}}\right) }{\sqrt{3 n +2}\, \sqrt{|B|}\, \left( n +1\right) } = z, \quad n\in \mathbb {Z}. \end{aligned}$$

(36)

Solving (36) for u, we get

$$\begin{aligned} {u^\pm _{hom}}_2(z) = \pm \left( \frac{\left( 3 n +2\right) {| B |} \left( 1-\left( \tanh ^{2}\left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) \right) \right) }{\left( 2 n +1\right) D}\right) ^{\frac{2 n +1}{2 n +2}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(37)

The expression for ${v^\pm _{hom}}_2(z)$ is obtained by differentiating (37).

Appendix 2: Explicit expressions for $K_i, \ L_i$ and $N_i$.

Here we give values of $K_i, L_i$ and $N_i$ more explicitly.

$$\begin{aligned} K_1&= F\int _{-\infty }^{\infty }\frac{{| B |}^{\frac{n +1}{2 n}} \left( n +1\right) ^{\frac{1}{2 n}} \sinh \! \left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) \sin \! \Omega z dz}{\sqrt{n}\, D^\frac{1}{2n} \cosh \! \left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) ^\frac{n}{n+1}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(38)

$$\begin{aligned} L_1&= k\int _{-\infty }^{\infty }\frac{{| B |}^{\frac{n +1}{n}} \left( n +1\right) ^{\frac{1}{n}} \sinh ^{2}\left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) dz}{n D^{\frac{1}{n}} \cosh \! \left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) ^\frac{2(n+1)}{n}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(39)

$$\begin{aligned} N_1&= F_1\int _{-\infty }^{\infty }\frac{\left( n +1\right) ^{\frac{1}{n}} {| B |}^{\frac{2+n}{2 n}} \sinh \! \left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) \sin {\Omega _1z}dz}{\sqrt{n}\, D^{\frac{1}{n}} \cosh \! \left( \sqrt{{| B |}}\, \sqrt{n}\, z \right) ^\frac{n+2}{n}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(40)

$$\begin{aligned} K_2&= F\int _{-\infty }^{\infty }\frac{ {| B |}^{\frac{3 n +2}{2 n +2}} \left( 3 n +2\right) ^{\frac{2 n +1}{2 n +2}} \sinh \! \left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) \sin \! \Omega z dz}{\sqrt{n +1} \left( 2 n +1\right) ^{\frac{n}{2 n +2}}\,D^{\frac{2 n+1}{2 n +2}} \cosh \! \left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) ^\frac{3n+2}{n+1}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(41)

$$\begin{aligned} L_2&= k\int _{-\infty }^{\infty }\frac{ {| B |}^{\frac{3 n +2}{n +1}} \left( 3 n +2\right) ^{\frac{2 n +1}{n +1}} \left( \sinh ^{2}\left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) \right) dz}{\left( n +1\right) \left( 2 n +1\right) ^{\frac{n}{n +1}} D^{\frac{2 n +1}{n +1}} \cosh \! \left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) ^\frac{2(3n+2)}{n+1}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(42)

$$\begin{aligned} N_2&= F_1\int _{-\infty }^{\infty } \frac{ {| B |}^{\frac{5 n +3}{2 n +2}} \left( 3 n +2\right) ^{\frac{2 n +1}{n +1}} \sinh \! \left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) \sin \! \left( \Omega _{1} z \right) }{\sqrt{n +1}\, \left( 2 n +1\right) ^{\frac{3 n +1}{2 \left( n +1\right) }} D^{\frac{2 n +1}{n +1}} \cosh \! \left( \frac{\sqrt{{| B |}}\, \sqrt{n +1}\, z}{\sqrt{2 n +1}}\right) ^\frac{3n+2}{n+1}}, \quad n\in \mathbb {Z}. \end{aligned}$$

(43)