Investigation of the analytical and numerical solutions with bifurcation analysis for the (2+1)-dimensional Bogoyavlenskii-Kadomtsev-Petviashvili equation

Abstract

In this work, we investigate the solutions of the (2+1)-dimensional Bogoyavlenskii-Kadomtsev-Petviashvili (BKP) equation by three powerful analytical methods: the $\exp _{a}$ function method, the $(\frac{G'}{G})$-expansion method, and the Sine-Gordon expansion method. This equation describes the nonlinear wave propagation in many applications like waves of evolutionary shallow water, electrical networks, and engineering devices. Moreover, we study the solutions numerically via the finite difference method. We analyze the bifurcation of dynamical system resulting from the BKP equation. Finally, the majority of our solutions are displayed graphically to present the strength of imposed methods.

1 Introduction

The importance of treatise the nonlinear differential equations that it present complicated phenomenons in different fields like: plasma physics, physical science, fluid mechanics, biology, ecology, chemistry, nonlinear optics, engineering technology, mathematical physics, waves in shallow water, optical fibers, nano-fibers, metamaterials, and others. Many researchers employed different techniques such as: Hirota’s bilinear method Hirota (2004), long wave limit technique Tan et al. (2018), the inverse scattering transformation method Ablowitz and Clarkon (1991), sine-cosine method Bekir (2008), the two variable $(\frac{G^{\prime }}{G},\frac{1}{G})$-expansion methods Miah et al. (2019), modified kudryashov method Ali and Mehanna (2022), the extended tanh function method Ali et al. (2021), the improved F-expansion approach Almatrafi et al. (2021), and and recent techniques being used to find explicit solutions to different versions of nonlinear equations that are found in real-life applications such as Kudryashov-expansion method, updated rational sine-cosine method, updated rational sinh-cosh method, Cole-Hopf transformation, extended tanh-coth expansion, recent ansatze methods, extended sinh-Gordon equation expansion method, and Exp$(-\phi (\xi ))$-expansion method Alquran (2022); Alquran and Alqawaqneh (2022); Ali et al. (2022); Alquran (2022); Alhami and Alquran (2022); Mathanaranjan (2022); Mathanaranjan and Vijayakumar (2022); Mathanaranjan et al. (2022); Mathanaranjan (2022); Mathanaranjan et al. (2021).

Our goal in this work is concerned with the solution of the (2+1)-dimensional BKP equation

$$\begin{aligned} \begin{aligned}&u_{xxt}+u_{xxxxy}+12u_{xx}u_{xy}+8u_{x}u_{xxy}+4u_{xxx}u_{y}=\gamma u_{yyy},\ \ \ \gamma =\pm 1\\ {}&or\\ {}&(u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y})_{x}=\gamma u_{yyy}. \end{aligned} \end{aligned}$$

(1)

Where, u(x, y, t) presents the wave amplitude. The BKP equation is assorted as the equation of BKP-I when $\gamma =1$, and the equation of BKP-II when $\gamma =-1$. The BKP Eq. (1) is a protraction of the Bogoyavlenskii-Schiff (BS) equation and the Kadomtsev-Petviashvili (KP) Eq. Estevez and Hernaez (2000), If $\gamma =0$ then (1) can be converted to the Calogero-Bogoyavlenskii-Schiff (CBS) equation. The BKP Eq. (1) can be used to explain how nonlinear waves propagate in fluid, plasmas, biology, physics, and other scientific fields. The exact solutions have been covered in many literature using a variety of techniques: Wang et al. used Hermitian quadratic form and the bilinear structure Wang and Fang (2020), Wazwaz applied the Hirota’s direct method Wazwaz (2020), Cheng et al. constructed Wronskian determinant solutions Chenga et al. (2021), Wang et al. employed the bilinear representation and Grammian determinant Wang and Fang (2020), Rui et al. applied Hirota-s direct method and the KP hierarchy reduction method Rui and Zhang (2020), Wang et al. utilized the truncated Painlevé method and consistent Riccati expansion Wang and Fang (2017), Moretlo et al. employed the multiple exp-function algorithm and the modern group analysis method Moretlo et al. (2022), Khan utilized Lie analysis, the reduced differential equations were studied by: the new extended direct algebraic method and the tanh method Jhangeer et al. (2020), Zhao et al. used the polynomial function method Zhao et al. (2022), Wang et al. employed Taylor expansion approach and the perturbation method Wang and Fang (2019), Fang et al. utilized differential constraint technique and the binary Bell polynomials method Wang and Fang (2017), Fan et al. employed the bifurcation method Fan and Zhou (2018). In this work, we use three efficient analytical techniques, the first one is the $\exp _{m}$ function method Method Ali et al. (2020); Hosseini et al. (2017, 2019), the second one is the $(\frac{G'}{G})$-expansion method Nisar et al. (2022); Almusawa et al. (2021); Shehata et al. (2019); Akçagil and Aydemir (2016); Aminakbari et al. (2021) and the Sine-Gordon expansion method Ali and Mehanna (2021); Ali et al. (2020). We introduce a numerical solution using finite difference method Raslan and Ali (2020); ELDanaf et al. (2014); Raslan et al. (2022). We analyze the bifurcation of the traveling wave solutions of the BKP equation El-Labany et al. (2018); Saha et al. (2021); Karakoca et al. (2023).

Our work is streaked as: we demonstrate the main steps of the present methods in Sect. 2. We exhibit the application of the suggested methods in Sect. 3. We present some graphs to illustrate our solutions in Sect. 4. The numerical solution is presented in Sect. 5 using the finite difference method. We study the bifurcation analysis in Sect. 6. Lastly, in Sect. 7, we give a compact conclusion.

2 A Summary for the proposed methods

2.1 The $\exp _{m}$-function method

Assume that we have the following nonlinear PDF

$$\begin{aligned} F(u,u_{t},u_{x},u_{y},u_{xx},u_{xy},u_{xxx},u_{xxt},...)=0, \end{aligned}$$

(2)

where, $u=u(x,y,t)$ is an unknown function to be determined, F is a polynomial in u and its first and higher order partial derivatives.

Step 1::

Employing the traveling wave transformation to the PDE switch the PDE to an ODE

$$\begin{aligned} u(x,y,t)=u(\eta ),\,\ \eta =ax+by-ct \end{aligned}$$

(3)

where a, b are arbitrary constants and c is the wave speed. Inserting (3) into (2), we get the following ODE:

$$\begin{aligned} H(u^{\prime },u^{\prime \prime },u^{\prime \prime \prime },u^{\prime \prime \prime \prime },...)=0, \end{aligned}$$

(4)

where H is a polynomial in $u(\eta )$ and its derivatives.

Step 2::

Suppose that the solution of (4) is presented by the next form:

$$\begin{aligned} u(\eta )=\frac{A_{0}+A_{1}m^{\eta }+\cdots +A_{N}m^{N\eta }}{B_{0}+B_{1}m^{\eta }+\cdots +B_{N} m^{N \eta }}, \end{aligned}$$

(5)

where $A_{\texttt{i}}$ and $B_{\texttt{i}}$ $(0 \le i \le N)$ are constants to be evaluated, N is a positive integer.

Step 3::

By balancing the term with the highest order derivative and the highest power nonlinear term in (4), we determine the positive integer N.

Step 4::

Substituting (5) into (4), we obtain the next polynomial

$$\begin{aligned} R(m^{\eta })=p_{0}+p_{1}m^{\eta }+\cdots +p_{r}m^{r\eta }=0. \end{aligned}$$

(6)

Putting the coefficients $p_{j}(0\leqslant j\leqslant r)$ equal to zero. We get a system of nonlinear algebraic equations which can be solved by using Mathematica program to achieve the solution of Eq. (1).

2.2 The $(\frac{G'}{G})$-expansion method

The $(\frac{G'}{G})$-expansion method is given by the following steps:

Step 1::

Assume that the solution of Eq. (4), is presented by:

$$\begin{aligned} u(\eta )=\sum _{\texttt{i}=0}^N f_{\texttt{i}}(\frac{G'}{G})^{i}, \end{aligned}$$

(7)

where $G=G(\eta )$ fulfill the next linear ODE:

$$\begin{aligned} G''(\eta )+\lambda G'(\eta )+\mu G(\eta )=0, \end{aligned}$$

(8)

where $f_{\texttt{i}}(i=0,1,2,...,N),b_N\ne 0, \lambda$ and $\mu$, are constants to be studied.

Step 2::

The positive integer N is calculated as mentioned before by the homogeneous balance technique.

Step 3::

Here, we present three groups of solutions for (8): Group 1: Hyperbolic function solutions, when $\lambda ^{2}-4 \mu >0,$

$$\begin{aligned} \frac{G'}{G}=\frac{-\lambda }{2}+\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\frac{h_{1}\sinh (\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta )+h_{2}\cosh (\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta )}{h_{1}\cosh (\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta )+h_{2}\sinh (\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta )}. \end{aligned}$$

(9)

Group 2: Trigonometric function solutions, when $\lambda ^{2}-4 \mu <0,$

$$\begin{aligned} \frac{G'}{G}=\frac{-\lambda }{2}+\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\frac{-h_{1}\sin (\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta )+h_{2}\cos (\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta )}{h_{1}\cos (\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta )+h_{2}\sin (\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta )}. \end{aligned}$$

(10)

Group 3: Rational function solutions, when $\lambda ^{2}-4 \mu =0,$

$$\begin{aligned} \frac{G'}{G}=\frac{-\lambda }{2}+\frac{h_{2}}{h_{1}+h_{2}\eta }. \end{aligned}$$

(11)

Step 4::

Replacing (7) with (8) into (4), then gathering all terms with the same powers of $(\frac{G'}{G})$ and equaling their coefficients to zero, we achieve a set of equations can be solved by using Mathematica program to obtain the exact solution of equation (1).

2.3 The sine-Gordon expansion method(SGEM)

The sine-Gordon equation:

$$\begin{aligned} u_{xx}-u_{tt}=m^{2}\sin (u), \end{aligned}$$

(12)

where m is a constant and $u=u(x,t)$. Suppose that the wave transformation $u(x,t)=U(\eta ), \eta =x-ct$ in (12) which converted to the nonlinear ODE:

$$\begin{aligned} U''=\frac{m^{2}}{(1-c^{2})}\sin (U), \end{aligned}$$

(13)

where, $U=U(\eta )$, $\xi$ is the traveling waves amplitude and c is the traveling waves speed. By integrating (13) once and putting the integration constant equal zero, we obtain

$$\begin{aligned}{}\left[(\frac{U}{2})'\right]^{2}=\frac{m^{2}}{(1-c^{2})}\sin ^{2}\left(\frac{U}{2}\right), \end{aligned}$$

(14)

let $w(\xi )=\frac{U}{2}$ and $a^{2}=\frac{m^{2}}{(1-c^{2})}$, so (14) becomes:

$$\begin{aligned} w'=a \sin (w). \end{aligned}$$

(15)

Set $a=1$ in (15), we obtain:

$$\begin{aligned} w'=\sin (w). \end{aligned}$$

(16)

The solution of (16), can be become as follow:

$$\begin{aligned} \sin (w)= & {} \sin (w(\eta ))=\frac{2pe^{\eta } }{p^{2}e^{2\eta }+1}\Bigg |_{p=1}=sech(\eta ), \end{aligned}$$

(17)

$$\begin{aligned} \cos (w)= & {} \cos (w(\eta ))=\frac{p^{2}e^{2\eta }-1}{p^{2}e^{2\eta }+1}\Bigg |_{p=1}=-\tanh (\eta ), \end{aligned}$$

(18)

where p is non zero constant of integration.

It is presumed that the solution $U(\eta )$ of (4) can be given as:

$$\begin{aligned} U(\eta )=A_{0}+\sum _{\texttt{i}=1}^N ((-\tanh (\eta ))^{i-1} (B_{\texttt{i}}sech(\eta )-A_{\texttt{i}} \tanh (\eta )). \end{aligned}$$

(19)

Use (17) and (18), we get:

$$\begin{aligned} U(w)=A_{0}+\sum _{\texttt{i}=1}^N (\cos ^{i-1}(w)) (B_{\texttt{i}}\sin (w)+A_{\texttt{i}}\cos (w)). \end{aligned}$$

(20)

Computing the value of N by using the balance principle. Assuming that the coefficients of $\sin ^{i}(w) \cos ^{i}(w)$ with like power are equal to zero, we acquire an algebraic system of equations that can be solved by Mathematica software.

3 Applications

Start by reducing the PDE (1) into the ODE via the wave transformation (3), we obtain:

$$\begin{aligned} 12a^{3}bu^{\prime \prime }(\eta )^{2}-(b^{3}+a^{2}c-12a^{3}bu^{\prime }(\eta ))u^{(3)}(\eta )+a^{4}bu^{(5)}(\eta )=0. \end{aligned}$$

(21)

Integrating twice with respect to $\eta$

$$\begin{aligned} -(b^{3}+a^{2}c)u^{\prime }(\eta )+6a^{3}bu^{\prime }(\eta )^{2}+a^{4}bu^{(3)}(\eta )=0. \end{aligned}$$

(22)

Determine the value of N by Balancing $u^{(3)}(\eta )$ with $u^{\prime }(\eta )^{2}$ in (14), we obtain $N+3=2(N+1)$, then $N=1$.

3.1 Solutions via the $\exp _{m}$-function method

The solution of (22)is assumed to be:

$$\begin{aligned} u(\eta )=\frac{A_{0}+A_{1}m^{\eta }}{B_{0}+B_{1}m^{\eta }}. \end{aligned}$$

(23)

Inserting (23) into (22) and setting the coefficients that have the same powers of $m^{\eta }$ equal to zero, we acquire the nonlinear system:

$$\begin{aligned} \begin{aligned}&-b^{3}A_{1}B_{0}^{3}\log (m)-a^{2}c A_{1}B_{0}^{3}\log (m)+a^{4}b A_{1}B_{0}^{3}\log (m)^{3}+b^{3}A_{0}B_{0}^{2}B_{1}\log (m)\\ {}&+a^{2}c A_{0}B_{0}^{2}B_{1}\log (m)-a^{4}b A_{0}B_{0}^{2}B_{1}\log (m)^{3}=0,\\ {}&6a^{3}b A_{1}^{2}B_{0}^{2}\log (m)^{2}-12a^{3}b A_{0} A_{1}B_{0}B_{1}\log (m)^{2}-2b^{3} A_{1}B_{0}^{2}B_{1}\log (m)\\ {}&-2a^{2}cA_{1}B_{0}^{2}B_{1}\log (m)-4a^{4}b A_{1}B_{0}^{2}B_{1}\log (m)^{3}+6a^{3}b A_{0}^{2}B_{1}^{2}\log (m)^{2}\\ {}&+2b^{3}A_{0}B_{0}B_{1}^{2}\log (m)+2a^{2}c A_{0}B_{0}B_{1}^{2}\log (m)+4a^{4}b A_{0}B_{0}B_{1}^{2}\log (m)^{3}=0,\\ {}&-b^{3}A_{1}B_{0}B_{1}^{2}\log (m)-a^{2}c A_{1}B_{0}B_{1}^{2}\log (m)+a^{4}b A_{1}B_{0}B_{1}^{2}\log (m)^{3}\\ {}&+b^{3}A_{0}B_{1}^{3}\log (m)+a^{2}cA_{0}B_{1}^{3}\log (m)-a^{4}bA_{0}B_{1}^{3}\log (m)^{3}=0. \end{aligned} \end{aligned}$$

(24)

We get the following set of solution, using (3) and (23):

$$\begin{aligned} \begin{aligned}&A_{1}=\frac{(A_{0}+aB_{0}\log (m))B_{1}}{B_{0}},\,\,\,\,c=\frac{b(-b^{2}+a^{4}\log (m)^{2})}{a^{2}},\\ {}&u(x,y,t)=\frac{A_{0}+A_{1}m^{\eta }}{B_{0}+B_{1}m^{\eta }}. \end{aligned} \end{aligned}$$

(25)

3.2 Solutions via the $(\frac{G'}{G})$-expansion method

Presenting the solution of (22) by:

$$\begin{aligned} u(\eta )=f_{0}+f_{1} \frac{G'}{G}, \end{aligned}$$

(26)

inserting (26) into (22), gathering and putting the coefficients of terms that have the same power of $\frac{G'}{G}$ equal to zero, we obtain the next set of equations:

$$\begin{aligned} \begin{aligned}&b^{3}\mu f_{1}+a^{2}c\mu f_{1}-a^{4}b\mu \lambda ^{2}f_{1}-2a^{4}b\mu ^{2}f_{1}+6a^{3}b\mu ^{2}f_{1}^{2}=0,\\ {}&\lambda f_{1}(b^{3}+a^{2}c-a^{4}b(\lambda ^{2}+8\mu )+12a^{3}b\mu f_{1})=0,\\ {}&f_{1}(b^{3}+a^{2}c-a^{4}b(7\lambda ^{2}+8\mu )+6a^{3}bf_{1}(\lambda ^{2}+\mu ))=0,\\ {}&12a^{3}b\lambda f_{1}(-a+f_{1})=0,\\ {}&6a^{3}bf_{1}(-a+f_{1})=0. \end{aligned} \end{aligned}$$

(27)

The traveling wave solutions of (1) are presented by:

$$\begin{aligned} f_{1}=a,\,\,\,c=-\frac{b(b^{2}-a^{4}\lambda ^{2}+4a^{4}\mu )}{a^{2}} \end{aligned}$$

(28)

Group 1: Hyperbolic function solutions, when $\lambda ^{2}-4 \mu >0,$

$$\begin{aligned} u(x,y,t)=f_{0}+f_{1}\bigg (\frac{-\lambda }{2}+\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\frac{h_{1}\sinh \frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta +h_{2}\cosh \frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta }{h_{1}\cosh \frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta +h_{2}\sinh \frac{1}{2}\sqrt{\lambda ^{2}-4\mu }\eta }\bigg ). \end{aligned}$$

(29)

Group 2: Trigonometric function solutions, when $\lambda ^{2}-4 \mu <0,$

$$\begin{aligned} u(x,y,t)=f_{0}+f_{1}\bigg (\frac{-\lambda }{2}+\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\frac{-h_{1}\sin \frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta +h_{2}\cos \frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta }{h_{1}\cos \frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta +h_{2}\sin \frac{1}{2}\sqrt{4\mu -\lambda ^{2}}\eta }\bigg ). \end{aligned}$$

(30)

Group 3: Rational function solutions, when $\lambda ^{2}-4 \mu =0,$

$$\begin{aligned} u(x,y,t)=f_{0}+f_{1}\bigg (\frac{-\lambda }{2}+\frac{h_{2}}{h_{1}+h_{2}\eta }\bigg ). \end{aligned}$$

(31)

3.3 Solutions via the Sine-Gordon expansion method(SGEM)

Using (20), we introduce the solution of (22) by the next form:

$$\begin{aligned} U(w)=A_{0}+B_{1}\sin (\omega )+A_{1}\cos (\omega ). \end{aligned}$$

(32)

substitute from (32) in (22), and putting the coefficients of trigonometric functions that have like powers equal to zero, we acquire the following algebraic set of equations:

$$\begin{aligned} \begin{aligned}&-b^{3}B_{1}-a^{2}cB_{1}-a^{4}bB_{1}=0,\\ {}&-5a^{4}bB_{1}-12a^{3}bA_{1} B_{1}-a^{4}bB_{1}=0,\\ {}&b^{3}A_{1}+a^{2}cA_{1}-4a^{4}bA_{1}+6a^{3}bB_{1}^{2}=0,\\&2a^{4}bA_{1}+6a^{3}bA_{1}^{2}+4a^{4}bA_{1}-6a^{3}bB_{1}^{2}=0. \end{aligned} \end{aligned}$$

(33)

By the help of mathematica program, we attain the following groups of solutions:

Group 1:

$$\begin{aligned} \begin{aligned}&A_{1}=\frac{1}{2}\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,a =-\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,B_{1} =\pm \frac{1}{2}\sqrt{\frac{-c+\sqrt{4b^{4}+c^{2}}}{2b}},\\&u_{1,2}(x,y,t)=A_{0}-\frac{1}{2}\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct)\\ {}&\pm \frac{1}{2}\sqrt{\frac{-c+\sqrt{4b^{4}+c^{2}}}{2b}}sech(ax+by-ct). \end{aligned} \end{aligned}$$

(34)

Group 2:

$$\begin{aligned} \begin{aligned}&A_{1}=-\frac{1}{2}\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,a =\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,B_{1}=\pm \frac{1}{2} \sqrt{\frac{-c+\sqrt{4b^{4}+c^{2}}}{2b}},\\ {}&u_{3,4}(x,y,t)=A_{0} +\frac{1}{2}\sqrt{\frac{c-\sqrt{4b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct)\\&\pm \frac{1}{2}\sqrt{\frac{-c+\sqrt{4b^{4}+c^{2}}}{2b}}sech(ax+by-ct). \end{aligned} \end{aligned}$$

(35)

Group 3:

$$\begin{aligned} \begin{aligned}&A_{1}=\frac{1}{2}\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,a =-\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,B_{1}=\pm \frac{1}{2} \sqrt{\frac{-c-\sqrt{4b^{4}+c^{2}}}{2b}},\\ {}&u_{5,6}(x,y,t)=A_{0} -\frac{1}{2}\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct)\\&\pm \frac{1}{2}\sqrt{\frac{-c-\sqrt{4b^{4}+c^{2}}}{2b}}sech(ax+by-ct). \end{aligned} \end{aligned}$$

(36)

Group 4:

$$\begin{aligned} \begin{aligned}&A_{1}=-\frac{1}{2}\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,a =\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}},\,\,\,B_{1}=\pm \frac{1}{2} \sqrt{\frac{-c-\sqrt{4b^{4}+c^{2}}}{2b}},\\ {}&u_{7,8}(x,y,t)=A_{0} +\frac{1}{2}\sqrt{\frac{c+\sqrt{4b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct)\\&\pm \frac{1}{2}\sqrt{\frac{-c-\sqrt{4b^{4}+c^{2}}}{2b}}sech(ax+by-ct). \end{aligned} \end{aligned}$$

(37)

Group 5:

$$\begin{aligned} \begin{aligned}&A_{1}=\pm \frac{1}{2}\sqrt{\frac{c-\sqrt{16b^{4}+c^{2}}}{2b}},\,\,\,a =\mp \sqrt{\frac{c-\sqrt{16b^{4}+c^{2}}}{2b}},\,\,\,B_{1}=0, \\ {}&u_{9,10}(x,y,t)=A_{0}\mp \frac{1}{2}\sqrt{\frac{c-\sqrt{16b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct). \end{aligned} \end{aligned}$$

(38)

Group 6:

$$\begin{aligned} \begin{aligned}&A_{1}=\pm \frac{1}{2}\sqrt{\frac{c+\sqrt{16b^{4}+c^{2}}}{2b}},\,\,\,a =\mp \sqrt{\frac{c+\sqrt{16b^{4}+c^{2}}}{2b}},\,\,\,B_{1}=0, \\ {}&u_{11,12}(x,y,t)=A_{0}\mp \frac{1}{2}\sqrt{\frac{c+\sqrt{16b^{4}+c^{2}}}{2b}}\tanh (ax+by-ct). \end{aligned} \end{aligned}$$

(39)

4 Graphical illustrations

Hither, we graphically demonstrate our solutions (see Figs. 1, 2, 3, 4, 5, 6 and 7):

Fig. 1

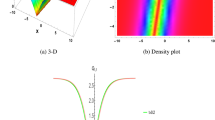
Kink solution plots of (25) by the $\exp _{m}$-function method when $a=1, b=0.3, m=0.3,A_{0}=0.006, B_{0}=0.001, B_{1}=0.001$

Fig. 2

Kink solution plots of (29) by the $(\frac{G'}{G})$-expansion method when $a=1.4, b=0.9, f_{0}=0.1, h_{1}=7, h_{2}=0.6, \mu =0.4, \lambda =1.3$

Fig. 3

Cusp solution plots of (30) by the $(\frac{G'}{G})$-expansion method when $a=1.1, b=0.8, f_{0}=0.01, h_{1}=0.3, h_{2}=0.1, \mu =0.01, \lambda =0.1$

Fig. 4

Periodic solution plots of (34) by the Sine-Gordon expansion method when $b=0.6, c=0.13, A_{0}=0.001$

Fig. 5

Periodic solution plots of (35) by the Sine-Gordon expansion method when $b=0.6, c=0.14, A_{0}=0.1$

Fig. 6

Kink solution plots of (37) by the Sine-Gordon expansion method when $b=0.3, c=0.2, A_{0}=0.4$

Fig. 7

Periodic solution plots of (38) by the Sine-Gordon expansion method when $b=0.8, c=0.13, A_{0}=0.01$

5 Numerical solutions

To solve the (2+1)-dimensional Bogoyavlenskii-Kadomtsev-Petviashvili Eq. (1) numerically by finite difference method, we impose $x,y\in [\texttt{a},\texttt{b}]$ and divide this interval into sub-intervals with horizontal distance $\texttt{h}=\frac{\texttt{b}-\texttt{a}}{\texttt{N}}=x_{\texttt{i}+1}-x_{\texttt{i}}, \texttt{i}=0,1,...,\texttt{N}$ and vertical distance $\texttt{k}=\frac{\texttt{b}-\texttt{a}}{\texttt{M}}=y_{\texttt{j}+1}-y_{\texttt{j}}, \texttt{j}=0,1,...,\texttt{M}$ at time levels $t_l=l\Delta {t}, l=0,1,...,\texttt{K}$ where $\Delta {t}>0$ and $\texttt{K}$ is +ve integer.

Put the governing conditions to solve Eq. (1)

$$\begin{aligned} \begin{aligned}&u_{\texttt{i},\texttt{j}}^{0}=f_1(x_\texttt{i},y_\texttt{j}),\ \ (u_{t})_{\texttt{i},\texttt{j}}^{0}=f_2(x_\texttt{i},y_\texttt{j}),\\ {}&u_{0,\texttt{j}}^{l}=f_3(y_\texttt{j},t_l),\ \ u_{n,\texttt{j}}^{l}=f_4(y_\texttt{j},t_l),\\ {}&u_{\texttt{i},0}^{l}=f_5(x_\texttt{i},t_l),\ \ u_{\texttt{i},m}^{l}=f_6(x_\texttt{i},t_l). \end{aligned} \end{aligned}$$

(40)

We obtain the numerical solution $\tilde{u}(x,y,t)$ equivalent to the exact solution u(x, y, t) by constructing finite difference scheme for Eq. (1)

$$\begin{aligned} \begin{aligned}&(\tilde{u}_{xxt})_{\texttt{i},\texttt{j}}^{l}+(\tilde{u}_{xxxxy})_{\texttt{i}, \texttt{j}}^{l}+c_{1}+12(\tilde{u}_{xx})_{\texttt{i},\texttt{j}}^{l} (\tilde{u}_{xy})_{\texttt{i},\texttt{j}}^{l}+8(\tilde{u}_{x})_{\texttt{i}, \texttt{j}}^{l}(\tilde{u}_{xxy})_{\texttt{i},\texttt{j}}^{l}\\&+4(\tilde{u}_{xxx})_{\texttt{i},\texttt{j}}^{l}(\tilde{u}_{y})_{\texttt{i}, \texttt{j}}^{l}=\gamma (\tilde{u}_{yyy})_{\texttt{i},\texttt{j}}^{l}, \end{aligned} \end{aligned}$$

(41)

where,

$$\begin{aligned} \begin{aligned}&\tilde{u}(x_\texttt{i},y_\texttt{j},t_l)=\delta _{\texttt{i},\texttt{j}}^{l}, \end{aligned} \end{aligned}$$

(42)

and its first and higher order partial derivatives

$$\begin{aligned} \begin{aligned}&\tilde{u}_{x}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\texttt{h}} \bigg (\delta _{\texttt{i}+1,\texttt{j}}^{l}-\delta _{\texttt{i}-1,\texttt{j}}^{l}\bigg ),\\ {}&\tilde{u}_{y}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\texttt{k}} \bigg (\delta _{\texttt{i},\texttt{j}+1}^{l}-\delta _{\texttt{i},\texttt{j}-1}^{l}\bigg ),\\ {}&\tilde{u}_{xx}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{\mathtt {h^2}} \bigg (\delta _{\texttt{i}-1,\texttt{j}}^{l}-2 \delta _{\texttt{i},\texttt{j}}^{l}+\delta _{\texttt{i}+1,\texttt{j}}^{l}\bigg ),\\ {}&\tilde{u}_{xy}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{4 \texttt{h k}}\bigg (\delta _{\texttt{i}+1,\texttt{j}+1}^{l}-\delta _{\texttt{i}+1, \texttt{j}-1}^{l}-\delta _{\texttt{i}-1,\texttt{j}+1}^{l}+\delta _{\texttt{i}-1,\texttt{j}-1}^{l}\bigg ),\\ {}&\tilde{u}_{xxy}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\mathtt {h^2 k}}\bigg (\delta _{\texttt{i}+1,\texttt{j}+1}^{l}-\delta _{\texttt{i}+1, \texttt{j}-1}^{l}-2\delta _{\texttt{i},\texttt{j}+1}^{l}+2\delta _{\texttt{i},\texttt{j}-1}^{l}\\ {}&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\delta _{\texttt{i}-1,\texttt{j}+1}^{l}-\delta _{\texttt{i}-1,\texttt{j}-1}^{l}\bigg ),\\ {}&\tilde{u}_{xxt}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\mathtt {h^2} \Delta {t}}\bigg (\delta _{\texttt{i}+1,\texttt{j}}^{l+1}-\delta _{\texttt{i}+1,\texttt{j}}^{l-1}-2 \delta _{\texttt{i},\texttt{j}}^{l+1}+2\delta _{\texttt{i},\texttt{j}}^{l-1}\\ {}&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\delta _{\texttt{i}-1,\texttt{j}}^{l+1}-\delta _{\texttt{i}-1,\texttt{j}}^{l-1}\bigg ),\\ {}&\tilde{u}_{xxx}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\mathtt {h^3}} \big (\delta _{\texttt{i}+2,\texttt{j}}^{l}+2\delta _{\texttt{i}-1,\texttt{j}}^{l}-2 \delta _{\texttt{i}+1,\texttt{j}}^{l}-\delta _{\texttt{i}-2,\texttt{j}}^{l}\big ),\\ {}&\tilde{u}_{yyy}(x_\texttt{i},y_\texttt{j},t_l)\simeq \frac{1}{2\mathtt {k^3}} \bigg (\delta _{\texttt{i},\texttt{j}+2}^{l}+2\delta _{\texttt{i},\texttt{j}-1}^{l}-2 \delta _{\texttt{i},\texttt{j}+1}^{l}-\delta _{\texttt{i},\texttt{j}-2}^{l}\bigg ). \end{aligned} \end{aligned}$$

(43)

As before, we formulate system of difference equations as follows

$$\begin{aligned} \begin{aligned}&\frac{1}{2\mathtt {h^2} \Delta {t}}\bigg (\delta _{\texttt{i}+1,\texttt{j}}^{l+1}- \delta _{\texttt{i}+1,\texttt{j}}^{l-1}-2\delta _{\texttt{i},\texttt{j}}^{l+1}+2 \delta _{\texttt{i},\texttt{j}}^{l-1}+\delta _{\texttt{i}-1,\texttt{j}}^{l+1}-\delta _{\texttt{i} -1,\texttt{j}}^{l-1}\bigg )+\\ {}&\frac{1}{2\mathtt {h^4 k}}\bigg (\delta _{\texttt{i}-2,\texttt{j}+1}^{l}-\delta _{\texttt{i}-2,\texttt{j}-1}^{l} -4\delta _{\texttt{i}-1,\texttt{j}+1}^{l}+4\delta _{\texttt{i}-1,\texttt{j}-1}^{l}+6 \delta _{\texttt{i},\texttt{j}+1}^{l}-\\ {}&6\delta _{\texttt{i},\texttt{j}-1}^{l}-4 \delta _{\texttt{i}+1,\texttt{j}+1}^{l}+4\delta _{\texttt{i}+1,\texttt{j}-1}^{l} +\delta _{\texttt{i}+2,\texttt{j}+1}^{l}-\delta _{\texttt{i}+2,\texttt{j}-1}^{l}\bigg )+\\ {}&\frac{3}{\mathtt {h^3 k}}\bigg (\delta _{\texttt{i}-1,\texttt{j}}^{l}-2 \delta _{\texttt{i},\texttt{j}}^{l}+\delta _{\texttt{i}+1,\texttt{j}}^{l}\big ) \big (\delta _{\texttt{i}+1,\texttt{j}+1}^{l}-\delta _{\texttt{i}+1,\texttt{j}-1}^{l} -\delta _{\texttt{i}-1,\texttt{j}+1}^{l}+\delta _{\texttt{i}-1,\texttt{j}-1}^{l}\bigg )+\\ {}&\frac{2}{\mathtt {h^3 k}}\bigg (\delta _{\texttt{i}+1,\texttt{j}}^{l}-\delta _{\texttt{i}-1,\texttt{j}}^{l}) (\delta _{\texttt{i}+1,\texttt{j}+1}^{l}-\delta _{\texttt{i}+1,\texttt{j}-1}^{l}-2 \delta _{\texttt{i},\texttt{j}+1}^{l}+2\delta _{\texttt{i},\texttt{j}-1}^{l}+\delta _{\texttt{i}-1, \texttt{j}+1}^{l}\\ {}&-\delta _{\texttt{i}-1,\texttt{j}-1}^{l}\bigg )+\frac{1}{\mathtt {h^3 k}}\bigg (\delta _{\texttt{i}+2,\texttt{j}}^{l}+2\delta _{\texttt{i}-1,\texttt{j}}^{l} -2\delta _{\texttt{i}+1,\texttt{j}}^{l}-\delta _{\texttt{i}-2,\texttt{j}}^{l}) (\delta _{\texttt{i},\texttt{j}+1}^{l}-\delta _{\texttt{i},\texttt{j}-1}^{l}\bigg )\\&=\frac{\gamma }{2\mathtt {k^3}}\bigg (\delta _{\texttt{i},\texttt{j}+2}^{l}+2 \delta _{\texttt{i},\texttt{j}-1}^{l}-2\delta _{\texttt{i},\texttt{j}+1}^{l} -\delta _{\texttt{i},\texttt{j}-2}^{l}\bigg ). \end{aligned} \end{aligned}$$

(44)

can be solved using the conditions (40). We show the accuracy of the presented numerical scheme by calculating error norm

$$\begin{aligned} \begin{aligned}&{L_2}=\sqrt{\texttt{h k}\sum _{\texttt{i}=0}^{\texttt{N}}\sum _{j=0}^{\texttt{M}}(u_{\texttt{i}, \texttt{j}}^{l}-\tilde{u}_{\texttt{i},\texttt{j}}^{l})^2}\\ {}&{L_\infty }= \max _{\texttt{i},\texttt{j}=0}^{\texttt{N},\texttt{M}}\left| u_{\texttt{i},\texttt{j}}^{l}-\tilde{u}_{\texttt{i},\texttt{j}}^{l} \right| , \end{aligned} \end{aligned}$$

(45)

Table 1 presents error norms using ${L_2}$ and ${L_\infty }$ formulas (45) at different time levels and Fig. 8(a, b) display the numerical and exact solutions at time level $t=0.5$ with step size $\texttt{h}=\texttt{k}=1.0$ and $\Delta {t}=0.01, 0.001$ for Eq. (25), respectively. Figure 9 shows the maximum absolute error at different time levels $t=1, 3, 5$ using the analytical solution (25) with step size $\texttt{h}=\texttt{k}=0.5$ and $\Delta {t}=0.001$.

Table 2 exhibits ${L_2}$ and ${L_\infty }$ error norms at different time levels and Fig. 10(a, b) compare between the numerical and exact solutions at $t=0.1$ with $\texttt{h}=\texttt{k}=1.0, 0.5$ and $\Delta {t}=0.01, 0.001$ for Eq. (29), respectively. The maximum absolute error at different time levels $t=3, 5, 10$ appear as in Fig. 11 using the analytical solution (29) with $\texttt{h}=\texttt{k}=1.0$ and $\Delta {t}=0.001$.

Table 3 shows ${L_2}$ and ${L_\infty }$ at different time levels and Fig. 12(a, b) display the analytical and numerical solutions at time level $t=0.5$ with $\texttt{h}=\texttt{k}=1.0$ and $\Delta {t}=0.01$ for Eqs. (37) and (39), respectively.

Table 1 $L_2$ and $L_\infty$ errors with step sizes $\texttt{h}=\texttt{k}=1.0$ and different values of $\Delta {t}$ for Problem (1)

Table 2 $L_2$ and $L_\infty$ errors with step sizes $\texttt{h}=\texttt{k}$ and different values of $\Delta {t}$ for Problem (1)

Table 3 $L_2$ and $L_\infty$ errors with step size $\texttt{h}=\texttt{k}=1.0$ and $\Delta {t}=0.01$ for Problem (1)

Fig. 8

Analytical and exact solutions of problem (1) using (25) at $a=1, b=0.3, m=0.3,A_{0}=0.006, B_{0}=0.001, B_{1}=0.001$

Fig. 9

Maximum absolute error of problem (1) at $t=1, 2, 3$ using (25) at $a=1, b=0.3, m=0.3,A_{0}=0.006, B_{0}=0.001, B_{1}=0.001$

Fig. 10

Analytical and exact solutions of problem (1) using (29) at $a=1.4, b=0.9, f_{0}=0.1, h_{1}=7, h_{2}=0.6, \mu =0.4, \lambda =1.3$

Fig. 11

Maximum absolute error of problem (1) at $t=1, 2, 3$ using (29) at $a=1.4, b=0.9, f_{0}=0.1, h_{1}=7, h_{2}=0.6, \mu =0.4, \lambda =1.3$

Fig. 12

Analytical and exact solutions of problem (1) using (37) and (39) at $b=0.03, c=0.01, A_{0}=1.2$

6 Bifurcation analysis

In this section, we discuss the bifurcation analysis of the (2+1)-dimensional BKP Eq. (1). For this analysis, we use the bifurcation theory Guckenheimer and Holmes (1983) and formulate equation (22) as a three-dimensional dynamical system as follows:

$$\begin{aligned} \begin{aligned}&u_{\eta }=f,\\&f_{\eta }=g,\\&g_{\eta }=\frac{1}{a^4b}\left[ \left( b^3+a^2c\right) f-6a^3b f^2 \right] . \end{aligned} \end{aligned}$$

(46)

Let $\textbf{F}=\left<f,g,\frac{\left( b^3+a^2c\right) f-6a^3b f^2}{a^4b}\right>$ is a vector field with $\mathbf {\nabla }.\textbf{F}=\frac{\partial {u_{\eta }}}{\partial {u}}+\frac{\partial {f_{\eta }}}{\partial {f}}+\frac{\partial {g_{\eta }}}{\partial {g}}=0$, Then the dynamical system (46) is conservative. The dynamical system (46) with three parameters a, b, c has infinite equilibrium points $p_{\texttt{i}}=(u_{\texttt{i}},0,0), i=1,2,...$ in the $ufg-$ phase plane, where $u_{\texttt{i}}$ arbitrary constant, it’s Jacobian matrix is as follows:

$$\begin{aligned} \begin{aligned} J(u_{\texttt{i}},0,0)=\begin{pmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} \frac{b^3+a^2c}{a^4b} &{} 0 \end{pmatrix}. \end{aligned} \end{aligned}$$

(47)

Then, the characteristic equation and eigenvalues of the system (46) are

$$\begin{aligned} \begin{aligned} \det [J-\zeta I]=\zeta ^3-\frac{b^3+a^2c}{a^4b}\zeta =0, \end{aligned} \end{aligned}$$

(48)

$$\begin{aligned} \begin{aligned}&\zeta _{1}=0, \ \ \zeta _{2}=\frac{\sqrt{b}\sqrt{b^3+a^2c}}{a^2}, \ \ \zeta _{3}=\frac{-\sqrt{b}\sqrt{b^3+a^2c}}{a^2}. \end{aligned} \end{aligned}$$

(49)

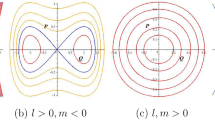
It obviously, from (49) that there is an eigenvalue $\zeta _{1}=0$. Consequently, these equilibrium points are non-hyperbolic equilibrium points. When parameters $a=1.0, b=0.3, c=0.4$ the phase plots of the dynamical system are attractors shaped like a wave in the 2D plot and are strange attractors in the 3D plot, as shown in Fig. 13.

Fig. 13

2D and 3D Phase plots of the dynamical system (46) at $a=1.0, b=0.3, c=0.4$

7 Conclusion

In this work, we introduced new solutions for the (2+1)-dimensional BKP Eq. (1) which characterize the wave phenomena in scientific applications as fluid mechanics and others. The introduced solutions are gained by three powerful and simple analytical methods, namely: the $\exp _{m}$-function method, the $(\frac{G'}{G})$-expansion method, the Sine-Gordon expansion method. Furthermore, we exhibited the acquired results graphically. We successfully attain solutions in different forms: trigonometric, exponential, hyperbolic, and rational functions which presented different types of waves as kink, cusp, and periodic wave solutions. The aforementioned results demonstrate that the suggested techniques are straightforward, effective, and good tools that give conclusive results when solving the proposed model and possibly be applied to different kinds of NPDE. We applied a numerical scheme via finite difference method of the BKP Eq. (1). Tables 1, 2, 3 and Figs. 8, 9, 10, 11, 12 showed efficiency and accuracy of the imposed numerical scheme and compatible it with the corresponding analytical solutions. We analyzed the traveling wave solutions of the dynamical system (46) consisting of the BKP equation (1) and found all equilibrium points are nonhyperbolic equilibrium points. In future work, we will be concerned about searching for other types of wave solutions to the presented BKP equation (1) by trying other analytical and numerical techniques.