1 Introduction

The perturbed stochastic nonlinear Schrödinger equation (NLSE) is a model used in the study of stochastic nonlinear dynamics, describing the evolution of a quantum system under the influence of external perturbations. The perturbed stochastic NLSE has attracted notable attention in the field of quantum optics, where it has been used to analyze the propagation of light in nonlinear media. This equation is a generalization of the standard nonlinear Schrödinger equation, which plays a foundational role in quantum mechanics. Several studies have been conducted on the perturbed stochastic NLSE in the past few decades, focusing on various aspects of the equation (Khan 2020, 2021; Zayed et al. 2022; Albosaily et al. 2020; Abdelrahman et al. 2021; Mohammed and El-Morshedy 2021; Biswas 2004; Saleh etal. 2007; Al-Ghafri et al. 2018; Biswas et al. 2017; Khan 2020; Zayed et al. 2022). These include the derivation of exact analytical solutions, the investigation of the effects of various types of perturbations on the system, and the analysis of the system’s stability and asymptotic behavior. The perturbed stochastic NLSE has also been used in the study of various nonlinear phenomena such as soliton propagation, dispersive shocks, turbulence, and optical rogue waves.

Optical solitons are a form of solitary wave that can propagate without scattering for long distances and thus retain their shape. Solitons models are extensively helpful in the mechanism of solitary wave-based communications links, optical pulse compressors, fiber optics, amplifiers, and several others (Seadawy et al. 2021). Finding the optical soliton solutions to stochastic differential equations is one of the fundamental physical problems (Foroutan et al. 2018; Jawad et al. 2017; Krishnan et al. 2018). So, the search for mathematical techniques to deduce exact solutions for these equations is a fundamental action.

In recent years, various mathematical techniques were proposed to search for solitary solutions of the nonlinear evolution equations, such as the simplest equation method (Arnous etal. 2017), exp-function method (Ekici etal. 2017), \(G^{^{\prime }}/G\)-expansion method (Mirzazadeh etal. 2014), first integral method (Ekici etal. 2016), sine-cosine function method (Mirzazadeh etal. 2015), extended trial equation method (Biswas etal. 2018), semi-inverse variational principle (Biswas etal. 2017), F-expansion method (Zhou etal. 2004), and Lie point symmetry (Abdel Kader etal. 2016, 2018). Zerarka et al. (2010), proposed an effective method for solving a wide class of linear and nonlinear wave equations which is called the functional variable method. After then, this method became popular among researchers, and more studies dealt with it for finding accurate solutions to some real and complex nonlinear evolution equations have been published (Zerarka and Ouamane 2010; Cevikel et al. 2012; Mirzazadeh and Eslami 2013; Eslami and Mirzazadeh 2013).

In this article, the main objective is constructing the optical soliton solutions to the perturbed stochastic NLSE that would be addressed with the generalized anti-cubic (GAC) law nonlinearity and the spatio-temporal dispersion (STD) having multiplicative noise by using the functional variable method.

The stochastic NLSE with multiplicative noise is given by Zayed et al. (2022)

$$\begin{aligned} iu_{t}+au_{xx}+bu_{xt}+\left[ \frac{c_{1}}{\left| u\right| ^{2n+2}} +c_{2}\left| u\right| ^{2n}+c_{3}\left| u\right| ^{2n+2} \right] u+\sigma \left( u-ibu_{x}\right) \frac{dW\left( t\right) }{dt}=0,~i= \sqrt{-1}, \end{aligned}$$
(1)

where \(u=u(x,t)\) is a complex-valued function that represents the wave profile, while \(c_{j}~(j=1,2,3),~a,~b,~\)and\(~\sigma\) are real-valued constant parameters. The first term is the linear temporal evolution, a represents the coefficient of chromatic dispersion (CD), b represents the coefficient of the STD, and the constants \(c_{j}~(j=1,2,3)\) are constants that arise from the GAC law nonlinearity with n being the generalized parameter, where \(-1<\) n \(<3~\) (Zayed et al. 2022). Finally, \(\sigma\) is the coefficient of noise strength and \(W\left( t\right)\) is the typical Wiener process, such that \(\frac{dW\left( t\right) }{dt}\) is the white noise. When \(\sigma =0\), the newly structured model turns into the NLSE without the stochastic factor in Biswas (2019); Kudryashov (2022) andZayed et al. (2020).

In Zayed et al. (2022), Eq. (1) is solved by Jacobi’s elliptic function approach and the modified Kudryashov’s algorithm with setting \(c_{2}=0\). In this paper, we study Eq. (1) when \(c_{2}\ne 0\) by using the functional variable method which is reliable and effective. Moreover, we obtain new doubly periodic solutions in the form of Weierstrass, hyperbolic, rational, and Jacobi elliptic functions for Eq. (1) when n equals \(1,~\frac{-4}{3},~\)and \(\frac{-1}{3}\). Several optical soliton solutions were proposed, including dark, bright, and compacton soliton solutions.

This paper has the following manner: in Sect. 2, we introduce the functional variable method. In Sect. 3, the functional variable method is applied to the stochastic NLSE Eq. (1). While in Sects. 4, 5, and 6, we obtain the optical soliton solution of Eq. (1) at n equals 1, \(\frac{-4}{3}\), and \(\frac{-1}{3},\) respectively. Finally, in Sect. 7, we give the conclusion of this paper.

2 Functional variable method

Consider a nonlinear evolution equation

$$\begin{aligned} P(u,u_{t},u_{x},u_{tt},u_{xx},u_{xt},...)=0, \end{aligned}$$
(2)

where P is a polynomial in u and its partial derivatives.

To find the travelling wave solution of Eq. (2) we introduce the wave variable \(\xi =x-ct\) (Eslami and Mirzazadeh 2013) such that

$$\begin{aligned} u(x,t)=U(\xi ). \end{aligned}$$
(3)

Then Eq. (2) can be converted to an ordinary differential equation as

$$\begin{aligned} Q(U,U^{\prime },U^{\prime \prime },...)=0, \end{aligned}$$
(4)

where Q is a polynomial in U and its total derivatives, and \((.)^{\prime }=\frac{d(.)}{d\xi }.\)

Let us make a transformation in which the unknown function \(U(\xi )\) is considered as a functional variable in the form (Zerarka et al. 2010)

$$\begin{aligned} U^{\prime }=F(U), \end{aligned}$$
(5)

and some successive derivatives of U are

$$\begin{aligned} U^{\prime \prime }& {} = \frac{dF(U)}{dU}\frac{dU}{d\xi }=\frac{dF(U)}{dU}F(U)= \frac{1}{2}\frac{d}{dU}(F^{2}(U)), \nonumber \\ U^{\prime \prime \prime }& {} = \frac{1}{2}\frac{d^{2}(F^{2}(U))}{dU^{2}}\sqrt{ F^{2}(U)}, \\ U^{\prime \prime \prime \prime }& {} = \frac{1}{2}\left[ \frac{d^{3}(F^{2}(U))}{ dU^{3}}F^{2}(U)+\frac{1}{2}\frac{d^{2}(F^{2}(U))}{dU^{2}}\frac{d(F^{2}(U))}{ dU}\right] . \nonumber \end{aligned}$$
(6)

Eq. (4) can be reduced in terms of U,  F,  and its derivatives upon using the expressions of Eq (6) into Eq. (4) gives

$$\begin{aligned} Q(U,F,\frac{dF(U)}{dU},\frac{d^{2}(F(U))}{dU^{2}},\frac{d^{3}(F(U))}{dU^{3}},...)=0. \end{aligned}$$
(7)

This particular equation, Eq. (7), is particularly noteworthy because it allows for analytical solutions for a large class of nonlinear wave-type equations. Following integration, Eq. (7) yields the expression of F, combined with Eq. (5), resulting in appropriate solutions for the original problem.

3 Application to perturbed stochastic NLSE

To solve the perturbed stochastic NLSE Eq. (1), we use a wave transformation involving the noise coefficient \(\sigma\) and the Wiener process W(t) as:

$$\begin{aligned} u(x,t)=\psi (z)e^{i\left[ \beta (x,t)+\sigma W(t)\right] }, \end{aligned}$$
(8)

where \(\psi (z)\) and \(\beta (x,t)\) are real non-zero functions, and

$$\begin{aligned} z=x-\nu t,~\beta (x,t)=-kx+(\omega -\sigma ^{2})t, \end{aligned}$$
(9)

where \(\nu ,~k,\) and \(\omega\) are real constants that represent soliton velocity, soliton frequency, and wave number, respectively. Plugging Eq. ( 8) into Eq. (1) causes to the real part

$$\begin{aligned} c_{1}-\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) \psi ^{2+2n}+c_{2}\psi ^{2+4n}+c_{3}\psi ^{4+4n}+(a-b\nu )\psi ^{1+2n}\psi ^{\prime \prime }=0, \end{aligned}$$
(10)

and the imaginary part

$$\begin{aligned} (2ak-(-1+bk)\nu +b(\sigma ^{2}-\omega ))\psi ^{1+2n}\psi ^{\prime }=0. \end{aligned}$$
(11)

Eq. (11) gives the soliton velocity

$$\begin{aligned} \nu =\frac{2ak+b(\sigma ^{2}-\omega )}{bk-1},~bk\ne 1. \end{aligned}$$
(12)

Substituting the soliton velocity to the real part, Eq. (10) becomes

$$\begin{aligned}{} & {} c_{1}-\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) \psi ^{2+2n}+c_{2}\psi ^{2+4n}\nonumber \\{} & {} +c_{3}\psi ^{4+4n}-\frac{(a+abk+b^{2}(\sigma ^{2}-\omega ))}{bk-1}\psi ^{1+2n}\psi ^{\prime \prime }=0. \end{aligned}$$
(13)

According to the functional variable method, let

$$\begin{aligned} \psi ^{\prime }(z)=F(\psi (z)), \end{aligned}$$
(14)

then, Eq. (13) reduces to

$$\begin{aligned} c_{1}-\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) \psi ^{2+2n}+c_{2}\psi ^{2+4n}+c_{3}\psi ^{4+4n}- \end{aligned}$$
$$\begin{aligned} \frac{(a+abk+b^{2}(\sigma ^{2}-\omega ))}{bk-1}\psi ^{1+2n}F(\psi )F^{\prime }(\psi )=0. \end{aligned}$$
(15)

Solving the differential equation (15), we can get

$$\begin{aligned} F^{2}& {} = 2A-\frac{(-1+bk)\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{ (a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{2}-\frac{c_{1}(-1+bk)}{ n(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{-2n} \nonumber \\ & {}\quad+ \frac{c_{2}(-1+bk)}{(1+n)(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{2+2n}+ \frac{c_{3}(-1+bk)}{(2+n)(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{4+2n}, \end{aligned}$$
(16)

where A is the constant of integration. From Eqs. (14) and (16 ), we get

$$\begin{aligned} (\psi ^{\prime })^{2}=2A-\frac{(-1+bk)\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{2}-\frac{ c_{1}(-1+bk)}{n(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{-2n}+ \end{aligned}$$
$$\begin{aligned} \frac{c_{2}(-1+bk)}{(1+n)(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{2+2n}+ \frac{c_{3}(-1+bk)}{(2+n)(a+abk+b^{2}(\sigma ^{2}-\omega ))}\psi ^{4+2n}. \end{aligned}$$
(17)

Taking the transformation

$$\begin{aligned} \psi (z)=g^{\frac{1}{n+1}}(z), \end{aligned}$$
(18)

Eq. (17) becomes

$$\begin{aligned} (g^{\prime })^{2}& {} = -\frac{c_{1}(-1+bk)(1+n)^{2}}{n(a+abk+b^{2}(\sigma ^{2}-\omega ))}-\frac{(-1+bk)(1+n)^{2}\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{2} \nonumber \\& \quad+ \frac{c_{3}(-1+bk)(1+n)^{2}}{(2+n)(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{4}+ \frac{c_{2}(-1+bk)(1+n)}{(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{\frac{2+4n}{ 1+n}} \nonumber \\& \quad+ 2A(1+n)^{2}g^{\frac{2n}{1+n}}. \end{aligned}$$
(19)

In the following sections, we will obtain the soliton solution of Eq. (19) for some cases of n, and hence the soliton solution of the perturbed stochastic NLSE Eq. (1).

4 Exact solutions of Eq. (1) at \(n=1\)

Taking \(n=1\) and \(A=0\), Eq. (19) reduces to

$$\begin{aligned} (g^{\prime })^{2}& {} = -\frac{4c_{1}(-1+bk)}{(a+abk+b^{2}(\sigma ^{2}-\omega )) }-\frac{4(-1+bk)\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{ (a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{2}+ \nonumber \\{} & {} \frac{2c_{2}(-1+bk)}{(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{3}+\frac{ 4c_{3}(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{4}. \end{aligned}$$
(20)

Introducing the new variable H(z) such that

$$\begin{aligned} g(z)=H(z)+j, \end{aligned}$$
(21)

Eq. (20) converts to

$$\begin{aligned} (H^{\prime })^{2}=a_{0}+a_{1}H+a_{2}H^{2}+a_{3}H^{3}+a_{4}H^{4}, \end{aligned}$$
(22)

where

$$\begin{aligned} a_{0}& {} = -\frac{2(-1+bk)(6c_{1}+j^{2}(-3c_{2}j-2c_{3}j^{2}+6ak^{2}+6(-1+bk)( \sigma ^{2}-\omega )))}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ a_{1}& {} = \frac{2j(-1+bk)(9c_{2}j+8c_{3}j^{2}-12ak^{2}-12(-1+bk)(\sigma ^{2}-\omega ))}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ a_{2}& {} = -\frac{2(-1+bk)(-3c_{2}j-4c_{3}j^{2}+2ak^{2}+2(-1+bk)(\sigma ^{2}-\omega ))}{(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ a_{3}& {} = \frac{2(3c_{2}+8c_{3}j)(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ a_{4}& {} = \frac{4c_{3}(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}. \end{aligned}$$

Eq. (22) has many solutions listed in Zhang et al. (2008); Hong and Lu (2012); Zhou et al. (2004). The following soliton solutions are chosen.

4.1 The first solution is

$$\begin{aligned} H(z)=cn(z|m), \end{aligned}$$
(23)

where cn is the Jacobi elliptic cosine function with modulus m. Equation (23) is satisfied under the following conditions:

$$\begin{aligned} c_{1}& {} = -\frac{a}{8m^{2}(-2+4bk+b^{2}(-1-2k^{2}+2m^{2}))},~c_{2}=\frac{2am \sqrt{-2+4m^{2}}}{-2+4bk+b^{2}(-1-2k^{2}+2m^{2})}, \\ c_{3}& {} = \frac{3am^{2}}{4-4bk+b^{2}(2+4k^{2}-4m^{2})},~\omega =\frac{ a(1-2k^{2}-2m^{2}+b(k+2k^{3}-2km^{2}))}{2-4bk+b^{2}(1+2k^{2}-2m^{2})}+\sigma ^{2}, \\ ~j& {} = \pm \frac{\sqrt{-1+2m^{2}}}{\sqrt{2}m}. \end{aligned}$$

By inserting Eq. (23) and pairing it with Eqs. (21) and (18 ) into Eq. (8), we get

$$\begin{aligned} \left| u\right| =\left( cn(z|m)\pm \frac{\sqrt{-1+2m^{2}}}{\sqrt{2}m} \right) ^{\frac{1}{2}}. \end{aligned}$$
(24)

When \(m=1,\) the solution given in Eq. (24) degenerates to

$$\begin{aligned} \left| u\right| =(\mathrm{}{sech}(z)\pm \frac{1}{\sqrt{2}})^{\frac{1}{ 2}}. \end{aligned}$$
(25)
Fig. 1
figure 1

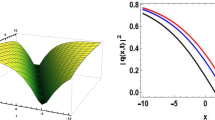
Simulations of the Eq. (25), for parameteric values \(b=a=\sigma =1,~k=2,~\)and j= \(\frac{1}{\sqrt{2}}\)

Full size image
Fig. 2
figure 2

Simulations of the Eq. (25), for parameteric values \({\small b=a=\sigma =1,~k=2,\ }\text {and }{\small ~j=} \frac{-1}{\sqrt{2}}\)

Full size image

4.2 The second solution is

$$\begin{aligned} H(z)=\frac{mdn(z|m)cn(z|m)}{1+msn^{2}(z|m)}, \end{aligned}$$
(26)

where sn and dn are the Jacobi elliptic functions with modulus m. Equation ( 26) is satisfied under the following conditions:

$$\begin{aligned} c_{1}& {} = \frac{am(1+m)^{4}}{32(2-4bk+b^{2}(1+2k^{2}-6m+m^{2}))},~c_{2}=- \frac{4a\sqrt{2m(-1+6m-m^{2})}}{m(2-4bk+b^{2}(1+2k^{2}-6m+m^{2}))}, \\ c_{3}& {} = \frac{6a}{m(2-4bk+b^{2}(1+2k^{2}-6m+m^{2}))},~~j=\frac{\sqrt{ m(-1+6m-m^{2})}}{2\sqrt{2}}, \\ \omega& {} = \frac{a(1-2k^{2}-6m+m^{2}+bk(1+2k^{2}-6m+m^{2}))}{ 2-4bk+b^{2}(1+2k^{2}-6m+m^{2})}+\sigma ^{2}. \end{aligned}$$

By inserting Eq. (26) and pairing it with Eqs. (21) and (18 ) into Eq. (8), we get

$$\begin{aligned} \left| u\right| =\left( \frac{mdn(z|m)cn(z|m)}{1+msn^{2}(z|m)}+\frac{ \sqrt{m(-1+6m-m^{2})}}{2\sqrt{2}}\right) ^{\frac{1}{2}}. \end{aligned}$$
(27)

Substituting \(m=1\) in Eq. (27), we get the bright soliton solution

$$\begin{aligned} \left| u\right| =\left( \frac{\mathrm{}{sech}^{2}(z)}{1+\tanh ^{2}(z)} +\frac{1}{\sqrt{2}}\right) ^{\frac{1}{2}}. \end{aligned}$$
(28)
Fig. 3
figure 3

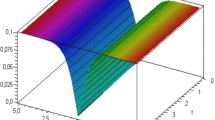
Simulations of the Eq. (28), for parameteric values \({\small b=a=\sigma =1,~}\text {and}{\small ~k=2}\)

Full size image

4.3 The third solution is

$$\begin{aligned} H(z)=\frac{1}{1+\mathrm{}{sech}^{2}(z)}, \end{aligned}$$
(29)

with

$$\begin{aligned} a& {} = -\frac{(32-64bk+b^{2}(17+9\sqrt{17}+32k^{2}))(\sigma ^{2}-\omega )}{17+9 \sqrt{17}-32k^{2}+bk(17+9\sqrt{17}+32k^{2})}, \\ c_{1}& {} = \frac{(107+51\sqrt{17})(\sigma ^{2}-\omega )}{128(17+9\sqrt{17} -32k^{2}+bk(17+9\sqrt{17}+32k^{2}))}, \\ c_{2}& {} = -\frac{32(3+\sqrt{17})(\sigma ^{2}-\omega )}{17+9\sqrt{17} -32k^{2}+bk(17+9\sqrt{17}+32k^{2})}, \\ ~c_{3}& {} = \frac{192(\sigma ^{2}-\omega )}{17+9\sqrt{17}-32k^{2}+bk(17+9\sqrt{ 17}+32k^{2})}, \\ j& {} = \frac{1}{16}(-7+\sqrt{17}). \end{aligned}$$

By inserting Eq. (29) and pairing it with Eqs. (21) and (18 ) into Eq. (8), we get the dark soliton solution

$$\begin{aligned} \left| u\right| =\left( \frac{1}{1+\mathrm{}{sech}^{2}(z)}+j\right) ^{ \frac{1}{2}}. \end{aligned}$$
(30)
Fig. 4
figure 4

Simulations of the Eq. (30), for parameteric values \({\small b=\sigma =1,~k=\omega =2}\)

Full size image

5 Exact solutions of Eq. (1) at \(n=-\frac{4}{3}\)

Equation (19) at \(n=-\frac{4}{3}\) can be written as the following

$$\begin{aligned} (g^{\prime })^{2}& {} = \frac{c_{1}(-1+bk)}{12(a+abk+b^{2}(\sigma ^{2}-\omega )) }-\frac{(-1+bk)\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{ 9(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{2}+ \nonumber \\{} & {} \frac{c_{3}(-1+bk)}{6(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{4}+\frac{2}{9} Ag^{8}-\frac{c_{2}(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{10}. \end{aligned}$$
(31)

Applying the transformation

$$\begin{aligned} g(z)=\sqrt{H(z)+j}, \end{aligned}$$
(32)

Eq. (31) converts to

$$\begin{aligned} (H^{\prime })^{2}=b_{0}+b_{1}H+b_{2}H^{2}+b_{3}H^{3}+b_{4}H^{4}+b_{5}H^{5}+b_{6}H^{6}, \end{aligned}$$
(33)

where

$$\begin{aligned} b_{0}& {} = j(3c_{1}(-1+bk)+6c_{3}j^{2}(-1+bk)+4j(-3c_{2}j^{4}(-1+bk)+a(k^{2}-bk^{3}+2Aj^{3}(1+bk))\\{} & {}\quad +(2Ab^{2}j^{3}-(-1+bk)^{2})(\sigma ^{2}-\omega )))/(9(a+abk+b^{2}(\sigma ^{2}-\omega ))), \\ b_{1}& {} = (3c_{1}(-1+bk)+2j(9c_{3}j(-1+bk)+4(-9c_{2}j^{4}(-1+bk)+a(k^{2}-bk^{3}+5Aj^{3}(1+bk))\\{} & {}\quad +(5Ab^{2}j^{3}-(-1+bk)^{2})(\sigma ^{2}-\omega ))))/(9(a+abk+b^{2}(\sigma ^{2}-\omega ))), \\ b_{2}& {} = 2(9c_{3}j(-1+bk)-90c_{2}j^{4}(-1+bk)+2a(k^{2}-bk^{3}+20Aj^{3}(1+bk))+2(20Ab^{2}j^{3}-\\{} & {} (-1+bk)^{2})(\sigma ^{2}-\omega ))/(9(a+abk+b^{2}(\sigma ^{2}-\omega ))),\\ b_{3}& {} = (6c_{3}(-1+bk)+80j^{2}(-3c_{2}j(-1+bk)+aA(1+bk)+Ab^{2}(\sigma ^{2}-\omega )))/(9(a+abk \\{} & {} +b^{2}(\sigma ^{2}-\omega ))), \\ b_{4}& {} = 20j(-9c_{2}j(-1+bk)+2aA(1+bk)+2Ab^{2}(\sigma ^{2}-\omega ))/(9(a+abk+b^{2}(\sigma ^{2}-\omega ))), \\ b_{5}& {} = 8(-9c_{2}j(-1+bk)+aA(1+bk)+Ab^{2}(\sigma ^{2}-\omega ))/(9(a+abk+b^{2}(\sigma ^{2}-\omega ))), \\ b_{6}& {} = -4c_{2}(-1+bk)/(3(a+abk+b^{2}(\sigma ^{2}-\omega ))). \end{aligned}$$

Eq. (33) has the following solution (Zhang et al. 2008):

$$\begin{aligned} H(z)=\sqrt{\frac{-b_{2}b_{4}\mathrm{}{sech}^{2}(\sqrt{b_{2}}z)}{ b_{4}^{2}-b_{2}b_{6}(1+\tanh (\sqrt{b_{2}}z))^{2}}}, \end{aligned}$$
(34)

with

$$\begin{aligned} c_{1}& {} = \frac{104aAj^{4}}{3(61Ab^{2}j^{3}+3(-1+bk)^{2})},c_{2}=-\frac{aA}{ 3j(61Ab^{2}j^{3}+3(-1+bk)^{2})}, \\ \omega& {} = \frac{3ak^{2}(-1+bk)+61aAj^{3}(1+bk)+(61Ab^{2}j^{3}+3(-1+bk)^{2}) \sigma ^{2}}{61Ab^{2}j^{3}+3(-1+bk)^{2}}, \\ c_{3}& {} = \frac{80aAj^{2}}{3(61Ab^{2}j^{3}+3(-1+bk)^{2})},~j>0,~A<0. \end{aligned}$$

By inserting Eq. (34) and pairing it with Eqs. (32) and (18 ) into Eq. (8), we get the dark soliton solution

$$\begin{aligned} \left| u\right| =\left( \sqrt{\frac{-b_{2}b_{4}\mathrm{}{sech}^{2}( \sqrt{b_{2}}z)}{b_{4}^{2}-b_{2}b_{6}(1+\tanh (\sqrt{b_{2}}z))^{2}}}+j\right) ^{\frac{-3}{2}}. \end{aligned}$$
(35)
Fig. 5
figure 5

Simulations of the Eq. (35), for parameteric values \({\small b=j=\sigma =1,~k=a=2,~}\)and \({\small A=-1}\)

Full size image

6 Exact solutions of Eq. (1) at \(n=-\frac{1}{3}\)

Equation (19) at \(n=-\frac{1}{3}\) and \(A=0\) takes the form

$$\begin{aligned} (g^{\prime })^{2}& {} = \frac{4c_{1}(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega )) }+\frac{2c_{2}(-1+bk)}{3(a+abk+b^{2}(\sigma ^{2}-\omega ))}g- \nonumber \\{} & {} \frac{4(-1+bk)\left( ak^{2}+(-1+bk)(\sigma ^{2}-\omega )\right) }{ 9(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{2}+\frac{4c_{3}(-1+bk)}{ 15(a+abk+b^{2}(\sigma ^{2}-\omega ))}g^{4}. \end{aligned}$$
(36)

Applying the transformation

$$\begin{aligned} g(z)=H(z)+j, \end{aligned}$$
(37)

Eq. (36) becomes

$$\begin{aligned} (H^{\prime })^{2}=d_{0}+d_{1}H+d_{2}H^{2}+d_{3}H^{3}+d_{4}H^{4}, \end{aligned}$$
(38)

where

$$\begin{aligned} d_{0}& {} = \frac{2(-1+bk)(30c_{1}+j(15c_{2}+6c_{3}j^{3}-10j(ak^{2}+(-1+bk)( \sigma ^{2}-\omega ))))}{45(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ d_{1}& {} = \frac{2(-1+bk)(15c_{2}-4j(-6c_{3}j^{2}+5ak^{2}+5(-1+bk)(\sigma ^{2}-\omega )))}{45(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ d_{2}& {} = -\frac{4(-1+bk)(-18c_{3}j^{2}+5ak^{2}+5(-1+bk)(\sigma ^{2}-\omega )) }{45(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ d_{3}& {} = \frac{16c_{3}j(-1+bk)}{15(a+abk+b^{2}(\sigma ^{2}-\omega ))}, \\ d_{4}& {} = \frac{4c_{3}(-1+bk)}{15(a+abk+b^{2}(\sigma ^{2}-\omega ))}. \end{aligned}$$

As mentioned above, Eq. (38) has many solutions listed in Zhang et al. (2008); Hong and Lu (2012); Zhou et al. (2004), so we select the soliton solutions as follow:

6.1 The first solution is

$$\begin{aligned} H(z)=\frac{1}{1+qz+rz^{2}}, \end{aligned}$$
(39)

with

$$\begin{aligned} c_{1}& {} = \frac{9ar^{4}}{ 2(q^{2}-4r)^{2}(2(-1+bk)^{2}q^{2}-r(8-16bk+b^{2}(8k^{2}+27r)))}, \\ c_{2}& {} = -\frac{24ar^{3}}{ (q^{2}-4r)(2(-1+bk)^{2}q^{2}-r(8-16bk+b^{2}(8k^{2}+27r)))}, \\ c_{3}& {} = -\frac{15a(q^{2}-4r)^{2}}{ 4(-1+bk)^{2}q^{2}-2r(8-16bk+b^{2}(8k^{2}+27r))}, \\ \omega& {} = \frac{a(-2k^{2}(q^{2}-4r)+2bk^{3}(q^{2}-4r)-27r^{2}(1+bk))}{ 2(-1+bk)^{2}q^{2}-r(8-16bk+b^{2}(8k^{2}+27r))}+\sigma ^{2}, \\ j& {} = \frac{r}{q^{2}-4r}, \end{aligned}$$

where q and r are constants and \(q^{2}<4r.\) By inserting Eq. (39) and pairing it with Eqs. (37) and (18) into Eq. (8), we get the compacton soliton solution

$$\begin{aligned} \left| u\right| =\left( \frac{1}{1+qz+rz^{2}}+\frac{r}{q^{2}-4r} \right) ^{\frac{3}{2}}. \end{aligned}$$
(40)
Fig. 6
figure 6

Simulations of the Eq. (40), for parameteric values \({\small b=a=\sigma =r=q=1,~k=2}\)

Full size image

6.2 The second solution is

$$\begin{aligned} H(z)=\frac{1}{q+\wp (\frac{\sqrt{C_{3}}}{2}z;\{\frac{-4C_{1}}{C_{3}},\frac{ -4C_{0}}{C_{3}}\})}, \end{aligned}$$
(41)

with

$$\begin{aligned} C_{0}& {} = -\frac{ 8(-1+bk)^{2}(c_{3}(1+10jq+24j^{2}q^{2}+16j^{3}q^{3})-5c_{2}q^{3})}{ 30a(1+6jq)-27b^{2}(5c_{2}q+4c_{3}j^{2}(1+2jq))}, \\ C_{1}& {} = -\frac{4(-1+bk)^{2}(8c_{3}j(1+6jq+6j^{2}q^{2})-15c_{2}q^{2})}{ 30a(1+6jq)-27b^{2}(5c_{2}q+4c_{3}j^{2}(1+2jq))}, \\ C_{3}& {} = -\frac{4(-1+bk)^{2}(5c_{2}-16c_{3}j^{3})}{ 30a(1+6jq)-27b^{2}(5c_{2}q+4c_{3}j^{2}(1+2jq))}, \\ c_{1}& {} = \frac{-5c_{2}j(1+3jq)+2c_{3}j^{4}(5+6jq)}{10+60jq}, \\ \omega& {} = \frac{ -36c_{3}j^{2}(1+2jq)+5(-9c_{2}q+2ak^{2}(1+6jq)+2(-1+bk)(1+6jq)\sigma ^{2})}{ 10(-1+bk)(1+6jq)}. \end{aligned}$$

By inserting Eq. (41) and pairing it with Eqs. (37) and (18 ) into Eq. (8), we get

$$\begin{aligned} \left| u\right| =\left( \frac{1}{q+\wp (\frac{\sqrt{C_{3}}}{2}z;\{ \frac{-4C_{1}}{C_{3}},\frac{-4C_{0}}{C_{3}}\})}+j\right) ^{\frac{3}{2}}. \end{aligned}$$
(42)

Where q is a constant and \(\wp\) is a Weierstrass elliptic function (Farahat et al. 2023). For

$$\begin{aligned} c_{2}& {} = \frac{-16c_{3}j^{3}(135-35\sqrt{3(3+4jq)(1+12jq)}+12jq(55+48jq-4 \sqrt{3(3+4jq)(1+12jq)}))}{45(9+4jq(15-32jq)+3\sqrt{3(3+4jq)(1+12jq)})}, \\ d& {} = -\frac{3+4jq+\sqrt{3(3+4jq)(1+12jq)}}{8j}, \end{aligned}$$

the solution given in Eq. (42) degenerates to the following bright soliton solution (Farahat et al. 2023; Gradshteyn , Ryzhik 2007)

$$\begin{aligned} \left| u\right| =\left( \frac{1}{q+(-d+\frac{3d}{2}\coth ^{2}(\sqrt{ \frac{3d}{2}}\frac{\sqrt{C_{3}}}{2}z))}+j\right) ^{\frac{3}{2}}. \end{aligned}$$
(43)

When

$$\begin{aligned} a> & {} \frac{\sqrt{3}}{40}\sqrt{\frac{b^{4}c_{3}^{2}(3+4jq)^{3}(1+12jq)}{q^{4}} }+\frac{3b^{2}c_{3}(3+24jq+32j^{2}q^{2})}{40q^{2}},q<0,c_{3}>0,b>0, \\ j> & {} \frac{-3}{4q},k>\frac{1}{b}. \end{aligned}$$
Fig. 7
figure 7

Simulations of the Eq. (43), for parameteric values \({\small b=\sigma =1,~c}_{3}{\small =0.5,} {\small k=3,~j=2,~q=-3,~}\)and \({\small a=10}\)

Full size image

6.3 The third solution is

$$\begin{aligned} H(z)=\frac{-2d_{2}d_{3}\mathrm{}{sech}^{2}(\frac{\sqrt{d_{2}}}{2}z)}{ d_{3}^{2}-d_{2}d_{4}(1-\tanh (\frac{\sqrt{d_{2}}}{2}z))^{2}}, \end{aligned}$$
(44)

with

$$\begin{aligned} c_{1}& {} = \frac{3c_{3}j^{4}}{5}-\frac{1}{3}j^{2}(ak^{2}+(-1+bk)(\sigma ^{2}-\omega )),~c_{2}=\frac{4j(-6c_{3}j^{2}+5ak^{2}+5(-1+bk)(\sigma ^{2}-\omega ))}{15}, \\ a> & {} -\frac{b^{2}(\sigma ^{2}-\omega )}{1+bk},c_{3}>\frac{ 5(ak^{2}+(-1+bk)(\sigma ^{2}-\omega ))}{18j^{2}},k>0,~j>0,~b>\frac{1}{k},\omega <0. \end{aligned}$$

By inserting Eq. (44) and pairing it with Eqs. (37) and (18 ) into Eq. (8), we get the dark soliton solution

$$\begin{aligned} \left| u\right| =\left( \frac{-2d_{2}d_{3}\mathrm{}{sech}^{2}(\frac{ \sqrt{d_{2}}}{2}z)}{d_{3}^{2}-d_{2}d_{4}(1-\tanh (\frac{\sqrt{d_{2}}}{2} z))^{2}}+j\right) ^{\frac{3}{2}}. \end{aligned}$$
(45)
Fig. 8
figure 8

Simulations of the Eq. (45), for parameteric values \({\small b=2,~\sigma =3,~j=k=1,}{\small \omega =-2,~a=-1,~}\) and \({\small c}_{3} {\small =4}\)

Full size image

7 Conclusions

In this work, we obtained optical soliton solutions for the perturbed stochastic NLSE with generalized anti-cubic nonlinearity and multiplicative white noise. Using the traveling wave transformation Eq. (8), the perturbed stochastic NLSE is transformed into the ODE (13). Using the functional variable method, Eq. (13) is transformed into the first-order ODE (17) which is solved at some different values of n. New doubly periodic solutions in the form of Jacobi elliptic functions are given in Eqs. (24) and (27), Weierstrass elliptic function is given in Eq. (42), hyperbolic functions are given in Eqs. (30), (35), and (45), and rational function is given in Eq. (40) are obtained for Eq. (1). For \(n=1\), we obtain bright soliton solutions given in Eqs. (25) and (28), compacton soliton solution given in Eq. (25), and dark soliton solution given in Eq. (30). For \(n=\frac{-4}{3}\), the dark soliton solution given in Eq. (35) obtained of Eq. (1). For \(n=\frac{-1}{3}\), the compacton soliton solution given in Eq. (40), bright soliton solution given in Eq. (43), and dark soliton solution given in Eq. (45) are obtained. In addition, 3D, contour plots, and soliton propagation of solutions, were introduced to show the physical movements of observed solutions by assigning different values to parameters. The perspective view of the dark solutions for the Eqs. (30), (35), and (45) can be seen in Figs. 4, 5, and 8, respectively. Also, the bright solutions for Eqs. (25), (28), and (43) can be seen in Figs. 1, 3, and 7, respectively. While the compacton solutions for the Eqs. (25) and (40) can be seen in Figs. 2 and 6, respectively.