1 Introduction

The SOAs technology has become increasingly important for the use, improvement, and optimization of photonic circuits, networks, and subsystems in recent years (Zoiros 2018, Volet et al. 2017 and Perin et al. 2016). The SOAs demonstrate numerous fundamental characteristics, such as broad band, significant nonlinearities, wide dynamic range, minimum power consumption, flexible range of wavelengths, rapid response, varied operations and small footprint (Pleros et al. 2007). These desirable characteristics have made the SOAs essential elements to accomplish the major and at fundamentally critical tasks (Rizou et al. 2017). Despite all these desirable characteristics, the usage of SOAs is quite restricted in linear amplification systems, however there is utilize of SOAs in such applications (Bonk et al. 2012).

One of the major limitation of SOAs is its low output saturation power, Psat. There are many methods to improve the output saturation power including decreasing the optical confinement factor (Brenot et al. 2005), the use of flared waveguides (Bendelli et al. 1991), gain clamping (Giuliani and D’Alessandro 2000), and pump beams (Yoshino and Inoue 1996).

Recently, high efficient, high gain, and high saturation output power quantum-dot SOAs grown on Si and its applications are demonstrated by Liu et al. (2020). Moreover, the fundamental study of saturation output power on quantum-dot SOA under high temperature was presented by Kuwahata et al. (2019). Additionally, the characterization of the wideband semiconductor optical amplifier was investigated by Beshr et al. numerically and by simulation (Beshr and Aly 2023).

In this paper, we present a comprehensive model of output saturation power and fiber-to-fiber gain of wideband SOAs. We investigate the effects of optical confinement factor and bias current on improving the output power saturation and fiber-to-fiber gain, Moreover, we study the impact of bias current, input signal power, temperature, and amplifier length on the fiber-to-fiber gain spectrum in the C-band. The obtained numerical results show a good accordance with the ones obtained by simulation.

The format of this paper is as follows. In Sect. 2, a comprehensive model of output saturation power and fiber-to-fiber gain of wideband SOAs is described. Section 3 presents and discusses the numerical results, including comparisons between numerical and simulation approaches. Section 4 is dedicated to main conclusions.

2 Mathematical model

2.1 Improvement of output power saturation

One of the major characteristics of SOA is the high output power saturation; mainly for power booster and multichannel applications. A simple rate equation model is utilized to define the parameters that affect SOA gain at high input power. At the signal wavelength, the coefficient of material gain, gm, is thought to be a linear function of carrier density, n, such as

$$ {\text{g}}_{{\text{m}}} = {\text{a}}_{1} \left( {{\text{n}} - {\text{n}}_{0} } \right) $$
(1)

where a1 is the differentiation of gm with respect to n, n0 is the transparency carrier density.

The coefficient of material gain gm (m−1) showing the bulk-material active area of InGaAsP with direct bandgap as a function of wavelength of the signal is determined as (Connelly 2001).

$$ {\text{g}}_{{\text{m}}} \left( {\lambda , n} \right) = \frac{{\lambda^{2} }}{{4 \sqrt 2 \pi^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} n_{eq} \tau }} \left( {\frac{{2 m_{e} m_{hh} }}{{\hbar \left( {m_{e} + m_{hh} } \right)}}} \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \chi \sqrt {\frac{c}{\lambda } - \frac{{E_{go} - \Delta E_{g } \left( n \right)}}{h}} \left( {f_{c} \left( \lambda \right) - f_{\upsilon } \left( \lambda \right)} \right) $$
(2)

where mhh stands for the effective mass of the heavy hole in the valance band and me stands for the effective mass of the electron in the conduction band. The probability distributions of Fermi–Dirac for conduction and valance band are denoted by fc(λ) and fυ(λ), correspondingly, Eg0, the no carrier injection bandgap energy, ΔEg (n) is the shrinkage band-gap caused by injection (Adachi 1992).

The carrier density rate equation

$$ \frac{dn}{{dt}} = \frac{J}{ed} - \frac{n}{\tau } - a_{1} \left( {n - n_{0} } \right)\frac{{I_{s} }}{h\nu } $$
(3)

The travelling-wave equation describes how the signal intensity, Is, moves across the SOA

$$ \frac{{{\text{dI}}_{{\text{s}}} }}{{{\text{dz}}}} = { }\left[ {{\Gamma a}_{1} \left( {{\text{n}} - {\text{n}}_{0} } \right) - {\upalpha }} \right]{\text{I}}_{{\text{s}}} $$
(4)

where the time is denoted by t, z is the direction of propagation, J stands for the active region’s current density, e for the electron’s charge, d for the thickness of the active region, τ for the lifespan of the spontaneous carrier, h for Planck’s constant, υ for the optical signal’s frequency, and α for the coefficient of waveguide loss.

The output power saturation is well-described as the output power obtained by the SOA when the gain is decreased by 3 dB.

The output power saturation is determined by (Connelly 2007)

$$ P_{sat } = \frac{{A I_{sat,out} }}{\Gamma } $$
(5)

where A represents the size of the active region, Γ stands for confinement factor, and \(I_{sat,out} \) represents the saturation output intensity, given by (Connelly 2007)

$$ I_{sat,out} = \frac{{\ln \left( 2 \right) G_{0} I_{sat} }}{{G_{0} - 2}} $$
(6)

The unsaturated gain, G0 is defined as (Connelly 2007)

$$ {\text{G}}_{0} = \exp \left( {{\Gamma g}_{{0{ }}} {\text{ L}}} \right) $$
(7)

where the intensity of saturation, \(I_{sat }\)., and the power of saturation, \(P_{sat} , \) are determinedrespectively, as

$$ I_{sat } = \frac{h \nu }{{a_{1} \tau }} $$
(8)
$$ P_{sat} = \frac{{AI_{sat} }}{\Gamma } $$
(9)

where L is the amplifier length and g0 is the coefficient of unsaturated material gain.

2.2 Fiber to fiber gain of SOA

The intrinsic gain, G, taking into account coupling losses at the input and output is referred to as the fiber to fiber gain, G(υ), at the optical frequency υ.

The fiber to fiber gain at the optical frequency, υ, is given by (Connelly 2001)

$$ {\text{G}}_{{\text{s}}} ({\upupsilon }) = \exp \left\{ {\int\limits_{0}^{L} {\left[ {{\text{g}}_{{\text{m}}} ({\upupsilon },\;{\text{n}}) - {\upalpha }({\text{n}}){\text{dz}}} \right]} } \right. $$
(10)

where α(n) is the coefficient of material loss (Connelly and O’Dowd 1995).

3 Results and discussion

In this section, we present the numerical findings from MATLAB and compare them with the simulation results that are performed by OptiSystem. An excellent accordance is achieved between numerical and simulation results. Table 1 shows the material parameters and geometrical for the SOA use in this simulation.

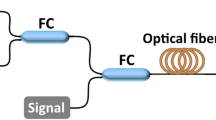
Table 1 Material parameters and geometrical used in simulation (M.J. Connelly 2001)
Full size table

The setup configuration, used in simulation, is built using OptiSystem as shown in Fig. 1.

Fig. 1
figure 1

Setup configuration using OptiSystem

Full size image

3.1 Output power saturation: impact of confinement factor

As a function of output power saturation at various optical confinement factors, the numerical and simulated fiber to fiber gain is provided in Figs. 2, 3, respectively, at.

Fig. 2
figure 2

Relationship between numerical fiber-to-fiber gain and output power at various confinement parameters (using MATLAB)

Full size image
Fig. 3
figure 3

Simulated fiber-to-fiber gain as a function of output power at various confinement parameters (using OptiSystem)

Full size image

1550 nm input signal wavelength and 150 mA bias current.

It is noticed that, the amplifier with small optical confinement factor, Γ, exhibits high output power saturation as predicted from Eq. (4). At a small confinement factor of 0.3, the peak gain numerically achieved is ~ 26.3 dB and the output power saturation is 8.21 dBm. This compares favorably to the equivalent stimulated maximum gain of 26.9 dB and the output power saturation is 8.2 dBm.

At higher confinement factor, 0.45, the numerically maximum gain achieved is ~ 25.6 dB and the output power saturation is decreased to 7.74 dBm. This compares approvingly to the corresponding stimulated value (~ 26 dB) when the output power saturation is decreased to 7.8 dBm.

3.2 Output power saturation: impact of bias current

Figures 4, 5 show, respectively, the numerical and simulated gain saturation characteristics of SOA as a function of output power. The function of output power saturation is used to illustrate the numerical and simulated fiber to fiber gain for the assigned bias currents 100, 120 and 150 mA with 1550 nm input signal wavelength.

Fig. 4
figure 4

Relationship between numerical fiber- to-fiber gain and output power at various bias currents (using MATLAB)

Full size image
Fig. 5
figure 5

Simulated fiber-to-fiber gain with respect to output power at various bias currents (using OptiSystem)

Full size image

At a higher bias current of 150 mA, the numerical and simulated maximum gain obtained are 25.6 dB and 25.9 dB, and the output power saturation values are.

7.744 dBm and 7.8 dBm, respectively, showing an excellent agreement. At100 mA (low bias current), the numerical and simulated maximum gain obtained are 23.2 dB and 24 dB, and the output power saturation values are reduced to 5.3 dBm and 5.4 dB, respectively. Again, this reveals an excellent agreement between numerical analysis and simulation. Evidently, an improvement of the output power from 5.4 to 7.8 dBm are predicted from Eq. (4) by improving the bias current from 100 to 150 mA.

3.3 Fiber-to-fiber gain spectrum: impact of bias current

We introduce the effect of input bias current on the improving the fiber-to-fiber gain spectrum for C-band at power of input signal—10 dBm in Figs. 6, 7, numerically and by simulation, respectively. The bias current, I, is assigned values of 150, 120 and 100 mA. It is noticed that, the fiber to fiber gain improving with increasing the bias current, until getting its maximum value at ~ 1565 nm, then decreases. As shown, the SOA optical gain spectrum is very diverse. Cleary, the maximum gain increases also with the bias current. The discrepancy between both the numerical and simulation results is insignificant showing a fair agreement.

Fig. 6
figure 6

Numerical gain spectrum at different bias current (using MATLAB)

Full size image
Fig. 7
figure 7

Simulated fiber-to-fiber gain spectrum at multiple bias currents (using OptiSystem)

Full size image

3.4 Fiber-to-fiber gain spectrum: impact of input signal power

Assigned signal powers of − 10, − 5, and 0 dBm in the C-band at an input bias current of 150 mA are presented in Fig. 8 along with the simulated fiber-to-fiber gain. Evidently, increasing the power of input signal leads to a decrease in the fiber-to-fiber gain. This can be explained as follows. As the signal power rises, the number of carriers in the active zone decreases, which causes the gain to fall and the wavelengths to shift towards longer ones. The maximum obtained gain of 17.7, 12.8, and 7.8 dB at − 10, − 5 and 0 dBm input signal power of, respectively, at 1550 nm wavelength.

Fig. 8
figure 8

Simulated spectrum of fiber-to-fiber gain at various input signal powers (using OptiSystem)

Full size image

3.5 Fiber to fiber gain spectrum: impact of temperature

Figure 9 displays the simulated SOA fiber-to-fiber gain spectrum at multiple temperatures, T, 220, 250 and 300 K, at 150 mA bias current and − 10 dBm input signal power.

Fig. 9
figure 9

Simulated gain spectrum at different temperatures, at 150 mA bias current and − 10 dBm input signal power (using OptiSystem)

Full size image

It was observed that as the temperature rose, the fiber-to-fiber gain decreased. This is because at high temperatures, the electron distribution spans a greater energy range. As a result, there are less electrons accessible at a given energy to take part in an optical transition, which results in a gain. This result is in a fair agreement with work of Dutta and Wang (2013). Cleary, the maximum gain is achieved at 1550 nm and then reduces towards longer wavelengths when temperature is increased.

3.6 Fiber-to-fiber gain spectrum: impact of amplifier length

Figure 10 displays the simulated gain spectrum at multiple amplifier lengths, L = 600, 700 and 800 μm, at 150 mA bias current and − 10 dBm input signal power. We observe that, the fiber-to-fiber gain falls with increased amplifier lengths.

Fig. 10
figure 10

Simulated gain spectrum at multiple amplifier lengths, L, at input signal power = − 10 dBm and bias current = 150 mA (using OptiSystem)

Full size image

The maximum gain, 18.55, 17.71, and 16.95 dB is obtained at amplifier lengths of 600, 700, and 800 μm, respectively, at 1550 nm wavelength.

3.7 The coefficient of material gain spectrum: impact of carrier density

Figure 11 displays the coefficient of material gain versus carrier density, n, in the C-band Clearly, the coefficient of material gain increases with the carrier density, showing a peak at 1550 nm, which is in a fair agreement with the work of Agrawal et al. (2022).

Fig. 11
figure 11

The coefficient of material gain at different values of carrier density, n, in the C-band

Full size image

4 Conclusion

The saturation output power and fiber-to-fiber gain of wideband SOAs are discussed in length in this study. Bias current and optical confinement factor effects are examined numerically and through simulation. It is discovered that raising the bias current and lowering the confinement factor improve fiber-to-fiber gain and output power saturation. The maximum gain and output power saturation obtained are 25.9 dB and 7.8 dBm, respectively, at 150 mA (high bias current). While the minimum gain and output power saturation achieved are 24 dB and 5.4 dBm, respectively, at 100 mA (low bias current). Also, the output power saturation is improved from 7.8 to 8.2 dBm by decreasing the optical confinement factor from 0.45 to 0.3. The numerical results are validated by simulated ones, showing excellent agreement.

Moreover, we studied the impact of input signal power, temperature and amplifier length on the fiber-to-fiber gain spectrum. A maximum gain of 17.7, 12.8 and 7.8 dB is obtained at an input signal power of − 10,− 5 and 0 dBm, respectively, at 1550 nm wavelength. Additionally, the fiber-to-fiber gain falls with increasing the temperature and the maximum gain is achieved at 220 K, at 1550 nm wavelength. Moreover, the maximum fiber-to-fiber gain, 18.55 dB, is obtained at minimum amplifier length of 600 μm at 1550 nm wavelength. We also studied the impact of the carrier density on coefficient of material gain spectrum, where the coefficient of material gain peaks near 1550 nm and gets better as the carrier density rises. Finally, the discrepancy among both the numerical and simulation results is insignificant showing a fair agreement.