1 Introduction

Challenge-response authentication schemes based on Physical Unclonable Functions (PUFs) have been proposed and are being actively investigated as an alternative to standard authentication protocols, especially for the Internet of Things (IoT) applications (Shamsoshoara 2020, Velasquez 2018, Suh 2007, Babaei 2019, Idriss 2016, Mall 2022, Najafi 2009, Gao 2022, Zang 2014). With PUFs, authentication is based on secrets, which are produced in the unsecure environment from complex physical characteristics of integrated circuits or other electronic devices, and which are the response to a specific stimulus (challenge) sent from the secure environment. The main advantage of these methods is that they provide a good security level, without requiring neither to store the key in the unsecure environment nor extended computation capabilities, which is important especially on the user (unsecure) side.

In the optoelectronic domain, semiconductor lasers are interesting candidates for such hardware-based method of authentication, because of the dispersion of their parameters. Lasers in the chaotic regime are especially suitable to this scope, because of the strong sensitivity of chaos to parameter variations.

A semiconductor laser can be routed to chaos by delayed optical feedback provided by back-reflection from a local mirror, or by injection from another laser. Chaos in lasers has been extensively analyzed since the last 1990s, both theoretically and experimentally, finding bifurcation diagrams and attractors (Annovazzi-Lodi 1994, Annovazzi-Lodi 1998, Ohtsubo 1999, Ryan 1994, Masoller 1995, Kanno 2012). Applications of chaos to secure transmission of data have been investigated starting from the early 2000s (Donati 2002, Larger 2004, Argiris 2005). An important characteristic of the chaotic regime is that two lasers never produce the same chaotic waveform, (i.e., the same pseudo-random amplitude modulation, which, for telecommunication lasers, is typically in the GHz range), unless they are synchronized. Different schemes have been proposed to synchronize two lasers in the chaotic regime (Donati 2002, Larger 2004). A fundamental condition, to obtain a stable and robust synchronization, is that the lasers must be ‘twins’, i.e., they must have very well matched, almost identical, parameters. This can be obtained by selecting them from the same wafer, which is possible only for the Authorized user. For the Adversary, instead, it is very difficult to generate an identical chaotic waveform, because of the unavoidable differences between nominally identical but physically different devices.

This property has been already exploited in chaos-secured communication experiments (Donati 2002, Larger 2004). Different methods have been investigated to hide a message in chaos, and chaos-protected digital transmission on a metropolitan network (Argiris 2005) has been demonstrated years ago. Integrated optics cryptosystems have been also designed and manufactured (Syvridis 2009).

In a previous paper (Annovazzi-Lodi 2022), a challenge-response authentication scheme has been proposed, which is inspired by the so-called three-laser chaos-protected transmission scheme (Yamamoto 2007, Annovazzi-Lodi 2010, Annovazzi-Lodi 2011, Uchida 2003, Oowada 2009) in which synchronization is obtained by driving the two lasers (called Slaves, SL) by the common optical injection of a third chaotic laser (Driver, DRV).

In transmission applications, two main topologies have been considered so far in the literature (Donati 2002, Larger 2004): the close loop, when the isolated SL lasers are already chaotic, and the open loop, where they are chaotic only due to injection from DRV.

In (Annovazzi-Lodi 2022), only the basic open loop has been evaluated in detail for authentication. However, in transmission applications it has been demonstrated that the close loop offers a much better security level, because it has more parameters to be optimized and stricter tolerances to match (Donati 2002, Larger 2004, Annovazzi-Lodi 2011). In (Annovazzi-Lodi 2022) the close loop has been only preliminarily considered without sweeping parameters. In (Lombardi 2022), the close loop has been addressed by sweeping parameters, but only in selected cases.

Thus, we have now studied the close loop in detail, to check if the increased complexity of the scheme results into a better performance in terms of security also when applied to authentication.

A specific advantage of our approach is that both the challenge and the responses are generated on the fly in both environments, and thus they do not need to be stored, not even in the secure environment. Moreover, the challenge changes at every attempt in a virtually random way.

A preliminary numerical evaluation on the validity of this approach could open the route to a new PUF based authentication method, which could then be investigated in detail both theoretically and experimentally. This is the goal of our contribution.

2 The authentication scheme

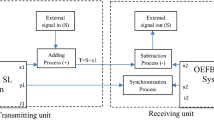
In Fig. 1 we show the proposed scheme of challenge-response authentication with chaotic lasers.

Fig.1
figure 1

Authentication scheme based on chaotic lasers (M: mirrors, PD: photodiodes, PROC: electronic processing)

Full size image

The driver laser DRV is routed to chaos by delayed optical feedback, provided by an external mirror M, and injects (this is the challenge) two Slave lasers: SL1, in the secure environment, and SL2 in the unsecure environment. Slave lasers also work in the chaotic regime, due to delayed optical feedback produced by local mirrors (M). If SL1, SL2 are twins, in suitable operating conditions they synchronize, i.e., they produce the same chaotic modulation. A bit sequence can be easily obtained from the chaotic waveform by photodetection and electronic processing. The response in the unsecure environment is the bit stream produced by Slave SL2. The reference response in the secure environment is the bit stream generated by SL1. Only if the responses match (as detected by the EXOR block), authorization is granted.

As usual with PUFs, a small number of errors in the response bit sequence must be tolerated, because synchronization is never perfect in practice. A threshold is to be defined, to offer a probability of success of (or next to) 100% to the Authorized user, while keeping the probability of success of the Adversary as low as possible.

This can really be obtained, in practice, not only because the Authorized user can own a SL2 laser which is twin to SL1, while getting a matched laser is a very difficult task for the Adversary; moreover, the Authorized user can train his system, by optimizing pump current and optical injection to minimize errors, before using it in the field (Annovazzi-Lodi 2022). This is not possible for the Adversary, who can only sweep his parameters, trying many different lasers and working points. As already observed, the responses need not to be stored, not even in the secure environment, but they are produced on the fly, which improves security.

3 Numerical model

The well-known Lang-Kobayashi model (Lang 1980) is used to describe the lasers. The set of equations for the driver and the two slave lasers of the setup of Fig. 1 is the same used for the three-laser chaos-protected transmission (Annovazzi-Lodi 2011), without, however, including a message. The different devices are described by varying index J in Eqs. 1–3:

$$\begin{gathered} \frac{{dE_{J} \left( t \right)}}{dt} = \frac{1}{2}\left( {1 + i\alpha } \right)\left[ {G_{J} \left( t \right) - \frac{1}{{\tau_{p} }}} \right]E_{J} \left( t \right) + \hfill \\ \quad \quad \quad \;\;\; + \frac{{K_{J} }}{{\tau_{in} }}E_{J} \left( {t - \tau } \right)\exp \left( { - i\omega \tau } \right) + L_{{E_{J} }} \left( t \right) + \hfill \\ \quad \quad \quad \;\;\; + \Delta_{D,J} \frac{{K_{D,J} }}{{\tau_{in} }}E_{D} \left( {t - T_{D,J} } \right)\exp \left( { - i\omega T_{D,J} } \right) \hfill \\ \end{gathered}$$
(1)
$$\frac{{dN_{J} \left( t \right)}}{dt} = \frac{\eta }{eV}I_{J} - \frac{{N_{J} \left( t \right)}}{{\tau_{s} }} - G_{J} \left( t \right)\left| {E_{J} \left( t \right)} \right|^{2} - L_{{N_{J} }} \left( t \right)$$
(2)
$$G_{J} \left( t \right) = \frac{{\xi \left[ {N_{J} \left( t \right) - N_{0} } \right]}}{{1 - \varepsilon \Gamma \left| {E_{J} \left( t \right)} \right|^{2} }}$$
(3)

For J = D, we have the equations describing the DRV dynamics, while for J = 1 and J = 2 we have the equations describing the SL1 and SL2 dynamics, respectively. Coefficient ΔD,J is zero for J = D, otherwise it is ΔD,J = 1.

In these equations, EJ(t) is the slowly varying, complex electric field, NJ(t) the carrier density, GJ(t) the linear gain coefficient, the pump current, e the electron charge and KJ, τ are the feedback parameter and the time of flight to the external mirrors. For J = T,R the terms KD,J/τin and TD,J represent the injection rate and the propagation time from the driver into transmitter and receiver, respectively. For simplicity, in the simulations we have taken TD,T = TD,R = 0. Other parameters are defined in Table 1.

Table 1 Laser parameters
Full size table

The Langevin noise terms LEj(t) LEJ(t) and LNj(t) (Ju 2004), are given by:

$$L_{{E_{J} }} \left( t \right) = \frac{{E_{J} \left( t \right)}}{{\left| {E_{J} \left( t \right)} \right|}}\sqrt {\frac{{2R_{sp} }}{\Delta t}} \left[ {\frac{1}{2}\chi_{e} \left( t \right) + i\chi_{\phi } \left( t \right)} \right]$$
(4)
$$L_{{N_{J} }} \left( t \right) = \sqrt {\frac{{2N_{J} \left( t \right)}}{{\tau_{s} \Delta t}}} \chi_{n} \left( t \right) - \left| {E_{J} \left( t \right)} \right|\sqrt {\frac{{2R_{sp} }}{\Delta t}} \chi_{e} \left( t \right)$$
(5)

where \(R_{sp} = {{\beta N_{J} \left( t \right)\Gamma } \mathord{\left/ {\vphantom {{\beta N_{J} \left( t \right)\Gamma } {\tau_{s} }}} \right. \kern-0pt} {\tau_{s} }}\) is the spontaneous emission rate.

The terms\(\chi_{e}\), \(\chi_{\phi}\) and \(\chi_{n}\) are time series with zero-mean, unit-variance Gaussian distribution, and Δt is the time resolution in the modeling of white noise.

It is worth noting that the equation set 1–3 differs from that of the open-loop scheme (Annovazzi-Lodi 2022) for the inclusion of a term describing the reflection from each laser mirror in the equations for the electric fields (second term in Eq. 1).

As usual, the electric fields are normalized in (m−3/2). The true value of each electric field (in [V/m]) is given by:

$$E_{True} (t) = \left( {\xi \hbar \omega \frac{{Z_{0} }}{n\zeta }} \right)^{\frac{1}{2}} E\left( t \right)$$
(6)

where \(\hbar\) is the Planck’s constant, Z0 = (1/ε0c) the vacuum impedance, ε0 the vacuum permittivity and c the speed of light. The photodetected currents of PD1, PD2 are obtained by computing \(I = \sigma AZ_{0}^{ - 1} \left| {E_{True} \left( t \right)} \right|^{2}\) for both SL1 and SL2.

In the next Section, we report the numerical results obtained with this model. In all simulations, in addition to the Langevin noise, the photodetector noise has been taken into account. This has been done by assuming Johnson noise and shot noise as white Gaussian processes of variance 4KBTB/R and 2e < I > B, respectively, where KB is the Boltzmann constant, T is the absolute temperature (T = 300 K), R is the load resistance (R = 50 Ω) and < I > is the mean detected current. For the simulations, time samples for each noise source have been obtained by a standard numerical routine.

In our previous paper (Annovazzi-Lodi 2022) the proposed authentication method was evaluated in the open loop (Kj = 0 for both SLs). The parameters of DRV and SL1,2, and the working point, were optimized to obtain a robust synchronization. Then, the main internal parameters, i.e., the linewidth enhancement factor α, the carrier lifetime τs, the photon lifetime τp, the gain coefficient \(\xi\) had been swept in numerical simulations from 1 to 10%, to test different levels of mismatch of SL2 with respect to SL1. For each combination of the internal parameters, the external parameters of the lasers, i.e., the supply current and the injection from the DRV, were also varied, on more that 16 million combinations.

In the present analysis, two more parameters have been added to describe the close loop, i.e., the reflectivity Kj of the mirrors in front of each slave laser, and the time of flight τ from each mirror to its laser. Figure 2 shows the chaotic waveforms generated by the DRV, SL1 and SL2 in a typical close loop simulation. The time series generated by the SLs are identical since the lasers are twins in this case. The time series generated by the DRV is significatively different, since this laser has been intentionally selected to be unmatched with respect to SL1,2. This is required to prevent the Adversary from recovering the bit stream directly from processing the DRV emission.

Fig. 2
figure 2

Chaotic waveforms produced by Driver, and by matched SL1 and SL2 lasers, in the close loop scheme

Full size image

For the Authorized user, who can select the laser, we have assumed a parameter mismatch of 2%, while for the Adversary the assumed mismatch was from 3 to 10%. For each internal parameter combination, the external parameters of the lasers have been also varied, as for the open loop. For the Authorized user, who can train his system, the error number was minimized by properly selecting the external parameters, while, for the Adversary, these parameters were simply swept, and all combinations were added to the statistics.

In principle, all the parameters of the close loop should be swept in the numerical analysis, getting a total number of more than 56 million combinations for each single percentage of mismatch. Due to the large number of combinations, we have begun by assuming, as a reasonable starting point, a 2% mismatch for the Authorized user, and a 5% for the Adversary, as often done with chaos-protected transmission. For these two values, all parameter combinations have been tested. For the other cases, to reduce the machine time, we have first considered the results obtained with constant nominal values for the two new parameters. From them, we have selected the combinations giving the least number of errors, and only for these lasers we have swept the two new parameters, for approximately 7 million combinations per laser. In this way, we have been able to get the results for a mismatch of 3, 4, 7 and 10% in a relatively short time.

For 2% (Authorized) and 5% (Adversary) the number of detected errors is reported in Table 2, for a 128-bit sequence (2 ns bit time) obtained from the chaotic waveforms with a low-pass filter followed by a comparator to obtain a two-level signal (where the time of each level over the full sequence is approximately the same), which is then sampled by a clock. In Fig. 3 the reference response SL1, in the secure environment, is shown together with those of the Authorized user (SL2, in optimized condition), and of the Adversary (SL2, typical case).

Table 2 Error number on a 128-bit sequence (Authorized, 2% mismatch, vs. Adversary, 5% mismatch) for the open loop and for the close loop
Full size table
Fig. 3
figure 3

Bit sequences obtained from lasers SL1 (Reference), SL2 (Authorized user, 2% mismatch), and SL2 (Adversary, 5% mismatch) in the close loop scheme

Full size image

The results for the open loop (Annovazzi-Lodi 2022) are also shown in Table 2, for comparison.

From Table 2, we would like to point out the difference in the performance of the Authorized user vs. the Adversary, which is large for both the open and the close loop. Even if for the Adversary the minimum error number is low, because sweeping parameters occasionally results in a well performing device, this event is very unlikely (Fig. 4). The mean error number is very small, instead, for the Authorized user.

Fig. 4
figure 4

Close loop error occurrence for the Adversary (5% mismatch)

Full size image

Finally, we have calculated (Table 3) the authentication success rate, for different levels of mismatch.

Table 3 Success rate (Authorized, 2% mismatch, vs. Adversary 3–10% mismatch) for the open loop (threshold: 6 errors) and for the close loop (threshold: 9 errors)
Full size table

As already observed, this implies to define a maximum acceptable error number. From Table 2, for 2% mismatch at least 7 errors should be tolerated, in order to obtain a success rate of 100%, for the Authorized user with the close loop. Even if we select a threshold of 9 errors, to get some margin, the success rate of the Adversary with 5% mismatch is only 0.0004%. In comparison, the open loop (Annovazzi-Lodi 2022) performs, with the same mismatch levels and a 6-error threshold, an authentication success of 0.004% (i.e., ten times lower) for the Adversary, while it is 100% for the Authorized user.

Similar results have been obtained with different mismatch levels for the Adversary, which are also shown in Table 3.

From these outcomes, we conclude that the proposed scheme is well performing in both versions, and thus it represents a new promising method of network authentication. Moreover, based on the new available data, the close loop is found to offer a significative improvement vs. the open loop. Thus, the close loop scheme should be considered for applications where the security improvement it offers overcompensates the increased complexity of the setup.

Following the numerical analysis, next step will be the experimental evaluation of the authentication scheme. We are confident that both versions can be successfully implemented, based on the experiments already performed on similar setups in chaos-secured transmission (Donati 2002, Larger 2004, Annovazzi-Lodi 2011). In these papers stable synchronization is demonstrated and since the time series of chaos are matched (they can be subtracted almost to zero), we expect that also bit sequences obtained from them should be equal, but for a small percentage of occurrences. As in (Syvridis 2009) a suitable photonic integration technology could be considered to produce a conveniently compact and stable system.

About the statistical properties of the authentication key obtained by our method, the digital sequence should reflect the characteristics of chaos, i.e., it should be pseudo-random. However, the exact statistics is expected to depend on the source characteristics and working point, as well as on the electronic processing (Li 2019, 2022, Aromataris and Annovazzi-Lodi 2012), and thus it should be evaluated in a real implementation.

4 Conclusions

In this paper we have proposed an authentication method based on twin chaotic lasers, synchronized by the common optical injection from a third chaotic laser. Our numerical analysis demonstrates the good performance of both the open and the close loop version of our scheme. However, the results for the close loop, where both lasers are chaotic even before injection, are far better than for the open loop, in spite of a somewhat more complex setup. Based on our findings, we conclude that the proposed scheme represents a promising approach for a new authentication method.