Performance investigation of dual-hop relaying for hybrid FSO/RF system based on optimum threshold SNR

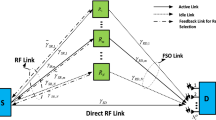
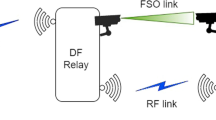
Abstract

A less-complex and efficient time-hysteresis switching algorithm assisted hybrid free-space optics (FSO)/millimeter wave (mm)-radio frequency (RF) system is presented in the paper. A time-hysteresis switching algorithm is utilized for link transient for selection of FSO or RF links. For improving the long-haul communication efficiency and coverage a selective decode-and-forward relay scheme is blended with hybrid FSO/RF system along with maximal-ratio-combining (MRC) for signal reconstruction at the receiver end. However, the pointing errors due to misalign apertures and building sway, which have the potential to suppress the benefits of the relay assisted hybrid system. The impact of pointing errors and path loss attenuation are modeled with Gamma–Gamma distribution and generalised Nakagami-m is used to model the RF channel fading. The exact closed-form expressions of average symbol-error-rate (ASER) and outage-probability (OP) have been derived for the performance evaluation of the proposed system with and without pointing errors. We also present an asymptotic-analysis of the ASER and outage with lower computational-complexity for the proposed system and obtain the diversity order. To achieve target ASER value for the proposed switching scheme, the optimum-threshold signal-to-noise ratio (SNR) value has been obtained numerically in this work. The derived theoretical outcomes have been validated with Monte-Carlo simulation. In addition, we present comparative results of ASER and OP performance for proposed system with Gamma–Gamma and generalised Málaga distribution under various adverse weather conditions. It is observed that the proposed hybrid FSO/RF system outperforms a cooperative single FSO system as well as single-hop hybrid FSO/RF system on account of diversity as well as switching technique benefits. The presented hybrid FSO/RF system achieves ASER of 10^–7 in the lower SNR regimes.

Appendices

Appendix A: Average SER of the FSO link

We derive the ASER of the FSO link through the Eq. (38) in this post script section. The term ${B}_{MRC}^{fso}\left({\gamma }_{th}^{fso}\right)$ can be represented as

$${B}_{MRC}^{fso}\left({\gamma }_{th}^{fso}\right)= \int_{{\gamma }_{th}^{fso}}^{\infty }P\left(e\backslash \gamma \right) {f}_{{\gamma }_{MRC}^{fso}}\left(\gamma \right)d\gamma = {B}_{MRC}^{fso}- {B}_{MRC}^{{fso}_{out}}\left({\gamma }_{th}^{fso}\right),$$

(A1)

where ${B}_{MRC}^{fso}$ is the ASER of FSO link given as

$${B}_{MRC}^{fso}= \int_{0}^{\infty }P\left(e\backslash \gamma \right) {f}_{{\gamma }_{MRC}^{fso}}\left(\gamma \right)d\gamma .$$

(A2)

Hence the ASER of the FSO link for the outage time i.e. ${\gamma }_{MRC}^{fso}< {\gamma }_{th}^{fso}$, is expressed as

$${B}_{MRC}^{{fso}_{out}}\left({\gamma }_{th}^{fso}\right)= \int_{0}^{{\gamma }_{th}^{fso}}P\left(e\backslash \gamma \right) {f}_{{\gamma }_{MRC}^{fso}}\left(\gamma \right)d\gamma .$$

(A3)

From Eqs. (A2) and (A3), all phrase mentioned in Eq. (38) can be solved, and the term ${B}_{i, j}^{fso}\left({\gamma }_{th}^{fso}\right)$ from Eq. (38), where $i\,\epsilon\,\left\{S-D, S-R\right\}$ and $\epsilon \left\{S-R,S-D\right\}$, has been solved from Eq. (A1). Putting Eqs. (10), (11), and (33) in Eq. (A2) and utilizing Equation (07.34.21.0013.01) of Anees and Bhatnagar (2015), ${B}_{i, j}^{fso}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$B_{i, j}^{fso} \left( {\gamma_{th}^{fso} } \right) = \frac{A}{2\sqrt \pi }\ell_{1}^{j} \varOmega_{i} \mathop \sum \limits_{g = 1}^{2} \mathop \sum \limits_{n = 0}^{\infty } \frac{{{\mathcal{L}}_{1,g} }}{{D^{{2\mu_{g,n}^{i} }} }}\varOmega_{g,n}^{i} G_{3,6}^{4,2} \left( {\frac{{\upsilon_{j} }}{{D^{2} }}\left| {\begin{array}{*{20}c} {\varLambda_{3,g,n}^{i} } \\ {\varLambda_{4,g,n}^{i,j} } \\ \end{array} } \right.} \right),$$

(A4)

For the case of pointing errors the term ${B}_{i, j}^{{fso}^{PE}}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$B_{i, j}^{{fso^{PE} }} \left( {\gamma_{th}^{fso} } \right) = \frac{{A\pi^{2} {\text{K}}_{1}^{j} {\text{K}}_{2}^{j} }}{2\sqrt \pi }\mathop \sum \limits_{g = 1}^{3} \mathop \sum \limits_{n = 0}^{\infty } \frac{{{\mathcal{M}}_{g,n}^{j} }}{{D^{{2\mho_{g,n}^{j} }} }}G_{6,9}^{6,4} \left( {\frac{{\upsilon_{j} }}{{D^{2} }}\left| {\begin{array}{*{20}c} {\frac{1}{2}, {\mathcal{N}}_{6,g,n}^{j,i} } \\ {{\mathcal{N}}_{7,g,n}^{j,i} } \\ \end{array} } \right.} \right)$$

(A4′)

where $\ell_{1}^{j}$, $\varOmega_{i}$, ${\mathcal{L}}_{1,g}$, $\varOmega_{g,n}^{i}$, and ${\upupsilon }_{j}$ as well as $\varLambda_{3,g,n}^{i}$, $\varLambda_{4,g,n}^{j,i}$, ${\mathcal{N}}_{6,g,n}^{j,i}$ and ${\mathcal{N}}_{7,g,n}^{j,i}$ have been mentioned in Table 1 and Table

Table 4 Notations used in appendix equations

4, respectively. By putting Eqs. (10), (11), and (34) in Eq. (A3) and utilizing Equation (07.34.21.0084.01) of Anees and Bhatnagar (2015), the exact equation for ${B}_{i, j}^{fso}\left({\gamma }_{th}^{fso}\right)$ is given as

$$B_{i, j}^{fso} \left( {\gamma_{th}^{fso} } \right) = \frac{{A\ell_{1}^{j} \varOmega_{i} }}{2} \mathop \sum \limits_{g = 1}^{4} \mathop \sum \limits_{n = 0}^{\infty } {\mathcal{T}}_{3,g,n}^{i} G_{2,6}^{4,2} \left( {\upsilon_{j} \gamma_{th}^{fso} \left| {\begin{array}{*{20}c} {\varLambda_{5,g,n}^{i} } \\ {\varLambda_{6,g,n}^{i,j} } \\ \end{array} } \right.} \right).$$

(A5)

For the case of pointing errors the term ${B}_{i, j}^{{fso}_{out}^{PE}}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{i, j}^{{fso_{out}^{PE} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{j} {\text{K}}_{2}^{j} \pi^{2} }}{2}\mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{l = 1}^{2} \mathop \sum \limits_{g = 1}^{3} q_{l,n}^{j} {\mathcal{M}}_{g,n }^{j} \\ & \quad \times G_{5,9}^{6,3} \left( {\upsilon_{j} \gamma_{th}^{fso} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{1,l,g}^{j,i,n} } \\ {{\mathcal{N}}_{2,l,g}^{j,i,n} } \\ \end{array} } \right.} \right), \\ \end{aligned}$$

(A5′)

where ${\mathcal{T}}_{3,g,n }^{{i, n_{4} }}$, $\varLambda_{5,g,n}^{{i, n_{4} }}$, $\varLambda_{6,g,n}^{{i,j,n_{4} }}$, $q_{l,n}^{j}$, ${\mathcal{M}}_{g,n }^{j}$, ${\mathcal{N}}_{1lg}^{j,i,n}$ and ${\mathcal{N}}_{2lg}^{j,i,n}$ have been mentioned in Table 4. In Eq. (38), the term, ${B}_{C}^{fso}\left({\gamma }_{th}^{fso}\right)$ has been solved from Eq. (A1). Now Putting Eqs. (28) and (33) in Eq. (A2) as well as utilizing Equation (07.34.21.0013.01) from Anees and Bhatnagar (2015), the term ${B}_{C}^{fso}$ is expressed as

$$\begin{aligned} B_{C}^{fso} \left( {\gamma_{th} } \right) & = \frac{{A\ell_{1}^{R - D} \varOmega_{S - D} }}{2\sqrt \pi }\sum\limits_{n = 0}^{\infty } {\sum\limits_{{n_{1} }}^{\infty } {\mathop \sum \limits_{g = 1}^{2} } }\frac{{\mathcal{L}}_{1,g}{\varOmega }_{g,n}^{S-D}B\left(\frac{{\alpha }_{R-D}}{2}+1, {\mu }_{g,n}^{S-D}+{n}_{1}\right)}{{n}_{1}!{D}^{2{\mu }_{g,n}^{S-D}}} \\ & \quad \times \left[ {\frac{1}{{D^{2} }}G_{4,7}^{4,4} \left( {\frac{{\upsilon_{R - D} }}{{D^{2} }}\bigg|\begin{array}{l} { - 1,0,\mu_{g,n}^{S - D} ,\mu_{g,n}^{S - D} - \frac{1}{2}} \\ {\varLambda_{{2,n_{1} }}^{R - D} - 1,\mu_{g,n}^{S - D} - 1,0, - 1 } \\ \end{array} } \right)} \right. \\ & \quad \times \left. {\mu_{g,n}^{S - D} G_{3,6}^{4,3} \left( {\frac{{\upsilon_{R - D} }}{{D^{2} }}\left| {\begin{array}{l} {1, 1 - \mu_{g,n}^{S - D} , \frac{1}{2} - \mu_{g,n}^{S - D} } \\ {\varLambda_{{2,n_{1} }}^{R - D} , - \mu_{g,n}^{S - D} , 0} \\ \end{array} } \right.} \right)} \right]. \\ \end{aligned}$$

(A6)

Similarly, for the case of pointing errors the term ${B}_{C}^{{fso}_{out}^{PE}}\left({\gamma }_{th}\right)$ can be expressed as

$$\begin{aligned} B_{C}^{{fso_{out}^{PE} }} \left( {\gamma_{th} } \right) & = \frac{A}{2\sqrt \pi }{\text{K}}_{1}^{S - D} {\text{K}}_{2}^{R - D} \pi^{2} \mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{g = 1}^{3} \frac{1}{n!}\frac{{{\mathcal{M}}_{g,n}^{S - D} }}{{D^{{2\mu_{g,n}^{S - D} }} }}{\text{B}}\left( {{\rm C}\!\!\!\cdot ,{\rm C}\!\!\!\cdot_{{n_{1} }}^{n} } \right) \\ & \quad \times \left[ {\frac{1}{{D^{2} }}G_{6,9}^{6,4} \left( {\frac{{\upsilon_{R - D} }}{{D^{2} }}\left| {\begin{array}{*{20}c} {0,{\mathcal{N}}_{6,g,n}^{S - D, R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} , - \mu_{g,n}^{S - D} ,1,0} \\ \end{array} } \right.} \right)} \right. \\ & \quad + \left. {\mu_{g,n}^{S - D} G_{5,8}^{6,3} \left( {\frac{{\upsilon_{R - D} }}{{D^{2} }}\left| {\begin{array}{*{20}c} {{\mathcal{N}}_{6,g,n}^{S - D,R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} , - \mu_{g,n}^{S - D} , 0} \\ \end{array} } \right.} \right)} \right], \\ \end{aligned}$$

(A6′)

where ${\mu }_{g,n}^{j}$ has been mentioned in Table 1. Putting Eq. (28) in Eq. (A3) and similarly from Eq. (A5), the exact equation for the term ${B}_{C}^{{fso}_{out}}\left({\gamma }_{th}^{fso}\right)$ is expressed as

$$\begin{aligned} B_{C}^{{fso_{out} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A\ell_{1}^{R - D} \varOmega_{S - D} }}{2}\mathop \sum \limits_{{n_{1} }}^{\infty } \frac{1}{{n_{1} !}}\mathop \sum \limits_{g = 1}^{4} \mathop \sum \limits_{n = 0}^{\infty } {\mathcal{T}}_{3, g, n}^{S - D} B\left( {\frac{{\alpha_{R - D} }}{2} + 1, \mu_{g,n}^{S - D} + n_{1} } \right) \\ & \quad \times \left[ {\gamma_{th}^{fso} G_{3,7}^{4,3} \left( {\upsilon_{R - D} \gamma_{th}^{fso} \left| {\begin{array}{*{20}c} {\varLambda_{7,g,n}^{S - D} } \\ {\varLambda_{8,g,n}^{R - D,S - D} } \\ \end{array} } \right.} \right)} \right. \\ & \quad + \left. {\mu_{g,n}^{S - D} G_{2,6}^{4,2} \left( {\upsilon_{R - D} \gamma_{th} \left| {\begin{array}{*{20}c} {\varLambda_{5,g,n}^{S - D} } \\ {\varLambda_{6,g,n}^{R - D,S - D} } \\ \end{array} } \right.} \right)} \right]. \\ \end{aligned}$$

(A7)

Similarly, for the case of pointing errors the term ${B}_{C}^{{fso}_{out}^{PE}}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{C}^{{fso_{out}^{PE} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{S - D} {\text{K}}_{2}^{R - D} \pi^{2} }}{2}\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{g = 1}^{3} \mathop \sum \limits_{l = 1}^{2} \frac{{q_{l,n}^{S - D} {\mathcal{M}}_{g,n}^{S - D} {\text{B}}\left( {{\text{C}}\!\!\cdot ,{\text{C}}\!\!\cdot_{{n_{1} }}^{n} } \right)}}{{n_{1} !}} \\ & \quad \times \left[ {\gamma_{th}^{fso} G_{5,9}^{6,3} \left( {\upsilon_{R - D} \gamma_{th}^{fso} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{3,l,R - D,g}^{S - D,n} } \\ {{\mathcal{N}}_{4,l,R - D,g}^{S - D,n} } \\ \end{array} } \right.} \right)} \right. \\ & \quad + \left. {\mu_{g,n}^{S - D} G_{4,8}^{6,2} \left( {\upsilon_{R - D} \gamma_{th}^{fso} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{5,l,R - D,g}^{S - D,n} } \\ {{\mathcal{N}}_{6,l,R - D,g}^{S - D,n} } \\ \end{array} } \right.} \right)} \right], \\ \end{aligned}$$

(A7′)

where $\varLambda_{7,g,n}^{S - D}$, $\varLambda_{8,g,n}^{R - D,S - D}$, ${\mathcal{N}}_{3,l,R - D,g}^{S - D,n}$, ${\mathcal{N}}_{4,l,R - D,g}^{S - D,n}$, ${\mathcal{N}}_{5,l,R - D,g}^{S - D,n}$, and ${\mathcal{N}}_{6,l,R - D,g}^{S - D,n}$ has been mentioned in Table 4. The CDF of ${\gamma }_{j}^{fso}$ is obtained from Equation (07.34.21.0084.01) of Mathematica Edition (2021) and expressed as

$$F_{{\gamma_{j}^{fso} }} \left( \gamma \right) = {\text{K}}_{2}^{j} G_{3,7}^{6,1} \left( {\upsilon_{j} \gamma \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{j} } \\ {{\mathcal{N}}_{3}^{j} ,0} \\ \end{array} } \right.} \right),$$

The term ${B}_{C, S-R}^{fso}\left({\gamma }_{th}^{fso}\right)$ in Eq. (28) has been solved using Eq. (A1). By putting Eqs. (11), (28), and (30) in Eq. (A3) and using Equation (9.301) of Douik et al. (2016) to expand the Meijer G-functions as well as the integral has been solved from the help of Equation (4.1.11) of Ho (2007) and Ng and Geller (1969). Thus we find the generalised Meijer G-function of two-variables using (Singh and Tiwari 2022a) and (Sharma and Abiodun (1975)). The exact expression of ${B}_{C, S-R}^{fso}$ is expressed as

$$\begin{aligned} B_{C, S - R}^{fso} & = \frac{{A\ell_{1}^{S - R} \ell_{1}^{R - D} \varOmega_{S - D} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} }}^{\infty } \frac{1}{{n_{1} !}}\mathop \sum \limits_{g = 1}^{2} {\mathcal{L}}_{1,g} \mathop \sum \limits_{n = 0}^{\infty } \varOmega_{g,n}^{S - D} B\left( {\frac{{\alpha_{R - D} }}{2} + 1, \mu_{g,n}^{S - D} + n_{1} } \right) \\ & \quad \times \left[ {\frac{{G_{2,1:1,5:2,6}^{{2,0{ }:4,1:4,2}} { }\left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - D} + \frac{3}{2},\mu_{g,n}^{S - D} + 1} \\ {\mu_{g,n}^{S - D} + 2} \\ \end{array} } \right|\begin{array}{*{20}c} 1 \\ {\varLambda_{1}^{S - R} } \\ \end{array} \left| {\begin{array}{*{20}c} { - 1,0} \\ {\varLambda_{{2,n_{1} }}^{R - D} , - 1,0, - 1} \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - R} }}{{D^{2} }},{ }} \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right)}}{{D^{{2\left( {\mu_{g}^{S - D} + 1} \right)}} }}} \right. \\ & \quad + \left. {\frac{{\mu_{g,n}^{S - D} G_{2,1:1,5:1,5}^{{2,0{ }:4,1:4,2}} \left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - D} + 1,\mu_{g,n}^{S - D} + \frac{1}{2}} \\ {\mu_{g,n}^{S - D} + \frac{3}{2}} \\ \end{array} } \right|\begin{array}{*{20}c} 1 \\ {\varLambda_{1}^{S - R} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} 1 \\ {\varLambda_{{2,n_{1} }}^{R - D} ,0} \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - R} }}{{D^{2} }},{ }} \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right)}}{{D^{{2\mu_{g,n}^{S - D} }} }}} \right]. \\ \end{aligned}$$

(A8)

Similarly, for the case of pointing errors the term ${B}_{C, S-R}^{{fso}^{PE}}$ can be expressed as

$$\begin{aligned} B_{C, S - R}^{{fso^{PE} }} & = \frac{{A{\text{K}}_{1}^{S - D} {\text{K}}_{2}^{R - D} {\text{K}}_{2}^{S - R} \pi^{2} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{g = 1}^{3} \frac{1}{{n_{1} !}}{\mathcal{M}}_{g,n}^{S - D} B\left( {{\text{C}}\!\!\cdot ,{\text{C}}\!\!\cdot_{{n_{1} }}^{n} } \right) \\ & \quad \times \left[ {\frac{{G_{2,1:4,8:3,7}^{2,0 :6,2:6,1} \left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - D} + \frac{3}{2},\mu_{g,n}^{S - D} + 1} \\ {\mu_{g,n}^{S - D} + 2} \\ \end{array} } \right|\begin{array}{*{20}c} {0,{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,1,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{S - R} } \\ {{\mathcal{N}}_{3}^{S - R} ,0} \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - R} }}{{D^{2} }}, } \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right)}}{{D^{{2\left( {\mu_{g}^{S - D} + 1} \right)}} }}} \right. \\ & \quad + \left. {\frac{{\mu_{g,n}^{S - D} G_{2,1:3,7:3,7}^{2,0 :6,1:6,1} \left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - D} + \frac{1}{2},\mu_{g,n}^{S - D} } \\ {\mu_{g,n}^{S - D} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{S - R} } \\ {{\mathcal{N}}_{3}^{S - R} ,0} \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - R} }}{{D^{2} }}, } \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right)}}{{D^{{2\left( {\mu_{g}^{S - D} } \right)}} }}} \right]. \\ \end{aligned}$$

(A8′)

By putting Eqs. (11), (28), and (34) in Eq. (A3), and use of Equation (9.301) of Douik et al. (2016) in expansion of the Meijer G-functions, and the integral has been calculated using Equation (3.191.1) of Douik et al. (2016). Thus we find the generalised Meijer G-function of two variables and the exact final equation for ${B}_{C, S-R}^{fso}\left({\gamma }_{th}^{fso}\right)$ is represented as

$$\begin{aligned} & B_{C, S - R}^{fso} \left( {\gamma_{th}^{fso} } \right) = \frac{{A\ell_{1}^{S - R} \ell_{1}^{R - D} \varOmega_{S - D} }}{2}\mathop \sum \limits_{{n_{1} }}^{\infty } \frac{1}{{n_{1} !}}\mathop \sum \limits_{g = 1}^{4} \mathop \sum \limits_{n = 0}^{\infty } {\mathcal{T}}_{3,g,n}^{S - D} B\left( {\frac{{\alpha_{R - D} }}{2} + 1, \mu_{g,n}^{S - D} + n_{1} } \right) \\ & \quad \times \left[ {\gamma_{th}^{f} G_{1,1:1,5:2,6}^{1,0 :4,1:4,2} \left( {\left. {\begin{array}{*{20}c} {\varLambda_{7,g,n}^{S - D} + 1} \\ {\varLambda_{7,g,n}^{S - D} + 2} \\ \end{array} } \right|\begin{array}{*{20}c} 1 \\ {\varLambda_{1}^{S - R} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} { - 1,0} \\ {\varLambda_{{2,n_{1} }}^{R - D} - 1,0, - 1} \\ \end{array} } \right.\left| {\upsilon_{S - R} \gamma_{th}^{fso} ,\upsilon_{R - D} \gamma_{th}^{fso} } \right.} \right)} \right. \\ & \quad + \left. {G_{1,1:1,5:1,5}^{1,0:4,1:4,1} \left( {\left. {\begin{array}{*{20}c} {\varLambda_{7,g,n}^{S - D} } \\ {\varLambda_{7,g,n}^{S - D} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} 1 \\ {\varLambda_{1}^{S - R} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} 1 \\ {\varLambda_{{2,n_{1} }}^{R - D} ,0} \\ \end{array} } \right.\left| {\upsilon_{S - R} \gamma_{th}^{fso} ,\upsilon_{R - D} \gamma_{th}^{fso} } \right.} \right)} \right]. \\ \end{aligned}$$

(A9)

Similarly, for the case of pointing errors the term ${B}_{C, S-R}^{{fso}^{PE}}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{C, S - R}^{{fso^{PE} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{S - D} {\text{K}}_{2}^{R - D} {\text{K}}_{2}^{S - R} \pi^{2} }}{2}\mathop \sum \limits_{{n_{1 = 0} }}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{g = 1}^{3} \frac{{\mu_{g,n}^{S - D} B\left( {{\text{C}}\!\!\!\cdot ,{\text{C}}\!\!\!\cdot_{{n_{1} }}^{n} } \right)}}{{n_{1} !}} \\ & \quad \times \mathop \sum \limits_{l = 1}^{2} q_{1,l}^{S - D} \left[ {\gamma_{th}^{fso} G_{1,1:4,8:3,7}^{1,0 :6,2:6,1} \left( {\left. {\begin{array}{*{20}c} {{\mathcal{N}}_{7,l,g}^{S - D} + 1} \\ {{\mathcal{N}}_{7,l,g}^{S - D} + 2} \\ \end{array} } \right|\begin{array}{*{20}c} {0,{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,1,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{S - R} } \\ {{\mathcal{N}}_{3}^{S - R} ,0} \\ \end{array} } \right.\left| {\begin{array}{*{20}c} {\upsilon_{R - D} \gamma_{th}^{fso} } \\ {\upsilon_{S - D} \gamma_{th}^{fso} } \\ \end{array} } \right.} \right)} \right. \\ & \quad + \left. {\mho_{g}^{S - D} G_{1,1:3,7:3,7}^{1,0 :6,1:6,1} \left( {\left. {\begin{array}{*{20}c} {{\mathcal{N}}_{5,l,g}^{S - D} } \\ {{\mathcal{N}}_{7,l,g}^{S - D} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} { {\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{S - R} } \\ {{\mathcal{N}}_{3}^{S - R} ,0} \\ \end{array} } \right.\left| {\begin{array}{*{20}c} {\upsilon_{R - D} \gamma_{th}^{fso} } \\ {\upsilon_{S - D} \gamma_{th}^{fso} } \\ \end{array} } \right.} \right)} \right], \\ \end{aligned}$$

(A9′)

The term ${\mathcal{N}}_{7,l,g}^{j,n}$ is mentioned in Table 4. From Eq. (38), the term ${B}_{S-R, C}^{fso}\left({\gamma }_{th}^{fso}\right)$ is calculated from Eq. (A1) and putting Eqs. (10), (25), and (30) in Eq. (A2) as well as similar approach as in Eq. (A8) has been utilized, then the final exact expression of ${B}_{S-R, C}^{fso}$ is represented as

$$\begin{aligned} B_{S - R, C}^{fso} & = \frac{{A\varOmega_{S - R} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} }}^{\infty } \ell_{{n_{1} }} \mathop \sum \limits_{g = 1}^{2} {\mathcal{L}}_{1,g} \mathop \sum \limits_{n = 0}^{\infty } \frac{{\varOmega_{g,n}^{S - R} }}{{D^{{2\mu_{g,n}^{S - R} }} }} \\ & \quad \times G_{2,1:1,5:1,5}^{2,0:4,1:4,1} \left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - D} + \frac{1}{2},\mu_{g,n}^{S - D} } \\ {\mu_{g,n}^{S - D} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} {1 - n_{1} } \\ {\varLambda_{1}^{S - R} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} 1 \\ {\varLambda_{{2,n_{1} }}^{R - D} } \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - D} }}{{D^{2} }}, } \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right). \\ \end{aligned}$$

(A10)

Similarly, for the case of pointing errors the term ${B}_{S-R, C}^{{fso}^{PE}}$ can be expressed as

$$\begin{aligned} B_{S - R, C}^{{fso^{PE} }} & = \frac{{A{\text{K}}_{1}^{S - R} \pi^{2} }}{2\sqrt \pi }\mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{g = 1}^{3} \frac{{{\mathcal{M}}_{g,n}^{S - R} {\text{K}}_{{n_{1} }} }}{{D^{{2\mu_{g,n}^{S - R} }} }} \\ & \quad \times G_{2,1:3,7:3,7}^{2,0:6,1:6,1} \left( {\left. {\begin{array}{*{20}c} {\mu_{g,n}^{S - R} + \frac{1}{2},\mu_{g,n}^{S - R} } \\ {\mu_{g,n}^{S - R} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{{4,n_{1} }}^{S - D} } \\ {{\mathcal{N}}_{3}^{S - D} , - \left( {\frac{{\zeta_{R - D}^{2} }}{2} + n_{1} } \right)} \\ \end{array} } \right.\left| {\frac{{\upsilon_{S - D} }}{{D^{2} }}, } \right.\frac{{\upsilon_{R - D} }}{{D^{2} }}} \right). \\ \end{aligned}$$

(A10′)

By putting Eqs. (10), (25), and (34) in Eq. (A3), and solving rest expressions from similar approach as in Eq. (A9), the exact final equation of ${B}_{S-R, C}^{fso}\left({\gamma }_{th}^{fso}\right)$ is represented as

$$\begin{aligned} B_{{S - R,{ }C}}^{fso} \left( {\gamma_{th}^{fso} } \right) & = { }\frac{{A\varOmega_{S - R} }}{2}\mathop \sum \limits_{{n_{1} }}^{\infty } \ell_{{n_{1} }} \mathop \sum \limits_{g = 1}^{4} \mathop \sum \limits_{n = 0}^{\infty } {\mathcal{T}}_{3,g,n}^{S - R} { } \\ & \quad \times G_{1,1:1,5:1,5}^{1,0:4,1:4,1} \left( {\left. {\begin{array}{*{20}c} {\varLambda_{7,g}^{S - R} } \\ {\varLambda_{7,g}^{S - R} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} {1 - n_{1} } \\ {\varLambda_{1}^{S - D} } \\ \end{array} \left| {\begin{array}{*{20}c} 1 \\ {\varLambda_{{2,n_{1} }}^{R - D} } \\ \end{array} } \right.\left| {\upsilon_{S - D} \gamma_{th}^{fso} ,\upsilon_{R - D} \gamma_{th}^{fso} } \right.} \right). \\ \end{aligned}$$

(A11)

Similarly, for the case of pointing errors the term ${B}_{S-R, C}^{{fso}^{PE}}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{S - R,C}^{{fso^{PE} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{S - R} \pi^{2} }}{2}\sum\limits_{n = 0}^{\infty } {\sum\limits_{{n_{1} = 0}}^{\infty } {\sum\limits_{g = 1}^{3} {\sum\limits_{l = 1}^{2} {\frac{{{\mathcal{M}}_{g,n}^{S - R} {\text{K}}_{{n_{1} }} q_{1,l}^{S - R} }}{{D^{{2\mu_{g,n}^{S - R} }} }}} } } } \\ & \quad \times G_{1,1:3,7:3,7}^{1,0:6,1:6,1} \left( {\left. {\begin{array}{*{20}c} {{\mathcal{N}}_{7,l,g}^{S - R} } \\ {{\mathcal{N}}_{7,l,g}^{S - R} + 1} \\ \end{array} } \right|\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,0} \\ \end{array} \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{{4,n_{1} }}^{S - D} } \\ {{\mathcal{N}}_{3}^{S - D} , - \left( {\frac{{\zeta_{R - D}^{2} }}{2} + n_{1} } \right)} \\ \end{array} } \right.\left| {\begin{array}{*{20}c} {\upsilon_{R - D} \gamma_{th} } \\ {\upsilon_{S - D} \gamma_{th} } \\ \end{array} } \right.} \right). \\ \end{aligned}$$

(A11′)

Appendix B: Aser of the MM-RF link

From Eq. (38), the terms are express to derive the ASER for the RF link. To derive Eq. (38) the functions are expressed as

$$\begin{aligned} N\left( {\lambda ,\mho ,\phi ,a} \right) & = \int_{\phi }^{\infty } {{\rm erfc}\left( {a\sqrt Y } \right)Y^{\lambda - 1} e^{ - \mho Y} dY} \\ N\left( {\lambda ,\mho ,\phi ,a} \right) & = {\rm erfc}\left( {a\sqrt \phi } \right)\frac{{\Gamma \left( {\lambda , \mho \phi } \right)}}{{\mho^{\lambda } }} \\ & \quad - \frac{a}{\sqrt \pi }\mathop \sum \limits_{r = 0}^{\lambda - 1} \frac{{\mho^{r} }}{r!}\frac{{\Gamma \left( {r + \frac{1}{2},\left( {a^{2} + \mho } \right)\phi } \right)}}{{\left( {a^{2} + \mho } \right)^{{r + \frac{1}{2}}} }}, \\ \end{aligned}$$

(B1)

From Eq. (18) of Sharma et al. (2019) and utilize Equations (2.33.10 & 11) of Douik et al. (2016), the above equation has been solved using integration by parts and the upper incomplete gamma-function $\Gamma \left( { \cdot , \cdot } \right)$ from Equation (8.350.2) of Douik et al. (2016). Hence

$$\begin{aligned} P\left( {\lambda ,\phi ,a} \right) & = \mathop \smallint \limits_{\phi }^{\infty } erfc\left( {a\sqrt Y } \right)Y^{\lambda - 1} dY \\ P\left( {\lambda ,\phi ,a} \right) & = \frac{{\left( { - \phi } \right)^{\lambda } }}{\lambda }erfc\left( {a\sqrt \phi } \right) + \frac{{a^{ - 2\lambda } }}{\lambda \sqrt \pi }\Gamma \left( {\lambda + \frac{1}{2},a^{2} \phi } \right). \\ \end{aligned}$$

(B2)

By putting Eqs. (19), (20), and (32) into Eq. (38) and solving the term ${B}_{j,i}^{RF}\left({\gamma }_{th}^{RF}\right),$ where $j\,\epsilon\,\left\{S-D,S-R\right\}$ and $i\,\epsilon\,\left\{S-R, S-D\right\}$, the Eq. (B2) has been solved by MATHEMATICA. From Eq. (B1) and utilizing Equation (8.352.6) of Douik et al. (2016), the ${B}_{j,i}^{RF}\left({\gamma }_{th}^{RF}\right)$ is represented as

$$B_{j,i}^{RF} \left( {\gamma_{th}^{RF} } \right) = \frac{{A\Psi_{j}^{{m_{j} }} }}{{2\Gamma \left( {m_{j} } \right)}}\left[ {N\left( {m_{j} ,\Psi_{j} ,\gamma_{th}^{RF} ,D} \right) - \mathop \sum \limits_{{k_{2} = 0}}^{{m_{i} - 1}} \frac{{\Psi_{i}^{{k_{2} }} }}{{k_{2} !}}N\left( {m_{j} + k_{2} ,\Psi_{j,i} ,\gamma_{th}^{RF} ,D} \right)} \right],$$

(B3)

where the term $\Psi_{j,i} \triangleq \Psi_{j} + \Psi_{i}$. Putting Eqs. (31) and (32) in Eq. (38) and utilizing Eqs. (B1) and (B2), the term ${B}_{C}^{RF}\left({\gamma }_{th}^{RF}\right)$ is expressed as

$$\begin{gathered} B_{C}^{RF} \left( {\gamma_{th}^{RF} } \right) = \frac{A}{2}\sum\limits_{{n_{2} = 0}}^{\infty } {\sum\limits_{{k_{1} = 0}}^{{m_{R - D} + n_{2} }} {C_{{n_{2} }}^{{k_{1} }} } } \left( {C_{{k_{1} }}^{m} - 1} \right)! \hfill \\ \left[ {P\left( {C_{{n_{{2,k_{1} }} }}^{m} ,\gamma_{th}^{RF} ,D} \right) \times C_{{n_{2,} k_{1} }}^{m} - \sum\limits_{{p_{1} = 0}}^{{C_{{k_{1} }}^{m} - 1}} {\frac{{\Psi_{S - D}^{{p_{1} }} }}{{p_{1} !}}} C_{{n_{2} ,k_{1} }}^{{m,p_{1} }} N\left( {C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} ,\Psi_{S - D} ,\gamma_{th}^{RF} ,D} \right) + \sum\limits_{{p_{1} = 0}}^{{C_{{k_{1} }}^{m} - 1}} {\frac{{\Psi_{S - D}^{{p_{1} + 1}} }}{{p_{1} !}}} N\left( {C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} + 1,\Psi_{S - D} ,\gamma_{th}^{RF} ,D} \right)} \right]. \hfill \\ \end{gathered}$$

(B4)

Putting Eqs. (31) and (20) in Eq. (38) as well as utilizing Equations (B1), (B2) and (8.352.6) of Touati et al. (2016). We solve the term ${B}_{C,S-R}^{RF}\left({\gamma }_{th}^{RF}\right)$, represented as

$$\begin{gathered} B_{C,S - R}^{RF} \left( {\gamma_{th}^{RF} } \right) = \frac{A}{2}\sum\limits_{{n_{2} = 0}}^{\infty } {\sum\limits_{{k_{1} = 0}}^{{m_{R - D} + n_{2} }} {C_{{n_{2} }}^{{k_{1} }} } } \left( {C_{{k_{1} }}^{m} - 1} \right)! \hfill \\ \left[ {C_{{n_{{2,k_{1} }} }}^{m} \left\{ {P(C_{{n_{{2,k_{1} }} }}^{m} ,\gamma_{th}^{RF} ,D) - \sum\limits_{{k_{2} = 0}}^{{m_{S - R} - 1}} {\frac{{\Psi_{S - R}^{{k_{2} }} }}{{k_{2} !}}} N(C_{{n_{{2,k_{1} }} }}^{m} + k_{2} + 1,\Psi_{S - D} ,\gamma_{th}^{RF} ,D)} \right\}} \right. \hfill \\ - \sum\limits_{{p_{1} = 0}}^{{C_{{k_{1} }}^{m} - 1}} {\frac{{\Psi_{S - D}^{{p_{1} }} }}{{p_{1} !}}} \left( {C_{{n_{2} ,k_{1} }}^{{m,p_{1} }} + p_{1} } \right) \hfill \\ \left\{ {N\left( {C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} ,\Psi_{S - D} ,\gamma_{th}^{RF} ,D} \right) - \sum\limits_{{k_{2} = 0}}^{{m_{S - R} - 1}} {\frac{{\Psi_{S - R}^{{k_{2} }} }}{{k_{2} !}}} N(C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} + k_{2} ,\Psi_{S - D,S - R} ,\gamma_{th}^{RF} ,D)} \right\} \hfill \\ + \left. {\sum\limits_{{p_{1} = 0}}^{{C_{{k_{1} }}^{m} - 1}} {\frac{{\Psi_{S - D}^{{p_{1} + 1}} }}{{p_{1} !}}} \left\{ {N(C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} + 1,\Psi_{S - D} ,\gamma_{th}^{RF} ,D) - \sum\limits_{{k_{2} = 0}}^{{m_{S - R} - 1}} {\frac{{\Psi_{S - R}^{{k_{2} }} }}{{k_{2} !}}} N(C_{{n_{{2,k_{1} }} }}^{{m,p_{1} }} + k_{2} + 1,\Psi_{S - D,S - R} ,\gamma_{th}^{RF} ,D)} \right\}} \right]. \hfill \\ \end{gathered}$$

(B5)

Putting Eqs. (26), (19) in Eq. (38) and utilizing Eqs. (B1), (B2) as well as (8.352.6) of Touati et al. (2016), the term ${B}_{S-R, C}^{RF}\left({\gamma }_{th}^{RF}\right)$ is represented as

$$\begin{aligned} B_{S - R, C}^{RF} \left( {\gamma_{th}^{RF} } \right) & = \frac{A}{2}\mathop \sum \limits_{{n_{2} = 0}}^{\infty } \mathop \sum \limits_{{k_{1} = 0}}^{{m_{R - D} + n_{2} }} C_{{n_{2} }}^{{k_{1} }} \frac{{\Psi_{S - R}^{{m_{S - R} }} }}{{\Gamma \left( {m_{S - R} } \right)}}\left( {C_{{k_{1} }}^{m} - 1} \right)! \\ & \quad N\left( {C_{{n_{{2,k_{1} }} }}^{m} + m_{S - R} ,\Psi_{S - R} ,\gamma_{th}^{RF} ,D} \right) \\ & \quad - \mathop \sum \limits_{{k_{2} = 0}}^{{m_{S - D} - 1}} \frac{{\Psi_{S - D}^{{k_{2} }} }}{{k_{2} !}}N\left( {C_{{n_{{2,k_{1} }} }}^{m} + k_{2} + m_{S - R} ,\Psi_{S - D, S - R} ,\gamma_{th}^{RF} ,D} \right). \\ \end{aligned}$$

(B6)

Appendix C: Asymptotic aser analysis of FSO link

In this postscript, we derive the asymptotic-SER analysis of blended FSO/RF system and express all the terms of Eq. (51). With the help of Equation (07.34.06.0040.01) of Anees and Bhatnagar (2015) and Eqs. (9) and (11), the outcome expression along with Eq. (33) has been putted in Eq. (51) and remaining part of integrand has been solved utilizing Equation (07.34.21.0085.01) of Anees and Bhatnagar (2015). The resultant closed-form equation of the term ${B}_{j,i}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$, where $j\,\epsilon\,\left\{S-R,S-D\right\}$ as well as $i\,\epsilon\,\left\{S-D,S-R\right\}$ is represented as

$$\begin{aligned} B_{j,i}^{{fso^{\infty } }} \left( {\gamma_{th}^{fso} } \right) & = \mathop \sum \limits_{k = 1}^{4} \mathop \sum \limits_{{k_{3} = 1}}^{2} \frac{{A\ell_{1}^{j} \ell_{1}^{i} }}{2\sqrt \pi }{\text{J}}_{{4,k_{3} }}^{j} {\text{J}}_{1,k}^{i} {\text{J}}_{{x_{{1,k_{3} ,k}} }} \\ & \quad \times \left[ {\overline{\gamma }_{j}^{fso} } \right]^{{ - \upsilon_{j} }} \left[ {\overline{\gamma }_{i}^{fso} } \right]^{{ - \upsilon_{i} }} , \\ \end{aligned}$$

(C1)

Similarly, for the case of pointing errors the term ${B}_{j,i}^{{fso}^{PE\infty }}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{j,i}^{{fso^{PE\infty } }} \left( {\gamma_{th}^{fso} } \right) & = \mathop \sum \limits_{k = 1}^{3} \mathop \sum \limits_{{k_{3} = 1}}^{3} \frac{{A{\text{K}}_{1}^{j} {\text{K}}_{1}^{i} }}{2\sqrt \pi }{\text{J}}_{{4,k_{3} }}^{j} {\text{J}}_{1,k}^{i} {\text{J}}_{{x_{{1,k_{3} ,k}} }} \\ & \quad \times \left[ {\overline{\gamma }_{j}^{fso} } \right]^{{ - \upsilon_{j} }} \left[ {\overline{\gamma }_{i}^{fso} } \right]^{{ - \upsilon_{i} }} . \\ \end{aligned}$$

(C1′)

where $\mathrm{J}_{1,k}^{i}$ is mentioned in Table 2, and $\mathrm{J}_{4,{k}_{3}}^{j}, \mathrm{J}_{{x}_{1,{k}_{3},k}}$ as well as ${x}_{1,{k}_{3},k}$ in Table

Table 5 Notations used in appendix equations

5.

Differentiating Eq. (25) with respect to $\gamma$ to re-calculate the term ${f}_{{\gamma }_{C}^{fso}}\left(\gamma \right)$, we find the equations for the terms ${B}_{C}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$ and ${B}_{C, S-R}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$ as

$$\begin{aligned} f_{{\gamma_{C}^{fso} }} \left( \gamma \right) & = \mathop \sum \limits_{{n_{1} = 0}}^{\infty } \frac{{\ell_{{n_{1} }} }}{\gamma } \times \left[ {G_{2,6}^{4,2} \left( {\upsilon_{R - D} \gamma {|}\begin{array}{*{20}c} {0,1} \\ {\varLambda_{{2,n_{1} }}^{R - D} ,1,0} \\ \end{array} } \right)G_{1,5}^{4,1} \left( {\upsilon_{S - D} \gamma {|}\begin{array}{*{20}c} {1 - n_{1} } \\ {\varLambda_{1}^{S - D} , - n_{1} - \frac{{\alpha_{R - D} }}{2}} \\ \end{array} } \right)} \right. \\ & \quad + \left. {G_{1,5}^{4,1} \left( {\upsilon_{R - D} \gamma {|}\begin{array}{*{20}c} 1 \\ {\varLambda_{{2,n_{1} }}^{R - D} ,0} \\ \end{array} } \right)G_{2,6}^{4,2} \left( {\upsilon_{S - D} \gamma {|}\begin{array}{*{20}c} {1 - n_{1} } \\ {\varLambda_{1}^{S - D} , - n_{1} - \frac{{\alpha_{R - D} }}{2},1} \\ \end{array} } \right)} \right]. \\ \end{aligned}$$

(C2)

Similarly, for the case of pointing errors the term ${f}_{{\gamma }_{C}^{{fso}^{PE}}}\left(\gamma \right)$ can be expressed as

$$\begin{aligned} f_{{\gamma_{C}^{{fso^{PE} }} }} \left( \gamma \right) & = \mathop \sum \limits_{{n_{1} = 0}}^{\infty } \frac{{{\text{K}}_{{n_{1} }} }}{\gamma } \times \left[ {G_{4,8}^{6,2} \left( {\upsilon_{R - D} \gamma \left| {\begin{array}{*{20}c} {0,{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,1,0} \\ \end{array} } \right.} \right)} \right. \\ & \quad \times G_{3,7}^{6,1} \left( {\upsilon_{S - D} \gamma \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{4}^{S - D} } \\ {{\mathcal{N}}_{3}^{S - D} , - (n_{1} + \frac{{\zeta_{SD}^{2} }}{2})} \\ \end{array} } \right.} \right) + G_{3,7}^{6,1} \left( {\upsilon_{R - D} \gamma \left| {\begin{array}{*{20}c} {{\mathcal{N}}_{2}^{R - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} ,0} \\ \end{array} } \right.} \right) \\ & \quad \times \left. {G_{4,8}^{6,2} \left( {\upsilon_{S - D} \gamma \left| {\begin{array}{*{20}c} {0,{\mathcal{N}}_{4}^{S - D} } \\ {{\mathcal{N}}_{{5,n_{1} }}^{R - D} , - \left( {n_{1} + \frac{{\zeta_{SD}^{2} }}{2}} \right),1} \\ \end{array} } \right.} \right)} \right]. \\ \end{aligned}$$

(C2′)

Similarly, following the similar approach as for Eq.  (C1), the final closed form representation of ${B}_{C}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$ as

$$B_{C}^{{fso^{\infty } }} \left( {\gamma_{th}^{fso} } \right) = \frac{A}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{4} \ell_{{n_{1} }} {\text{J}}_{{x_{{2,n_{1} ,k}} }} \left[ {{\text{J}}_{2,k}^{S - D} {\text{J}}_{{5,n_{1} k}}^{R - D} + {\text{J}}_{{3,n_{1} k}}^{R - D} {\text{J}}_{6,k}^{S - D} } \right]\left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} ,$$

(C3)

Similarly, for the case of pointing errors the term ${B}_{C}^{{fso}^{PE \infty }}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$B_{C}^{{fso^{PE\,\infty } }} \left( {\gamma_{th}^{fso} } \right) = \frac{A}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{6} {\text{K}}_{{n_{1} }} {\text{J}}_{{x_{{2,n_{1} ,k}} }} \left[ {{\text{J}}_{2,k}^{{R - D,n_{1} }} {\text{J}}_{6,k}^{S - D} + {\text{J}}_{3,k}^{{S - D,n_{1} }} {\text{J}}_{5,k}^{{R - D,n_{1} }} } \right]\left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} .$$

(C3′)

From Eq. (C3), the terms $\mathrm{J}_{2,k}^{S-D}$ and $\mathrm{J}_{3,{n}_{1}k}^{R-D}$ have been mentioned in Table 2, as well as $\mathrm{J}_{5,{n}_{1}k}^{R-D}$, $\mathrm{J}_{6,k}^{S-D}$, $\mathrm{J}_{{x}_{2,{n}_{1},k}}$, and ${x}_{2,{n}_{1},k}$ have been mentioned in Table 5. From the similar approach as for Eq. (C1), a closed-form expression for the term ${B}_{C,S-R}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$ is given as

$$\begin{aligned} B_{C,S - R}^{{fso^{\infty } }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A\ell_{1}^{S - R} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{4} \ell_{{n_{1} }} {\text{J}}_{{x_{{3,n_{1} ,k}} }} \left[ {{\text{J}}_{2,k}^{S - D} {\text{J}}_{{5,n_{1} k}}^{R - D} {\text{J}}_{1,k}^{S - R} } \right. \\ & \quad + \left. {{\text{J}}_{{3,n_{1} k}}^{R - D} {\text{J}}_{6,k}^{S - D} {\text{J}}_{1,k}^{S - R} } \right]\left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} \left[ {\overline{\gamma }_{S - R}^{fso} } \right]^{{ - \upsilon_{S - R} }} , \\ \end{aligned}$$

(C4)

Similarly, for the case of pointing errors the term ${B}_{C,S-R}^{{fso}^{PE \infty }}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{C,S - R}^{{fso^{PE \infty } }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{S - R} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{6} {\text{K}}_{{n_{1} }} {\text{J}}_{{x_{{3,n_{1} ,k}} }} {\text{J}}_{1,k}^{S - R} \left[ {{\text{J}}_{2,k}^{{R - D,n_{1} }} {\text{J}}_{6,k}^{{S - D,n_{1} }} + {\text{J}}_{3,k}^{{S - D,n_{1} }} {\text{J}}_{5,k}^{{R - D,n_{1} }} } \right] \\ & \quad \times \left[ {\overline{\gamma }_{S - R}^{fso} } \right]^{{ - \upsilon_{S - R} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} \left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} . \\ \end{aligned}$$

(C4′)

From Eq. (C4), the terms $\mathrm{J}_{{x}_{3,{n}_{1},k}}$ and ${x}_{3,{n}_{1},k}$ have been mentioned in Table 5. Hence, with similar approach followed as for Eq. (C4), the final closed-form expression for ${B}_{S-R,C}^{{fso}^{\infty }}\left({\gamma }_{th}^{fso}\right)$ is given as

$$\begin{aligned} B_{S - R,C}^{{fso^{\infty } }} \left( {\gamma_{th}^{fso} } \right) & = { }\frac{{A\ell_{1}^{S - R} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{4} \mathop \sum \limits_{{k_{3} = 1}}^{2} \ell_{{n_{1} }} {\text{J}}_{{4,k_{3} }}^{S - R} {\text{J}}_{3,k}^{{R - D,{ }n_{1} }} {\text{J}}_{2,k}^{S - D} \\ & \quad \times {\text{J}}_{{x_{{4,n_{1} ,k,k_{3} }} }} \left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} \left[ {\overline{\gamma }_{S - R}^{fso} } \right]^{{ - \upsilon_{S - R} }} , \\ \end{aligned}$$

(C5)

Similarly, for the case of pointing errors the term ${B}_{S-R,C}^{{fso}^{PE \infty }}\left({\gamma }_{th}^{fso}\right)$ can be expressed as

$$\begin{aligned} B_{S - R,C}^{{fso^{{PE{ }\infty }} }} \left( {\gamma_{th}^{fso} } \right) & = \frac{{A{\text{K}}_{1}^{S - R} }}{2\sqrt \pi }\mathop \sum \limits_{{n_{1} = 0}}^{\infty } \mathop \sum \limits_{k = 1}^{6} \mathop \sum \limits_{{k_{3} = 1}}^{3} {\text{K}}_{{n_{1} }} {\text{J}}_{{4,k_{3} }}^{S - R} {\text{J}}_{3,k}^{{R - D,{ }n_{1} }} {\text{J}}_{2,k}^{{S - D,n_{1} }} \\ & \quad \times {\text{J}}_{{x_{{4,n_{1} ,k,k_{3} }} }} \left[ {\overline{\gamma }_{S - D}^{fso} } \right]^{{ - \upsilon_{S - D} }} \left[ {\overline{\gamma }_{R - D}^{fso} } \right]^{{ - \upsilon_{R - D} }} \left[ {\overline{\gamma }_{S - R}^{fso} } \right]^{{ - \upsilon_{S - R} }} . \\ \end{aligned}$$

(C5′)

From Eq. (C5), the terms $\mathrm{J}_{{x}_{4,{n}_{1},k,{k}_{3}}}$ and ${x}_{4,{n}_{1},k,{k}_{3}}$ have been mentioned in Table 5.

Appendix D: Power series representation

From (Roach 1997), the Eq. (16) can be expressed the Meijer G function in terms of simple hypergeometric functions. The probability distribution function ${f}_{{\gamma }_{j}^{fso}}\left(\gamma \right)$ is represented in terms of a regularized generalised hypergeometric function from Equation (07.32.02.0001.01) of Mathematica Edition (2021) as

$$\begin{aligned} f_{{\gamma_{j}^{fso} }} \left( \gamma \right) & = {\mathcal{K}}_{1}^{j} \frac{{\pi^{2} }}{\gamma }\left[ {\aleph_{1}^{j} \left( {\upsilon_{j}^{fso} \sqrt \gamma } \right)^{{\zeta^{2} }} 1{\tilde{\text{F}}}_{2} \left( {0;1 - {\upalpha } + {\upzeta }^{2} ,{ }1 - {\upbeta } + {\upzeta }^{2} ;\upsilon_{j}^{fso} \sqrt \gamma } \right)} \right. \\ & \quad + \aleph_{2}^{j} \left( {\upsilon_{j}^{fso} \sqrt \gamma } \right)^{\alpha } 1{\tilde{\text{F}}}_{2} \left( {{\upalpha } - {\upzeta }^{2} ;{ }1 - {\upzeta }^{2} + {\upalpha },{ }1 - {\upbeta } + {\upalpha }; \upsilon_{j}^{fso} \sqrt \gamma } \right) \\ & \quad + \aleph_{3}^{j} \left( {\upsilon_{j}^{fso} \sqrt \gamma } \right)^{\beta } 1{\tilde{\text{F}}}_{2} \left. {\left( {{\upbeta } - {\upzeta }^{2} ;{ }1 - {\upzeta }^{2} + {\upbeta },{ }1 - {\upalpha } + {\upbeta }; \upsilon_{j}^{fso} \sqrt \gamma } \right)} \right] \\ \end{aligned}$$

(D1)

where $p{\widetilde{\mathrm{F}}}_{\mathrm{q}}\left({\mathrm{a}}_{1,\dots ..,}{\mathrm{a}}_{\mathrm{p}};{\mathrm{b}}_{1,\dots .,}{\mathrm{b}}_{\mathrm{q}};\mathrm{z}\right)$ represents a regularized generalised hypergeometric-function, ${\mathrm{\aleph }}_{1}^{\mathrm{j}}$, ${\mathrm{\aleph }}_{2}^{\mathrm{j}}$, and ${\mathrm{\aleph }}_{3}^{\mathrm{j}}$ have been mentioned in Table 1. The regularized hypergeometric function is represented as

$$p{\tilde{\text{F}}}_{{\text{q}}} \left( {{\text{a}}_{1, \ldots ..,} {\text{a}}_{{\text{p}}} ;{\text{b}}_{1, \ldots .,} {\text{b}}_{{\text{q}}} ;{\text{z}}} \right) = \mathop \sum \limits_{{{\text{n}} = 0}}^{\infty } \frac{{\mathop \prod \nolimits_{{{\text{j}} = 1}}^{{\text{p}}} \left( {{\text{a}}_{{\text{j}}} } \right)_{{\text{n}}} {\text{z}}^{{\text{n}}} }}{{{\text{n}}!\mathop \prod \nolimits_{{{\text{j}} = 1}}^{{\text{q}}} \Gamma \left( {{\text{n}} + {\text{b}}_{{\text{j}}} } \right)}},$$

(D2)

where ${\left({\mathrm{a}}_{\mathrm{j}}\right)}_{\mathrm{n}}$ reprsesents the Pochhammer symol from Equation (06.10.02.0001.01) of Mathematica Edition (2021). Hence, the PDF of instantaneous SNR of FSO channel using power series terms is expressed as

$$f_{{\gamma_{j}^{fso} }} \left( \gamma \right) = {\mathcal{K}}_{1}^{j} \pi^{2} \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{g = 1}^{3} {\mathcal{M}}_{g,n}^{j} \gamma^{{\mho_{g,n}^{j} - 1}} ,$$

(D3)

where ${\mathcal{M}}_{{{\text{g}},{\text{n}}}}^{{\text{j}}}$ and ${\upgamma }^{{\mho_{{{\text{g}},{\text{n}}}}^{{\text{j}}} - 1}}$ have been metioned in Table 1. It is observed that the power series in (D3) contains summation terms with only exponents of $\gamma$. Therefore, it is simple to calculate an integral containing the proposed series representation as compared to a Meijer-G function based representation in Eq. (16).