1 Introduction

In a high-quality power supply, power generation and demand are matched. The integration of renewable energy sources (RES), such as photovoltaic (PV), wind turbines, and biodiesel generators, into interconnected power systems (IPSs) to supply electricity has attracted the interest of researchers because it can minimize air pollution and alleviate economic difficulties experienced by electricity consumers due to rising fuel costs. As the customer demand changes, the frequency and tie-line power of an IPS vary. RES can increase the frequency and tie-line power deviations in IPS endangering the stability of the power system. By using load frequency control (LFC), which is the main part of automatic generation control (AGC), these frequency deviations and tie-line power fluctuations can be minimized and a reliable IPS can be ensured. In an IPS, the LFC signal is fed to a controller and set to zero to minimize tie-line power and frequency variations (Barakat et al. 2019, 2021a). The tasks of an LFC are summarized as (Barakat 2022):

  • Each area should be capable of supporting its own load at steady state;

  • Throughout a sudden load disruption and any interruptions, the system must be kept under control;

  • To improve system stability, frequency and tie-line power variations in terms of undershoot, overshoot, and settling time must be lessened.

Accordingly, designing an outstanding basic structure controller to get the AGC optimum performance in the presence of nonlinearity is a struggle. Because of their dependability, low cost, and structural simplicity, conventional proportional–integral–derivative (PID) and proportional–integral (PI) controllers are in use universally (Barakat et al. 2021b, c). Recently, the fine-tuning of the parameters of the controllers, such as PI and PID single controllers, using different optimization algorithms, such as differential evolution algorithm (DE) (Mohanty and Sahu 2019), bacterial foraging optimization algorithm (Ali and Abd-Elazim 2013), genetic algorithm (GA), firefly algorithm (FA) (Abd-Elazim and Ali 2018), and teaching–learning-based optimization algorithm (Sahu et al. 2015a), have been widely reported. The physical nonlinearities of a power system, such as governor dead band, generation rate constraint (GRC), and time/communication delay, that degrade power system performance have been studied in Jagatheesan et al. (2017), Çelik (2021). Because of its wide availability, solar PV has become a popular RES that should be integrated into IPSs. Due to the advantages of PID controller and its relevant, numerous soft computing-based conventional PI, PID, and PID with filter (PIDn) controllers have been used in two-area PV–thermal IPSs (Abd-Elazim and Ali 2018; Khadanga et al.2020a, b; Fathy and Kassem 2019; Khamies et al. 2021; Panwar et al. 2019). The particle swarm optimization algorithm (PSO) is used to adjust the scaling factors of fuzzy controller to demonstrate the effectiveness of the fuzzy controller compared to conventional controllers is carried out in Davtalab et al. (2020). In Çelik et al. (2022), authors studied the impact of energy storage on ameliorating the performance of LFC for thermal–PV power system. Also, in Revathi and Mohan Kumar (2020), a three-area PV–thermal–thermal IPSs under the action of fuzzy gain scheduling-based PI controller to improve performance of the IPSs is conducted. Perhaps, conventional controllers are simple and economical; they operate under explicit conditions. In addition, single controllers are inappropriate when the conditions fluctuate because of the nonlinear behavior of IPSs (Barakat 2022; Guha et al. 2019).

Because a cascade controller (CC) has more tuning knobs than a single controller, it can produce better results than a single controller (Barakat et al. 2021b). The CC is well known for its superior dynamic responsiveness and exceptional resilience to uncertainties and large disturbances (Çelik 2021). Therefore, CC has been used to improve IPS performance by overcoming LFC issues (Barakat et al. 2021c; Behera et al. 2019). Furthermore, the AGC of PV–thermal using capacitive energy storage based multi-stage fuzzy PIDF-(1 + PI) cascade controller is performed in Arya (2019). For practical employment, it is highly desirable to keep the controller structure simple. Accordingly, the multi-stage fuzzy PIDF-(1 + PI) controller is highly complex. Also, the use of PV power systems to overcome problems associated with LFC and the physical constraints of LFC design using optimization has not been studied so far.

Solar PV systems deserve close attention because of their advantages, such as pollution reduction, silent, easy to install, and versatility. Designing a powerful controller for an IPS is a challenging task, especially when the system has RES and nonlinearities. Although the literature mentions efficient algorithms, the number of algorithms that can be used in PV systems is limited. Moreover, only a little attention has been paid to the impact of PVs on LFC using CCs. Because of the specific advantages of PID controllers, they can be effectively used in CCs (Barakat et al. 2021b; Behera et al. 2019). Therefore, in this study, the PIDn followed by PI to form PIDn-PI CC is chosen to study the LFC issues of the PV–reheat thermal IPS. Finally, to attain the best performance, a powerful optimizer must be applied (Barakat 2022). Therefore, an innovative and powerful algorithm such as the chaos game optimizer (CGO) was introduced (Talatahari and Azizi 2020). The main idea of the CGO technique is based on some principles of chaos theory (CT) wherein the structure of fractals by the chaos game principle and the fractal problems of self-similarity are considered. The CGO has some advantages over other swarm schemes, such as fast convergence characteristics, and avoiding trapping in a local minimum (Talatahari and Azizi 2020). Thus, CGO is used in solving many engineering problems (Ramadan et al. 2021; Jiang et al. 2021). Accordingly, in this study, the CGO is chosen to fine tune the scaling factors of the proposed PIDn-PI CC.

The key objectives of the study were as follows:

  1. i.

    To identify a superior algorithm, such as CGO, for use with conventional PI and PIDn controllers and the proposed PIDn-PI CC to resolve LFC issues present in PV–reheat thermal IPSs.

  2. ii.

    To study the dynamic performance of different controllers operating in different situations with different types of disturbances.

  3. iii.

    To investigate the controller performance by altering the loading conditions and changing the controller parameters by ± 50%.

  4. iv.

    To verify the superiority of the proposed CGO:PIDn-PI CC compared with other recently introduced controllers.

  5. v.

    To investigate the performance of the proposed controller by conducting a sensitivity analysis using a random load pattern (RLP).

  6. vi.

    To study the nonlinearities of PV–reheat thermal IPSs, such as GRC and time delay (TD), and confirm the effectiveness of the proposed controller in addressing AGC-related issues.

2 System modeling

2.1 Modeling of the photovoltaic unit

PV panels are a renewable energy system that relies on the variations in solar irradiance and temperature. To manage its boost converter, a PV system requires a maximum power point tracking (MPPT) device as illustrated in Fig. 1. The fundamental function of the MPPT device is to manage the operating point of the system by varying the maximum power that can be produced through the adjustment of the duty cycle; the boost converter increases the low output voltage of the PV panels. An inverter will supply AC power to the grid from the PV system at an appropriate voltage and frequency. The entire PV system is explained in Abd-Elazim and Ali (2018). The transfer function (TF) of a complete PV unit comprising an MPPT device, a PV panel, a converter, and a filter is given below (Davtalab et al. 2020).

Fig. 1
figure 1

Block diagram of the PV unit

Full size image
$${G}_{PV}\left(s\right)=\frac{-\mathrm{AS}+\mathrm{B}}{{S}^{2}+\mathrm{C}S+D}$$
(1)

Because the PV unit does not have a primary/droop controller, the area control error (ACE)/input of the controller will be equal to the tie-line power deviation (\(\Delta {P}_{tie})\).

2.2 Modeling of the reheat thermal unit

The reheat thermal unit contains a governor, a generator, and a reheater. Each component of the unit can be represented using TFs (Barakat et al. 2021b; Khadanga et al. 2020a). The TF of a steam turbine is straightforward, being a first-order TF with a constant time \({T}_{t}\) as (Barakat et al. 2021b):

$${G}_{T}\left(s\right)=\frac{1}{1+{T}_{t}S}$$
(2)

The TFs of the speed governor valve, reheater, and generator load can be expressed using Eqs. 3–5, respectively.

$${G}_{G}\left(s\right)=\frac{1}{1+{T}_{g}S}$$
(3)
$${G}_{R}\left(s\right)=\frac{1+{{K}_{r} T}_{r} S}{1+{T}_{r }S}$$
(4)
$${G}_{P}\left(s\right)=\frac{{K}_{P}}{1+{T}_{P}S}$$
(5)

The ACE of the reheat thermal plant can be expressed using Eq. 6.

$${ACE}_{2}=B\Delta {f}_{2}+\Delta {P}_{tie}$$
(6)

where \({B}_{i}, {P}_{tie},\) and \(\Delta {f}_{i}\) are the frequency bias parameter, tie-line power deviation, and frequency deviation of the \(i\mathrm{th}\) area, respectively.

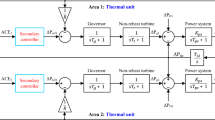
The IPS investigated in this study used a PV unit and a reheat thermal generator. Figure 2 displays the TFs of the IPS. Each generating unit in the IPS will have its own controller. The power generation rate will be limited by the physical constraints imposed by system dynamics and mechanics. In a reheat thermal plant, the GRC limits the generation rate. The physical limitations caused by GRC degrade system performance by increasing the magnitude and settling time of the oscillations. In a thermal plant, the GRC is typically 3% per min (Çelik 2021). To study the performance of the proposed controller under different conditions, a constant TD of 2 s was considered for each area to show how the TD can significantly degrade LFC. The system parameter values are shown in Appendix.

Fig. 2
figure 2

Simulink model for the two-area PV–reheat thermal IPS with a PI/PID single controller

Full size image

3 Controller-based performance function

3.1 Controller structure

Because of their dependability, ease of construction, unnecessary greater skill, and satisfactory performance, PID controllers are in high demand and are the most popular PID controllers, which can be attributed to their wide applications. They are used whenever stability and fast reaction are required (Dash et al. 2015). A CC has inner and outer control loops (Dash et al. 2015; Crowe 2005). In the CC used in this study, the outer control loop contained a PIDn controller, and the inner control loop a PI controller. Figure 3 shows the structure of the proposed PIDn-PI CC. Figure 4 illustrates a CC containing the inner and outer control loops.

Fig. 3
figure 3

Proposed PIDn-PI cascade controller

Full size image
Fig. 4
figure 4

Cascade controller structure

Full size image

3.1.1 Outer control loop

The outer process is represented by \({G}_{1}\left(s\right)\), and the entire process is subjected to the load perturbation d1 (s) (Dash et al. 2015) as shown in Fig. 4. The output of the outer control loop is \(Y\left(s\right)\). U1(s), which is the output of the inner control loop, is the input to the outer control loop. The outer control loop equation can be expressed as

$$Y\left(s\right)={G}_{1}\left(s\right) {U}_{1}\left(s\right)+{d}_{1}\left(s\right)$$
(7)

The outer control process is adjusted to obtain the reference signal R(s) (Dash et al. 2015).

3.1.2 Inner control loop

The inner control loop includes the source process \(G\)2\(\left(s\right)\). The input of the outer control loop is the output of the inner control loop. \({U}_{2}\left(s\right)\) is the input of the inner control loop (Crowe 2005). The inner control loop equation can be expressed as

$${U}_{1}\left(s\right)={G}_{2}\left(s\right){ U}_{2}\left(\mathrm{s}\right)$$
(8)

A PIDn controller is in the outer control loop and a PI controller is in the inner control loop as shown in Fig. 4. The ACE signal is fed to the PIDn-PI CC. \({U}_{1}\left(s\right)\) is subtracted from the output of the PIDn controller to obtain the input to the PI controller in the inner control loop. Reference tracking and perturbation rejection are used to compare the two control system reactions. The PIDn and PI controllers are the outer and inner control loop controllers, respectively, and can be represented by \({C}_{1}\left(s\right)\) and \({C}_{2}\left(s\right),\) respectively, as given below.

$${C}_{1}\left(s\right)= {K}_{P1}+{\frac{{K}_{I1}}{S} +SK}_{D}\frac{N}{N+S}$$
(9)
$${C}_{2}\left(s\right)= {K}_{P2}+\frac{{K}_{I2}}{S}$$
(10)

The final output of the closed loop Y(s) can be expressed as

$$Y\left(s\right)={Y}_{R}\left(s\right)-{Y}_{d1}\left(s\right)$$
(11)

where:

$${Y}_{R}\left(s\right)=\left[\frac{{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]R\left(s\right)$$
(12)
$${Y}_{d1}\left(s\right)=\left[\frac{{G}_{1}(s)}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]{d}_{1}\left(s\right)$$
(13)

where \({d}_{1}\left(s\right)\) is the perturbation load, \({G}_{1}\left(s\right)\) is the outer process loop, and \({G}_{2}\left(s\right)\) is the inner process loop (Barakat et al. 2021b).

The final output \({Y}_{th}\)(s) of the reheat thermal generator (area 2) can be expressed as

$${Y}_{th}\left(s\right)={Y}_{R}\left(s\right)-{Y}_{d2}\left(s\right)$$
(14)

where

$${Y}_{R}\left(s\right)=\left[\frac{{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]R\left(s\right)$$
$${Y}_{d2}\left(s\right)=\left[\frac{{G}_{1}(s)}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{1}\left(s\right){G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]{d}_{2}\left(s\right)$$

where \({d}_{2}\left(s\right)\) is the disturbance load in area 2.

In the case of the PV unit (area 1), the TF of the output \(Y\left(s\right)\) is substituted by \({U}_{1}\left(s\right)\) because the outer process loop \({G}_{1}\left(s\right)\) is unused. Therefore, the TF of the PV unit output can be expressed as

$${Y}_{PV}\left(s\right)={Y}_{R}\left(s\right)-{Y}_{d1}\left(s\right)$$
(15)

where

$${Y}_{R}\left(s\right)=\left[\frac{{G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]R\left(s\right)$$
$${Y}_{d1}\left(s\right)=\left[\frac{1}{1+ {G}_{2}\left(s\right){C}_{2}\left(s\right)+{G}_{2}\left(s\right){C}_{1}\left(s\right){C}_{2}\left(s\right)}\right]{d}_{1}\left(s\right)$$

Each of the two TFs of the PV unit and reheat thermal generator has two components with identical denominators. The first component is used for the reference tracking of R(s), whereas the other component is used for suppressing the second input disturbance \({d}_{1}\left(s\right)\). A CC has several advantages, which make it more stable than a single controller. A CC, therefore, exhibits superior performance with the inner control loop addressing the disturbances caused by the inner controller PI before they can spread to all system elements. Therefore, the reaction time of the system has been greatly enhanced (Dash et al. 2016; Padhy et al. 2017). Figure 5 shows the linear phase of the IPS using the proposed PIDn-PI CC. Figure 6 shows the PV–reheat thermal IPS containing nonlinearities.

Fig. 5
figure 5

Power system with the proposed cascade controller

Full size image
Fig. 6
figure 6

PV–Reheat IPS with TD and GRC (Phase 2)

Full size image

The IPS investigated in this study was developed using a single loop controller (PI/PIDn) and a PIDn-PI CC. The strong algorithm CGO was used in the PI and PID controllers and in the PIDn-PI CC. The gains of the \(\mathrm{PIDn}\) outer controller were \({K}_{P1i}\), \({K}_{I1i},\) \({K}_{D1i},\) and \({N}_{i }\) and those of the PI inner controller were \({K}_{P2i}\) and \({K}_{I2i}\) the gains were the input variables of the CGO.

3.2 Design of the performance function

An appropriate objective function has to be used before using the heuristic optimization-based controllers to enhance LFC. The integral time multiply absolute error (ITAE) criterion has been used in previous AGC studies (Sahu et al. 2014a, b). Thus, it was used in this study also to fine tune PIDn-PI CC parameters. The equivalent integral square error (ISE), integral absolute error (IAE), and integral time square error (ITSE) values also were calculated.

The objective functions (\({J}_{S}\)) can be characterized as follows:

$${J}_{1}=ITAE={\int }_{0}^{{t}_{sim}}(\left|\Delta {F}_{1}\right|+\left|\Delta {F}_{2}\right|+|\Delta {P}_{tie-line}|).t.\mathrm{d}t$$
(16)
$${J}_{2}=ITSE={\int }_{0}^{{t}_{sim}}[(\Delta {F}_{1}{)}^{2}+(\Delta {F}_{2}{)}^{2}+(\Delta {P}_{tie-line}{)}^{2}].t.\mathrm{d}t$$
(17)
$${J}_{3}=IAE={\int }_{0}^{{t}_{sim}}(\left|\Delta {F}_{1}\right|+\left|\Delta {F}_{2}\right|+|\Delta {P}_{tie-line}|).\mathrm{d}t$$
(18)
$${J}_{4}=ISE={\int }_{0}^{{t}_{sim}}[(\Delta {F}_{1}{)}^{2}+(\Delta {F}_{2}{)}^{2}+(\Delta {P}_{tie-line}{)}^{2}].\mathrm{d}t$$
(19)

where \(\Delta {F}_{1}\) \(\mathrm{and}\) \(\Delta {F}_{2}\) are the frequency deviations \(, \Delta {P}_{tie-line}\) is the tie-line power variation, and \({t}_{sim}\) is the simulation time. The optimal performance corresponds to the lowest value of \(J\) (Sahu et al. 2015b).

The ITAE of the PIDn-PI controller has to be minimized, subjected to the following conditions:

$$\begin{aligned} & K_{P1}^{min} \le K_{P1} \le K_{P1}^{max} , \,K_{P2}^{min} \le K_{P2} \le K_{P2}^{max} , \\ & K_{I1}^{min} \le K_{I1} \le K_{I1}^{max} , \, K_{I2}^{min} \le K_{I2} \le K_{I2}^{max} , \\ & K_{D}^{min} \le K_{D} \le K_{D}^{max} , \,N^{min} \le N \le N^{max} , \\ \end{aligned}$$
(20)

where the superscripts min and max indicate the \(\mathrm{minimum}\) and \(\mathrm{maximum}\) values of the relevant parameters, respectively. All gains considered during the optimization process were in the − 4 to + 4 range, whereas the coefficient of the filter \(N\) in the PIDn controller was in the 1–200 range (Sharma et al. 2018; Abou El-Ela et al. 2021).

4 Chaos game optimization

The CGO algorithm's main premise is based on some notions of CT wherein the construction of fractals by chaos game rules and the self-similarity problems of fractals are explored (Talatahari and Azizi 2020). Nowadays, design challenges have gotten so complicated that existing approaches based on mathematical principles are incapable of producing good answers. Implementing an effective new optimization method is thus of tremendous relevance to prepare for superior efficiency, high accuracy, and enhanced speed when dealing with complicated situations. Chaos game theory is employed as the core algorithm concept in the CGO algorithm, and the algorithm formula is based on game theory.

4.1 Inspiration

The unpredictability of complex systems that are sensitive to beginning circumstances is the subject of CT. CT is relevant to contemporary important patterns such as fractals, repetitive templates, and so on, (Karaboga and Basturk 2007). The CT shows that a little alteration in the system’s starting circumstances might cause disproportionate changes in the subsequent conditions. Furthermore, the present system state may settle on the system’s future state, whereas the approximate current state could rarely define the system’s future state.

Many chaotic techniques incorporate fractal graphical shapes. A fractal is a geometry form that can be repeated at different scales and displays self-similar systems. The chaotic game is a way of producing fractals in mathematics that uses an initial polygon shape with a random beginning point. In this case, the vertices of the primary polygon/fractal should be placed first. Previously, a random point was picked as the beginning point for fractal formation. The following point is defined as a fraction of the length between the starting point and one of the polygon’s vertices. The fractal is created by repeatedly repeating this procedure, considering the stochastic starting point and the random selection of the vertex in each iteration. The CGO inspiration is shown in Fig. 7. The triangle of Sierpinski is composed of 3-vertices with a factor of half. As the number of initial fractal vertices is extended to N, a Sierpinski with \(\mathrm{N}-1\) dimensions may be constructed, as seen in Fig. 8.

Fig. 7
figure 7

Inspiration for CGO

Full size image
Fig. 8
figure 8

Formation of the final shape and self-similarity of the Sierpinski triangle at different scales

Full size image

4.2 Mathematical model

The triangle of Sierpinski is first regarded as the search space for solutions possibilities in the CGO technique. CGO analyses many solutions (S), which represent some suitable seeds within a Sierpinski triangle (Zaldivar et al. 2018). Each solution (\({S}_{i}\)) is made up of certain decision variables (\({S}_{i,j}\)) that represent the seed positions:

$$S=\left[\begin{array}{c}\begin{array}{c}{S}_{1}\\ {S}_{2}\end{array}\\ \begin{array}{c}\vdots \\ {S}_{i}\\ \vdots \end{array}\\ {S}_{n}\end{array}\right]=\left[\begin{array}{cccccc}{s}_{1}^{1}& {s}_{1}^{2}& \cdots & {s}_{1}^{j}& \cdots & {s}_{1}^{d}\\ {s}_{2}^{1}& {s}_{2}^{2}& \cdots & {s}_{2}^{j}& \cdots & {s}_{2}^{d}\\ \vdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ {s}_{i}^{1}& {s}_{i}^{2}& \cdots & {s}_{i}^{j}& \cdots & {s}_{i}^{d}\\ \vdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ {s}_{n}^{1}& {s}_{n}^{2}& \cdots & {s}_{n}^{j}& \cdots & {s}_{n}^{d}\end{array}\right], \mathrm{where} \left\{\begin{array}{c}i=1, 2, \dots ,n.\\ j=1, 2, \dots ,d.\end{array}\right.$$
(21)

where \(n\) is the number of eligible-seeds/solutions inside the Sierpinski triangle, and \(d\) is the dimension of these solutions, (Gao et al. 2020). The initial positions \({s}_{i}^{j}\) of seeds are revealed randomly as:

$${s}_{i}^{j}={x}_{i,min}^{j}+r.\left({s}_{i,max}^{j}-{s}_{i,min}^{j}\right)$$
(22)

where \({s}_{i,max}^{j}\), \({s}_{i,min}^{j}\) are the upper boundary (LB) and lower boundary (UB) for the \(jth\) decision variable of the \(ith\) solution, respectively, and \(r\) is a random within \([\mathrm{0,1}]\). The first seeds created mirror the fundamental patterns of dynamical systems that rely on chaos theory. A temporary position triangle is formed with three seeds for each of the eligible seeds in the search space (\({\mathrm{S}}_{\mathrm{i}}\)): The so far defined Global Best (\(\mathrm{GB}\)), calculating the mean value for each Group (\({\mathrm{M}}_{\mathrm{Gi}}\)), and the \(\mathrm{ith}\) solution (\({S}_{\mathrm{i}}\)) as the certain seed. The three seeds are in the \({\mathrm{S}}_{\mathrm{I}}\), GB, and \({\mathrm{M}}_{\mathrm{Gi}},\) respectively. The first seed process is mathematically represented as follows:

$${Seed}_{i}^{1}={S}_{\mathrm{i}}+{\mathrm{x}}_{\mathrm{i}}*\left({\mathrm{y}}_{\mathrm{i}}*GB-{\mathrm{z}}_{\mathrm{i}}*{\mathrm{M}}_{\mathrm{Gi}}\right)$$
(23)

where \({\mathrm{x}}_{\mathrm{I}}{,\mathrm{ y}}_{\mathrm{I}}, {\mathrm{z}}_{\mathrm{I}}\) are the random number of \(0\) or \(1\) for modelling the possibility of rolling a dice, (Deepthi and Ravikumar 2015). The following is a representation of the stated process of the second, third, and fourth seeds:

$${Seed}_{i}^{2}=\mathrm{GB}+{\mathrm{x}}_{\mathrm{i}}*\left({\mathrm{y}}_{\mathrm{i}}*{S}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}*{\mathrm{M}}_{\mathrm{Gi}}\right)$$
(24)
$${Seed}_{i}^{3}={\mathrm{M}}_{\mathrm{Gi}}+{\mathrm{x}}_{\mathrm{i}}*\left({\mathrm{y}}_{\mathrm{i}}*{S}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}*GB\right)$$
(25)
$${Seed}_{i}^{4}={S}_{\mathrm{i}}\left({s}_{i}^{k}={s}_{i}^{k}+r\right)$$
(26)

where k is a random integer within [1, d]. Four distinct formulations for \({\mathrm{x}}_{\mathrm{I}}\) which regulates the displacement limits of the seeds, are offered to control the exploitation and exploration rate of the CGO algorithm (Talatahari and Azizi 2020):

$${\text{x}}_{{\text{i}}} \; = \;\left\{ {\begin{array}{*{20}l} r \hfill \\ {2*r } \hfill \\ {\delta *r + 1 } \hfill \\ {\varepsilon *r + \sim \varepsilon } \hfill \\ \end{array} } \right.$$
(27)

Where \(\delta\) and \(\varepsilon\) are random integers within [0, 1]. The flowchart of CGO scheme is displayed in Fig. 9. The constancy of the new solution possibilities is assessed to the old ones, and the seed with the lowest value is preserved, while the seeds with the lowest fitness values are removed in proportion to their degree of self-similarity. Once the solution of (\({s}_{i}^{j}\)) violates the boundary conditions, a measured flag is given, and a boundary change for the \({s}_{i}^{j}\) beyond the range outside the range of is ordered. After a certain number of iterations, the optimization process is ended.

Fig. 9
figure 9

CGO flowchart

Full size image

After all, to accomplish the finest gains of the PIDn-PI CC, the CGO needs to set one parameter, which is the number of seeds \(({N}_{seeds})\). This makes it a low number of runs, which makes it highly suitable for online tuning controllers. The CGO algorithm has matured and is one of the most likely evolutionary strategies for solving complicated engineering optimization issues. CGO was used in LFC investigations in this study. The CGO’s resilience and exploratory capabilities are determined by the type and complexity of the challenges.

5 Simulation results and discussion

On an Intel Core i-5 10210U with 2.1 GHz and 8 GB of RAM, the PV–reheat thermal IPS was evaluated within the MATLAB/SIMULINK (2019b) environment with a 10 ms step size and 20 s of simulation time \({(T}_{sim})\) for linear phase and 100 s for nonlinear phase. The settling time is computed at 2% of the SLP value. The CGO technique and the ITAE cost function are written in. mfile and the file of CGO is connected to the Simulink model for the \({J}_{\mathrm{ITAE}}\) estimation. Initially, CGO is examined using a comparison to determine its applicability in dealing with LFC difficulties. In this study, to evaluate the resilience of the proposed CGO:PIDn-PI scheme, various scenarios are explored.

5.1 Scenario 1: application of CGO to LFC studies

In the literature, the mouth-flame optimization (MFO) algorithm and PSO algorithms are powerful in solving LFC issues (Sharma et al. 2018; Lal and Barisal 2019; Veerasamy et al. 2020; Safari et al. 2021). Thus, to test the fitness of CGO for LFC studies, a comparison with the MFO and PSO based on the PIDn controller under the ITAE cost function with 10% SLP at areas 1 and 2 is executed. These algorithms have one parameter, population size, to determine. According to Barakat (2022), large population sizes do not dominate small ones in terms of determining the best solution. As a result, from the literature, the population size (\({N}_{POP}\)) is set to 50 for PSO and MFO algorithms, which is sufficient to attain the best controller gains, and the CGO seed number is set to 20, which is adequate to get an optimal solution while requiring less processing time. The iteration number is set to 50, which is performed 20 times to pick the best controller gains equivalent to the lowest ITAE value for all algorithms.

The standard deviation, average, maximum, and minimum of ITAE values are displayed in Table 1. From the statistical analysis in Table 1, the minimum value of ITAE is obtained using the proposed CGO algorithm (ITAE = 0.374) compared with MFO (ITAE = 0.393) corresponding to (\({N}_{POP}=48)\) and PSO (ITAE = 0.398) corresponding to (\({N}_{POP}=54).\) It is concluded that the proposed CGO algorithm is superior to other schemes in terms of the maximum, minimum, average, and standard deviation values.

Table 1 Comparison of ITAE values over different independent runs for various algorithms
Full size table

5.2 Scenario 2: 10% change in the demands of areas 1 and 2

First, the CGO-based PI and PIDn controllers were used to compare the performance of the CGO with those of the GA and FA (Abd-Elazim and Ali 2018), modified whale optimization algorithm (MWOA) c, and mouth-flame optimization (MFO) algorithm (Sharma et al. 2018) in addressing AGC issues. A 10% step load perturbation (SLP) (\(\Delta {P}_{d1}=\Delta {P}_{d2}=0.1\) puMW was used at t = 0 s. Table 2 displays the parameter values of the proposed controller. Figure 10 depicts the frequency changes in areas 1 and 2 and the tie-line power change. Table 3 compares the effectiveness of the proposed CGO-based PIDn-PI CC, and PIDn and PI controllers with GA:PI, FA:PI, MFO:PI, MFO:PIDn, and MWOA:PIDn controllers. The comparisons were conducted by varying two key indices: settling time and objective functions. CGO:PIDn-PI CC had the lowest cost function \((\mathrm{ITAE }= 0.05597\)) among CGO:\(\mathrm{PIDn}\) \(\left(\mathrm{ITAE }= 0.3740\right),\) MFO:\(\mathrm{PIDn}\) \(\left(\mathrm{ITAE }= 0.3933\right),\) MWOA:PIDn \(\left(\mathrm{ITAE }=1.6160 \right),\) CGO:PI (\(\mathrm{ITAE }=2.2130\)), MFO:PI \(\left(\mathrm{ITAE }= 2.6985\right),\) FA:PI (ITAE = 6.8292), GA:PI \(\left(\mathrm{ITAE }= 10.9780\right).\) The settling time of the proposed PIDn-PI controller in the 0.002 band was reduced to 0.67 and 2.24 s for frequency variations in areas 1 and 2, respectively, and 0.82 s for the power variation in the tie line, which can be attributed to the reduction of the ITAE value of the controller. Thus, the CGO is found to be more effective and superior in dealing with AGC-related issues in a single controller system than GA, FA, MFO algorithm, and MWOA. The proposed CC PIDn-PI CC was found to be better than any of the other controllers.

Table 2 Controller parameter values
Full size table
Fig. 10
figure 10

System responses for 10% SLP in areas 1 and 2: a frequency variation in area 1, b frequency variation in area 2, and c tie-line power change

Full size image
Table 3 Comparative analysis of the different controllers for 10% SLP in areas 1 and 2
Full size table

To explain the dynamic operation of the proposed controller, the values of the undershoots (Us), overshoots (Os), and root mean square (RMS) of the signal were calculated as demonstrated in Table 4. Us, Os, and RMS ensure that the proposed CGO:PIDn-PI CC handles AGC well with the controller exhibiting a smooth and quick behavior with few oscillations unlike the single controllers and other recently reported controllers.

Table 4 Sensitivity analysis for 10% SLP in areas 1 and 2
Full size table

5.3 Scenario 3: performance and uncertainty of area 2 for a 10% SLP

To compare the proposed controller with the controllers mentioned in the literature, performance and uncertainty studies pertaining to area 2 were conducted for a 10% SLP. Figure 11 shows the system responses for the 10% SLP in area 2. The time-domain analysis of the uncertainty for a ± 50% of the turbine time constant (\({T}_{t}\)), governor time constant (\({T}_{g}\)), and synchronization coefficient (\({T}_{12}\)) was conducted. Figures 12, 13, and 14 show the dynamic responses of the controllers to the frequency deviations in area 1 and tie-line power change. Moreover, synchronized uncertainties and high load disturbances in areas 1 and 2 (+ 50% change in \({ T}_{12}\), − 33% change in \({T}_{t},\) and − 25% change in \({T}_{g},\) under 10% SLP at area 1 and 20% SLP at area 2) were determined (Fig. 15). Figure 15 shows the settling time boundary in the ± 0.002 band taken in this study. This scenario demonstrates that the proposed PIDn-PI CC is robust and that it can resist the changes in the system parameters up to 50% and withstand synchronized uncertainties.

Fig. 11
figure 11

System responses for 10% SLP in area 2: a \(\Delta {F}_{1}\), b \(\Delta {F}_{2}\), and c \(\Delta {P}_{tie-line}\)

Full size image
Fig. 12
figure 12

Dynamic response with steam turbine (\({T}_{t})\) uncertainty: a \(\Delta {F}_{1}\) and b \(\Delta {P}_{tie-line}\)

Full size image
Fig. 13
figure 13

Dynamic response with governor (\({T}_{g})\) uncertainty: a \(\Delta {F}_{1}\) and b \(\Delta {P}_{tie-line}\)

Full size image
Fig. 14
figure 14

Dynamic response with synchronizing coefficient \(({T}_{12})\) uncertainty: a \(\Delta F_{1} { }\)and b \(\Delta {\mathrm{P}}_{tie-line}\)

Full size image
Fig. 15
figure 15

Transient response with synchronized uncertainties (+ 50% change in \({ T}_{12}\), − 33% change in \({T}_{t},\) and − 25% change in \({T}_{g}\)) and for 10% SLP in area 1 and 20% SLP in area 2: a \(\Delta {\mathrm{F}}_{1}\) and b \(\Delta {\mathrm{P}}_{tie-line}\)

Full size image

5.4 Scenario 4: RLPs are applied in areas 1 and 2

For the dynamic analysis of the CGO:PI/PIDn controller and CGO:PIDn-PI CC, areas 1 and 2 were simultaneously exposed to random step load perturbations as shown in Fig. 16. Figure 16a, b show the input of SLP for areas 1 and 2, respectively. Figure 17 depicts the transient responses of the controllers to an RLP. Table 5 shows a comparison of several objective functions. Figure 17 and Table 5 indicate that under a random step load, the proposed PIDn-PI CC ensures system stability with only minor variations.

Fig. 16
figure 16

Random load patterns a \({\Delta P}_{D1}\) in area 1 and b \({\Delta P}_{D2}\) in area 2

Full size image
Fig. 17
figure 17

Transient performance with the RLP: a \(\Delta {F}_{1}\), b \(\Delta {F}_{2}\), and c \(\Delta {P}_{tie-line}\)

Full size image
Table 5 Comparison of different objective functions for 160 s of RLP
Full size table

5.5 Scenario 5: performance analysis considering nonlinearities

The effect of physical nonlinearities of the controllers on system performance also was studied. The nonlinearities, such as the GRC (saturation block limited by ± 0.005) and TD (2 s), were considered as shown in Fig. 6. To investigate the enhanced performance of the proposed CGO:PIDn-PI CC, a 1% SLP was used in areas 1 and 2 at \(t=0\). Table 2 lists the tuned parameter values. Figure 18 presents the dynamic responses of the controllers, which indicates that the PIDn-PI CC has few oscillations and a satisfactory settling time. Table 6 presents the results of the comparative analysis conducted for different cost functions and settling times. The performance enhancement of the CGO:PID-PI CC was approximately 85% and 90% when compared with CGO:PIDn and PI, respectively. Thus, the proposed PIDn-PI CC is robust and powerful in dealing with various issues, including nonlinearities.

Fig. 18
figure 18

Transient response considering TD and GRC for 1% SLP in areas 1 and 2: a \(\Delta {F}_{1}\), b \(\Delta {F}_{2}\), and c \(\Delta {P}_{tie-line}\)

Full size image
Table 6 Comparative analysis of different controllers considering TD and GRC nonlinearities for 1% SLP in areas 1 and 2
Full size table

6 Conclusion

An ITAE criterion was used to examine the deployment of the novel CGO-based PIDn-PI CC in a PV–reheat thermal IPS with and without nonlinearities, and the associated ISE, ITSE, and IAE criteria were also determined. The PV unit of the PV–reheat thermal IPS that was investigated with and without the nonlinearities in the study had a MPPT method. To conduct a detailed LFC analysis and validate the applicability of the proposed PIDn-PI CC, the dynamic LFC response profiles of the controller are compared with those of the CGO:PI/PIDn single controller and with those of previously reported controllers. In linear phase, the results demonstrated that the proposed PIDn-PI CC outperformed the other reported and studied controllers by more than 85% under all scenarios, and the uncertainty for a ± 50% change in the system parameters is diminished. An RLP is used to verify the performance of the proposed controller. Finally, in the nonlinear phase, the GRC and TD of the IPS are used to determine the effectiveness of the proposed controller for AGC. The performance enhancement of the proposed CGO:PID-PI CC was approximately 85% and 90% when compared with CGO:PIDn and PI, respectively. Therefore, the time-domain studies demonstrated that the proposed CGO:PIDn-PI scheme outperformed all other techniques in terms of the oscillation magnitude and settling time in all the scenarios considered.

In the near future, prior to validating its reliability, the proposed approach will be assessed with complex application scenarios such as LFC with incorporated electric vehicles, wind, and PV system based on random solar irradiation level.