1 Introduction

The satellite categories are based on the different types of orbits and their altitudes (Kota et al. 2003). SatCom downlink and uplink communications, which are affected by space turbulence, atmospheric attenuation, and angle of arrival variations, can be used effectively with a frequency spectrum spanning 20 to 375 THz (ITU 2019). A satellite can be used as a relay to help a source get around channel turbulence and improve system performance. Using binary pulse position modulation (BPPM) and IM/DD with a large number of optical ground stations (OGS), the examination of the physical layer performance for optical downlink between low earth orbit (LEO) and OGS has been presented in Erdogan et al. (2021). In Zheng et al. 2016, the direct optical inter-satellite link was discussed using BPPM and IM/DD, and the closed form of outage probability (OP) was obtained. Ma et al. (2015) analyzed the performance of satellite-to-ground uplink/downlink with coherent optical communications in the case of the number of OGS over the Gamma–Gamma turbulence channel. They concluded that the system’s performance could be significantly enhanced by the multiple aperture receiver systems. The new mechanism for improving the performance analysis is investigated in Kong et al. (2022) where the authors discuss improving the performance analysis using rate-splitting uplink NOMA transmission in high-throughput satellite systems. The use of artificial intelligence (AI) or machine learning (ML) can enhance satellite communication performance, as explained in Huaicong et al. (2022). The author in Erdogan et al. (2022) discusses how to choose the best SNR for a high altitude platform station (HAPS) using the DF technique and how to derive a closed form for outage probability. Serial relays, as discussed in Refaai et al. (2018), can improve the performance of optical relay communication systems. The author in Tan et al. (2018) discusses the all-optical forwarding relay (AOFR) system and uses various system parameters to empirically show the benefits of a satellite relay system for interplanetary optical communication networks. Do et al. (2020) discusses the analysis of geostationary earth orbit (GEO) and low-earth orbit (LEO) laser communication under the influence of pointing errors on the transmitting side.

The performance analysis of serial relay orbital optical satellite communication in existing turbulent channels with different primary downlink system models is investigated in Refaai et al. (2022). In this study, the performance of the end-to-end uplink optical signal system is compared to the optical direct link relayed from OGS to GEO through multiple LEO satellites and the downlink optical relay at the same system parameters. For end-to-end serial relay optical satellite communication, the closed-form outage probability and bit error rate are examined in terms of various channel parameters and compare the results to clarify the superiority of our model we compare our results with direct link and downlink optical relay with the same system parameters. The results show that the suggested system performs much better than a direct link for different system parameter values at various permissible zenith angles. We also go over how key satellite optical communication link characteristics affect system performance. The remaining sections of the paper are structured as follows. Section 2 describes mathematical analysis and problem formulation. Section 3 presents our numerical results, and Sect. 4 concludes our results.

2 Mathematical analysis

2.1 System model

We take into account end-to-end uplink optical relay SatCom, where perfect channel state information (CSI) is taken into account and a different number of interconnected LEO satellites are relayed between OGS and GEO using DF technique (Abaza et al. 2016). Consider inter-orbit pointing errors while assuming the LEO satellites are aligned with the incoming beam from OGS to correct bore-sight pointing problems. The number of connected LEO satellites in the first hop can be used to form a constellation and communicate with the best OGS by using opportunistic scheduling method to increase the performance of our suggested system. To show how altitude affects system performance, the location of the ground station in two different scenarios above the sea surface was investigated.

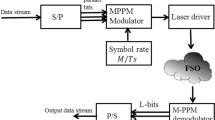
The direct link is used to compare with our outcomes to more clearly illustrate the benefits of the suggested model (Erdogan et al. 2021). The proposed model employs the proper system parameter values in Fig. 1 to make up for the connection performance degradation brought on by channel turbulence in the two hops of laser communication between orbits.

Fig. 1
figure 1

Satellite uplink with LEO relay communication

Full size image

2.2 OGS/LEO and total link analysis

We were able to create an instantaneous SNR channel model that takes space turbulence brought on by Mie scattering and geometric scattering into account, as well as fading and attenuation. The optical links can be improved by deploying additional LEO satellites, provided that they are directed with the incoming beam from OGS, in order to adjust for bore-sight pointing error (Refaai et al. 2018). Because the Gamma–Gamma model is accepted to be valid in all turbulence regimes for a point receiver (direct link), Nevertheless, the Gamma–Gamma model does not hold at different apertures; averaging takes place in the exponentiated weibull model, and the scintillation index for the two models is approximately the same at our aperture radius range (Song et al. 2016). The instantaneous SNR (\({\gamma }\)) can be expressed as

$$\begin{aligned} \gamma =\frac{P_t}{N_0} I^2, \end{aligned}$$
(1)

where I is the aggregated channel model, and \(P_t\) is the transmitted power, which is reduced by half in the case of relaying due to atmospheric attenuation compounded by turbulence due to fading and N0/2 is the white Gaussian noise variance. The atmospheric attenuation, which is mostly brought on by minute water particles, can be expressed by extracting its values (Refaai et al. 2022; Barrios 2013). The attenuation due to geometric scattering, \(I^{g}\), is closed to surface of the earth and can be expressed as

$$\begin{aligned} I^g= \exp ( - \Theta L), \end{aligned}$$
(2)

where L is the propagation distance and \(\Theta \) is the attenuation coefficient given by

$$\begin{aligned} \Theta&=\left( \frac{3.91}{V}\right) \left( \frac{\lambda }{550}\right) ^{- \Psi },\\ V&=\frac{1.002}{{L_w N}^{0.6473}}, \end{aligned} $$
(3)

where V is the visibility measured in kilometres, \(\lambda \) represent the operating wavelength which equal to 1.55 um, \(L_w\) is the amount of liquid water, and N is the concentration of clouds. We assume that the cloud type is thin cirrus, and that \(\Psi \) is the particle size-related coefficient provided by Kim’s model (Erdogan et al. 2021). The OP is defined as the likelihood that the instantaneous SNR (\(\gamma \)) is less than a predefined threshold value (\(\gamma _{th}\)). Then, in the case of turbulence-induced fading, the outage probability of the first hop \(OP_1\), where the best LEO satellite is selected among numerous candidates by using opportunistic scheduling, can be expressed as an exponentiated Weibull fading channel that is chosen to make a fair comparison with direct link characteristics in terms of our model parameters, and can be written as

$$\begin{aligned} OP_1= \prod _{j=1}^{K}\left( 1-\exp [- (\frac{\gamma _{th}}{{({\eta _j} {I_j}^{a})^2}{ \gamma ^-_j}})^ {{\beta _j} /2}]\right) ^{\alpha _j}, \end{aligned}$$
(4)

where j denote to the dedicated number of the available LEO satellites, \(\alpha _j\), \(\beta _j\) , and \(\eta _j\) are the two shape parameters component and the scale parameter, respectively, and can be derived as (Erdogan et al. 2021; Refaai et al. 2022).

$$\begin{aligned} \alpha _j&= \frac{7.220 \times \sigma _{i}^{2/3}}{\Gamma (2.487 \sigma _{i} ^{2/6} - 0.104)},\\ \beta _j&= 1.012 (\alpha _j \sigma _{i}^{2})^{-13/25} + 0.142,\\ \eta _j&= \frac{1}{\alpha _j \Gamma (1+1/\beta _j) g(\alpha _j,\beta _j)}, \end{aligned} $$
(5)

where \(\sigma _{i}\) denotes the scintillation index and can be given as

$$\begin{aligned} {\sigma _{i}}^2&=\exp \left[\frac{0.49 {\sigma _{R}}^2}{(1+1.11 {\sigma _{R}}^{12/5})^{7/6}} + \frac{0.51 \sigma _{R}^2}{(1+0.69 {\sigma _{R}}^{12/5})^{5/6}}\right]-1,\\ \sigma _{R}^2&= 2.25 k^{7/6} sec^{11/6} (\xi ) \int _{h_0}^{H} {C_{n}}^{2}(h) (h-h_{0})^{5/6} dh, \end{aligned} $$
(6)

where \(k={2 \pi }/{\lambda }\) is the wave number, \(\xi \) is the zenith angle, \(h_0\) stands for the height of the GS above ground level, H represents the altitude of the satellite, \({C_{n}}^{2}(h)\) is refractive index constant at altitude h and can be written as (ITU 2019).

$$\begin{aligned} {C_{n}}^{2}(h)&= 8.148 \times 10^{-56} {{v_r}^2} h^{10} {\exp ^{-h/1000}}+ 2.7 \times {10^{-16}} \\ &\quad {\times \exp ^{-h/1500}} + C_0 {\exp ^{-h/100}} m^{-2/3}, \end{aligned} $$
(7)

where \({v_r}\) is r.m.s. ground wind speed, \(C_0= 1.7 \times 10^{-17}\) is the nominal value of refractive index.

2.3 LEO/GEO link analysis

This is an orbit-to-orbit optical link for which the IM/DD and BPPM are employed (Zheng et al. 2016). The OP can be expressed in terms of the receiver’s instantaneous electrical SNR as (Safari and Uysal 2018), which tends to

$$\begin{aligned} OP_2&=Pr(\gamma<\gamma _{th})\\ &=Pr\left( \frac{1}{N_0 Be} [R P_t h_{SD} G_R]^2 <\gamma _{th}\right) =(\chi /A)^{\xi ^2}, \end{aligned} $$
(8)

where R is the responsivity of the photodiode, \({h_{SD}}\) is the channel attenuation from source to destination, \({G_R}\) is the amplifier gain, \({N_0}\) is the noise variance under the assumption of white Gaussian noise for the bandwidth of the electrical band pass filter Be and \(\xi =\frac{\omega _z}{2 \sigma }, A=\frac{2 a^2}{\omega _z ^2}\), \({\omega _z}\) represent the beam radius at the receiver, which is due to turbulent free equal to half divergence angle \({\theta _d}\) multiplied by distance z, a is the aperture radius, \(\chi =\frac{\sqrt{\gamma _{th} N_0 Be}}{R P_t G_R}\) and \(\sigma \) is the pointing error displacement standard deviation \({\theta _p}\) multiplied by z (Safari and Uysal 2018).

The end to end outage probability (\(OP_{T}\)) for the proposed model can be represented as:

$$\begin{aligned} OP_T = 1-((1-OP_1)(1-OP_2))=F_{\gamma }(\gamma _{th}) \end{aligned} $$
(9)

Then, the general form for average BER can be calculated using the cumulative distribution function (CDF) of SNR at BPPM for an optical point-to-point link as

$$\begin{aligned} BER= d E [Q(\sqrt{c\gamma })]=\frac{d}{\sqrt{2 \pi }}\times \int _{0}^{\infty }F_{\gamma }\left(\frac{y^2}{c}\right) \exp \left(\frac{-y^2}{2}\right) dy, \end{aligned} $$
(10)

where Q(.) is the average over channel fading distributions and (d, c) are constants depending on the modulation format BPPM and equal to (1, 0.5) in our model (Abaza et al. 2016).

2.4 General direct link analysis

We consider IM/DD with BPPM and AWGN channel expressing the combined channel PDF in terms of Meijer-G function and the heterodyne detection is proposed. Then, the direct link \(OP_d\) as (AlQuwaiee et al. 2015).

$$\begin{aligned} OP_d&= \frac{\alpha \beta ^{(\alpha + \beta ) /2}}{\Gamma (\alpha ) \Gamma (\beta ) {h^{-}}^{(\alpha + \beta )/2}} \times \left(\frac{\gamma _{th}}{\gamma _{elec}}\right)^{(\alpha + \beta )/4} \\ &\quad \times G_{1,3}^{2,1} \left( \begin{matrix}{-(\alpha + \beta )}/2 \\ {(\alpha - \beta ) /2}, {(\beta - \alpha ) /2}, {- (\alpha + \beta )/2} \end{matrix} \Vert {\frac{\alpha \beta }{h^{-}} \sqrt{\frac{\gamma _{th}}{\gamma _{elec}}}} \right) , \end{aligned} $$
(11)

where \({\gamma _{elec}}\) represents the average electrical SNR, \({h^{-}}\) represent Gamma–Gamma distribution for atmospheric turbulence. \(\alpha \) and \(\beta \), respectively, represent the small scale and large scale eddies of the scattering process.

3 Numerical results

A series of simulations performed using the Matlab 2016 and Maple programmes have also confirmed our theoretical findings. The ground level and high ground level in the windy weather scenario are then validated in terms of the likelihood of an outage. A number of suitable LEO satellites (\(K = 1, 8\)), thin cirrus clouds, and various zenith angles (\(\xi \)) are considered. Simulation results verify the efficiency of our used analytical model with Monte-Carlo (MC) simulation using \(10^{6}\) samples, and the pointing error standard deviation and half beam divergence angle for the second hop of our proposed model are determined in Song et al. (2016). All simulation parameters and values are shown in Table 1.

Table 1 List of symbols and parameters [3];[4];[5];[7];[14]
Full size table

In Fig. 2, at \( h_0 = 0\), \( K=1 \), OP target \(10^{-6}\), decrease zenith angle \( \xi \), increase the system performance by assisting the signal in overcoming channel turbulence, where \( SNR= 50, 55, 78\) dB for \(\xi = 10^\circ , 30^\circ , 60^\circ \), respectively, compared to 70 dB for direct link which clearly indicate the poor system performance at higher values of \(\xi \).

Fig. 2
figure 2

Effect of zenith angle and the number of LEO satellites at ground level deployment

Full size image

At \( K = 8\), this improvement becomes obvious and significant. As can be observe, the SNR can bring at \( \xi =10^\circ \) up to 20 dB using \( K=8 \) compared to \( K=1 \).

This illustrates the significance of selecting the system’s primary characteristics as well as the availability of LEO satellites.

The system performance in Fig. 3 is significantly influenced by the relay receiver aperture radius. This fact makes it necessary to understand the ideal design for our suggested model in order to achieve the same OP that while maintaining the proposed model’s superiority in terms of direct link at the minimum SNR.

Fig. 3
figure 3

Effect of relay receiver aperture at different ground level deployment

Full size image

Correspondingly, we noticed that the OGS altitude 1000 m has an enhancement effect up to 1 cm at receiving aperture radius of the relay satellite no matter where the ground station altitude, for example, at \(h_0= 0\), \( \xi = 10^{\circ }, 30^{\circ }, 60^{\circ } \) then, the required aperture are 20, 22, 30 cm, respectively, to target the required outage probability \(10^{-6}\) at \( K=1 \).

But, the performance of the system is enhance at \(K=8\) up to 10 cm with the same \(\xi \) compared to the same properties and \(K=1\) .

In the second state, OGSs are deployed at \(h_0 = 1000\) m from the ground level. There is an improvement of system performance over ground level deployment up to 2 to 4 dB (5:10%), while maintaining the same enhancement properties with respect to both \(\xi \), and the number of LEO satellites at the same OP target as shown in Fig. 4.

Fig. 4
figure 4

Effect of zenith angle and the number of LEO satellites at high ground level deployment

Full size image

To demonstrate the superiority of the proposed system, we compare the results to the downlink serial relay optical communication model (Refaai et al. 2022) at \(\lambda = 1550\) nm and \(h_0 = 0\) m, which concludes that the proposed system outperforms the downlink system by up to 1 dB at \(\xi = 10^{\circ }\) due to the change in the half beam divergence angle with distance. This value increases to 3 dB at \(\xi =60^{\circ }\), which can be explained as the overall OP performance of the proposed system improves as both atmospheric turbulence and atmospheric attenuation effects decrease due to shorter propagation distances to the fading and atmospheric region, which can be close to the earth. Thereby, keeping the zenith angle small can boost the overall performance compared to a direct link, as indicated in Fig. 5.

Fig. 5
figure 5

Comparing uplink and downlink optical satellite relay at various zenith angles

Full size image

In other words, to maximize the value of this study, which has a significant indicator on contemporary studies, BER, other analysis have been merged to corroborate the benefits of our conclusions as discussed in Fig. 6.

Fig. 6
figure 6

Effect of the number of LEO satellites on bit error rate performance of the system at \(h_0 =0\), \(\xi =30^{\circ }\)

Full size image

It is evident that increasing the number of LEO satellites generally improves system performance; for instance, increasing the number of available LEO satellites from \(K=2\) to \(K=4\) tends to increase system performance up to 10 dB, but at higher numbers of available LEO satellites, the improvements gradually diminish.

4 Conclusion

The uplink laser relay satellite communication is considered in this paper. Some key design considerations, including the ideal zenith angle, the number of possible LEO orbit satellites, the receiver aperture cross-section area, and the altitude of the ground station, can improve optical OGS-GEO satellite communications. We looked at two potential ground station deployment scenarios as well as the impact of the key system parameters on our proposed end-to-end system design. Due to the relationship between the channel turbulence and the beam divergence angle over system performance, the uplink optical SatCom is better than the downlink optical SatCom by up to 3 dB. Our findings show that reducing the zenith angle has a significant impact on system performance; however, at \(\xi \ge 70^{\circ }\), satellite communication is lost. The number of available LEO satellites can achieve greater system performance, up to 57% under the same channel conditions, whereas the OGS altitude increase has a considerable impact on system performance. The best selection of govern parameters allows for a 10% reduction in the receiver aperture radius. Last but not least, end-to-end relay SatComs parameters like aperture design, operating wavelength, OGS deployment, and diversity order are crucial for enhancing system performance over a direct link (OGS-GEO).