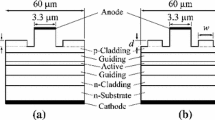
Abstract
In this work, a simulation-based analysis of a CW-driven tapered ridge-waveguide laser design is presented. Measurements of these devices delivered high lateral brightness values of \({4}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) at \({2.5}\,\hbox {W}\) optical output power. First, active laser simulations are performed to reproduce these results. Next, the resulting complex valued intra-cavity refractive index distributions are the basis for a modal and beam propagation analysis, which demonstrates the working principle and limitation of the underlying lateral mode filter effect. Finally, the gained understanding is the foundation for further design improvements leading to lateral brightness values of up to \({10}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) predicted by simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
High-brightness diode lasers emitting in the 9xx nm spectral region are of interest for several applications, including direct material processing (Schulz and Poprawe 2000). In general, the brightness \(B\propto P/M^2\) of a laser source can be improved if its output power P can be increased at a higher rate then its beam propagation ratio \(M^2\). The output power of continuous-wave (CW) driven ridge-waveguide lasers, however, is limited by its high intra-cavity optical power and current densities. Both effects result in increased device temperatures which further leads to thermal power saturation as well as a rising risk of catastrophic optical damage (COD) (Wenzel et al. 2010; Tomm et al. 2011).
These effects can be reduced by increasing the biased contact area. Unfortunately, this leads to wider waveguides with an increased number of supported lateral modes, which eventually diminishes the resulting beam quality (Koester et al. 2020a). Therefore, the round-trip gain of unwanted higher-order lateral modes has to be limited. One possibility to archive both, a larger overall electrical contact area and lateral mode filtering, is to widen the contact and waveguide width in longitudinal direction. The idea is that the narrowest waveguide limits the number of supported lateral modes inside the whole cavity. The concept of the resulting tapered ridge-waveguide (TRW) lasers, also known as tapered waveguide lasers (Williams et al. 1999) or index-guided tapered lasers (Auzanneau et al. 2003). These devices typically possess a small total opening of \(\Theta _t < {1}^{\,\circ }\) leading to astigmatism-free emission (Krakowski et al. 2003).
Recently, results of TRW lasers emitting at \({970}\,\hbox {nm}\) were reported resulting in lateral brightness \(B_\sigma\) values of \({4}\,{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) at \({2.5}\,\hbox {W}\) with \({55}\,{\%}\) conversion efficiency (Wilkens et al. 2020). In this work, we investigate the underlying TRW laser design as schematically shown in Fig. 1 using the traveling-wave-based simulation tool WIAS-BALaser which takes into account all relevant carrier and temperature effects (Radziunas 2018). Subsequently, the resulting time-averaged intra-cavity complex index distributions are used to perform a modal analysis as well as a beam-propagation method (BPM) based cavity round-trip investigation to reveal the design-related lateral mode filter properties.
This study is organized as follows. First the lateral-longitudinal device design is introduced in Sect. 2. Next, the used simulation tools and applied data post-processing procedure are introduced in Sect. 3. Subsequently, the obtained results are presented and discussed in Sect. 4. Finally, in Sect. 5 this work is concluded.
2 Device design
The TRW lasers investigated are based on the design first presented in Wilkens et al. (2020). Its vertical structure relies on an extreme double asymmetric (EDAS) large optical cavity (LOC) design which combines a low electrical series resistance, low carrier leakage, free-carrier absorption and optical losses leading to high conversion efficiencies (Hasler et al. 2014).
The lateral-longitudinal layout is shown in Fig. 1. Here, the ridge width w increases linearly from \(w_\textrm{r}\) at the rear to \(w_\textrm{f}\) at the front facet. This is achieved by a \(L_\textrm{t}= 4.4\,{mm}\) long taper connecting a straight rear and front waveguide having a length of \({1}\,\hbox {mm}\) and \({0.6}\,\hbox {mm}\), respectively. The width B of the index guiding trenches changes linearly within the tapered section such that \(w + 2B = {27}\,{\upmu }\hbox {m}\) is held constant over the whole \({6}\,\hbox {mm}\) long device. In addition to the TRW lasers, reference ridge-waveguide (RW) lasers were evaluated in this work. To enable a fair comparison of their results the width of these straight lasers was chosen to result in the same contact area as the TRW devices. The ridge and trench widths of both devices are summarized in Table 1.
Using the effective index approximation and assuming a symmetrical waveguide with infinitely extended index trenches as well as neglecting any heating and carrier effects present in CW-driven diode lasers the number N of lateral guides modes at any position inside the cavity can be estimated by
where the \(\textrm{ceil}\{x\}\)-operator rounds its argument x to the least integer greater than or equal to x.
Figure 2 shows the results of Eq. (1) as function of the ridge width w and effective index \(\Delta n_0\) for an emission wavelength of \(\lambda _0 = {970}\,\hbox {nm}\) and a reference index of \(\bar{n} = 3.36\). The index trenches of both device types result in \(\Delta n_{0}\) of \(-0.004\). It follows that the narrow and wide RW sections of the tapered waveguide support up to \(N = 2\) and 8 modes, respectively. The reference RW laser on the other hand supports 5 modes within its whole cavity.
3 Simulation tool and analysis procedure
Here, the used active laser simulation tool is introduced in Sect. 3.1. Subsequently, in the Sects. 3.2 and 3.3, the methods that form the basis for the study of the mode filtering properties of the tapered laser design are laid out.
3.1 Laser simulation tool: BALaser
The laser simulations were performed using WIAS-BALaser (Radziunas 2018). Here, the forward and backward traveling slowly varying fields \(u^\pm (x,z,t)\) within the lateral-longitudinal (x-z) plane (see Fig. 1) are described by paraxial traveling-wave equations assuming a reference refractive index \(\bar{n} = 3.36\) and wavelength \(\lambda _0 = {970}\,\hbox {nm}\):
Here, \(n_g = 3.81\), \(c_0\) and \(k_0 = \frac{2\pi }{\lambda _0}\) are the group index, the vacuum speed of light and the free space propagation constant, respectively. The operator \(\mathcal{D}\) accounts for the dispersion of the optical gain in Lorentzian approximation, whereas \(f^\pm _\textrm{sp}\) are Langevin forces incorporating spontaneous emission (Ning et al. 1997; Wünsche et al. 2003). The refractive index variation relative to the reference index is modeled as in Zeghuzi et al. (2019)
where the first bracketed expression on the right-hand side accounts for the built-in effective index contrast \(\Delta n_0\) caused by the etched index trenches as well as carrier density (\(\Delta n_N\)) and temperature (\(\Delta n_T\)) dependent index changes. The first and second terms of the imaginary part account for the intra-cavity gain g and loss \(\alpha\) distributions. For details about the specific dependencies, the reader is referred to Zeghuzi (2020).
Together with the Eq. (2), equations modeling the relevant carrier and temperature effects are considered. These include an effective diffusion equation of the excess carrier density N(x, z) to model the lateral diffusion of carriers within the active region as well as a Laplace equation for the quasi-Fermi potential of the holes in the p-doped region to account for current spreading and obtain the current density injected into the active region (Zeghuzi 2020).
The temperature distribution is calculated by solving a stationary heat flow equation for the self-consistently obtained time-averaged heat sources h within each vertical-lateral cross-section of the laser cavity. However, since h is not known in advance an iterative approach is used. In the first simulation all heat sources are neglected (\(h = 0\)) leading to \(T = T_\textrm{HS}\), where \(T_\textrm{HS} = 300\,\hbox {K}\) is the heat sink temperature. In all following iterations, h consisting of Joule heat, absorption heat, recombination heat and quantum-defect heat is computed from the results of the previous electro-optical simulation. More details on the implementation of the thermal model can be found in Radziunas et al. (2019).
All BAlaser simulations were performed considering a \({0.4}\,\hbox {mm}\) wide and \({6}\hbox {mm}\) long domain having a lateral and longitudinal resolution of \(dx = {0.25}\,\upmu \hbox {m}\) and \(dz = {6}\,\upmu \hbox {m}\), respectively. At each working point, three iterations of the thermal model have been performed, were each one represents a \({2}\,\hbox {ns}\) long transient simulation. The results presented in this work were obtained by averaging over the last \({2}\,\hbox {ns}\) of the final iteration step. The rear and front facets of all devices are modeled to have power reflectivity values of \({98}\,{\%}\) (HR) and \({0.1}\,{\%}\) (LR), respectively.
The effective densities of states as well as the dependence of the refractive index on the carrier density were fitted to results obtained by the microscopic model proposed by Wenzel et al. (1999). Most of the remaining parameters entering the simulation tool were taken from the literature (Gehrsitz et al. 2000; Vurgaftman et al. 2001; Piprek 2013). The temperature dependencies of the simulation parameters are summarized in Zeghuzi (2020).
Finally, in order to achieve a good agreement between simulated and experimental power-current characteristics the Shockley-Read-Hall recombination rate and the material absorption were used as fitting parameters resulting in values of \(A = 4.95 \cdot 10^{8}\,{\hbox {s}^{-1}}\) and \(\alpha _0 ={126}\,{\hbox {m}^{-1}}\), respectively.
3.2 Analysis of the time-averaged index distribution
Figure 3 depicts the time-averaged intensity \(\langle \Vert u(x,z)\Vert ^2\rangle = \langle \vert u^+ \vert ^2 + \vert u^- \vert ^2 \rangle\), carrier density \(\langle N(x,z) \rangle\) and temperature \(\langle T(x,z)\rangle\) distributions at \({2.5}\,\hbox {W}\) output power obtained by the laser simulation tool introduced above. Using these quantities Eq. (3) can be used to calculate a time-averaged complex refractive index distribution as:
The resulting complex refractive index profile is shown in Fig. 4 as real valued refractive index \(\Re \{\langle n(x,z) \rangle \}\) (top) and gain/loss \(\Im \{2k_0\langle n(x,z) \rangle \}\) distribution (bottom). It can be seen that the complex index also resembles the non-uniformities already present in the intra-cavity distributions \(\langle \Vert u(x,z)\Vert ^2\rangle\), \(\langle N(x,z) \rangle\) and \(\langle T(x,z)\rangle\), see Fig 3.
In this work, \(\langle n(x,z) \rangle\) is the basis to obtain a deeper understanding of the mode-filter properties resulting from the tapered cavity of the TRW laser design. This is done by calculating the local 1D lateral TE modes \(\Phi ^{(m)}(x)\) of the time-averaged waveguide which obey the Helmholtz equation
giving the profiles of local guided and radiation modes \(\Phi ^\mathrm {(m)}\) and its corresponding eigenvalues \(\beta ^{(m)} = k_0 n^{(m)}\) holding information about the corresponding modal index and gain values. Here, \(n^{(m)}\) is the complex modal index and m the mode number.
Additionally, \(\langle n(x,z) \rangle\) is used in a beam propagation method (BPM) based cavity round-trip analysis of the first three waveguide modes revealing information about the modal cross coupling inside the laser as well as round-trip gain/loss. The governing equation can be obtained from Eq. (2) by assuming only forward traveling fields and neglecting the time derivative as well as the terms accounting for dispersion and spontaneous emission (Chung and Dagli 1990). To avoid reflections of radiated light at the domain boundaries transparent boundary conditions were used (Hadley 1991). The spatial discretisation in the mode and BPM calculations were set to the values used in BALaser.
3.3 Modal power fraction
As mentioned above, in BALaser the optical field is modeled by traveling-wave equations. However, often it is also of interest how much power each mode contributes to the emitted laser field. Utilizing the orthogonality relation
the time-dependent complex forward traveling field \(u^+\) at the front facet (\(z = L\)) is assumed to be decomposable into lateral modes of the time-averaged waveguide \(\langle n(x,L) \rangle\) as
with \(b^{(m)}(t)\) being the complex-valued time-dependent expansion coefficient of the \(m^\textrm{th}\) lateral mode. Since the CW output power P is proportional to the time-averaged lateral integrated near-field intensity \(\left\langle \int \vert u^{+}(x, L, t) \vert ^{2} {d} x\right\rangle\) it can be expressed as
where \(\left<b^{(m)} b^{(n)*}\right>= c^{(m,n)}\) represents the power coupling and \(M^{(m,n)} = \int \Phi ^{(m)}(x) \Phi ^{(n)*}(x) \textrm{d} x\) the non-orthogonality between individual modes. Numerical experiments of the lasers investigated in this paper showed that \(M^{(m,n)}\approx 0\) for \(m \ne n\). Note, that the eigenmodes \(\Phi ^{(m)}(x)\) are normalized such that \(M^{(m,n)} = 1\) for \(m = n\). Finally, by inserting Eq. (7) into Eq. (8) and neglecting modal cross-coupling the modal power can be expressed as
with \(\eta ^{(m)}\) being the modal power fraction which is dependent on the injection current.
4 Results
Here, in Sect. 4.1 the mode-resolved power-current characteristics are presented. This is followed by the results obtained by modal and BPM-based analyses of the time-averaged waveguide which are shown in Sect. 4.2 and 4.3, respectively. Finally, in Sect. 4.4 the gained understanding is used to suggest further design improvements to the TRW laser.
4.1 Modal power-current characteristics
Simulated power-current (black lines, right axis) and \(M^2_{\sigma }\)-current characteristics (red lines, left axis) of the TRW laser (left panel) and a reference RW laser (right panel). The dashed/dotted lines represent the calculated modal power fractions of the power contributing lateral modes indicated by \(m = \{1,2,3,4\}\). In the left panel experimental results are represented as gray and red-dotted lines
Figure 5 shows the simulated (solid lines) and measured (partially transparent lines) output power P and beam propagation ratio \(M^2_{\sigma }\) as a function of the applied current I for the TRW laser (left panel) and the reference RW laser. Here, the subscript \(\sigma\) refers to the fact that the \(M^2\)-values were calculated by using the second-moment beam width criterion. The modal power fractions calculated by applying Eq. (9) are represented as dashed/dotted black lines within each plot.
Even though the power-current curves of both devices show a similar trajectory, it is visible that only two instead of four modes contribute to the output power of the TRW compared to the reference RW laser. In addition, the second-order mode (\(m=2\)) has a higher threshold in the tapered device. Consequently, the TRW laser leads to lower \(M^2_{\sigma }\) values than the reference device. The former shows an increase from \(M^2_{\sigma }\approx 1.1\) to 1.9 at \(P = {1}\,\hbox {W}\) and stays nearly constant thereafter. The reference RW laser, in contrast, leads to \(M^2_{\sigma }\approx 2.8\) at \(P = {1}\,\hbox {W}\), however, its \(M^2_{\sigma }\) further increases with the higher injection currents.
These results indicate that the tapered cavity design increases the threshold of higher-order lateral modes compared to the conventional straight RW-based cavity. The reason for the underlying mode filtering is further investigated next.
4.2 Modal analysis
Refractive index (black lines, left axis) and gain profiles (red lines, right axis) obtained at the rear a and front b facet at \(P\approx \,{2.5}\,\hbox {W}\) output power. The resulting modal indices and gain values are represented as different types of dotted/dashed horizontal lines. Panel c and d present the longitudinally resolved relative modal gain of the first five local lateral waveguide modes (\(m = \{1,2,3,4,5\}\)) of the TRW and the reference RW laser, respectively
In this section, a modal analysis is performed based on the complex refractive index profiles at the facets obtained at \({2.5}\,\hbox {W}\). Figure 6a and b depicts the index and gain profiles (solid lines) at the rear and front facet, respectively, as calculated applying Eq. (4). In addition, the modal index \(\Re \{n^{(m)}\}\) and gain \(g^{(m)} = \Im \{2k_0n^{(m)}\}\) obtained by solving the Helmholtz Eq. (5) for these profiles are shown as dashed/dotted horizontal lines.
The increased refractive index values and the lower gain at the front compared to the rear is a consequence of the nonuniform intensity, carrier density, and temperature distributions as visible in Fig. 3. The underlying effects are known as longitudinal temperature variation and longitudinal spatial hole burning, respectively. The high gain at the waveguide edges is the consequence of accumulated excess carriers caused by the low intensity at these positions induced by thermally induced index guiding which narrows the beam towards the front facet (Rauch et al. 2017; Koester et al. 2020b).
It can be seen that the waveguide profile corresponding to the rear facet only supports two guided modes with \(\Re \{n^{(m)}\} > \textrm{min}(\Re \{\langle n \rangle \})\). This agrees with the number of modes contributing to the laser emission at this working point, c.f. Fig. 5. In addition, the fundamental mode experiences a slightly higher gain than the first higher-order mode since the latter has a larger spatial overlap with the absorptive regions next to the ridge. The \({23}{\upmu \,\hbox {m}}\) wide waveguide at the front facet supports a larger number of modes (only \(m\le 5\) are shown). Here, the lateral carrier accumulation at the ridge edges leads to an increased modal gain for higher-order modes compared to the fundamental mode.
To get more information about the modal gain inside the cavity panels (c) and (d) show the relative modal gain \(\frac{g^\mathrm {(m)}-g^{(1)}}{g^{(1)}}\) as a function of the longitudinal position for the TRW and the reference RW laser, respectively. The results for the TRW design indicate that the modes with \(m \le 2\) experience a positive relative gain at positions \(z >\,{1.5}\,{\upmu \,\hbox {m}}\). However, the modes \(m \ge 3\) do not reach the laser threshold since they are not guided within the narrow \({5}{\upmu \,\hbox {m}}\) wide rear waveguide and consequently experience high optical losses. The situation is different for the reference RW laser. Here, the first four modes which all contribute to the laser emission (c.f. Fig. 5) show a relative gain of close to zero for all longitudinal positions. All of the corresponding modes are well-guided within the whole cavity. The mode \(m = 5\) is guided but does not reach the laser threshold.
4.3 Beam propagation analysis
Intensity distributions \(\vert u_\textrm{BPM,m}\vert ^2\) obtained by BPM calculations. Left panels: Backward propagation \(u^-_\textrm{BPM,m}\) of the first three modes \(\Phi ^{(1,2,3)}(x,L)\). Right panels: Forward propagation \(u^+_\textrm{BPM,m}\) of the field profile \(u^-_\textrm{BPM,m}(x,0)\)
In this section, the results of the BPM-based propagation analysis are presented. Figure 7 shows the intensity distributions \(\vert u_\textrm{BPM,m}\vert ^2\) obtained by propagating the first three modes one round-trip through the waveguide formed by the index and gain distribution as shown in Fig. 4. First the modes \(\Phi ^{(1,2,3)}(x,L)\) where calculated by solving Eq. (5) at \(z = L\) serving as starting conditions. Subsequently, these modes were propagated from the front to the rear facet (left panels). The resulting complex fields \(u^-(x,0)_\textrm{BPM,m}\) served as input for the forward propagation back to the front (right panels). After the full round-trip, the resulting field profile \(u^+_\textrm{BPM,m}(x,L)\) was decomposed into the local waveguide modes using an ansatz similar to Eq. (7).
The propagation of the fundamental and first higher modes \(\Phi ^{(1,2)}(x,L)\) are shown in the first and second row, respectively. Here, after a full round-trip, still \({99}\,{\%}\) of the total power remain in the corresponding input modes. This indicates that the waveguide taper achieves an adiabatic mode conversion. In addition, both modes experience a net power gain of \({18.5}\,\hbox {dB}\).
The results of the third mode \(m = 3\) (bottom row) show a somewhat different picture. Here, the resulting intensity profile \(\vert u^-_\textrm{BPM,3}\vert ^2\) shows, in agreement with the rapidly decreasing relative modal gain in Fig. 6c, that most of the modal power is radiated at \(z<1.5~\,\hbox {mm}\). The spatial overlap of the resulting field \(u^-_\textrm{BPM,3}(x,0)\) at the rear facet with the corresponding local lateral modes \(\Phi ^{(m)}(x,0)\) indicates that \({13}\,{\%}\) of the power gets coupled into the fundamental mode. The remaining power, however, is contained in several radiation modes. After a full round-trip the field at front facet \(u^+_\textrm{BPM,3}(x,L)\) predominantly (\({80}\,{\%}\)) consists of the fundamental mode. However, \({20}\,{\%}\) of the power is still carried by the second higher-order mode. Nevertheless, \(\Phi ^{(3)}(x,L)\) experiences no amplification but rather gets attenuated by about \({-1.5}\,\hbox {dB}\) which prevents it from reaching the laser threshold.
4.4 Further design optimization
Beam propagation ratio \(M^2_{\sigma }\) and linear brightness \(B_{\sigma }\) as function of the optical output power. The black, red and blue lines correspond to an effective refractive index \(\Delta n_0\) of \(-4\cdot 10^{-3}\), \(-2\cdot 10^{-3}\) and \(-4\cdot 10^{-4}\), respectively. The experimental results are represented as black-dotted lines
The black lines in Fig. 8 represent the lateral beam propagation factor \(M^2_{\sigma }\) (left panel) and the lateral brightness \(B_{\sigma }\) (right panel) as a function of the output power. At \(P = {2.5}\,\hbox {W}\) the experimental and simulated results lead to \(M^2_{\sigma } \approx 1.9\) and \(B_{\sigma }\approx {4}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\). In comparison, the authors of Auzanneau et al. (2003) and Michel et al. (2005) reported values of \(M^2_{\sigma } \approx 4\) and \(M^2_{\sigma } \approx 3\) at \({1}\,\hbox {W}\) output power, respectively. However, it is noteworthy that the corresponding devices were \({2.5}\,\hbox {mm}\) long and therefore significantly shorter than the \({6}\,\hbox {mm}\) long lasers investigated in this work.
The results of the previous sections have shown that the TRW laser restricts the power contribution to only two lateral modes. However, to further increase the brightness only the fundamental mode should reach the laser threshold even at high injection currents. This can be done by designing the rear waveguide to be purely single-mode. Following Eq. (1), this can be achieved by either decreasing w or \(\vert \Delta n_0\vert\).
The red and blue lines in Fig. 8 represent the latter possibility. It is visible that the diffraction-limited output power is increased from \({0.5}\,\hbox {W}\) to about \({1.5}\,\hbox {W}\) by changing \(\Delta n_0\) from \(-4\cdot 10^{-3}\) to \(-2\cdot 10^{-3}\). For the value of \(\Delta n_0 = -6\cdot 10^{-4}\), the laser supports only the fundamental mode for all investigated power levels. This leads to very high lateral brightness values of about \({8}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) and \({10}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) at output powers of \({2.5}\,\hbox {W}\) and \({3}\,\hbox {W}\), respectively.
5 Conclusion
We presented the simulation-based analysis of a CW-driven TRW laser design which was measured to achieve high lateral brightness values of \({4}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) at \({2.5}\,\hbox {W}\). First, active laser simulations were performed to reproduce these results. In the next step, the obtained time-averaged intra-cavity intensity, carrier density, and temperature were used to calculate complex refractive index distributions which formed the basis of further investigations, namely, a modal waveguide analysis and BPM-based propagation analysis. Following this approach, it was shown that higher-order lateral modes experience an increasing relative modal gain towards the front but get partially radiated during their propagation through the resonator. The resulting high round-trip losses prevent those unwanted modes from reaching the laser threshold. Finally, the gained insights were used to suggest ways to further increase the achievable brightness. A TRW laser with reduced effective index contrast was simulated to deliver a brightness of almost \({10}{\hbox {W}\cdot \hbox {mm}^{-1} \hbox {mrad}^{-1}}\) at \({3}\,\hbox {W}\) output power.
Data availability
The data presented in this paper are available upon reasonable request.
References
Auzanneau, S.C., Krakowski, M.M., Berlie, F. et al: High-power and high-brightness laser diode structures using Al-free active region. In: Proceeding SPIE Integrated Optoelectronics Devices, pp. 184 (2003)
Chung, Y., Dagli, N.: An assessment of finite difference beam propagation method. IEEE J. Quantum Electron. 26(8), 1335–1339 (1990). https://doi.org/10.1109/3.59679
Gehrsitz, S., Reinhart, F.K., Gourgon, C., et al.: The refractive index of AlxGa1-xAs below the band gap: accurate determination and empirical modeling. J. Appl. Phys. 87(11), 7825–7837 (2000). https://doi.org/10.1063/1.373462
Hadley, G.R.: Transparent boundary condition for beam propagation. Opt. Lett. 16(9), 624 (1991). https://doi.org/10.1364/OL.16.000624
Hasler, K.H., Wenzel, H., Crump, P., et al.: Comparative theoretical and experimental studies of two designs of high-power diode lasers. Semicond. Sci. Technol. 29(4), 045010 (2014). https://doi.org/10.1088/0268-1242/29/4/045010
Koester, J.P., Putz, A., Wenzel, H., et al.: Mode competition in broad-ridge-waveguide lasers. Semicond. Sci. Technol. 36(1), 015014 (2020). https://doi.org/10.1088/1361-6641/abc6e7
Koester, J.P., Radziunas, M., Zeghuzi, A., et al: Traveling wave model-based analysis of tapered broad-area lasers. In: Proceeding SPIE Physics and Simulation of Optoelectronic Devices, pp. 112,740I (2020b)
Krakowski, M., Auzanneau, S., Berlie, F., et al.: 1 W high brightness index guided tapered laser at 980 nm using Al-free active region materials. Electron. Lett. 39(15), 1122 (2003). https://doi.org/10.1049/el:20030720
Michel, N., Hassiaoui, I., Calligaro, M., et al: High-power diode lasers with an aluminium-free active region at 915 nm. In: Proceeding SPIE European Symposium on Optics and Photonics for Defence and Security, pp. 598,909 (2005)
Ning, C., Indik, R., Moloney, J.: Effective bloch equations for semiconductor lasers and amplifiers. IEEE J. Quantum Electron. 33(9), 1543–1550 (1997). https://doi.org/10.1109/3.622635
Piprek, J.: Semiconductor Optoelectronic Devices: Introduction to Physics and Simulation. Elsevier, Amsterdam (2013)
Radziunas, M.: Modeling and simulations of broad-area edge-emitting semiconductor devices. Int. J. High. Perform. Comput. Appl. 32(4), 512–522 (2018). https://doi.org/10.1177/1094342016677086
Radziunas, M., Fuhrmann, J., Zeghuzi, A., et al.: Efficient coupling of dynamic electro-optical and heat-transport models for high-power broad-area semiconductor lasers. Opt. Quantum Electron. 51(3), 69 (2019). https://doi.org/10.1007/s11082-019-1792-1
Rauch, S., Wenzel, H., Radziunas, M., et al.: Impact of longitudinal refractive index change on the near-field width of high-power broad-area diode lasers. Appl. Phys. Lett. 110(26), 263–504 (2017). https://doi.org/10.1063/1.4990531
Schulz, W., Poprawe, R.: Manufacturing with novel high-power diode lasers. IEEE J. Sel. Top. Quantum Electron. 6(4), 696–705 (2000). https://doi.org/10.1109/2944.883386
Tomm, J.W., Ziegler, M., Hempel, M., et al.: Mechanisms and fast kinetics of the catastrophic optical damage (COD) in GaAs-based diode lasers. Laser Photonics Rev. 5(3), 422–441 (2011). https://doi.org/10.1002/lpor.201000023
Vurgaftman, I., Meyer, J.R., Ram-Mohan, L.R.: Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 89(11), 5815–5875 (2001). https://doi.org/10.1063/1.1368156
Wenzel, H., Erbert, G., Enders, P.: Improved theory of the refractive-index change in quantum-well lasers. IEEE J. Sel. Top. Quantum Electron. 5(3), 637–642 (1999). https://doi.org/10.1109/2944.788429
Wenzel, H., Crump, P., Pietrzak, A., et al.: Theoretical and experimental investigations of the limits to the maximum output power of laser diodes. New J. Phys. 12(8), 085007 (2010). https://doi.org/10.1088/1367-2630/12/8/085007
Wilkens, M., Erbert, G., Wenzel, H., et al.: Highly efficient high-brightness 970-nm ridge waveguide lasers. IEEE Photonics Technol. Lett. 32(7), 406–409 (2020). https://doi.org/10.1109/LPT.2020.2978243
Williams, K., Penty, R., White, I., et al.: Design of high-brightness tapered laser arrays. IEEE J. Sel. Top. Quantum Electron. 5(3), 822–831 (1999). https://doi.org/10.1109/2944.788456
Wünsche, H.J., Radziunas, M., Bauer, S., et al.: Modeling of mode control and noise in self-pulsating phase COMB lasers. IEEE J. Sel. Top. Quantum Electron. 9(3), 857–864 (2003). https://doi.org/10.1109/JSTQE.2003.818854
Zeghuzi, A.: Analysis of Spatio-Temporal Phenomena in High-Brightness Diode Lasers using Numerical Simulations. Cuvillier Verlag, Berlin (2020)
Zeghuzi, A., Radziunas, M., Wünsche, H., et al.: Traveling wave analysis of non-thermal far-field blooming in high-power broad-area lasers. IEEE J. Quantum Electron. 55(2), 1–7 (2019). https://doi.org/10.1109/JQE.2019.2893352
Acknowledgements
The authors want to thank G. Erbert for the discussions contributing to this work. Furthermore, we are indebted to M. Radziunas (WIAS Berlin) for providing the simulation tool BALaser.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.-P.K. and H.W. wrote the main text of the manuscript. J.-P.K. performed the simulations and prepared the figures. M.W. contributed the experimental data shown. H.W. and A.K. supervised this work. A.K. performed the project administration. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interest
The authors declare to have no competing interests that might be perceived to influence the results and/or discussion reported in this paper.
Ethics approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koester, JP., Wenzel, H., Wilkens, M. et al. Simulation and analysis of high-brightness tapered ridge-waveguide lasers. Opt Quant Electron 55, 285 (2023). https://doi.org/10.1007/s11082-022-04511-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-022-04511-z