Landau–Khalatnikov subcircuit based equivalent circuit model for hybrid perovskite solar cells

Abstract

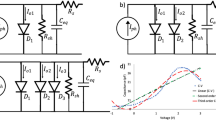
Hybrid perovskite solar cell technology has a distinct advantage over the conventional solar cell technologies due to its high predicted efficiency and low manufacturing cost. However, its commercialization is hindered by the unpredictability existing in its J-V characteristics leading to ambiguous efficiency estimation. Modeling the hysteresis in the J-V characteristics is a means of curtailing this ambiguity. It is established in literature that hysteresis models can be derived from the non-linear behavior of ferroelectric materials. Perovskite, which forms the light absorbing region of the solar cell is a ferroelectric material. In this paper, an equivalent circuit model for the hybrid perovskite solar cell is proposed in which the reasons for origin of hysteresis is characterized as varying capacitance to model hysteresis. A Landau–Khalatnikov subcircuit which portrays this variation is the principal addition to the conventional model to include hysteresis effect. The model parameters of the subcircuit are estimated from the inherent properties of perovskites. Hence, the proposed equivalent circuit model is completely physics based and it links the material property of perovskite to its equivalent circuit model parameters.

Appendix

To derive ${C_{0}}$ and ${C_{\hbox {F}}}$, the Eq. (21) in section III is used

$$\begin{aligned} P=D-\epsilon _0E= \left( \frac{Q}{A}-\epsilon _0 \frac{V}{d} \right) \end{aligned}$$

(31)

$$\begin{aligned} P= \frac{1}{A}\left( Q- \frac{\epsilon _0A}{d}V \right) \end{aligned}$$

(32)

Here, denoting $C_0=\frac{\epsilon _0A}{d}$, P is obtained as

$$\begin{aligned} P= \frac{1}{A}\left( Q- C_0V \right) \end{aligned}$$

(33)

The corresponding equilibrium Eq. (20) is given by

$$\begin{aligned} E=\alpha P + \beta P^3 \end{aligned}$$

(34)

Substituting for P, it is re-written as

$$\begin{aligned} \frac{\alpha }{A} (Q- C_0V) + \frac{\beta }{A^3} (Q- C_0V)^3 = \frac{V}{d} \end{aligned}$$

(35)

where A is the area, d is the distance and V is the voltage between the two electrodes of the capacitor.

Re-arranging terms,

$$\begin{aligned} Q + \frac{\beta }{\alpha A^2} (Q- C_0V)^3 = \Bigg (\frac{A}{d \alpha } + C_0 \Bigg ) V \end{aligned}$$

(36)

By re-substituting ${C_{0}}$

$$\begin{aligned} Q + \frac{\beta }{\alpha A^2} (Q- C_0V)^3 = \Bigg (\Bigg (1 + \frac{1}{\epsilon _0 \alpha } \Bigg ) C_0 \Bigg )V \end{aligned}$$

(37)

or

$$\begin{aligned} Q + \frac{\beta }{\alpha A^2} (Q- C_0V)^3 = C_FV \end{aligned}$$

(38)

From this, the equation for ${C_{\hbox {F}}}$ is obtained as

$$\begin{aligned} C_F = \Bigg (1 + \frac{1}{\epsilon _0 \alpha } \Bigg ) C_0 \end{aligned}$$

(39)

where, ${\alpha }$ is the molecular polarizability of the material under study.