1 Introduction

One of the promising and reliable evolution in the field of optics is the photonic crystal fibers (PCFs) (Birks et al. 1997; Knight et al. 1998; Russell 2003). The PCF has high field confinement, low attenuation loss, large effective mode area and good design flexibility with different filling materials (Hameed et al. 2009). As a result, PCFs can be used in different applications such as biomedical sensors (Knight et al. 1998; Azab et al. 2017a), and polarization handling devices (Hameed et al. 2010; Hameed et al. 2011; Hameed et al. 2013). Moreover, PCF can be selectively infiltrated by plasmonic material where a coupling between the surface plasmon (SP) mode and core guided modes can be easily obtained (Hassani and Skorobogatiy 2006; Azab et al. 2019). Plasmonic PCF has been extensively used for sensing applications (Azab et al. 2017b; Xiao et al. 2014). In this context, SP resonance (SPR) PCF with sensitivity (S) of 3000 nm/RIU has been reported by Hassani and Skorobogatiy (2006). Also, an analyte filled PCF biosensor with two resonance peaks has been designed with corresponding sensitivities of 2280 nm/RIU and 4354.3 nm/RIU (Qin et al. 2014). Moreover, birefringent plasmonic PCF with supported HEy11 HEx11 modes offered sensitivities of 2000 nm/RIU and 1700 nm/RIU, respectively (Otupiri et al. 2014). Azzam et al. (2016) have also designed multichannel plasmonic PCF sensor. Further, plasmonic PCF sensor with extra air holes achieved sensitivity of 4000 nm/RIU (Akowuah et al. 2012a). In addition, high temperature sensitivity of 10 nm/°C based on SPR liquid crystal PCF sensor has been also reported by Hameed et al. (2015). Further, sensitivities of 1500 nm/RIU and 2000 nm/RIU were achieved by a multi-channel PCF biosensor (Akowuah et al. 2012b). Moreover, Hameed et.al have reported self-calibration SPR PCF biosensor with sensitivities of 10,000 nm/RIU and 6700 nm/RIU, corresponding to x-polarized and y-polarized modes, respectively (Hameed et al. 2016). Further, sensitivity of 4000 nm/RIU has been obtained by metallic layer based PCF (Rifat et al. 2015). A bimetallic PCF biosensor has offered a sensitivity of 3200 nm/RIU (Akowuah et al. 2012c). An et al. (2017) reported D-shaped SPR biosensor as sensitive as 10,493 nm/RIU for refractive index detection range (1.33–1.38). In addition, high wavelength sensitivity of 9000 nm/RIU has been achieved using gold-coated circular lattice PCF biosensor (Chakma et al. 2018). Further, SPR PCF sensor with dual layers of symmetrical square air holes has been reported with sensitivity of 6000 nm/RIU (Hossen et al. 2018). An ultra-low loss SPR- PCF has been presented for biosensing applications with wavelength sensitivity of 8500 nm/RIU (Asaduzzaman and Ahmed 2018). On the other hand, Lu et al. (2014) have fabricated PCF temperature sensor with selectively filled nanowires with sensitivity of 2.7 nm/°C. In addition, cascaded PCF interferometers for analyte refractive index sensing with sensitivity of 252 nm/RIU has been experimentally reported by Lim et al. (2012). Moreover, Wu et al. (2017) have fabricated SPR biosensor based on gold-coated side-polished hexagonal structure PCF with a maximum theoretical sensitivity of 21,700 nm/RIU.

This research paper presents a SPR PCF biosensor for refractive index sensing, where analysis, fabrication and characterization are carried out. The suggested biosensor is based on plasmonic D-shape configuration via side etching of the PCF structure. A silver layer is used as a plasmonic material with a silica background material. The full vectorial finite element method (FVFEM) (Obayya et al. 2000, 2002) is deployed to make the modal analysis of the suggested sensor. Further, the geometrical parameters are studied to maximize the sensor sensitivity through refractive index range 1.33–1.354. Therefore, the reported RI sensor can be used for glucose concentration detection where the analyte refractive index changes with the glucose concentration within the studied RI range. Then, the stack and draw method (Knight et al. 1998) is used to fabricate the optimized design. The proposed PCF biosensor experimentally offers high sensitivity of 294.11 nm/RIU with a resolution of \(3.4 \times 10^{ - 4} \;{\text{RIU}}\).

2 Design considerations and numerical approach

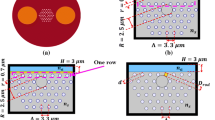
Figure 1a shows the 3D schematic diagram of the reported biosensor. The suggested PCF is based on silica background material with triangular lattice of hole pitch \({\Lambda } = 2.8\;{\mu m}\) and air hole diameter \({\text{d}} = 2.4\;{\mu m}\). In order to obtain the D-shape surface, a horizontal etching is applied at a distance h of 2.9 μm from the core region as shown in Fig. 1. The stacked view of the proposed biosensor is illustrated in Fig. 1b where a solid silica rod is introduced in the central region to form the core region. As may be seen from Fig. 1a, a silver layer is deposited on the etched surface with thickness t. The silver layer serves as a plasmonic material where the core guided mode in the core region is coupled with the SP mode at the silica-silver interface when the matching condition is attained.

Fig. 1
figure 1

a 3-D diagram of the suggested D-shape biosensor and b Cross-section of the proposed PCF’s stacked preform

Full size image

The silica glass background material has the Sellmeier equation given by (Otupiri et al. 2014):

$$\upvarepsilon _{{\text{s}}} = 1 + \frac{{{\text{B}}_{1}\uplambda ^{2} }}{{\uplambda ^{2} - {\text{C}}_{1} }} + \frac{{{\text{B}}_{2}\uplambda ^{2} }}{{\uplambda ^{2} - {\text{C}}_{2} }} + \frac{{{\text{B}}_{3}\uplambda ^{2} }}{{\uplambda ^{2} - {\text{C}}_{3} }}$$
(1)

where \({\upvarepsilon }_{{\text{s}}}\) is the silica dielectric permittivity, λ is the operating wavelength in μm. Further, the values for the constants C1 through C3 are equal to 0.00467914826 μm2, 0.0135120631 μm2 and 97.9340025 μm2, respectively. On the other hand, B1, B2 and B3 have the values of 0.6961663, 0.4079426 and 0.8974794, respectively. Additionally, the relative permittivity of the silver can be obtained using Drude-Lorentz model which is given by (Rakic et al. 1998):

$$\upvarepsilon _{{{\text{Ag}}}} = 1 - \frac{{\Omega_{{\text{p}}}^{2} }}{{\upomega \left( {\upomega - {\text{i}}\Gamma_{0} } \right)}} + \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{n}}} \frac{{{\text{f}}_{{\text{j}}}\upomega _{{\text{p}}}^{2} }}{{\left( {\upomega _{{\text{j}}}^{2} -\upomega ^{2} } \right) + {\text{i}}\upomega \Gamma_{{\text{j}}} }}$$
(2)

where \({\upomega }_{{\text{p}}}\) represents the plasma angular frequency, n refers to the oscillators number with angular frequency \({\upomega }_{{\text{j}}}\), oscillator strength \({\text{f}}_{{\text{j}}}\), and decay time 1/\({\Gamma }_{{\text{j}}}\), whereas \({\Omega }_{{\text{p}}} { } = \sqrt {{\text{f}}_{0} } {\upomega }_{{\text{p}}}\) is the intraband transitions associated plasma frequency with damping constant \({\Gamma }_{0}\) and oscillator strength \({\text{f}}_{0}\).

The sensing mechanism for the suggested biosensor is based on the coupling between the core guided mode and the surface plasmon mode around the metallic layer. When the wavelength of the light source is changed, the refractive indices of the structure materials are changed. As a result, the effective indices of the SP and fundamental core guided modes are varied accordingly. When both the real parts for the effective indices for the core guided mode and SP mode are equal, the coupling takes place. Therefore, a matching between the two modes is attained. In this case, the power transfer from the core mode to the SP mode is maximum with high confinement loss at the resonance wavelength. Such resonance wavelength depends on the analyte refractive index where RI sensing can be achieved.

3 Numerical results

The analysis for the suggested sensor is performed via FVFEM using Comsol-Multiphysics package (COMSOL Multiphysics). In this study, non-uniform meshing element is used with 0.0008 μm minimum element size and degrees of freedom of 135,076. Further, the computational domain is truncated using perfect matched layer (PML) to calculate the confinement losses of the supported modes.

Figure 2 presents the dependence of the real parts of the effective indices of the quasi TM core guided and the SP modes on the wavelength. Additionally, the confinement loss for the quasi TM core guided mode is presented in Fig. 2 as well. The analysis is carried out at \(\Lambda = 2.8\;\upmu {\text{m}}\), \({\text{d}} = 2.4\;\upmu {\text{m}}\), \({\text{t}} = 40{\text{ nm}}\) and \({\text{n}}_{{\text{a}}} =\) 1.33. The inset field plots of Fig. 2 reveal that at \(\uplambda = 1000\;{\text{nm}}\) far from the coupling wavelength, there is a good confinement of the quasi TM core guided mode. Accordingly, the real parts of the effective index of both the SP and core guided modes have considerable difference where no coupling occurs. However, at resonance wavelength λ = 1163 nm, the real parts of the effective indices of the quasi TM core guided mode and SP mode are equal. As a result, maximum power transfer is achieved from the core mode to the SP mode with low confinement of the quasi TM core guided mode as concluded from the inset of Fig. 2.

Fig. 2
figure 2

Dependence of confinement losses of the quasi TM-polarized core mode and the real parts of the effective index for the quasi TM-polarized core mode and the TM SP modes at \({\text{n}}_{{\text{a}}} = 1.33\) on the wavelength. The inset figures present the field plot of the fundamental components of quasi TM core and SP modes at \({\uplambda } = 1000\;{\text{nm}}\;{\text{and }}\;1163\;{\text{nm}}\)

Full size image

As may be seen from Fig. 1a, planar silver layer covers the surface of the D-shaped PCF where the surface plasmon modes are excited at the metal/dielectric interface. Accordingly, the quasi-TM core mode is strongly coupled to the surface plasmon modes. At the matching condition, the real parts of the effective indices of the core guided mode and surface plasmon mode are equal. Then, maximum power transfer occurs from the core mode to the SP mode with high losses as may be seen in Fig. 2. However, the coupling between the quasi-TE mode and SP mode is weak with low losses. Therefore, the sensing performance is calculated thoroughly using the quasi TM mode.

The wavelength sensor sensitivity can be calculated based on the shift in the resonance wavelength for the two analyte cases (n = 1.33 and 1.3538) via the following relation (Otupiri et al. 2014):

$${\text{S}}_{{\uplambda }} = \frac{{\partial {\uplambda }_{0} \left( {{\text{n}}_{{\text{a}}} } \right)}}{{\partial {\text{n}}_{{\text{a}}} }}\quad {\text{nm}}/{\text{RIU}}$$
(3)

where λ0 is the resonance wavelength for a specific analyte refractive index \({\text{n}}_{{\text{a}}}\). Additionally, the amplitude sensitivity can be obtained using the following equation (Otupiri et al. 2014):

$${\text{S}}_{{\text{A}}} = - \frac{{\partial {\upalpha }\left( {{\text{n}}_{{\text{a}}} ,{\uplambda }} \right)/\partial {\text{n}}_{{\text{a}}} }}{{{\upalpha }\left( {{\text{n}}_{{\text{a}}} ,{\uplambda }} \right)}}\quad {\text{RIU}}^{ - 1}$$
(4)

such that \({\upalpha }\left( {{\text{n}}_{{\text{a}}} ,{\uplambda }} \right)\) represents the confinement loss of the core guided mode which depends on the analyte refractive index \({\text{n}}_{{\text{a}}}\) and the wavelength \({\uplambda }\). It is worth noting that the amplitude sensitivity is an alternative method to specify the sensitivity of the suggested device based on the change in the loss amplitude rather than the resonance wavelength. In this regard, the analysis is performed at a wavelength close to the plasmonic resonance where the loss amplitude is calculated at different analyte refractive indices. This method is simple and low in cost compared to the spectral method. However, based on the smaller dynamic range of detection, the corresponding sensitivity is relatively low compared to the wavelength method (Hassani et al. 2008).

The geometrical parameters of the proposed biosensor are adjusted by performing a parametric sweep over arbitrary values to improve the wavelength and amplitude sensitivities. In this study, the effect of air holes diameter d, hole pitch \({\Lambda }\), the and the silver layer thickness t are studied. First, the silver layer thickness is investigated whereas the hole pitch \({\Lambda }\) and the air hole diameter d are kept constant at 2.4 μm and 2.8 μm, respectively. Figure 3 shows the dependency of the confinement loss and amplitude sensitivity on the wavelength at different silver layer thicknesses. Figures 3a, d and Table 1 show that at \({\text{t}} = 40{\text{ nm}}\), the resonance wavelengths at \({\text{n}}_{{\text{a}}} = 1.33\) and 1.34 occur at 1163 nm and 1168 nm, respectively. Accordingly, the obtained amplitude and wavelength sensitivities are 7.38 \({\text{RIU}}^{ - 1}\) and 500 nm/RIU, respectively as listed in Table 1. At a silver layer thickness of 60 nm, the coupling wavelengths are shifted to 1088 and 1087 for analyte refractive indices 1.34 and 1.33, respectively. The corresponding amplitude and wavelength sensitivities are obtained as 3.47 \({\text{RIU}}^{ - 1}\) and 100 nm/RIU, respectively. Further, Table 1 and Fig. 3c, f show that when 80 nm silver layer is used, the resonance wavelengths are 1051 nm and 1051 nm corresponding to analyte refractive indices of 1.34 and 1.33, respectively. Accordingly, a wavelength sensitivity of zero and a decreased amplitude sensitivity of 1.31 \({\text{RIU}}^{ - 1}\) are obtained. Therefore, t = 40 nm will be used for the subsequent simulations.

Fig. 3
figure 3

Dependency of confinement losses and amplitude sensitivity of the quasi TM-polarized core mode at \({\text{n}}_{{\text{a}}} = 1.33,\;{\text{and }}\;1.34\) on the wavelength, at a, d \({\text{t }} = 40\;{\text{nm}}\), b, e \({\text{t }} = 60\;{\text{nm}}\), and c, f \({\text{t}} = 80\;{\text{nm}}\)

Full size image
Table 1 Summary of the resultant values of the amplitude sensitivity, resonance wavelength, wavelength sensitivity based on the parametric study for the analyte sensing
Full size table

Next, the hole pitch is considered with three values of \(2.8\;\upmu {\text{m}},\;2.9\;\upmu {\text{m}}\;{\text{and}}\;3\;\upmu {\text{m}}\) while the air hole diameter and the silver thickness are kept constant at 2.4 μm and \(40{\text{ nm}}\), respectively. Figure 4 shows the change in the wavelength dependent loss spectra and amplitude sensitivity at \({\text{n}}_{{\text{a}}} = 1.33\) and 1.34 with the variation in the hole pitch. It can be realized from Fig. 4a that at \({\Lambda } = 2.8\;\upmu {\text{m}}\), the coupling wavelength is equal to 1163 nm at \({\text{n}}_{{\text{a}}} = 1.33.\) However, at \({\text{n}}_{{\text{a}}} = 1.34\), the resonance wavelength is achieved at 1168 nm. The resultant wavelength shift is equal to 5 nm and the corresponding wavelength sensitivity is 500 nm/RIU. In addition, the amplitude sensitivity for the same \({\Lambda }\) is equal to 7.38 \({\text{RIU}}^{ - 1}\) as shown in Fig. 4d. At \(\Lambda = 2.9\;\upmu {\text{m}}\), the resonance wavelength has a red shift to 1172 nm and 1177 nm for \({\text{n}}_{{\text{a}}} = 1.33\) and \({\text{n}}_{{\text{a}}} = 1.34\), respectively. Accordingly, Fig. 4b, e show that the wavelength sensitivity has the same value of 500 nm/RIU while a slight increase to 7.88 \({\text{RIU}}^{ - 1}\) is noticed in the amplitude sensitivity. When a hole pitch of 3.0 μm is used, the resonance wavelengths shift to 1183 nm and 1188 nm as may be seen from Fig. 4c at \({\text{n}}_{{\text{a}}} = 1.33\) and 1.34, respectively as shown in Table 1. Figure 4c, f show that the corresponding wavelength sensitivity is still 500 nm/RIU, whereas a decrease in the amplitude sensitivity to 7.27 \({\text{RIU}}^{ - 1}\) is observed.

Fig. 4
figure 4

Dependency of confinement losses and amplitude sensitivity of the quasi TM-polarized core mode at \({\text{n}}_{{\text{a}}} = 1.33,{ }1.34\) on the wavelength at different values of Λ from 2.8 to \(3.0\;{\mu m}\)

Full size image

Finally, the diameter of the air holes is considered with values of 2.3 μm, 2.4 μm and 2.5 μm, where the hole pitch and silver layer thickness are kept constant at 2.8 μm and 40 μm, respectively. Figure 5a reveals that at \({\text{d}} = 2.3\;\upmu {\text{m}}\), the coupling wavelengths occur at 1163 nm and 1168 nm at \({\text{n}}_{{\text{a}}} = 1.33\) and 1.34, respectively. Therefore, the corresponding amplitude and wavelength sensitivities are equal to 7.14 \({\text{RIU}}^{ - 1}\) and 500 nm/RIU, respectively as observed from Fig. 5a, d and Table 1. In addition, Table 1 shows that using air holes diameter of 2.4 μm results in the same resonance wavelengths. Therefore, wavelength sensitivity has the same value of 500 nm/RIU whereas the amplitude sensitivity is slightly increased to 7.38 \({\text{RIU}}^{ - 1}\) as presented in Fig. 5b, e. If a further increase in the air holes diameter to 2.5 μm is to take place, the resonance wavelength is obtained at 1163 nm for \({\text{n}}_{{\text{a}}} = 1.33\) while it is at1169 nm for \({\text{n}}_{{\text{a}}} = 1.34\). As a result, the corresponding amplitude and wavelength sensitivities are increased to 7.56 \({\text{RIU}}^{ - 1}\) and 600 nm/RIU, respectively.

Fig. 5
figure 5

Variation of the a, b, c quasi TM core mode loss and d, e, f amplitude sensitivity with the wavelength for \({\text{n}}_{{\text{a}}} = 1.33\;{\text{and}}\;1.34\) at different values of d from 2.3 to 2.5 μm

Full size image

To ensure the linearity of the suggested sensor over the refractive index range under study, the resonance wavelength variation with the analyte RI is investigated. The linearity study is performed within refractive index range from 1.33 to 1.354 with a step of 0.002. It may be seen from Fig. 6 that the suggested design has high degree of linearity over the desired range with R-squared value of 0.98508. Further the corresponding fitting equation is obtained as follows:

$${\uplambda }_{{{\text{Res}}}} = 675.8{\text{ n}}_{{{\text{analyte}}}} + 263.5$$
(5)
Fig. 6
figure 6

Linear fitting for the resonance wavelength dependency on the sample refractive index

Full size image

The performance of the proposed sensor is also evaluated via figure of merit FOM over the desired range of refractive index 1.33–1.354. A well-known FOM for optical sensors is defined as the ratio of the sensitivity to the full width at half maximum (FWHM). It may be seen from Fig. 7 that the value of FOM increases with the increase in the analyte refractive index because of the corresponding decrease of the FWHM. Moreover, if the minimum detectable change in the refractive index is 0.1 nm then the suggested sensor is characterized with theoretical resolution of \(1.58 \times 10^{ - 4} \;{\text{RIU}}^{ - 1}\).

Fig. 7
figure 7

FOM variation with the change of the analyte refractive index

Full size image

4 Fabrication and characterization

Based on the geometrical parameters’ analysis, the optimum PCF biosensor is fabricated via the common stack-and-draw method (Russell 2003, Knight et al. 1998). In this context, the PCF is fabricated using fused silica material in 3-steps drawing processes. First a suitable diameter of capillaries and rods were pulled. The capillaries and rods were cleaned and stacked into a suitable wall thickness silica jacket. The stacked preform was then drawn into canes of around 2–3 mm diameter followed by a very precise side grinding and polishing. A short length of a PCF cane, around 30 cm, was then selected and side polished. Prior to polishing, the PCF cane was aligned under microscope to find the right side that need to be polished. Both ends of the PCF cane were closed to avoid polishing dusts enter to the PCF holes. One side of the PCF cane was then precisely grinded and polished to the desired depth. After the PCF cane was side-polished and well cleaned, it has been directly re-drawn into the final D-shaped PCF fiber of outer diameter around 250 µm and core of around 3 μm. Figure 8 shows the SEM images of the final fabricated D-shaped PCF. Figure 9 shows visible light guiding in the core of the fabricated D-shaped PCF before silver coating. The D-shaped PCF fiber was then undergoing silver coating using electron beam evaporation method.

Fig. 8
figure 8

SEM of the fabricated D-shaped PCF

Full size image
Fig. 9
figure 9

SEM for single mode guiding of light through the fabricated D-shaped PCF

Full size image

The fabricated PCF biosensor is characterized through applying different analytes with different refractive indices where the shift in the resonance wavelength is noticed. For further clarification of the sensing mechanism, a schematic diagram of the experimental setup is shown in Fig. 10. A tunable laser source (TLS) through an objective lens is first applied to a polarization controller to obtain a TM mode as desired for the proposed fiber design. The output of the polarization controller is then applied to the D-shaped PCF through a polarization maintaining fiber (PMF). The output of the D-shaped PCF was spliced with a single mode fiber (SMF) and connected to a spectrum analyzer. Analytes with different refractive indices are applied to the coated surface of the D-shaped PCF and the output spectrum was recorded per analyte. The next analytes was applied only after washing and drying of the fiber under the test. Figure 11 shows the measured transmission spectrum of the fabricated biosensor for two analyte refractive indices: \({\text{n}}_{{\text{a}}} = 1.33\;{\text{and}}\;1.3538\). It may be realized from Fig. 11 that the highlighted peaks for \({\text{n}}_{{\text{a}}} = 1.33\) and 1.3538 occurred at \({\uplambda }\) = 1606 nm and 1613 nm, respectively. Accordingly, the resulting wavelength sensitivity is 294.11 nm/RIU. If the minimum detectable variation in the resonance spectral is 0.1 nm, the suggested design is capable of detecting a change in the refractive index as small as \(3.4 \times 10^{ - 4} \;{\text{RIU}}\). A comparison is performed between the theoretical calculation and the practical results as shown in Table 2. It may be seen that the theoretical sensitivity is equal to 630.25 nm/RIU while measured sensitivity of 294.11 nm/RIU is obtained. It is worth noting that in the theoretical calculations, the confinement loss is only considered. However, the measured transmission includes the total loss through the propagation of the suggested design. Further, the geometrical parameters may have some fluctuations than the optimum values. Therefore, an acceptable difference in the resonance wavelength and average sensitivity is expected. In general, the fabricated biosensor has a good potential for RI sensing applications.

Fig. 10
figure 10

Schematic diagram of the real-time online measurement system

Full size image
Fig. 11
figure 11

Transmission spectra through the fabricated biosensor at refractive index of 1.33 and 1.3538 for the tested analyte

Full size image
Table 2 Comparison between the theoretical and experimental results
Full size table

It is worth noting that most of the human blood consists of water. Therefore, the basis refractive index for human blood will be 1.33. When the glucose concentration in the blood increases, the refractive index is also increased above 1.33 according to the following relation (Yeh 2008):

$${\text{n}} = 1.1889 \times 10^{ - 4} {\text{C}} \left( {\text{g/l}} \right) + 1.3323054$$
(6)

such that n is the average refractive index, C is the glucose concentration (g/l). Therefore, the proposed biosensor can be used to monitor the glucose concentration in the blood of human body within the studied RI range. Additionally, it is convenient to use pure water (n = 1.33) and water/alcohol mix (n = 1.3538) for the calibration process. Accordingly, the corresponding glucose concentration to refractive index 1.34 and 1.3538 is equal to 64.72 (g/l) and 180.79 (g/l), respectively. Hence, different glucose concentrations can be obtained via the obtained refractive index values (Yeh 2008). Therefore, the proposed sensor can play a significant role in the biomedical sensor industry.

5 Conclusion

A novel design of SPR D-shaped PCF biosensor to monitor the RI change and hence blood glucose concentration is reported and analyzed. The reported PCF is first studied using full vectorial finite element method. Then, the optimum structure is fabricated using stack and draw method. The fabricated biosensor is also characterized which shows practical wavelength sensitivity of 294.11 nm/RIU with resolution of \(3.4 \times 10^{ - 4} \;{\text{RIU}}\) which is in a good agreement with the theoretical predictions.