1 Introduction

The need for high bandwidth has expeditiously increased for the future generation of communication networks. Free-Space Optical (FSO) communication is very promising, as it offers less expenses and more flexibility in designing optical networks at high speed. It also can emerge radio frequency (RF) communication as it provides a solution to the last-mile distribution of high bandwidth networks with a higher data rates, immunity to RF interference, secure communication links, and unlicensed spectrum (Majumdar 2019; Chaudhary et al. 2014; Amphawan et al. 2015; Chaudhary et al. 2014). It can be an alternative solution in areas where the traditional optical fiber wired communication systems is hardly installed and can be applied in hospitals and in healthcare (Yang et al. 2020; Amphawan et al. 2015; Zhang et al. 2021a, b).

The FSO communication is a wireless transmission of data through modulated optical beam directed via the atmosphere or vacuum as a communication channel between transceivers with a line of sight (LOS) (Kanno et al. 2011). On the other hand, the effect of the atmospheric conditions is considered an enormous challenge to FSO communication links, such as fog which affects the FSO links and causes a signal attenuation (Chaudhary et al. 2020; Sharma et al. 2021).

Optical Code Division Multiple Access (OCDMA) is based on binary 1 and 0, where 1 represents the presence of light, which supports considerable users to share the same medium asynchronously and simultaneously without any interruption (Wang et al. 2009). Spectral Amplitude Coding (SAC) is selected among many coding techniques that can be implemented in OCDMA due to less cost. In SAC-OCDMA, each user is assigned a unique code sequence that serves as its address providing security to each user during their accessing time on the same transmission channel. Many codes are used with SAC-OCDMA. Some have zero cross correlation like random diagonal (Chaudhary et al. 2020), multi diagonal (Mostafa et al. 2017) and others have unity cross correlation like enhanced double weight (EDW) (Abd El-Mottaleb et al. 2018) and diagonal permutation shift code (DPS) (Ahmed et al. 2017, 2022). Although, code construction of zero cross correlation code is easy but their implementation in a real experiment is difficult.

Comparisons between different OCDMA codes are carried out in (Mrabet et al. 2021). The authors used these codes with optical fiber communication systems only, not in optical wireless communication.

However, unity cross correlation codes suffer from multiple access interference (MAI) caused by various noises that lead to performance degradation. This undesired effect of MAI can be resolved by using detection techniques at the receiver, such as single photodiode detection (SPD) technique (Abd El-Mottaleb et al. 2018).

Recently, researchers integrated multiplexing techniques with OCDMA to enhance the capacity of the optical communication system. A hybrid space division multiplexing (SDM) with OCDMA using balanced incomplete block chain code (BIBC) was proposed in the FSO/passive optical network by Farghal (2019). Atmospheric turbulence was considered while atmospheric attenuation due to different weather conditions was not considered. Conducted results showed successful transmission of eight channels with an overall capacity of 8 × 0.5 = 4 Gbps.

Multiple polarization signals are combined in polarization division multiplexing (PDM) to generate a new parallel polarization state. PDM also improves transmission capacity by allowing distinct signals to be carried at the same wavelength in an orthogonal condition (Zhou et al. 2017; Goossens et al. 2017; Upadhyay et al. 2019).

Chaudhary et al. (2019), a hybrid PDM/SAC-OCDMA was proposed but with RD codes for inter-satellite communication. Chaudhary et al. (2020), the performance of hybrid PDM with SAC-OCDMA in the FSO system was solely tested for random diagonal (RD) code using direct detection approach and under different fog weather conditions only. Although the results showed enhancement in transmission capacity as its overall capacity was 50 Gbps, the implementation of this code in a real experiment was difficult due to its code property that has zero cross correlation.

In this paper, a hybrid PDM/SAC-OCDMA based FSO communication system is used for transmitting three different channels, on x-polarization signals and on y-polarization to increase transmission capacity. A DPS code with SPD detection scheme is used. The performance is investigated under various weather conditions: fog {light (LF), medium (MF) and heavy (HF)}, dust storm {low (LD), medium (MD), and heavy (HD)}, and rain {low (LR), medium (MR), and heavy (HR)}. The system performance is evaluated in terms of maximum allowable number of users, maximum propagation link, minimum bit error rate (BER), Q-factor and received power.

The remainder of the paper is organized as follows. SAC-OCDMA code construction and property are explained in Sect. 2. Performance analysis of our proposed model is illustrated in Sect. 3. Section 4 describes the schematic diagram of PDM/SAC-OCDMA-FSO system, followed by results and discussion in Sect. 5. Finally, Sect. 6 is devoted to the main conclusions.

2 Code properties and code construction

2.1 Code properties

A DPS code is proposed to our FSO model, and its code property is given in Table 1 (Ahmed et al. 2017).

Table 1 DPS code property (Ahmed et al. 2017)
Full size table

2.2 Code construction

The DPS code is driven from prime code sequences that are based on Galois field GF (w) = {0, 1,…, w − 1}, where w is any prime number greater than 2 (Ahmed et al. 2017). Four process are used for making DPS code which are sequent diagonal, permutation, shifting and joining.

In the diagonal process, primary diagonal (\({d}_{x,y}\)) sequences of integer number are constructed according to Ahmed et al. (2017)

$${d}_{x,y}=\left(x \cdot y\right)\,mod\,w$$
(1)

where x and y represent the location of each element over GF and mod is the modulo operation.

Based on \({d}_{x,y}\), the construction of generator sequence, \({D}_{w}\), is Ahmed et al. (2017)

$${D}_{w}= \left\{{d}_{0,0} {d}_{1,1} {d}_{2,2} \cdots {d}_{w-1,w-1}\right\}$$
(2)

For any value of w, the following diagonal sequences are fixed as Ahmed et al. (2017)

$$\begin{aligned} d_{0,0} &= 0, \hfill \\ d_{1,1} &= 1, \hfill \\ d_{w - 1,w - 1} &= \left( {w - 1} \right) \cdot \left( {w - 1} \right)mod\,P = \left( {w^{2} - 2w + 1} \right)mod\, \left( w \right) = 1 \hfill \\ \end{aligned}$$
(3)

Then, the value of \({D}_{w}\) at w = 3 can be written as

$${D}_{3}= \left\{0\;\,1\;\,1\right\}$$
(4)

Now, the permutation process can be done and by first constructing a basic matrix, \({B}_{w}^{0}\), having \({D}_{w}\) in the first row. Then, in the next rows, making permutation of \({D}_{w}\) one time to get a \(w\times w\) zero-diagonal symmetric matrix without repeating any row as follows Ahmed et al. (2017)

$${B}_{w}^{0}= \left[\begin{array}{c}{d}_{\mathrm{0,0}}\\ {d}_{w-1,w-1}\\ \begin{array}{c}{d}_{w-1,w-2}\\ \begin{array}{c}\vdots \\ {d}_{\mathrm{1,1}}\end{array}\end{array}\end{array} \begin{array}{c}{d}_{\mathrm{1,1}}\\ {d}_{\mathrm{0,0}}\\ \begin{array}{c}{d}_{w-1,w-1}\\ \begin{array}{c}\vdots \\ {d}_{\mathrm{2,2}}\end{array}\end{array}\end{array} \begin{array}{c}{d}_{\mathrm{2,2} }\\ {d}_{\mathrm{1,1} }\\ \begin{array}{c}{d}_{\mathrm{0,0}} \\ \begin{array}{c}\vdots \\ {d}_{\mathrm{3,3}}\end{array}\end{array}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \begin{array}{c}\dots \\ \begin{array}{c}\ddots \\ \dots \end{array}\end{array}\end{array} \begin{array}{c}{d}_{w-1,w-1}\\ {d}_{w-2,w-2}\\ \begin{array}{c}{d}_{w-3,w-3}\\ \begin{array}{c}\vdots \\ {d}_{\mathrm{0,0}}\end{array}\end{array}\end{array}\right]$$
(5)

So, \({B}_{w}^{0}\) at w = 3, can be written as Ahmed et al. (2022)

$${B}_{3}^{0}= \left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 1\\ 1& 1& 0\end{array}\right]$$
(6)

Here, a shifting process can be applied through constructing (w − 1) shifted matrices, \({B}_{w}^{H}\), by adding H to each element of the matrix \({B}_{w}^{0}\), where H = 1, 2, 3,…, w − 1 as follows

$$\begin{aligned} B_{3}^{1} & = \left[ {\begin{array}{*{20}c} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \\ \end{array} } \right] \\ B_{3}^{2} & = \left[ {\begin{array}{*{20}c} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] \\ \end{aligned}$$
(7)

Finally, the matrix K is obtained in a joining process through joining \({B}_{w}^{H}\) in each sequence, then an extra column of matrix \({m}_{w}\) is added to each corresponding \({B}_{w}^{H}\) as Kanno et al. (2011) and Ahmed et al. (2017)

$$K= \left[\begin{array}{c}\left[{B}_{w}^{0}\right]\\ \begin{array}{c}\left[{B}_{w}^{1}\right]\\ \vdots \end{array}\\ \left[{B}_{w}^{w-1}\right]\end{array} \begin{array}{c}\vdots \\ \begin{array}{c}\vdots \\ \vdots \end{array}\\ \vdots \end{array}\begin{array}{c}\left[{m}_{w}\right]\\ \begin{array}{c}\left[{m}_{w}\right]\\ \vdots \end{array}\\ \left[{m}_{w}\right]\end{array}\right]$$
(8)

where \({m}_{w}\) is a w \(\times\) 1 matrix containing the elements \(\left\{0, 1, 2, \ldots , w-1\right\}\) in an arbitrary order. The matrix K size is \({w}^{2}\times (w-1)\) and its elements are \({K}_{x,y}\) where x = 0, 1, 2, \(\cdots\), \({w}^{2}-1\), and y = 0, 1, 2, \(\cdots\), w.

As an example, for w = 3, the DPS code is shown in Table 2 (Ahmed et al. 2022).

Table 2 DPS code sequence for w = 3
Full size table

According to Table 1, channel 1 will have the code word 100010010100. So, it will have wavelengths \({\lambda }_{1}\),\({\lambda }_{5}\),\({\lambda }_{8}\),\({\lambda }_{10}\) corresponding to the number of “1s” bit that will carry its information. While for channels 2 and 3, their code words are 010100010010 and 010010100001, respectively, and their corresponding wavelengths are \({\lambda }_{2}\),\({\lambda }_{4}\),\({\lambda }_{8}\),\({\lambda }_{11}\) and \({\lambda }_{2}\),\({\lambda }_{5}\),\({\lambda }_{7}\),\({\lambda }_{12}\), respectively.

3 Performance analysis

The received power for FSO link is Singh and Malhotra (2019)

$${S}_{rx}= {S}_{tx}{\left(\frac{{d}_{rx}}{{d}_{tx}+\theta F}\right)}^{2}{10}^{\frac{-{\propto }_{w}F}{10}}$$
(9)

where \({S}_{rx}\) and \({d}_{rx}\) are the received power and received aperture angle, respectively. \({S}_{tx}\) and \({d}_{tx}\) represent the transmitted power and transmitted aperture angle, respectively. \(\theta\), F and \({\propto }_{w}\), respectively, are the beam divergence angle, FSO range and attenuation due to weather conditions.

The fog attenuation,\({\propto }_{f}\), in dB/km is expressed as Kim et al. (2001)

$$\propto_{f} = \frac{3.912}{V}\left( {\frac{\lambda }{550nm}} \right)^{ - z}$$
(10)

where V and \(\lambda\), respectively, are the visibility in km and the wavelength in nm while \(z\) is the size distribution of the scattering particle that can be determined according to Kim model as Singh et al. (2022a, b)

$$z= \left\{\begin{array}{cc}1.6 & V>50 \\ 1.3 & 6 <V<50 \\ 0.16 V+0.34 &1<V<6 \\ V-0.5 & 0.5 <V<1 \\ 0 & V<0.5\end{array}\right.$$
(11)

As dust storms affect the FSO channel and cause attenuation, the dust storm attenuation, \({\propto }_{D}\), in dB/km, is expressed as Singh et al. (2022a, b)

$$\propto_{D} = 52 \times V^{ - 1.05}$$
(12)

Also, the different rain conditions cause attenuation that causes degradation in the received signal power and can be expressed as Muhammad et al. (2005)

$$\alpha_{R} = \beta R^{q}$$
(13)

where \(\beta\) (dB/km), R (mm/hr), \(\gamma\) and q, respectively, indicate the rain attenuation, the rain rate, a coefficient that depends on frequency, and a coefficient that depends on ambient temperature. At the R = 100 mm/hr, \(\gamma\) = 1.076 and q = 0.67, yielding \({\alpha }_{R}\) of ~ 18.3 dB/km (Mohammed et al. 2013).

At PD, the power spectral density (PSD), \(P(\upsilon )\), is Al-Khafaji et al. (2013)

$$P\left( \upsilon \right) = \frac{{S_{rx} }}{{B_{op} }}\mathop \sum \limits_{i = 1}^{U} d_{U} \left( {\mathop \sum \limits_{i = 1}^{L} H_{a} \left( i \right) \cdot H_{b} \left( i \right) - \mathop \sum \limits_{i = 1}^{L} (H_{a} \left( i \right) \cdot H_{b} \left( i \right)(H_{a} \left( i \right))} \right)\left\{ {u\left[ {\frac{{B_{op} }}{L}} \right]} \right\}$$
(14)

where \(B_{op}\) and \(u\left[ {\frac{{B_{op} }}{L}} \right]\), respectively, represents optical bandwidth and unit step function. \({H}_{a}\left(i\right)\) and \({H}_{b}\left(i\right)\) represent the ith element of the element of a and b code sequence.

The DPS code property when SPD detection is used as

$$\sum_{i=1}^{L}{H}_{a}\left(i\right).{H}_{b}\left(i\right)-\sum_{i=1}^{L}{(H}_{a}\left(i\right).{H}_{b}\left(i\right){(H}_{a}\left(i\right))=\left\{\begin{array}{ll}{w}_{PD}, &\quad for\;a=b\\ 0, &\quad for\;a \ne b\end{array}\right.$$
(15)

where \({w}_{PD}\) is the number of “1′s” that reach PD and is equal to w + 1.

The average received optical power, \({P}_{u}\), by the PD for the desired channel with SPD detection is Abd El-Mottaleb et al. (2021)

$$P_{u} = \Re\int_{0}^{\infty } P\left( \upsilon \right)d\upsilon = \frac{{S_{rx} B_{op} }}{L}w_{PD}$$
(16)

where \(\mathfrak{R}\) is the PD responsivity.

The shot noise, \({Sh}_{N}\), can be expressed as Ahmed et al. (2022)

$$Sh_{N} = 2\,e\,B_{e} \left( {P_{u} } \right) = \frac{{2eB_{e} \Re S_{rx} B_{0p} }}{L}w_{PD}$$
(17)

where e is electron charge and \({B}_{electric}\) is electrical bandwidth.

The phase induced intensity noise (PIIN) noise power, \({PN}_{N}\), is Ahmed et al. (2022)

$${PN}_{N}={{S}^{2}}_{rx}{B}_{e}\frac{{B}_{0p}}{L}\sum_{i=1, a=b}^{L}{\left[{H}_{a}(i)\right]}^{2}.{\left[{H}_{b}(i)\right]}^{2}= \frac{{{{S}^{2}}_{rx}B}_{e}{B}_{op}{w}_{PD}}{L}$$
(18)

Thermal noise, \({Th}_{N}\), can be expressed as Abd El-Mottaleb et al. (2021)

$${Th}_{N}= \frac{4{k}_{B}T{B}_{e}}{{R}_{L}}$$
(19)

where \({k}_{B}\) is Boltzmann constant, \({T}_{n}\) is the receiver noise absolute temperature, and \({R}_{L}\) is the receiver load resistance.

The SNR is expressed as Abd El-Mottaleb et al. (2021), Moghaddasi et al. (2015), 2017 and Kakati and Arya (2019a, 2019b)

$$SNR=\frac{{\left({P}_{u}\right)}^{2}}{\frac{{{{S}^{2}}_{rx}B}_{e}{B}_{op}{w}_{PD}}{L}+\frac{{2e{B}_{e}\mathfrak{R}S}_{rx}{B}_{0p}}{L}{w}_{PD}+\frac{4{{K}_{B}T}_{n}{B}_{e}}{{R}_{L}}}$$
(20)

Using Gaussian approximation, the BER can be expressed as a function of SNR as Abd El-Mottaleb et al. (2021) and Al-Khafaji et al. (2013)

$$BER=0.5 erfc\left(\frac{\sqrt{SNR}}{2}\right)$$
(21)

Also, the BER can be expressed in term of Q-factor as Ahmed et al. (2022):

$$BER=0.5 erfc\left(\frac{Q}{\sqrt{2}}\right)$$
(22)

4 Proposed PDM/SAC-OCDMA-FSO model

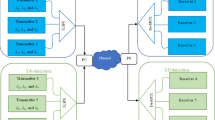
Figure 1 shows the schematic diagram for six users of a PDM/SAC-OCDMA-FSO system. Channel 1 will assign 100010010100 DPS code according to Table 1. So, the transmitter consists of continuous wave (CW) source for generating optical signals and also delivers azimuthal angle of 0° and 90° for x and y polarizations. Channels 1 and 4 have the same code but one is transmitted on x-polarization while the other on y-polarization and the same applies for the other channels. The information signal, that is 10 Gbps, is then generated from the pseudo random bit generator (PRBG) and the non-return to zero (NRZ) modulator. Further, Mach–Zehnder modulator (MZM) is used for encoding the information signal onto optical signals. Then, the three channels from x-polarization are combined together through an ideal multiplexer (MUX) and the same sequence is done for the other channels from y-polarization. Both signals that transmitted on x-polarization and y-polarization are combined through PDM before transmitting to the FSO channel.

Fig. 1
figure 1

Proposed PDM/SAC-OCDMA-FSO

Full size image

At the receiver, the six channels are split using the PDM splitter into x-polarization and y-polarization. For channel 1, as an example, its receiver consists of a single branch that has a decoder, a subtractive decoder, a low pass filter (LPF), and a BER analyzer (Ahmed et al. 2022). In the decoder, the SPD detection technique is used to detect the right code (desired information), which is 100010010100. The decoder consists of four fiber Bragg gratings having the same spectral width as the encoder, while a subtractive decoder has an interference bit with channel 2, which is the eighth bit as channel 2 has the code 010100010010. So, after subtracting the subtractive decoder from the decoder, the desired channel (channel 1) is detected. Then, the output passes through the photodiode (PD) for optical/electrical conversion. Finally, the received signal passes to the LPF for rejecting unwanted noise, and the BER is visualized to evaluate the performance of the signal. The same sequence is done at the receiver of the other channels, either on x-polarization or y-polarization, but according to their assigned codes.

The recommended PDM/SAC-OCDMA-FSO system is evaluated and simulated using Optisystem software version 19 with the parameters mentioned in Table 3 (Kakati and Arya 2019a, 2019b; Imtiaz and Ahmad 2014; Zhang et al. 2021a, b).

Table 3 Simulation parameters (Al-Khafaji et al. 2013; Kakati and Arya 2019a, 2019b; Imtiaz and Ahmad, 2014; Zhang et al. 2021a, b)
Full size table

5 Simulation results

In this section, the obtained results are displayed and discussed for our proposed model PDM/SAC-OCDMA-FSO system using DPS code with the given parameters in Table 2. The performance of the model is evaluated under different fog conditions: LF, MF and HF in terms of maximum allowable number of users and propagation range, Q-factor, BER, and optimum received power.

Figure 2 shows BER versus number of users for SAC-OCDMA-FSO system code at different bit rates, under LF condition and at propagation range 1.5 km. As noticed, when the number of users increases, the BER increases and as the bit rates increases, the number of users that the system can support decreases. At BER \(\sim {10}^{-6}\), the maximum allowable number of users that the system can support is 50 at 2.5 Gbps, 25 at 5 Gbps and 11at 10 Gbps.

Fig. 2
figure 2

BER versus number of users at different bit rates

Full size image

Figure 3 shows BER versus FSO propagation range under LF, MF and HF for channels 1 and 3 on x-polarization and channels 4 and 6 on y-polarization. These specific channels are chosen for simplicity as these channels give the highest and lowest performance. Fog is atmospheric phenomenon that causes water particles to stay in the atmosphere. So, it affects the LOS link between transmitter and receiver and causes degradation to the performance of FSO transmission system. As the level of fog increases from light to heavy, the propagation link range decreases as declared in Fig. 3. The maximum FSO range achieved for channels 1and 4 is 2 km, and for channels 3 and 6 it is 1.8 km under LF condition with BER value < \({10}^{-6}\). When the level of fog slightly increases and becomes MF, these ranges are decreased to 1.3 km for channels 1 and 4, and to 1.2 km, for channels 3 and 4. Furthermore, increasing the fog level until becoming heavy leads to minimum propagation distance; 1 km (channels 1 and 4) and 0.92 km (channels 3 and 6). Table 4 summarizes the simulation results of the BER for the different channels at propagation ranges 2 km under LF, 1.3 km under MF and 1 km under HF.

Fig. 3
figure 3

BER versus range for PDM/SAC-OCDMA using DPS under a LF, b MF and c HF

Full size image
Table 4 BER values for different ranges
Full size table

The Q-factor versus FSO propagation range is displayed in Fig. 4 under LF, MF and HF for different channels. As the fog level rises from light to heavy, both the propagation range and the Q-factor decrease. Figure 4. As an example, the maximum range and Q-factor, respectively, for channel 1 is 2 km and 4.5 under LF, 1.3 km and 4.3 under MF, and 1 km and 4.7 under HF, respectively.

Fig. 4
figure 4

Q-factor versus range for PDM/SAC-OCDMA and DPS under a LF, b MF and c HF

Full size image

Table 5 summarizes the simulation results of the Q-factor for the different channels at propagation ranges of 2 km under LF, 1.3 km under MF and 1 km under HF.

Table 5 Q-factor values for different ranges
Full size table

Figure 5 shows the received power versus FSO propagation range under LF, MF and HF for channels 1 and 3 on x-polarization and channels 4 and 6 on y-polarization. As the propagation range increases, the received power decreases. The LF achieves the highest received power as Fig. 5 depicts. Channel 1 has the highest received power under different weather conditions while channel 6 has the lowest. The received power for channel 1 is − 26.123 dBm at 2 km under LF, − 26.293 dBm at 1.3 km under MF and − 26.015 dBm at 1 km under HF. As for channel 6, the received powers at the same ranges (2 km under LF, 1.3 km under MF and 1 km under HF), are − 27.852 dBm, − 28.001 dBm and − 27.777 dBm, respectively. Table 6 summarizes the simulation results of the received power for the different channels at the mentioned propagation ranges.

Fig. 5
figure 5

Received power versus range for PDM/SAC-OCDMA using DPS under a LF, b MF and c HF

Full size image
Table 6 Received power values for different ranges
Full size table

Figure 6 displays the BER versus propagation range under LD, MD and HD for channels 1 and 3 with the x-polarization and channels 4 and 6 with y-polarization. Dust introduces aerosols into the atmospheric channel. Therefore, it affects the LOS link between transmitter and receiver and causes degradation to the performance of FSO transmission system. As the level of dust increases from light to heavy, the propagation link range decreases as declared in Fig. 6. The maximum FSO range achieved for channels 1and 4 is 0.9 km, and for channels 3 and 6 it is 0.85 km under LD condition with BER value < 10–6. When the level of dust slightly increases and becomes MD, these ranges are decreased to 0.25 km for channels 1 and 4, and to 0.23 km for channels 3 and 4. Further increasing the dust level until becoming heavy leads to minimum propagation distances; 0.095 km (channels 1 and 4) and 0.09 km (channels 3 and 6). Table 7 summarizes the simulation results of the BER for the different channels at propagation ranges 0.9 km under LD, 0.25 km under MD and 0.095 km under HD.

Fig. 6
figure 6

BER versus range for PDM/SAC-OCDMA using DPS under a LD, b MD and c HD

Full size image
Table 7 BER for different ranges under dust conditions
Full size table

The Q-factor versus FSO propagation range is displayed in Fig. 7 under LD, MD and HD for different channels. As the dust level rises from light to heavy, both the propagation range and the Q-factor decrease. As an example, the maximum range and Q-factor, respectively, for channel 1 are 0.9 km and 4.4 under LD, 0.25 km and 4.8 under MD, and 0.095 km and 5.3 under HD, respectively.

Fig. 7
figure 7

Q-factor versus range for PDM/SAC-OCDMA and DPS under a LD, b MD and c HD

Full size image

Table 8 summarizes the simulation results of the Q-factor for the different channels at propagation ranges of 0.9 km under LD, 0.25 km under MD and 0.095 km under HD.

Table 8 Q-factor for different ranges under dust conditions
Full size table

Figure 8 shows the received power versus FSO propagation range under LD, MD and HD for channels 1 and 3 with x-polarization and channels 4 and 6 with y-polarization. As the propagation range increases, the received power decreases. The LD achieves the highest received power as Fig. 8 depicts. Channel 1 has the highest received power under different weather conditions while channel 6 has the lowest one. Table 9 summarizes the simulation results of the received power for the different channels at the mentioned propagation ranges.

Fig. 8
figure 8

Received power versus range for PDM/SAC-OCDMA using DPS under a LD, b MD and c HD

Full size image
Table 9 Received power for different ranges under dust conditions
Full size table

Figure 9 shows the BER versus FSO propagation range under LR, MR and HR for channels 1 and 3 with x-polarization and channels 4 and 6 with y-polarization. The difference between rain and fog is the density and size of water particles in the atmospheric channel. Attenuation of the optical beam due to the rain is lower as compared to the fog. Rain affects the LOS link between transmitter and receiver and causes degradation to the performance of FSO transmission system. As the scale of rain increases from light to heavy, the propagation link range decreases as declared in Fig. 9. The maximum FSO range achieved for channels 1and 4 is 2.4 km, and for channels 3 and 6 it is 2.3 km under LR condition with BER value < 10–6. When the level of rain slightly increases and becomes MR, these ranges are decreased to 1.8 km for channels 1 and 4, and to 1.7 km for channels 3 and 4. Furthermore, increasing the rain level until becoming heavy leads to minimum propagation distance; 1.1 km (channels 1 and 4) and 1.05 km (channels 3 and 6). Table 10 summarizes the simulation results of the BER for the different channels at propagation ranges 2.4 km under LR, 1.8 km under MR and 1.1 km under HR.

Fig. 9
figure 9

BER versus range for PDM/SAC-OCDMA using DPS under a LR, b MR and c HR

Full size image
Table 10 BER for different ranges under rain conditions
Full size table

The Q-factor versus FSO propagation range is displayed in Fig. 10 under LR, MR and HR for different channels. As level of rain rises from light to heavy, both the propagation range and the Q-factor decrease. Table 11 summarizes the Q-factor for the different channels at propagation ranges of 2.4 km under LR, 1.8 km under MR and 1.1 km under HR.

Fig. 10
figure 10

Q-factor versus range for PDM/SAC-OCDMA and DPS under a LR, b MR and c HR

Full size image
Table 11 Q-factor for different ranges under rain conditions
Full size table

Figure 11 shows the received power versus FSO propagation range under LR, MR and HR for channels 1 and 3 with x-polarization and channels 4 and 6 with y-polarization. As the propagation range increases, the received power decreases. Table 12 summarizes the simulation results of the received power for the different channels and ranges.

Fig. 11
figure 11

Received power versus range for PDM/SAC-OCDMA using DPS under a LR, b MR and c HR

Full size image
Table 12 Received power for different ranges under rain conditions
Full size table

Table 13 performs a comparison between our work and previously published related work.

Table 13 Comparison between our work and previously published related work
Full size table

6 Conclusion

A hybrid PDM/SAC-OCDMA based FSO communication system with DPS code is proposed. Three different channels, each carrying 10 Gbps, are transmitted on two different polarization directions signals, x at azimuthal angle \({0}^{0}\) and y at azimuthal angle of 90°. The system performance is studied in terms of maximum allowable number of users, different propagation ranges, Q-factor, BER, and received power under different fog weather conditions: LF, MF and HF. The simulation results assure that as the level of fog increases, the propagation link length decreases and the received power decreases. Accordingly, the LF weather condition achieves the longest propagation distance with the highest received power. In the proposed model, the signal travels up to 2 km with a Q-factor of 4 and a received power of − 27 dBm under LF. At the same value for Q-factor and received power, the propagation range is decreased to 1.3 km and 1 km, under MF and HF, respectively. Additionally, the impact of dust storms is also considered. The maximum achievable FSO link length is 0.9, 0.25, and 0.095 km, respectively, under LD, MD, and HD. Furthermore, the system performance under LR, MR and HR is performed and the results show that the signal can propagate up to 2.4 km under LR, 1.8 km under MR, and 1.1 km under HR. We recommend this work to be carried out in future 5G wireless transmission communications networks and in remote areas.